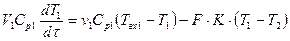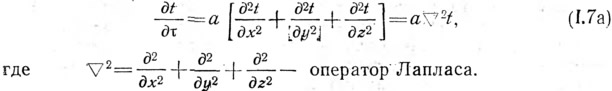Уравнение температурного поля в общем виде

Температурное поле

Температурным полем называется совокупность значений температур в данный момент времени во всех точках рассматриваемого пространства, занятого теплом.

Если температура поля с течением времени t изменяется, то оно называетсянестационарным и описывается уравнением:

где x,y,z – координаты точки поля.

Если же температура в каждой точке поля с течением времени t, остается неизменной, то такое температурное поле называетсястационарным. Температура, в этом случае, является функцией только пространственных координат

В каждый момент времени в температурном поле можно выделить поверхности, имеющие одинаковые температуры. Такие поверхности называются изотермическими. В стационарном температурном поле изотермические поверхности с течением времени не меняют свой вид и расположение, в то время как в нестационарном поле они со временем изменяются.

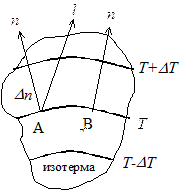
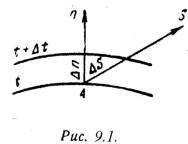
Одной из характеристик температурного поля является температурный градиент, представляющий собой вектор, направленный по нормали к изотермической поверхности в сторону возрастания температуры. На рис.4.1. изображены изотермические поверхности, температуры которых отличаются на DТ.

Рис. 1. К понятию температурного градиента

Из рисунка видно, что интенсивность изменения температуры по разным направлениям (из точки А лучи п и l) неодинакова. Наибольшая разность температур на единицу длины наблюдается в направление нормали п к изотермической поверхности в точке А, так как расстояние между соседними изотермами Dn при этом меньше, чем в точке В.

Предел отношения изменения температуры DТ к расстоянию между изотермами по нормали Dn, когда Dn стремится к нулю, называетсятемпературным градиентом:

В общем случае для различных точек одной и той же изотермической поверхности (например, для точек А и В) градиент температуры различен не только по направлению, но и по величине. За положительное направление градиента принято направление возрастания температур.

Основы теплового расчета

Несмотря на многообразие конструкций и принципов работы теплообменных аппаратов, процессы теплообмена в них подчиняются общим закономерностям, а основные положения методики их расчета могут быть рассмотрены в общей постановке.

До недавнего времени расчет теплообменных аппаратов приводился только для стационарных режимов, и при этом в основном решались две задачи:

1. Для заданных параметров на входе и выходе из аппарата и типе теплообменной поверхности определить требуемую площадь поверхности теплообмена и произвести его конструктивную разработку. Это есть проектный расчет.

2. Для реально существующего аппарата при заданных параметрах потоков на входе определить количество передаваемой теплоты и параметры потоков на выходе из аппарата. Это задача проверочного расчета.

К этим двум задачам можно добавить третью, так называемый оптимальный расчет теплообменного аппарата. Решение этой задачи возможно благодаря использованию ЭВМ. Суть этой задачи сводится к расчету оптимального теплообменника по выбранному критерию.

Тепловой расчет теплообменных аппаратов базируется на уравнениях теплового баланса и теплопередачи.

Решение нестационарных задач теплообмена возможно только при использовании математических моделей, записанных на основе моделей структуры потоков теплоносителей.

Проектный расчет теплообменного аппарата

Задачей проектного расчета является определение геометрических размеров и режима работы теплообменника, необходимого для отвода или подвода заданного количества теплоты к теплоносителю.

При проектном расчете задают:

1. Тип аппарата и общие геометрические характеристики поверхности теплообмена (размеры труб, оребрения, толщина стенок и др.).

2. Параметры теплоносителей на входе и выходе из аппарата (температура, давление и т.д.)

3. Тепловую мощность аппарата Q или расход сред.

Взаимность изменений температур теплоносителей определяется условием теплового баланса, которое для бесконечно малого элемента теплообменника имеет вид:

Здесь G₁, G₂, C_p1, C_P2 – расходы и теплоемкости теплоносителей 1 и 2, T₁ и Т₂ – их температуры в произвольном сечении аппарата. Уравнение теплового баланса для всего аппарата получается путем интегрирования уравнения (4.4) и имеет вид:

Уравнение (4.5) содержит две неизвестные: G₁ или G₂ и T_k1 или T_k2. Следовательно, это уравнение является неопределенным. Общий прием решения этих задач заключается в использовании метода последовательных приближений, состоящего в том, что в начале принимаются определенные решения относительно конструкции аппарата и неизвестных технологических параметров, затем путем пересчета проверяется до получения результатов с желаемой степенью точности.

Проверочный расчет теплообменного аппарата

Целью проверочного расчета теплообменного аппарата заданной конструкции является определение его мощности и температур потоков на выходе Т_k1, T_k2 при заданных площадях поверхности теплообмена F, расхода сред G₁, G₂ и их температурах на входе Т_h1 и Т_h2.

Математические модели теплообменников

Обычно принимают, что движение потоков теплоносителя и хладоагента характеризуется гидродинамическими моделями идеального смешения, идеального вытеснения, ячеечной моделью ОДМ или их комбинацией.

Если гидродинамическая структура потоков в теплообменном аппарате соответствует модели идеального смешения, то во всем потоке происходит полное смешение молекул потока. В таком случае любое изменение температуры потока на входе в зону идеального смешения мгновенно распространяется по всему объему зоны.

Гидродинамическая структура потоков теплоносителя, соответствующая модели идеального смешения, имеет место в теплообменных аппаратах с изменением агрегатного состояния потоков – в конденсаторах, кипятильниках, испарителях. Уравнение, описывающее изменение температуры для теплообменника в зоне идеального смешения, имеет вид:

, (6)

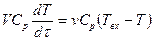
где V – объем зоны идеального смешения; v – объемная скорость; Т_вх, Т – температура потока на входе и в зоне идеального смешения; С_р – теплоемкость потока; t – время.

Условие физической реализуемости модели идеального вытеснения выполняются в случае поршневого потока, когда предполагается, что в направлении его движения смещение полностью отсутствует, а в направлении, перпендикулярном движению, происходит идеальное смешение. Гидродинамическая структура потоков, соответствующая модели идеального вытеснения, характерна для движения потоков в трубном пространстве кожухотрубчатых теплообменников различных конструкций, а также для теплообменного аппарата типа «труба в трубе».

Уравнение, описывающее изменение температуры в зоне идеального вытеснения, имеет вид:

, (7)

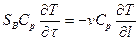
где S_b – сечение зоны идеального вытеснения; l – координата длины аппарата.

Диффузионная модель гидродинамической структуры потоков соответствует такому движению потоков, когда в направлении его движения существует продольное смещение, а перпендикулярном направлении предполагается наличие идеального смешения.

Диффузионная модель значительно лучше, чем модель идеального вытеснения, описывает гидродинамические условия в реальных кожухотрубчатых теплообменниках. Уравнение, характеризующее изменение температуры по длине зоны, имеет вид:

, (8)

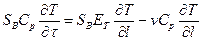
где е_т – коэффициент продольного переноса теплоты.

Температуры потоков в теплообменных аппаратах могут изменяться в каждой точке потока не только в результате его движения, но также из-за теплообмена с окружающей средой или за счет источника теплоты. Интенсивность источника теплоты записывается следующим образом:

где F – поверхность теплообмена, отнесенная к единице объема; К – коэффициент теплопередачи; DТ – разность температур.

Уравнения (4.6) и (4.7) для температур потока с учетом источника теплоты в потоке имеет вид:

;(10)

. (11)

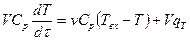
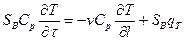
Учитывая (4.9) и зная, что V = S*L из (4.11) получим:

или

. (12)

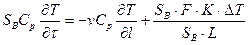
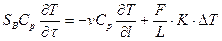
Аналогично для ДДМ с учетом (4.9) имеем:

. (13)

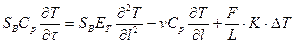
Для описания гидродинамической структуры потоков в реальных теплообменных аппаратах используются комбинированные модели движения потоков: ячеечная модель; модель идеального смешения с застойной зоной; модель идеального смешения с байпасом; последовательное соединение двух моделей МИС и МИВ. Применение таких моделей для описания гидродинамической структуры потоков позволяет описать изменение профиля температур как по длине, так и в объеме теплообменного аппарата.

Теплообменник типа «перемешивание-перемешивание»

Математическая модель такого теплообменника (рис.4.2) представляет собой систему уравнений типа (4.7), записанных для теплоносителя и хладоагента:

, (14)

где T₁ – T₂ = DT, при этом T₁ и T₂ имеют постоянные значения в каждой точке объема идеального перемешивания V₁ и V₂; Т_вх1, Т_вх2 – температуры первичного и вторичного теплоносителей на входе в аппарат; Т_к1 = Т₂ и Т_к2 = Т₂ – конечные температуры первичного и вторичного теплоносителей. Величина FK(T₁ – T₂) имеет знак «минус» в уравнении описания потока теплоносителя, который отдает тепло, и знак «плюс», если тепло воспринимается теплоносителем.

Рис. 2. Схематическое изображение теплообменника типа «перемешивание-перемешивание»

Теплообменник типа «перемешивание-вытеснение»

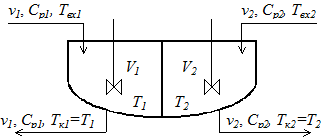
Математическая модель такого теплообменника (рис.4.3) включает уравнение модели идеального перемешивания для потока теплоносителя и уравнение модели идеального вытеснения для хладоагента:

;

, (15)

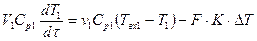
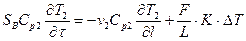
где DT = T₁ – T₂ при этом значения T₁ остается одинаковыми в каждой точке объема идеального перемешивания, а Т₂ изменяются по длине зоны идеального вытеснения.

Рис. 3. Схематическое изображение теплообменника типа «перемешивание — вытеснение»

Теплообменник типа «вытеснение-вытеснение»

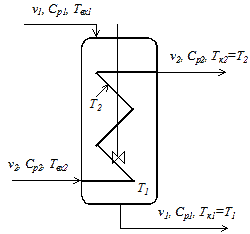
Рассмотрим моделирование широко распространенного в химической технологии теплообменника «труба в трубе», структура потоков которого соответствует модели «вытеснение – вытеснение» (рис.3.1).

Рис.4. Схема теплообменника типа «труба в трубе»

Это так называемый прямоточный теплообменник, для которого модель имеет вид:

;

, (16)

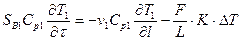
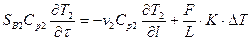
где DT = T₁ – T₂, при этом Т₁ и Т₂ изменяются по длине соответствующих зон идеального вытеснения. Цель работы: построить математическую модель и рассчитать теплообменный аппарат с известной структурой потоков.

Тема 9.Теплопроводность

9.1. Температурное поле. Уравнение теплопроводности

Будем рассматривать только однородные и изотропные тела, т.е. такие тела, которые обладают одинаковыми физическими свойствами по всем направлениям. При передачи теплоты в твердом теле, температура тела будет изменяться по всему объему тела и во времени. Совокупность значений температуры в данный момент времени для всех точек изучаемого пространства называется температурным полем:

где:t –температура тела;

x,y,z -координаты точки;

Такое температурное поле называется нестационарным ∂t/∂ i ¹ 0, т.е. соответствует неустановившемуся тепловому режиму теплопроводности

Если температура тела функция только координат и не изменяется с течением времени, то температурное поле называется стационарным:

t = f(x,y,z) , ∂t/∂ i = 0 (9.2)

Уравнение двухмерного температурного поля:

для нестационарного режима:

t = f(x,y,τ) ; ∂t/∂z = 0 (9.3)

для стационарного режима:

t = f(x,y) , ∂t/∂z = 0; ∂t/∂ i = 0 (9.4)

Уравнение одномерного температурного поля:

для нестационарного режима:

t = f(x,τ) ; ∂t/∂y = ∂t/∂z = 0; ∂t/∂ i ¹ 0 (9.5)

для стационарного режима:

t = f(x) ; ∂t/∂y = ∂t/∂z = 0; ∂t/∂ i = 0 (9.6)

Изотермической поверхностью называется поверхность тела с одинаковыми температурой.

Рассмотрим две изотермические поверхности (Рис.9.1) с температурами t и t + ∆t. Градиентом температуры называют предел отношения изменения температуры∆t к расстоянию между изотермами по нормали ∆n, когда стремится к нулю:

Температурный градиент-это вектор, направленной по нормали к изотермической поверхности в сторону возрастания температуры и численно равный производной температуры t по нормалиn:

Количество теплоты, проходящее через изотермическую поверхность F в единицу времени называется тепловым потоком – Q, [Вт=Дж/с].

Тепловой поток, проходящий через единицу площади называют плотностью теплового потока – q = Q / F, [Вт/м 2 ]

Для твердого тела уравнение теплопроводности подчиняется закону Фурье:

Тепловой поток, передаваемая теплопроводностью, пропорциональна градиенту температуры и площади сечения, перпендикулярного направлению теплового потока.

q = -λ ∙ ∂t/∂n ∙n_o = -λ∙gradt , (9.9)

где: q – вектор плотности теплового потока;

Численное значение вектора плотности теплового потока равна:

q = -λ∙ ∂t/∂n = -λ∙|gradt| , (9.10)

Коэффициент теплопроводности является физическим параметром вещества, характеризующим способность тела проводит теплоту, Она зависит от рода вещества, давления и температуры. Также на её величину влияет влажность вещества. Для большинства веществ коэффициент теплопроводности определяются опытным путем и для технических расчетов берут из справочной литературы.

Уравнения теплопроводности и температурного поля

Количество тепла Q₁ (в ккал), распространяющееся путем теплопроводности в направлении х, в течение единицы времени составит:

Минус в выражении (1.4) означает, что для получения положительной величины Q₁ температура в направлении х должна уменьшаться, а не возрастать. Величина dt/dx, называемая градиентом температуры, выражается в град/м; λ — представляет коэффициент теплопроводности материала в ккал/м·ч·град.

При неустановившихся условиях количество тепла Q₁, распространяющееся в направлении х, изменяется, что связано с поглощением или отдачей тепла частицами материальной среды при изменении их температуры с течением времени т (т. е. наличии величины dt/dx≠0.

Изменение потока тепла dQ₁/dx пропорционально теплоемкости материала сγ (с — удельная теплоемкость в ккал/кг·град; γ — объемный вес материала в кг/мг); тогда

Знак минус в правой части уравнения означает, что повышение температуры материала связано с поглощением им тепла и соответствующим уменьшением теплового потока Q₁.

Величина изменения потока тепла Q₁ в направлении х может быть получена также дифференцированием уравнения (1.4), т. е.

При отсутствии внутренних источников или стоков тепла, изменение величины теплового потока связано только с поглощением тепла материалом, и выражения (1,5) и (1.6) должны быть равны. Из этого равенства выводится дифференциальное уравнение теплопроводности при одномерном распространении тепла в направлении х, а именно:

Это выражение известно как дифференциальное уравнение Фурье. Величина λ/cγ называется коэффициентом температуропроводности материала, имеет кинематическую размерность, в которую не входят измерители массы и энергии, и характеризует скорость перераспределения температуры, выражаемую обычно в м 2 /ч или см 2 /сут при нагреве или охлаждении материальной среды.

Материалы и конструкции с высоким коэффициентом температуропроводности быстро нагреваются или охлаждаются до температуры, соответствующей равновесному состоянию с окружающей средой.

В самом общем виде, при неустановившемся распространении тепла по всем трем осям координат, дифференциальное уравнение теплопроводности приобретает трехмерный вид:

Путемч интегрирования одномерного (1.7), двухмерного или трехмерного уравнения теплопроводности могут быть получены любые конкретные решения, раскрывающие закономерности распространения тепла в материальных средах, в частности, ограждающих конструкциях зданий.

Чтобы получить из множества возможных конкретное решение, соответствующее определенному рассматриваемому процессу распространения тепла, необходимо располагать дополнительными условиями, не содержащимися в исходном дифференциальном уравнении. Эти дополнительные условия, которые вместе с исходным уравнением однозначно определяют все особенности рассматриваемого процесса, называются условиями однозначности 1 .

Условия однозначности разделяются на временные (характеризующие рассматриваемый физический процесс во времени) и пространственные, относящиеся к поверхностям, ограничивающим изучаемый объект или конструкцию, и особенностям физического процесса, происходящего на этих граничных поверхностях.

Различают три вида граничных условий:

• 1) граничное условие I рода, устанавливающее распределение температуры на поверхности и ее изменения во времени;
• 2) граничное условие II рода, устанавливающее величину потока тепла, проходящего через поверхность, и его изменения во времени;
• 3) граничное условие III рода, определяющее температуру окружающей среды и закон теплообмена между поверхностью и этой средой.

В строительной теплофизике обычно задаются граничные условия III рода, устанавливаемые значениями температуры среды t и коэффициентов теплообмена α 2 .

При рассмотрении теплопередачи в однородной среде и в установившихся условиях (когда dt/dτ=0), временные условия исключаются и значение имеют только пространственные.

В этих случаях, поскольку а≠0, уравнение (1.7а) приобретает вид:

Уравнение относится к температурному полю в установившихся условиях. Выражение (1.8) известно как уравнение Лапласа. Физический смысл этого уравнения состоит в том, что сумма изменений количеств тепла, поступающего к любой рассматриваемой точке конструкции, равна нулю. Следовательно, температуры ее неизменны и имеют установившиеся значения, отвечающие постоянным условиям воздействий внешней среды, окружающей конструкцию. При практических расчетах температурного поля проектируемых конструкций на основе уравнения (1.8) расчетные температуры внешней среды принимаются соответствующими возможности завершения процесса предельного охлаждения рассматриваемой конструкции. Этот процесс происходит постепенно и требует определенного времени: незначительного для легких конструкций и длительного — для массивных, поэтому расчетные значения температуры наружного воздуха в наиболее холодные зимние периоды зависят от степени массивности конструкции и связаны с возможностью более или менее длительной стабилизации теплового состояния во времени.

Для многих практических случаев достаточно исследования плоского температурного поля (в плане или разрезе конструкции). Для двумерных условий уравнение (1.8) имеет вид:

Исследование на основе уравнения (1.8а) температурных полей неоднородных в теплофизическом отношении облегченных конструкций (панелей с контурными ребрами, сопряжений крупных элементов ограждающих конструкций и т. д.) имеет весьма важное значение при проектировании индустриальных конструкций зданий, особенно в достаточно суровых климатических условиях, когда низкие температуры наружного воздуха длительны во времени и вызывают полное охлаждение, для которого характерно неизменное установившееся распределение предельно низких температур.

Порядок проведения подобных практических расчетов и применение для этих целей счетно-решающих устройств типа электроинтегратора, изложены далее в гл. IV.

Дифференциальное уравнение Фурье (1.7) в обобщающем смысле является уравнением нестационарного поля любого потенциала переноса (в данном случае — поля потенциала переноса тепла, т. е. температуры). С определенными ограничениями это уравнение может быть использовано и для изучения процессов влагообмена, происходящих в материальных системах при неизменной температуре.

Если рассматривать какую-либо материальную систему, например, ограждающую конструкцию, выполненную из влажного капиллярно-пористого материала и находящуюся в изотермической воздушной среде 3 , то за потенциал переноса влаги может быть принято влагосодержание материала (со, г/кг). Уравнение (1.7), записанное применительно к исследованию одномерного поля потенциала переноса влаги называют уравнением влагопроводности. Оно имеет вид:

где ω — влагосодержание материала (часто выражаемое через весовую влажность материала); а_m — коэффициент нестационарной влагопроводности 4 , зависящий от природы материала и его влажностного состояния.

Уравнение влагопроводности, в частности, используется для обоснования простейших приближенных сравнительных расчетов длительности естественной сушки ограждающих конструкций из капиллярно-пористых материалов.

Примечания

1. Иногда условия однозначности называют краевыми условиями.

2. В теплотехнической литературе эти коэффициенты часто называют коэффициентами теплоотдачи, имея в виду особенности теплообмена материальных систем нагретых выше температуры окружающей среды.

3. То есть в среде с неизменной постоянной температурой.

4. Аналог коэффициента температуропроводности: