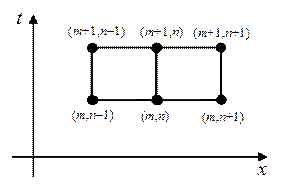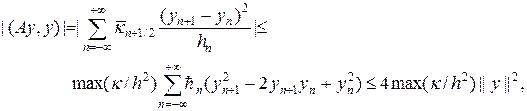Уравнение теплопроводности какого типа параболического

Основные типы уравнений математической физики

Основные типы уравнений

К основным уравнениям математической физики относятся следующие дифференциальные уравнения в частных производных второго порядка.

1. Волновое уравнение:

.

Это уравнение является простейшим уравнением гиперболического типа. К его исследованию приводит изучение процессов поперечных колебаний струны, продольных колебаний стержня, электрических колебаний в проводах и т. д.

2. Уравнение теплопроводности, или уравнение Фурье:

.

Это уравнение является простейшим уравнением параболического типа. К его исследованию приводит рассмотрение процессов распространения тепла, фильтрации жидкости и газа в пористой среде, изучение некоторых вопросов теории вероятностей и т. д.

3. Уравнение Лапласа:

.

Это уравнение относится к простейшим уравнениям эллиптического типа. К его исследованию приводит изучение задач об электрических и магнитных полях, о стационарном тепловом состоянии, задач гидродинамики и т. д.

В выписанных уравнениях искомая функция u зависит от двух переменных t, x или x, y. Рассматриваются также уравнения и для функций с большим числом переменных. Например, волновое уравнение с тремя независимыми переменными имеет вид

,

и уравнение Лапласа

.

Уравнение колебаний струны.

Формулировка краевой задачи

В математической физике струной называют гибкую упругую нить. Пусть струна в начальный момент времени расположена на отрезке 0≤x≤l оси Ox. Предположим, что ее концы закреплены в точках x=0 и x=l. Если струну отклонить от первоначального положения, а потом предоставить самой себе или придать ее точкам некоторую скорость, то точки струны будут совершать движение. Задача заключается в определении формы струны в любой момент времени и в определении закона движения каждой точки струны в зависимости от времени.

Если предположить, что движение точек струны происходит перпендикулярно оси Ox и в одной плоскости, то процесс колебания струны описывается одной функцией u(x,t), которая определяет величину перемещения точки струны с абсциссой x в момент t.

Доказано, что при отсутствии внешней силы функция u(x,t) должна удовлетворять дифференциальному уравнению в частных производных второго порядка

.

Для полного определения движения струны одного уравнения недостаточно. Искомая функция u(x,t) должна удовлетворять граничным условиям, указывающим, что делается на концах струны (при x=0 и x=l), и начальным условиям, описывающим состояние струны в начальный момент (t=0). Совокупность граничных и начальных условий называется краевыми условиями.

Пусть, например, концы струны при x=0 и x=l неподвижны. Тогда при любом t должны выполняться равенства

Это – граничные условия для рассматриваемой задачи. В начальный момент t=0 струна имеет определенную форму, которую мы ей придали. Пусть эта форма определяется функцией f(x), т. е.

Далее в начальный момент должна быть задана скорость в каждой точке струны, которая определяется функцией φ(x), т. е.

.

Эти два условия называются начальными условиями.

Колебания бесконечной струны.

Формула Даламбера решения задачи Коши

для волнового уравнения

Прежде чем решать задачу о колебаниях закрепленной струны, рассмотрим более простую задачу – о колебаниях бесконечной струны. Если представить очень длинную струну, то ясно, что на колебания, возникающие в ее средней части, концы струны не будут оказывать заметного влияния.

Рассматривая свободные колебания, мы должны решить однородное уравнение

при начальных условиях

, ,

где функции f(x) и g(x) заданы на всей числовой оси. Такая задача называется задачей с начальными условиями или задачей Коши.

Преобразуем волновое уравнение к каноническому виду, содержащему смешанную производную. Уравнение характеристик

распадается на два уравнения:

интегралами которых служат прямые

Введем новые переменные ξ=x – at, η=x + at и запишем волновое уравнение для переменных ξ и η.

, ,

,

,

и подставляя их в исходное уравнение, видим, что уравнение колебания струны в новых координатах будет

.

Интегрируя полученное равенство по η при фиксированном ξ, придем к равенству . Интегрируя это равенство по ξ при фиксированном η, получим

,

где φ и ψ являются функциями только переменных ξ и η соответственно. Следовательно, общим решением исходного уравнения является функция

. (8)

Найдем функции φ и ψ так, чтобы удовлетворялись начальные условия:

.

,

.

Интегрируя последнее равенство, получим:

,

где х0 и С – постоянные. Из системы уравнений

Таким образом, мы определили функции φ и ψ через заданные функции f и g, причем полученные равенства должны иметь место для любого значения аргумента. Подставляя в (8) найденные значения φ и ψ, будем иметь

.

Найденное решение называется формулой Даламбера решения задачи Коши для волнового уравнения

Пример. Решить уравнение при начальных условиях , .

Используя формулу Даламбера, сразу получаем

.

Решение волнового уравнения

методом разделения переменных

Метод разделения переменных применяется для решения многих задач математической физики. Пусть требуется найти решение волнового уравнения

, (9)

удовлетворяющее краевым условиям

u(x,0)=f(x), . (12),(13)

Частное решение уравнения (9), удовлетворяющее граничным условиям (10) и (11), ищут в виде произведения двух функций:

Подставляя функцию u(x,t) в уравнение (9) и преобразовывая его, получим

.

В левой части этого уравнения стоит функция, которая не зависит от x, а в правой – функция, не зависящая от t. Равенство возможно только в том случае, когда левая и правая части не зависят ни от x, ни от t, т. е. равны постоянному числу. Обозначим

, где λ>0. (14)

Из этих уравнений получаем два однородных дифференциальных уравнения второго порядка с постоянными коэффициентами

и . (15)

Общее решение этих уравнений

,

,

где A, B, C, D – произвольные постоянные.

Постоянные A и B подбирают так, чтобы выполнялись условия (10) и (11), из которых следует, что X(0)=X(l)=0, так как T(t)≠0 (в противном случае u(x,t)=0). Учитывая полученные равенства, находим

А=0 и .

Так как B≠0 (иначе, было бы X=0 и u=0, что противоречит условию), то должно выполняться равенство

,

.

Найденные значения λ называют собственными значениями для данной краевой задачи. Соответствующие им функции X(x) называются собственными функциями.

Заметим, что, если в равенстве (14) вместо – λ взять число λ (λ>0), то первое из уравнений (15) будет иметь решение в виде

.

Отличное от нуля решение в такой форме не может удовлетворять граничным условиям (10) и (11).

Зная , можем записать

.

Для каждого n получаем решение уравнения (9)

.

Так как исходное уравнение (9) линейное и однородное, то сумма решений также является решением, и потому функция

(16)

будет решением дифференциального уравнения (9), удовлетворяющим граничным условиям (10) и (11).

Найденное частное решение должно еще удовлетворять начальным условиям (12) и (13). Из условия (12) получим

.

Далее, дифференцируя члены ряда (16) по переменной t, из условия (13) будем иметь

.

Правые части двух последних равенств есть ряды Фурье для функций f(x) и φ(x), разложенных по синусам на интервале (0, l). Поэтому

. (17)

Итак, ряд (16), для которого коэффициенты Cn и Dn определяются по выписанным формулам, если он допускает двукратное почленное дифференцирование, представляет решение уравнения (9), удовлетворяющее граничным и начальным условиям.

Пример. Найти решение краевой задачи для волнового уравнения

, 0

Одномерные уравнения

Лекция №11

Параболические уравнения

Одномерные уравнения

К параболическим уравнениям относятся задачи описания процессов теплопроводности, диффузии, вязкости и ряд других. Типична, например, следующая постановка для линейной теплопроводности в однородной среде:

(1)

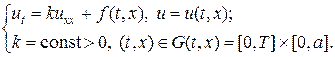
Помимо самого уравнения (1) необходимо определить начальное и граничные условия:

; (2)

. (3)

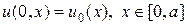
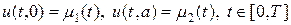
Граничные условия (3) означают, что на левой и правой границе изменения температуры следуют заданным функциональным зависимостям. Эти условия еще называют граничными условиями первого рода. Граничные условия второго рода отвечают заданию на границах потоков тепла, т.е.

. (4)

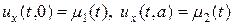
Для граничных условий третьего рода можно записать следующее представление:

. (5)

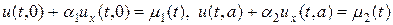
В терминах теплообмена граничные условия третьего рода описывают так называемый линейный (ньютоновский) теплообмен с окружающей средой. Для задачи (1) с начальным (2) и граничными условиями (3) — (5) корректность постановки доказана[1].

Рассмотрим простейшие разностные схемы для численного решения уравнения теплопроводности (1). Выберем в области G(t,x) = [0,T]´[0,a] прямоугольную равномерную сетку с шагами t и h по времени и пространству. В качестве шаблона разностной схемы выберем шеститочечный шаблон, представленный на рис.1. Учитывая шаблон на рис.1, запишем следующую разностную схему

(6)

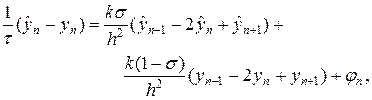
где n = 1,2,…,N-1, s = const. Уравнение (6) необходимо дополнить граничными условиями, например, первого рода:

. (6¢)

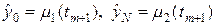
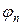
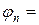
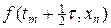
В качестве правой части часто выбирают значение . Параметр s в (6) выступает в качестве свободного параметра, его вариация порождает целое семейство разностных схем от явных до неявных.

Рис.1. Шеститочечный шаблон разностной схемы (6)

Исследуем схему (6), (6¢). Начнем с существования решения и его вычисления. Если s = 0, то схема (6) переходит уже в рассмотренную ранее явную разностную схему (9.26). В этом случае разностное решение легко находится, т.е. его существование и единственность очевидна.

При s ¹ 0 разностная схема (6), (6¢) неявная и ее можно переписать в трехдиагональном форме:

(7)

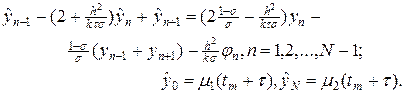
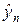
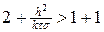
Разностное уравнение на каждом временном слое может быть решено относительно неизвестных методом прогонки. Достаточным условием устойчивости прогонки является условие диагонального преобладания (5.16), которое, согласно (7), выполнено ( ), когда s > 0.

В итоге, решение разностных схем (6), (6¢) существует и единственно при s ³ 0 и при любых ограниченных начальных и краевых условиях. При s = 1 схему называют чисто неявной, а при s = ½ — схемой с полусуммой или симметричной.

Для оценки порядка аппроксимации проведем разложение решений схемы (6) в ряд Тейлора относительно центра разложения (t_m+t / 2,x_n), тогда, опуская довольно утомительные выкладки, можно получить

(8)

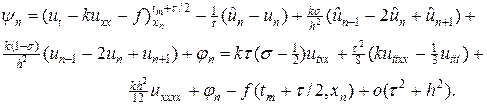
Из (8) видно, что, если положить 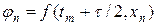, то при s ¹ ½ схема (6) имеет порядок аппроксимации O(t + h 2 ). Для симметричной схемы, у которой s = ½, порядок аппроксимации выше — O(t 2 + h 2 ).

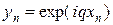
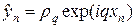
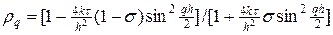
Устойчивость по начальным данным исследуем методом разделения переменных. Поскольку схема (6) линейная, отбросим правую часть и осуществим подстановку и , тогда можно получить множитель роста гармоники

. (9)

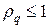
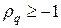
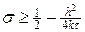
Непосредственной проверкой можно убедиться, что множитель роста гармоники (9) меньше единицы при s ³ 0. Проверяя условие , находим

. (10)

Условие (10) обеспечивает условие равномерной устойчивости схемы (6) по начальным данным в норме 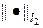. Условие устойчивости по правой части (9.65) выполняется при любых t и h. Таким образом, схема устойчива по начальным данным и по правой части при условии того, что верно неравенство (10).

Для чисто неявной схемы (s = 1), симметричной схемы (s = ½ ) условие (10) выполняется при любых значениях t и h, т.е. эти схемы являются безусловно устойчивыми. Для явной схемы (s = 0) условие (10) выполняется только при условии, что t £ h 2 /(2k), т.е. явная схема является условно устойчивой, что уже было установлено в лекции №9.

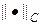
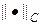
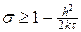
Отметим, что справедливо более сильное утверждение об устойчивости схем (6): они устойчивы в норме . Так из принципа максимума (9.66), (9.67) легко получить достаточное условие устойчивости в норме :

. (10¢)

По сравнению с (10) условие (10¢) более жесткое, но для явной и чисто неявной схем выводы об устойчивости аналогичны тем, которые сделаны выше.

Изучим разностную схему (6), (6¢) на численном примере решения уравнения вида:

(11)

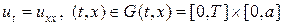
с начальным распределением температуры u₀ в виде равнобедренного треугольника с основанием длиной a и высотой b:

(12)

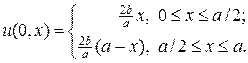
В качестве граничных условий выберем нулевые условия, т.е.

. (13)

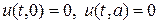
Аналитическое решение задачи (11) — (13) можно представить в виде следующего бесконечного ряда:

. (14)

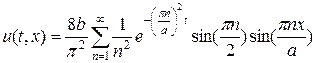
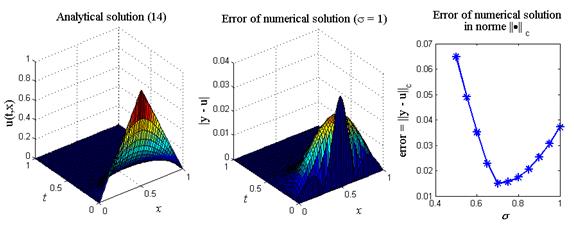
На листинге_№1 приведен код программы численного решения задачи (11) — (13) при различных значениях параметра s. При каждом значении параметра численное решение сравнивалось с аналитическим решением (14) в норме , т.е. находилась ошибка вида: error = .

%Программа решения задачи (11) — (13) при

%различных значениях параметра sigma

%Задаем размеры области интегрирования G=[0,T]x[0,a]

%Определяем размеры сеток по времени и пространству

%Определяем шаги по времени и пространству

%Определяем сетки по времени и пространству

%Находим в узлах сетки значения аналитического

%Рисуем аналитическое решение (14)

%Задаем набор значений параметра sigma, при которых

%будет численно решаться задача (11) — (13) по

%разностной схеме (6), (6′)

%Организуем цикл по времени

%Применяем метод прогонки

%Находим модуль отклонения численного решения от

%аналитического при некотором sigma

%Определяем ошибку численного решения в норме C

%Рисуем 3D график ошибки при sigma=1

%Рисуем 2D график зависимости ошибки численного

%решения от значений параметра sigma

%Функция для вычисления значений аналитического

%решения (14) в точке (t,x)

Итог работы кода программы листинга_№1 приведен на рис.2. На левом рисунке приведено 3D изображение аналитического решения (14). На среднем рисунке приведено 3D изображение абсолютного значения ошибки численного решения задачи (11) — (13) с помощью полностью неявной разностной схемы (6), (6¢), т.е. при s = 1. Видно, что пик ошибки приходится на центральный излом в начальном распределении температуры. На рисунке справа приводится ошибка численного решения задачи (11) — (13) в норме 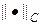в зависимости от значений параметра s (s Î [0,5;1]). Отчетливо виден довольно заметный провал графика в окрестности s = 0,7.

Наилучшая схема. Обобщим разностную схему (6) на случай уравнения теплопроводности с переменным коэффициентом теплопроводности:

. (15)

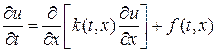
Исследуем общий случай, когда функции k(t,x) и f(t,x) могут быть кусочно-непрерывными. Сильные разрывы могут возникнуть на границе областей, для слоистых сред в случае появления ударных волн и в ряде других приложений. В этом случае решение уравнения (15) следует рассматривать как обобщенное. Обобщенное решение в общем случае не единственно.

Для выделения допустимого решения из множества обобщенных решений необходимо из физических соображений определиться с величинами, которые считаются непрерывными. Для уравнения (15) такими величинами выступают температура u(t,x) и поток тепла W = —k¶u/¶x. Производные этих величин u_x и W_x разрывны в точках разрыва коэффициента теплопроводности и источника тепла соответственно.

Рис.2. Левый рисунок — аналитическое решение (14). Средний и правый
рисунки — решение задачи (11) — (13) с помощью разностной
схемы (6), (6¢) при различных значениях параметра s

Для сходимости к допустимому обобщенному решению составим методом баланса консервативную разностную схему. Для этого перепишем исходное уравнение (15) в явной дивергентной форме, т.е.

. (16)

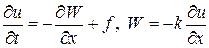
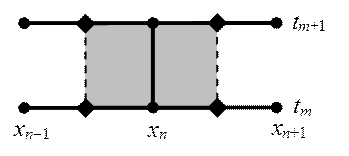
Шаблон и соответствующая ячейка для искомой разностной схемы представлены на рис.3.

Рис.3. Шаблон для разностной схемы уравнения (16)
и ячейка для метода баланса

Запишем для первого уравнения в (16) закон сохранения энергии в виде интеграла по ячейке, заштрихованной на рис.3.

(17)

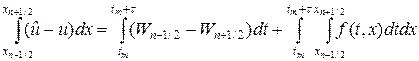
Второе уравнение в (16) проинтегрируем по интервалу сетки [x_n,x_n+1], тогда

. (18)

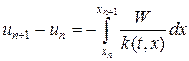
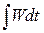
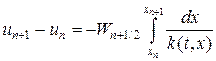
Значения температур припишем узлам сетки, а потоки тепла — серединам интервалов (ромбики на рис.3). Интегралы в (17) аппроксимируем квадратурными формулами. Так, интеграл оценим, исходя из того, что подынтегральное выражение берется с текущего и верхнего слоев. В (18) поток тепла в силу того, что он непрерывен, вынесем из под знака интеграла в средней точке

.

В итоге получим консервативную разностную схему, называемую наилучшей:

, (19)

, (19¢)

,

. (20)

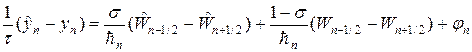
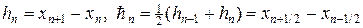
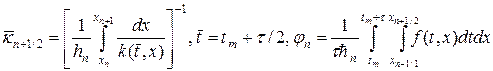
Для аппроксимации интегралов (20) применяют следующий набор формул:

, (21)

, (21¢)

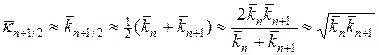
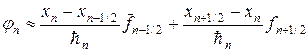
где черта сверху означает отнесение к моменту времени 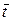. Если разрывы функций k(t,x) и f(t,x) отнесены к узлам сетки, то подстановки в (21) и (21¢) следует понимать, как подстановки односторонних пределов.

Исследуем наилучшую схему (19), (19¢). После подстановки (19¢) в (19) получим обычную трехточечную по пространству схему относительно неизвестных значений 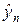на верхнем слое, которая решается методом прогонки. Поскольку имеется диагональное преобладание, т.е. метод прогонки устойчив, постольку может быть получено единственное решение.

Устойчивость по начальным данным разностной схемы (19), (19¢) изучим с помощью метода операторных неравенств. Рассмотрим задачу Коши на всей прямой, считая, что .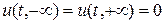

Перепишем схему (19), (19¢) в так называемой канонической операторной форме:

, (22)

где операторы A и B имеют следующий вид:

,

.

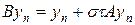
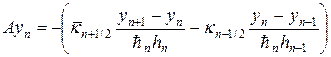
Скалярное произведение определим по формуле:

.

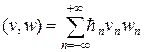
Покажем, что операторы A и B неотрицательные и самосопряженные. Действительно,

.

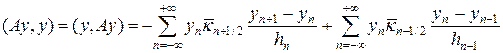
Сдвинем во второй сумме индекс на единицу, тогда

, (23)

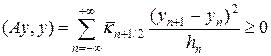
Отметим, что из (23) следует оценка

. (24)

(25)

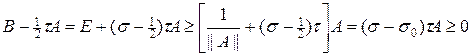
s ³ s₀, 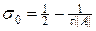. (26)

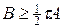
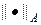
Условие (25) означает, что и по теореме (лекция №9, формулы (9.76) — (9.82)) устойчивости двухслойных разностных схем в канонической форме схема (19) — (20) устойчива в энергетической норме . Таким образом, неравенство (26) является достаточным условием устойчивости схемы (19) — (20).

Учитывая (24), можно получить более сильное достаточное условие устойчивости разностной схемы (19) — (20) в форме:

. (27)

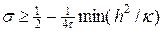
Изучим численно достаточное условие устойчивости (27) на примере использования наилучшей разностной схемы с разрывными функциями, описывающими теплопроводность и правую часть. На листинге_№2 приведен код соответствующей программы.

%Программа тестирования критерия устойчивости (27)

%для наилучшей схемы (19) -(20) численного решения

%Определяем размеры области интегрирования

%Определяем количество узлов в сетках по времени

%вычисляем шаги по времени и пространству

%формируем сетки по времени и пространству

%вычисляем значения коэффициента теплопроводности

%и правой части (источника тепла) в узлах сетки

%рисуем профили коэффициента теплопроводности k(x)

%и источника тепла f(x)

%Находим пороговое значение параметра sigma0 для

%изучения устойчивости наилучшей разностной схемы

%Строим начальное распределение u(0,x)=u0(x)

%температуры в виде треугольного профиля

%Определяем нулевые граничные условия

%Определяем пару значений параметра sigma0 и

%sigma0-eps. При втором значении параметра

%ожидается появление неустойчивости

%Организуем цикл по значением параметра sigma,

%а также по времени и пространству

%определяем левое граничное условие

%Рисуем профили температуры при пороговом значении

%sigma0 и подкритическим значением sigma0-eps

%Определяем функцию коэффициента

if ((x>=0)&(x =(2*a)/3)&(x a/3)&(x =0)&(x =(2*a)/3)&(x a/3)&(x s (s > 0). В лекции №9 аналитически и численно исследовалась бегущая волна для квазилинейного уравнения теплопроводности без источника тепла. И, наконец, в той же лекции аналитически и численно изучалось квазилинейное уравнение теплопроводности с источником тепла, степенным образом, зависящим от температуры, т.е. при f

u s +1 . Во всех трех случаях использовалась чисто неявная схема с весом s = 1. Запишем ее в следующем виде:

. (29)

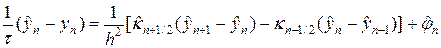
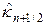
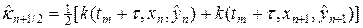
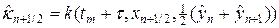
В (29) под понимаются выражения типа (21), т.е.

(30)

. (30¢)

Аналогично (30), (30¢) можно аппроксимировать в (29) источник тепла .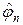

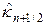
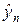
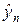
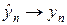
Можно показать, что схема (29) абсолютно устойчива и консервативна и на четырежды непрерывно дифференцируемых решениях имеет погрешность аппроксимации O(t + h 2 ). Вследствие зависимости от неизвестного решения на следующем слое алгебраическая схема (29) является нелинейной относительно . Понятно, что, когда t ® 0 — , т.е. при достаточно малом t существует вещественное решение системы (29). Понятно также, что при большом значении t вещественное решение может отсутствовать.

Решать алгебраическую систему уравнений можно несколькими способами. Рассмотрим подробно метод последовательных приближений, в котором и берутся с предыдущей итерации, т.е.

, (31)

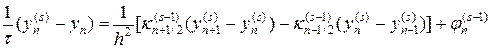
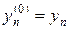
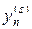
где индекс s = 1,2,… описывает номера итераций. В (31) в качестве нулевого приближения берутся решения с предыдущего слоя, т.е. . Величины находятся из (31) методом прогонкой. Итерации в (31) сходятся линейно и обычно не быстро. Итерации могут и расходиться. В этом случае расчет можно вести с фиксированным числом итераций (обычно 2, 3 итерации).

В качестве критерия сходимости итераций можно использовать условие

(32)

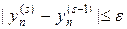
или более жесткое условие

, (32¢)

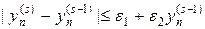
где e, e₁, e₂ — некоторые малые неотрицательные числа. Критерий сходимости (32) либо (32¢) должен выполняться для всех узлов сетки n. Если за разумное число итераций критерий сходимости не выполняется необходимо уменьшить шаг по времени и повторить процедуру повторно. После выполнения одного из критериев (32), (32¢) полагают 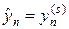и цикл перехода на следующий слой завершается.

Рассмотрим пример численного решения квазилинейного уравнения теплопроводности с источником, в котором коэффициент теплопроводности и источник тепла степенным образом зависят от температуры. Запишем это уравнение в виде

, (33)

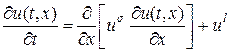
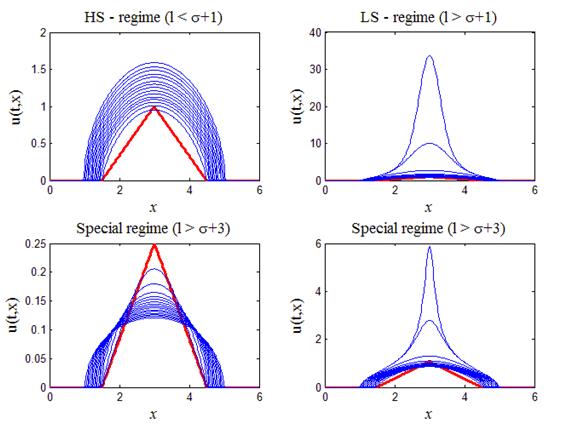
В лекции №9 уже рассмотрено аналогичное уравнение (9.18), точнее рассмотрено аналитическое решение (9.19) — (9.21) этого уравнения при l = s + 1. Продолжим изучение уравнения (33) численным методом в еще трех случаях[2]: 1) так называемый HS-режим, когда l s + 1; 3) особый случай, когда l > s + 3. Третий случай интересен тем, что в зависимости от начального распределения температуры, последующая эволюция решения может пойти по двум прямо противоположным направлениям. Если амплитуда начального распределения ниже некоторого порогового значения, то в дальнейшем тепло будет “расползаться” по пространству неограниченно и амплитуда решения будет стремиться к нулю. Если амплитуда начального распределения температуры является надпороговой, то дальнейшее изменение решения происходит в режиме с обострением, т.е. за конечное время решение обращается в бесконечность.

%Программа решения квазилинейного уравнения

%теплопроводности с источником (33) с помощью

%разностной схемы (31)

%Очищаем рабочее пространство

%Определяем число шагов по времени и

%максимальное количество итераций на

%Определяем диапазон изменения переменной x и

%число узлов сетки на отрезке [0,a]

%Определяем шаг и сетку по пространству

%Определяем степень температурной зависимости

%Определяем четыре расчета:1)HS-режим, когда

%1 sigma+1; 3)режим

%l>sigma+3 с двумя типами начальных данных:

%подпороговый пик возмущения и надпороговый

l=[sigma sigma+2 sigma+4 sigma+4];

%Вариация высоты пика начального возмущения

%для четырех расчетов

%Основной цикл для четырех расчетов

%Начальное распределение температуры в

%виде равнобедренного треугольника с

%высотой b(k) и основанием длиной 0.5*a

if (x(n)>=0.25*a)&(x(n) =0.5*a)*(x(n) s + 3 в зависимости от амплитуды начального распределения возможны два прямо противоположных режима динамики. На левом нижнем рисунке, при подпороговой начальной амплитуде тепло “расползается” неограниченно по пространству, амплитуда распределения стремится к нулю, при этом источник тепла не перестает действовать. На правом нижнем рисунке, при надпороговой начальной амплитуде температура в центре в начале падает, а потом начинает расти неограниченно в режиме с обострением, причем полуширина пика, как и LS-режиме, стремится к нулю. На всех четырех рисунках жирной (красной) линией выделен начальный температурный профиль.

Рис.5. Различные типы динамики решений уравнения (33) в
зависимости от соотношения параметров s и l

Дифференциальные уравнения в частных производных¶

Дифференциальные уравнениями в частных производных с дополнительными уравнениями, выражающими граничные и начальные условия описывают большинство физических процессов. В общем случае линейное дифференциальное уравнение в частных производных второго порядка имеет вид

Классификация проводится в соответствии с характеристическими кривыми второго порядка для данных уравнений. По соотношению значений a, b и c уравнение относят к эллиптическим, параболическим или гиперболическим в данной точке. Тип ДУ определяется знаком выражения, называемого дискриминантом: \(D(x,y) = b^2-4ac\) .

• Если \(D(x, y) , дифференциальное уравнение является эллиптическим в точке (x, y).
• Если \(D(x, y) = 0\) , дифференциальное уравнение является параболическим в точке (x, y).
• Если \(D(x, y) > 0\) , дифференциальное уравнение является гиперболическим в точке (x, y).

Если коэффициенты a, b, c постоянные и значение D не зависит от точки, то в зависимости от знака D уравнение является полностью эллиптическим, гиперболическим или параболическим. В случае если коэффициенты не являются постоянными, для одного и того же уравнения возможны области, в которых оно является уравнением разного типа.

Эллиптические уравнения¶

Эллиптическими уравнениями являются уравнения Лапласа и Пуассона, возникающие в теории потенциала для электрического поля. Так же к уравнению этого тапа сводятся многие стационарные (установившиеся) решения параболических и гиперболических задач.

Простейший вид Эллиптического уравнения:

Такими уравнения описываются стационарное распределение температуры в процессе теплопереноса и стационарное распределение концентрации при диффузии. К уравнению Лапласа приводят и многие другие задачи, например, задача о распределении электростатического поля в однородной непроводящей среде в отсутствие электрических зарядов. В общем случае в векторной форме уравнение Пуассона имеет вид:

где \(u(x, y, z)\) – искомая функция; \(A(x, y, z)\) , \(f(x, y, z)\) – некоторые функции независимых переменных. Функция А описывает «коэффициент распространения» величины u и может являться тензорной величиной в случае анизотропной среды. Функция f это функция источников – скалярная величина, показывающая плотность «скорости появления» величины u в единице объема. В качестве величин, входящих в это уравнение могут использоваться, температура, коэффициент теплопроводности, плотность тепловых источников или потенциал эл. поля, диэлектрическая проницаемость и плотность зарядов и т.д

Параболические уравнения¶

Параболические уравнения появляются в нестационарных задачах теплопроводности, диффузии, иногда параболические задачи получаются из гиперболических уравнений (параболическое приближение в оптике) и т. д. Уравнение теплопроводности, например, имеет вид:

В первом слагаемом коэффициенты это плотность и удельная теплоемкость, во втором слгаемом – коэффициент теплопроводности, правая часть – плотность источников тепла.

Гиперболические уравнения¶

Гиперболические уравнения, часто называют волновыми уравнениями, т.к. с их помощью описывается распространения волн (упругих, электро — магнитных, сдвиговых). К этому же типу уравнений относится уравнение Шредингера квантовой механики.

Начальные и граничные условия¶

Из курса высшей математики известно, что дифференциальные уравнения, как правило, имеют бесконечное множество решений. Это связано с появлением в процессе интегрирования констант, при любых значениях которых решение удовлетворяет исходному уравнению. Решение задач физики связано с нахождением зависимостей от координат и времени определенных физических величин, которые, безусловно, должны удовлетворять требованиям однозначности, конечности и непрерывности. Иными словами, любая задача физики предполагает поиск единственного решения (если оно вообще существует). Поэтому математическая формулировка физической задачи должна помимо основных дифференциальных уравнений, описывающих искомые функции, включать дополнительные уравнения (дифференциальные или алгебраические), описывающие искомые функции на границах рассматриваемой области в любой момент времени и во всех внутренних точках области в начальный момент времени. Эти дополнительные уравнения называют соответственно граничными и начальными условиями задачи. Условия, относящиеся к точкам пространства, называются граничными. Обычно это неизменные условия, накладываемые на значение функции или на ее производную (поток через границу) на границе рассматриваемой области. Начальные условия – условия о значениях физической величины в начальный момент времени. Только после задания обоих типов условий можно получить описание развития процесса во времени. Для ДУЧП редко решают задачи, когда условия внутри области заданы для различных моментов времени, т.к. это сильно усложняет и без того не простую процедуру поиска решения.