Уравнение теплопроводности неявная схема паскаль

Уравнение теплопроводности в tensorflow

Привет, Хабр! Некоторое время назад увлекся глубоким обучением и стал потихоньку изучать tensorflow. Пока копался в tensorflow вспомнил про свою курсовую по параллельному программированию, которую делал в том году на 4 курсе университета. Задание там формулировалось так:

Линейная начально-краевая задача для двумерного уравнения теплопроводности:

Хотя правильнее было бы назвать это уравнением диффузии.

Задачу тогда требовалось решить методом конечных разностей по неявной схеме, используя MPI для распараллеливания и метод сопряженных градиентов.

Я не специалист в численных методах, пока не специалист в tensorflow, но опыт у меня уже появился. И я загорелся желанием попробовать вычислять урматы на фреймворке для глубокого обучения. Метод сопряженных градиентов реализовывать второй раз уже не интересно, зато интересно посмотреть как с вычислением справится tensorflow и какие сложности при этом возникнут. Этот пост про то, что из этого вышло.

Численный алгоритм

Разностная схема:

Чтобы проще было расписывать, введем операторы:

Явная разностная схема:

В случае явной разностной схемы для вычисления используются значения функции в предыдущий момент времени и не требуется решать уравнение на значения . Однако такая схема менее точная и требует значительно меньший шаг по времени.

Неявная разностная схема:

Перенесем в левую сторону все связанное с , а в правую и домножим на :

По сути мы получили операторное уравнение над сеткой:

что, если записать значения в узлах сетки как обычный вектор, является обычной системой линейных уравнений (). Значения в предыдущий момент времени константы, так как уже рассчитаны.
Для удобства представим оператор как разность двух операторов:

Заменив на нашу оценку , запишем функционал ошибки:

где — ошибка в узлах сетки.

Будем итерационно минимизировать функционал ошибки, используя градиент.

В итоге задача свелась к перемножению тензоров и градиентному спуску, а это именно то, для чего tensorflow и был задуман.

Реализация на tensorflow

Кратко о tensorflow

В tensorflow сначала строится граф вычислений. Ресурсы под граф выделяются внутри tf.Session. Узлы графа — это операции над данными. Ячейками для входных данных в граф служат tf.placeholder. Чтобы выполнить граф, надо у объекта сессии запустить метод run, передав в него интересующую операцию и входные данные для плейсхолдеров. Метод run вернет результат выполнения операции, а также может изменить значения внутри tf.Variable в рамках сессии.

tensorflow сам умеет строить графы операций, реализующие backpropagation градиента, при условии, что в оригинальном графе присутствуют только операции, для которых реализован градиент (пока не у всех).

Сначала код инициализации. Здесь производим все предварительные операции и считаем все, что можно посчитать заранее.

По-хорошему надо было считать значения функции на краях заданными и оптимизировать значения функции только во внутренней области, но с этим возникли проблемы. Способа сделать оптимизируемым только часть тензора не нашлось, и у операции присвоения значения срезу тензора не написан градиент (на момент написания поста). Можно было бы попробовать хитро повозиться на краях или написать свой оптимизатор. Но и просто добавление разности на краях значений функции и краевых условий в функционал ошибки хорошо работает.

Стоит отметить, что метод с адаптивным моментом показал себя наилучшим образом, пусть функционал ошибки и квадратичный.

Вычисление функции: в каждый момент времени делаем несколько оптимизационных итераций, пока не превысим maxiter или ошибка не станет меньше eps, сохраняем и переходим к следующему моменту.

Запуск:

Результаты

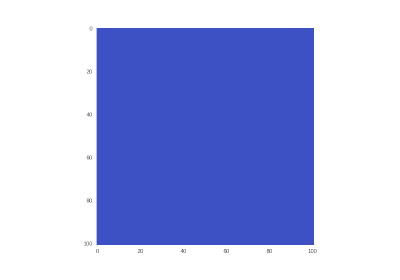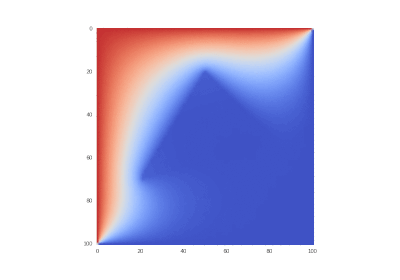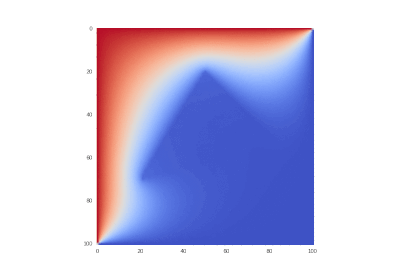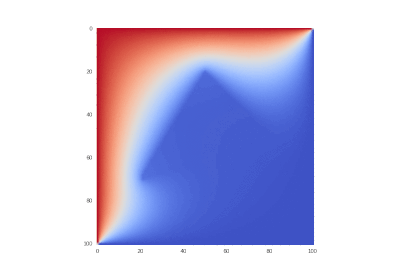
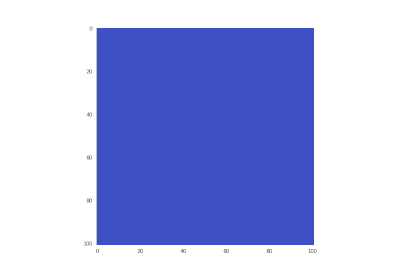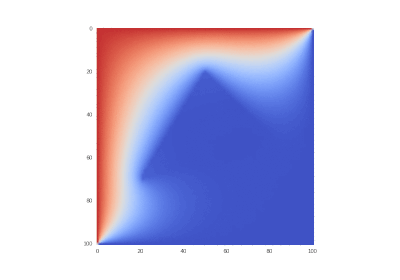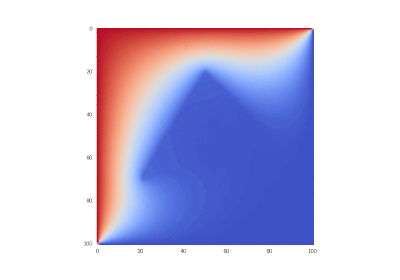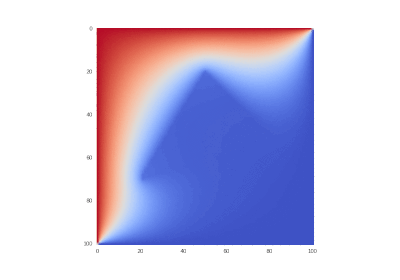
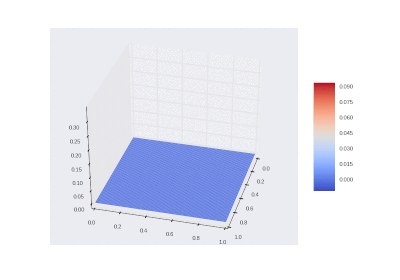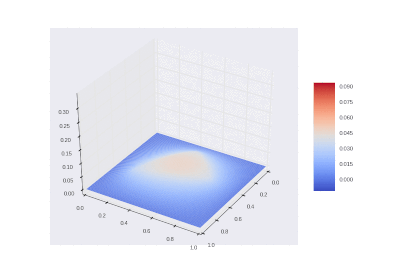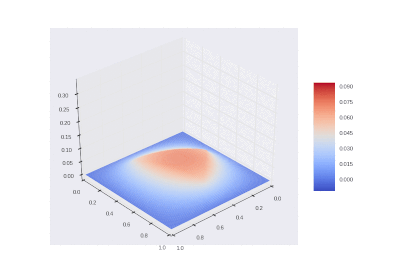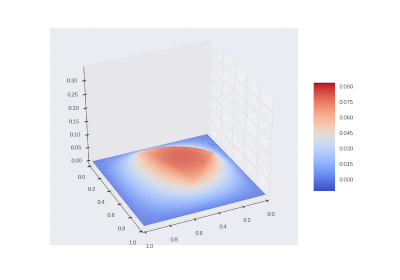
Условие как и оригинальное, но без в уравнении:

Что легко правится в коде:

Разницы почти нет, потому что производные имеют большие порядки, чем сама функция.

Условие с одним нагревающимся краем:

Условие с остыванием изначально нагретой области:

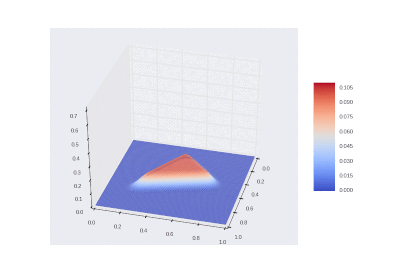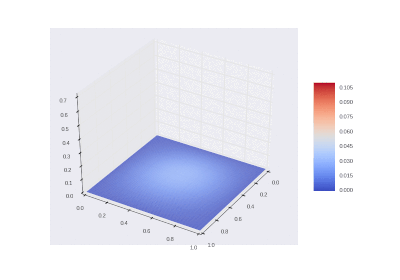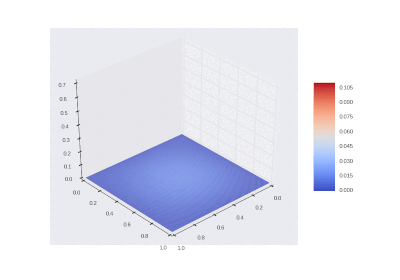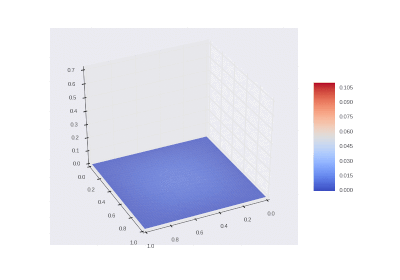
Условие с включением нагрева в области:

Рисование гифок

Функция рисования 3D-гифки:

В основной класс добавляем метод, возвращающий U в виде pandas.DataFrame

Функция рисования 2D-гифки:

Стоит отметить, что оригинальное условие без использования GPU считалось 4м 26с, а с использованием GPU 2м 11с. При больших значениях точек разрыв растет. Однако не все операции в полученном графе GPU-совместимы.

Intel Core i7 6700HQ 2600 МГц,
NVIDIA GeForce GTX 960M.

Посмотреть, какие операции на чем выполняются, можно с помощью следующего кода:

Это был интересный опыт. Tensorflow неплохо показал себя для этой задачи. Может быть даже такой подход получит какое-то применение — всяко приятнее писать код на питоне, чем на C/C++, а с развитием tensorflow станет еще проще.

Разностная аппроксимация начально-краевой задачи для уравнения теплопроводности. Понятие явной и неявной схемы.

Владислав Грузинский 5 лет назад Просмотров:

1 Разностная аппроксимация начально-краевой задачи для уравнения теплопроводности. Понятие явной и неявной схемы. 1 Разностная аппроксимация уравнения теплопроводности Рассмотрим различные варианты разностной аппроксимации линейного одномерного по пространству уравнения теплопроводности: где T > 0 некоторая константа. u t = u + fx, t, x 0, l, t 0, T ], 1.1 x Введем в области D = <0 x l, 0 t T >равномерную сетку с шагом по координате и шагом по времени: x =, = 0, 1. = l; t j = j, j = 0, 1. M, M = T. Уравнение 1.1 содержит как производные по пространственной переменной x, так и по времени t, поэтому для построения его разностной аппроксимации придется использовать узлы сетки, соответствующие различным j. Все узлы сетки, отвечающие фиксированному j, называют j-м временным слоем. Свойства разностных схем для уравнения 1.1 зависят от того, на каком слое j по времени аппроксимируется выражение u x. Рассмотрим возможные варианты. Вариант 1: явная схема. Для аппроксимации оператора L = t x приведенный на рис. 1. в уравнении 1.1 используем шаблон, 1

2 Рис. 1: Шаблон явной схемы для уравнения теплопроводности. Соответствующий разностный оператор L 0 u имеет вид: L 0 ux, t + ux, t ux +, t ux, t + ux, t u =. Далее для краткости будем использовать следующие стандартные обозначения: u = ux, t; û = ux, t +. Тогда: u t = û u, L 0 u = u t u xx. Найдем погрешность аппроксимации разностным оператором L 0 исходного дифференциального оператора L в точке x, t. В случае достаточно гладкой функции ux, t при достаточно малых шагах и имеем: u t = ux, t + ux, t = ux, t t + O, 1. Следовательно, разностный оператор L 0 аппроксимирует дифференциальный оператор L с погрешностью O + в точке x, t: L 0 u xx = ux, t x + O. 1.3 ux, t u = t ux, t x > << >L[ux,t] +O +. Введем сеточную функцию ϕ = ϕx, t j, аппроксимирующую правую часть fx, t уравнения 1.1 на всех внутренних узлах x, t j сетки с погрешностью O +. В качестве ϕ можно взять, например ϕx, t j = fx, t j. Тогда разностное уравнение L 0 y = ϕ будет аппроксимировать исходное дифференциальное уравнение теплопроводности 1.1 с первым порядком погрешности по и вторым по.

3 Вариант. Чисто неявная схема. Используем для аппроксимации оператора L = t x приведенный на рис.. в уравнении 1.1 шаблон, Рис. : Шаблон неявной схемы для уравнения теплопроводности. Тогда разностная аппроксимация оператора L уравнения теплопроводности будет выглядеть следующим образом: L 1 ux, t + ux, t ux +, t + ux, t + + ux, t + u = = u t û xx. Рассмотрим погрешность аппроксимации разностным оператором L 1 исходного дифференциального оператора L в точках x, t, x, t +. Так как для достаточно гладкой функции ux, t справедливы равенства û xx = ux, t + x + O = ux, t x + O +, 1.4 то с учетом 1. получаем, что оператор L 1 аппроксимирует дифференциальный оператор L в уравнении 1.1 с погрешностью O + в точках x, t и x, t + : L 1 ux, t u = t ux, t x > << >L[ux,t] +O + ux, t + = ux, t + +O +. > t << x >L[ux,t+] Беря в качестве сеточной аппроксимации правой части уравнения 1.1, например, функцию ϕx, t j = fx, t j+1, получим разностное уравнение L 1 y = ϕ, аппроксимирующее 1.1 с погрешностью O +. 3

4 Вариант 3. Неявная схема с весами. Используем шаблон, приведенный на рис. 3, и линейную комбинацию операторов L 0 и L 1 для аппроксимации дифференциального оператора L: L σ u = σl1 u+1 σl0 u = σu t σû xx +1 σu t 1 σu xx = u t σû xx + 1 σu xx, где σ 0, 1. Рис. 3: Шаблон неявной схемы с весами для уравнения теплопроводности. Пользуясь равенствами 1., 1.3 и 1.4, получаем, что оператор L σ аппроксимирует исходный дифференциальный оператор L с погрешностью O + в точках x, t, x, t+ при любом σ. По определению погрешность ψx, t = L σ u Lu 1.5 аппроксимации выражения Lu разностным выражением L σ u может вычисляться в любой точке x, t, а не обязательно в каком-либо узле сетки, так как в соотношении 1.5 функция ux, t это произвольная достаточно гладкая функция непрерывных аргументов x и t. Поэтому рассмотрим погрешность аппроксимации оператором L σ дифференциального оператора L в центральной точке x, t шаблона, приведенного на рис. 3. Пользуясь для достаточно гладкой функции ux, t разложением в ряд Тейлора в окрестности точки x, t + 0.5, при малых и получаем: ux, t + ux, t u t = = u t + O, x,t+0.5 û xx = u x + O = u x,t+ x + 3 u x,t+0.5 t x + O +, x,t+0.5 u xx = u x + O = u x,t x x,t u t x + O +. x,t+0.5 4

5 Следовательно, при σ = 0.5 в точке x, t оператор L 0.5 в силу своей симметрии аппроксимирует L со вторым порядком погрешности аппроксимации по и : L σ u = ux, t + t ux, t + x > << >L[ux,t+ ] 3 ux, t + σ 1 + O +. > <<>x t 0 при σ=0.5 Для того, чтобы получить разностное уравнение, аппроксимирующее дифференциальное уравнение u t = u + fx, t x с погрешностью O + в точке x, t +, достаточно взять в качестве сеточной аппроксимации правой части fx, t этого уравнения функцию ϕx, t j = fx, t j Итак, разностное уравнение L 0.5 y = ϕ, где ϕx, t j = fx, t j + 0.5, аппроксимирует уравнение 1.1 со вторым порядком погрешности по и. Реализация явной, неявной и симметричной разностных схем для начально-краевой задачи для уравнения теплопроводности на отрезке. Пример.1. Постройте явную разностную схему для следующей начально-краевой задачи на отрезке x [0, 1]: u t = u + x, 0 6 задаче с однородными граничными условиями: v t = v, 0 7 Итак, первый вариант явной разностной схемы для задачи.1, обладающей погрешностью аппроксимации O +, имеет вид: y j = yj 1 yj + yj +1 + x, = 1. 1, j = 0, 1. M 1, y 0 3πx = sn, = 0, 1. 4 y j 0 = 0, y j yj 1 = t j, j = 0, 1. M. Рассмотрим алгоритм решения системы.4. При j = 0 значения y j известны из начального условия. Следовательно, при каждом фиксированном j = 0, 1. M 1 неизвестными являются. Найти их можно следующим образом: 1 при = 1. 1 из первого уравнения системы.4 находим = y j + y j +1 yj + yj 1 + x ; при = 0 и = пользуемся граничными условиями, учитывая, что 1 и 1 уже известны: 0 = 0, = yj t j+1; 3 переходим на новый слой по времени, увеличивая j на единицу и повторяем действия 1 и. На рис.4-6 приведены результаты решения системы.4 для = 50 и M = Рис. 4: Аналитическое решение задачи.1. Если мы хотим, чтобы явная схема аппроксимировала исходную задачу с погрешностью O +, то можно использовать тот же прием, который применялся ранее для ап- 7

8 Рис. 5: Численное решение задачи.1 с помощью явной схемы. Рис. 6: Погрешность численного решения задачи.1 с помощью явной схемы. проксимации граничного условия, содержащего производную, в краевой задаче для обыкновенного дифференциального уравнения на отрезке. Пусть ux, t решение задачи.1. Рассмотрим выражение: u x = ux, t ux, t ux, t = ux, t + O = x x ux, t = ux, t x + O. x t Заменяя в нем производную u t конечной разностью: ux, t t = ux, t ux, t + O, 8

9 получим ux, t ux, t = ux, t x ux, t ux, t x + O +. Переходя в полученном равенстве к пределу при x 1 и учитывая, что по условию u x = t, x=1 находим, что при t = t j+1 имеет место равенство: u j+1 uj+1 1 = t j+1 u j+1 uj 1 + O +. Следовательно, разностное уравнение yj+1 1 = t j+1 yj 1.5 аппроксимирует граничное условие Неймана при x = 1 с погрешностью O +. Таким образом, меняя в схеме.4 уравнение.3 на.5, мы получим схему, аппроксимирующую исходную задачу на ее решении с погрешностью O +. Уравнение.5 удобно переписать в виде: 1 = t j yj, j = 0, 1. M 1, и использовать при уже найденных 1, yj для завершения перехода на слой j + 1. Результаты расчетов по соответствующей явной схеме на той же сетке, что и в предыдущем случае, приведены на рис Рис. 7: Численное решение задачи с помощью явной схемы с граничным условием.5. 9

10 Рис. 8: Погрешность решения задачи с помощью явной схемы с граничным условием.5. Также для получения схемы, имеющей погрешность аппроксимации O +, можно аппроксимировать граничное условие Неймана при x = 1 с помощью трехточечной первой разностной производной: 3 4yj yj+1 Переписывая это уравнение в виде = t j+1, j = 0, 1. M 1. = 4 3 yj yj+1 + t j+1 3,.6 мы можем использовать его для завершения перехода на слой j + 1 при уже найденных 1 и yj+1. Погрешность вычислений по схеме с условием.6 приведена на рис. 9. Рис. 9: Погрешность решения задачи с помощью явной схемы с граничным условием.6. 10

11 Пример.. Постройте чисто неявную разностную схему для начально-краевой задачи.1. Сравните численное решение с аналитическим и исследуйте зависимость погрешности от шагов сетки. Решение. Используем ту же сетку, что и в предыдущем примере с той лишь разницей, что соотношение шагов и теперь может быть любым. Разностная аппроксимация уравнения в соответствии с неявной схемой имеет вид: y j = yj+1 1 yj x, = 1. 1, j = 0, 1. M 1..7 Дополним разностное уравнение.7 начальными и граничными условиями на сетке. Как и в случае явной схемы, начальное условие и граничное условие Дирихле при x = 0 аппроксимируются точно: y 0 3πx = sn, = 0, 1. ; 0 = 0, j = 1. M 1. Для аппроксимации граничного условия при x = 1 используем те же три способа, что и в случае явной схемы, разобранной в предыдущем примере. Первый вариант аппроксимации граничного условия Неймана при x = 1: yj+1 1 = t j+1, j = 1. M 1. Получающаяся при этом неявная разностная схема: y 0 3πx = sn, = 0, 1. 0 = 0, j = 0, 1. M 1, y j yj+1 1 = yj+1 1 yj x, = 1. 1, j = 0, 1. M 1, = t j+1, j = 0, 1. M 1.8 имеет погрешность аппроксимации O +. Значения сеточной функции y j на нулевом слое по времени известны из начального условия, поэтому при каждом фиксированном j = 0, 1. M 1 неизвестными являются. Система уравнений, которым они удовлетворяют, имеет вид: 0 = 0, yj = yj t j+1, + yj+1 +1 = y j + x, = 1. 1,.9 11

12 то есть является системой с трехдиагональной матрицей: 0 = κ µ 1, A 1 C + B +1 = F, = 1. 1, = κ 1 + µ,.10 где κ 1 = 0, µ 1 = 0, A = B =, C = 1 +, F = y j + x, κ = 1, µ = t j+1. Очевидно, что достаточные условия устойчивости прогонки: A > 0, B > 0, C A + B, C A + B, = 1. 1, 0 κ p 1, p = 1, для системы.9 выполнены. Решая систему.9 методом прогонки и последовательно увеличивая значения j на единицу, мы полностью решим систему.8. Результаты вычислений по неявной схеме.8 в случае = M = 50 приведены на рис Рис. 10: Численное решение задачи.1 с помощью неявной схемы.8. Рис. 11: Погрешность численного решения задачи.1 с помощью неявной схемы.8. 1

13 Второй вариант аппроксимации граничного условия Неймана при x = 1: 1 = t j yj, j = 0, 1. M В этом случае для неизвестных при каждом фиксированном j получаем трехдиагональную систему вида.10, где κ = 1 1 +, µ = κ t j yj Погрешность расчетов по соответствующей неявной схеме в случае = M = 50 приведена на рис. 1.. Рис. 1: Погрешность решения задачи.1 с помощью неявной схемы с граничным условием.11. Третий вариант аппроксимации граничного условия Неймана при x = 1: = 4 3 yj yj+1 + t j+1 3 Для того, чтобы получить для неизвестных.1 систему с трехдиагональной матрицей при каждом фиксированном j, исключим из уравнения.1 неизвестное. Для этого воспользуемся уравнением.7 при = 1: yj yj yj+1 = F 1. Следовательно, = + 1 yj+1 F 1, 13

14 и уравнение.1 принимает вид: = 1 В результате для неизвестных.10, где κ = 1, 1 + F 1 + t j+1. приходим к системе с трехдиагональной матрицей вида µ = F 1 + t j+1. Погрешность расчетов по соответствующей схеме в случае = M = 50 приведена на рис. 13. Рис. 13: Погрешность численного решения задачи.1 с помощью неявной схемы с граничным условием.1. Пример.3. Постройте симметричную разностную схему схему с весом σ = 0.5 для начально-краевой задачи.1. Сравните численное решение с аналитическим и исследуйте зависимость погрешности от шагов сетки. Решение. Аппроксимация уравнения u t = u x + x в соответствии с симметричной разностной схемой имеет вид: y j = 1 y j+1 1 yj yj 1 yj + yj +1 + x,.13 где = 1. 1, j = 0, 1. M 1. Разностное уравнение.13 аппроксимирует исходное дифференциальное уравнение теплопроводности с погрешностью O + на всех внутренних узлах сетки. 14

15 Начальное условие и условие Дирихле при x = 0 аппроксимируются так же, как и в двух рассмотренных ранее случаях. Граничное условие Неймана при x = 1 можно аппроксимировать как с первым, так и со вторым порядком по. Если в качестве аппроксимации условия при x = 1 берется разностное уравнение yj+1 1 = t j+1, j = 1. M 1, то схема будет иметь погрешность аппроксимации O +. Соответствующая система для неизвестных будет трехдиагональной: 0 = 0, A 1 C + B +1 = F, = 1. 1, = yj t j+1,.14 где A = B =, C = 1 + A, F = y j + x + yj 1 yj + yj +1. Достаточные условия устойчивости прогонки для системы.14 выполнены. Погрешность решения задачи по схеме.14 для = M = 50 приведена на рис. 14. Рис. 14: Погрешность численного решения задачи.1 с помощью симметричной схемы. Построим аппроксимацию граничного условия Неймана при x = 1 с погрешностью O +. Рассмотрим равенство: ux, t ux, t = ux, t x ux, t t x + O,.15 где ux, t решение исходной задачи.1. Положим в равенстве.15 t = t j Так как ux, t j ux, t j =

16 и получаем: 1 = 1 u j uj 1 + uj+1 ux, tj ux, t j ux, t t t=tj +0.5 u j+1 1 = ux, t x + ux, t j+1 ux, t j+1 + O = ux, t j+1 ux, t j x,t j O, u j+1 u j x + O +. Перейдем в полученном равенстве к пределу при x 1 то есть при, учитывая граничные условия задачи: 1 u j uj 1 + uj+1 uj = t j Следовательно, разностное уравнение y j yj 1 + yj+1 yj+1 1 = t j +0.5 будет аппроксимировать условие u x = t x=1 yj u j+1 uj с погрешностью O +. Соответствующая система для вид: где 0 = 0, 1 1 A 1 C + B +1 = F, = 1. 1, = κ 1 + µ, 1 κ = 1 +, µ = κ 1 + yj + O +., j = 0, 1. M 1.16 при фиксированном j имеет + t j + y j + yj Погрешность, получаемая при численном решении задачи с использованием граничного условия.16, для = M = 50 приведена на рис. 15. Такой же порядок погрешности аппроксимации можно получить, используя граничное условие = 4 3 yj yj+1 + t j Исключим из этого уравнения неизвестное, используя уравнение.13 при = 1: Так как yj yj+1 = F 1. = + 1 yj+1 F 1, 16

17 Рис. 15: Погрешность численного решения задачи.1 с помощью симметричной схемы с граничным условием.16. уравнение.18 можно переписать в виде: = F 1 + t j+1. В результате мы снова придем к системе с трехдиагональной матрицей вида.17 для неизвестных при каждом фиксированном j = 0, 1. M 1, где теперь κ = 1, µ = F 1 + t j+1. Погрешность решения по предложенной схеме при = M = 50 приведена на рис. 16. Рис. 16: Погрешность решения задачи с помощью симметричной схемы с граничным условием

18 3 Задачи для самостоятельного решения Решите аналитически и численно при помощи явной, неявной и симметричной схем начальнокраевую задачу для уравнения теплопроводности на отрезке: u t = u a + fx, t, x 0, l, t 0, T ], x ux, 0 = u 0 x, u γ 0 x + δ 0u = g 0 t, x=0 u γ 1 x + δ 1u = g 1 t, x=l где: x а a =, f = cos e t, u 0 = π x, γ 0 = 1, δ 0 = 0, γ 1 = 0, δ 1 = 1, g 0 = 1, g 1 = 0, l = π; б a = 1, f = e t x / 1, u 0 = 1 + e t x /, γ 0 = 1, δ 0 = 0, γ 1 = 1, δ 1 = 0, g 0 = 0, g 1 = e t, l = 1; в a = 0.5, f = e t, u 0 = 1 + sn 3x, γ 0 = 0, δ 0 = 1, γ 1 = 1, δ 1 = 0, g 0 = e t, g 1 = 0, l = π/; 3πx г a = 1, f = 0, u 0 = 3 x + cos, γ 0 = 1, δ 0 = 0, γ 1 = 0, δ 1 = 1, g 0 = 1, g 1 = 1, l = ; 4 д a = 0.1, f = 0, u 0 = cosπx + x + x, γ 0 = 1, δ 0 = 0, γ 1 = 1, δ 1 = 0, g 0 = 1, g 1 = 5, l =. Сравните результаты численного решения по разным схемам между собой и с аналитическим решением задачи. 18

«А.И. Цаплин, И.Л. Никулин МОДЕЛИРОВАНИЕ ТЕПЛОФИЗИЧЕСКИХ ПРОЦЕССОВ И ОБЪЕКТОВ В МЕТАЛЛУРГИИ Утверждено Редакционно-издательским советом университета в качестве учебного . »

имеющий порядок шага сетки hx. В этом случае, имея в виду первую степень шага сетки в остаточном члене разложения, говорят, что формула (5.5) аппроксимации первой производной имеет первый порядок точности.

Используя нумерацию узловых точек, можно записать полученные формулы односторонних разностей для i-й узловой точки на k-м слое по времени:

Среднее арифметическое значение право- и левосторонних разностей дает формулу центральной разности:

Вторая производная может быть найдена формально как производная от производной с применением формул (5.6):

Последнее выражение может быть получено из ряда Тейлора с учетом пяти членов разложения. Действительно, подставляя в этот укороченный ряд значения x = x0 + hx, x = x0 – hx и складывая полученные выражения, получим:

Вторая производная определена с точностью до квадрата шага сетки, т.е. имеет второй порядок точности. С таким же вторым порядком точности может быть получена формула первой производной. Для этого в разложении (5.2), записанном через узловые точки k-го слоя, учтем еще один член ряда с учетом приближенного значения второй производной (5.8) получаем:

где O ( hx2 ) = 3 x. Таким образом, формула центральной разности имеет второй порядок точности, т.е. она на порядок точней формул односторонних разностей (5.6).

5.2. Схемы аппроксимации уравнения теплопроводности От отдельных производных перейдем к дискретному представлению всего уравнения теплопроводности:

Существующие схемы аппроксимации делятся на явные, когда все производные по координате в уравнении переноса записываются на «старом» (k–1)-м временном слое с известным распределением переносимого параметра Т, и неявные, когда все производные по координате в этом уравнении записываются на «новом» k-м временном слое с известным распределением Т.

Используя формулу односторонней разности для производной по времени, а также формулу центральной разности для конвективного члена, запишем примеры схем аппроксимации – явной:

и неявной Отметим, что полученные аналоги имеют второй порядок точности по пространственной переменной и лишь первый – по времени.

Найдем соотношение между шагами сетки для уравнения теплопроводности, обеспечивающее одинаковую точность аппроксимации его левой и правой частей. Производные по времени и координате в уравнении теплопроводности (5.12) имеют различные ошибки аппроксимации соответственно первого и второго порядков точности относительно шагов сетки. Погрешность всего уравнения определяется максимальным значением этой ошибки. Возникает вопрос нахождения такого соотношения между шагами сетки hx и h, при котором ошибки аппроксимации левой и правой частей этого уравнения равны.

Имея в виду тот факт, что ошибки аппроксимации должны удовлетворять уравнению теплопроводности, запишем:

или с учетом (5.5), (5.9):

Продифференцировав уравнение теплопроводности (5.12) по и дважды по x:

и подставив полученные выражения в (5.16), получим искомую зависимость:

Полученное условие показывает, что для обеспечения минимальной погрешности аппроксимации уравнения теплопроводности сгущение пространственной сетки в 2, 3, 4 раза должно вызывать соответствующее сгущение временной сетки в 4, 9, 16 раз.

Самая простая схема аппроксимации уравнения (5.12) заключается в замене его левой части односторонней разностью, имеющей первый порядок точности, и записи правой части Рис. 5.2. Сеточный шаблон явной схемы 1-го порядка точности для температуры:

Вычисления по явной схеме первого порядка точности устойчивы, если коэффициент при Тi,k оказывается положительным:

Это накладывает ограничение на выбор шага сетки по времени Условие устойчивости явной схемы является достаточно жестким. Так, при Hx = 0,01 м, а = 1,510–5 м2/c (сталь), N = 20, h 0,0083 c. Необходимость счета с мелким шагом по времени приводит к увеличению объема вычислений и является существенным недостатком, ограничивающим применение явной схемы первого порядка точности.

От этого недостатка свободна неявная схема первого порядка точности (5.14) (схема Лаасонена, рис. 5.3), согласно которой правая часть уравнения (12) записывается на k + 1-м временном слое с неизвестными значениями Т. Она не дает явной формулы для определения неизвестных значений S в узловых точках k-го слоя, а дает лишь распределение:

Соотношения (5.22) образуют для всех внутренних узловых точек k + 1-го слоя систему линейных алгебраических уравнений (N–1)-го порядка. Так как схема абсолютно Рис. 5.3. Сеточный шаблон устойчива, то счет можно неявной схемы 1-го порядка точности вести с достаточно крупными шагами по времени. Это, однако, приводит к увеличению ошибок аппроксимации уравнения теплопроводности.

Для уменьшения ошибок аппроксимации правую часть уравнения теплопроводности (5.12) усредняют по времени:

Эта схема, называемая схемой Кранка – Николсона (рис. 5.4), также абсолютно устойчива, имеет второй порядок точности и находит широкое применение в пракРис. 5.4. Сеточный шаблон тических расчетах. Соотно- неявной схемы 2-го порядка точности шения (5.23) образуют для всех узловых точек k-го слоя систему линейных алгебраических уравнений вида (5.22).

В рассмотренных схемах производная по времени аппроксимировалась односторонней разностью с использованием двух слоев сетки по времени. Такие схемы называются двухслойными.

Рис. 5.5. Сеточный шаблон явной схемы 2-го порядка точности может служить схема Дюфора – Из (5.24) можно получить явное выражение для неизвестного значения Тi,k+1 в каждом узле сетки:

Полученное соотношение дает необычную для явных схем абсолютную устойчивость счета при любых шагах сетки hx и h.

Однако следует отметить, что при больших шагах по времени рассматриваемая схема приводит к колебаниям, хотя и не возрастающим. Причиной этого являются ошибки аппроксимации.

Поэтому при больших шагах по времени метод Дюфора – Франкеля неточен.

Существуют и другие явные и неявные методы разностной аппроксимации уравнения переноса.

Ошибки, связанные с дискретным представлением уравнения переноса и проведением расчетов на компьютере, можно разделить на три вида: ошибки округления, ошибки аппроксимации, схемные ошибки.

Ошибки округления связаны с выполнением арифметических операций, в котором числа представляются в экспоненциальной форме с ограниченным числом разрядов. Ошибки округления можно уменьшить, изменяя метод решения матричных уравнений, последовательность арифметических операций и увеличивая число разрядов для записи чисел в компьютере (например, применяя двойную точность).

Ошибки аппроксимации обычно больше ошибок округления и связаны с дискретным представлением отдельных членов уравнения переноса, использованием разложения функции в укороченный ряд Тейлора. Порядок ошибки аппроксимации оценивается максимальным значением остаточного члена ряда Тейлора. Грубо ошибки аппроксимации можно оценить на следующем примере. При числе разбиений по толщине слоя N = = 10 шаг сетки hx 1/10, ошибка аппроксимации первой производной односторонними разностями равна О(hx) 1/10 10 %, второй производной – O ( hx2 ) 1 100 1 %. Более точно ошибки аппроксимации всего уравнения переноса можно оценить, находя решение на последовательности сгущающихся сеток.

На практике полезно строить график изменения функции в характерной точке при сгущении сетки. При этом схемы первого порядка точности в области достаточно густой сетки дают линейное приближение к точному решению, а схемы второго порядка точности – параболическое (рис. 5.6).

Рис. 5.6. Стремление численных решений к точному решению со сгущением сетки при схемах аппроксимации первого (1) и второго (2) порядков точности Общим свойством ошибок аппроксимации является их исчезновение при асимптотическом стремлении к нулю шагов сетки (сгущении сетки).

Схемная ошибка консервативности Схемные ошибки связаны со схемой конечно-разностного аналога всего уравнения переноса. В отличие от ошибок аппроксимации схемные ошибки не исчезают при асимптотическом уменьшении шагов сетки. Однако для уменьшения или исключения схемных ошибок совсем не обязательно устремлять к нулю шаги сеток.

Примером схемной ошибки является ошибка, связанная с нарушением свойства консервативности (закона сохранения) в конечно-разностном аналоге уравнения переноса энергии только конвекцией:

Явная схема аппроксимации этого уравнения имеет вид:

Получим это соотношение интегральным методом, интегрируя уравнение переноса по времени от до +h и по пространственной области Ф от x–hx/2 до x+hx/2 (рис. 5.7).

Поскольку порядок интегрирования по времени и координате несущественен, выберем его так, чтобы можно было провести одно точное интегрирование, а именно:

Проинтегрируем выражения в квадратных скобках Остальные интегралы можно определить численно, используя теорему о среднем, взяв за средние значения центральную точку x области интегрирования Ф и нижний предел времени интегрирования. В итоге получим:

Производные T x можно найти, используя формулы односторонних разностей:

Значения конвективных членов uТ можно вычислить как средние арифметические, например:

Подставляя (5.29) и (5.30) в (5.28), получим:

Поделим последнее уравнение на hhx и перейдем к индексным обозначениям, учитывая, что времени соответствует индекс k–1, а +h – индекс k, получим:

Отметим, что конечно-разностный аналог (5.31) уравнения переноса, полученный интегральным методом, отличается от соответствующего аналога (5.27), полученного применением приближенных конечно-разностных формул ряда Тейлора непосредственно к уравнению переноса, т.е. дифференциальным методом. Отличие касается аппроксимации конвективного члена уравнения.

Для того чтобы выявить это отличие, приведем полученную интегральным методом аппроксимацию конвективного члена к виду уравнения (5.27). Для этого предположим, что скорость линейно возрастает в направлении координаты x.

Пользуясь формулой усреднения (индекс k–1 опускаем):

преобразуем конвективный член уравнения (5.31):

Указанное отличие, как видно из сравнения (5.32) с соответствующей аппроксимацией конвективного члена уравнения (5.27), составляет u Ti hx и исчезает, когда u = 0, т.е. при постоянной скорости. Это свидетельствует о том, что интегральный и дифференциальный методы дают различные конечно-разностные аналоги дифференциального уравнения переноса, причем это различие увеличивается с возрастанием градиента скорости переноса. Интегральный метод позволил учесть закон сохранения в дискретном аналоге уравнения переноса. Следовательно, ошибку u Ti hx можно трактовать как нарушение закона сохранения переносимого параметра в дискретном аналоге уравнения переноса, полученном дифференциальным методом.

Заметим, что указанная схемная ошибка в отличие от ошибок аппроксимации при сгущении сетки ( hx 0 ) не только не стремится к нулю, но даже возрастает.

Другая схемная ошибка связана с неодинаковой точностью конечно-разностного представления отдельных членов уравнения переноса. Поясним ее на следующем примере. Запишем стационарное уравнение переноса энергии:

Получим конечно-разностный аналог этого уравнения, применяя для аппроксимации правой части (диффузионного члена) формулу второго порядка точности, а для левой части (конвективного члена) – формулу правосторонней разности первого порядка точности:

Уравнение (5.34) имеет низший, первый порядок точности, поэтому погрешностью O ( hx2 ), имеющей более высокий второй порядок, можно пренебречь. Подставляя в (5.34) погрешность O ( hx ) из (5.5), получим:

Усредним скорость в пределах шага сетки u = u и объединим коэффициенты при вторых производных, в результате получим:

Из последнего уравнения видно, что погрешность влияет на коэффициент при диффузионном члене уравнения переноса, поэтому ее называют схемной искусственной температуропроводностью (диффузией). Вынесем в уравнении (5.36) температуропроводность за скобку:

Введем сеточное число Пекле по локальной скорости и характерной длине, равной шагу сетки:

Тогда при переносе тепла получаем схемную температуропроводность:

Так как коэффициент а не может быть отрицательными, то Последнее соотношение является условием, при котором счетная температуропроводность не проявляется. Это соотношение накладывает ограничение на шаг сетки:

Однако в практических расчетах ограничение (5.40) оказывается очень жестким, поэтому диффузия, которую мы будем в дальнейшем называть счетной диффузией, всегда присутствует. С математической точки зрения счетная диффузия увеличивает физическую температуропроводность:

где счетное значение температуропроводности Счетная диффузия проявляется в «размазывании» внешних возмущений, в стремлении сделать распределение переносимых величин более однородным.

Отметим, что аппроксимация всех членов уравнения переноса с одинаковым порядком точности, например вторым, приводит к исключению счетной диффузии, такие схемы называют бездиффузионными.

Схемная ошибка транспортивности Схемная ошибка транспортивности приводит к тому, внешнее возмущение переносится за счет конвекции не только в направлении, но и против скорости потока. Проиллюстрируем её на уравнении переноса, учитывая в нем только нестационарный и конвективный члены:

Конечно-разностный аналог этого уравнения запишем с помощью формул правосторонней и центральной разностей:

Рассмотрим некоторое возмущение Т = только в одной точке i = n, полагая u 0. Тогда в точке i = n+1 по потоку Таким образом, возмущение, которое должно переноситься только в направлении скорости, т.е. по потоку, при использовании формулы центральной разности для конвективного члена переносится и против потока. Схема (5.44) не обладает, поэтому, свойством транспортивности, а (5.46) характеризует схемную ошибку в точке i = n 1, связанную с нарушением этого свойства. Нарушение свойства транспортивности эквивалентно возникновению фиктивных (счетных) источников (стоков) в конечноразностном аналоге уравнения переноса.

Существуют и другие схемные ошибки, связанные главным образом с нестационарностью и многомерностью уравнения переноса. Схемы аппроксимации уравнения переноса, свободные от схемных ошибок, называются нейтральными.

5.4. Способы аппроксимации конвективных членов Как мы уже убедились при анализе схемных ошибок, аппроксимация конвективного члена уравнения переноса играет важную роль в численном решении этого уравнения. Поэтому целесообразно провести сравнительный анализ нескольких наиболее распространенных разностных схем на регулярной сетке.

Схема с центральными разностями консервативна, так как конвективный член записан в дивергентной форме, имеет второй порядок точности, поэтому она свободна от счетной диффузии. Однако главным недостатком этой схемы является, как мы уже убедились ранее, ее нетранспортивность. Поэтому схема (5.47) применяется в расчетной практике редко, в основном при малых числах Пекле.

В первой схеме с разностями против потока используются односторонние разности, а не центральная разность, причем при положительной скорости потока используется формула лево-, а при отрицательной – правосторонней разности, т.е.

Зависимость односторонних разностей от знака скорости приводит в отличие от предыдущей схемы, к выполнению свойства транспортивности, при котором перенос возмущения обеспечивается всегда в направлении потока. Однако схема (5.48) не консервативна, имеет первый порядок точности, т.е.

обладает счетной диффузией, пропорциональной сеточному числу Пекле.

Вторая схема с разностями против потока известна как схема с донорными ячейками. В ней используются усредненные значения скоростей на границах ячейки, содержащей узловую точку где uп = ( ui +1 + ui ) 2, uл = ( ui 1 + ui ) 2, а значения Т выбираются в зависимости от знака усредненных скоростей:

Схема с донорными ячейками обладает как свойством транспортивности, так и свойством консервативности. Формально она имеет первый порядок точности, однако усреднение скоростей сохраняет в ней кое-что от второго порядка точности. Поэтому схема (5.49) имеет меньшую по сравнению со схемой (5.48) величину счетной диффузии.

Способы аппроксимации конвективных членов можно продолжить. Однако уже рассмотренные способы достаточно иллюстрируют сложность проблемы устранения схемных ошибок и построения нейтральных разностных схем уравнений переноса.

5.5. Аппроксимация граничных условий Аппроксимацию граничных условий рассмотрим на примере граничных условий теплообмена 3-го рода для правой границы (рис. 5.8) Рис. 5.8. Фрагмент сетки у правой границы Применяя формулу односторонней разности, получим приближение:

из которого определяется температура на поверхности тела Полученную формулу, имеющую первый порядок точности, можно использовать для получения граничных значений температуры в сочетании со схемами аппроксимации уравнения переноса энергии, имеющими такой же порядок точности.

При работе со схемами второго порядка точности (Кранка – Николсона и др.) необходимо использовать более точную аппроксимацию граничных условий. Для этого запишем разложение температуры в ряд Тейлора в окрестности границы i = N:

Учитывая три члена разложения, получим:

Запишем вторую производную в конечных разностях:

Полученное выражение имеет второй порядок точности, с его учетом из граничного условия:

получается более точное по сравнению с (5.59) значение температуры на границе:

Отметим нелинейность граничных условий для температуры, т.е. зависимость ее на поверхности от значений во внутренних узлах сетки. Это приводит к итерационному процессу удовлетворения граничным условиям, который заканчивается при достижении наперед заданной точности.

5.6. Методы решения сеточных уравнений Разностные уравнения, полученные из неявных и явнонеявных схем, являются, как было показано, линейными алгебраическими уравнениями. На фиксированном временном слое для всех внутренних узловых точек эти уравнения образуют систему:

которую можно записать в векторно-матричном виде:

или где [H] матрица коэффициентов;вектор-столбец неизвестных значений искомого параметра Т в узловых точках;

неизвестный вектор столбец, характеризующий краевые условия и распределение параметра Т на предыдущем временном слое.

Матрица [H] обладает рядом специальных свойств, которые необходимо использовать при решении системы уравнений. Она имеет высокий порядок, зависящий от густоты сетки, которая может достигать для современных компьютеров нескольких десятков тысяч. Матрица является редко заполненной с размещением ненулевых элементов по диагонали в три ряда.

Такие матрицы называются ленточными трехдиагональными.

Важным свойством является симметрия матрицы относительно ее диагонали, вытекающая из равенства коэффициентов А и С.

Указанные свойства матрицы [H] позволяют занимать незначительное место для ее хранения в запоминающем устройстве компьютера, поэтому матрицу [H] называют порождающейся в отличие от хранящейся матрицы.

Перейдем к рассмотрению эффективных способов решения системы (5.62).

Метод прогонки является модификацией метода исключения Гаусса, учитывающей свойства матрицы H. Решение системы (5.64) в узловой точке ищется в виде линейной функции.

В частности, для (i1)-ой точки эта функция имеет вид:

где i, zi неизвестные пока вспомогательные коэффициенты. Подставим (5.65) в (5.62):

Полученное соотношение имеет ту же форму, что и функция (5.65), только для i-й точки откуда заключаем, что Полученные коэффициенты называются прогоночными коэффициентами, а формулы (5.68–5.69) дают процедуру решения.

Сначала при i = 1, 2. N–1 считаются прогоночные коэффициенты (5.69), при этом начальные значения прогоночных коэффициентов 1, z1 определяются из граничных условий на левой границе. Эта операция называется прямой прогонкой. После определения всех i, zi в обратном направлении (i = N1. 1) с учетом значения параметра TN, найденных из граничного условия на правой границе, по формуле (5.68) последовательно находятся неизвестные значения Ti в узловых точках сетки.

Определение начальных значений прогоночных коэффициентов рассмотрим на примере граничных условий теплообмена. На левой границе условие конвективного теплообмена:

может быть представлено в конечно-разностном виде (рис. 5.9):

Рис. 5.9. Фрагмент сетки у левой (а) и правой (б) границ Отсюда находим:

Сравнивая эту формулу с соотношением (5.68) для левой границы получаем начальные значения прогоночных коэффициентов:

Запишем условие теплообмена на правой границе:

в конечных разностях:

Запишем соотношение (5.68) для правой границы:

Приравнивая правые части (5.77), (5.78), получим искомое значение температуры на правой границе Запишем алгоритм метода прогонки:

Пример программы, реализующий алгоритм метода прогонки, приведён в лабораторной работе № 3.

Основным недостатком метода прогонки являются ошибки округления при вычислении прогоночных коэффициентов. Эти ошибки возрастают с увеличением порядка системы. Для уменьшения этих ошибок рекомендуется считать эти коэффициенты с повышенной точностью.

Метод последовательной линейной верхней релаксации Наряду с прямыми методами для решения сеточных уравнений применяются итерационные методы, дающие решения в виде предела последовательности однообразных итераций.

Основное их преимущество перед прямыми методами заключается в самокорректирующемся решении, дающем минимальные ошибки округления. Привлекает в них и простота вычислительного алгоритма.

Рассмотрим один из эффективных итерационных методов – метод последовательной линейной верхней релаксации, итерационная процедура которого применительно к разностному уравнению (5.62) имеет вид Ti q = где q – номер итерации; – параметр релаксации. При = получаем процесс последовательных смещений, или процесс Зейделя. Введение параметра верхней релаксации 1 2 позволяет ускорить сходимость итерационного процесса (21), причем наибольшая скорость сходимости имеет место при оптимальном значении параметра релаксации = опт. Последнее зависит от порядка системы и может быть вычислено через число разбиений расчетной области:

Эта формула применима для одномерной области с регулярной сеткой. Расчет по формуле (5.82) с учетом (5.83) продолжается до тех пор, пока искомое решение не будет удовлетворять требуемой точности:

где – требуемая точность.

сопряженных уравнений теплообмена Рассмотрим в общих чертах процедуру решения сопряженной задачи конвективного теплообмена, в которой совместно решаются уравнения конвекции, например, в переменных завихренность и функция тока (–) и уравнение переноса энергии для температуры Т. Рассмотрим вычислительный цикл для нестационарных уравнений ––T-системы (рис. 5.10).

Исследуемая область покрывается конечно-разностной сеткой, в узлах которой определяется решение. Процедура счета начинается с задания начальных условий для функций,, T, причем для нахождения стационарного решения вид начальных условий несущественен.

Далее для некоторого приращения по времени вычисляются завихренность и температура во внутренних узлах сетки с помощью конечно-разностных аналогов соответствующих уравнений переноса. Затем решается конечно-разностный аналог уравнения Пуассона для функции тока, в котором используются новые значения завихренности, вычисленные во внутренних узловых точках. Отметим, что решение уравнения Пуассона включает в себя итерации, которые называются внутренними. В процессе внутренних итераций завихренность не изменяется. После выхода из внутренних итераций по наперед заданной точности вычисляются компоненты скорости.

Рис. 5.10. Блок-схема решения задачи конвективного теплообмена Следующий шаг вычислительного цикла связан с уточнением граничных условий для завихренности и температуры.

При этом используются новые (уже вычисленные) значения,, Т во внутренних приграничных точках области. Расчет – – Т-системы с уточнением граничных условий повторяют до достижения наперед заданной точности. Одновременно могут уточняться неоднородные свойства, например вязкость, температуропроводность и др. Эти повторения называются внешними итерациями (в отличие от внутренних итераций для уравнения Пуассона).

При выходе из внешних итераций проводится расчет чисел Нуссельта (безразмерной теплоотдачи), и вычислительный цикл повторяется для нового слоя по времени. Если находится стационарное решение задачи, то необходимость во внешних итерациях отпадает, и расчет чисел Нуссельта откладывается до выхода решения на стационарное с заданной степенью точности.

Выход из внутреннего итерационного цикла осуществляется по условию:

Выход из внешнего цикла определяется условиями:

где р – номер внешней итерации. При значениях чисел Прандтля, близких к единице, скорости сходимости итерационных процессов по температуре и завихренности примерно одинаковы. При числах Прандтля, меньших единицы, что соответствует расплавленным металлам, сходимость по температуре может достигаться медленнее, чем по завихренности. В этом случае «замораживание» температурного поля в течение нескольких шагов по времени и расчет только завихренности может привести к экономии времени счета.

Общие затраты компьютерного времени зависят также от задаваемой точности внутренних и внешних итераций,, Т. Рекомендуется задавать = 0,005, = Т = 0,01. С уменьшением указанных значений допустимых погрешностей увеличиваются затраты компьютерного времени при практически неизменном решении, увеличение погрешностей приводит к колебаниям решения.

1. Основы метода сеток. Запись первой и второй производных с первым и вторым порядками точности.

2. Явная и неявная схемы аппроксимации уравнения переноса энергии.

3. Схемы аппроксимации первого и второго порядков точности для уравнения теплопроводности.

4. Сравнительная характеристика ошибок округления, аппроксимации и схемных ошибок в вычислительном эксперименте.

5. Как оценить погрешность в вычислительном эксперименте?

6. От чего зависит схемная ошибка консервативности в уравнении переноса?

7. Каковы условия существования схемной ошибки искусственной диффузии, как она проявляется в численном решении?

8. Причины возникновения и проявление схемной ошибки транспортивности.

9. Способы аппроксимации конвективных членов уравнения переноса. Понятие о нейтральных разностных схемах.

10. Формулы аппроксимации граничных условий конвективного теплообмена первого и второго порядков точности.

11. Векторно-матричное представление сеточных уравнений.

12. Метод прогонки решения матричных уравнений и его реализация на компьютере.

13. Итерационный метод последовательной линейной верхней релаксации решения матричных уравнений и его реализация на компьютере.

14. Как организовать алгоритм решения сопряженных уравнений тепломассопереноса на компьютере?

ЧАСТЬ II

ЛАБОРАТОРНЫЙ ПРАКТИКУМ

Статистическая обработка массива случайных данных Цель работы: ознакомиться с методами обработки массива случайных данных.

Приборы и принадлежности: калькулятор.

Случайной величиной называют переменную величину, которая в результате опыта может принимать различные значения.

Случайные величины обычно обозначают большими буквами, например Х. Значения случайной величины, которые она принимает в результате опыта, обозначают малыми буквами x1, x2. xn. При массовых испытаниях каждое из возможных значений случайной величины x1, x2. xn может встретиться m1, m2, …, mn раз. Эти числа называют частотами. Весь набор значений случайной величины образует генеральную совокупность Nx. Отсеянные из генеральной совокупности Nx значения грубых ошибок образуют выборку объемом N. Если всего было проведено Nx опытов, то в результате выборки получаем n, и отношеmi = N ние mi /N называют частостью или относительной частотой.

Распределение случайной величины X (рис. 1.1), определяющей вероятность того, что эта величина примет значения, не превосходящие хi, т.е. попадет в интервал (, xi ), называется интегральной функцией распределения F(xi):

Рис. 1.1. Плотность распределения случайной величины Плотность вероятности f (х) задает распределение случайной величины и количественно оценивается вероятностью события р(x1 X x2) = f(x)dx. Функция распределения F(x) является первообразной для плотности f(x), поэтому f(x) называют также дифференциальной функцией распределения.

Распределение случайной величины представляют гистограммой частот – ступенчатой функцией, состоящей из прямоугольников, основанием которой служат частичные интервалы длиной h, а высоты равны отношению ni/h (плотность частоты). Площадь гистограммы частот равна сумме всех частот, т.е. объему выборки.

Модой распределения (Mо) называется значение случайной величины X, при котором f(x) принимает максимальное (наиболее вероятное) значение в окрестности какого-либо значения случайной величины х.

Математическим ожиданием дискретной случайной величины называется сумма произведений всех возможных значений случайной величины на вероятности этих значений:

Стандартное (или среднее квадратическое) отклонение служит мерой рассеяния случайной величины Х около ее математического ожидания:

Другая мера рассеяния – дисперсия Д x характеризует разброс значений случайной величины относительно ее математического ожидания и определяется по формуле Д x = 2.

В качестве примера в табл. 1.1 представлены результаты выборочного взвешивания отливок (xi, кг, i = 1, 2, …, n). Было взвешено 100 отливок, т.е. объем выборки n = 100. Требуется построить функцию распределения F(x) и плотность вероятности f(x), а также представить график функции распределения и гистограмму частот.

1) Экстремальные значения веса отливок xmin = 4,97; xmax = 5,85;

2) число интервалов группирования s = log 2 n + 1 = 7,62 8 ;

3) ширина интервала группирования 4) левый (сj–1) и правый (сj) концы j-го интервала:

5) середины интервалов группирования x 0 = ( c j 1 + c j ) 2 ;

6) подсчитываем число выборочных данных vj, попавших в каждый (j-й) интервал группирования (j = 1, 2, …, s);

7) подсчитываем количество выборочных данных, попавших в j-й интервал группирования h (v1 + … + vjx);

8) подсчитываем выборочную функцию распределения где ix – номер самого правого из интервалов группирования, правый конец которых не превосходит заданного значения x;

9) посчитываем выборочную функцию плотности:

в которой k(x) – порядковый номер интервала группирования, накрывающего заданную точку x, а vk(x) – число выборочных данных, попавших в этот интервал;

10) результаты группировки сводим в табл. 1.2.

11) Строим гистограмму (рис. 1.2).

12) Строим функцию распределения (рис. 1.3).

Рис. 1.3. График функции распределения 1. Сформировать из табл. 1.1 массив случайных чисел, пользуясь для своего варианта данными поправок из табл. 1.3.

Поправку x прибавить к первым пяти строкам и вычесть из последних пяти строк табл. 1.1, например, для варианта 6 x = = ± 0,06.

2. Построить гистограмму частот.

3. Построить график функции распределения.

4. Найти для данного распределения моду, математическое ожидание и дисперсию.

1. Сформулируйте основные причины появления неопределенностей. Какие из них являются субъективными, а какие – объективными?

2. Как описывается неопределенность математически?

3. Приведите примеры математического описания неопределенностей в металлургии.

4. Когда в задаче математического моделирования применяется стохастическое описание переменных?

5. Дайте определение функции и плотности распределения.

6. Меры положения и рассеяния кривой распределения.

Объясните различие между модой, медианой и математическим ожиданием.

Цель работы: ознакомиться с методами обработки массива случайных данных.

Приборы и принадлежности: калькулятор.

Целью моделирования любого технологического процесса является установление количественной зависимости выходного параметра от одного или группы случайных входных параметров. В функциональной связи Y = f (X) каждому значению независимой переменной X отвечает одно или несколько вполне определенных значений зависимой переменной Y. В этом случае связь между переменными X и Y в отличие от функциональной приобретает статистический характер и называется корреляционной.

Простейшей и распространенной зависимостью между величинами X и Y является линейная регрессия (рис. 2.1). Оценка тесноты или силы связи между величинами X и Y осуществляется методами корреляционного анализа.

При линейной регрессии от одного параметра для произвольного фиксированного значения x может быть получено несколько значений y.

Рис. 2.1. Корреляционное поле зависимости y = f (x) Для линейной зависимости линия регрессии задается уравнением прямой:

неизвестные коэффициенты которой определяются по методу наименьших квадратов. В соответствии с этим методом квадрат расстояния по вертикали между опытными точками с координатами xi, yi и соответствующими точками на линии регрессии должно быть минимальным:

Из уравнений для определения неизвестных коэффициентов k, b :

откуда С учетом обозначений следует Таким образом, уравнение линейной регрессии принимает вид:

1. Построить для своего номера задания линейную зависимость регрессии по семи экспериментальным точкам, заданным в табл. 2.1., результаты промежуточных расчетов представить в форме табл. 2.2.

задания 2. Построить график y =f (x), на котором представить экспериментальные точки и линию линейной регрессии. Оценить максимальную относительную погрешность отклонения экспериментальной точки от линии регрессии.

1. Что такое корреляционное поле, линии регрессии?

2. Метод наименьших квадратов для получения уравнения линейной регрессии.

3. Коэффициент корреляции, его смысл.

Метод прогонки решения сеточных уравнений Цель работы: ознакомиться с прямым методом решения сеточных уравнений на компьютере.

Приборы и принадлежности: компьютер.

Метод прогонки является модификацией метода исключения Гаусса. В соответствии с этим методом решение для системы линейных алгебраических уравнений ищется в виде линейной функции неизвестные коэффициенты которой определяются из соотношений:

Формулы (3.1–3.3) дают процедуру решения. Сначала при i = 2, 3. N считаются прогоночные коэффициенты (3.3), при этом начальные значения прогоночных коэффициентов 2, z определяются из граничных условий на левой границе (i = 1). Эта операция называется прямой прогонкой. После определения всех i, zi в обратном направлении (i = N, N1. 2) с учетом значения параметра TN +1, найденных из граничного условия на правой границе (i = N + 1), по формуле (3.2) последовательно находятся неизвестные значения Ti в узловых точках сетки.

При решении задачи стационарной теплопроводности плоского слоя на поверхностях задаются граничные условия конвективного теплообмена:

где – коэффициент теплопроводности; – коэффициент теплоотдачи; Тп, Тс – соответственно температуры поверхности и окружающей среды; знаки (+) и (–) соответственно для левой (i = 0) и правой (i = N) границ; N – число разбиений сетки по толщине плоского слоя. Тогда начальные значения прогоночных коэффициентов принимают вид:

Значение температуры на правой границе;

Алгоритм метода прогонки:

Пример Паскаль-программы, реализующей решение стационарного уравнения теплопроводности методом прогонки.

var T: array [0..n] of real;

beta,zeta : array [1..n] of real;

beta[1]:= lah/(1. + lah);

zeta[i+1]:= (ff-aa*zeta[i])/(aa*beta[i] + bb);

T[n]:= (lah*zeta[n] + T2)/(1. + lah*(1-beta[n]));

В качестве теста для проверки программы предлагается задача стационарной теплопроводности плоского слоя толщиной, на поверхностях которого x = 0 и x = поддерживаются температуры соответственно Тл и Тп, т.е. заданы граничные условия первого рода ( = ). Математическая формулировка краевой задачи теплопроводности имеет вид Решением ее является линейное распределение температуры:

Точное значение температуры в центре слоя T ( x = 2 ) = = (Tл + Tп ) 2.

Решение задачи на регулярной сетке дает систему уравнений с граничными условиями:

В этом случае при численном решении на регулярной сетке с четным числом разбиений N точное значение температуры в центре слоя TN 2 +1 = (Т л + Т п ) 2, а приближенное значение отличается от точного из-за ошибок округления при вычислении прогоночных коэффициентов.

Алгоритм прогонки (3.7) реализуется для этой системы при N = 4, Тл = 100, Тп = 200, A = C = 1, B = 2 следующим образом:

T3 = 4T4 + z4 = 200 + 25 = 175 ;

Ввести в программу исходные данные: Тл = 0 и Тп в соответствии с табл. 3. № задания 1 2 3 4 5 6 7 8 9 10 11 12 13 2. Проверить работоспособность алгоритма метода прогонки, т.е. просчитать «вручную» температуры в узловых точках сетки при N = 4.

3. Определить относительную погрешность в центральной точке слоя численного ТN/2+1 и аналитического T ( x = 2 ) = 4. Провести вычислительный эксперимент на сгущающейся сетке, построить график зависимости R(N) и определить, при каких числах разбиений N погрешность округления R вычисления прогоночных коэффициентов начинает превышать 5 %.

5. Внести коррективы в программу, предусмотрев в ней расчет прогоночных коэффициентов (3.3) с двойной точностью. Провести вычислительный эксперимент на сгущающейся сетке, построить график зависимости R(N) и убедиться на графике в эффективности этой коррективы.

1. Конечно-разностное представление первой и второй производных.

2. Явная и неявная схемы аппроксимации уравнения теплопроводности.

3. Оценка ошибок аппроксимации уравнения теплопроводности.

4. Соотношение между временным и пространственным шагами сетки, обеспечивающее минимальную ошибку аппроксимации уравнения теплопроводности.

5. Векторно-матричное представление сеточных уравнений.

6. Метод прогонки решения матричных уравнений и его реализация на компьютере.

7. Запись основных операторов программирования на языке Паскаль.

Цель работы: ознакомиться с итерационным методом решения сеточных уравнений на компьютере.

Приборы и принадлежности: компьютер.

Итерационные методы дают решение сеточных уравнений в виде предела последовательности однообразных итераций.

Решение системы линейных алгебраических уравнений в соответствии с итерационным методом последовательных смещений (методом Зейделя) определяется по итерационной процедуре:

где q – номер итерации. Расчет по формуле (4.2) продолжается до тех пор, пока искомое решение не будет удовлетворять требуемой наперед заданной точности :

Недостатком метода Зейделя является медленная сходимость, поэтому для ускорения сходимости метод последовательной линейной верхней релаксации:

где – параметр релаксации. При = 1 итерационные процедуры (4.2) и (4.4) совпадают. Введение параметра верхней релаксации 1 2 позволяет ускорить сходимость итерационного процесса (4.4), причем наибольшая скорость сходимости имеет место при оптимальном значении параметра релаксации = опт. Последнее зависит от порядка системы и может быть вычислено в области с регулярной сеткой с числом разбиений N по формуле:

где – требуемая точность.

Решением ее является линейное распределение температуры:

Решение задачи на регулярной сетке дает систему уравнений с граничными условиями:

В табл. 4.1 представлена реализация итерационного алгоритма при N = 4, Тл = 200, Тп = 100, A = C = 1, B = 2, = 1 для первых пяти итераций.

Значения переменных при решении задачи решение Относительная ошибка в точке i = 2: 1 T1( 4) T1( 5) = 162,5 168,75 = 0,037, что составляет 3,7 %, это далеко от требуемой точности, которую выбирают в пределах = 103. 104, поэтому итерационный процесс необходимо продолжить.

Пример Паскаль-программы, реализующей метод последовательной линейной верхней релаксации.

var T,Tx: array [0..n] of real;

if abs(1-T[i]/Tx[i]) delta then delta:=abs(1-T[i]/Tx[i]);

until (delta epsilon) or (iter 100);

1. Ввести в программу исходные данные: Тл = 0 и Тп в соответствии с табл. 4. № задания 1 2 3 4 5 6 7 8 9 10 11 12 13 2. Проверить работоспособность алгоритма метода последовательной линейной верхней релаксации, т.е. просчитать «вручную» температуры в узловых точках сетки при N = 4 на первых пяти итерациях.

3. Определить относительную погрешность в центральной точке слоя численного ТN/2+1 и аналитического T ( x = 2 ) = 4. Провести вычислительный эксперимент на сгущающейся сетке при фиксированной погрешности = 10–3, построить график зависимости R(N).

5. При фиксированной сетке (N) и наперед заданной погрешности () провести расчеты с варьированием параметра релаксации в интервале 1 2, построить график зависимости q().

1. Оценка ошибок аппроксимации уравнения теплопроводности.

2. Соотношение между временным и пространственным шагами сетки, обеспечивающее минимальную ошибку аппроксимации уравнения теплопроводности.

3. Векторно-матричное представление сеточных уравнений.

4. Метод последовательной линейной верхней релаксации и его реализация на компьютере.

5. Запись основных операторов программирования на языке Паскаль.

Расчет времени охлаждения плоского слоя Цель работы: ознакомиться с численным методом решения задач нестационарной теплопроводности.

Приборы и принадлежности: компьютер.

При охлаждения плоского слоя толщиной 2 рассматривается половина слоя толщиной с адиабатной левой и охлаждаемой правой поверхностями. Математическая формулировка краевой задачи нестационарной теплопроводности имеет вид:

где Т – температура; – время; а – коэффициент температуропроводности; – коэффициент теплопроводности; – коэффициент теплоотдачи; Тп, Тс – температуры поверхности и окружающей среды.

В частном случае, в соответствии с методом регулярного теплового режима пренебрегают внутренним тепловым сопротивлением по сравнению с внешним. Решение задачи (5.1–5.2) принимает вид где = Т – Тс – избыточная температура; Bi =, Fo = = a 2 – числа Био и Фурье. На практике решение (5.3) используется уже при Bi 0,1.

Для численного решения задачи на расчетную область наносится регулярная сетка с координатами узлов:

где N – число разбиений по толщине слоя ; hx, h – соответственно шаги пространственной (по x) и временной (по ) сеток;

i, k – номера узловых точек в направлении координат x,.

Уравнение теплопроводности (5.1) может быть представлено в дискретном виде по явной схеме, в соответствии с которой вторая производная по координате записывается на текущем k-м временном слое с известным распределением температуры (рис. 5.1). В результате из аппроксимации уравнения (5.1) получается явная формула для температуры:

вычисления по которой устойчивы при следующем ограничении на шаг сетки по времени.

При неявной схеме вторая производная по координате записывается на «новом» k-м временном (рис. 5.2):

В результате получаем систему уравнений (N–1)-го порядка:

Схема абсолютно устойчива при больших, чем в ограничении (5.7), шагах по времени, однако с увеличением шага по времени возрастают ошибки аппроксимации.

С применением формулы односторонней разности записывается граничное условие (5.2) при x = :

из которого определяется температура на поверхности тела:

а также граничное условие при x = Алгоритм решения задачи по явной схеме представлен на рис. 5.3.

Рис. 5.3. Алгоритм решения задачи теплопроводности по явной схеме Пример Паскаль-программы, реализующей расчет времени охлаждения плоского слоя по явной схеме.

var T,TT: array [0..n] of real;

for i:=0 to n do T[i]:= Tstart;

until delta = epsilon;

<3. Вывод результата>writeln(‘Время установления стационара:’,tau);

writeln(‘Распределение температуры по слою’);

Алгоритм решения задачи по неявной схеме представлен на рис. 5.4.

Пример Паскаль-программы, реализующей расчет времени охлаждения плоского слоя по неявной схеме.

var T,TT: array [0..n] of real;

beta,zeta : array [1..n] of real;

delta, tau, htau : real;

for i:=0 to n do TT[i]:= Tstart;

bb := 1 + 2*a*htau/sqr(hx);

T[n]:= (lah*zeta[n] + Tc2)/(1. + lah*(1beta[n]));

until delta = epsilon;

writeln(‘Время установления стационара:’,tau);

writeln(‘Распределение температуры по слою’);

Рис. 5.4. Алгоритм решения задачи теплопроводности по неявной схеме 1. Составить Паскаль-программу расчета времени охлаждения плоского слоя по явной и неявной схемам.

2. Ввести в программу исходные данные: полутолщину слоя = 2 см; температуру окружающей среды Тс = 0 оС, теплофизические свойства стали: коэффициент теплопроводности = 50 Вт/(м·К), коэффициент температуропроводности а = 1,4·10–5 м2/c, коэффициент теплоотдачи и начальную температуру слоя в соответствии с табл. 5. ·10–1 Вт/(м2·К) 20 21 22 23 24 25 26 27 28 29 30 31 32 3. Определить по методу регулярного теплового режима время охлаждения слоя (к) до температуры, отличающейся от температуры окружающей среды на 1 %. Построить график зависимости Т() (аналитическое решение).

4. Провести вычислительный эксперимент по явной схеме на сгущающейся пространственной сетке (шаг временной сетки выбирать равным h = 0,9 hx2 ( 2a ) ) и определить число разбиений N построением на графике зависимостей Т(0,) при различных числах N. Сравнить времена охлаждения, полученные аналитическим и численным методами на различных сетках. Построить (при выбранном N) график зависимости Т(x) для четырех-пяти моментов времени в интервале 0 к.

5. Вычислительным экспериментом при выбранном числе N провести сравнительный анализ эффективности явной и неявной схем (в неявной схеме шаг временной сетки увеличивать по сравнению с шагом в п. 4). Сравнение провести по времени счета одного варианта, обеспечивающего примерно одинаковую погрешность, оцениваемую по графику зависимости Т(0,).

1. Конечно-разностное представление первой и второй производных.

2. Явная и неявная схемы аппроксимации уравнения теплопроводности.

3. Оценка ошибок аппроксимации уравнения теплопроводности.

5. Аппроксимация граничных условий теплообмена по формулам первого и второго порядков точности.

6. Векторно-матричное представление сеточных уравнений.

7. Запись основных операторов программирования на языке Паскаль.

Цель работы: ознакомиться с численным методом решения двумерных задач нестационарной теплопроводности.

Приборы и принадлежности: компьютер.

Охлаждение бруса квадратного сечения (блюмса) размерами 2·2 симметрично относительно осей координат, выбранных в центре бруса. Поэтому рассматривается четверть сечения бруса с охлаждаемой поверхностью и адиабатными осями симметрии (рис. 6.1).

Математическая формулировка краевой задачи нестационарной теплопроводности в этом слу- Рис. 6.1. Разбиение расчетной области чае имеет вид:

В частном случае, в соответствии с методом регулярного теплового режима пренебрегают внутренним тепловым сопротивлением по сравнению с внешним. Решение задачи (6.1–6.2) принимает вид:

где = Т – Тс – избыточная температура; Bi =, Fo = = a 2 – числа Био и Фурье. На практике решение (6.3) используется уже при Bi 0,1.

Для численного решения задачи на расчетную область наносится регулярная сетка с координатами узлов:

где N, М – числа разбиений расчетной области соответственно в направлении координат x, y; hx, hy, h – соответственно шаги пространственной (по x, y) и временной (по ) сеток; i, j, k – номера узловых точек в направлении координат x, y,.

Уравнение теплопроводности (6.1) может быть представлено в дискретном виде по явной схеме, в соответствии с которой вторая производная по координатам записывается на текущем kм временном слое с известным распределением температуры (рис. 6.2). В результате аппроксимации уравнения (6.1) получается явная формула для температуры:

вычисления по которой устойчивы при следующем ограничении на шаг сетки по времени:

С применением формул односторонней разности записываются граничные условия (2) на поверхностях блюмса:

из которых определяется температура на поверхностях блюмса:

а также граничные условия на осях симметрии 0,М; N,0; N,M) в расчетах не участвуют. Для вычисления температур в угловых точках применяют аппроксимацию стационарного уравнения теплопроводности (1). Например, для Рис. 6.3. Фрагмент разбиения из которого в частном случае при hx = hy получаем формулу аппроксимации:

Аналогично для других угловых точек Для вывода на экран (печать) массива поля температур Тi, j в плоскости 0xy в виде изотерм можно воспользоваться алгоритмом перевода цифрового массива в символьный. Для этого интервал температур T = T0 Tc делится на n подинтервалов, в каждом из которых записываются цифровые символы, разделенные символами пробелов (рис. 6.4). Правые границы интервалов определяются по формуле:

где Тl – значение температуры на правой границе l-го подинтервала.

Рис. 6.4. Представление температурного поля в символьном виде Алгоритм решения задачи по явной схеме представлен на рис. 6.5.

Рис. 6.5. Алгоритм решения нестационарной задачи 1. Составить Паскаль-программу расчета времени охлаждения блюмса. Блок-схема программы приведена на рис. 6.5.

Ниже приведён пример Паскаль-программы, реализующей расчет времени охлаждения блюмса по явной схеме.

var T,TT : array [0..n,0..m] of real;

for i:=0 to n do for j:=0 to m do T[i,j]:= Tstart;

writeln(‘Время установления стационара:’, writeln(‘Распределение температуры по слою’);

2. Ввести в программу исходные данные: полутолщину блюмса = 10 см; температуру окружающей среды Тс = 0 оС, теплофизические свойства стали: коэффициент теплопроводности = 50 Вт/(м·К), коэффициент температуропроводности а = 1,4·10–5 м2/c, коэффициент теплоотдачи и начальную температуру слоя в соответствии с табл. 6. ·10–1 Вт/(м2·К) 20 21 22 23 24 25 26 27 28 29 30 31 32 3. Определить по методу регулярного теплового режима время охлаждения блюмса (к) до температуры, отличающейся от температуры окружающей среды на 1 %. Построить график зависимости Т() (аналитическое решение).

4. Провести вычислительный эксперимент на сгущающейся пространственной сетке (принять N = M, в этих условиях hx = hy = h, шаг временной сетки выбирать равным h = 0,9 h 2 ( 4a ) ) и определить необходимое число разбиений сетки построением на графике зависимостей Т(0, 0, ) при различных числах разбиений. Сравнить времена охлаждения, полученные аналитическим и численным методами на различных сетках. Используя символьный метод вывода температурного поля, построить изотермы для трех-четырех моментов времени в интервале 0 к, при выбранном числе разбиений расчетной области.

1. Конечно-разностное представление первой и второй производных.

2. Явная и неявная схемы аппроксимации уравнения теплопроводности.

3. Оценка ошибок аппроксимации уравнения теплопроводности.

5. Аппроксимация граничных условий теплообмена по формулам первого и второго порядков точности.

6. Векторно-матричное представление сеточных уравнений.

7. Запись основных операторов программирования на языке Паскаль.

непрерывного плоского слитка (сляба) Цель работы: ознакомиться с численным методом решения одномерных задач затвердевания слитков.

Приборы и принадлежности: компьютер.

Непрерывный плоский слиток (сляб) толщиной 2 вытягивается из неподвижного кристаллизатора с постоянной скоростью u (рис. 7.1). При охлаждении на поверхностях сляба из жидкой фазы формируется корка затвердевшего металла толщиной. На глубине lк или в момент времени к = lк/u формирование сляба завершается. Математическая формулировка задачи включает дифференциальное уравнение переноса энергии которое в стационарном случае ( T = = 0 ) принимает вид:

а с учетом кинематического соотношения (u = y/) T ( y u ) = = T имеем квазистационарное уравнение переноса энергии где aэфф = ( cэфф ) – эффективная температуропроводность;, – коэффициент теплопроводности и плотность; эффективная теплоемкость скачком возрастает в интервале температур ликвидуса (Tлик) и солидуса (Тсол) двухфазной зоны и учитывает выделение скрытой теплоты затвердевания (L) Начальная температура расплава в кристаллизаторе граничные условия для расчетной области (0 x ) имеют вид:

где Т – перегрев расплава над температурой ликвидуса; Тп – температура поверхности слитка.

В частном случае, когда температура по толщине корки сляба изменяется по линейному закону, решение краевой задачи (7.3–7.5) принимает вид:

где Тзат – температура затвердевания, которая находится в интервале температур ликвидуса и солидуса и которая может быть вычислена по формуле Тзат = (Тлик + Тсол) / 2.

Для численного решения задачи на расчетную область наносится регулярная сетка с координатами узлов:

i, k – номера узловых точек в направлении координат x,.

Уравнение переноса энергии (7.3) может быть представлено в дискретном виде по явной схеме, в соответствии с которой вторая производная по координате записывается на «старом»

k-м временном слое с известным распределением температуры (рис. 7.2). В результате из аппроксимации уравнения (7.3):

получается явная формула для явной схемы 1-го порядка точности температуры:

вычисления по которой устойчивы при следующем ограничении на шаг сетки по времени:

С применением формулы односторонней разности записывается граничное условие на оси симметрии:

Текущая толщина твердой фазы может быть получена по формуле линейной интерполяции:

Алгоритм решения задачи представлен на рис. 7. Рис. 7.3. Алгоритм решения задачи затвердевания сляба 1. Составить Паскаль-программу расчета затвердевания сляба. Блок-схема программы приведена на рис. 7.3. Ниже приведён пример Паскаль-программы, реализующей расчет времени охлаждения блюмса по явной схеме.

2. Ввести в программу исходные данные: полутолщину сляба = 10 см; температуру окружающей среды Тс = 0 оС, температуры ликвидуса Тлик = 1500 оС, солидуса Тсол = 1430 оС, перегрев расплава Т = 10 оС, теплофизические свойства стали: коэффициент теплопроводности = 50 Вт/(м·К), коэффициент температуропроводности а = 1,4·10–5 м2/c, плотность = 7900 кг/м3;

скрытую теплоту затвердевания L = 270 кДж/кг, температуру поверхности сляба в соответствии с табл. 7. program Example_7;

var T,TT,ae : array [0..n] of real;

writeln(‘Время установления стационара:’, writeln(‘Распределение температуры по слою’);

for i:=0 to n do write(T[i]:8:2);

№ задания 1 2 3 4 5 6 7 8 9 10 11 12 13 Тп·10–1 оС 70 72 74 76 78 80 82 84 86 88 90 92 94 3. Определить по формуле (7.6) время окончания затвердевания сляба (к) до. Построить график зависимости () (аналитическое решение).

4. Провести вычислительный эксперимент на сгущающейся пространственной сетке (шаг временной сетки выбирать равным h = 0,9 hx2 ( 2amax ) ) и сравнить полученные решения на графике зависимости (). Сравнить на этом же графике численные решения с аналитическим.

1. Конечно-разностное представление первой и второй производных.

2. Явная и неявная схемы аппроксимации уравнения теплопроводности.

3. Оценка ошибок аппроксимации уравнения теплопроводности.

5. Аппроксимация граничных условий теплообмена по формулам первого и второго порядков точности.

6. Векторно-матричное представление сеточных уравнений.

7. Запись основных операторов программирования на языке Паскаль.

непрерывного слитка квадратного сечения (блюмса) Цель работы: ознакомиться с численным методом решения двумерных задач нестационарной теплопроводности.

Приборы и принадлежности: компьютер.

времени к = lк/u формирование блюмcа завершается. Математическая формулировка задачи по методу сквозного счета включает дифференциальное формирования блюмса а с учетом кинематического соотношения (u = z/) T ( z u ) = = T имеем квазистационарное уравнение переноса энергии:

где aэфф = ( cэфф ) – эффективная температуропроводность;, – коэффициент теплопроводности и плотность; эффективная теплоемкость скачком возрастает в интервале температур ликвидуса (Tлик) и солидуса (Тсол) двухфазной зоны и учитывает выделение скрытой теплоты затвердевания (L) Начальная температура расплава в кристаллизаторе граничные условия для расчетной области (0 x, 0 y ) имеют вид:

где Т – перегрев расплава над температурой ликвидуса; Тп – температура поверхности слитка.

В частном случае, когда температура по толщине корки сляба изменяется по линейному закону, решение краевой задачи (8.3–8.5) принимает вид:

Для численного решения задачи на расчетную область наносится регулярная сетка с координатами узлов:

Рис. 8.2. Расчетная область с указананием положения получается явная формула для температуры:

вычисления по которой устойчивы при следующем ограничении на шаг сетки по времени:

С применением формул односторонней разности записываются граничные условия (8.5) на поверхностях блюмса:

а также граничные условия на осях симметрии:

T0, j = T1, j, Ti,0 = Ti,1, i = 1, 2. N 1; j = 1, 2. M 1. (8.12) Угловые точки области (0, 0; 0, М; N, 0; N, M) в расчетах не участвуют. Для вычисления температур в угловых точках применяют аппроксимацию стационарного уравнения переноса энергии (8.3).

Например, для угловой точки (N, M) (рис. 8.3) это уравнение мает вид:

из которого в частном случае при hx = hy получаем формулу аппроксимации:

Аналогично для других угловых точек:

T0,0 = T1,0 + T0,1 (T2,0 + T0,2 ) 2; T0, M = T0, M 1 ; TN,0 = TN 1,0. (8.14) Для вывода на экран (печать) массива поля температур Тi, j в плоскости 0xy в виде изотерм можно воспользоваться алгоритмом перевода цифрового массива в символьный. Для этого интервал температур T = Tсол Tп делится на n подинтервалов, в каждом из которых записываются цифровые символы, разделенные символами пробелов (рис. 8.4). Правые границы интервалов определяются по формуле Tl = Tп + T l n, l = 1, 2. n, где Тl – значение температуры на правой границе l-го подынтервала. Для интервала температур фазового перехода (Тлик–Тсол) рекомендуется применять буквенный символ «Ф», а для температур перегрева – символ пробела.

Рис. 8.4. Представление температурного поля в символьном виде Алгоритм решения задачи по явной схеме представлен на рис. 8.5.

1. Составить Паскаль-программу расчета затвердевания сляба. Блок-схема программы приведена на рис. 8.5. Ниже приведён пример Паскаль-программы, реализующей расчет времени охлаждения блюмса по явной схеме.

var T,TT,ae : array [0..n,0..m] of double;

Tstart,Tc1,Tc2,alpha1,alpha,a,lambda,rho,cp,L,af,TS,TL, delta,tau,htau,ahtx,ahty,htx,hty,lahx,lahy,tau1 : double;

var mode,driver : smallint;

Рис. 8.5. Алгоритм решения задачи затвердевания блюмса procedure gColorField;

for i:=0 to n do for j:=0 to m do T[i,j]:= Tstart;

until delta = epsilon;

writeln(‘Время установления стационара:’, writeln(‘Распределение температуры по слою’);

2. Ввести в программу исходные данные: полутолщину блюмса = 10 см, температуры ликвидуса Тлик = 1500 оС, солидуса Тсол = 1430 оС, перегрев расплава Т = 10 оС, теплофизические свойства стали: коэффициент теплопроводности = 50 Вт/(м·К), коэффициент температуропроводности а = 1,4·10–5 м2/c, скрытую теплоту затвердевания L = 270 кДж/кг, температуру поверхности блюмса в соответствии с табл. 8. 3. Определить по формуле (8.6) время окончания затвердевания блюмса (к).

№ задания 1 2 3 4 5 6 7 8 9 10 11 12 13 Тп·10–1 оС 70 72 74 76 78 80 82 84 86 88 90 92 94 4. Провести вычислительный эксперимент на сгущающейся пространственной сетке при N = M (шаг временной сетки выбирать равным h = 0,9 hx2 ( 4amax ) ) и сравнить полученные решения на графике зависимости к(N). Построить (при выбранном числе разбиений расчетной области) изотермы для трех – четырех моментов времени в интервале 0 к.

1. Конечно-разностное представление первой и второй производных.

2. Явная и неявная схемы аппроксимации уравнения теплопроводности.

3. Соотношение между временным и пространственным шагами сетки, обеспечивающее минимальную ошибку аппроксимации уравнения теплопроводности.

4. Чем объясняется рост корки слитка по закону квадратного корня?

5. Запись основных операторов программирования на языке Паскаль.

ЧАСТЬ III

МАТЕРИАЛЫ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ

для самостоятельного изучения курса Методика изучения дисциплины «Моделирование процессов и объектов в металлургии» на заочном отделении существенно отличается от методик для дневной формы обучения. Так, если на дневном отделении основной формой обучения являются лекции, практические и лабораторные занятия, где преподаватель излагает программный материал, решает со студентами задачи, проводит лабораторные занятия, проверяет знания студентов, то учебный процесс на заочном отделении связан с углубленной самостоятельной работой и предусматривает:

1) изучение материала программы по учебникам или учебным пособиям;

2) самостоятельное решение задач;

3) выполнение контрольных работ;

4) выполнение лабораторных работ;

5) сдачу зачета и экзаменов.

Для успешного овладения материалом и сдачи экзаменов по физике необходимо руководствоваться несколькими правилами.

1. Следует изучать курс систематически в течение всего учебного года. Попытка изучить предмет в сжатые сроки перед экзаменом не даст глубоких, прочных знаний и приведет к неудаче.

2. Выбрав какое-либо учебное пособие в качестве основного для определенной части курса, придерживайтесь данного пособия при изучении всей части или, по крайней мере, ее целого раздела. Замена одного пособия другим в процессе изучения может привести к утрате логической связи между отдельными вопросами. Но если выбранное пособие не дает полного или ясного ответа на некоторые вопросы программы, необходимо обращаться к другим учебным пособиям.

3. При чтении учебного пособия составляйте конспект, в котором записывайте законы и формулы, выражающие эти законы, определения физических величин и их единиц, делайте чертежи и решайте типовые задачи. При решении задач следует пользоваться Международной системой единиц (СИ).

4. Самостоятельную работу над курсом необходимо подвергать систематическому контролю. Для этого после изучения очередного раздела следует ставить вопросы и отвечать на них.

При этом надо использовать рабочую программу курса.

5. Очень полезно прослушать установочный курс лекций, организуемых для студентов-заочников, а также пользоваться очными консультациями преподавателей.

2. Методические указания к решению задач Решение задач по моделированию процессов и объектов в металлургии способствует более глубокому пониманию изучаемого материала и помогает закреплению в памяти понятий, формулировок, определений, формул и физических законов, развивает у студентов логическое мышление, навык в применении полученных знаний для решения конкретных вопросов, имеющих практическое и познавательное значение. Поэтому в пособии приводится список тренировочных задач, работа над которыми закрепит знания и навыки студентов.

Задачи по дисциплине разнообразны, и дать единый «рецепт» для их решения невозможно. Умение решать задачи приобретается в процессе систематических упражнений. Можно лишь указать условия, соблюдение которых необходимо для успешного решения задач.

В основу каждой задачи положен тот или иной частный случай проявления общих законов моделирования. Поэтому без твердого знания теории нельзя рассчитывать на успешное решение и анализ даже самых простых задач.

При решении задач необходимо:

1. Хорошо вникнуть в условие задачи и установить, какие физические закономерности лежат в ее основе.

2. Записать все данные в задаче физические величины в одной системе единиц (в системе единиц СИ).

3. Если позволяет характер задачи, обязательно сделать схематический чертеж (эскиз), поясняющий ее сущность.

4. Записать законы и формулы, на которых базируется решение, и дать словесную формулировку этих законов, разъяснить буквенные обозначения.

5. Если при решении задачи применяется формула, полученная для частного случая, не выражающая какой-нибудь физический закон или не являющаяся определением какойнибудь физической величины, то ее следует вывести.

6. Получить решение задачи в общем виде, т.е. выразить искомую величину в буквенных обозначениях величин, заданных в условии задачи. Правильность решения задачи в общем виде можно проверить, используя правило размерностей (наименований). При правильном решении размерность правой части формулы совпадает с размерностью искомой величины.

Несоблюдение этого условия (оно необходимо, но недостаточно) свидетельствует об ошибке, допущенной в ходе решения.

7. Решение задачи следует сопровождать краткими, но исчерпывающими пояснениями.

8. Подставить числовые данные в полученные для искомых величин формулы, произвести с ними необходимые действия.

Проанализировать результат (оценить его правдоподобность).

9. Проводя арифметические расчеты, нужно использовать правила приближенных вычислений, позволяющие экономить время без ущерба для точности. Точность ответа не должна превышать точности, с которой даны исходные величины.

В тех задачах, где требуется начертить график, следует рационально выбрать масштаб и начало координат.

Умение решать задачи приобретается длительными и систематическими упражнениями. При подготовке к выполнению контрольной работы следует после изучения каждой темы решить тренировочные задачи. Они содержат элементы задач, предлагаемых для контрольных работ.

Задачи для тренировки призваны подготовить студента к выполнению контрольной работы. Решение этих задач крайне полезно и необходимо.

При оформлении контрольных работ нужно помнить следующее:

1. Контрольная работа включает 15 задач с десятью вариантами исходных данных к каждой задаче. Номер варианта определяется последней цифрой номера зачетной книжки.

2. Контрольные работы для проверки оформляются в тонкой ученической тетради синими или черными чернилами.

3. Текст задачи из контрольного задания должен быть переписан полностью и выписаны столбиком значения величин с их стандартными обозначениями и размерностями. Размерности указываются в СИ.

4. При решении задач необходимо придерживаться правил, приведенных выше.

Числовые значения величин, с которыми приходится иметь дело при решении задач, являются большей частью приближенными. Прежде чем вести разговор о правилах приближенных вычислений дадим определение значащей цифры числа. Значащими цифрами числа называются все его цифры, кроме нулей, стоящих левее первой, отличной от нуля цифры, а также кроме нулей, стоящих в конце числа взамен неизвестных или отброшенных цифр. Нуль в конце числа может быть значащим, если он является представителем сохраненного десятичного разряда.

Такими величинами являются, в частности, многие константы, приводимые в справочниках. Например: ускорение свободного падения g = 9,81 м/с2, число пи = 3,14 и т.п. При более точном вычислении или измерении числовые значения этих величин будут содержать большее число значащих цифр g = 9,80655 м/с2, = 3,1416. Однако и эти значения, в свою очередь, являются приближенными или в силу недостаточной точности измерения, или в силу того, что получены путем округления еще более точных значений.

Часто неопытные лица при вычислениях добиваются такой точности результатов, которая не оправдывается точностью исходных данных. Это приводит к бесполезной затрате труда и времени.

Рассмотрим следующий пример. Пусть требуется определить плотность вещества некоторого тела. При взвешивании тела на весах с точностью до 0,01 г определили массу тела:

Затем с точностью до 0,01 см3 был измерен объем тела:

Без критического подхода к вычислениям можно получить такой результат:

Но числа 9,38 и 3,46 – приближенные. Последние цифры в этих числах сомнительные. Эти числа при измерении могли быть получены такими: первое – 9,39 или 9,37, второе – 3, или 3,47. В самом деле, при взвешивании с указанной выше точностью могла быть допущена ошибка на 0,01 как в сторону увеличения массы, так и в сторону ее уменьшения. То же самое и в отношении объема. Таким образом, плотность тела, если ее вычислять с точностью до пятого десятичного знака, как это сделано выше, могла оказаться:

= 9,39/3,45 = 2,7214 г/см3 или = 9,37/3,47 = 2,70029 г/см3.

Сравнение всех трех результатов показывает, что они отличаются уже вторыми десятичными знаками и что достоверным является лишь первый десятичный знак, а второй – сомнительным. Цифры, выражающие остальные десятичные знаки, совершенно случайны и способны лишь ввести в заблуждение пользователя вычисленными результатами. Следовательно, работа по вычислению большинства знаков затрачена впустую. Во избежание бесполезных затрат труда и времени принято вычислять кроме достоверных знаков еще только один сомнительный. В рассмотренном примере надо было вести вычисление до второго десятичного знака:

Приближенные вычисления следует вести с соблюдением следующих правил.

1. При сложении и вычитании приближенных чисел окончательный результат округляют так, чтобы он не имел значащих цифр в тех разрядах, которые отсутствуют хотя бы в одном из слагаемых. Например, при сложении чисел 4,462 + 2,38 + + 1,17273 + 1,0262 = 9,04093 следует сумму округлить до сотых долей, т.е. принять ее равной 9,04, так как слагаемое 2,38 задано с точностью до сотых долей.

2. При умножении следует округлить сомножители так, чтобы каждый из них содержал столько значащих цифр, сколько их имеет сомножитель с наименьшим числом таких цифр.

Например, вместо вычисления выражения 3,723 2,4 5, следует вычислять выражение 3,7 2,4 5,2. В окончательном результате следует оставлять такое же количество значащих цифр, какое имеется в сомножителях после их округления.

В промежуточных результатах следует сохранять на одну значащую цифру больше. Такое же правило следует соблюдать и при делении приближенных чисел.

3. При возведении в квадрат или куб следует в степени брать столько значащих цифр, сколько их имеется в основании степени. Например, 1,322 1,74.

4. При извлечении квадратного или кубического корня в результате следует брать столько значащих цифр, сколько их в подкоренном выражении. Например, 1,17 1,08.

При вычислении сложных выражений следует применять указанные правила в соответствии с видом производимых действий. Например, при вычислении дроби сомножитель 5,1 имеет наименьшее число значащих цифр – две. Поэтому результаты всех промежуточных вычислений должны округляться до трех значащих цифр:

После округления до двух значащих цифр получаем результат 3,810–3.

Задача 1. Найти математическое ожидание и моду случайной величины, заданной таблицей значений x и вероятностей р.

Задача 2. В табл. 1 представлены результаты выборочного взвешивания отливок (xi, кг, i = 1, 2, …, n). Было взвешено отливок, т.е. объем выборки n = 100. Требуется построить функции распределения F(x) и плотности вероятности f(x).

Решение. Экстремальные значения веса отливок xmin = 4,97;

xmax = 5,85; Число интервалов группирования s = log 2 n + 1 = = 7,62 8 ; ширина интервала группирования h = ( xmax xmin ) s = = ( 5,85 4,97 ) 8 = 0,11 ; левый (сj–1) и правый (сj) концы j-го интервала:

середины интервалов группирования x 0 = ( c j 1 + c j ) 2.

Подсчитываем число выборочных данных vj, попавших в каждый (j-й) интервал группирования (j=1, 2, …, s); подсчитываем количество выборочных данных, попавших в j-й интервал группирования h (v1+…+vjx); подсчитываем выборочную функцию распределения:

где ix – номер самого правого из интервалов группирования, правый конец которых не превосходит заданного значения x.

Посчитываем выборочную функцию плотности:

в которой k(x) – порядковый номер интервала группирования, накрывающего заданную точку x, а vk(x) – число выборочных данных, попавших в этот интервал. Результаты группировки сводим в табл. j–номер интервала cj–1xcj интервалов vj v1+…+vix вания Последние два столбца этой таблицы дают искомые функции.

Задача 3. На металлургическом заводе проведено контрольное определение твердости по Шору рабочего слоя большой партии однотипных листопрокатных валков. Установлено, что твердость (случайная величина x) распределена нормально с математическим ожиданием 60 ед. по Шору и средним квадратическим отклонением 5 ед. по Шору. Необходимо найти вероятность того, что значение твердости валков заключено в пределах 57…65 ед. Шора, оговоренных ГОСТом.

Решение. Используем формулу р < x1 x x2 >= Ф (t2) – – Ф (t1), в соответствии с которой указанная вероятность сводится к разности нормальных функций Лапласа. По условию задачи x1 = 57; x2 = 65; M x = 60; = 5, следовательно, По таблице функции Лапласа из приложения находим:

Ф(1,0) = 0,3413; Ф(0,6) = 0,2257. Отсюда искомая вероятность Задача 4. Построить линейную зависимость регрессии по семи экспериментальным точкам:

Решение. Для линейной зависимости y = y + k ( x x ) определяем:

Искомое уравнение регрессии:

Задача 1. Тонкая пластина длиной l0 = 2 м и шириной а = = 1,5 м обтекается продольным потоком воздуха. Скорость и температура набегающего потока равны соответственно w0 = = 3 м/c; t0 = 20 oC. Температура поверхности пластины tп = 90 oC.

Определить средний по длине пластины коэффициент теплоотдачи и количество теплоты, отдаваемой пластиной воздуху.

Решение. Для воздуха при t0 = 20 oC = 15,06·10–6 м2/c; = = 2,59·10–2 Вт/(м·К); Рr = 0,703. Число Рейнольдса следовательно, режим течения в пограничном слое ламинарный. В этих условиях средняя по длине теплоотдача может быть рассчитана по формуле:

где Nu = l0 ; Re = w0 l0, а физические свойства выбираются по температуре набегающего потока t0.

В рассматриваемом случае и коэффициент теплоотдачи Количество передаваемой теплоты с обеих сторон пластины Задача 2. Плоская пластина длиной l = 1 м обтекается продольным потоком воздуха. Скорость и температура набегающего потока воздуха w0 = 80 м/c; t0 = 10 oC. Перед пластиной установлена турбулизирующая решетка, вследствие чего движение в пограничном слое на всей длине пластины турбулентное.

Вычислить среднее значение коэффициента теплоотдачи с поверхности пластины и значение местного коэффициента теплоотдачи на задней кромке. Вычислить также толщину гидродинамического пограничного слоя на задней кромке пластины.

Решение. При температуре набегающего потока t0 = 10 oC физические свойства воздуха: = 14,16 · 10–6 м2/c; = 2, 10–2 Вт/(м·К). Число Рейнольдса следовательно, режим течения в пограничном слое турбулентный.

Среднее значение коэффициента теплоотдачи при обтекании пластины воздухом для турбулентного пограничного слоя можно вычислить по формуле:

и коэффициент теплоотдачи Для вычисления местного коэффициента теплоотдачи при обтекании пластины воздухом и турбулентном пограничном слое можно воспользоваться следующей формулой:

Значение местного коэффициента теплоотдачи на задней кромке пластины найдем, положив x = l0; тогда Re x = 5,65 106, Местную толщину турбулентного гидродинамического пограничного слоя можно вычислить по формуле Подставив значения известных величин, получаем при x = l Таким образом, средний коэффициент теплоотдачи = = 202 Вт/(м2·К). Значение местного коэффициента теплоотдачи при x = l0 x = l0 = 157,5 Вт/(м2·К); Толщина гидродинамического пограничного слоя при x = l0 т = 16,5 мм.

Задача 3. Вычислить средний коэффициент теплоотдачи при течении трансформаторного масла в трубе диаметром d = =8 мм и длиной l = 1 м, если средняя по длине трубы температура масла tж = 80 oC, средняя температура стенки трубы tс = = 20 oC и скорость масла w = 0,6 м/с.

Решение. Для определения режима течения масла вычисляем значение числа Рейнольдса. При tж = 80 oC кинематическая вязкость масла ж = 3,66·10–6 м2/c и число Так как Re ж 2300, режим течения ламинарный.

Для того чтобы установить, оказывает ли влияние на теплоотдачу естественная конвекция, нужно вычислить значение произведения (Gr·Pr)г, где в качестве определяющей температуры принимается В рассматриваемом случае tг = 0,5 ( 80 + 20 ) = 50 о С.

При этой температуре г = 7,58·10–6 м2/c; г=7,05·10–4 K–1; Prг = 111;

Так как ( Gr Pr )г 8 105, естественная конвекция не оказывает существенного влияния на теплоотдачу и режим течения масла – вязкостный.

Расчет средней теплоотдачи при вязкостном режиме течения жидкости в трубах при постоянной температуре стенки (tс = const) можно производить по следующей формуле где Индексы «с» и «г» означают, что физические свойства жидкости выбираются соответственно при температуре стенки tс и температуре tг = 0,5 ( tж + tс ) ; – поправка на участок гидродинамической стабилизации:

Эта поправка вводится, когда перед обогреваемым участком трубы нет участка гидродинамической стабилизации и Формула (1) справедлива при В рассматриваемом случае tж = 80 oC; tс = 20 oC и tг = 50 oC.

Физические свойства масла: ж = 844 кг/м3; µж = 30,8·104 Па·с;

г = 0,108 Вт/(м·К); срг = 1,846 кДж/(кг·K); µс = 198,2·10–4 Па·с.

Расход масла 0,05 и, следовательно, формула (1) применима.

Peг d Поправка на гидродинамический начальный участок Коэффициент теплоотдачи Задача 4. По трубам вертикального теплообменника снизу вверх течет вода. Внутренний диаметр труб d = 16 мм; их длина l = 1,2 м. Расход воды через одну трубу G = 58 кг/ч. Температура воды на входе в теплообменник tж1 = 30 оС.

Определить количество теплоты, передаваемой от стенки одной трубы к воде, и температуру воды на выходе, если температура стенок труб поддерживается равной 80 оС.

Решение. Секундный расход воды G = 58/3600 = 1, 10 кг/c. При tж1 = 30 оС µж1 = 801·10–6 Па·с и Режим течения ламинарный.

Далее необходимо вычислить произведение (Gr·Pr)г. Так как нам неизвестно значение температуры воды на выходе tж и, следовательно, нельзя найти ее среднюю температуру tж, то задачу решаем методом последовательных приближений.

Задаемся tж2 = 50 оС, тогда При этой температуре г = 0,478·10–6 м2/c; г = 5,11·10–4 K–1; Prг = 2,98;

Режим течения вязкостно-гравитационный.

При вязкостно-гравитационном режиме течения в вертикальных трубах и совпадении направлений вынужденной и свободной конвекций у стенки (охлаждение жидкости и течение сверху вниз или нагревание и течение снизу вверх) для расчета средней теплоотдачи можно воспользоваться следующей формулой:

где коэффициент теплоотдачи отнесен к начальной разности температур tc – tж1:

Индексы «с» и «г» означают, что соответствующие физические свойства выбираются по температуре стенки tс и температуре tг = 0,5 ( tж + tс ). Формула (1) справедлива при Reж 2300:

В рассматриваемом случае при tг = 60 oC аг = 1,6·10–7 м2/c;

при tс = 80 oC с = 0,635 Вт/(м·К); при tж = 40 oC ж = 992 кг/м3.

«Список книг для чтения (1 – 10 классы) 1 класс Литературное чтение Н. Носов Фантазеры. Живая шляпа. Дружок. И другие рассказы. В. Драгунский Он живой и светится. В. Бианки, Н. Сладков Рассказы о животных. Г.Х. Андерсен Принцесса на горошине. Стойкий оловянный солдатик. П. Бажов Серебряное копытце. В. Катаев Дудочка и кувшинчик. Цветик-семицветик. Русский язык И.Р. Калмыкова 50 игр с буквами и словами. В.В. Волина Занимательное азбуковедение. Н. Павлова Читаем после Азбуки с крупными буквами. »

«Научное обоснование развития сети особо охраняемых природных территорий в Республике Карелия Карельский научный центр Российской академии наук Научное обоснование развития сети особо охраняемых природных территорий в Республике Карелия Петрозаводск 2009 УДК 502.172 (470.22) ББК 20.18 (2Рос. Кар.) Н 34 Научное обоснование развития сети особо охраняемых природных территорий в Республике Карелия. Петрозаводск: Карельский научный центр РАН, 2009. 112 с.: ил. 14, табл. 6. Библиограф. 96 назв. ISBN. »

«RMC-M20 Уважаемый покупатель! Благодарим вас за то, что вы отдали предпочтение бытовой технике REDMOND. REDMOND — это качество, надежность и неизменно внимательное отношение к потребностям наших клиентов. Надеемся, что вам понравится продукция нашей компании, и вы также будете выбирать наши изделия в будущем. Мультиварка REDMOND RMC-M20 — современный многофункциональный прибор для приготовления пищи, в котором компактность, экономичность, простота и удобство использования гармонично сочетаются. »

«Международный консорциум Электронный университет Московский государственный университет экономики, статистики и информатики Евразийский открытый институт П.В. Бахарев Арбитражный процесс Учебно-практическое пособие Москва 2008 УДК – 347.9 ББК – 67.410 Б – 30 Бахарев П.В. АРБИТРАЖНЫЙ ПРОЦЕСС: Учебнометодический комплекс. – М.: Изд. центр ЕАОИ, 2008. – 327 с. ISBN 978-5-374-00077-1 © Бахарев П.В., 2007 © Евразийский открытый институт, 2007 2 Оглавление Предисловие Раздел 1. Структура арбитражных. »

«Федеральное государственное образовательное бюджетное учреждение высшего профессионального образования ПОВОЛЖСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ И ИНФОРМАТИКИ РУКОВОДЯЩИЙ РД ПГУТИ ДОКУМЕНТ 2.64.7-2013 Система управления качеством образования ПОРЯДОК ПЕРЕВОДА, ОТЧИСЛЕНИЯ И ВОССТАНОВЛЕНИЯ СТУДЕНТОВ В ПГУТИ Положение Самара 2013 РД ПГУТИ 2.64.7 – 2013 ПОРЯДОК ПЕРЕВОДА, ОТЧИСЛЕНИЯ И ВОССТАНОВЛЕНИЯ СТУДЕНТОВ В ПГУТИ Положение Предисловие 1 РАЗРАБОТАН Отделом качества образования ПГУТИ. »

«министерство образования российской федерации государственное образовательное учреждение московский государственный индустриальный университет информационно-вычислительный центр Информационные технологии и программирование Межвузовский сборник статей Выпуск 3 (8) Москва 2003 ББК 22.18 УДК 681.3 И74 Информационные технологии и программирование: Межвузов ский сборник статей. Вып. 3 (8) М.: МГИУ, 2003. 52 с. Редакционная коллегия: д.ф.-м.н. профессор В.А. Васенин, д.ф.-м.н. профессор А.А. Пярнпуу. »

«Зарегистрировано в Минюсте РФ 16 декабря 2009 г. N 15640 МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ ПРИКАЗ от 9 ноября 2009 г. N 553 ОБ УТВЕРЖДЕНИИ И ВВЕДЕНИИ В ДЕЙСТВИЕ ФЕДЕРАЛЬНОГО ГОСУДАРСТВЕННОГО ОБРАЗОВАТЕЛЬНОГО СТАНДАРТА ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ ПО НАПРАВЛЕНИЮ ПОДГОТОВКИ 230100 ИНФОРМАТИКА И ВЫЧИСЛИТЕЛЬНАЯ ТЕХНИКА (КВАЛИФИКАЦИЯ (СТЕПЕНЬ) БАКАЛАВР) (в ред. Приказов Минобрнауки РФ от 18.05.2011 N 1657, от 31.05.2011 N 1975) КонсультантПлюс: примечание. Постановление. »

«СРГ ПДООС ПРЕДЛАГАЕМАЯ СИСТЕМА СТАНДАРТОВ КАЧЕСТВА ПОВЕРХНОСТНЫХ ВОД ДЛЯ МОЛДОВЫ: Технический доклад (сокращенная версия, без приложений) Настоящий доклад подготовлен Полом Бяусом (Нидерланды) и Кармен Тоадер (Румыния) для Секретариата СРГ ПДООС/ОЭСР в рамках проекта Содействие сближению со стандартами качества воды ЕС в Молдове. Финансовую поддержку проекту оказывает DEFRA (Соединенное Королевство). За дополнительной информацией просьба обращаться к Евгению Мазуру, руководителю проекта в ОЭСР. »

«152 Евсеенко Александр Васильевич Унтура Галина Афанасьевна доктор экономических наук, доктор экономических наук, профессор,ведущий научный Институт экономики и организации сотрудник Института экономи- промышленного производства ки и организации промышленного СО РАН. производства СО РАН. untura@ieie.nsc.ru evseenko@ieie.nsc.ru ИННОВАЦИОННАЯ ЭКОНОМИКА СИБИРИ1 Формирование инновационного сектора экономики Сибири Инновационный сектор экономики формируется в результате функционирования. »

«Предисловие Раздел 1. Общие вопросы методики преподавания информатики и ИКТ в школе Глава 1. Предмет информатики в школе 1.1. Информатика как наука и как учебный предмет 1.2. История введения предмета информатика в отечественной школе 1.3. Цели и задачи школьного курса информатики Контрольные вопросы и задания Глава 2. Содержание школьного курса информатики и ИКТ 36 2.1. Общедидактические подходы к определению содержания курса информатики. »

«1 Общие положения Полное наименование вуза на русском языке: федеральное государственное бюджетное образовательное учреждение высшего профессионального образования Тихоокеанский государственный университет. Сокращенные наименования вуза на русском языке: Тихоокеанский государственный университет, ФГБОУ ВПО ТОГУ, ТОГУ. Полное наименование на английском языке: Pacific National University. Сокращенное наименование на английском языке: PNU. Место нахождения вуза: 680035, г. Хабаровск, ул. »

«ТЕОРИЯ И МЕТОДОЛОГИЯ УДК 336.722.112:316 Т. А. Аймалетдинов О ПОДХОДАХ К ИССЛЕДОВАНИЮ ЛОЯЛЬНОСТИ КЛИЕНТОВ В БАНКОВСКОЙ СФЕРЕ АЙМАЛЕТДИНОВ Тимур Алиевич — директор по исследованиям ЗАО НАФИ, кандидат социологических наук, доцент кафедры социальной и педагогической информатики РГСУ. Email: aimaletdinov@nacfin.ru Аннотация. В статье приводится обзор классических и современных подходов к теоретической интерпретации и эмпирическим исследованиям лояльности клиентов к банкам. На основе анализа. »

«МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА РОССИЙСКОЙФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ СТАВРОПОЛЬСКИЙ ГОСУДАРСТВЕННЫЙ АГРАРНЫЙ УНИВЕРСИТЕТ УТВЕРЖДАЮ Проректор по учебной и воспитательной работе И. В. Атанов _2013 г. ОТЧЕТ о самообследовании основной образовательной программы высшего образования Направление подготовки: 230700.68 — Прикладная информатика Профиль: 230700.68.01 Системы корпоративного управления (код, наименование. »

«Международный консорциум Электронный университет Московский государственный университет экономики, статистики и информатики Евразийский открытый институт Иванов А.А., Олейников С.Я., Бочаров С.А. Риск-менеджмент Учебно-методический комплекс Москва 2008 1 УДК – 65.014 ББК – 65.290-2 И – 20 Иванов А.А., Олейников С.Я., Бочаров С.А. РИСК-МЕНЕДЖМЕНТ. Учебнометодический комплекс. – М.: Изд. центр ЕАОИ, 2008. – 193 с. ISBN 5-374-00013-6 © Иванов А.А., 2008 © Олейников С.Я., 2008 © Бочаров С.А., 2008. »

«Направление бакалавриата 210100 Электроника и наноэлектроника Профиль подготовки Электронные приборы и устройства СОДЕРЖАНИЕ ИСТОРИЯ ИНОСТРАННЫЙ ЯЗЫК ФИЛОСОФИЯ ЭКОНОМИКА И ОРГАНИЗАЦИЯ ПРОИЗВОДСТВА КУЛЬТУРОЛОГИЯ ПРАВОВЕДЕНИЕ ПОЛИТОЛОГИЯ СОЦИОЛОГИЯ МАТЕМАТИКА ФИЗИКА ХИМИЯ ЭКОЛОГИЯ ИНФОРМАТИКА ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА МЕТОДЫ МАТЕМАТИЧЕСКОЙ ФИЗИКИ ФИЗИЧЕСКИЕ ОСНОВЫ ЭМИССИОННОЙ ЭЛЕКТРОНИКИ И КАТОДЫ СПЕЦИАЛЬНЫЕ ВОПРОСЫ ФИЗИКИ СПЕЦИАЛЬНЫЕ ВОПРОСЫ МАТЕМАТИКИ ОСНОВЫ ТЕОРИИ НАДЁЖНОСТИ ТЕОРИЯ ИНЖЕНЕРНОГО. »

«Кирикчи Василий Павлович Эволюция развития, организация и экономические аспекты внедрения IPTV Специальность: 5А522104 – Цифровое телевидение и радиовещание Диссертация на соискание академической степени магистра Работа рассмотрена Научный руководитель и допускается к защите к.т.н., доцент Абдуазизов А.А. зав. кафедрой ТВ и РВ к.т.н., доцент В.А. Губенко (подпись) (подпись) _ 2012. »

«РОССИЙСКАЯ АКАДЕМИЯ НАУК Санкт-Петербургский институт информатики и автоматизации Посвящается 30-летию Санкт-Петербургского института информатики и автоматизации Российской академии наук В.В. Александров С.В. Кулешов О.В. Цветков ЦИФРОВАЯ ТЕХНОЛОГИЯ ИНФОКОММУНИКАЦИИ Передача, хранение и семантический анализ ТЕКСТА, ЗВУКА, ВИДЕО Санкт-Петербург НАУКА 2008 1 УДК 004.2:004.6:004.7 ББК 32.973 А Александров В.В., Кулешов С.В., Цветков О.В. Цифровая технология инфокоммуникации. Передача, хранение и. »

«Направление подготовки: 010400.68 Прикладная математика и информатика (очная) Объектами профессиональной деятельности магистра прикладной математики и информатики являются научно — исследовательские центры, государственные органы управления, образовательные учреждения и организации различных форм собственности, использующие методы прикладной математики и компьютерные технологии в своей работе. Магистр прикладной математики и информатики подготовлен к деятельности, требующей углубленной. »

«МИНОБРНАУКИ РОССИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ НОВОСИБИРСКИЙ НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ (НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ, НГУ) Кафедра систем информатики Иван Валентинович Гурлев Пространственный анализ амплитуд отраженных продольных волн в азимутально-анизотропных средах МАГИСТЕРСКАЯ ДИССЕРТАЦИЯ по направлению высшего профессионального образования 230100.68 ИНФОРМАТИКА И. »

«Э.А. Соснин, Б.Н. Пойзнер УНИВЕРСИТЕТ КАК СОЦИАЛЬНОЕ ИЗОБРЕТЕНИЕ: РОЖДЕНИЕ, ЭВОЛЮЦИЯ, НЕУСТОЙЧИВОСТЬ МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ Э.А. Соснин, Б.Н. Пойзнер УНИВЕРСИТЕТ КАК СОЦИАЛЬНОЕ ИЗОБРЕТЕНИЕ: РОЖДЕНИЕ, ЭВОЛЮЦИЯ, НЕУСТОЙЧИВОСТЬ Издательство Томского университета 2004 2 УДК 007 + 101+ 316+502 + 519 + 612 ББК 60.5 + 22.18 + 88 + 72. C Соснин Э.А., Пойзнер Б.Н. C54 Университет как социальное. »

Материалы этого сайта размещены для ознакомления, все права принадлежат их авторам.
Если Вы не согласны с тем, что Ваш материал размещён на этом сайте, пожалуйста, напишите нам, мы в течении 1-2 рабочих дней удалим его.

источники:

http://docplayer.com/28166744-Raznostnaya-approksimaciya-nachalno-kraevoy-zadachi-dlya-uravneniya-teploprovodnosti-ponyatie-yavnoy-i-neyavnoy-shemy.html

http://kniga.seluk.ru/k-informatika/96537-3-ai-caplin-nikulin-modelirovanie-teplofizicheskih-processov-obektov-metallurgii-utverzhdeno-redakcionno-izdatels.php