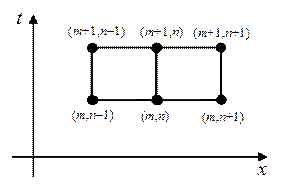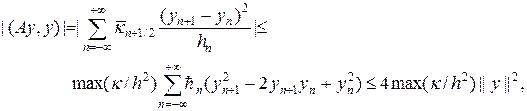Уравнение теплопроводности с разрывными коэффициентами

Одномерные уравнения

Лекция №11

Параболические уравнения

Одномерные уравнения

К параболическим уравнениям относятся задачи описания процессов теплопроводности, диффузии, вязкости и ряд других. Типична, например, следующая постановка для линейной теплопроводности в однородной среде:

(1)

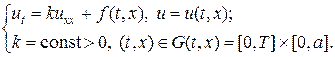
Помимо самого уравнения (1) необходимо определить начальное и граничные условия:

; (2)

. (3)

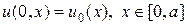
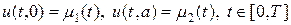
Граничные условия (3) означают, что на левой и правой границе изменения температуры следуют заданным функциональным зависимостям. Эти условия еще называют граничными условиями первого рода. Граничные условия второго рода отвечают заданию на границах потоков тепла, т.е.

. (4)

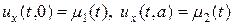
Для граничных условий третьего рода можно записать следующее представление:

. (5)

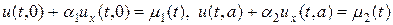
В терминах теплообмена граничные условия третьего рода описывают так называемый линейный (ньютоновский) теплообмен с окружающей средой. Для задачи (1) с начальным (2) и граничными условиями (3) — (5) корректность постановки доказана[1].

Рассмотрим простейшие разностные схемы для численного решения уравнения теплопроводности (1). Выберем в области G(t,x) = [0,T]´[0,a] прямоугольную равномерную сетку с шагами t и h по времени и пространству. В качестве шаблона разностной схемы выберем шеститочечный шаблон, представленный на рис.1. Учитывая шаблон на рис.1, запишем следующую разностную схему

(6)

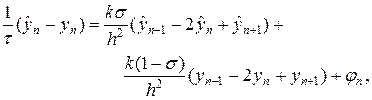
где n = 1,2,…,N-1, s = const. Уравнение (6) необходимо дополнить граничными условиями, например, первого рода:

. (6¢)

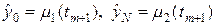
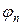
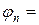
В качестве правой части часто выбирают значение . Параметр s в (6) выступает в качестве свободного параметра, его вариация порождает целое семейство разностных схем от явных до неявных.

Рис.1. Шеститочечный шаблон разностной схемы (6)

Исследуем схему (6), (6¢). Начнем с существования решения и его вычисления. Если s = 0, то схема (6) переходит уже в рассмотренную ранее явную разностную схему (9.26). В этом случае разностное решение легко находится, т.е. его существование и единственность очевидна.

При s ¹ 0 разностная схема (6), (6¢) неявная и ее можно переписать в трехдиагональном форме:

(7)

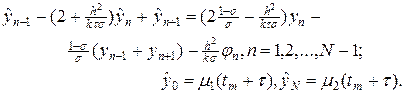
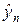
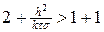
Разностное уравнение на каждом временном слое может быть решено относительно неизвестных методом прогонки. Достаточным условием устойчивости прогонки является условие диагонального преобладания (5.16), которое, согласно (7), выполнено ( ), когда s > 0.

В итоге, решение разностных схем (6), (6¢) существует и единственно при s ³ 0 и при любых ограниченных начальных и краевых условиях. При s = 1 схему называют чисто неявной, а при s = ½ — схемой с полусуммой или симметричной.

Для оценки порядка аппроксимации проведем разложение решений схемы (6) в ряд Тейлора относительно центра разложения (t_m+t / 2,x_n), тогда, опуская довольно утомительные выкладки, можно получить

(8)

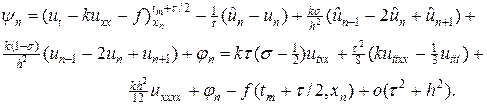
Из (8) видно, что, если положить 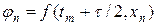, то при s ¹ ½ схема (6) имеет порядок аппроксимации O(t + h 2 ). Для симметричной схемы, у которой s = ½, порядок аппроксимации выше — O(t 2 + h 2 ).

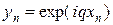
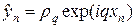
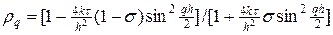
Устойчивость по начальным данным исследуем методом разделения переменных. Поскольку схема (6) линейная, отбросим правую часть и осуществим подстановку и , тогда можно получить множитель роста гармоники

. (9)

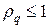
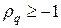
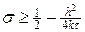
Непосредственной проверкой можно убедиться, что множитель роста гармоники (9) меньше единицы при s ³ 0. Проверяя условие , находим

. (10)

Условие (10) обеспечивает условие равномерной устойчивости схемы (6) по начальным данным в норме 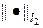. Условие устойчивости по правой части (9.65) выполняется при любых t и h. Таким образом, схема устойчива по начальным данным и по правой части при условии того, что верно неравенство (10).

Для чисто неявной схемы (s = 1), симметричной схемы (s = ½ ) условие (10) выполняется при любых значениях t и h, т.е. эти схемы являются безусловно устойчивыми. Для явной схемы (s = 0) условие (10) выполняется только при условии, что t £ h 2 /(2k), т.е. явная схема является условно устойчивой, что уже было установлено в лекции №9.

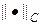
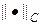
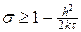
Отметим, что справедливо более сильное утверждение об устойчивости схем (6): они устойчивы в норме . Так из принципа максимума (9.66), (9.67) легко получить достаточное условие устойчивости в норме :

. (10¢)

По сравнению с (10) условие (10¢) более жесткое, но для явной и чисто неявной схем выводы об устойчивости аналогичны тем, которые сделаны выше.

Изучим разностную схему (6), (6¢) на численном примере решения уравнения вида:

(11)

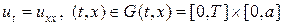
с начальным распределением температуры u₀ в виде равнобедренного треугольника с основанием длиной a и высотой b:

(12)

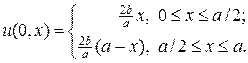
В качестве граничных условий выберем нулевые условия, т.е.

. (13)

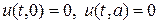
Аналитическое решение задачи (11) — (13) можно представить в виде следующего бесконечного ряда:

. (14)

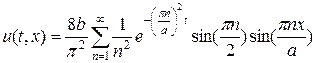
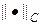
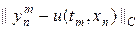
На листинге_№1 приведен код программы численного решения задачи (11) — (13) при различных значениях параметра s. При каждом значении параметра численное решение сравнивалось с аналитическим решением (14) в норме , т.е. находилась ошибка вида: error = .

%Программа решения задачи (11) — (13) при

%различных значениях параметра sigma

%Задаем размеры области интегрирования G=[0,T]x[0,a]

%Определяем размеры сеток по времени и пространству

%Определяем шаги по времени и пространству

%Определяем сетки по времени и пространству

%Находим в узлах сетки значения аналитического

%Рисуем аналитическое решение (14)

%Задаем набор значений параметра sigma, при которых

%будет численно решаться задача (11) — (13) по

%разностной схеме (6), (6′)

%Организуем цикл по времени

%Применяем метод прогонки

%Находим модуль отклонения численного решения от

%аналитического при некотором sigma

%Определяем ошибку численного решения в норме C

%Рисуем 3D график ошибки при sigma=1

%Рисуем 2D график зависимости ошибки численного

%решения от значений параметра sigma

%Функция для вычисления значений аналитического

%решения (14) в точке (t,x)

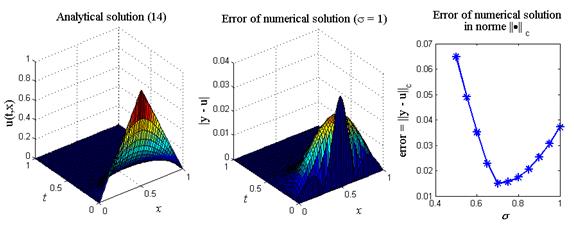
Итог работы кода программы листинга_№1 приведен на рис.2. На левом рисунке приведено 3D изображение аналитического решения (14). На среднем рисунке приведено 3D изображение абсолютного значения ошибки численного решения задачи (11) — (13) с помощью полностью неявной разностной схемы (6), (6¢), т.е. при s = 1. Видно, что пик ошибки приходится на центральный излом в начальном распределении температуры. На рисунке справа приводится ошибка численного решения задачи (11) — (13) в норме 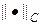в зависимости от значений параметра s (s Î [0,5;1]). Отчетливо виден довольно заметный провал графика в окрестности s = 0,7.

Наилучшая схема. Обобщим разностную схему (6) на случай уравнения теплопроводности с переменным коэффициентом теплопроводности:

. (15)

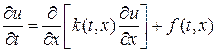
Исследуем общий случай, когда функции k(t,x) и f(t,x) могут быть кусочно-непрерывными. Сильные разрывы могут возникнуть на границе областей, для слоистых сред в случае появления ударных волн и в ряде других приложений. В этом случае решение уравнения (15) следует рассматривать как обобщенное. Обобщенное решение в общем случае не единственно.

Для выделения допустимого решения из множества обобщенных решений необходимо из физических соображений определиться с величинами, которые считаются непрерывными. Для уравнения (15) такими величинами выступают температура u(t,x) и поток тепла W = —k¶u/¶x. Производные этих величин u_x и W_x разрывны в точках разрыва коэффициента теплопроводности и источника тепла соответственно.

Рис.2. Левый рисунок — аналитическое решение (14). Средний и правый
рисунки — решение задачи (11) — (13) с помощью разностной
схемы (6), (6¢) при различных значениях параметра s

Для сходимости к допустимому обобщенному решению составим методом баланса консервативную разностную схему. Для этого перепишем исходное уравнение (15) в явной дивергентной форме, т.е.

. (16)

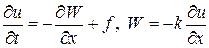
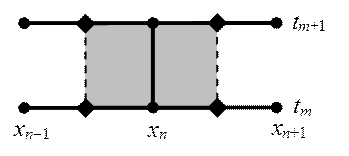
Шаблон и соответствующая ячейка для искомой разностной схемы представлены на рис.3.

Рис.3. Шаблон для разностной схемы уравнения (16)
и ячейка для метода баланса

Запишем для первого уравнения в (16) закон сохранения энергии в виде интеграла по ячейке, заштрихованной на рис.3.

(17)

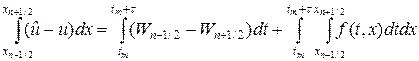
Второе уравнение в (16) проинтегрируем по интервалу сетки [x_n,x_n+1], тогда

. (18)

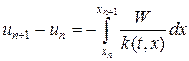
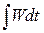
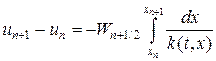
Значения температур припишем узлам сетки, а потоки тепла — серединам интервалов (ромбики на рис.3). Интегралы в (17) аппроксимируем квадратурными формулами. Так, интеграл оценим, исходя из того, что подынтегральное выражение берется с текущего и верхнего слоев. В (18) поток тепла в силу того, что он непрерывен, вынесем из под знака интеграла в средней точке

.

В итоге получим консервативную разностную схему, называемую наилучшей:

, (19)

, (19¢)

,

. (20)

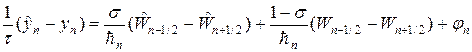
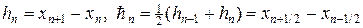
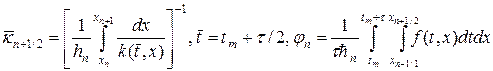
Для аппроксимации интегралов (20) применяют следующий набор формул:

, (21)

, (21¢)

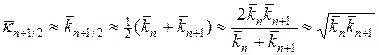
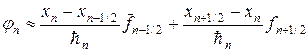
где черта сверху означает отнесение к моменту времени 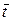. Если разрывы функций k(t,x) и f(t,x) отнесены к узлам сетки, то подстановки в (21) и (21¢) следует понимать, как подстановки односторонних пределов.

Исследуем наилучшую схему (19), (19¢). После подстановки (19¢) в (19) получим обычную трехточечную по пространству схему относительно неизвестных значений 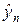на верхнем слое, которая решается методом прогонки. Поскольку имеется диагональное преобладание, т.е. метод прогонки устойчив, постольку может быть получено единственное решение.

Устойчивость по начальным данным разностной схемы (19), (19¢) изучим с помощью метода операторных неравенств. Рассмотрим задачу Коши на всей прямой, считая, что .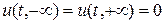

Перепишем схему (19), (19¢) в так называемой канонической операторной форме:

, (22)

где операторы A и B имеют следующий вид:

,

.

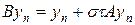
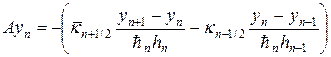
Скалярное произведение определим по формуле:

.

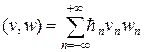
Покажем, что операторы A и B неотрицательные и самосопряженные. Действительно,

.

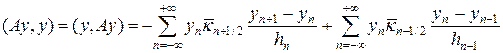
Сдвинем во второй сумме индекс на единицу, тогда

, (23)

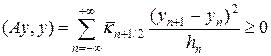
Отметим, что из (23) следует оценка

. (24)

(25)

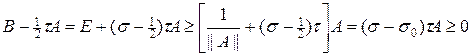
s ³ s₀, 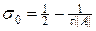. (26)

Условие (25) означает, что и по теореме (лекция №9, формулы (9.76) — (9.82)) устойчивости двухслойных разностных схем в канонической форме схема (19) — (20) устойчива в энергетической норме . Таким образом, неравенство (26) является достаточным условием устойчивости схемы (19) — (20).

Учитывая (24), можно получить более сильное достаточное условие устойчивости разностной схемы (19) — (20) в форме:

. (27)

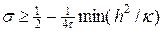
Изучим численно достаточное условие устойчивости (27) на примере использования наилучшей разностной схемы с разрывными функциями, описывающими теплопроводность и правую часть. На листинге_№2 приведен код соответствующей программы.

%Программа тестирования критерия устойчивости (27)

%для наилучшей схемы (19) -(20) численного решения

%Определяем размеры области интегрирования

%Определяем количество узлов в сетках по времени

%вычисляем шаги по времени и пространству

%формируем сетки по времени и пространству

%вычисляем значения коэффициента теплопроводности

%и правой части (источника тепла) в узлах сетки

%рисуем профили коэффициента теплопроводности k(x)

%и источника тепла f(x)

%Находим пороговое значение параметра sigma0 для

%изучения устойчивости наилучшей разностной схемы

%Строим начальное распределение u(0,x)=u0(x)

%температуры в виде треугольного профиля

%Определяем нулевые граничные условия

%Определяем пару значений параметра sigma0 и

%sigma0-eps. При втором значении параметра

%ожидается появление неустойчивости

%Организуем цикл по значением параметра sigma,

%а также по времени и пространству

%определяем левое граничное условие

%Рисуем профили температуры при пороговом значении

%sigma0 и подкритическим значением sigma0-eps

%Определяем функцию коэффициента

if ((x>=0)&(x =(2*a)/3)&(x a/3)&(x =0)&(x =(2*a)/3)&(x a/3)&(x s (s > 0). В лекции №9 аналитически и численно исследовалась бегущая волна для квазилинейного уравнения теплопроводности без источника тепла. И, наконец, в той же лекции аналитически и численно изучалось квазилинейное уравнение теплопроводности с источником тепла, степенным образом, зависящим от температуры, т.е. при f

u s +1 . Во всех трех случаях использовалась чисто неявная схема с весом s = 1. Запишем ее в следующем виде:

. (29)

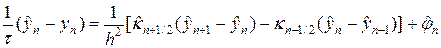
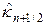
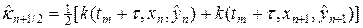
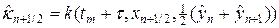
В (29) под понимаются выражения типа (21), т.е.

(30)

. (30¢)

Аналогично (30), (30¢) можно аппроксимировать в (29) источник тепла .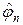

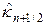
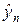
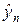
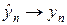
Можно показать, что схема (29) абсолютно устойчива и консервативна и на четырежды непрерывно дифференцируемых решениях имеет погрешность аппроксимации O(t + h 2 ). Вследствие зависимости от неизвестного решения на следующем слое алгебраическая схема (29) является нелинейной относительно . Понятно, что, когда t ® 0 — , т.е. при достаточно малом t существует вещественное решение системы (29). Понятно также, что при большом значении t вещественное решение может отсутствовать.

Решать алгебраическую систему уравнений можно несколькими способами. Рассмотрим подробно метод последовательных приближений, в котором и берутся с предыдущей итерации, т.е.

, (31)

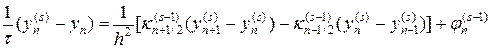
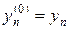
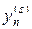
где индекс s = 1,2,… описывает номера итераций. В (31) в качестве нулевого приближения берутся решения с предыдущего слоя, т.е. . Величины находятся из (31) методом прогонкой. Итерации в (31) сходятся линейно и обычно не быстро. Итерации могут и расходиться. В этом случае расчет можно вести с фиксированным числом итераций (обычно 2, 3 итерации).

В качестве критерия сходимости итераций можно использовать условие

(32)

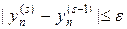
или более жесткое условие

, (32¢)

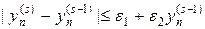
где e, e₁, e₂ — некоторые малые неотрицательные числа. Критерий сходимости (32) либо (32¢) должен выполняться для всех узлов сетки n. Если за разумное число итераций критерий сходимости не выполняется необходимо уменьшить шаг по времени и повторить процедуру повторно. После выполнения одного из критериев (32), (32¢) полагают 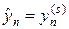и цикл перехода на следующий слой завершается.

Рассмотрим пример численного решения квазилинейного уравнения теплопроводности с источником, в котором коэффициент теплопроводности и источник тепла степенным образом зависят от температуры. Запишем это уравнение в виде

, (33)

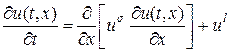
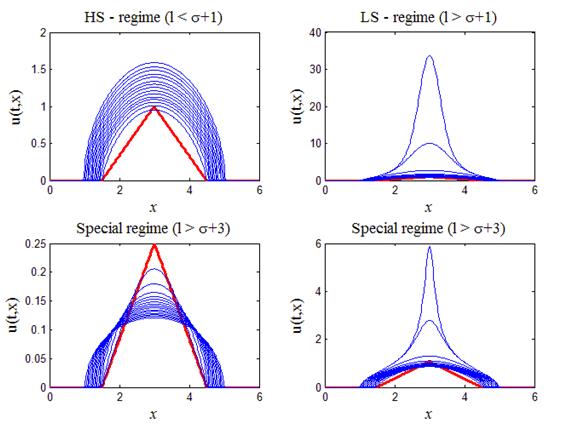
В лекции №9 уже рассмотрено аналогичное уравнение (9.18), точнее рассмотрено аналитическое решение (9.19) — (9.21) этого уравнения при l = s + 1. Продолжим изучение уравнения (33) численным методом в еще трех случаях[2]: 1) так называемый HS-режим, когда l s + 1; 3) особый случай, когда l > s + 3. Третий случай интересен тем, что в зависимости от начального распределения температуры, последующая эволюция решения может пойти по двум прямо противоположным направлениям. Если амплитуда начального распределения ниже некоторого порогового значения, то в дальнейшем тепло будет “расползаться” по пространству неограниченно и амплитуда решения будет стремиться к нулю. Если амплитуда начального распределения температуры является надпороговой, то дальнейшее изменение решения происходит в режиме с обострением, т.е. за конечное время решение обращается в бесконечность.

%Программа решения квазилинейного уравнения

%теплопроводности с источником (33) с помощью

%разностной схемы (31)

%Очищаем рабочее пространство

%Определяем число шагов по времени и

%максимальное количество итераций на

%Определяем диапазон изменения переменной x и

%число узлов сетки на отрезке [0,a]

%Определяем шаг и сетку по пространству

%Определяем степень температурной зависимости

%Определяем четыре расчета:1)HS-режим, когда

%1 sigma+1; 3)режим

%l>sigma+3 с двумя типами начальных данных:

%подпороговый пик возмущения и надпороговый

l=[sigma sigma+2 sigma+4 sigma+4];

%Вариация высоты пика начального возмущения

%для четырех расчетов

%Основной цикл для четырех расчетов

%Начальное распределение температуры в

%виде равнобедренного треугольника с

%высотой b(k) и основанием длиной 0.5*a

if (x(n)>=0.25*a)&(x(n) =0.5*a)*(x(n) s + 3 в зависимости от амплитуды начального распределения возможны два прямо противоположных режима динамики. На левом нижнем рисунке, при подпороговой начальной амплитуде тепло “расползается” неограниченно по пространству, амплитуда распределения стремится к нулю, при этом источник тепла не перестает действовать. На правом нижнем рисунке, при надпороговой начальной амплитуде температура в центре в начале падает, а потом начинает расти неограниченно в режиме с обострением, причем полуширина пика, как и LS-режиме, стремится к нулю. На всех четырех рисунках жирной (красной) линией выделен начальный температурный профиль.

Рис.5. Различные типы динамики решений уравнения (33) в
зависимости от соотношения параметров s и l

Lp-регулярность решения уравнения теплопроводности с разрывными коэффициентами Текст научной статьи по специальности « Математика»

Аннотация научной статьи по математике, автор научной работы — Кусем Сельма, Чикуче Видед

Вэтой статье мы рассмотрим задачу прохождения для уравнения теплопроводности на ограниченном плоском секторев пространствах Lp-Соболева. Применяя теорию сумм операторовДа Прато-ГрисвардаиДоре-Венни,мы доказываем, что решениеможно разбитьна регулярную частьв пространстве Lp-Соболеваи явную особую часть.

Похожие темы научных работ по математике , автор научной работы — Кусем Сельма, Чикуче Видед

LP REGULARITY OF THE SOLUTION OF THE HEAT EQUATION WITH DISCONTINUOUS COEffiCIENTS

Inthispaper,we considerthe transmission problemfortheheat equationonaboundedplane sector in Lp-Sobolev spaces. By Applying the theory of the sums of operators of Da Prato-Grisvard and Dore-Venni, we prove that the solution can be splited into a regular part in Lp-Sobolev space and an explicit singular part.

Текст научной работы на тему «Lp-регулярность решения уравнения теплопроводности с разрывными коэффициентами»

DOI: 10.17516/1997-1397-2020-13-4-466-479 УДК 517.9

L Regularity of the Solution of the Heat Equation with Discontinuous Coefficients

LMA, Department of Mathematics Abderrahmane Mira University Bejaia, Algeria

LMPA, Department of Mathematics Mohamed Seddik Ben Yahia University Jijel, Algeria

Received 16.02.2020, received in revised form 23.04.2020, accepted 06.06.2020 Abstract. In this paper, we consider the transmission problem for the heat equation on a bounded plane sector in Lp-Sobolev spaces. By Applying the theory of the sums of operators of Da Prato-Grisvard and Dore-Venni, we prove that the solution can be splited into a regular part in Lp-Sobolev space and an explicit singular part.

Keywords: transmission heat equation, sums of linear operators, singular behavior, non-smooth domains.

Citation: S. Kouicem, W. Chikouche, Lp Regularity of the Solution of the Heat Equation with Discontinuous Coefficients, J. Sib. Fed. Univ. Math. Phys., 2020, 13(4), 466-479. DOI: 10.17516/1997-1397-2020-13-4-466-479.

1. Introduction and preliminaries

Let B = Gx]0, T[, where G is a bounded plane sector constitued of two plane sectors Gi,G2 with respective opening wi and w2, separated by an interface E.

Gi = <(r cos 0,r sin 0); -wi 1) the Lebesgue spaces, and by Ws'p(D), s >0, the standard Sobolev spaces built on. The space Wq’p(D) is defined as usual by W^i’p(D) :=< v G W 1,p(D); v = 0 on dD>. When p = 2, we use the common notation Hi(D) instead of W^,p(D).

For any separable Banach space X provided with the norm || • ||x, we denote by Lp(]0, T[; X) the space of measurable functions v from ]0, T[ in X such that

mlpq0,t [;x) = ( j0 M^t)Hpx p n and p(-A) contains the truncated sector

sa = R, | arg A| R, | arg A| v and Lvn —> f in E.

2.2. The second strategy

Here we just recall from [6] an application of the theory of sums of operators of Dore-Venni. Let X be an U.M.D. complex Banach space and A : D(A) ^ X a closed linear operator with dense domain in X satisfying the following assumptions

H4 p(A) d] — to, 0] and there exists MA > 0 such that

H5 Ais G L(X) for all s G R and there exist K > 0, ta such that 0 dx,

a(x) = ai > 0 for x G G^ i = 1, 2, with a1 = a2.

In what follows, we use the positive constant C to denote a generic constant and may take different values in different places.

Lemma 3.1. Let 0A G ]0,n[. Then problem (13) admits a unique solution u G Hq(G) for any f G Lp(G) and any z G C with | argz\ Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

is continuous on Hq(G), with the estimate

K(v)| 0 and *R(zeie) ^ 0, which implies thanks to Poincare’s inequality

eie az(v, v)) > cos 0 / a\Vvl2dx > C||v||Hi(G),

for all v G Hq(G). We conclude using the Lax-Milgram lemma. □

For R> 0 and 0 a G

fixed, we define the sets S + and SA as follows

S+ = 0>, Sa = R and | arg z | 0 and 0A e ,n be fixed. Let z e S+ U SA and u e Hq(G) be the solution of (13), then u satisfies the estimate

\Iuhr(G) 0. Due to (17) and Poincare’s inequality, we deduce that

Case 2 : K(z) psin0a.

Consequently, from (18) we obtain

Note that Lp(G) = Lp(G1) x Lp(G2) and ui = uG; i = 1,2.

Theorem 3.1 ([1]). Let f G Lp(G), z G C with №(z) > 0 and u G H^(G) be the solution of (13), then u satisfies the estimates

As in [3], we can prove the estimate (20) for z in a larger part of the complex plane.

Corollary 3.2. There exists 0A G ,n such that, for all f G Lp(G), all z G C with \ arg z\ 0 and t G R*

\a + iT\!(Ap + (a + iT)/)-i|| 0 such that

PWsp(G) := , is the space of piecewise Ws’p functions on G. Let S(m) be the function defined by

where n is a radial cut-off function such that n = 1 in a small ball centered at the origin and n = 0 outside a larger ball of radius strictly less than 1, Am is a nonnegative real number and Am, tm are respectively the eigenvalues and eigenfunctions of the following Sturm-Liouville problem:

-t’m(0)=A2mtm(0) for 0 e [-wi,w2], 0 = 0, tm(0-)=tm(0+), a2tm(0-)=aitm(0+), tm(-Wi) = tm(w2) = 0.

Theorem 3.2. If Am = — for all m e N*, then there exists 0A e

such that, for all

f e Lp(G), all z e S+ U Sa, the unique solution u e Hq(G) of problem (9)-(12) admits the decomposition

u = ur + E cm^m(z), (25)

e-rVz S(m) e-r^ (1 + r^z)S(m)

if 7 — 1 Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

From the previous estimate and inequality (28), we deduce that we have (29). □

With the notation introduced above, we can write

consequently the decomposition (25) implies a similar decomposition of the resolvent of Ap. Namely we may write

(Ap + z)-1 = R(z)+ ]T Tm(z) ® Vm(z), (30)

(Tm(z) ® Vm(z))(f) = ^m(z). The estimates (27) and (29) imply that

||R(z)»lp(g)^fw2,p(G) + \z\2 ||R(z)»lp(g)^wi.p(G) + \z\ ||R(z)»lp(g)^lp(g) 0 such that

Proof. We proceed as in [9, Proposition 6.2] and [5, Proposition 2.2]. First we consider the extension of g to G x R, defined by

g(x,t) if t € [0,T], 0 if t € [0,T],

and denote by uz = (zI — B^,) 1g , the solution of

where Bis the operator, defined by

Observe that, by uniqueness of the solution of the Cauchy problem, we have uz |gx[ot] = = (zI — B)-1g.

Consider the functions

g)*m(z) dz, qm(t) = n J (Tm(z), (zI — B^)-1

We assume that g € D(G x R), a dense subspace of LP(G x R). Then we can apply partial Fourier transform in t, to (40) and (41). By Fubini’s theorem, we obtain

= -ni U Tm(z), 1—ir) *m(z) dz,

The decaly at infinity of Tm(z) and ^m(z) due to (31) and (26) allows us to apply Cauchy’s foumula. We get

Ftum(x, 0 = -(Tm№, Ft g(, 0) ^m(ii), (42)

Ftqm(£) = -(Tm(i0, dt g(-,0)-According to (26), the identity (42) can be written as follows

-(Tm(i^), Ft g(-,0) e-rV^ S(m) if Am > 1 .

-(Tm(i0, Ft g(-,0) (1 + rv/ie) S(m) if Am 1 — -,

FtEm(x,e) = p(g)) u and gn —» g in E.

Moreover, as in Section 4, for every n, we have

0 gi — E (dtu—,i — Au—,i).

It is obvious that wR is a strong solution of (47)-(51). Consequently, by applying the first strategy to (47)-(51), we have by uniqueness of the strong solution that wR = uR.

This implies that uR € LP (I; D(AP)) n WI; LP(G)). With the help of (44), this yields

ur € LP(I; D(Ap) n PWs’P(G)).

Then, from [1, Lemma 5.4], we deduce that

ur € LP(I; PW2’p(G) n W1’P(G)) n W 1p(I; LP(G)).

Summing up, we have proved the following Theorem.

Theorem 5.1. Let p > 2 , suppose that Xm = — Vm € N*. Then for every g € LP(I; LP(G)),

there exists a unique solution u € LP(I; LP(G)) to the transmission problem (1)-(5). Moreover u admits the decomposition

u = ur + (Em *t Qm)S(m),

0 Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы.