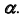Пересечение прямой с плоскостью в начертательной геометрии с примерами
Содержание:
Пересечение прямой с плоскостью:
Рассмотрим три варианта, а соответственно и три алгоритма решения задачи по определению точки пересечения прямой с плоскостью:
- прямая — проецирующая, плоскость — общего положения;
- прямая — общего положения, плоскость — проецирующая;
- прямая и плоскость — общего положения.
Пересечение проецирующей прямой с плоскостью общего положения
При решении задач на определение точки пересечения проецирую- щей прямой с плоскостью общего положения используется собирательное свойство вырожденной проекции проецирующей прямой. Вырожденная проекция прямой совпадает с одноименной проекцией искомой точки. Другая проекция точки пересечения прямой с плоскостью определяется по принадлежности точки заданной плоскости.
Задача:
На эпюре Монжа построить проекции точки пересечения проецирующей прямой
Алгоритм решения
- Так как прямая
— горизонтально- проецирующая, то вторая проекция точки пересечения заданной прямой с плоскостью совпадает с вы- рожденной проекцией прямой
Отметим горизонтальную проекцию
- Фронтальную проекцию
определим по принадлежности точки K плоскости
(задача 3).
Видимость прямой 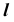
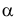
Пересечение прямой общего положения с проецирующей плоскостью
При решении задач на определение точки пересечения проецирующей плоскости с прямой общего положения используется собирательное свойство вырожденной проекции проецирующей плоскости. Одна из проекций искомой точки определяется на пересечении вырожденной проекции плоскости с одноименной проекцией заданной прямой. Другая проекция точки пересечения прямой с плоскостью определяется по принадлежности точки заданной прямой.
Задача:
На эпюре Монжа построить проекции точки пересечения прямой общего положения 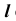
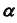
Алгоритм решения
- Так как точка K — общий элемент прямой и плоскости, а плоскость
— фронтально- проецирующая, следовательно, проекция
определится на пересечении фронтальных проекций прямой и плоскости
- Горизонтальную проекцию
определим по принадлежности точки K прямой
(задача 1).
Видимость прямой 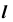
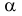
Пересечение прямой общего положения с плоскостью общего положения
Для построения точки пересечения прямой общего положения 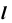
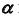
1. Заключим прямую 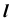
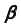
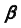
2. Строим линию пересечения заданной плоскости 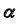
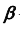
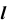
Так как линия m принадлежит заданной плоскости 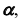
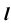
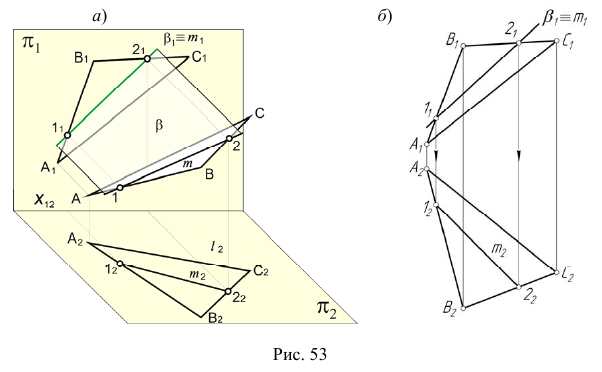
Перед решением задачи по определению точки пересечения прямой общего положения с плоскостью общего положения рассмотрим отдельно реализацию на эпюре Монжа п. 2 — построение линии пересечения проецирующей плоскости с плоскостью общего положения рис. 53, а.
Задача:
На эпюре Монжа построить проекции линии пересечения плоскости общего положения 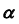
При решении этой задачи используем собирательное свойство вырожденной проекции проецирующей плоскости.
Алгоритм решения
- Определим фронтальную проекцию линии m. Так как плоскость
— фронтально-проецирующая, то первая проекция линии m совпадает с вырожденной (фронтальной) проекцией плоскости
(рис. 53, б).
- Горизонтальную проекцию линии m построим, учитывая ее принадлежность плоскости
(задача 2).
- Заказать чертежи
Задача:
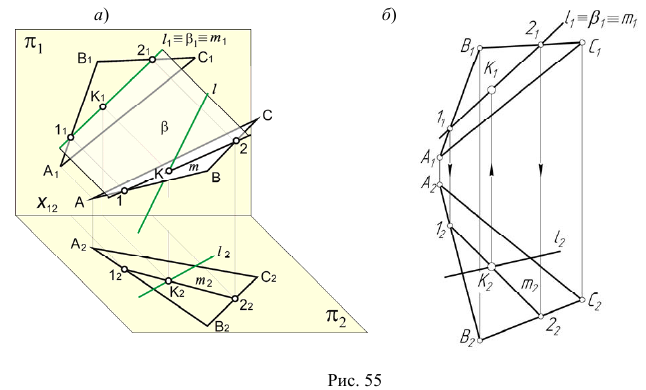
На эпюре Монжа построить проекции точки пересечения прямой общего положения l с плоскостью общего положения (ABC) (рис. 54, а).
Алгоритм решения
1. Заключим прямую линию l во вспомогательную проецирующую плоскость 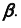
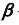
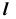
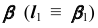
2. Построим проекции линии пересечения m заданной плоскости 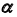
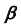
3. Определим проекции точки пересечения K прямой линии 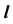
- отметим проекцию
- на пересечении
и линии проекционной связи отметим проекцию
(рис. 55, б).
4. Определим видимость прямой 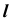
Точка K делит прямую 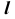
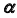
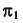
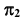
Определим видимость прямой 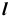
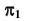
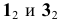
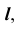
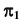
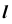
Видимость прямой 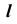
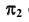
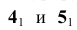
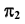
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Пересечение прямой с поверхностью
- Пересечение поверхностей
- Способы преобразования чертежа
- Ортогональное проецирование: точка, прямая, плоскость
- Отображение пространственных объектов на плоскость
- Моделирование линии на эпюре Монжа
- Моделирование плоскости на эпюре Монжа
- Моделирование поверхностей на эпюре Монжа
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Координаты точки пересечения прямой и плоскости — примеры нахождения
Данная глава рассказывает о том, как найти координаты точки пересечения прямой с плоскостью при заданных уравнениях, определяющих эту плоскость. Будет рассмотрено понятие точки пересечения прямой с плоскостью, два способа нахождения координат точки пересечения прямой с плоскостью.
Точка пересечения прямой и плоскости – определение
Для углубленного изучения теории необходимо начать рассмотрение с понятия точки, прямой, плоскости. Понятие о точке, прямой линии рассматривается как на плоскости, так и в пространстве. Для детального рассмотрения необходимо обратиться к теме о прямой и плоскости в пространстве.
Существует несколько вариаций расположения прямой относительно плоскости и пространства:
- прямая лежит в плоскости;
- прямая параллельна плоскости;
- прямая пересекает плоскость.
Если рассмотреть третий случай, то отчетливо видно, что прямая с плоскостью при пересечении образуют общую точку, которую называют точкой пересечения прямой и плоскости. рассмотрим данный случай на примере.
Нахождение координат точки пересечения прямой и плоскости
Была введена прямоугольная система координат О х у z трехмерного пространства. Каждая прямая имеет свое собственное уравнение, а каждая плоскость соответствует своему заданному уравнению, каждая точка имеет определенное количество действительных чисел – координат.
Чтобы подробно разобраться в теме координат пересечения, необходимо знать все виды уравнения прямой в пространстве и уравнений плоскости. в данном случае пригодятся знания о переходе от одного вида уравнения к другому.
Рассмотрим задачу, которая основывается на заданном пересечении прямой и плоскости. она сводится к нахождению координат пересечений.
Вычислить, может ли точка М 0 с координатами — 2 , 3 , — 5 являться точкой пересечения прямой x + 3 — 1 = y — 3 = z + 2 3 с плоскостью x — 2 y — z + 3 = 0 .
Когда точка принадлежит некоторой прямой, координаты точки пересечения являются решением обоих уравнения. Из определения имеем, что при пересечении образуется общая точка. Для решения задания необходимо подставить в оба уравнения координаты точки М 0 и вычислить. Если она является точкой пересечения, то оба уравнения будут соответствовать.
Представим координаты точки — 2 , 3 , — 5 и получим:
— 2 + 3 — 1 = 3 — 3 = — 5 + 2 3 ⇔ — 1 = — 1 = — 1 — 2 — 2 · 3 — ( — 5 ) + 3 = 0 ⇔ 0 = 0
Так как получаем верные равенства, делаем вывод, что точка М 0 — точка пересечения заданной прямой с плоскостью.
Ответ: заданная точка с координатами является точкой пересечения.
Если координаты точки пересечения являются решением обоих уравнений, то они пересекаются.
Первый способ нахождения координат пересечения прямой и плоскости.
Когда задается прямая a с плоскостью α прямоугольной системы координат, известно, что они пересекаются в точке М 0 . Для начала займемся поиском координат заданной точки пересечения при заданном уравнении плоскости, имеющего вид A x + B y + C z + D = 0 с прямой линией a , являющейся пересечением плоскостей A 1 x + B 1 y + C 1 z + D 1 = 0 и A 2 x + B 2 y + C 2 z + D 2 = 0 . Данный способ задания прямой в пространстве рассматривается в статье уравнения прямой и уравнения двух пересекающихся плоскостей.
Необходимые нам координаты прямой a и плоскости α должны удовлетворять обоим уравнениям. Таким образом задается система линейных уравнений, имеющая вид
A x + B y + C z + D = 0 A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0
Решение системы подразумевает обращение каждого тождества в верное равенство. Следует отметить, что при таком решении мы определяем координаты пересечения 3 плоскостей вида A x + B y + C z + D = 0 , A 1 x + B 1 y + C 1 z + D 1 = 0 , A 2 x + B 2 y + C 2 z + D 2 = 0 . Для закрепления материала рассмотрим решение данных задач.
Прямая задана уравнением двух пересекающихся плоскостей x — y + 3 = 0 5 x + 2 z + 8 = 0 , причем пересекает еще одну 3 x — z + 7 = 0 . Необходимо найти координаты точки пересечения.
Необходимые координаты получим при составлении и решении системы, имеющей вид x — y + 3 = 0 5 x + 2 z + 8 = 0 3 x — z + 7 = 0 .
Следует обратить внимание на тему решения систем линейных уравнений.
Возьмем систему уравнений вида x — y = — 3 5 x + 2 z = — 8 3 x — z = — 7 и произведем вычисления по определителю основной матрицы системы. Получаем, что
∆ = 1 — 1 0 5 0 2 3 0 — 1 = 1 · 0 · ( — 1 ) + ( — 1 ) · 2 · 3 + 0 · 5 · 0 — 0 · 0 · 3 — 1 · 2 · 0 — ( — 1 ) · 5 · ( — 1 ) = — 11
Так как определитель матрицы не равен нулю, система имеет только одно решение. Для этого мы применим метод Крамера. Он считается очень удобным и подходящим для данного случая.
∆ x = — 3 — 1 0 — 8 0 2 — 7 0 — 1 = ( — 3 ) · 0 · ( — 1 ) + ( — 1 ) · 2 · ( — 7 ) + 0 · ( — 8 ) · 0 — — 0 · 0 · ( — 7 ) — ( — 3 ) · 2 · 0 — ( — 1 ) · ( — 8 ) · ( — 1 ) = 22 ⇒ x = ∆ x ∆ = 22 — 11 = — 2 ∆ y = 1 — 3 0 5 — 8 2 3 — 7 — 1 = 1 · ( — 8 ) · ( — 1 ) + ( — 3 ) · 2 · 3 + 0 · 5 · ( — 7 ) — — 0 · ( — 8 ) · 3 — 1 · 2 · ( — 7 ) — ( — 3 ) · 5 · ( — 1 ) = — 11 ⇒ y = ∆ y ∆ = — 11 — 11 = 1 ∆ z = 1 — 1 — 3 5 0 — 8 3 0 — 7 = 1 · 0 · ( — 7 ) + ( — 1 ) · ( — 8 ) · 3 + ( — 3 ) · 5 · 0 — — ( — 3 ) · 0 · 3 — 1 · ( — 8 ) · 0 — ( — 1 ) · 5 · ( — 7 ) = — 11 ⇒ z = ∆ z ∆ = — 11 — 11 = 1
Отсюда следует, что координаты точки пересечения заданной прямой и плоскости имеет значение ( — 2 , 1 , 1 ) .
Ответ: ( — 2 , 1 , 1 ) .
Система уравнений вида A x + B y + C z + D = 0 A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 имеет одно единственное решение. Когда прямая a определена такими уравнениями, как A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 , а плоскость α задается уравнением A x + B y + C z + D = 0 , то они пересекаются. Когда прямая лежит в плоскости, система выдает бесконечное множество решений. При их параллельности уравнение решений не имеет, так как нет общих точек пересечения.
Найти точку пересечения прямой z — 1 = 0 2 x — y — 2 = 0 и плоскости 2 x — y — 3 z + 1 = 0 .
Заданные уравнения необходимо преобразовать в систему z — 1 = 0 2 x — y — 2 = 0 2 x — y — 3 z + 1 = 0 . Когда она будет иметь единственное решение, то получим искомые координаты пересечения в точке. При условии, если нет решений, то они параллельны, либо прямая лежит в этой же плоскости.
Получим, что основная матрица системы – A = 0 0 1 2 — 1 0 2 — 1 — 3 , расширенная – T = 0 0 1 1 2 — 1 0 2 2 — 1 — 3 — 1 . Нам необходимо определить ранг матрицы A и T методом Гаусса:
1 = 1 ≠ 0 , 0 1 — 1 0 = 1 ≠ 0 , 0 0 1 2 — 1 0 2 — 1 — 3 = 0 , 0 1 1 — 1 0 2 — 1 — 3 — 1 = 0
Тогда получим, что ранг основной матрицы равен рангу расширенной. Применим теорему Кронекера-Капелли, отсюда видно, что у системы есть бесконечное множество решений. Получим, что прямая z — 1 = 0 2 x — y — 2 = 0 принадлежит плоскости 2 x — y — 3 z + 1 = 0 , что говорит об их невозможности пересечения и наличии общей точки.
Ответ: нет координат точки пересечения.
Задано пересечение прямой x + z + 1 = 0 2 x + y — 4 = 0 и плоскости x + 4 y — 7 z + 2 = 0 , найти координаты точки пересечения.
Необходимо собрать заданные уравнения в систему вида x + z + 1 = 0 2 x + y — 4 = 0 x + 4 y — 7 z + 2 = 0 . Для решения применяем метод Гаусса. С его помощью мы определим все имеющиеся решения коротким путем. Для этого запишем
x + z + 1 = 0 2 x + y — 4 x + 4 y — 7 z + 2 = 0 ⇔ x + z = — 1 2 x + y = 4 x + 4 y — 7 z = — 2 ⇔ ⇔ x + z = — 1 y — 2 z = 6 4 y — 8 z = — 1 ⇔ x + z = — 1 y — 2 z = 6 0 = — 25
Применив метод Гауса, стало понятно, что равенство неверное, так как система уравнений решений не имеет.
Делаем вывод, что прямая x + z + 1 = 0 2 x + y — 4 = 0 с плоскостью x + 4 y — 7 z + 2 = 0 не имеют пересечений. Отсюда следует, что невозможно найти координаты точки, так как они не пересекаются.
Ответ: нет точек пересечения, так как прямая параллельна плоскости.
Когда прямая имеет задана параметрическим или каноническим уравнением, то отсюда можно найти уравнение пересекающихся плоскостей, которые определяют прямую a , после чего искать необходимые координаты точки пересечений. Имеется еще один метод, который применяется для нахождения координат точки пересечения прямой и плоскости.
Второй способ нахождения точки начинается с задания прямой a , пересекающей плоскость α в точке М 0 . Необходимо найти координаты заданной точки пересечения при заданном уравнении плоскости A x + B y + C z + D = 0 . Прямую а определяем параметрическими уравнениями, имеющими вид x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ , λ ∈ R .
Когда в уравнение A x + B y + C z + D = 0 производится подстановка x = x 1 + a x · λ , y = y 1 + a y · λ , z = z 1 + a z · λ , выражение примет вид уравнения с неизвестной λ . Необходимо разрешить его относительно λ , тогда получим λ = λ 0 , которое соответствует координатам точки, в которой они пересекаются. Вычисление координат точки производится из x = x 1 + a x · λ 0 y = y 1 + a y · λ 0 z = z 1 + a z · λ 0 .
Подробнее этот способ будет рассмотрен на примерах, приведенных ниже.
Найти координаты точки пересечения прямой x = — 1 + 4 · λ y = 7 — 7 · λ z = 2 — 3 · λ , λ ∈ R с плоскостью x + 4 y + z — 2 = 0 .
Для решения системы, необходимо произвести подстановку. Тогда получаем, что
— 1 + 4 · λ + 4 · 7 — 7 · λ + 2 — 3 · λ — 2 = 0 ⇔ — 27 · λ + 27 = 0 ⇔ λ = 1
Найдем координаты точки пересечения плоскости с прямой, используя параметрические уравнения, со значением λ = 1 .
x = — 1 + 4 · 1 y = 7 — 7 · 1 z = 2 — 3 · 1 ⇔ x = 3 y = 0 z = — 1
Ответ: ( 3 , 0 , — 1 ) .
Когда прямая вида x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ , λ ∈ R принадлежит плоскости A x + B y + C z + D = 0 , тогда необходимо подставить туда уравнение плоскости выражения x = x 1 + a x · λ , y = y 1 + a y · λ , z = z 1 + a z · λ , тогда получим тождество такого вида 0 ≡ 0 . При параллельности плоскости и прямой получаем неверное равенство, так как нет точек пересечения.
Если прямая задана каноническим уравнением, имеющим вид x — x 1 a x = y — y 1 a y = z — z 1 a z , тогда необходимо переходить от канонических к параметрическим при поиске координат точки пересечения прямой с плоскостью A x + B y + C z + D = 0 , то есть получим x — x 1 a x = y — y 1 a y = z — z 1 a z ⇔ x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ и применим необходимы способ для нахождения координат точки пересечения заданной прямой и плоскости в пространстве.
Точка пересечения прямой и плоскости онлайн
С помощю этого онлайн калькулятора можно найти точку пересечения прямой и плоскости. Дается подробное решение с пояснениями. Для нахождения координат точки пересечения прямой и плоскости задайте вид уравнения прямой («канонический» или «параметрический» ), введите данные в уравнения прямой и плоскости и нажимайте на кнопку «Решить». Теоретическую часть и численные примеры смотрите ниже.
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Точка пересечения прямой и плоскости − теория, примеры и решения
- Содержание
- 1. Точка пересечения плоскости и прямой, заданной в каноническом виде.
- 2. Точка пересечения плоскости и прямой, заданной в параметрическом виде.
- 3. Примеры нахождения точки пересечения прямой и плоскости.
1. Точка пересечения плоскости и прямой, заданной в каноническом виде
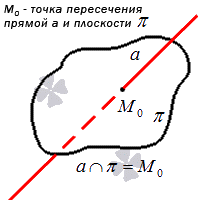
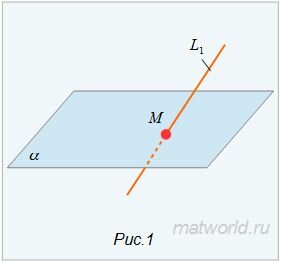
Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат заданы прямая L1:
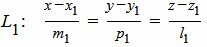 , , | (1) |
| α: Ax+By+Cz+D=0. | (2) |
Найти точку пересечения прямой L1 и плоскости α (Рис.1).
 |
Запишем уравнение (1) в виде системы двух линейных уравнений:
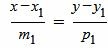 , , | (3) |
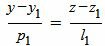 | (4) |
Сделаем перекрестное умножение в уравнениях (3) и (4):
| p1(x−x1)=m1(y−y1) |
| l1(y−y1)=p1(z−z1) |
Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:
| p1x−m1y=p1x1−m1y1, | (5) |
| l1y−p1z=l1y1−p1z1. | (6) |
Решим систему линейных уравнений (2), (5), (6) с тремя неизвестными x, y, z. Для этого в уравнении (2) переведем свободный член в правую часть уравнения и запишем эту систему в матричном виде:
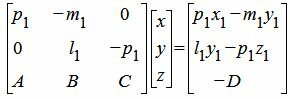 | (7) |
Как решить систему линейных уравнений (11)(или (2), (5), (6)) посмотрите на странице Метод Гаусса онлайн или на примерах ниже. Если система линейных уравнениий (7) несовместна, то прямая L1 и плоскость α не пересекаются. Если система (7) имеет множество решений, то прямая L1 лежит на плоскости α. Единственное решение системы линейных уравнений (7) указывает на то, что это решение определяет координаты точки пересечения прямой L1 и плоскости α.
Замечание. Если прямая задана параметрическим уравнением, то уранение прямой нужно приводить к каноническому виду и применить метод, описанный выше, или же
2. Точка пересечения плоскости и прямой, заданной в параметрическом виде.
Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат задана прямая L1 в параметрическом виде:
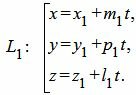 | (8) |
| α: Ax+By+Cz+D=0. | (9) |
Задачу нахождения нахождения точки пересечения прямых L1 и плоскости α можно решить разными методами.
Метод 1. Приведем уравнения прямой L1 к каноническому виду.
Для приведения уравнения (8) к каноническому виду, выразим параметр t через остальные переменные:
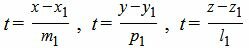 | (10) |
Так как левые части уравнений (10) равны, то можем записать:
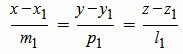 | (11) |
Далее, для нахождения точки пересечения прямой и плоскости нужно воспользоваться параграфом 1.
Метод 2. Для нахождения точки пересечения прямой L1 и плоскости α решим совместно уравнения (8) и (9). Из уравнений (8) подставим x, y, z в (9):
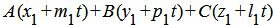 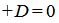 | (13) |
Откроем скобки и найдем t:
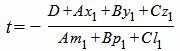 | (14) |
Если числитель и знаменатель в уравнении (14) одновременно равны нулю, то это значит, что прямая L1 лежит на полскости α. Если в уравнении (14) числитель отличен от нуля, а знаменатель равен нулю, то прямая и плоскость параллельны.
Если же числитель и знаменатель в уравнении (14) отличны от нуля, то прямая и плоскость пересекаются в одной точке. Для нахождения координат точки пересечения прямой L1 и плоскости α подставим полученное значение t из (14) в (8).
3. Примеры нахождения точки пересечения прямой и плоскости.
Пример 1. Найти точку пересечения прямой L1:
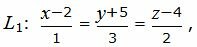 | (15) |
| α: 7x−5y+2z+19=0. | (16) |
Представим уравнение (15) в виде двух уравнений:
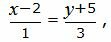 | (17) |
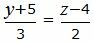 | (18) |
Сделаем перекрестное умножение в уравнениях (17) и (18):
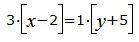 |
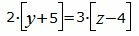 |
Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:
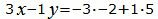 |
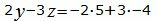 |
Для нахождения точки пересечения прямой L1 и плосклсти α нужно решить совместно уравнения (2), (19) и (20). Для этого переведем в уравнении (2) свободный член на правую сторону уравнения и построим матричное уравнение для системы линейных уравнений (2), (19) и (20):
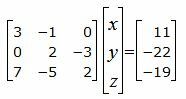 | (21) |
Решим систему линейных уравнений (21) отностительно x, y, z. Для решения системы, построим расширенную матрицу:
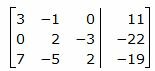 |
Обозначим через aij элементы i-ой строки и j-ого столбца.
Первый этап. Прямой ход Гаусса.
Исключим элементы 1-го столбца матрицы ниже элемента a1 1. Для этого сложим строку 3 со строкой 1, умноженной на −7/3:
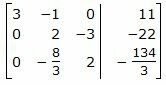 |
Исключим элементы 2-го столбца матрицы ниже элемента a22. Для этого сложим строку 3 со строкой 2, умноженной на 4/3:
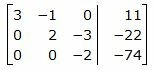 |
Второй этап. Обратный ход Гаусса.
Исключим элементы 3-го столбца матрицы выше элемента a33. Для этого сложим строку 2 со строкой 3, умноженной на −3/2:
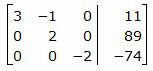 |
Исключим элементы 2-го столбца матрицы выше элемента a22. Для этого сложим строку 1 со строкой 2, умноженной на 1/2:
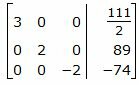 |
Делим каждую строку матрицы на соответствующий ведущий элемент (если ведущий элемент существует):
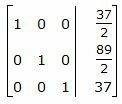 |
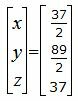 |
Ответ. Точка пересечения прямой L1 и плоскости α имеет следующие координаты:
| M (37/2, 89/2, 37). |
Пример 2. Найти точку пересечения прямой L1:
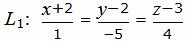 | (22) |
| α: 6x+2y+z+7=0. | (23) |
Представим уравнение (22) в виде двух уравнений:
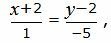 | (24) |
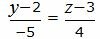 | (25) |
Сделаем перекрестное умножение в уравнениях (24) и (25):
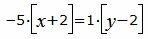 |
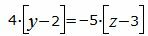 |
Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:
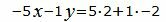 |
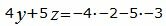 |
Для нахождения точки пересечения прямой L1 и плосклсти α нужно решить совместно уравнения (2), (26) и (27). Переведем в уравнении (2) свободный член на правую сторону уравнения и построим матричное уравнение для системы линейных уравнений (2), (26) и (27):
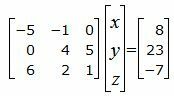 | (28) |
Решим систему линейных уравнений (21) отностительно x, y, z. Для этого построим расширенную матрицу:
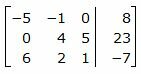 |
Обозначим через aij элементы i-ой строки и j-ого столбца.
Исключим элементы 1-го столбца матрицы ниже элемента a11. Для этого сложим строку 3 со строкой 1, умноженной на 6/5:
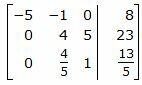 |
Исключим элементы 2-го столбца матрицы ниже элемента a22. Для этого сложим строку 3 со строкой 2, умноженной на −1/5:
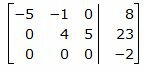 |
Из расширенной матрицы восстановим систему линейных уравнений:
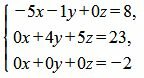 | (29) |
Легко можно заметить, что последнее уравнение в (29) несовместна, так как несуществуют такие x, y, z чтобы выполнялось это равенство. Следовательно система линейных уравнений (2), (26) и (27) несовместна. Тогда прямая L1 и плоскость α не пересекаются, т.е. они параллельны.
Ответ. Прямая L1 и плоскость α параллельны, т.е. не имеют общую точку.
Пример 3. Найти точку пересечения прямой в параметрическом виде L1:
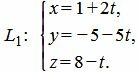 | (30) |
| α: 2x+y−z+11=0. | (31) |
Решение. Для нахождения точки пересечения прямой L1 и плоскости α нужно найти такое значение t, при котором точка M(x, y, z) удовлетворяет уравнению (31). Поэтому подставим значения x, y, z из (30) в (31):
| 2(1+2t)+(−5−5t)−(8−t)+11=0. |
| 2+4t−5−5t−8+t+11=0. | (32) |
Упростив уравнение, получим:
Как видим, любое значение t удовлетворяет уравнению (33), т.е. любая точка на прямой L1 удовлетворяет уравнению плоскости α. Следовательно прямая L1 лежит на плоскости α.
Ответ. Прямая L1 лежит на плоскости α.
http://zaochnik.com/spravochnik/matematika/prjamaja-ploskost/koordinaty-tochki-peresechenija-prjamoj-i-ploskost/
http://matworld.ru/analytic-geometry/tochka-peresechenija-prjamoj-i-ploskosti.php
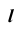
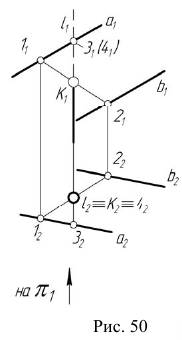
 — горизонтально- проецирующая, то вторая проекция точки пересечения заданной прямой с плоскостью совпадает с вы- рожденной проекцией прямой
— горизонтально- проецирующая, то вторая проекция точки пересечения заданной прямой с плоскостью совпадает с вы- рожденной проекцией прямой  Отметим горизонтальную проекцию
Отметим горизонтальную проекцию 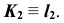
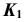 определим по принадлежности точки K плоскости
определим по принадлежности точки K плоскости 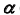 (задача 3).
(задача 3).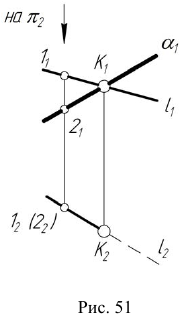
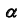 — фронтально- проецирующая, следовательно, проекция
— фронтально- проецирующая, следовательно, проекция 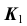 определится на пересечении фронтальных проекций прямой и плоскости
определится на пересечении фронтальных проекций прямой и плоскости 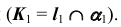
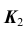 определим по принадлежности точки K прямой
определим по принадлежности точки K прямой 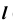 (задача 1).
(задача 1).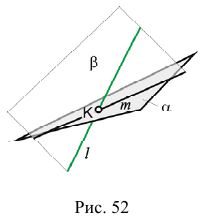
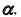
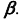
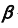 — фронтально-проецирующая, то первая проекция линии m совпадает с вырожденной (фронтальной) проекцией плоскости
— фронтально-проецирующая, то первая проекция линии m совпадает с вырожденной (фронтальной) проекцией плоскости 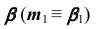 (рис. 53, б).
(рис. 53, б).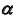 (задача 2).
(задача 2).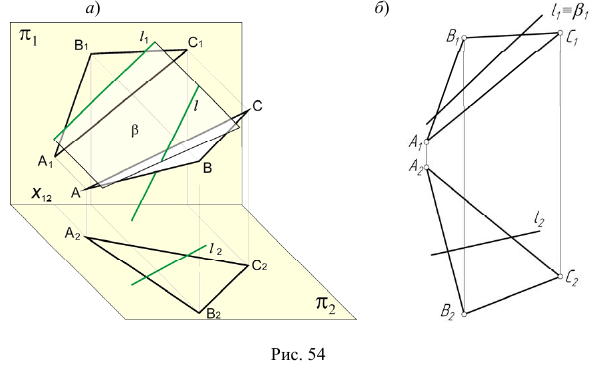
 и линии проекционной связи отметим проекцию
и линии проекционной связи отметим проекцию  (рис. 55, б).
(рис. 55, б).