Уравнение траектории снаряда имеет вид

Как рассчитать движение снаряда

Когда объект запускается, он следует параболическому пути и движению, известному как движение снаряда. В этом посте мы рассмотрим параметры и способы их расчета. движение снаряда в подробном анализе.

Когда объект запускается и движется по симметричной параболической траектории, движение называется движением снаряда, а параболический путь объекта называется его траекторией. В этом случае объект перемещается одновременно по вертикали и горизонтали. В результате движение снаряда становится двумерным. При движении снаряда вам нужно только приложить силу в начале траектории; после этого на объект действует только сила тяжести.

Теперь давайте посмотрим, как рассчитать движение снаряда:

Предположим, вы стреляете пушечным ядром. Он начинает двигаться вверх и вперед, пока не достигнет максимальной высоты. С этого момента он будет продолжать двигаться вперед, но в нисходящем направлении. Он отслеживает этот изогнутый маршрут, известный как траектория, имеющая форму параболы. Любой объект, движущийся таким образом, называется движущимся снарядом. Поскольку траектория движения снаряда всегда параболическая, она представляется как:

у = ах + bx 2

Прежде чем достичь Земли, пушечное ядро ​​во время своего путешествия пойдет по параболическому маршруту. скорость по оси X остается постоянной на протяжении всего движения, тогда как скорость по оси Y изменяется в зависимости от его положения. Только ускорение свободного падения 9.8 м / с 2 , управляет этим типом движения. Ускорение, направленное вниз, остается постоянным во время полета ядер.

Кинематические уравнения движения снаряда:

Формула начальной скорости:

Предположим, что начальная скорость равна u, а угол полета снаряда равен. У начальной скорости есть две составляющие: горизонтальная и вертикальная.

Горизонтальная составляющая начальной скорости u_x и предоставлено:

u_x = ты ᐧ потому что𝛳

Вертикальная составляющая начальной скорости равна uy и определяется выражением:

Время полета снаряда:

Время полета снаряда — это промежуток времени между запускаемым объектом и достижением земли. Величина стартовой скорости и угол полета снаряда определяют время полета, которое обозначается T.

Формула ускорения:

В горизонтальном направлении ускорение отсутствует, поскольку горизонтальная составляющая ускорения остается постоянной на протяжении всего движения. Единственное ускорение в вертикальном направлении происходит за счет силы тяжести.

Отрицательный знак означает ускорение вниз.

Формула скорости в момент времени t:

На протяжении всего движения горизонтальная составляющая скорости остается постоянной. Однако, поскольку вертикальное ускорение постоянно, вертикальная составляющая скорости изменяется линейно.

В результате скорость может быть рассчитана в любой момент времени t по следующей формуле:

v_y = u ᐧ sin𝛳 — g ᐧ t

Используя теорему Пифагора, можно найти величину скорости.

Формула смещения в момент времени t:

В момент времени t смещение может быть определено как:

y = (u ᐧ sin𝛳) ᐧ t — ½ (gt 2 )

Формула параболической траектории:

Мы можем использовать уравнения смещения в направлениях x и y, чтобы вывести уравнение для параболической формы движения снаряда:

Формула дальности снаряда:

Общее горизонтальное расстояние, пройденное объектом за время полета, определяется как его дальность. Если объект запускается с земли (начальная высота = 0), формула выглядит следующим образом:

Согласно приведенному выше уравнению, максимальная дальность полета по горизонтали может быть получена при угле полета снаряда 𝛳 = 45 °. Rm представляет собой максимальный диапазон.

Формула максимальной высоты:

Когда вертикальная составляющая скорости равна нулю, v_y = 0, максимальная высота может быть достигнута. Поскольку время полета — это полное время снаряда, для достижения максимальной высоты потребуется половина этого времени. Таким образом, время для достижения максимальной высоты составляет:

Таким образом, из уравнения перемещения максимальная высота может быть определена как:

Формула движения снаряда по горизонтали:

Горизонтальный снаряд Движение — это тип движения снаряда, при котором объект запускается горизонтально с возвышенной плоскости, а не с земли.

Угол запуска указывать не нужно, поскольку он параллелен земле (т. Е. Угол равен 0 °). В результате у нас есть только одна начальная составляющая скорости: Vx = V, тогда как Vy = 0.

В этом случае уравнения движения следующие:

Скорость горизонтального движения снаряда:

Горизонтальная скорость: v_x = V

И вертикальная скорость: v_x = -g ᐧ т

Расстояние, пройденное объектом при горизонтальном движении снаряда:

В этом случае горизонтальное расстояние рассчитывается следующим образом:

А расстояние по вертикали можно определить как:

y = — (g ᐧ t 2 ) / 2

Ускорение при горизонтальном движении снаряда:

Горизонтальное ускорение а_x = 0, поскольку горизонтальная скорость постоянна.

Вертикальное ускорение а_y = -г

Уравнение траектории горизонтального движения снаряда:

Уравнение траектории в этом случае может быть задано следующим образом:

Время полета при горизонтальном движении снаряда:

Время полета в этом случае может быть определено как:

Дальность полета снаряда при горизонтальном движении снаряда:

Дальность полета снаряда при горизонтальном движении снаряда составляет:

Поскольку мы запускаем объект с максимальной высоты, нам не нужно рассчитывать максимальную высоту в этом сценарии.

Давайте посмотрим на некоторые проблемы движения снаряда.

Проблема 1: Каким будет θmax, при котором расстояние от частицы до метателя всегда увеличивается до конца пути снова у земли?

Решение: Горизонтальное расстояние, пройденное объектом, называется его горизонтальным диапазоном и определяется по формуле:

Максимальная дальность полета может быть достигнута при угле выстрела 45 °.

Таким образом, для максимального угла Rm θmax = 45 °.

Задача 2: Если мяч брошен вертикально вверх со скоростью u, расстояние, пройденное за последние t секунд его всплытия, будет:

Решение: Поскольку мяч брошен вертикально, угол полета снаряда 𝛳 = 90 °.

Где Tm — время, необходимое объекту для достижения максимальной высоты.

Предположим, что h представляет собой расстояние, пройденное объектом за последние t секунд его подъема. Затем скорость в этот момент рассчитывается следующим образом:

Таким образом, расстояние, пройденное за последнюю t секунду, составляет:

3 задачи: Частица проецируется под углом 60 ° над горизонтом со скоростью 10 м / с. Через некоторое время скорость составит угол 30 ° от горизонтали. Скорость частицы в этот момент составляет?

Решение: Горизонтальная составляющая скорости определяется как:

v_x = ты ᐧ потому что𝛳

Здесь в первом случае угол проекции составляет 60 °, а начальная скорость u = 10 м / с. Таким образом,

Теперь вертикальная составляющая скорости v_y изменяется во время движения, но v_x остается постоянным. Таким образом,

Где 𝛳2 = 30 °, а v — скорость, когда объект составляет угол 𝛳 = 30 ° с горизонтом.

Последние выпуски в области передовой науки и исследований

Уравнение траектории снаряда имеет вид

2017-10-05
Зенитное орудие может сообщить снаряду начальную скорость $v_<0>$ в любом направлении. Требуется найти зону поражения, т. е. границу, отделяющую цели, до которых снаряд из данного орудия может долететь, от недостижимых целей. Сопротивлением воздуха пренебречь.

рис.1

рис.2
Попробуем сначала выяснить, что можно сказать об этой границе, не решая задачи. Сам факт существования такой границы сомнений не вызывает, так что поставленный в задаче вопрос имеет смысл (кстати, начиная решать задачу, никогда не вредно подумать об этом). Попытаемся представить себе искомую границу. Очевидно, что она представляет собой некоторую поверхность. Если цель находится точно над орудием, то стрелять нужно вертикально вверх. Снаряд при этом поднимается на высоту $h = v_<0>^<2>/2g$, после чего начинает падать вниз, так что граница достижимых целей пересекает вертикаль в точке, находящейся на высоте $h$.

Если ограничиться целями, находящимися на горизонтальной плоскости, то очевидно, что граница представляет собой окружность, радиус которой равен максимальной дальности полета снаряда по горизонтали $s = v_<0>^<2>/g$ (напомним, что максимальная дальность полета по горизонтали достигается при угле возвышения ствола орудия $\alpha = \pi /4$). Эта окружность есть пересечение искомой поверхности с горизонтальной плоскостью (рис.). Вообще из симметрии можно сделать вывод, что искомая поверхность представляет собой поверхность вращения некоторой кривой вокруг вертикали, проходящей через орудие, и задача сводится к нахождению этой кривой. Отметим, что кривая есть огибающая всех возможных траекторий (рис. 2).

Приступим к решению задачи. Выберем систему координат: орудие расположим в начале координат, ось х направим горизонтально, ось $y$ — вертикально. Тогда зависимость координат снаряда от времени имеет вид

$x(t) = v_ <0>\cos \alpha t, y(t) = v_ <0>\sin \alpha t — \frac><2>$.

Исключив из этих уравнений $t$, получим уравнение траектории снаряда $y=f(x)$:

$y = x tg \alpha — \frac><2v_<0>> (1 + tg^ <2>\alpha)$. (1)

Это уравнение параболы. Коэффициенты при $x$ и $x^<2>$ зависят от угла $\alpha$, т. е. при разных направлениях начальной скорости получаются различные траектории. Таким образом, данное уравнение описывает семейство траекторий при одних и тех же по модулю, но различных по направлению начальных скоростях $v_<0>$.

Но этому же уравнению можно придать и другой смысл. Будем теперь рассматривать х и у как координаты определенной цели, в которую попадает снаряд, двигаясь по некоторой траектории. Тогда при заданных координатах цели х и у уравнение (1) определяет угол, под которым нужно выпустить снаряд с начальной скоростью $v_<0>$ для того, чтобы он попал в эту цель. Решая это квадратное относительно $tg \alpha$ уравнение, находим

Если уравнение имеет вещественное решение, т. е. дискриминант неотрицателен:

то в цель попасть можно. Если вещественных решений нет, т. е.

то в цель попасть нельзя. Это значит, что цель находится за пределами искомой границы. Координаты цели, расположенной на границе, должны удовлетворять соотношению $v_<0>^ <4>— g(gx^ <2>+ 2v_<0>^ <2>y) = 0$. Выражая отсюда у как функцию х, получаем уравнение границы в явном виде:

Это уравнение параболы с вершиной при $x = 0, y = v_<0>^<2>/2g$. Коэффициент при $x^<2>$ отрицателен, т. е. ветви параболы направлены вниз и пересекают горизонтальную ось в точках $x = \pm v_<0>^<2>/g$ (рис. 2), Итак, полученная граница действительно проходит через точки, которые вначале были нами установлены из элементарных соображений.

Мы нашли сечение граничной поверхности вертикальной плоскостью, проходящей через начало координат. Вся поверхность может быть получена вращением этой параболы вокруг оси у.

В связи с приведенным решением сделаем еще несколько замечаний. Рассмотрим какую-либо точку, находящуюся ближе границы (например, точку А на рис. 2). Для такой точки подкоренное выражение в формуле (2) положительно, и, следовательно, через нее проходят две траектории (при заданном значении начальной скорости), соответствующие двум возможным значениям угла $\alpha$.

В баллистике одна из этих траекторий называется настильной, а другая, касающаяся границы до попадания в цель,— навесной. Через каждую точку, принадлежащую границе, проходит лишь одна траектория. Отметим, что граница является огибающей для семейства траекторий при различных направлениях начальной скорости и фиксированном значении начальной скорости $v_<0>$.

Приведем другой возможный путь решения этой задачи, связанный с еще одной трактовкой уравнения (1). Рассмотрим цели, находящиеся на одной вертикали, отстоящей от орудия на расстояние $x$, и найдем на ней самую высокую точку, в которую еще может попасть снаряд. Эта точка, очевидно, принадлежит границе. Таким образом, задача сводится к нахождению максимума у, т. е. правой части уравнения (1), рассматриваемой как функция угла $\alpha$. Правая часть есть квадратный трехчлен относительно $tg \alpha$ и имеет максимум при $tg \alpha = v_<0>^ <2>/ gx$. Соответствующее максимуму значение у получается подстановкой этого значения $tg \alpha$ в уравнение (1):

что совпадает с полученным ранее уравнением границы (4).

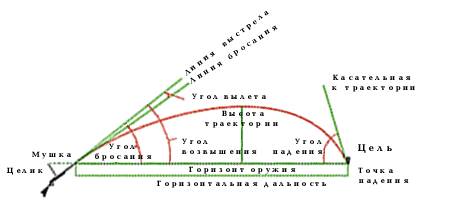
ЭЛЕМЕНТЫ Траектории полета снаряда

Свободным полётом снаряда называется фаза его движения после выстрела до попадания в твёрдое препятствие (цель, грунт) или до дистанционного подрыва. В этом процессе на снаряд действуют только сила тяжести и силы, возникающие при движении тела в газообразной среде (атмосфере Земли). В общем случае в атмосфере Земли также могут существовать упорядоченные движения масс воздуха (ветер), которые оказывают определённое влияние на полёт снаряда.

Путь, описываемый центром тяжести снаряда в пространстве после вылета его из канала ствола, называется траекторией.

Принято считать за траекторию полёта снаряда кривую, которую при движении описывает его центр масс. Эта кривая также имеет название баллистической. В самом общем случае она не является ни прямой, ни параболической, ни даже плоской.

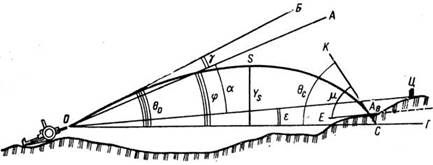
Основные элементами траектории (рис.1) являются:

Рис.1. Элементы траектории артиллерийского снаряда и пули

1. Точка вылетаО — центр дульного среза орудия.

2. Горизонт орудия ОС— горизонтальная плоскость, проходящая через точку вылета.

3. Точка падения С — точка пересечения траектории с горизонтом орудия.

4. Точка встречи Ав — точка встречи снаряда с преградой.

5. Линия выстрела ОА — направление оси канала ствола наведенного орудия.

6. Линия бросания ОБ — направление оси канала ствола в момент вылета снаряда; из-за вибрации ствола в момент вылета снаряда, линия бросания не совпадает с линией выстрела.

7. Линия цели ОЦ — прямая, проходящая через точку вылета и цель,

8. Угол прицеливания α(альфа) — угол между линией цели ОЦ и линией выстрела ОА.

9. Угол места цели ε(эпсилон) — угол между горизонтом орудия ОС и линией цели ОЦ, угол места цели считается положительным, когда цель выше горизонта орудия, и отрицательным, когда цель ниже горизонта орудия.

10. Угол возвышения φ(фи) — угол между горизонтом орудия ОС и линией выстрела ОА.

11. Угол вылета γ(гамма) — угол между линией выстрела ОА и линией бросания ОБ.

12. Угол бросания θ₀ (тета) — угол между горизонтом орудия ОС и линией бросания ОБ.

13. Угол падения θ_с (тета) — угол между горизонтом орудия ОС и касательной к траектории в точке падения.

14. Угол встречи μ(мю) — угол между касательной к траектории в точке встречи и плоскостью, касательной к поверхности цели (преграды) в той же точке; угол встречи может быть от 0 до 90°.

15. Вершина траектории S — точка траектории, превышение которой над горизонтом орудия ОС является наибольшим.

16. Высота траектории — вертикальное расстояние от горизонта орудия ОС до вершины траектории S.

17. Восходящая ветвьОS — отрезок траектории от точки вылета до вершины траектории.

18. Нисходящая ветвь SС — отрезок траектории от ее вершины до точки падения.

19. Дальность до цели ОЦ — расстояние по прямой от орудия до цели.

С увеличением угла возвышения увеличивается и дальность падения снаряда, однако увеличение дальности имеет предел. В безвоздушном пространстве наибольшая дальность получилась бы при угле возвышения 45°. При дальнейшем увеличении угла возвышения снаряд полетел бы выше, но дальность падения уменьшилась бы. То же происходит и при стрельбе в действительных условиях, но траектория снаряда имеет другую форму.

Мерой крутизны траектории является величина угла возвышения φ (фи). Траекторию с углом возвышения не более 20° принято называть отлогой, а траекторию с углом возвышения более 20°— крутой.

Стрельбу, при которой траектория получается отлогой, называют настильной. Стрельбу, при которой траектория получается крутой, называют навесной.

Навесную стрельбу при углах возвышения более 45° называют мортирной.

Траектория снаряда в воздухе значительно отличается от траектории в безвоздушном пространстве (рис.2).

В безвоздушном пространстве траектория снаряда симметрична относительно вершины траектории, а в действительных условиях траектория несимметрична, нисходящая ветвь траектории короче и круче восходящей; угол падения больше угла возвышения; вершина траектории находится ближе к точке падения.

Восходящие Ветви

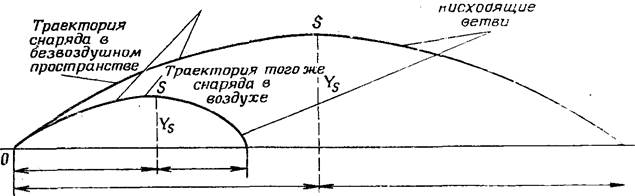Рис. 2. Траектория снаряда в безвоздушном пространстве и в воздухе

Под действием силы сопротивления воздуха снаряд за каждую секунду проходит меньшее расстояние по направлению оси канала ствола, а понижается на ту же величину, что и в безвоздушном пространстве. В результате этого траектория в воздухе будет ниже и короче, чем в безвоздушном пространстве.

Угол бросания, отвечающий наибольшей дальности, при стрельбе в воздухе зависит от начальной скорости, массы и формы снаряда, а также от способа стабилизации снаряда на полете и может находиться в пределах от 28 до 55°.

При стрельбе из танков, БМП, противотанковых орудий и гранатометов и стрелкового оружия используются обычно настильные траектории. Чем меньше высота траектории и чем меньше угол падения, тем траектория более настильна.

Траектория в воздухе имеет следующие свойства:

§ траектория несимметрична, ее нисходящая ветвь короче и круче восходящей.

§ вершина траектории находится ближе к точке падения.

§ угол падения больше угла бросания.

У снаряда, движущегося в воздухе, окончательная скорость меньше начальной.