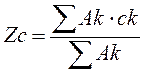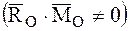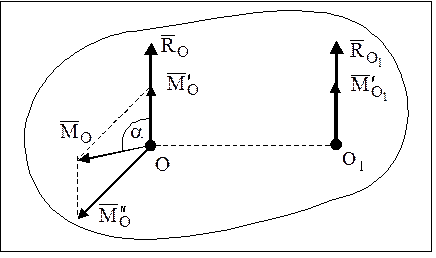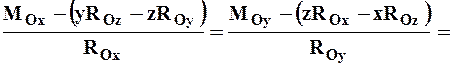Приведение системы сил к динаме. Уравнение центральной оси.
R0*≠0 и М0*≠0(R* перпенд М0*; R* парал М0*) – система сил сходится в динаме, ось которой не проходит через центр приведения (сложное движение)
25-26) Если произвольная пространственная система сил приведена к равнодействующей, то момент этой равнодействующей относительно произвольного центра равен геометрической сумме моментов составляющих сил относительно этого же центра.
28) 



Центр тяжести тела – точка приложения его силы тяжести. Силы тяжести элементов тела представляют собой систему сходящихся сил, линии действия которых пересекаются в центре земли, однако угла между ними настолько малы. что ими пренебрегают, поэтому эту систему можно рассматривать как систему параллельных сил и используются те же формулы.




центр тяжести плоской фигуры (Ак – площадь)
29 Методы нахождения центра тела:
(1) Метод симметрии. Если объемное тело имеет плоскость или ось симметрии, то центр тяжести тела расположен на этой оси в этой плоскости. Если плоское тело имеет 2 оси симметрии то центр тяжести расположен на пересечении этих осей. (2) Метод разбиения на части. Любой тело можно разбить на части для которых известны координаты центра тяжести этих частей, а также площади массы объёмы элементов известны. Если плоское тело состоит из 3-х элементов, то центр тяжести такого тела находится в пределах треугольника, ограниченного линиями соединяющими центр тяжести элементов сечении. (3)Метод ортогональных площадей. В том случае если тело имеет вырезы, полости и т.д. необходимо применять метод разбиения на части при условии, что массы площади и объёмы свободных полостей считаются отрицательными.
Центры тяжести некоторых фигур.
Прямоугольник – центр тяжести на пересечении диагоналей.
Треугольник – центр тяжести на пересечении медиан.
Дуга окружности: 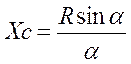
Круговой сектор 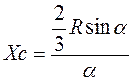
Полукруг: 
Круговой сегмент: Для получения координаты необходимо разбивать сечение на круговой сектор и равнобедренный треугольник и затем применить метод отрицательных площадей.
Конус, пирамида: Центр тяжести находится от основания пирамиды на расстоянии равной ¼ высоты.
Кинематика
1) Кинематика – раздел теоретической механики изучающий законы механического движения материальных точек или тел без учёта причин, вызывающих это движение. Механическое движение – изменение положения тела в пространстве с течением времени. Любое движение точки или тела рассматривается относительно какой-либо системы отсчёта. Обычно систему отсчёта связывают с землёй, считая её неподвижной. Если рассматривать движение тела относительно подвижной системы отсчёта, то при расчётах необходимо учитывать движение подвижной системы отсчёта относительно неподвижной. Траектория точки – геометрическое место последовательных положений точки в процессе её движения. Прямолинейное, если траектория-прямая, в других случаях криволинейное.
Основные задачи кинематики: — определение закона движения точки или тела в выбранной системе отсчёта. — По заданному закону определить кинематические характеристики движения.
2)Движение точки считается заданным, если существует зависимость, позволяющая определить положение точки в пространстве в произвольный момент времени, эта зависимость называется законом движения. Способы задания движения: (1) Естественный – используется. Если известна траектория движения, уравнение движения точки по этой траектории, начало отсчёта и положительное направлении движения. S=S(t) – угловая координата. (2) Векторный – положение описывается радиус-вектором проведённым из некоторой неподвижной точки. r=r(t) уравнение движения при векторном способе. Траектори в данном случае является гадографом радиус-вектора. (3) координатный – положение точки задаётся зависящими от времени дифференцируемыми функциями координат. X=x(t) y=y(t) z=z(t). y=f(x) – уравнение траектории.
3) Величина равная отношению приращения дэльта(r) вектора r к промежуточному времени дэльта(t) за который произошло это приращение называется средней скоростью точки за это время Vср.= дэльта(r)/дэльта(t). При дэльта(t) стремящимся к 0: V= dr/dt скорость точки в данный момент времени. Скорость всегда направлена по касательной к траектории движения.
4)Величина равная отношению приращения дэльта(V) вектора r к промежуточному времени дэльта(t) за который произошло это приращение называется средним ускорением точки за это время a cр.= дэльта(V)/дэльта(t). При дэльта(t) стремящимся к 0: a= dV/dt ускорение точки в данный момент времени. Ускорение всегда направлена по касательной к гадографу вектора скорости.
5)V= dr/dt = d(xi+yj+zk)/dt = Vxi + Vyj + Vzk где Vx=dx/dt, Vy=dy/dt, Vz=dz/dt – проекции вектора скорости на оси координат V=корень(Vx^2+Vy^2+Vz^2)Положени вектора Vопределяется направлением косинусов , а именно углов между направлением вектора V и положительно направленной соответствующей оси координат.
6)V= dS/dt*dr/dS сдесь dS/dt – v – алгебраическая скорость точки, а dr/ds – ŧ(тау) – вектор, направленный по направлению вектора dr. V= ŧ(тау)*v.
7) Если выбрать в качестве осей координат независимые оси ŧ(тау), n, в — которые связаны с движущейся точкой при этом ŧ(тау)-является касательной, n – нормалью , в – бинормалью, тогда ŧ(тау) и n образуют касательную плоскость, n и в нормальную плоскость, в и ŧ(тау) – спрямляющуюся плоскость, это и есть естественный трёхгранник. Нормальное ускорение точки всегда направлено к центру кривизны траектории(a норм. =V^2/q, где q – радиус кривизны траектории), а касательное по касательной к траектории, если знаки касательного ускорения и скорости совпадают, то и направления их тоже совпадают, или наоборот(а ŧ(тау)=dV/dt)
8) Касательное ускорение показывает изменение скорости по величине, нормально – по направлению. Если (а ŧ(тау)=0) и ( a норм.=0) – движение равномерное и прямолинейное, если (а ŧ(тау)=0) и ( a норм. не равно 0) то криволинейное и равномерное, если (а ŧ(тау)не равно 0) и ( a норм.=0) то прямолинейное равномерное, если (а ŧ(тау) не равно 0) и ( a норм. не равно 0) то криволинейное неравномерное. При постоянном а ŧ(тау) движение либо равноускоренное, либо равнозамедленное.
9 Поступательнымназывается такое движение, при котором в теле можно выделить прямую, остающуюся параллельной самой себе в процессе движения. Т-ма: Все точки тела, движущиеся поступательно имеют в данный момент геометрически равные скорости и ускорения и движутся по одинаковым траекториям. Для изучения тела, движущегося поступательно достаточно изучить движение одной его точки, обычно рассматривают центр тяжести.
10 Вращательное движение тела – такое движение твердого тела, при котором точки, принадлежащие некоторой прямой, остаются неподвижными, а остальные точки описывают окружности в плоскости перпендикулярно оси вращения. Уравнение (закон) вращательного движения: j=f(t) – угол поворота тела в радианах. Угловая ск-сть: 
Вектор угловой скорости тела, совершающего вращение вокруг неподвижной оси, направлен вдоль оси вращения так, что если смотреть ему навстречу вращение будет против час. стрелке. Угловое ускорение тела: 
11 Частные случаи вращения тела:
1) Равномерное вращение: w=const, j=wt, w=j/t,
2) Равнопеременное вращение: w=w0+et; 

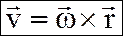
12 Передаточные механизмыпредназначены для передачи вращения от ведущего вала к ведомому. Они реализуются в виде различного рода передач с жёсткой или гибкой связью. Фрекционные передачи функционируют за счёт сцепления между колёсами, зубчатые передают крутящий момент за счёт зацепления между зубьями. Отношение угловой скорости ведущего вала к угловой скорости ведомого называется передаточным числом i. Иногда хар-ка вращательного движения задаётся в виде числа оборотов в минуту.
13 j,w,ε – основные кинематические характеристики вращательного движения твёрдого тела. Они одинаковы для всех точек вращательного твёрдого тела. Скорости и ускорения точек вращающегося тела. 
a=корень((a вращ.)^2+ (a центр.)^2) = (СМ)*корень(w^4+ε^2)
14 
а вращ. равняется (ε x r) где r это (СМ), а центр. равняется (w x V) из этого выразим а:
a=корень((a вращ.)^2+ (a центр.)^2) = (СМ)*корень(w^4+ε^2)

Вопрос 16. Определение скоростей точек плоской фигуры. Теорема о проекциях скоростей точек плоской фигуры.
Теорема: Скорость любой точки принадлежащей плоской фигуре равна геометрической сумме скорости полюса и той скорости которую имела бы точка при вращательном движении вокруг оси проходящей через полюс
Теорема: при плоском движении проекции скоростей двух точек тела на ось, проходящую через эти точки, равны между собой: vAcosa = vBcosb.
Вопрос 17. Мгновенный центр скоростей. Определение скорости с помощью МЦС. Частные случаи нахождения МЦС.
МЦС – точка плоскости движения плоской фигуры, скорость которой в данном положении равна 0.
Скорости всех точек будут направлены перпендикулярно отрезкам соединяющим точку и МЦС в сторону угловой скорости и пропорциональны длинам этих отрезков.
Частные случаи определения м.ц.с.: 1) м.ц.с. – точка пересечения перпендикуляров, восстановленных к скоростям точек (напр. в точке В и точке К); 2) если скорости точек А и В параллельны между собой и перпендикулярны АВ, то для определения м.ц.с. должны быть известны модули и направления скоростей (см. vA и vB); 3) если они при этом равны между собой, то м.ц.с. находится в ¥, а угловая скорость w=vA/¥=0; 4) если известно, что скорости двух точек А и В равны, параллельны и не перпендикулярны АВ, то м.ц.с. в ¥, и угловая скорость w=vA/¥=0, если это имеет место только к некоторый момент времени, то имеем мгновенное поступательное движение; 5) если плоская фигура катится без скольжения по неподвижной поверхности, то м.ц.с. плоской фигуры будет в точке соприкасания.
Вопрос 18. Определение ускорений точек плоской фигуры. Мгновенный центр ускорений.
Ускорение любой точки плоской фигуры равно векторной сумме ускорения полюса и ускорения точки которое она имела бы при вращательном движении тела вокруг оси проходящей через полюс.
Существует 2 способа определения ускорений:
Построение многоугольника ускорений
Мгновенный центр ускорений – точка (Q) плоской фигуры, ускорение которой в данный момент времени равно нулю. Для его построения из точки А откладываем под углом 



Вопрос 19. Сферическое движение твёрдого тела. Углы Эйлера. Определение ускорений точек тела при сферическом движении.
Сф.движ – движение твердого тела, одна из точек которого во все время движения остается неподвижной (напр. движение волчка).
Точки тела движутся по сферическим поверхностям. Положение тела определяют при помощи трех углов. Для этого задаются две системы координат: неподвижная Оxyz и подвижная ОxhV, связанная с твердым телом. Линия ОJ – линия узлов, задаются углы: Y – угол прецессии, q – угол нутации, j – угол собственного вращения — углы Эйлера. Таким образом уравнения сферического движения: Y=f1(t); q=f2(t); j=f3(t). Углы отсчитываются от осей против хода час.стр.
Уравнение центральной винтовой оси




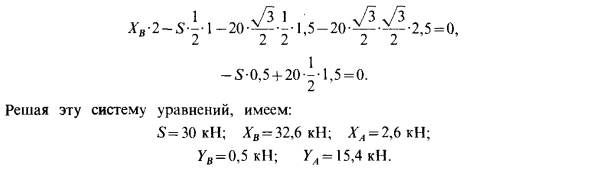
Уравнение центральной винтовой оси
- Предположим, что главный вектор Lo проецируется на координатные оси Rx, Ry и Rz, а главный момент Lo получается на проекции Lx и Ly с центром редукции ^ в качестве начала координат. Когда система сил движется к центру редукции O (рис. 78), обнаруживается динамо с главным вектором A, = A и главным моментом LOl. Векторы LO1 и A, как генераторы динамо, параллельны, поэтому отличается только скалярный коэффициент k0. У нас есть Lo-k0R, _ _ (9) Согласно (2), поскольку Rt = R, основные моменты LOi и Lo удовлетворяют следующему соотношению: EOi = Lo
OO, xR. (2 ‘) Подставляя LOi из (2 ‘) в (9) Lo-Od, xR = knR. (9 ‘) Координаты точки O, из которой получается динамо, обозначены x, y, z.
Тогда проекция вектора OOt на оси координат равна координатам x, y, r. Учитывая это, (9 ‘) можно выразить в следующем виде: (Lxi + Lj + LZE) -x Jy AH A, = k0 (Rxi + Ryj + Rjc), Aj Где i, j и А — единичные векторы векторного произведения осей координат и OO, а x A выражается определителем. Векторное уравнение (9 «) соответствует трем скалярным уравнениям и может быть выражено следующим образом после отбрасывания Lo: £, — (yY, -? I,) _ £, — (rY, -xY,) _ I, I, (9 «) Рисунок 78 Рис. 79 Линейное уравнение (10) для координат x, y и z является уравнением спиральной оси с линейным центром. Таким образом, в точке, где система сил сводится к двойственности, есть прямая линия. Пример 1.
Такая линеаризация, конечно, в некоторой степени искажает действительное изображение движения, но чем меньше отклонение системы от устойчивого положения равновесия, тем точнее получается линеаризованное изображение. Людмила Фирмаль
В конце куба с длиной стороны 1 = 3 м действуют силы Fj = Fr = 2_H и F3 = l H (рис. 79). Приносит систему питания F, F2. Е3 в простейшем виде. Решения. Выберите точку O (начало координат) в качестве центра уменьшения силы и рассчитайте главный вектор R и главный момент Lo. для Проекции на оси этих векторов K = Y.Fix = F2 = 2B; Rr = ^ Flt = F3 = i H-. Rn- £ /? = £, = 2 H; ix = XWx (F;) = 0; Координаты у нас есть: Z.z = £ m, (F) = F3 / -F2 / = -3Hm.
Значение основного вектора и значение главного момента составляют R = ^ R2x + R ^ + R ^ = y / 9 = 3 Н. £ 0 = V / ZJ + ZJ + IJ = V / 45 = 6,8 Нм Определите угол a между векторами Eo и R. Для этого сформируем скалярное произведение. Это выражается в двух формах: Eo-R = LoRcos
- Один конец — это сечение _A, и нормальная сила P прикладывается в точке B (рис. 81, а). Надежно прикрепите балку CD к балке AB секции C под прямым углом. На конце балки I в плоскости, параллельной координатной плоскости Ayz, действует пара сил с моментом M = Ra. Направление вращения пары размеров и сил показано на рисунке. Определяет момент силы пары вложенных сил. Решения. Лучи B и CD, рассматриваемые вместе, освобождаются от галстуков. Вложение системы пространства сил создает неизвестную силу Ra, спроецированную на ось координат силы X с вектором. Момент Отологон Динат М.Л., (Рисунок £ Flx = 0; * l = 0; £ f (, = 0; ya = Q; £ F „= 0; ZA — P = O; Y.
Для того, чтобы определить силу реакции упорного подшипника, п Людмила Фирмаль
Что касается проекции сил на оси координат, то здесь есть следующее. EG (x = 0;% 4 + Uv-Psin asin p-Ssiny = 0; 1 EFf = 0; Ul + rB + Pcosa-Scosy = 0;> EF (, = 0; Z4-Psin acos P = 0. При определении проекции силы P на оси координат сначала разбейте ее на две вертикальные составляющие. Одна параллельна оси Oy и имеет проекцию на эту ось P = Pcosa. Вертикальный компонент расположен в плоскости оси и имеет проекционное значение в этой плоскости. (А) Спроецируйте силу P как вектор на оси Ax и Ar. В P, = -P „sin p = -Psin a sin p; P, = P„ cosp = Psinacosp.
За момент силы вокруг осей получим … МЖ (Р,) = О; -Gv (/, + / 2) + Scosy /, -Pcosa (Z, + / 2 + / 3) = 0;] EM, (A) = 0; XB (Z, + / 2) -Ссины / 1- Я -Psin acos pZ „-Psin asin p (Z, + 12 + Z3) = 0; EA / I (F,) = 0; -SP + PcosaZ4 = 0. По определению, при расчете момента силы вокруг координатной оси, спроецируйте силу на плоскость, перпендикулярную оси, и рассчитайте момент проекции силы относительно пересечения оси и плоскости. Сила, параллельная или пересекающая ось, дает нулевой момент вокруг этой оси.
При определении момента силы S для осей координат он разлагается на компоненты, параллельные осям координат, вычисляет момент каждого компонента для соответствующих координатных осей на основе теоремы Баринона и добавляет их алгебраически. Значения составляющих сил равны проекции этих сил на оси и могут быть получены из уравнения (а). Момент силы R. рассчитывается аналогично. Решите систему линейных уравнений (а) и (б) для проекции неизвестных сил. Могу решить Подставляя уравнение (а) и угол, оно становится следующим.
Если вам потребуется помощь по теоретической механике вы всегда можете написать мне в whatsapp.




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Приведение системы сил к динаме
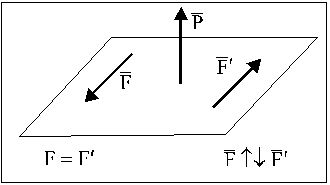
Определение: Система, состоящая из силы и пары сил, момент которой коллинеарен силе (плоскость пары перпендикулярна линии действия силы), называется динамой или динамическим винтом (рис. 30) .
Если при приведении системы сил к центру О второй инвариант не равен нулю, то эта система сил приводится к динаме (рис. 31).
Разложив 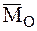
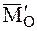
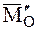
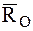
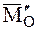
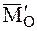
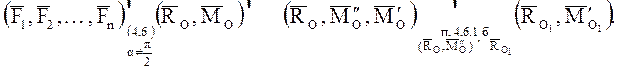
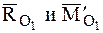
где 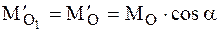
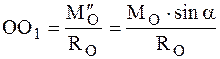
В рассматриваемом случае приведения системы сил главный момент 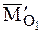
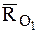
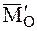
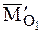
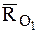
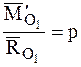
В соответствии с соотношениями (4.16) и (4.17)
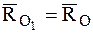
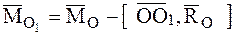
тогда уравнение центральной оси динамы в векторной форме можно записать так:
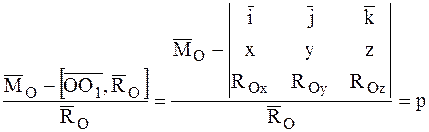
Проектируя это соотношение на оси декартовой системы координат с началом в центре приведения О, получим:
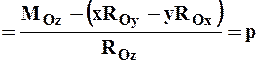
Здесь x, y, z – координаты точек, лежащих на центральной оси, а р – постоянная линейная величина, называемая параметром динамы.
4.7. Алгоритм решения задач по приведению систем сил к простейшим системам – схема алгоритма
Дата добавления: 2015-08-01 ; просмотров: 2411 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
http://lfirmal.com/uravnenie-centralnoj-vintovoj-osi/
http://helpiks.org/4-41341.html