Уравнение цепной линии для провода

Уравнение цепной линии для провода

Кривая, форма которой соответствует однородной гибкой нерастяжимой тяжелой нити, закрепленной с обоих концов и находящейся под действием силы тяжести, называется цепной линией. Очевидно, цепная линия является плоской кривой, то есть такой кривой, все точки которой лежат в одной плоскости.

Долгое время считалось, что цепная линия представляет собой параболу, подобно тому, как траектория движения камня в поле земного тяготения есть парабола. Однако уже в начале 17 века великий итальянский мыслитель Галилео Галилей высказал предположения, что цепная линия не является параболой. Строгое решение задачи с выводом уравнения цепной линии впервые было найдено в трудах великих немецких мыслителей Готфрида Лейбница и Иоганна Бернулли, а также великого нидерландского естествоиспытателя Христиана Гюйгенса в 1691 году.

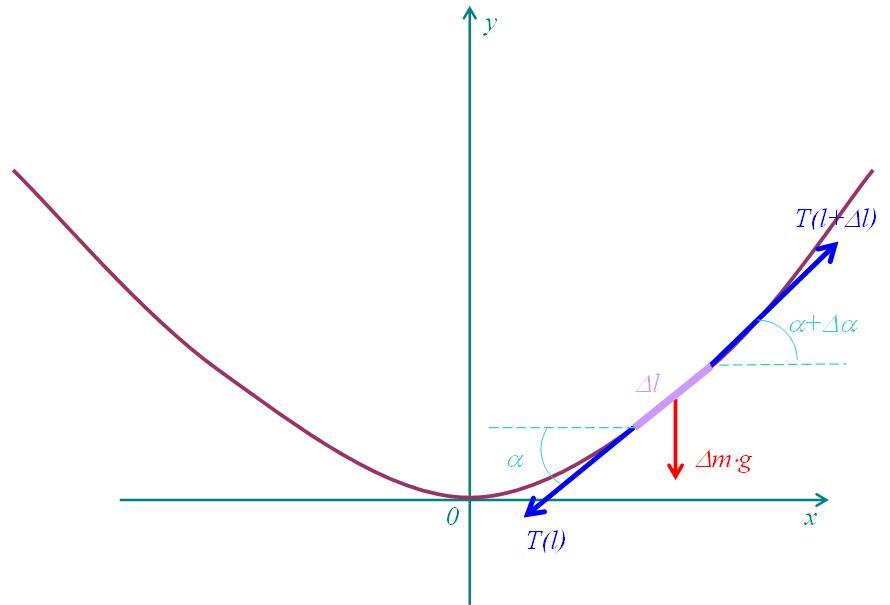
Рассмотрим элементарный участок нити длиной \(\Delta l\) (Рисунок 3). Масса этого участка равна \(\Delta m = \rho S \Delta l\) и на него действуют распределенная по длине сила тяжести интенсивности \(\rho gS\), направленная вниз и равная \(\Delta m g = \rho g S \Delta l\). Здесь \(\rho\) — объемная плотность материала нити, \(g\) — ускорение свободного падения, \(S\) — площадь поперечного сечения нити.

Также на концах данного участка действуют силы натяжения \(T(l)\) и \(T(l+\Delta l)\).

Рисунок 1. Цепи, используемые при штабелирование парахода “Бремен”. Фото из Федерального архива Германии.
Bundesarchiv Bild 102-06406, Bremen, Stapellauf des Dampfers «Bremen».

Рисунок 2. Цепи ограждения Царь-пушки в московском кремле. http://www.fotokonkurs.ru/photo/58515

Условие равновесия рассматриваемого участка запишется в виде: $$ \vec T(l) + \vec T(l+\Delta l) + \Delta m\vec g = 0. $$ В проекции на оси координат получим $$ — T(l)\cos(\alpha) + T(l+\Delta l)\cos(\alpha + \Delta \alpha) = 0. $$ $$ — T(l)\sin(\alpha) + T(l+\Delta l)\sin(\alpha + \Delta \alpha) — \rho gS\Delta l = 0.$$ Из первого уравнения получаем, что горизонтальная компонента силы натяжения \(T(l)\) всегда постоянна: \( T(l)\cos\alpha(l) = T_0 = const.\) Второе уравнение перепишем в виде: $$ d(T(l)\sin(\alpha(l)) = d(\rho gSl).$$ С учётом сказанного, можем записать $$ T_0 d(tg(\alpha(l)) = \rho gSdl).$$ Памятуя о геометрическом смысле производной, запишем \(tg\alpha = y’\) и тогда получим $$\frac

= \frac<\rho gS>.$$ Переходя к переменной x, используя правило дифференцирования сложной функции и выражение для дифференциала дуги кривой, получим $$\frac

= \frac \cdot \frac

= \frac \cdot \frac> = $$ $$ = \frac \cdot \frac <1><\sqrt<1+(y')^2>> = \frac <\rho gS>.$$ Отсюда, учитывая, что производная от первой производной есть вторая производная, получаем $$y» = \frac <\rho gS> \cdot \sqrt<1+(y')^2>.$$
Последнее уравнение называется дифференциальным уравнением цепной линии. Это уравнение второго порядка, допускающее понижение порядка. Чтобы понизить порядок уравнения сделаем замену \(z(x)=y’\). Тогда \(y»=z’\). Подставляя в последнее дифференциальное уравнение, получим $$\frac = z’ \frac <\rho gS> \cdot \sqrt<1+z^2>.$$

Рисунок 3. Ценная линия и расчётная схема.

Получили уравнение с разделяющимися переменными, которое после элементарных преобразований принимает вид $$\frac<\sqrt<1+z^2>> = \frac<\rho gS> \cdot dx.$$ Интегрируем последнее уравнение $$\int\frac<\sqrt<1+z^2>> = \frac<\rho gS> \int dx,$$ $$\ln|z + \sqrt<1+z^2>| = \frac<\rho gS> \cdot x + C_1.$$ Принимая за начало координат нижнюю точку цепной линии, заметим, что касательная в нижней точке горизонтальная, другими словами, нижняя точка является точкой экстремума для функции \(y(x)\). Следовательно, \(y’(0)=z(0)=0\). Подставим в последнее выражение \(x=0, y=0, z=0\). В результате получим \(С_1 = 0\). Тогда уравнение цепной линии перепишется в виде $$\ln|z + \sqrt<1+z^2>| = \frac<\rho gS> \cdot x.$$ Потенцируя полученное уравнение, перепишем его в показательной форме

Здесь для сокращения записи мы ввели обозначение \(\frac<\rho gS> = \kappa.\)
Умножим обе части уравнение (1) на выражение сопряжённое к левой части \(z-\sqrt<1+z^2>\). Получим $$(z + \sqrt<1+z^2>)\cdot(z — \sqrt<1+z^2>) = e^<\kappa x>\cdot(z — \sqrt<1+z^2>).$$ Нетрудно заметить, что $$(z + \sqrt<1+z^2>)\cdot(z — \sqrt<1+z^2>) = z^2 — (\sqrt<1+z^2>)^2 = z^2 -1 + z^2 = -1.$$ Вследствие последнего замечания, уравнение можно переписать в виде $$e^<\kappa x>\cdot(z — \sqrt<1+z^2>) = -1.$$ или в виде $$z — \sqrt <1+z^2>= -e^<\kappa x>. $$ Прибавим последнее выражением к выражению (1), и поделим полученное равенство на 2. В результате получим $$z = \frac — e^<-\kappa x>><2>. $$ Определение 1. Гиперболическим синусом от \(x\) называется функция, определённая следующим выражением $$sh(x) = \frac — e^<-x>><2>. $$ Определение 2. Гиперболическим косинусом от \(x\) называется функция, определённая следующим выражением $$sh(x) = \frac + e^<-x>><2>. $$ Предложение 1. Производная от гиперболического косинуса есть гиперболический синус, производная от гиперболического синуса есть гиперболический косинус, то есть$$sh'(x) = ch(x),$$ $$ch'(x) = sh(x).$$ Доказательство. $$sh'(x) = \left(\frac — e^<-x>><2>\right)’ = \frac <(e^— e^<-x>)’> <2>= \frac <(e^)’ — (e^<-x>)’> <2>= \frac <(e^)’ + (e^<-x>)’> <2>= ch(x);$$ $$ch'(x) = \left(\frac + e^<-x>><2>\right)’ = \frac <(e^+ e^<-x>)’> <2>= \frac <(e^)’ + (e^<-x>)’> <2>= \frac <(e^)’ — (e^<-x>)’> <2>= sh(x).$$ Доказательство завершено. ❑

Следствие 1. Первообразная от гиперболического косинуса есть гиперболический синус, а первообразная от гиперболического синуса есть гиперболический косинус.

Следствие 2. $$\int sh(x)dx = ch(x) + C, $$ $$ \int ch(x)dx = sh(x) + C.$$
С учётом сформулированных определений, а также памятуя о сделанной ранее замене \(z(x)\), перепишем выражение для прогиба в следующем виде $$ y’ = z = \frac — e^<-\kappa x>> <2>= sh(\kappa x).$$
На основании предложения 1 и следствий к нему, после интегрирования получим $$ y(x) = \int sh(\kappa x)dx = \frac <1> <\kappa>\cdot ch(\kappa x) + C.$$
В принятой системе координат, когда нижняя точка цепной линии является началом системы координат, справедливо следующее начальное условие \(y(0)=0\). Подставим это условие в найденное уравнение цепной линии и получим $$ y(0) = \frac <\kappa>+ C = 0,$$ $$ \frac <1> <\kappa>\cdot \frac <2>+C = \frac <1> <\kappa>\cdot \frac <1+1> <2>+C = \frac <1> <\kappa>+ C = 0. $$ Отсюда \(С=-\frac <1><\kappa>\) и уравнение цепной линии запишется в виде $$ y(x) = \frac <1> <\kappa>\left(ch(\kappa x) — 1\right).$$
Таким образом, форма цепной линии определяется как гиперболический косинус с параметром \(\kappa\). Кроме гиперболического синуса и гиперболического косинуса существуют также гиперболический тангенс и котангенс, которые определяются по тому же принципу, что и тригонометрический тангенс и котангенс, а именно:

Определение 3. Гиперболическим тангенсом от \(x\) называется функция, определённая следующим выражением $$th(x) = \frac .$$
Определение 4. Гиперболическим котангенсом от \(x\) называется функция, определённая как частное гиперболического скосинуса и гиперболического синуса. То есть гиперболический котангенс это функция, определённая следующим выражением $$cth(x) = \frac .$$
Из сделанных определений следуют равенства $$th(x) \cdot cth(x) = 1;$$ $$th(x) =\frac >>;$$ $$cth(x) =\frac >>.$$
Исследуем ряд других замечательных свойств гиперболических функций.

Предложение 2. Справедливы следующие тождества $$сh^2(x) — sh^2(x) = 1;$$ $$1-th^2(x) = \frac <1>,$$ $$cth^2(x) — 1 = \frac <1>.$$ Доказательство.

Из определений гиперболического косинуса и гиперболического синуса следует: $$ch^2(x) — sh^2(x) = \left(\frac + e^<-x>><2>\right)^2 — \left(\frac <(e^— e^<-x>)><2>\right)^2 = $$ $$ = \frac <(e^)^2 + 2e^xe^ <-x>+ (e^<-x>)^2> <4>— \frac <(e^)^2 — 2e^xe^ <-x>+ (e^<-x>)^2> <4>= e^xe^ <-x>= e^ = e^0 = 1.$$ Первое тождество доказано. Из него следует $$ch^2(x) = 1 + sh^2(x);$$ $$sh^2(x) = ch^2(x) — 1.$$ Тогда $$1 — th^2(x) = 1 — \frac = \frac = \frac <1>.$$ $$cth^2(x) — 1 = \frac — 1 = \frac = \frac <1>.$$ Все три тождества доказаны. ❑

Задание.
Найти производные гиперболического тангенса и гиперболического котангенса.

Решение.
По правилу дифференцирования частного, получим для производной гиперболического тангенса $$th'(x) = \left(\frac\right)’ = \frac = $$ $$ = \frac = \frac = \frac <1>.$$
Аналогично получим производную для функции гиперболический котангенс $$cth'(x) = \left(\frac\right)’ = \frac = $$ $$ = \frac = \frac = — \frac <1>.$$
Таким образом, мы доказали следующие соотношения $$ th'(x) = \frac <1>;$$ $$ cth'(x) = — \frac <1>.$$
Обратим внимание на некоторое сходство полученных тождеств с соответствующими тригонометрическими тождествами.

Уравнение цепной линии для провода

3.4. Расчет натяжений и высотных положений проводов простых контактных подвесок и воздушных ЛЭП

Точное уравнение провисания гибкой нити. В литературе, посвященной расчетам воздушных линий, можно встретить изложение выводов и расчетных формул в двух формах. В первой из них, по­лучившей распространение при расчетах контактной сети, фигу­рируют полные значения натяжений и нагрузок, приходящихся на данный провод. Во второй форме натяжения и нагрузки относят к единице поперечного сечения. В этом случае натяжение заменяет­ся напряжением в проводе, а полная нагрузка — удельной нагруз­кой. Эта форма получила исключительное распространение при расчетах ЛЭП. Ниже все выводы будут даны применительно к пер­вой форме, а расчетные формулы будут даваться в обеих формах.

При изучении работы любой подвески все провода рассматриваются как гибкие нити. Если абсолютно гибкая однородная нить постоянного поперечного сечения подвешена между двумя точками, то под действи­ем собственного веса в нити возникают растягивающие напряжения.

Для исследования кривой провисания нити в ее плоскости проведем оси координат Ох и Оу (рис. 3.18). Выделим элемент нити dL , на который действуют натяжения Т и , заменяющие действие отброшенных частей нити и направленные по касательной к нити. Нагрузку , действующую на этот элемент, можно принять пропорциональной его длине:

,

где q — нагрузка на 1 пог. м нити.

Из условия, что сумма горизонтальных проекций всех сил на ось равна| нулю, получим

,

где — приращение на длине угла , образованного касательной с осью ; — горизонтальная составляющая натяжения нити, равная натяжению нити в самой низшей ее точке.

Из этого уравнения видно, что горизонтальная составляющая на­тяжения по всей длине нити — величина постоянная и, следова­тельно, изменение натяжения по длине нити может иметь место лишь за счет вертикальной составляющей.

Рис. 3.18. Элемент сво­бодно подвешенной нити

Из условия, что сумма проекций всех сил на ось у равна нулю, получим

,

где — приращение углового коэффициента касательной (величины ). Из этого уравнения имеем:

,

, (3.5)

Разделив переменные, находим

(3.6)

(3.7)

Интегрируя уравнение, получим:

(3.8)

Разделив переменные, будем иметь

Интегрируя еще раз, получим уравнение искомой кривой

(3.9)

Поместив начало координат в точку (- , — ), заменим при­веденное уравнение более простым

(3.10)

Кривая, соответствующая полученному уравнению, называет­ся цепной линией.

В выбранной новой системе координат ось ординат является осью симметрии кривой, так как положительные и отрицательные значения при равной их абсолютной величине дают одно и то же значение у. Заменив в уравнении (3.10) х = 0, получим у= т, т.е. равен отрезку на оси между началом координат и наинизшей точ­кой нити (рис. 3.19).

Во многих случаях удобнее располагать начало координат в точке наибольшего провеса нити О. При этом будем иметь при = 0; у = 0 и у’ = 0 (рис. 3.20 ).

Подставляя = 0 в выражения (3.8) и (3.9), найдем

=0 и ₂= , после чего из (3.9) получим

(3.11)

При составлении дальнейших расчетных формул, учитывающих изменение натяжения и стре­лы провеса нити при измене­нии температуры или на­грузки, приходится опериро­вать с длиной нити. Длину нити между точкой начала координат О (см. рис. 3.20) и точкой (х, у) можно найти, проинтегрировав уравнение (3.5). Тогда

(3.12)

Рис. 3.19. Кривая провисания свобод­но подвешенной нити

Длину между точками подвеса можно получить, заменив один раз расстоянием от точки наибольшего провеса (вершины цепной линии) до одной точки подвеса и второй раз — до другой, а затем сложить эти длины. Длина нити на этих участках (см. рис. 3.20) будет равна

.

Если точки подвеса лежат на одной высоте и, следовательно, , где — расстояние между точками подвеса нити (длина пролета), то длина нити равна

.

Упрощенное уравнение провисания гибкой нити. В случае располо­жения точек подвеса проводов на одной высоте выведенные уравнения провисания нити для практически встречающихся в контактной сети условий можно заменить уравнением параболы. Это значительно уп­ростить определение по заданному или наоборот. При учете же из­менения Н или у в зависимости от изменения температуры и нагрузки, о чем будет сказано ниже, та­кая замена становится необхо­димой. Это объясняется тем, что составление точных рас­четных формул в этом случае встречает большие математи­ческие трудности.

Раскладывая правую часть уравнения (3.11) в ряд Маклорена, получим

Рис. 3.20. Кривая провисания свободно подвешенной нити с началом координат в точке наибольшего провисания

Разложив также правую часть уравнения (3.14) в ряд Маклорена, будем иметь

(3.16)

Для встречающихся в практике условий, т. е. когда пролет во много раз больше стрелы провеса , подсчет стрел провеса и длины проводов можно производить приближенно, оставляя в урав­нении (3.15) первый член и в уравнении (3.16) первые два члена. Эти упрощения дают возможность представить уравнение кривой провисания нити в виде параболы. Подставив значение т в формулу (3.15), получим

(3.17)

Разделив числитель и знаменатель этого выражения на S , где S — площадь поперечного сечения нити, и заменив , где -удельная нагрузка на провод, кг/ммм , и напряжение в проводе, кг/мм 2 , получим эту же формулу, выраженную через удельные значения:

. (3.18)

Если точки опоры (точки подвеса нити) расположены на одном уровне, то значение стрелы провеса в точке О (рис. 3.21) может быть получено из уравнения (3.17) подстановкой x = l /2:

(3.19)

или через удельные значения

. (3.20)

Воспользовавшись формулой (3.19), представим y в виде

(3.21)

Рис. 3.21. Кривая провисания свободно подвешенной нити со стрелой провеса

Длина нити после подстановки значения т в уравнение (3.16) будет равна

(3.22)

или после преобразования при помощи уравнения (3.19) получим

(3.23)

Если перенести начало координат в точку подвеса нити (рис. 3.22), заменив у на и на , что в некоторых случаях более удоб­но, то уравнение кривой провисания нити получит вид

(3.24)

Максимальное усилие в нити в общем случае будет иметь мес­то в точке подвеса у той опоры, где имеется наибольшая верти­кальная составляющая опорной реакции или _, где и (см. рис. 3.20 и 3.19).

Если принять, что вес отрезка провода приближенно равен весу провода, имеющего длину, равную длине горизонтальной проекции рассматриваемого отрезка, то при расположении точек подвеса нити на одном уровне:

(3.25)

Рис. 3.22. Кривая провисания нити с расположением начала координат в точке подвеса

Дифференцируя уравнение (3.17), можно получить формулу для тангенса угла наклона касательной к оси , который в значитель­ной степени определяет условия прохода токоприемником точек подвеса:

(3.26)

Для точки опоры, т. е. при х =1/2 , получим

(3.27)

или, выразив при помощи геометрических размеров, из формулы (3.19) получим

(3.28)

Упрощенные формулы (3.17), (3.19), (3.22) могут быть также по­лучены непосредственно из рассмотрения условий равновесия при принятом допущении, что сила тяжести пропорциональна не дли­не элемента, а его проекции на горизонтальную ось. Рассмотрим, исходя из этого допущения, отрезок нити (см. рис. 3.20). В этом случае, взяв относительно точки сумму моментов всех сил, приложенных к отрезку (рис. 3.23), получим

и отсюда уравнение (3.17)

.

Длина нити в этом случае может быть определена из уравнения

(3.29)

Рис. 3.23. Кривая прови­сания отрезка нити

Воспользовавшись тем, что величина значительно меньше единицы, можно без большой погрешности представить подкорен­ное выражение в виде

(3.30)

как бы произвольно добавить к правой части малую величину

Используя это приближение и произведя интегрирование, по­лучим приведенную уже ранее формулу (3.22).

При замене в этом уравнении Н на его значение из уравнения (3.19) получим также формулу (3.23).

Ситуация, когда точки подвеса расположены на разной высоте, мо­жет представить интерес при расчетах контактных сетей только в слу­чае небольшой по сравнению с длиной пролета разности высот точек подвеса, так как они ограничены допускаемым уклоном железнодорож­ного пути. Это позволяет для проводов контактной сети во всех случа­ях ввести в расчет те же упрощения, что и выше, т.е. считать нагрузку равномерно распределенной не по длине нити, а по длине ее проекции. Приводимые ниже формулы могут использоваться и для расчетов лю­бых воздушных линий с небольшой разностью высот точек подвеса.

Обозначим через a и расстояния по горизонтали от точек под­веса до вершины кривой О (рис. 3.24). Принимая, как и выше, вес нити пропорциональным длине ее проекции, найдем, что вес час­тей АО и ОВ нити соответственно будет равен qa и qb . Обозначив через проекции частей АО и ОВ нити на вертикаль, получим следу­ющее уравнение моментов сил относительно точки В:

(3.31)

(3.32)

(3.33)

Из уравнений (3.32) и (3.33) видно, что а и b положительны и что точка наибольшего провеса находится между точками подвеса. Это соответствует случаю, при котором растягивающее усилие так велико, что вершина параболической кривой провисания нити находится слева от опоры А (см. рис. 3.24 штриховую линию).

Если в уравнение (3.17) подставить один раз х=а и в другой раз х= b , то получим соответственно y=f и y = f .

и

Заменив а и b их значениями из формул (3.32) и (3.33), получим

и (3.34)

Эти формулы устанавливают связь между стрелами провеса и на­тяжением подобно тому, как это установлено формулой (3.19) для случая расположения точек подвеса на одном уровне.

Для определения натяже­ния и стрел провеса можно случаи с разной высотой то­чек подвеса привести к слу­чаю с расположением точек подвеса на одном уровне. Продолжим кривую нити AOB до пересечения в точке B с горизонтальной прямой, проведенной из высшей точки подвеса В (рис. 3.25), тогда

и

Рис.3.24. Расчётная схема провисания нити с точками подвеса на различной высоте

Из сопоставления рис. 3.19 и 3.20 можно видеть, что l₂=2a и l =2b, следовательно, согласно формулам (3.22) и (3.23) имеем

(3.35)

, (3.36)

Длины пролетов, определяемые формулами (3.35) и (3.36), называ­ются фиктивными пролетами. Фиктивный пролет дает возможность привести случай расположения точек подвеса нити на разной высоте к случаю расположения точек под­веса на одном уровне. Вводимая в рассмотрение фиктивная нить ВОВ (см. рис. 3.25) имеет кривую провисания, совпадающую с кривой действительной нити АОВ, а следовательно, натяжение (при одинаковых атмосферных условиях) будет равно натяжению действительной нити.

Рис.3.25. Кривая провисания нити с точками подвеса на различной высоте.

Однако введение фиктивного пролета для пересчетов при изменяющихся атмосферных условиях дает некоторую неточность, тем большую, чем больше отношение разности высот точек подвеса нити к действительной длине пролета l . При указанная ошибка равна 3—4%. Эта неточность объясняется тем, что при изменении натяжения провода вследствие изменения режима температуры и нагрузки фиктивный пролет также будет изменяться.

Длина нити для рассматриваемого случая может быть определена таким же образом, как и для случая расположения точек подвеса на одной высоте, т.е. по уравнениям (3.29) и (3.30) с соответствующим изменением пределов интегрирования.

(3.37)

Интегрируя в указанных пределах, получим

При h = 0 уравнение (3.37) обращается в уравнение (3.22). Очевидно, что уравнения (3.32) — (3.37) могут быть выражены и через удельные значения. Для этой цели везде надлежит заменить отношение отношением .

Натяжение и стрела провеса провода при изменении атмосферных условий (уравнение состояния провода). При изменении температуры, а также нагрузки на провод изменяется его длина и, как следствие этого, изменяются его стрела провеса и натяжение. Зная стрелы провеса и натяжение, соответствующие одному режиму температуры и нагрузки, необходимо иметь возможность определять стрелы провеса и натяжение, соответствующие другому режиму.

Обозначим: t — начальная температура, соответствующая пер­вому режиму, °С;

q — нагрузка, приходящаяся на единицу длины провода при начальной температуре, кг/м;

H — натяжение провода при начальной температуре, кг;

L — длина провода, м;

F — стрела провеса, м;

t , q , H , L и f — те же величины, соответствующие какому-то другому режиму;

— коэффициент линейного удлинения материала провода, 1 / °С;

Е — модуль упругости провода, кг/мм 2 ;

S — площадь поперечного сечения провода, мм 2 .

При температуре t длина провода, если считать, что натяже­ние осталось неизменным, будет равна

.

Однако изменение длины провода поведет к изменению стрелы провеса, а следовательно, и к изменению натяжения; изменение на­грузки, приходящейся на единицу длины, в свою очередь, вызовет изменение натяжения в проводе и тем самым изменение стрелы провеса. Изменение натяжения изменит начальную длину L со­гласно закону Гука до величины

Следовательно, одновременное изменение температуры и на­грузки вызовет такое изменение длины провода, что окончатель­но длина его будет равна

Раскрыв квадратные скобки, получим

Пренебрегая последним членом как малой величиной второго порядка (произведение двух малых величин) и вычитая из обеих частей уравнения начальную длину L ₁ , получим приращение длины провода

Учитывая, что длина провода L для обычных соотношений незначительно отличается от длины пролета l , примем для определения приращения L ₁ = l . Тогда

(3.38)

С другой стороны, приращение длины может быть представлено как разность между начальной и конечной длиной (3.22)

(3.39)

Приравняв уравнения (3.39) и (3.38) и разделив обе части на l , получим

(3.40)

Умножив обе части уравнения на Е S , будем иметь

(3.41)

Уравнение (3.41) симметрично. Это ясно видно, если в крайнем члене правой части открыть скобки и перенести αЕ St_x , влево.

В таком виде этим уравнением можно пользоваться, полагая величины для режима с индексом «1» известными и определяя величины для режима с индексом «х», или наоборот. Однако наибольшее распространение уравнение (3.41) получило в том виде, как оно написано. При проведении расчета для ряда режимов удобно заменять индекс «х» последовательно индексами «2», «3», «4» и т. д. Уравнение (3.41) по подстановке известных величин получает вид:

(3.42)

Стрела провеса провода f определяется по формуле (3.19)

Это же уравнение, выраженное через удельные значения нагрузок и натяжений, имеет вид

(3.43)

Стрела провеса может быть определена по формуле (3.41). В том случае, когда нагрузка q представляет собой геометрическую сумму вертикальных и горизонтальных нагрузок, плоскость расположен b я провода будет наклонена к вертикали на не который угол β. Этот же угол β будет составлять равнодействующая нагрузка q_x с вертикалью. Если требуется установить для этого режима высоту провода от земли, то нужно определить вертикальную проекцию стрелы провеса провода f_x (рис. 3.26):

(3.44)

Решение кубического уравнения (3.42) можно произвести графическим способом, придав ему вид Н_х=А_х/Н_х 2 +В_х и находя точку пересечения прямой у = Н_х и кривой Н_х=А_х/Н_х 2 +В_х. Однако на практике уравнение (3.42) обычно решают подбором, на что требуется несколько минут, причем может быть достигнута любая степень точности.

Рис. 3.26. Расчетная схема определения вертикальной составляющей стрелы провеса нити

Расчет стрел провеса провода при различных режимах. Если в уравнении (3.41) заменить Н его значением из уравнения (3.19), то после несложных преобразований получим

(3.45)

Решение этого уравнения может быть произведено тем же путем, что и уравнение (3.41). После подстановки всех известных величин в уравнение оно получит вид

(3.46)

В уравнении (3.45) также можно заменить отношение q / S величиной γ, т.е. перейти к удельным нагрузкам.

Уравнения (3.41) и (3.45) дают возможность по известной величине стрелы провеса или натяжения для какого-либо режима температуры и нагрузки определить эти величины для любого другого режима, характеризуемого заданной нагрузкой и температурой. Таким образом, чтобы приступить к расчету, необходимо предварительно задаться какой-либо одной величиной (натяжением или стрелой провеса) для какого-либо режима. Это даст возможность перейти к любому другому режиму.

Прежде чем говорить о выборе этой исходной величины, нужно ясно представить сущность механического расчета подвески. Подвешивая провод, можно получать различные стрелы провеса, задаваясь различной величиной натяжения. Если основная задача подвески — подвод энергии к поездам при помощи перемещающихся токоприемников, то, как будет показано ниже, для улучшения процесса токоснимания нужно обеспечить возможно большее натяжение провода.

Даже в том случае, когда подвешиваемый провод не служит для снятия тока (например, питающий провод, или провод ВЛ), часто целесообразно давать ему большее натяжение с целью уменьшения высоты опор, что во многих случаях снижает стоимость подвески. В некоторых случаях, когда указанные условия не играют роли (на пример, если высота опор определяется другими факторами или используют готовые опоры, имеющие достаточный запас высоты), а также, когда нагрузка опор уменьшается при снижении натяжения, задаются максимально допускаемой стрелой провеса провода.

Независимо от того, какие условия будут положены в основу расчета, его производят не только для режимов, дающих наибольшее натяжение или наибольшие стрелы провеса, но и для ряда других режимов. Так, для определения отклонений подвески под действием ветра устанавливают величину натяжения в проводе при этом режиме. Учитывая, что монтаж подвески может происходить при различных температурах, производят расчеты для ряда режимов, обычно отличающихся один от другого температурой 5—10°С.

Получив ряд значений для натяжений и стрел провеса сводят эти данные в таблицу или представляют их в виде кривых зависимости натяжения и стрел провеса от температуры. При монтаже подвески монтер или бригадир, производящий работу, для каждой температуры выбирает соответствующее натяжение. Назначение этих кривых и таблиц определило их название – монтажные кривые и монтажные таблицы.

Выяснив, что для большинства случаев желательно иметь в проводе возможно большее натяжение, нужно определить, при каком из режимов натяжение достигает наибольшей величины. Как указывалось, увеличение натяжения провода может возникнуть вследствие понижения температуры и повышения нагрузки (вес гололеда, давление ветра).

Если изучение метеорологических условий района приведет к выводу, что при каком-либо режиме возможно совпадение всех указанных выше явлений, то, несомненно, что наибольшее натяжение в проводе будет иметь место именно при этом режиме. Однако результаты наблюдений метеорологических станций в течение ряда лет свидетельствуют о том, что при наименьшей температуре воздуха обычно не бывает добавочной нагрузки. Это обстоятельство вносит в расчет не которую неопределенность, так как заранее не представляется возможным указать, какой из режимов (режим наименьшей температуры или режим наибольшей добавочной нагрузки) нужно считать при расчете исходным, т.е. дающим в проводе наибольшее натяжение.

Предположив произвольно, что какой-либо из этих режимов даст наибольшее натяжение в проводе, можно принять его за исходный, т.е., допустив, что Н₁ = Н _{m ах} (Н _{m ах} — наибольшее натяжение, допускаемое по прочности провода), пользуясь формулой (3.41), можно найти Н_х, где Н_х и будет относиться ко второму тяжелому режиму. Возможно, что во втором режиме даст Н_х>Н₁ и, следовательно, больше допускаемого. В этом случае необходимо произвести весь расчет сначала, взяв за исходный второй режим и предположив, что именно при этом режиме Н =Н _{m ах} , после чего определять по тем же формулам натяжения и стрелы провеса для других режимов.

Этой неопределенности можно избежать, сравнивая длину за данного пролета с «критическим», определение которого будет рас смотрено ниже.

Влияние длины пролета на изменение натяжения провода. Критический пролет и критическая нагрузка. Если при каком-либо режиме провод имеет некоторое натяжение, то, как ясно из изложенного ранее, при изменении температуры и нагрузки величина натяжения изменяется.

При этом расчеты и практика показывают, что соотношение натяжения в проводе при различных условиях температуры и нагрузки в большей степени зависит от величины пролета.

С практической точки зрения особый интерес представляет характер зависимости величины изменения натяжения от длины пролета для случаев понижения температуры и увеличения нагрузки. Очевидно, что натяжение провода при понижении температуры и неизмененной нагрузке, так же как и при увеличении нагрузки, но неизменной температуре, будет увеличиваться.

В первом случае при жестком закреплении провода в точках подвеса длина его в пролете будет уменьшаться за счет температурных изменений, что равносильно подтягиванию провода. Во втором случае при неизменной температуре и увеличении нагрузки провод получит удлинение, которому по закону упругости будет соответствовать приращение величины натяжения. Чтобы определить влияние длины пролета на величину изменения натяжения при понижении температуры или увеличении нагрузки, представим уравнение (3.4 1) в виде

(3.47)

где Н_г, q _г , t _г — соответственно натяжение, нагрузка и температура при режиме наибольшей добавочной нагрузки; Н _{t min} , q_{t min} , t_min — те же величины при минимальной температуре. Покажем прежде всего, что входящая в выражение (3.5) разность

всегда положительна. Для этого предположим вначале, что t _г = t_min . При этом Н_г будет, конечно, больше Н _min так как при неизменной температуре натяжение с увеличением нагрузки растет. Следовательно, в этом случае разность должна быть положительна, так как только тогда Н_г будет больше Н _{t min} , в соответствии с выражением (3.47).

Если же t _г > t_min , что имеет место в действительности, то натяжение Н_г будет меньше, чем при первом предположении (когда t _г = t_min ). В этом случае первый член рассматриваемой разности q _г 2 /Н_г 2 возрастает, а сама эта разность не изменит знака.

Из выражения (3.47) можно сделать заключение, что натяжение Н_г при

(3.48)

при наибольшей добавочной нагрузке будет выше, чем натяжение Н _{t min} , при минимальной температуре.

Соотношение (3.48), очевидно, возможно только при достаточно больших значениях пролета l . Наоборот, уменьшая величину пролета, можно получить неравенство

(3.49)

при котором натяжение Н_г будет меньше натяжения Н _min .

Таким образом, при малых пролетах натяжение провода при минимальной температуре будет выше, чем при режиме наибольшей добавочной нагрузки.

При некоторой величине пролета l может иметь место равенство

В этом случае натяжение Н_г и Н _{t min} будут равны между собой по выражению (3.47), и оба равны некоторому Н, а l будет функцией этого натяжения Н.

Положив Н_г = Н _{t min} = Н _{m ах} п обозначив соответствующее значение l через l _к , получим

(3.50)

Пролет l _к , называется критическим.

Разделив числитель и знаменатель уравнения (3.50) на S , выразим величину критического пролета через удельные значения:

(3.51)

Итак, критическим пролетом будем называть такой, при котором натяжения при минимальной температуре и режиме максимальной нагрузки одинаковы и равны максимально допустимому натяжению. При критическом пролете за исходный, наиболее тяжелый режим можно взять как режим минимальной температуры, так и режим наибольшей добавочной нагрузки. Если расчетный пролет больше критического, то за исходный (более тяжелый) режим надо брать режим наибольшей добавочной нагрузки. Наоборот, при расчетном пролете меньше критического за исходный режим следует взять режим минимальной температуры.

Иногда при расчетах проводов воздушных линий для выбора исходного режима пользуются вместо величины критического пролета величиной критической нагрузки.

Для определения критической нагрузки следует в выражениях (3.48) или (3.49) заменить q _г на q_k , затем Н_г и Н _min – на Н _max и приравнять левую часть выражения правой.

(3.52)

По аналогии с уравнением (3.50) можно и величину критической нагрузки выразить через удельные значения:

(3.53)

Расчет провода в анкерном участке. Выше при рассмотрении расчета провода предполагалось, что имеется один пролет. Если пролеты между всеми опорами в анкерном участке одинаковы, то все сказанное выше для одного пролета полностью сохраняет свое значение и для этого случая. Таким образом, расчет провода такого анкерного участка нужно вести, как для одного пролета между смежными опорами. Если же расстояния между смежными опорами различны, то расчет провода несколько изменится, так как при изменениях температуры и нагрузок в смежных пролетах возникнут различные изменения натяжения, и, следовательно, к точке подвеса (если она неподвижна) будут приложены с двух сторон различные натяжения. Разность этих натяжений стремится сместить точку подвеса в сторону большей силы. Изменение натяжения про вода в случае изменения атмосферных условий при неподвижных точках подвеса будет отличаться от варианта с подвижными. В первом случае длина пролета будет неизменна, во втором же за счет смещения точки подвеса будет несколько изменяться. Вследствие этого и изменение натяжения в проводах будет происходить по различным законам.

Разберем сначала случай жесткого закрепления точек подвеса. Прежде всего рассмотрим, как влияет длина пролета на изменение натяжения в проводе при изменении температуры и нагрузки. Для этого предположим, что при некоторой температуре монтажа t и нагрузке q ₀ проводу во всех пролетах дано натяжение Н. Тогда при режиме, который характеризуется температурой t и нагрузкой q ₁ натяжение Н₁ может быть найдено из уравнения (3.41), которое запишем в следующем виде

(3.54)

Чтобы оценить влияние длины пролета на изменение натяжения, когда нагрузка изменяется при изменении температуры, примем вначале, что меняется только нагрузка, температура остается постоянной, т.е. q ₁ > g и t = t ₁ . Тогда получим

(3.55)

Как было доказано ранее, второй член этого уравнения всегда положителен. Следовательно, уравнение (3.55) показывает, что при увеличении нагрузки натяжение провода будет интенсивнее возрастать в больших пролетах.

Если теперь принять, что температура понижается, а нагрузка остается неизменной, т.е. считать q ₁ = g и t t ₁ , то получим

(3.56)

Так как Н₁>Н (температура понижается), то последний член отрицателен. Следовательно, из выражения (3.56) можно заключить, что за счет изменения температуры натяжение будет интенсивнее изменяться в пролетах меньшей длины.

Перейдем теперь к установлению расчетного пролета при жестком закреплении провода на опорах. Рассмотрим три возможных случая: все пролеты меньше критического; все пролеты больше критического; величина критического пролета заключена между значениями наибольшего и наименьшего пролетов.

Если все пролеты меньше критического, то исходным будет режим минимальной температуры. При этом расчет надо вести по наименьшему пролету, так как, дав при монтаже для всех пролетов равное натяжение, получим при минимальной температуре наибольшее натяжение в наименьшем пролете.

Если все пролеты больше критического, то за исходный режим надо взять режим гололеда. Выбор расчетного пролета будет зависеть от температуры, при которой производится монтаж. Действительно, если монтаж ведется при относительно высоких температурах, то при переходе к режиму гололеда натяжение растет вследствие увеличения нагрузки и понижения температуры. При этом за счет первой причины больше возрастает натяжение в больших пролетах, а за счет второй — в меньших. Из этого следует, что при некоторой достаточно высокой температуре монтажа можно получить при гололеде равные натяжения в максимальном и минимальном пролетах, а при дальнейшем повышении температуры монтажа натяжение при гололеде в минимальном пролете станет более высоким, чем в максимальном.

Нетрудно показать, что натяжение при гололеде будет одинаковым во всех пролетах, если температура монтажа равна критической температуре действительно, при критической температуре для любого пролета

где Н_г – натяжение провода при гололеде; Н _k — натяжение про вода при критической температуре.

Из последнего равенства найдем

Следовательно, если при критической температуре t _к создать во всех пролетах одинаковое натяжение то при режиме гололеда натяжение также будет одинаковым для всех пролетов. Это видно из того, что в последнее выражение не входит длина пролета.

Изменения натяжения в зависимости от температуры для минимального и максимального пролетов удобно рассматривать в виде графиков (рис. 3.27). Таким образом, если все пролеты выше критического, то, приняв за исходный режим гололеда, надо исходить из максимального пролета, а для более высоких температур — исходить из минимального.

В третьем случае, когда наибольший пролет больше критического, а наименьший — меньше, необходимо вести расчет (для темпера тур, меньших критической) как для того, так и для другого пролета и при составлении монтажных таблиц выбрать для одной и той же температуры наименьшее из полученных значений. При температурах выше критической надо также рассчитать натяжения для пролета, превышающего критический на наименьшую величину.

Рис. 3.27. Кривые изменения натяжения провода при изменении температуры для разных длин пролетов

Для случая, когда точки подвеса про вода имеют возможность перемещаться, применяется другой метод расчета, так как натяжение по всей длине анкерного участка будет одинаковым (для каждого режима). Изменение натяжения будет в общем случае отлично от того, как оно менялось бы в каждом пролете при закрепленных точках подвеса. Нетрудно доказать, что для каждого анкерного участка с любым сочетанием расстояний между точками подвеса можно подобрать такой пролет, при котором изменение натяжения будет происходить таким же образом, как и в этом анкерном участке. Введение в расчет такого пролета позволяет вместо анкерного участка, в котором имеются различные расстояния между точками подвеса провода, рассматривать один «эквивалентный пролет» и тем самым значительно упростить задачу.

Обозначим l ₁ , l ₂ , l ₃ …, l _n — длины пролетов анкерного участка (рис. 3.28) и l _э величину эквивалентного пролета. Воспользовавшись уравнением (3.22) можно представить длину провода анкерного участка при первоначальном режиме с нагрузкой q ₁ , температурой t ₁ и натяжением Н₁ в следующем виде:

Рис. 3.28. Анкерный участок провода с различными длинами пролетов

Точно так же для режима «х» длина провода может быть представлена выражением

Приращение длины провода в анкерном участке при переходе от первоначального режима к режиму «х», таким образом, может быть представлено в виде:

С другой стороны, как и при выводе уравнения состояния для одного пролета, это удлинение можно представить как сумму удлинений, в результате изменений температуры и натяжения, т.е. в виде

Приравняв одно выражение другому, получим

Упростив это уравнение и разделив обе его части на , получим

(3.57)

Отнеся уравнение (3.40) к эквивалентному пролету l э будем иметь

(3.58)

Сравнивая уравнения (3.57) и (3.58), можно заметить, что при равных натяжениях, нагрузках и температурах, входящих в формулы для анкерного участка и эквивалентного пролета с одинаковыми индексами, должно иметь место равенство

(3.59)

Заменив этой величиной различные пролеты одного и того же анкерного участка, можно вести расчет по эквивалентному пролету, зная, что в дальнейшем натяжения в различных пролетах будут равны натяжению, полученному в расчете для эквивалентного пролета.

Что касается стрел провеса, то они, конечно, будут в разных пролетах различны. Стрелы провеса могут быть определены для каждого пролета в отдельности по формуле (3.19).

Последовательность расчета свободно подвешенного провода. Основные задачи расчета подвески были изложены выше. Там же были выведены основные формулы для расчета подвески. Расчет подвески следует начинать с определения нагрузок, действующих на провод при всех заданных для расчета режимах.

После расчета нагрузок определяют максимально допустимое для провода натяжение. Оно равно:

(3.60)

где σ_доп – допускаемое напряжение в проводе.

Допускаемое напряжение σ_доп находят путем деления временного сопротивления на запас прочности. При этом надо учитывать, что для многопроволочных проводов временное сопротивление снижается на 10% по сравнению с однопроволочными.

По рассчитанным нагрузкам и натяжению Н _max , по формуле (3.50) находят критический пролет l _k .

Если подвеска выполнена на подвесных изоляторах, то далее расчет ведут в следующем порядке. По плану трассировки линии находят действительные пролеты в анкерном участке и по ним определяют эквивалентный пролет по формуле (3.59). Затем, сравнивая эквивалентный пролет с критическим, находят наиболее тяжелый режим и принимают его за исходный. Приписывая нагрузке, натяжению и температуре при этом режиме индекс «1», определяют по уравнению (3.41) натяжения при других заданных режимах. Натяжение Н₁ при выбранном исходном режиме приравнивают к максимальному, т.е. полагают Н₁ = Н _max .

В случае, когда такой расчет по уравнению (3.41) дает натяжение Н_х выше Н₁ = Н _max , при расчете критического пролета допущена ошибка.

Затем по уравнению (3.41) находят натяжение при других расчетных режимах. Обычно рассчитывают еще только один режим – при ветре максимальной интенсивности.

Кроме этого необходимо произвести расчеты для построения монтажных кривых и составления монтажной таблицы. Эти расчеты так же производят по уравнению (3.41). При этом считают, что при монтаже провода дополнительных нагрузок от ветра и гололеда не будет.

Пользуясь уравнением (3.4 1), можно, задаваясь различными температурами, определять соответствующие им натяжения провода. Однако при этом придется каждый раз решать это уравнение подбором. Можно, наоборот, задаваться натяжениями и определять, каким температурам они соответствуют. При этом упомянутое уравнение (3.41) лучше переписать в следующем виде:

(3.61)

В этом уравнении принято q_x = g ₀ , где g ₀ – масса 1 м провода.

После преобразования уравнения (3.61) через удельную нагрузку

(3.62)

будет легко найти искомые температуры.

Расчет комбинированных проводов. Методы расчета комбинированных проводов могут быть даны в общем виде, т.е. для любого сочетания металлов. Однако в России наибольшее применение получили сталеалюминиевые провода.

Отличия поведения сталеалюминиевого провода от однородно го провода заключаются в следующем:

1) возникающее при подвеске провода напряжение в стали не равно напряжению в алюминии, тогда как в однородном проводе все нити имеют одинаковое напряжение;

2) изменение температуры вызывает перераспределение усилий между стальной и алюминиевой частями, тогда как в однородном проводе все нити всегда нагружены равномерно;

3) допускаемое напряжение, а следовательно, и допускаемое усилие на провод в целом зависит от температуры провода, тогда как у однородного провода допускаемое напряжение или усилие не зависит от температуры.

Рассмотрим причины, вызывающие эти особенности. Очевидно, что если комбинированный провод нагрузить растягивающим усилием, то удлинения стальной и алюминиевой частей будут одинаковыми. Возникающие напряжения согласно закону Гука равны произведению из относительного удлинения на модуль упругости Е, т. е.

(3.63)

Другими словами, отношение напряжений в стали σ_с и алюминии σ_а будут равны отношению их модулей упругости Е_с и Е_а, т. е.

(3.64)

Если умножить числители на площадь сечения стальной части S_c , а знаменатели — на площадь сечения алюминиевой части S_a и заменить произведение σ_с S_c через Н _c (усилие в стальной части), а σ_а S_a через На (усилие в алюминиевой части), то получим

(3.65)

Для того чтобы понять, как влияет изменение температуры на напряжения в комбинированном проводе, представим себе, что провод, изготовленный при температуре t ₀ , не имеет никаких напряжений ни в стальной, ни в алюминиевой части. Если теперь подвергнуть такой провод воздействию температуры, например нагреванию, то провод удлинится. Если стальная b алюминиевая части провода могли бы удлиняться независимо одна от другой, то они получили бы различное удлинение, так как коэффициент линейного удлинения алюминия α_а больше, чем коэффициент линейного удлинения стали α_с, и поэтому алюминиевая часть удлинилась бы на большую величину, чем стальная.

Но металлы механически между собой связаны и могут иметь только одинаковое удлинение. Следовательно, при повышении температуры стальная часть будет задерживать удлинение алюминиевой, т.е. вызывать в ней усилие сжатия и одновременно сама стальная часть получит такое же по величине растягивающее усилие.

Если провод предварительно был растянут (например, подвешенный), то повышение температуры кроме обычного своего влияния, оказываемого на подвешенный провод (увеличение стрелы провеса и уменьшение общего натяжения), приведет к некоторому увеличению натяжения в стальной части и дополнительному уменьшению натяжения в алюминиевой. Наоборот, при понижении температуры будет дополнительно сжиматься стальная часть и растягиваться алюминиевая другими словами, при любом изменении температуры напряжение в стальной части будет изменяться медленнее, чем в алюминиевой.

Из сказанного ясно, что отношение напряжений в стальной и алюминиевой частях комбинированного провода при всех прочих равных условиях будет зависеть от температуры провода.

Вместе с тем в пределах расчетного диапазона изменений температур напряжение в стали и алюминии не должно выходить за допускаемые пределы. Следовательно, и общее усилие натяжения будет зависеть от температуры провода.

Определение стрелы провеса комбинированного провода по заданному натяжению Н можно вести нотой же формуле (3.19), что и для однородного провода. При изменении температуры приходится учитывать, что комбинированный провод будет вести себя так, как не который эквивалентный однородный провод с модулем упругости Е₀ и коэффициентом линейного удлинения α₀, лежащими в пределах Е_с> Е₀> Еа и α_с

Общее натяжение комбинированного провода Н₀ может быть представлено в виде суммы натяжений Н_с и Н_а

(3.66)

или в виде произведения соответствующих напряжений на площадь поперечного сечения

(3.67)

где σ₀ — так называемое фиктивное напряжение, т.е. условное напряжение, взятое по суммарному сечению эквивалентного однородного провода. Воспользовавшись формулой (3.63), выразим напряжение через модули упругости и удлинение, одинаковое для всего провода:

(3.68)

(3.69)

Эквивалентный коэффициент линейного расширения можно вы вести следующим образом.

При переходе от температуры изготовления провода t ₀ , обычно принимаемой равной 15 0 C , к некоторой другой температуре стальная и алюминиевая части, если бы они не были между собой связаны, получили бы относительное удлинение, соответственно равное

(3.70)

(3.71)

Фактическое удлинение комбинированного провода ε₀, равное удлинению некоторого эквивалентного провода с коэффициентом линейного удлинения α₀, можно рассчитать по формуле

(3.72)

Следовательно, под действием возникших сил стальная часть получит дополнительное удлинение, равное

(3.73)

алюминиевая часть получит сокращение длины:

(3.47)

Усилие растяжения в стальной части, вызванное температурным удлинением, будет равно

то, использовав выражение (3.73), получим:

(3.75)

По аналогии усилие сжатия в алюминиевой части будет равно

(3.76)

но так как ΔН_с =ΔН_а то, приравняв выражения (3.75) и (3.76) и упростив полученное уравнение, найдем

(3.77)

Таким образом, по заданным параметрам комбинированного провода S_c , Е _c , S _а , Е_а и α_а можно найти по формуле (3.69) общий для всего провода модуль упругости Е₀, а по формуле (3.77) — коэффициент линейного удлинения α₀ и рассчитать комбинированный провод, как однородный. При этом под поперечным сечением провода надо понимать суммарное сечение стали и алюминия, а под натяжением —суммарное натяжение провода.

Если расчет ведется не по общему натяжению провода [формулы (3.19), (3.41), (3.45)], а по удельным нагрузкам [ формулы (3.19), (3.42)], то под напряжением σ_х следует понимать фиктивное напряжение σ_0х, где

(3.78)

Допускаемое усилие на комбинированный провод, как уже было показано выше, зависит от температуры провода. В той же степени оно зависит от отношения допустимых напряжений и модулей упругости стали и алюминия. Отношение временных сопротивлений или допускаемых напряжений для стали и алюминия равно примерно 7—8. Отношение же модулей упругости этих материалов равно примерно 3. Следовательно, если провод от механической нагрузки нагружается до предела по алюминию, то его стальная часть всегда будет недогружена. Кроме того, как было показано выше, понижение температуры (ниже t ₀ ) приводит к дополнительной нагрузке алюминия и некоторой разгрузке стали. Поэтому максимально допускаемое усилие на провод в целом следует определять исходя из допускаемого усилия на его алюминиевую часть.

Допускаемое усилие на алюминиевую часть комбинированного провода при температуре t t ₀ равно разности между абсолютным значением максимального усилия, равного σ_{а m ах} S_a , и усилием растяжения, возникшим от воздействия температуры на комбинированный провод. Последнее может быть определено из выражения (3.76). Тогда

(3.79)

Зная усилие в алюминиевой части, вызываемое нагрузкой, можно найти усилие в стальной части, вызываемое этой же нагрузкой, воспользовавшись уравнением (3.65).

Тогда усилие в стальной част ii , соответствующее Н_{а m ах} будет равно

(3.80)

Общее усилие в комбинированном проводе при допускаемом усилии в алюминиевой части будет равно

или, после подстановки значений и упрощений:

(3.81)

Если расчет ведется не по усилиям в проводе и полным нагрузкам, а по напряжениям я удельным нагрузкам, то надлежит обе части уравнения (3.81) разделить на общее сечение провода S ₀ . В этом случае:

(3.82)

где σ _max называют фиктивным максимальным напряжением комбинированного провода по допускаемому напряжению в алюминии.

Изложенный метод расчета получил наибольшее распространение в практике. Однако, хотя в нем исходят из предположения равномерного распределения усилий по алюминиевой и стальной частям, в действительности в комбинированном проводе усилия между алюминиевой и стальной частями перераспределяются таким образом, что внутренние слои алюминия воспринимают большую часть нагрузки от воздействия температуры, а наружные — меньшую. При этом некоторые слои могут работать за пределами текучести, но, поскольку стальная часть остается сильно недогруженной, это не должно приводить к опасным последствиям.

Цепная линия

Цепная линия

• Задание 13. 7. 30 метров гибкой нити и 7. 5 кг. Весь агрегат свободно подвешен на 2 опорах, расположенных на одном уровне на расстоянии возвратно-поступательного движения. Определите висячую стрелку в середине пролета и максимальное натяжение нити. Решение. Давайте набросаем положение равновесия yarn. In вопрос, расстояние между опорами. Длина всей нити g 3 м, вес единицы длины нити 5 7, 5 кг м.

Вот оно 2-й основной случай нагружения происходит, когда нить принимает форму цепной линии. Чтобы определить величину провисания нити f, необходимо составить уравнение для кривой равновесия нити. После выбора системы координат cx, как показано на рисунке, используйте основное дифференциальное уравнение 1, которое принимает следующий вид К заданию 13. 7. Функция азимутального — Длина дуги cd. Интегрируйте это уравнение и заранее выразите длину s как y. Используйте для этого хорошо известные Подставляя dyfdx из выражения 1, Вы получаете следующую форму Если мы интегрируем это уравнение — Арш с,. Вопрос п 2 Интегральная константа ci определяется из условий выбранной системы координат s 0.

После составления дифференциального уравнения движения (пункт 4) следует рассмотреть условие статического равновесия мате-риальпой точки, совершающей колебания. Людмила Фирмаль

Выражение 2 принимает вид 3 Подставляя эту формулу в Формулу 1, получаем следующую формулу Ферреневое уравнение кривой равновесия пряжи ды ш ДХ. После интегрирования, находим В если x 0, то координаты y-0, поэтому cr — h q и, наконец, Теперь у нас есть все уравнения, которые нам нужно решить problem. In факт, если задать Формулу 3 x z 2 Или после присвоения номера 112. 5, 56. 23 Это уравнение вида 2z shz.

Используйте таблицу гиперболических синусов, чтобы найти выбор ее решения Определить натяжение нити в точке 5, где h a 25, s4 кг. Искомая провисающая нить находится из Формулы 4 Если положить ее в x c2. Для определения натяжения нити используйте основное соотношение 2. Напомним, что q qs, применяя формулу 3, находим q f sh. Подставляя это в Формулу 2, получаем Или с помощью соединения 4 7 — я 4Р. Из последнего уравнения следует, что натяжение нити максимизируется в неподвижных точках a и b, где Гта я ФК 25. 84 7. 5-11. 94 115. 4 кг.

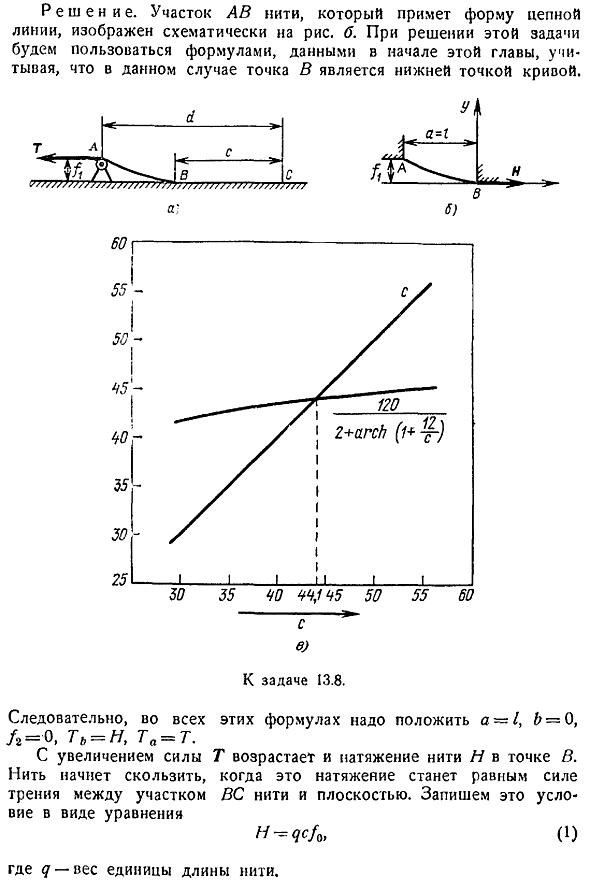
Задача 13. 8. Часть гибкой нити, равномерно распределенной по весу по длине, находится на горизонтальной плоскости. Остальные дачи проходят через небольшой блок а рисунок а. Постепенно увеличивая усилие t приложено к концам thread. In в этом случае длина линии контакта между ВС и плоскостью нити уменьшается и приближается к определенному пределу С, где нить начинает скользить вдоль плоскости.

Определить это предельное значение С, если d 60 м, l 6 м, а коэффициент трения между резьбой и плоскостью 0 0, 5. Другие способы решения такого уравнения см. В задаче 13. 8. Решение. На рисунке 2 показан участок av-потока, который принимает форму одной цепи. b. To решите эту задачу, используя выражение, показанное в начале этой главы, в котором точка b является нижней точкой кривой. С Задача 13. 8. Итак, для всех этих формул нужно разместить a-1, b-0, r 0, t h, ta t.

При увеличении силы Т натяжение нити Н в точке В также увеличивается, и когда это натяжение равно силе трения между частью ВС нити и плоскостью, нить начинает проскальзывать. Запишите это условие в виде уравнения Ч — qcfa, 1 Где d-вес единицы длины нити. Значение h должно удовлетворять формуле 14. В этом выпуске 2 Исключается из уравнения 1. 2 Значение h, получим следующее уравнение Из него определяется желаемый размер s. Быть l d-c. Уравнение эго Вот бы заменить знаменитые чудесные вещи 3 Вы не можете решить это трансцендентальное уравнение в отношении использования точных алгебраических методов. Поэтому, чтобы найти его корень, нужно воспользоваться приближенным методом.

Рассмотрим 2 таких ways. It это графический метод и итерационный метод. Графический способ заключается в создании левого и правого графика уравнений в 1 чертеже. Горизонтальная ось пересечения этих графиков показывает примерное значение маршрута. Для простоты сначала представим выражение 3 в следующем виде 120. 2 арка ий 4 График в левой части уравнения 4 является биссектрисой первой координаты angle. To постройте график правой стороны, вычислите значения некоторых значений в c, взятых рядом с расчетными значениями маршрута. Результаты расчетов сведены в таблицу. 1. 4 рефские. 4 2 арка 4 120 30 0. 4000 1. 4000 0. 8670 2. 8670 4186 35 0. 3429 1. 3429 0.

Если повторить этот процесс несколько раз, то можно получить значение корня с произвольной точностью, если f x 1 в интервале между корнем уравнения и первым приближением. Если это условие не выполняется, то уравнение должно быть преобразовано по крайней мере, путем передачи его в обратную функцию. Для 30 c 55 легко видеть, что модуль правой производной Формулы 4 меньше 1. Поэтому это выражение можно повторить, взяв значение c из заданного интервала первого приближения c0. C0 46 м. 120. 2 л 44, 3 м 44, 08 м 11a может завершить итерационный процесс, наконец, получив c 44. 1 m. Задача 13. 9. Гибкий поток без расширения приостанавливается от поддержки a и блока, который можно игнорировать.

• Вес q на единицу резьбы. Баланс определяет длину свободно висящей части нити, которая не нарушается. Третий блок игнорируется. Ты поешь. После выбора начальной точки самой нижней точки кривой, используйте уравнение 1, чтобы найти уравнение кривой. Где — напряжение в точке С. Тогда заметим, что вертикальное приращение нагрузки dq qds ды ЗДС Или заменить ДС У1 y 2 ДХ При разделении переменной Когда вы интегрируете ды И1 РТ 7г- с Для краткости укажите h q a. Как, о Тогда ci 0 и, наконец, выражение 2 имеет вид Г У1. Из Формулы 3 Вы можете легко проверить, умножив 3 на 4.

При добавлении выражений 3 и 4 Если мы интегрируем последнее уравнение если x 0 и y 0, то перенос начала координат 5 записывается в виде Точка o 0, — a. Ось ox называется основанием цепной линии. Это связано с тем, что я держусь только под действием вертикальной нагрузки, поэтому горизонтальное натяжение не изменяется. T h, или t h c- Согласно 1, это равенство может быть переписано в следующем виде 1 2 3 Ноль 5 1 равна Проекция Если вычесть равенство из 3 в 4 И, наконец, получить свободную точку кривой Натяжение нити по формуле Северный t — y1 chu1- В результате, если длина подвешенной части равна yt bd, то нить будет находиться в равновесии. Задание 13. 10.

При составлении дифференциального уравнения надо изобразить материальную точку в промежуточном положении, соответствующем ее положительной координате, предположив при этом, что точка перемещается в сторону возрастания этой координаты. Людмила Фирмаль

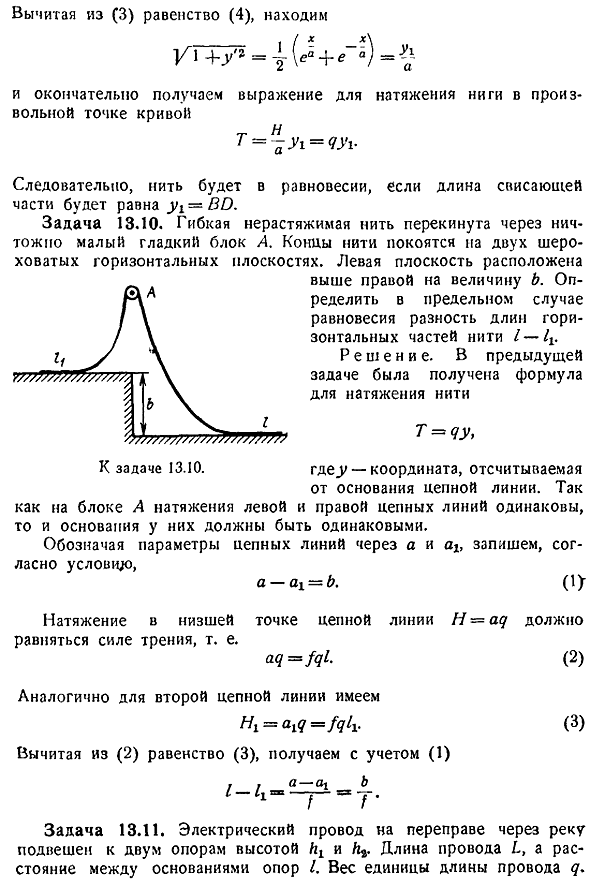
На небольшой и гладкий блок набрасывают гибкую, не натянутую нить. Нить лошади находится на 2 грубых горизонтальных плоскостях. Левая плоскость находится выше правой плоскости на величину b. In в предельном случае равновесия определяют разность длин горизонтальной части нити 1-1. Solution. In в предыдущем выпуске была получена формула натяжения нити Т Тип qy где y-координаты, измеренные от основания цепной линии. Правая прядь такая же Основа для этого должна быть одна и та же. В зависимости от условий, a и write указывают параметры линии цепи а-АИ б. 1 г, г Вопрос 13. 10. Для Как блок а в левом напряжении Натяжение в самой нижней точке цепной линии h aq должно быть равно силе трения.

Аналогично, для 2-й цепной линии 3 Если вычесть равенство 2 из равенства 3, то вы принимаете во внимание 1 Я Задание 13. 11. Проволока на пересечении реки подвешена к 2 столбам по высоте и c. Длина проволоки равна l, расстояние между основаниями опор равно i. Вес q на единицу длины проволоки. Для bx 30 м, b2 12 л, 20 м, 1 45 м, q 1. 25 кг м найти уравнение кривой, максимальное провисание и максимальное натяжение. Решение. Если выбрать начало координат в верхней части цепной линии o, то в соответствии с 10 уравнение кривой имеет вид В данном случае неизвестно следующее. Положение точки o, определяемое отрезком, также является горизонтальным натяжением n.

В определении используется выражение, определяющее условия прохождения цепной линии через точки соединения А и В, а также длину провода между опорами. У нас есть 2 НТ-н0 ч 1 3 Найти более длины провода В1 г ДХ г л ш ДХ х функции rfx 7shff e в sh4r shff 2 st, cht 4 От 2 до 3 Чтобы определить горизонтальное натяжение n, возьмем 4 и 5 2, Затем возьмем 2 и вычтем от 1-го до 2-го 4 Из этого уравнения 1д 2Н В Р П 2. 06 К1 2Н это трансцендентальное уравнение вида shz 2.

Графически решается с помощью fi z shz, g g 2. 06 z, которое создает или аппроксимирует 2 кривые в соответствии с таблицей. Их пересечение дает r 1d 2ч 2. 22, оттуда 6 4, 48 −1, 25 6, 6 кг. Чтобы найти a, разделите 5 на 4. У нас есть Откуда Учитывая 6, остается найти d0 из 2 Найти уравнение кривой, подставив значения, найденные в уравнении 1 Приступайте к решению о провисании самого большого провода. Максимальная слабина — это точка кривой, где касательная линия кривой параллельна линии ab. Из этого уравнения находим абсциссу искомой точки кривой Самые большие провалы Макс-е- а-xif по-Хо-у ХВ Т Н1 — ч дж а-х — н л- ч я-л педагогика 18. 74 м.

И согласно напряжению провода 7 l h a h 4 d1-l0 40, 5 кг, tb h qft h q h2-h0 m, 8 кг. Задание 13. 12. Цепь с равным сопротивлением представляет собой цепь переменной толщины, где толщина каждой точки пропорциональна напряжению t. in такая цепочка, вероятность обрыва во всех точках одинакова. Уравнение кривой равновесия и закон изменения толщины цепи определяются. Решение. Буква О обозначает переменный участок цепи, изменяющийся по ее длине. Если вес единицы объема цепи равен p, а ее длина равна s, то вес элемента ds равен puds. Выберите начало координат в самой нижней точке цепочки. Используйте уравнение 1, чтобы найти уравнение кривой 2 ДХ П О Где h-натяжение самой нижней точки цепи.

Приращение вертикальной нагрузки составляет rfq pa ds, и мы видим, что натяжение цепи согласно условию пропорционально толщине, то есть равно Т ka, k коэффициенту пропорциональности. При вычислении разности с обеих сторон уравнения 1 2 С другой стороны, проекция горизонтального натяжения оси x является постоянной величиной, так как на цепь действует только вертикальная нагрузка Ч Т — АО — const и Откуда 3 значение o вводится в Формулу 2. А потом мы это выясним. Здесь рассматривается ds j l dx.

Когда вы отделяете переменную, она выглядит так ды Ю Д Когда вы интегрируете arctgy г интернет. Происхождение выбран в самой низкой точке, где кривая сводится к минимуму. Так, если x 0, г 0, С1 0 4 диджей тг — xdx. Интеграция и поиск у — Линкос — х ХС. Если x 0, y 0, c2 0. — y lncos — — х, э к Кос- — х Или наконец-то е со −2-х 1. Это уравнение сопротивления curve. To найти закон изменения толщины цепи, используя уравнение 3.

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института