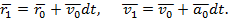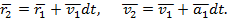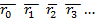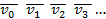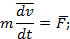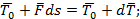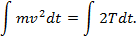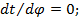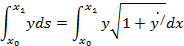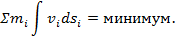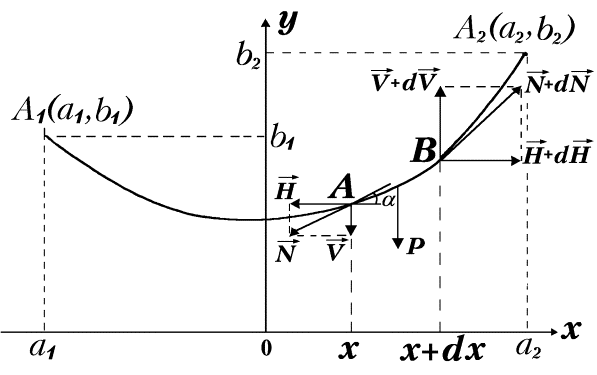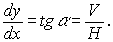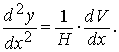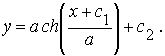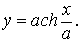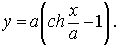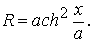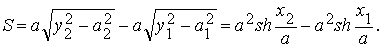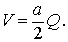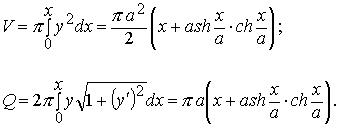Уравнение цепной линии принцип стационарного действия

Тема 29. Принцип наименьшего действия

Сущность динамики точки заложена во втором законе Ньютона. Дана точка, имеющая массу т и подверженная силе F; требуется определить движение этой точки.

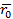
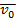
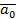
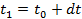
Если известно начальное положение точки, а также ее скорость, то при помощи уравнения Ньютона можно определить ускорение, а следовательно, и приращение скорости, которое точка получит в течение бесконечно малого времени dt . Если в начальный момент t₀ положение точки определяется радиусом-вектором r 0 , величина скорости v 0 , а определенное из уравнения Ньютона ускорение для начального момента. a 0 , то для момента t 1 = t 0 + dt положение точки и ее скорость определятся формулами

r 1 = r 0 + v 0 dt , v 1 = v 0 + a 0 dt .

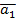
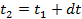
Момент t₁ можно рассматривать как начальный. Определив для него величину ускорения a 1 , для момента t 2 = t 1 + dt получим

r 2 = r 1 + v 1 dt , v 2 = v 1 + a 1 dt .

Переходя таким образом от одного момента к следующему за ним через бесконечно малый промежуток dt , для ряда моментов имеем

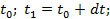
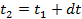
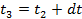
t 0 ; t 1 = t 0 + dt ; t 2 = t 1 + dt ; t 3 = t 2 + dt ; ….,

т. е. ряд величин, определяющих соответственно положение и скорости движущейся точки для этих моментов:

r 0 r 1 r 2 r 3 …

v 0 v 1 v 2 v 3 …

и таким образом можно определить движение точки за любой заданный конечный промежуток времени.

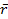
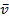
Математический анализ позволяет сразу определить величины r и v для любого момента времени, если можно проинтегрировать уравнение Ньютона

m dv dt = F ;

если же это уравнение нельзя проинтегрировать в элементарных функциях, то получаем интеграл приближенно при помощи операции, описанной выше.

Метод, который использован выше, основан на принципе, формулируемом вторым законом Ньютона; такие принципы, выражаемые при помощи дифференциального уравнения, носят название дифференциальных. При их применении общий процесс разбивается на ряд последовательных бесконечно малых процессов и устанавливаются способы перехода от одного момента времени к следующему.

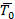
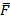
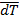
Не следует считать, что дифференциальные принципы обязательно связаны только с делением времени на бесконечно малые промежутки dt Можно воспользоваться тем же методом при определении формы равновесия гибкой нити, находящейся под действием заданной системы сил; можно разбить длину этой нити на бесконечно малые элементы ds . Зная положение начала первого элемента ds , соответствующее натяжение T 0 и действующую на этот элемент силу F можем получить соответствующее приращение натяжения dT , составляя уравнение равновесия для этого момента: если F — сила, приходящаяся на единицу длины элемента ds , то уравнение равновесия этого элемента имеет вид

T 0 + F ds = T 0 + d T ;

оно позволит найти натяжение T 1 = T 0 + d T 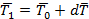в конце этого элемента и начале следующего.

Операция, аналогичная вышеописанной, позволит определить величину натяжения Т в функции длины s нити от начальной точки; поскольку же направление натяжения совпадает с направлением касательной к кривой, представляющей форму нити, то при помощи вторичного интегрирования можно определить положение концов последовательных участков ds , а следовательно, и форму нити.

Предположим, что нить является однородной и находится под действием силы тяжести. Известно, что положение устойчивого равновесия системы тяжелых материальных точек получается, если центр тяжести этой системы занимает наинизшее положение. Исходя из этого принципа, можно, получить уравнение искомой кривой, так называемой цепной линии, потребовав, чтобы интеграл ϱgyds 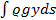имел наименьшую величину (ϱ — масса, приходящаяся на единицу длины нити, а у — координата точки рассматриваемой кривой). Такие принципы носят название интегральных или вариационных; для решения соответствующих задач в середине XVIII в. Эйлер изобрел вариационное исчисление. Теперь уже не требуется последовательное построение нужной кривой (или вообще функции, определяющей течение рассматриваемого процесса), а она выбирается из общего числа возможных при помощи условия, чтобы функция, дающая ответ на поставленную задачу, определялась из условия максимума или минимума некоторого интеграла.

В динамике интегральные принципы появились только во второй половине XVIII в., но в теории распространения света они были известны уже очень давно. Так, в эллинистическую эпоху было известно, что закон равенства углов падения и отражения светового луча мог быть получен из требования, чтобы при отражении луч света проходил из начального положения в. конечное в кратчайшее время. В XVII в. математик Пьер Ферма (1601—1665), познакомившись с опубликованным Декартом законом преломления света (этот закон был найден голландцем Снеллием ), усомнился в этом законе. Каково было его удивление, когда он, предположив, что при преломлении луч переходит из начального положения в конечное, вывел для преломления те же самые законы, которым не хотел доверять.

В дальнейшем подобные задачи стали встречаться чаще. В 1696 г. Иван Бернулли опубликовал знаменитую задачу о брахистохроне, или кривой наискорейшего ската. Это кривая, по которой должно спускаться, тяжелое тело, чтобы пройти в кратчайшее время из начального положения в конечное, не лежащее на одной вертикали с началом. Задача была решена рядом математиков, причем оказалось, что . и скомая кривая должна быть циклоидой.

В 1697 г. И. Бернулли поставил задачу — провести кратчайшую линию, между двумя точками, лежащими на произвольной поверхности. Он показал, что в любой точке кратчайшей линии главная нормаль перпендикулярна к касательной плоскости, т. е. искомая кривая является геодезической линией этой поверхности. И. Бернулли не опубликовал полученного результата, но предложил заняться этим вопросом своему ученику Эйлеру. Эйлер напечатал в 1728 г. (ему было тогда всего 21 год) решение поставленной перед ним задачи. Продолжая заниматься этим вопросом, он в 1744 г. показал, что для траекторий точек, описываемых под действием центральных сил, интеграл vds 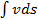равен максимуму или Минимуму. Специального названия этому выражению он, однако, не дал.

В области динамики первый интегральный принцип был введен в 1747 г. французским ученым Пьером-Луи Мопертюи (1690—1759). В истории науки Мопертюи известен прежде всего своим участием в экспедиции, отправленной в 1736 г. в Лапландию для измерения длины градуса земного меридиана. Это было сделано для проверки теоретических работ Гюйгенса и Ньютона, утверждавших, что Земля имеет форму сплюснутого эллипсоида вращения.

Основатель династии французских астрономов Джованни-Доменико Кассини держался мнения, что Земля представляет вытянутый эллипсоид вращения; это же мнение разделяли его сын Жак и внук Франсуа, при которых во Франции начали производить точные геодезические измерения. Чтобы разрешить вопрос об истинной форме Земли, французская Академия наук в 1735—1736 гг. снарядила две экспедиции — одну под руководством Мопертюи и Клеро в Лапландию, а другую под начальством Буге и Ла- Кондамина в Перу.

Результаты обоих градусных измерений показали, что Земля представляет сплюснутый эллипсоид вращения; таким образом, победа оказалась на стороне ньютоновцев , к которым принадлежал и Мопертюи . Попутно заметим, что лапландская экспедиция отражена и в философском романе Вольтера « Микромегас », где житель Сириуса Микромегас беседует с членами лапландской экспедиции. Вольтер очень высоко ставил Мопертюи , прославлял его деятельность в стихах и прозе, составил надпись для его портрета и в письменных обращениях к нему называл его « mon cher applatisseur des mondes et des Cassinis » («мой дорогой, приплюснувший миры и Кассини »).

Мопертюи в 1741 г. уехал в Берлин, где Фридрих II назначил его президентом Берлинской Академии. В 1747 г. он выпускает первый набросок своего «принципа наименьшего действия». Этому принципу знаменитый Эйлер оказал честь его защитой; одновременно он объяснил автору всю ширину и надлежащее употребление его принципа. Однако этот принцип вызвал большое количество возражений.

Одним из возражающих был член Берлинской Академии Кениг, библиотекарь принцессы Оранского дома и профессор общего права в университете Гааги, который тоже занимался математикой. Будучи сторонником Лейбница и теории живой силы, он доказал носящую его имя теорему о кинетической энергии в плоском движении твердого тела. Кениг не только опроверг этот принцип, но даже утверждал, что он не является новым, и цитировав отрывок из письма Лейбница, в котором содержалось указание на этот принцип.

Защищая Кенига, Вольтер написал остроумную «Диатрибу доктора Акакия», которая имела во Франции колоссальный успех. Репутация Мопертюи была уничтожена, ему пришлось уехать из Берлина во Францию, где он и умер в 1759 г. Как пишет Вольтер, вся литературная Европа ополчилась против него, кроме Эйлера и Мериана , которые приняли участие в этом процессе.

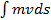
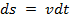
Решающим в этом вопросе является мнение Эйлера. Математическая формулировка принципа Мопертюи была бы таковой: интеграл mvds имеет минимальное значение. Эйлер воспользовался равенством ds = vdt и написал этот интеграл в виде

m v 2 dt = 2 Tdt .

Принцип наименьшего действия в форме Эйлера состоит в том, что при всяком действительном движении вышеприведенный интеграл должен иметь наименьшую величину. Постараемся выяснить, что это означает.

Как уже выяснено, при измерении движения в XVIII в. существенным было не само движение , а его изменение. Если независимым переменным является время, то движение нужно выражать формулой mv ; если же независимым переменным будет пройденный путь или перемещение, то для движения нужно взять выражение 1/2 mv 2 . Затем, как было известно еще Галилею, не всегда движение в кратчайшее время совпадает с движением по кратчайшему пути.

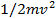
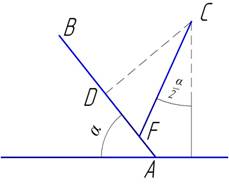
Предположим, что из точки С (рис. 38) надо опустить тяжелое тело на наклонную плоскость АВ, образующую с горизонтом угол α. Если сделать это по кратчайшему пути, то должны пустить тело по прямой CD, перпендикулярной к плоскости АВ; эта прямая образует с вертикалью угол, равный α. Если же выполнить этот переход в кратчайшее время, то должны пустить тело по более крутой прямой CF, образующей с вертикалью угол, равный лишь половине а. Решая эту задачу, можно выразить в зависимости от угла наклона φ прямой расстояние s от начальной точки С до плоскости АВ или время t, которое потребовалось бы для движения по этой прямой согласно законам равноускоренного движения.

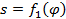
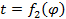
Получив зависимости s = f 1 φ и t = f 2 φ 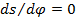, дифференцируем эти уравнения и из всех возможных значений угла φ выбираем нужные:

ds dφ =0 и dt dφ =0;

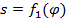
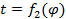
при этом обе зависимости s = f 1 ( φ ) и t = f 2 ( φ ) вполне определенные.

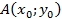
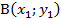
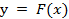
В задаче о цепной линии постановка является совершенно другой. Имеется начальная и конечная точки прикрепления нити A x 0 ; y 0 и В x 1 ; y 1 . Требуется найти такое выражение у = F ( x ) , при котором высота h центра тяжести нити была бы наименьшей возможной. Для этого необходимо, чтобы интеграл

x 0 x 1 yds = x 0 x 1 y 1+ y / dx

имел наименьшую величину. Если решать эту задачу подбором, то Нужно взять ряд кривых y = F 1 ( x ) , у = F 2 ( x ) и т. д., вычислить для них значение указанного интеграла и взять ту функцию, для которой величина интеграла окажется наименьшей. При этом пришлось бы рассматривать семейство линий, проходящих через точки А и В, причем для одного и того же значения х получим различные значения у; разности δу этих значений и представляют так называемые вариации. Только в точках А и В, где ординаты сохраняют постоянное значение, получаем, что вариация будет равна нулю.

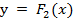
Такая переменность встречалась при рассмотрении принципа возможных перемещений, где возможные перемещения, обозначавшиеся δ, были, по существу, вариациями.

Таким образом, при отыскании минимума интеграла (основная задача вариационного исчисления) надо рассматривать уже не отдельные точки, а семейства кривых или изображаемых ими функций. Это семейство определяется уравнением у = f ( x , ε ) 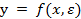, где ε — переменный параметр, позволяющий выделять различные кривые семейства.

Подобно тому как возможные перемещения подчинялись определенным условиям (удовлетворяли уравнениям связей), так и вариации тоже должны удовлетворять некоторым условиям. Например, при движении точки по линии или вообще при переходе системы из начального положения в конечное можно потребовать, чтобы все возможные переходы совершались в один и тот же промежуток времени: это будут так называемые изохронные вариации. В случае Эйлера требуемое условие заключалось в том, чтобы удовлетворялся закон сохранения механической энергии. Такое же требование было поставлено и Лагранжем, обобщившим принцип наименьшего действия на случай нескольких точек.

Σ m i v i d s i =минимум.

Применение принципа наименьшего действия в механике осложнялось тем, что нельзя сразу указать, какая величина должна иметь максимум или минимум, а от выбора этой величины зависели и условия, каким должны были удовлетворять вариации. Этим объясняется то, что в дальнейшем приходилось уточнять название применяемого принципа; кроме закона наименьшего действия Эйлера — Лагранжа в XIX в., как изложено ниже, появился принцип наименьшего действия по Гамильтону.

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Цепная линия

Цепная линия

• Задание 13. 7. 30 метров гибкой нити и 7. 5 кг. Весь агрегат свободно подвешен на 2 опорах, расположенных на одном уровне на расстоянии возвратно-поступательного движения. Определите висячую стрелку в середине пролета и максимальное натяжение нити. Решение. Давайте набросаем положение равновесия yarn. In вопрос, расстояние между опорами. Длина всей нити g 3 м, вес единицы длины нити 5 7, 5 кг м.

Вот оно 2-й основной случай нагружения происходит, когда нить принимает форму цепной линии. Чтобы определить величину провисания нити f, необходимо составить уравнение для кривой равновесия нити. После выбора системы координат cx, как показано на рисунке, используйте основное дифференциальное уравнение 1, которое принимает следующий вид К заданию 13. 7. Функция азимутального — Длина дуги cd. Интегрируйте это уравнение и заранее выразите длину s как y. Используйте для этого хорошо известные Подставляя dyfdx из выражения 1, Вы получаете следующую форму Если мы интегрируем это уравнение — Арш с,. Вопрос п 2 Интегральная константа ci определяется из условий выбранной системы координат s 0.

После составления дифференциального уравнения движения (пункт 4) следует рассмотреть условие статического равновесия мате-риальпой точки, совершающей колебания. Людмила Фирмаль

Выражение 2 принимает вид 3 Подставляя эту формулу в Формулу 1, получаем следующую формулу Ферреневое уравнение кривой равновесия пряжи ды ш ДХ. После интегрирования, находим В если x 0, то координаты y-0, поэтому cr — h q и, наконец, Теперь у нас есть все уравнения, которые нам нужно решить problem. In факт, если задать Формулу 3 x z 2 Или после присвоения номера 112. 5, 56. 23 Это уравнение вида 2z shz.

Используйте таблицу гиперболических синусов, чтобы найти выбор ее решения Определить натяжение нити в точке 5, где h a 25, s4 кг. Искомая провисающая нить находится из Формулы 4 Если положить ее в x c2. Для определения натяжения нити используйте основное соотношение 2. Напомним, что q qs, применяя формулу 3, находим q f sh. Подставляя это в Формулу 2, получаем Или с помощью соединения 4 7 — я 4Р. Из последнего уравнения следует, что натяжение нити максимизируется в неподвижных точках a и b, где Гта я ФК 25. 84 7. 5-11. 94 115. 4 кг.

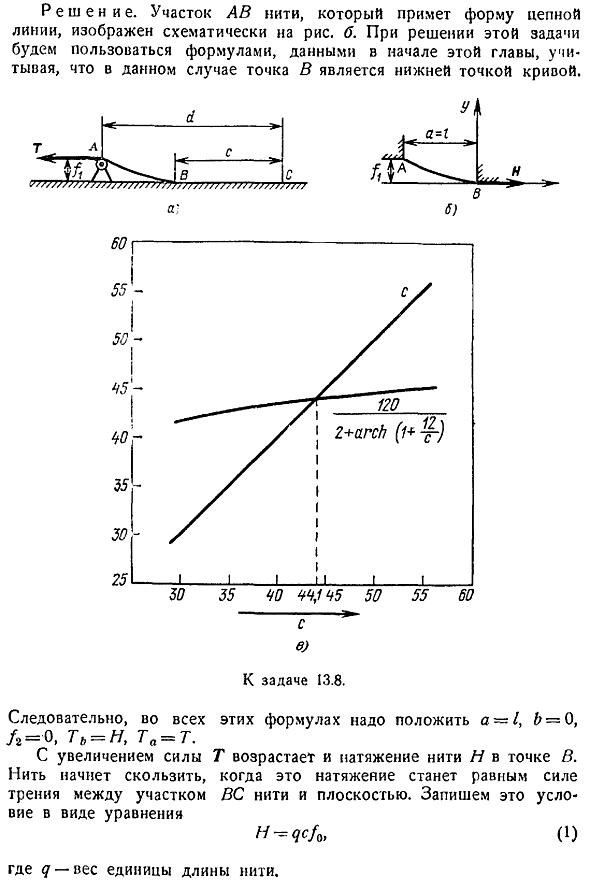
Задача 13. 8. Часть гибкой нити, равномерно распределенной по весу по длине, находится на горизонтальной плоскости. Остальные дачи проходят через небольшой блок а рисунок а. Постепенно увеличивая усилие t приложено к концам thread. In в этом случае длина линии контакта между ВС и плоскостью нити уменьшается и приближается к определенному пределу С, где нить начинает скользить вдоль плоскости.

Определить это предельное значение С, если d 60 м, l 6 м, а коэффициент трения между резьбой и плоскостью 0 0, 5. Другие способы решения такого уравнения см. В задаче 13. 8. Решение. На рисунке 2 показан участок av-потока, который принимает форму одной цепи. b. To решите эту задачу, используя выражение, показанное в начале этой главы, в котором точка b является нижней точкой кривой. С Задача 13. 8. Итак, для всех этих формул нужно разместить a-1, b-0, r 0, t h, ta t.

При увеличении силы Т натяжение нити Н в точке В также увеличивается, и когда это натяжение равно силе трения между частью ВС нити и плоскостью, нить начинает проскальзывать. Запишите это условие в виде уравнения Ч — qcfa, 1 Где d-вес единицы длины нити. Значение h должно удовлетворять формуле 14. В этом выпуске 2 Исключается из уравнения 1. 2 Значение h, получим следующее уравнение Из него определяется желаемый размер s. Быть l d-c. Уравнение эго Вот бы заменить знаменитые чудесные вещи 3 Вы не можете решить это трансцендентальное уравнение в отношении использования точных алгебраических методов. Поэтому, чтобы найти его корень, нужно воспользоваться приближенным методом.

Рассмотрим 2 таких ways. It это графический метод и итерационный метод. Графический способ заключается в создании левого и правого графика уравнений в 1 чертеже. Горизонтальная ось пересечения этих графиков показывает примерное значение маршрута. Для простоты сначала представим выражение 3 в следующем виде 120. 2 арка ий 4 График в левой части уравнения 4 является биссектрисой первой координаты angle. To постройте график правой стороны, вычислите значения некоторых значений в c, взятых рядом с расчетными значениями маршрута. Результаты расчетов сведены в таблицу. 1. 4 рефские. 4 2 арка 4 120 30 0. 4000 1. 4000 0. 8670 2. 8670 4186 35 0. 3429 1. 3429 0.

Если повторить этот процесс несколько раз, то можно получить значение корня с произвольной точностью, если f x 1 в интервале между корнем уравнения и первым приближением. Если это условие не выполняется, то уравнение должно быть преобразовано по крайней мере, путем передачи его в обратную функцию. Для 30 c 55 легко видеть, что модуль правой производной Формулы 4 меньше 1. Поэтому это выражение можно повторить, взяв значение c из заданного интервала первого приближения c0. C0 46 м. 120. 2 л 44, 3 м 44, 08 м 11a может завершить итерационный процесс, наконец, получив c 44. 1 m. Задача 13. 9. Гибкий поток без расширения приостанавливается от поддержки a и блока, который можно игнорировать.

• Вес q на единицу резьбы. Баланс определяет длину свободно висящей части нити, которая не нарушается. Третий блок игнорируется. Ты поешь. После выбора начальной точки самой нижней точки кривой, используйте уравнение 1, чтобы найти уравнение кривой. Где — напряжение в точке С. Тогда заметим, что вертикальное приращение нагрузки dq qds ды ЗДС Или заменить ДС У1 y 2 ДХ При разделении переменной Когда вы интегрируете ды И1 РТ 7г- с Для краткости укажите h q a. Как, о Тогда ci 0 и, наконец, выражение 2 имеет вид Г У1. Из Формулы 3 Вы можете легко проверить, умножив 3 на 4.

При добавлении выражений 3 и 4 Если мы интегрируем последнее уравнение если x 0 и y 0, то перенос начала координат 5 записывается в виде Точка o 0, — a. Ось ox называется основанием цепной линии. Это связано с тем, что я держусь только под действием вертикальной нагрузки, поэтому горизонтальное натяжение не изменяется. T h, или t h c- Согласно 1, это равенство может быть переписано в следующем виде 1 2 3 Ноль 5 1 равна Проекция Если вычесть равенство из 3 в 4 И, наконец, получить свободную точку кривой Натяжение нити по формуле Северный t — y1 chu1- В результате, если длина подвешенной части равна yt bd, то нить будет находиться в равновесии. Задание 13. 10.

При составлении дифференциального уравнения надо изобразить материальную точку в промежуточном положении, соответствующем ее положительной координате, предположив при этом, что точка перемещается в сторону возрастания этой координаты. Людмила Фирмаль

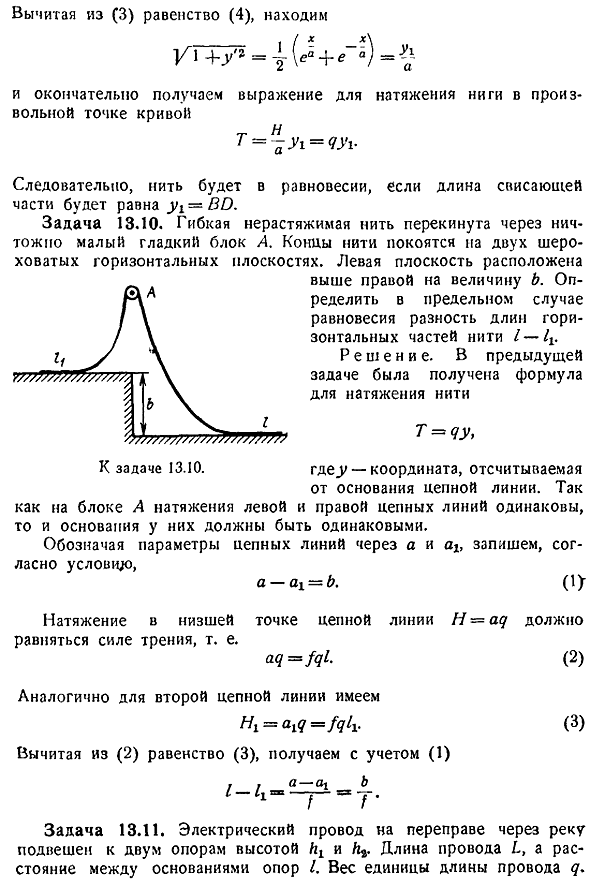
На небольшой и гладкий блок набрасывают гибкую, не натянутую нить. Нить лошади находится на 2 грубых горизонтальных плоскостях. Левая плоскость находится выше правой плоскости на величину b. In в предельном случае равновесия определяют разность длин горизонтальной части нити 1-1. Solution. In в предыдущем выпуске была получена формула натяжения нити Т Тип qy где y-координаты, измеренные от основания цепной линии. Правая прядь такая же Основа для этого должна быть одна и та же. В зависимости от условий, a и write указывают параметры линии цепи а-АИ б. 1 г, г Вопрос 13. 10. Для Как блок а в левом напряжении Натяжение в самой нижней точке цепной линии h aq должно быть равно силе трения.

Аналогично, для 2-й цепной линии 3 Если вычесть равенство 2 из равенства 3, то вы принимаете во внимание 1 Я Задание 13. 11. Проволока на пересечении реки подвешена к 2 столбам по высоте и c. Длина проволоки равна l, расстояние между основаниями опор равно i. Вес q на единицу длины проволоки. Для bx 30 м, b2 12 л, 20 м, 1 45 м, q 1. 25 кг м найти уравнение кривой, максимальное провисание и максимальное натяжение. Решение. Если выбрать начало координат в верхней части цепной линии o, то в соответствии с 10 уравнение кривой имеет вид В данном случае неизвестно следующее. Положение точки o, определяемое отрезком, также является горизонтальным натяжением n.

В определении используется выражение, определяющее условия прохождения цепной линии через точки соединения А и В, а также длину провода между опорами. У нас есть 2 НТ-н0 ч 1 3 Найти более длины провода В1 г ДХ г л ш ДХ х функции rfx 7shff e в sh4r shff 2 st, cht 4 От 2 до 3 Чтобы определить горизонтальное натяжение n, возьмем 4 и 5 2, Затем возьмем 2 и вычтем от 1-го до 2-го 4 Из этого уравнения 1д 2Н В Р П 2. 06 К1 2Н это трансцендентальное уравнение вида shz 2.

Графически решается с помощью fi z shz, g g 2. 06 z, которое создает или аппроксимирует 2 кривые в соответствии с таблицей. Их пересечение дает r 1d 2ч 2. 22, оттуда 6 4, 48 −1, 25 6, 6 кг. Чтобы найти a, разделите 5 на 4. У нас есть Откуда Учитывая 6, остается найти d0 из 2 Найти уравнение кривой, подставив значения, найденные в уравнении 1 Приступайте к решению о провисании самого большого провода. Максимальная слабина — это точка кривой, где касательная линия кривой параллельна линии ab. Из этого уравнения находим абсциссу искомой точки кривой Самые большие провалы Макс-е- а-xif по-Хо-у ХВ Т Н1 — ч дж а-х — н л- ч я-л педагогика 18. 74 м.

И согласно напряжению провода 7 l h a h 4 d1-l0 40, 5 кг, tb h qft h q h2-h0 m, 8 кг. Задание 13. 12. Цепь с равным сопротивлением представляет собой цепь переменной толщины, где толщина каждой точки пропорциональна напряжению t. in такая цепочка, вероятность обрыва во всех точках одинакова. Уравнение кривой равновесия и закон изменения толщины цепи определяются. Решение. Буква О обозначает переменный участок цепи, изменяющийся по ее длине. Если вес единицы объема цепи равен p, а ее длина равна s, то вес элемента ds равен puds. Выберите начало координат в самой нижней точке цепочки. Используйте уравнение 1, чтобы найти уравнение кривой 2 ДХ П О Где h-натяжение самой нижней точки цепи.

Приращение вертикальной нагрузки составляет rfq pa ds, и мы видим, что натяжение цепи согласно условию пропорционально толщине, то есть равно Т ka, k коэффициенту пропорциональности. При вычислении разности с обеих сторон уравнения 1 2 С другой стороны, проекция горизонтального натяжения оси x является постоянной величиной, так как на цепь действует только вертикальная нагрузка Ч Т — АО — const и Откуда 3 значение o вводится в Формулу 2. А потом мы это выясним. Здесь рассматривается ds j l dx.

Когда вы отделяете переменную, она выглядит так ды Ю Д Когда вы интегрируете arctgy г интернет. Происхождение выбран в самой низкой точке, где кривая сводится к минимуму. Так, если x 0, г 0, С1 0 4 диджей тг — xdx. Интеграция и поиск у — Линкос — х ХС. Если x 0, y 0, c2 0. — y lncos — — х, э к Кос- — х Или наконец-то е со −2-х 1. Это уравнение сопротивления curve. To найти закон изменения толщины цепи, используя уравнение 3.

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Уравнение цепной линии принцип стационарного действия

Цепная линия – плоская трансцендентная кривая, форму которой принимает под действием силы тяжести однородная, гибкая, не растяжимая, тяжелая нить (цепь) с закрепленными концами (см. рис. 10).

Для того, чтобы вывести уравнение цепной линии, выделим бесконечно малый элемент нити 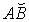от точки А (х , у) до точки В (х+dx , y+dy) и рассмотрим систему сил, действующих на него.

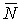
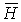
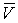
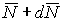
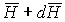
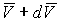
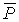
В точке А на нить действует натяжение , направленное по касательной к кривой. Обозначим через и его составляющие по осям координат. Соответственно в точке В имеется натяжение с составляющими и . Кроме того, на элемент АВ действует сила тяжести , направленная вертикально вниз и равная по абсолютной величине p=qds , где ds – дифференциал дуги АВ, а q – вес единицы длины нити. Для того, чтобы система сил находилась в равновесии, необходимо и достаточно, чтобы сумма проекций на каждую ось всех действующих сил была равна нулю. Приравнивая к нулю проекцию сил на ось Ох , получим:

т.е. горизонтальная составляющая натяжения нити есть величина постоянная.

Проецируя силы на ось Оу , получим:

-V-qds+(V+dV)=0 или dV=qds.

С другой стороны, обозначив через « a » угол, образованный касательной к кривой в точке А с осью Ох , получим:

Продифференцируем последнее равенство по х , учитывая, что H=const :

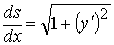
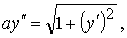
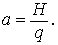
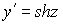
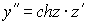
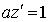
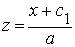
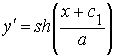
Учитывая, что dV=qds и (см. [1] ) , получим следующее дифференциальное уравнение: где обозначено Найдем общее решение данного уравнения. Для этого производим замену: . Тогда и уравнение примет вид: . Интегрируя последнее равенство по х, получим: . Следовательно и окончательно:

Получили семейство цепных линий. Подбирая произвольные постоянные с1 и с2 так, чтобы выполнялись начальные условия 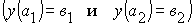, получим искомое уравнение линии провисания нити.

Предположим, что константы с1 и с2 уже подобраны, тогда уравнение цепной линии можно упростить. Произведем преобразование координат: 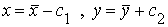, т.е. за новое начало координат принимается точка (-с1 , с2). В новой системе координат уравнение цепной линии с сохранением прежних обозначений для новых координат примет вид:

Если принять за начало координат нижнюю точку цепной линии, то с1=0 , с2=а и окончательно уравнение цепной линии примет вид :

Нетрудно рассчитать по известной формуле [1] радиус кривизны цепной линии в любой её точке:

Площадь, ограниченная дугой цепной линии прямыми х=х1 , х=х2 и осью абсцисс, будет :

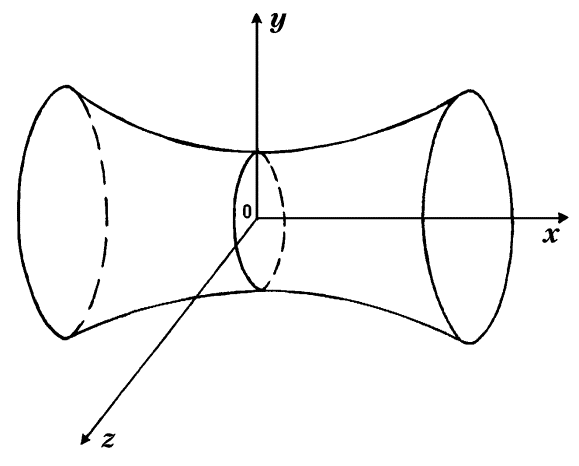
Если дугу цепной линии 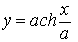вращать вокруг оси Ох , то образуется поверхность вращения, называемая катеноидом.

Можно показать, что катеноид представляет собой поверхность, имеющую минимальную площадь среди всех поверхностей вращения дуг линий, соединяющих две заданные точки плоскости.

Задача. Показать, что объём тела, ограниченного катеноидом, координатной плоскостью до уОz и плоскостью, параллельной ей и отстоящей от неё на расстояние х , и площадь Q поверхности этой же части катеноида связаны формулой:

Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter