Уравнение цилиндрической поверхности с образующей и направляющей

Цилиндрические поверхности

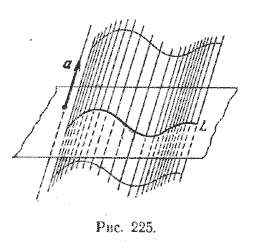
Если через каждую точку кривой L провести прямую, параллельно данному вектору а, то получим поверхность, которая называется цилиндрической поверхностью. Прямые, параллельные вектору а и принадлежащие цилиндрической поверхности, называются образующими этой поверхности, а кривая L называется направляющей цилиндрической поверхности (рис. 225).

Если в сечении цилиндрической поверхности плоскостью, перпендикулярной к ее образующим, (в нормальном сечении) получается окружность, то цилиндрическая поверхность называется круговой. Если в сечении получается эллипс, то цилиндрическую поверхность называют эллиптической, если гипербола — гиперболической, если парабола — параболической.

Пусть в пространстве дана прямоугольная система координат Oxyz, и пусть в плоскости хОу дана кривая L, уравнение которой в этой плоскости имеет вид

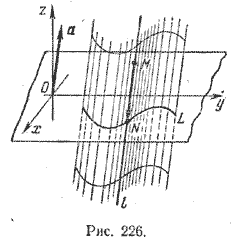
Составим уравнение цилиндрической поверхности с образующими, параллельными вектору a = (α; β; γ), γ =/= 0, если за направляющую принята кривая L (рис.226).

Рассмотрим произвольную точку этой поверхности М(х; у; z). Образующая l, проходящая через точку М, пересечет плоскость хОу в точке N, лежащей на кривой L. Если координаты точки N в пространстве обозначить (х₁; у₁; 0), то вектор \(\overrightarrow\) имеет координаты

По определению цилиндрической поверхности векторы а и \(\overrightarrow\) коллинеарны, т. е.

следовательно, имеем систему уравнений

Решив эту систему уравнений относительно λ, x₁и у₁, получим

Так как точка N лежит на кривой L, то F(х₁; у₁) = 0. Заменив х₁ и у₁ по формулам (2), получим уравнение

которое, очевидно, и будет уравнением данной цилиндрической поверхности.

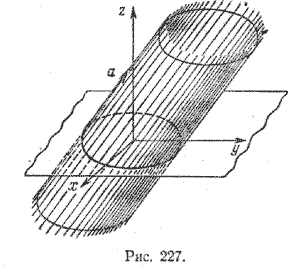
Задача 1. Составить уравнение цилиндрической поверхности, у которой направляющая лежит в плоскости хОу и имеет уравнение х 2 + у 2 = 4, а образующие параллельны вектору а = (0; 1; 1).

Так как, согласно условию задачи F(x; у) = х 2 + у 2 — 4 и α = 0, β = 1, γ = 1, то в силу формулы (3) уравнение данной цилиндрической поверхности имеет вид

Эта поверхность изображена на рис. 227.

Аналогично можно показать, что если направляющая цилиндрической поверхности L лежит в плоскости xOz и определяется уравнением F(x; z) = 0, а вектор а не параллелен этой плоскости, то цилиндрическая поверхность имеет уравнение

Наконец, если L определяется уравнением F(у; z) = 0 и а не параллелен плоскости yOz, то уравнение цилиндрической поверхности имеет вид

Отметим, что если направляющая цилиндрической поверхности лежит в плоскости

хОу, а образующие параллельны оси Oz, то уравнение цилиндрической поверхности в пространстве совпадает с уравнением направляющей и имеет вид

Уравнение (4), как уравнение множества точек плоскости, определяет кривую L, в то же самое время уравнение (4), как уравнение множества точек пространства, определяет цилиндрическую поверхность.

Итак, каждое из уравнений

можно истолковать двояко: если это уравнение множества точек плоскости, то это уравнение линии L, лежащей в плоскости своих переменных; если же это уравнение множества точек пространства, то каждое из этих уравнений определяет цилиндрическую поверхность с направляющей L и образующими, параллельными оси oтсутствующей переменной.

Рассмотрим несколько примеров.

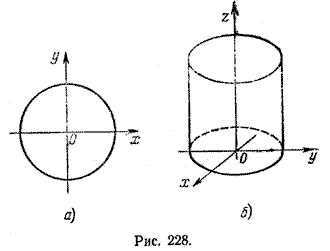
на плоскости хОу определяет окружность с центром в начале координат и радиусом r (рис. 228, а).

Это жe уравнение в пространстве определяет круговую цилиндрическую поверхность, направляющей которой является окружность, лежащая в плоскости хОу, а образующие параллельны оси Oz (рис. 228, б).

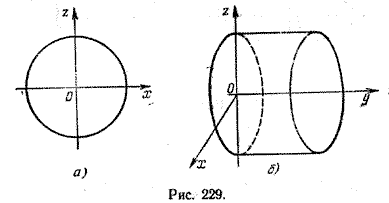
на плоскости xOz определяет окружность с центром в начале координат и радиусом

Это же уравнение в пространстве определяет круговую цилиндрическую поверхность, направляющей которой является окружность, лежащая в плоскости xOz, а образующие параллельны оси Оу (рис. 229, б).

и на плоскости, и в пространстве определяет пустое множество, так как сумма неотрицательных чисел не может быть числом отрицательным.

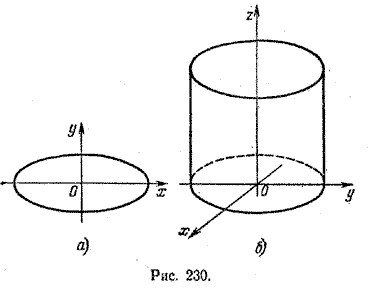
на плоскости хОу определяет эллипс с центром в начале координат и полуосями а и b (рис. 230, а).

Это же уравнение в пространстве определяет эллиптическую цилиндрическую поверхность с направляющей в плоскости хОу и образующими, параллельными оси Oz (рис. 230, б).

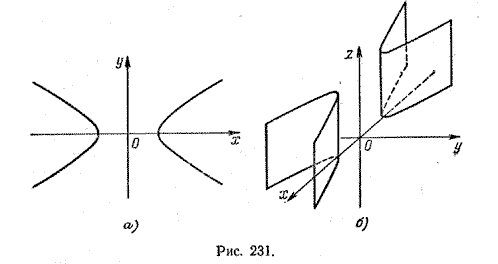
на плоскости хОу определяет гиперболу с центром в начале координат и полуосями а и b (рис. 231, а).

В пространстве это уравнение определяет гиперболическую цилиндрическую поверхность с образующими, параллельными оси Oz (рис. 231, б).

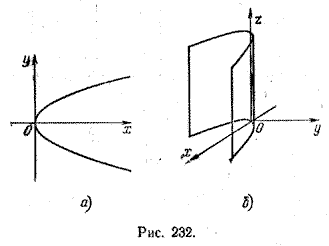
на плоскости хОу определяет параболу (рис. 232, а), а в пространстве — параболическую цилиндрическую поверхность с образующими, параллельными оси Oz (рис. 232, б).

Задача 2. Определить вид поверхности 3x 2 + 6y 2 — 24 = 0.

Данное уравнение приведем к виду:

Это уравнение в пространстве определяет эллиптическую цилиндрическую поверхность с направляющей в плоскости хОу и образующими, параллельными оси Oz.

Поверхности второго порядка. Цилиндрические поверхности.

Поверхность S называется цилиндрической поверхностью с образующей , если для любой точки M₀

этой поверхности прямая, проходящая через эту точку параллельно образующей , целиком принадлежит

Теорема (об уравнении цилиндрической поверхности).

Если в некоторой декартовой прямоугольной системе координат поверхность имеет

уравнение f(x,y)=0, то S — цилиндрическая поверхность с образующей, параллельной оси OZ.

Кривая, задаваемая уравнением f(x,y)=0 в плоскости z=0, называется направляющей цилиндрической

поверхности.

Если направляющая цилиндрической поверхности задаётся кривой второго порядка, то такая поверхность

называется цилиндрической поверхностью второго порядка.

Тема: Линейные операции над векторами. Скалярное произведение векторов

Главная > Документ

Тема: Поверхности вращения.
Цилиндрические поверхности

1. Поверхности вращения.

пределение. Поверхностью вращения называется поверхность, образованная вращением плоской линии  вокруг оси, лежащей в плоскости этой линии.

Пусть , тогда ее можно задать уравнениями

Уравнение поверхности, образованной вращением линии  вокруг оси Oz будет иметь вид:

(1)

2. Цилиндрические поверхности .

Пусть в пространстве дана некоторая плоская линия  и вектор , не параллельный плоскости этой линии.

Определение . Цилиндрической поверхностью называется множество точек пространства, лежащих на прямых параллельных данному вектору и пересекающих данную линию .

иния  называется направляющей цилиндрической поверхности, прямые называются образующими.

Рассмотрим частный случай: направляющая линия  лежит в плоскости xOy : и задается уравнениями: а направляющий вектор образующих имеет координаты , .

В этом случае уравнение цилиндрической поверхности имеет вид

. (2)

Получите уравнение поверхности вращения (1).

Получите уравнение цилиндрической поверхности (2).

Основные типовые задачи.

Составление уравнения поверхности вращения по уравнениям направляющей и оси вращения.

Составление уравнения цилиндрической поверхности по уравнениям направляющей и направляющему вектору образующих.

Примеры решения задач.

Задача 1. В плоскости yOz дана окружность с центром в точке (0; 4; 0) радиуса 1. Написать уравнение поверхности, образованной вращением данной окружности вокруг оси Oz .

Уравнения окружности, лежащей в плоскости yOz с центром в точке (0; 4; 0) радиуса 1, имеют вид

(3)

При вращении этой окружности вокруг оси Oz получается поверхность, называемая тором. Пусть М – произвольная точка на торе. Проведем через точку М плоскость , перпендикулярную оси вращения, т.е. оси Oz , в сечении получим окружность. Обозначим центр этой окружности P , а точку пересечения плоскости  с окружностью, образующей поверхность вращения, – N .

Обозначим координаты точки M ( x , y , z ), тогда P (0, 0, z ), а N(0,, z ). Так как точки M и N лежат на окружности с центром в точке P , то

,

.

Последнее равенство запишем в координатах

. (4)

Точка N лежит на окружности, при вращении которой образуется тор, значит ее координаты должны удовлетворять уравнениям (3), запишем первое уравнение системы (3)

,

,

.

Возведем последнее равенство в квадрат.

и подставим выражение для из равенства (4), получим

(5)

Уравнение (5) – искомое.

Ответ: .

Задача 2. Составить уравнение цилиндрической поверхности, если направляющая лежит в плоскости xOy и имеет уравнение , а образующие параллельны вектору <1; 2; –1>.

Пусть точка M ( x , y , z ) – произвольная точка цилиндрической поверхности. Проведем через точку М образующую l , она пересекает направляющую в точке . Так как направляющая лежит в плоскости xOy , то . Составим канонические уравнения прямой l

.

Приравняем первую и вторую дроби к последней

(6)

Точка N лежит на направляющей, значит ее координаты удовлетворяют ее уравнению:

.

Подставляя выражения для и из системы (6), получим

. (7)

(7) – искомое уравнение.

Ответ: .

Задачи для самостоятельного решения.

Составить уравнение поверхности, образованной вращением параболы , х= 0 вокруг оси Oz .

Составить уравнение поверхности, образованной вращением вокруг оси Oy каждой из следующих кривых, расположенной в плоскости xOy :

а) эллипса ;

б) гиперболы ;

в) параболы .

Написать уравнение поверхности, образованной вращением синусоиды вокруг оси Oz .

Напишите уравнение поверхности, образованной вращением прямой , вокруг оси Ox .

Докажите, что поверхность, образованная вращением вокруг оси Oz линии l , заданной уравнениями , имеет уравнение .

Составить уравнение цилиндрической поверхности в каждом из следующих случаев:

а) Направляющая лежит в плоскости и имеет уравнение , а образующие параллельны вектору <1; 0; 1>;

б) направляющая лежит в плоскости yOz и имеет уравнение , а образующие параллельны оси Ox ;

в) направляющая лежит в плоскости xOz и является окружностью , а образующие параллельны оси Oy.

Напишите уравнение цилиндрической поверхности, если:

а) направляющая задана уравнениями а образующая параллельна вектору ;

б) направляющая задана уравнениями а образующая параллельна прямой x = y = z .

Напишите уравнение цилиндрической поверхности, направляющая которой задана уравнениями а образующая параллельна оси Ox .

Напишите уравнение цилиндрической поверхности, направляющая которой задана уравнениями а образующая перпендикулярна плоскости направляющей.

Цилиндр, образующие которого перпендикулярны плоскости , описан около сферы . Составить уравнение этого цилиндра.

Написать уравнение цилиндрической поверхности вращения, если ось вращения совпадает с осью Oz , а радиус r= 5.

Составить уравнение круговой цилиндрической поверхности, если известны уравнения ее оси , , и координаты одной из ее точек .

Написать уравнение круговой цилиндрической поверхности, если известны уравнения ее оси l и координаты одной из ее точек М :

а) , , , М (2; 0; 1);

б) l : , М (2; –1; 1).

Тема: Конические поверхности.

Пусть в пространстве дана некоторая плоская линия  и точка S , не лежащая в плоскости этой линии.

Определение . Конической поверхностью называется множество точек пространства, лежащих на прямых проходящих через данную точку S и пересекающих данную линию .

Линия  называется направляющей конической поверхности, точка S – вершиной, прямые называются образующими.

ассмотрим частный случай: вершина S совпадает с началом координат, направляющая линия  лежит в плоскости, параллельной плоскости xOy : z = c , и задается уравнением: .

В этом случае уравнение конической поверхности имеет вид

. (1)

Если направляющая является эллипсом с центром на оси Oz ,

то получаем поверхность, называемую конусом второго порядка, уравнение этой поверхности имеет вид:

. (2)

Ось Oz в этом случае является осью конуса второго порядка.

Сечения конуса второго порядка:

Пусть плоскость  не проходит через вершину конуса второго порядка, тогда плоскость  пересекает конус:

а) по эллипсу, если  пересекает все образующие конуса;

б) по гиперболе, если  параллельна двум образующим конуса;

в) по параболе, если  параллельна одной образующей конуса.

Получите уравнение конической поверхности (1).

Получите уравнение конической поверхности второго порядка (2).

Основные типовые задачи.

Составление уравнения конической поверхности по координатам вершины и уравнению направляющей.

Примеры решения задач.

Задача 1. Написать уравнение конической поверхности, вершина которой находится в начале координат, а направляющая задана уравнениями

Пусть точка M ( x , y , z ) – произвольная точка конической поверхности. Проведем через эту точку образующую l , она пересечет направляющую в точке . Запишем канонические уравнения прямой l , как уравнения прямой, проходящей через точку N и вершину конуса О(0, 0, 0)

,

.

Выразим из последней системы и : , . Т.к. точка N лежит на направляющей конической поверхности, то ее координаты должны удовлетворять уравнениям направляющей:

(3)

Подставим найденные выражения во второе уравнение системы (3)

,

,

,

. (4)

, . (5)

Подставляем (4) и (5) в первое уравнение системы (3)

,

,

.

Полученное уравнение является искомым уравнением конической поверхности.

Задачи для самостоятельного решения.

Написать уравнение конической поверхности, если:

а) направляющая в плоскости xOy задана уравнением , а вершина имеет координаты (1; 0; 1);

б) направляющая в плоскости xOy задана уравнением , а вершина имеет координаты (0; 0; 1);

в) направляющая в плоскости xOy задана уравнением , а вершина имеет координаты (0; 0; 1).

г) направляющая в плоскости xOy задана уравнением , а вершина имеет координаты (0; 0; с ).

Составить уравнение конической поверхности с вершиной в точке S(1; 2; 4), образующие которой составляют с плоскостью угол =45.

Написать уравнение конической поверхности, направляющая которой задана уравнениями а вершина находится в точке .

Найти уравнение конической поверхности с вершиной в начале координат, которая проходит через линию пересечения:

а) гиперболоида и сферы ;

б) эллипсоида и плоскости .

Напишите уравнение круговой конической поверхности, если известны уравнения ее оси l : и координаты одной из ее точек М(3; –4; 5).

Доказать, что уравнение определяет конус с вершиной в начале координат.