Уравнение ударной адиабаты для идеального газа

Содержание (стр. 2 )

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4

12.5. Поверхности разрыва, ударные волны и скачки уплотнения

12.5.1. Конус Маха

С физической точки зрения сверхзвуковое движение газа отличается от дозвукового характером распространения малых возмущений в потоке.

Рассмотрим, как распространяются в движущемся потоке газа малые возмущения. Предположим, что в некоторой точке дозвукового течения газа возникло возмущение плотности газа. Это возмущение сносится вниз по потоку и распространяется в движении с газом со скоростью звука во все стороны. Если газ однороден, то поверхность распространения возмущения одинаковой фазы представляет собой поверхность шара, расширяющегося со скоростью звука (рис. 12.3а). При этом возмущение при дозвуковом движении газа распространяется как вниз, так и вверх по потоку.

При сверхзвуковом движении газа возмущения, распространяющиеся со скоростью звука, не могут проникнуть в область течения вверх по потоку (рис. 12.3б), а сносятся потоком вниз по течению.

Поверхность, ограничивающая область возмущения сверхзвукового потока, представляет собой поверхность конуса, который называют конусом Маха. Если движение газа прямолинейное, а газ однороден, то конус Маха

будет прямым круговым конусом. Из рисунка (12.3б) очевидно, что угол конуса определяется соотношением:

==. (12.5.1)

Угол называют углом Маха. Поверхность конуса Маха называют характеристической поверхностью, а линии пересечения ее с плоскостью, проходящей через ось конуса, называются характеристиками.

Из рассмотрения рисунков (12.3а, б) очевидно, что сверхзвуковой поток набегает на обтекаемое тело (являющееся, в частности, источником возмущения) »вслепую». Сверхзвуковой поток »не предчувствует» обтекаемое тело. В дозвуковом потоке влияние тела сказывается вверх по течению, т. е. дозвуковой поток »чувствует» обтекаемое тело значительно раньше, чем его достигнет.

12.5.2. Поверхности разрыва. Законы сохранения

До сих пор изучалось движение среды, при котором скорости и термодинамические параметры изменялись непрерывно, т. е. они были непрерывными функциями координат и времени.

Однако в действительности имеют место такие движения, при которых термодинамические параметры и скорости могут претерпевать разрыв непрерывности. Разрыв непрерывности скоростей и термодинамических параметров происходит на некоторых поверхностях, на которых они претерпевают скачок. Эти поверхности называют поверхностями разрыва.

При нестационарных движениях поверхности разрыва сами могут двигаться относительно тела, возмущающего покоящуюся среду, однако скорость их движения не имеет ничего общего со скоростью движения частиц газа, которые могут при своем движении пересекать поверхности разрыва.

Поверхности разрыва, которые перемещаются относительно обтекаемого тела, называют ударными волнами. Поверхности разрыва, которые неподвижны относительно обтекаемого тела, называют скачками уплотнения.

Рассмотрим малый участок поверхности разрыва, который можно считать плоским, и свяжем с ним оси координат. В этой системе координат поверхность разрыва покоится. Направим ось x по нормали к рассматриваемому участку поверхности разрыва (рис. 12.4).

Из физических соображений следует, что на поверхности разрыва должны соблюдаться определенные граничные условия, т. е. должны выполняться законы сохранения:

1. На поверхности разрыва должен выполняться закон сохранения массы, т. е. плотность потока вещества должна быть непрерывна:

2. На поверхности разрыва должен выполняться закон сохранения энергии, т. е. плотность потока энергии должна быть непрерывна. В разделе 1 было показано, что плотность потока энергии определяется вектором Умова-Пойтинга (6.8.9), который для ньютоновской среды () равен:

, .

Так как рассматривается сверхзвуковое движение газа, то можно считать газ идеальным. Пренебрегая потенциальной энергией и учитывая, что для идеальной среды коэффициенты теплопроводности, динамической и объемной вязкости равны нулю (), а, следовательно, плотность потока тепла и тензор вязких напряжений также равны нулю (), получим:

.

Непрерывность потока энергии на поверхности разрыва приводит к следующему соотношению:

Соотношение (12.5.3) с учетом равенства (12.5.2) дает:

, (12.5.4)

т. е. на поверхности разрыва выполняется уравнение Бернулли для изоэнтропического движения.

3. На поверхности разрыва должен выполняться закон сохранения количества движения, т. е. плотность потока импульса должна быть непрерывна. Это означает, что плотность потока импульса с обеих сторон поверхности разрыва должна быть одинакова; в противном случае на поверхность разрыва будет действовать некоторая сила, которая должна вызвать движение этой поверхности в выбранной системе координат. Плотность потока импульса и условие для него на поверхности разрыва имеют вид:

, .

Равенство плотностей потока в направлении оси x приводит к соотношению(i=k=x):

Равенство плотностей потоков импульсов в направлении осей y и z дает следующие равенства:

, , , . (12.5.6)

Последние два соотношения с учетом (12.5.2) дают:

, (12.5.7)

Соотношения (12.5.7) свидетельствуют о том, что на поверхности разрыва должны быть непрерывны касательные к ней скорости движения газа.

12.6. Прямая ударная волна в сжимаемом газе

12.6.1. Ударная адиабата (адиабата Гюгоньо)

Рассмотрим движение газа, при котором линии тока перпендикулярны поверхности разрыва. Поверхность разрыва называют прямой ударной волной, если она перемещается по отношению к обтекаемому телу, а линии тока перпендикулярны к ней. Если же поверхность разрыва неподвижна по отношению к обтекаемому телу, то её называют прямым скачком уплотнения.

Из (12.5.2,4,5) следует, что в прямой ударной волне или прямом скачке уплотнения скорости газа и термодинамические параметры должны удовлетворять следующим соотношениям:

, , . (12.6.1)

По определению прямой ударной волны . Равенство (12.5.7) свидетельствует о том, что и . Следовательно, если линия тока до прямой ударной волны перпендикулярна поверхности разрыва, то она останется перпендикулярной и после нее, т. е. линия тока при прохождении прямой ударной волны не испытывает излома. Поэтому в равенствах (12.6.1) , а и их можно записать в окончательном виде:

, , . (12.6.2)

Установим соотношение между термодинамическими параметрами и скоростями в прямой ударной волне. Введем следующие обозначения:

, , .

Из первого уравнения (12.6.2) имеем:

.

Воспользуемся третьим уравнением системы (12.6.2), умножив и разделив вторые слагаемые в нем на и , соответственно. Используя определение плотности потока массы , можно записать:

, , . (12.6.3)

Из второго уравнения (12.6.2) следует:

. (12.6.4)

Используя определение энтальпии h через скорость звука c, это равенство можно преобразовать:

. (12.6.5)

Данное уравнение называют уравнением ударной адиабаты или уравнением адиабаты Гюгоньо. Это уравнение при известных термодинамических параметрах набегающего потока и определяет зависимость за прямой ударной волной, представленную на (рис. 12.5). Угол между прямой, соединяющей точки 1 (,) и 2 (,), и осью на рис. 12.5 определяется соотношением:

. (12.6.6)

12.6.2. Связь между скоростями и термодинамическими параметрами в прямой ударной волне

Найдем связь между скоростями и термодинамическими параметрами в прямой ударной волне в сверхзвуковом потоке сжимаемого идеального газа. Если разделить уравнение ударной адиабаты (12.6.5) на P1 и V1, то, можно определить связь удельных объемов и давлений в прямой ударной волне.

(12.6.7)

Как видно из (12.6.7), функция является равнобочной гиперболой с асимптотами (см. рис.12.6):

. (12.6.8)

Из уравнения состояния идеального газа следует:

, , . (12.6.9)

Предельное отношение температур при и равно:

. (12.6.9а)

Таким образом, при очень большом скачке давления скачок температуры в ударной волне может быть сколь угодно большим. Однако отношение плотностей стремится к некоторому постоянному пределу, определяемому соотношением (см. 12.6.8):

(12.6.10)

Для воздуха () предельное значение плотности за прямой ударной волной при равно

Для скоростей можно получить следующие соотношения из первого граничного условия (12.5.2) на поверхности разрыва:

.

Если в этом определении использовать замену согласно (12.5.2), то

. (12.6.11)

Аналогичное выражение можно получить для :

. (12.6.12)

Используя определение плотностей потоков массы и (12.6.3), для разности скоростей получим соотношение:

В соответствии с (12.1.6) и (12.6.2) имеем:

.

Тогда критические скорости до и после ударной волны можно определить следующим образом:

.

Из данного соотношения следует, что

. (12.6.14)

Для изоэнтропического движения согласно уравнению Бернулли для произвольных точек и точек полного торможения потока на линии тока можно записать равенство:

= .

Из этого равенства следует, что температура торможения в прямой ударной волне сохраняется, т. е.

, (12.6.15)

Пользуясь вышеприведенными формулами можно доказать следующее соотношение:

. (12.6.16)

Интересующие нас соотношения можно выразить через число Маха. Так из формулы (12.6.12) можно получить следующее соотношение для давлений:

, (12.6.17)

В свою очередь можно выразить через , пользуясь формулами (12.6.12), (12.6.13) и (12.6.17):

, (12.6.18)

Отношение скоростей из (12.6.12, 13, 17) определяется по формуле:

, (12.6.19)

Наконец, пользуясь формулой (12.6.16), из последнего соотношения имеем:

, , , . (12.6.20)

12.7.Ударные волны слабой интенсивности

12.7.1. Изменение термодинамических параметров и скоростей в прямой ударной волне

Для определения направления изменения термодинамических параметров и скоростей в ударной волне рассмотрим ударные волны слабой интенсивности, т. е. будем полагать, что, например, изменение давления в ударной волне незначительно:

.

Из законов сохранения в прямой ударной волне следует, что при прохождении газа через нее, изменяются скорость и давление, а, следовательно, изменяется и энтропия идеального газа. Будем предполагать, что за счет изменения давления и энтропии изменяются энтальпия и удельный объем при прохождении газом прямой ударной волны, т. е.

.

Представим энтальпию после ударной волны в виде ряда Неймана около ее значения перед ударной волной (в состоянии 1):

Ограничимся в ряду (12.7.1) слагаемыми третьего порядка малости по , и в последующих выражениях будем пренебрегать слагаемыми, пропорциональными и . Аналогично удельный объем после прямой ударной волны представим в виде ряда:

Вспомним следующие термодинамические соотношения:

, .

. (12.7.3)

Подставляя (12.7.1,2) в уравнение ударной адиабаты (12.6.5), и используя (12.7.3), получим:

Из (12.7.4) следует, что скачок энтропии в ударной волне является величиной третьего порядка малости по отношению к скачку давления. Соотношение (12.7.4) замечательно тем, что оно указывает на изменение энтропии в ударной волне в идеальном газе, лишенном трения и теплопроводности. Следовательно, ударные волны являются еще одним механизмом (наряду с трением и теплопроводностью) возрастания энтропии в движущихся идеальных сжимаемых газах.

Во всех известных случаях производная положительна, и для идеального газа при изоэнтропическом движении, описываемом уравнением Пуассона, она равна

.

Поскольку энтропия может лишь возрастать (), то поэтому из соотношения (12.7.4) следует:

.

Из определения можно сделать вывод, что:

, .

Из граничных условий можно заключить:

.

Из уравнения ударной адиабаты (12.6.5) или уравнения Бернулли (второе уравнение в 12.6.2) можно прийти к следующему выводу:

, , .

Поскольку скорость звука зависит только от температуры, то имеем:

, .

Из определения скорости звука следует:

, . (12.7.5)

Скорости движения газа в ударной волне могут быть определены из равенства плотностей потока на поверхности разрыва (12.6.2), (12.6.3) и (12.6.6):

. (12.7.6)

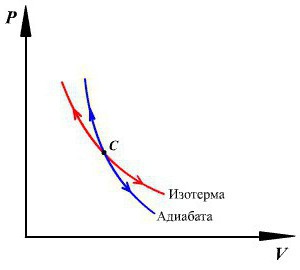
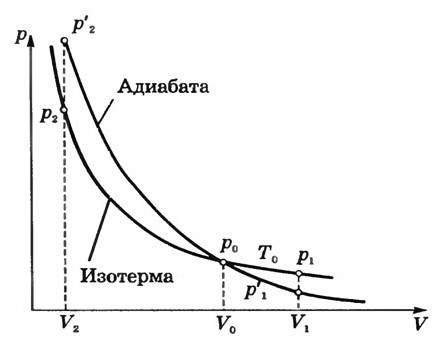
На графике ударной адиабаты (рис. 12.5) видно, что производная в точках () и () различны. Из сравнения (12.7.5) и (12.7.6) приходим к заключению:

, , , . (12.7.7)

Как видно из (12.7.7), для образования ударная волна необходимо, чтобы газ до ударной волны двигался со сверхзвуковой скоростью. Следовательно, в газе, прошедшем прямую ударную волну, не могут существовать новые ударные волны.

Таким образом, в прямой ударной волне выполняются следующие неравенства для скоростей и термодинамических параметров:

, , , , , , , , ,

, .

В газе, прошедшем прямую ударную волну, возрастают энтропия, давление, плотность и температура, уменьшаются лишь удельный объем и скорость движения газа, становясь дозвуковой.

До сих пор рассматривали неподвижную прямую ударную волну или скачок уплотнения. Если на рассматриваемое движение наложить скорость , направленную справа налево (рис. 12.6), то газ в области 1 окажется неподвижным относительно наблюдателя, а ударная волна будет двигаться справа налево со скоростью , за ударной волной в области 2 газ будет двигаться справа налево со скоростью — скоростью спутного потока. Из формулы (12.6.11) следует, что скорость движения плоской ударной волны тем больше, чем интенсивнее волна, т. е. чем больше отношение давлений .

12.7.2. Образование ударных волн

Образование прямой ударной волны с физической точки зрения можно понять, рассматривая следующий опыт. Пусть имеется некоторая бесконечная труба с газом, на одном конце которой расположен подвижный поршень (рис. 12.7). Пусть в некоторый момент времени поршень внезапно начинает двигаться с некоторой скоростью, а дальше продолжает двигаться со скоростью спутного потока. Тогда в первоначальный момент времени перед поршнем образуется уплотнение газа. Примерный график изменения плотности в трубе в этот момент изображен на рис. 12.7.

Разделим этот уплотненный участок газа на тонкие элементарные слои. Поскольку более интенсивное уплотнение распространяется в газе с большей скоростью, то в процессе движения более плотные задние слои будут догонять менее плотные передние слои, и в последующий момент график будет иметь более крутой вид. При дальнейшем движении крутизна увеличивается, и в конце концов возникнет разрыв, имеющий очень малую толщину и двигающийся слева направо со скоростью , т. е. возникнет ударная волна. За ударной волной газ будет двигаться со скоростью спутного потока . Таким образом, ударные волны являются самоформирующимися образованиями в газе. Не очень резко ограниченное уплотнение в газе по мере движения автоматически переходит в резко

ограниченную ударную волну. Очевидно, что толщина поверхности разрыва

термодинамических параметров и скоростей в прямой ударной волне должна быть порядка нескольких длин свободного пробега молекул газа. При последующем движении ударной волны в реальном газе ударная волна “размывается” и исчезает вследствие диссипации её кинетической энергии в окружающее пространство за счет вязких сил.

Если поршень резко сместить влево, то в начальный момент времени перед ним возникнет разрежение. Это разрежение будет в дальнейшем распространяться вправо. Однако те же рассуждения показывают, что в этом случае не происходит самоформирования резкого перехода между невозмущенным газом и областью разрежения. Наоборот, более или менее резкое возмущение — разрежение газа в начале движения поршня при дальнейшем движении “расползается”, занимая постепенно все большую и большую область пространства трубы. Это значит, что ударные волны разрежения, т. е. резкие переходы, при которых в газе после их прохождения давление уменьшается, существовать не могут. То же самое можно показать, пользуясь уравнением ударной адиабаты (12.6.5). Точки ударной адиабаты (рис. 12.5) правее точки (), которые соответствовали бы ударной волне разрежения () нереальны, т. к. они соответствуют такому процессу, при котором энтропия бы уменьшалась (см.(12.7.4)).

12.7.3.Численный пример

Рассмотрим численный пример. Оценим параметры ударной волны, образующейся при взрыве атомной бомбы. При взрыве атомной бомбы образуется сферическая или полусферическая ударная волна. Вдали от эпицентра взрыва участок сферической ударной волны можно приближенно рассматривать как плоский и для расчетов пользоваться полученными выше формулами для плоской ударной волны. Интенсивность волны характеризуют отношением давлений . Эксперимент показывает, что при взрыве мегатонной бомбы на расстоянии 2,5-5 километров от эпицентра взрыва . Скорость звука в неподвижном воздухе (γ = 1) при нормальных условиях равна =340м/сек.

Вычислим скорость движения ударной волны . Из формулы (12.6.11) имеем:

.

Таким образом, скорость распространения ударной волны в полтора раза больше, чем скорость звука в неподвижном газе. Поэтому наблюдатель сначала обнаружит ударную волну, а уж затем услышит звук взрыва. Причем, скорость распространения ударной волны тем больше, чем больше ее интенсивность, т. е. чем больше отношение .

Найдем скорость , необходимую для вычисления скорости спутного движения воздуха за ударной волной. Согласно (12.6.12) имеем:

.

Скорость спутного потока газа за ударной волной равна:

.

Таким образом, воздух за ударной волной движется с ураганной скоростью, производя большие разрушения. Найдем температуру воздуха за ударной волной, если температура неподвижного воздуха . То согласно (12.6.9) с использованием уравнения непрерывности на границе раздела можно получить:

,

Таким образом, объекты, подвергающиеся воздействию ударной волны, не только испытывают резкий, воспринимаемый как удар, перепад давления при ее прохождении (), но также могут разрушиться и даже при больших (Р1 /Р2) возгораться под воздействием горячего (

100C) ураганного ветра (

170м/c), создаваемого спутным потоком, движущимся вслед за ударной волной. Вблизи эпицентра взрыва к тепловому воздействию ударной волны добавляется еще тепловое излучение от вспышки.

Разбегающийся с большой скоростью от эпицентра взрыва воздух создает около него область очень низкого давления. Поэтому спустя некоторое время после прохождения ударной волны воздух устремляется по поверхности Земли обратно к эпицентру, неся с собой много пыли. Этот запыленный нагретый воздух, устремляясь вверх, и создает тот “гриб”, который характерен для наземных ядерных взрывов.

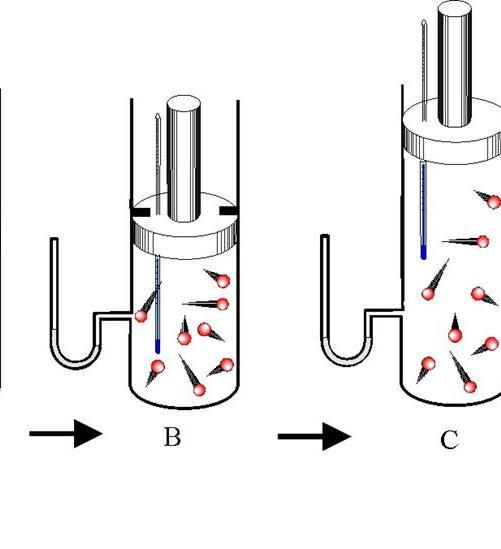
Адиабатический процесс и уравнения адиабаты для идеального газа. Пример задачи

Адиабатический переход между двумя состояниями в газах не относится к числу изопроцессов, тем не менее, он играет важную роль не только в различных технологических процессах, но и в природе. В данной статье рассмотрим, что представляет собой этот процесс, а также приведем уравнения адиабаты идеального газа.

Кратко об идеальном газе

Идеальным называется такой газ, в котором нет взаимодействий между его частицами, и их размеры равны нулю. В природе, конечно же, не существует идеальных на сто процентов газов, поскольку все они состоят из имеющих размеры молекул и атомов, которые взаимодействуют друг с другом всегда как минимум с помощью ван-дер-ваальсовых сил. Тем не менее, описанная модель часто выполняется с достаточной для решения практических задач точностью для многих реальных газов.

Вам будет интересно: Атеизм и антиклерикализм — это. В чем отличие понятий

Главным уравнением идеального газа является закон Клапейрона-Менделеева. Он записывается в следующей форме:

Это уравнение устанавливает прямую пропорциональность между произведением давления P на объем V и количества вещества n на абсолютную температуру T. Величина R — газовая константа, которая играет роль коэффициента пропорциональности.

Что это адиабатический процесс?

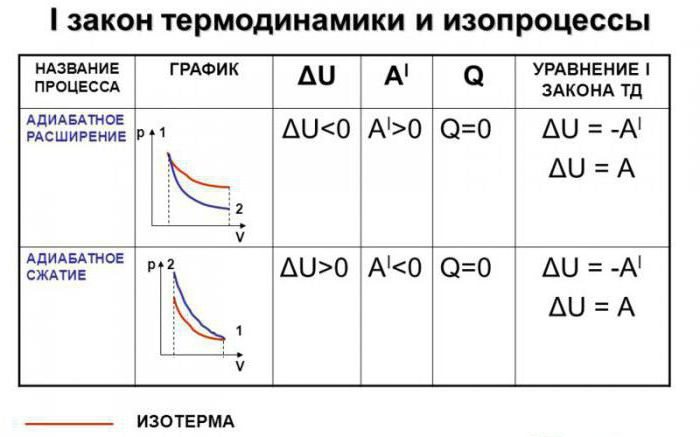
Адиабатический процесс — это такой переход между состояниями газовой системы, при котором обмена энергией с внешней средой не происходит. При этом изменяются все три термодинамических характеристики системы (P, V, T), а количество вещества n остается постоянным.

Различают адиабатическое расширение и сжатие. Оба процесса происходят только за счет внутренней энергии системы. Так, в результате расширения давление и особенно температура системы сильно падают. Наоборот, адиабатическое сжатие приводит к положительному скачку температуры и давления.

Чтобы не происходил обмен теплом между окружающей средой и системой, последняя должна обладать теплоизолированными стенками. Кроме того, сокращение длительности протекания процесса значительно уменьшает тепловой поток от и к системе.

Уравнения Пуассона для адиабатического процесса

Первый закон термодинамики записывается в таком виде:

Иными словами, сообщенная системе теплота Q идет на выполнение системой работы A и на повышение ее энергии внутренней ΔU. Чтобы написать уравнение адиабаты, следует положить Q=0, что соответствует определению изучаемого процесса. Получаем:

При изохорном процессе в идеальном газе все тепло идет на повышение внутренней энергии. Этот факт позволяет записать равенство:

Где CV — изохорная теплоемкость. Работа A, в свою очередь, вычисляется так:

Где dV — малое изменение объема.

Помимо уравнения Клапейрона-Менделеева, для идеального газа справедливо следующее равенство:

Где CP — изобарная теплоемкость, которая всегда больше изохорной, так как она учитывает потери газа на расширение.

Анализируя записанные выше равенства и проводя интегрирование по температуре и объему, приходим к следующему уравнению адиабаты:

Здесь γ — это показатель адиабаты. Он равен отношению изобарной теплоемкости к изохорной. Это равенство называется уравнением Пуассона для процесса адиабатического. Применяя закон Клапейрона-Менделеева, можно записать еще два аналогичных выражения, только уже через параметры P-T и P-V:

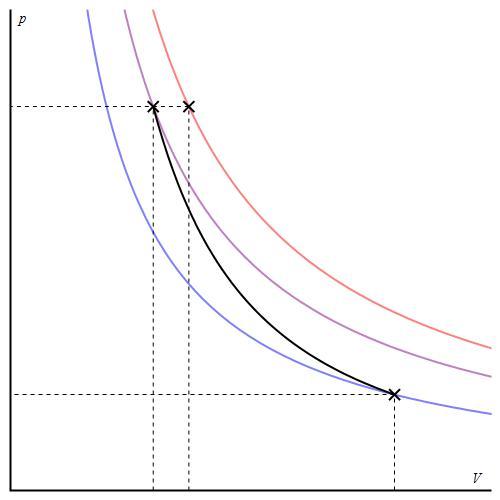
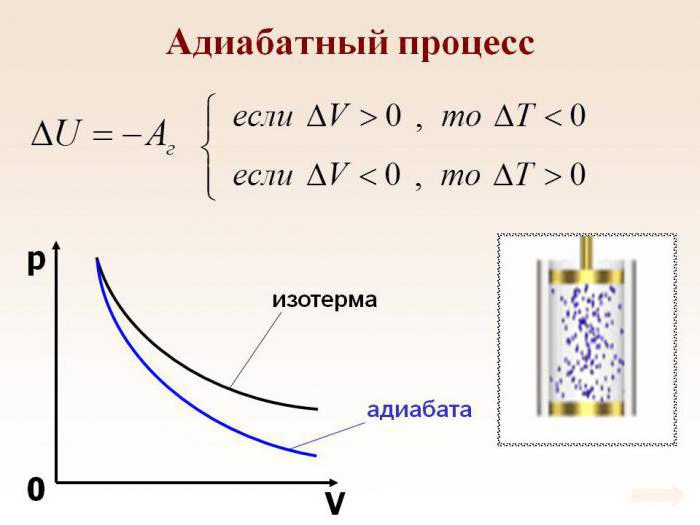
График адиабаты можно привести в различных осях. Ниже он показан в осях P-V.

Цветные линии на графике соответствуют изотермам, черная кривая — это адиабата. Как видно, адиабата ведет себя более резко, чем любая из изотерм. Этот факт просто объяснить: для изотермы давление меняется обратно пропорционально объему, для изобаты же давление изменяется быстрее, поскольку показатель γ>1 для любой газовой системы.

Пример задачи

В природе в горной местности, когда воздушная масса движется вверх по склону, то ее давление падает, она увеличивается в объеме и охлаждается. Этот адиабатический процесс приводит к снижению точки росы и к образованию жидких и твердых осадков.

Предлагается решить следующую задачу: в процессе подъема воздушной массы по склону горы давление упало на 30 % по сравнению с давлением у подножия. Чему стала равна ее температура, если у подножия она составляла 25 oC?

Для решения задачи следует использовать следующее уравнение адиабаты:

Его лучше записать в таком виде:

Если P1 принять за 1 атмосферу, то P2 будет равно 0,7 атмосферы. Для воздуха показатель адиабаты равен 1,4, поскольку его можно считать двухатомным идеальным газом. Значение температуры T1 равно 298,15 К. Подставляя все эти числа в выражение выше, получаем T2 = 269,26 К, что соответствует -3,9 oC.

Адиабатный процесс, его суть и и формулы

Адиабатный процесс (в некоторых источниках упоминается как адиабатический) — это термодинамический процесс, который происходит при отсутствии теплообмена с окружающей средой. Есть несколько факторов, которые характеризуют этот класс. Например, адиабатный процесс происходит динамично и укладывается в короткий срок времени. Происходят процессы данного класса, как правило, мгновенно.

Связь с первым началом термодинамики

Адиабатный процесс (адиабатический) можно напрямую связать с первым законом термодинамики. Его формулировка “по умолчанию” звучит следующим образом: изменение количества теплоты в системе при протекании в ней термодинамического процесса будет численно равно сумме изменения внутренней энергии идеального газа и работы, совершаемой этим газом.

Если мы попытаемся записать первое начало термодинамики в его стандартном виде, то получим следующее выражение: dQ = dU + dA. А теперь постараемся видоизменить эту формулу применительно к адиабатическому процессу. Как было сказано ранее, подобные процессы протекают при условии отсутствия теплообмена с окружающей (внешней, как ее называют некоторые литературные источники) средой.

В таком случае формула, описывающая первое начало термодинамики, примет следующий вид: dA = -dU. Теперь несколько подробнее о видоизменении. Если мы говорим о том, что теплообмена в системе не происходит, изменение количества теплоты (обозначенное в формуле первого закона термодинамики через dQ) будет равно нулю. Следовательно, мы можем перенести одно из слагаемых из правой части в левую, после чего получим формулу, приведенную к описанному ранее виду.

Следствие из первого начала термодинамики для адиабатического процесса

Допустим, что в системе произошел адиабатный процесс. В этом случае можно, не вдаваясь в мельчайшие детали, говорить о том, что газ при расширении совершает работу, но при этом он теряет свою внутреннюю энергию. Иными словами, работа, совершаемая при адиабатном расширении газа, будет осуществляться за счет убыли внутренней энергии. Следовательно, в качестве исхода этого процесса мы будем рассматривать понижение температуры самого вещества.

Абсолютно логично можно предположить, что если газ будет адиабатически сжат, его температура вырастет. Несложно заметить, что в ходе процесса будут изменяться все главные характеристики идеального газа. Речь идет о его давлении, объеме и температуре. Следовательно, грубой ошибкой стало название адиабатического процесса изопроцессом.

Адиабатный процесс. Формулы

Ранее была записана формула, выведенная из первого начала термодинамики. Используя ее, мы без особого труда можем вычислить работу в общем виде, которую будет выполнять газ при течении адиабатного процесса. Как вы уже могли догадаться, делать это мы будет при помощи интегрирования.

Итак, чтобы получить общую формулу работы для x молей газа, проинтегрируем выражение первого закона термодинамики для адиабатного процесса. Выглядеть все это будет следующим образом: A = — (интеграл) от dU. Раскроем это выражение, получим: A = — xCv (интеграл в пределах от T1 до T2) dT.

Теперь, когда мы привели интеграл к конечному виду, мы можем его упростить. На выходе получим формулу следующего вида: A = — xCv (T2 – T1). Ну и последним шагом станет небольшое упрощение. Избавимся от минуса перед формулой. Для этого сделаем в скобках небольшую перестановку, поменяв конечную температуру с начальной местами. В итоге получим: A = xCv (T1 – T2).

Уравнение адиабаты

Используя первое начало термодинамики для адиабатного процесса, мы можем найти уравнение адиабаты. При этом оно будет записано для произвольного числа молей идеального газа. Итак, запишем первоначальную формулу. Она имеет такой вид: dA + dU = 0. Но ведь мы прекрасно знаем, что работа идеального газа представляет численно собой не что иное, как произведение давления на изменение объема.

В то же время изменение внутренней энергии будет равно работе, взятой с обратным знаком. А ее-то мы уже нашли при помощи интегрирования. Значит, первое начало термодинамики для адиабатического процесса может принять следующий вид: pdV + xCvdT = 0. Из этого уравнения нам нужно исключить один показатель, а именно, температуру. Вернее, ее изменения. Чтобы сделать это, мы обратимся к достаточно часто используемому в молекулярной физики уравнению. А именно к уравнению Менделеева-Клапейрона.

Первичное выражение

Его нам нужно продифференцировать, чем мы и займемся. Итак, в общем виде уравнение выглядит следующим образом: PV = XRT. Вследствие дифференцирования оно будет приведено к такой форме: pdV + Vdp = xRdT. Отсюда мы можем выразить изменение энергии. Оно будет равно левой части, деленной на произведение количества вещества на универсальную газовую постоянную. Иными словами, формула будет такой: (pdV + Vdp)/xR. Остается только упростить ее. В итоге получим следующее выражение: dT = (pdV + Vdp)/x(Cp — Cv)

По сути дела, первая часть задачи выполнена. Остается только довести все до ума.

Вторичное выражение. Подстановка значения

Возьмем полученную в результате дифференцирования формулу Менделеева-Клапейрона и подставим ее в выражение, выведенное нами ранее для первого закона термодинамики по отношению к адиабатному процессу. Итак, что мы получим? Все это громоздкое выражение примет следующий вид: pdV + xCv ((pdV + Vdp)/x(Cp-Cv)) = 0.

Чтобы упростить все это, мы должны принять во внимание пару фактов. Во-первых, упростить выражение можно за счет приведения к общему знаменателю. Когда мы получим одну дробь, мы можем воспользоваться старым добрым правилом, которое гласит, что дробь равна нулю, когда ее числитель равен нулю, а знаменатель от нуля отличен. В результате совокупности всех этих действий мы получим следующее выражение: pCpdV – pCvdV + pCvdV + VCvdp = 0.

Теперь следующим шагом мы можем разделить данное выражение на pVCv. Получим сумму двух частей, дающих в итоге ноль. Это будет Cp/Cv * dV/V + dp/p = 0. Эту формулу необходимо проинтегрировать. Тогда мы получим следующее выражение: y (интеграл) dV/V + (интеграл) dp/p = (интеграл) 0.

Ну а дальше все достаточно просто. Воспользовавшись формулами интегрирования (можно использовать табличные интегралы, чтобы все было проще), получим в итоге следующую запись: y ln V + ln p = ln (const). Получается, что p(V)y = const. Данное выражение называется в молекулярной физике уравнением Пуассона. Многие литературные источники научной направленности также называют эту формулу уравнением адиабаты. В то же время величина y, которая имеет место в данной записи, называется показателем адиабаты. Она равна (i+2)/i. Нужно отметить, что показатель адиабаты всегда больше единицы, что, в принципе, логично.

Примеры адиабатных процессов

Вскоре после того, как был открыт адиабатический процесс, стартовало огромное количество различных исследований. Так, была создана первая теоретическая модель, имеющая отношение к циклу Карно. Именно она позволила установить условные пределы, ограничивавшие развитие тепловых машин. Но в случае некоторых реальных процессов осуществлять цикл Карно достаточно трудно. Все дело в том, что в его состав входят изотермы. А они, в свою очередь, требуют задания определенной скорости термодинамических процессов.

Заключение

С целью обойти подобные проблемы был придуман цикл Отто, а также цикл сжижения газа. Они стали широко применяться при решении конкретных задач на практике. Стартовавшие исследования показали возможность описания некоторых природных процессов в адиабатическом плане, что позволило выявлять общие закономерности соответствующих процессов. Примером адиабатического процесса можно смело назвать химическую реакцию, которая происходит внутри некоторого объема газа, если система является замкнутой, а обмен с внешней средой теплом отсутствует.