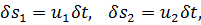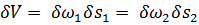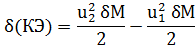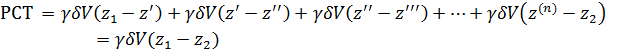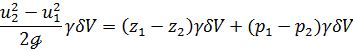Уравнение установившегося движения для элементарной струйки жидкости

Уравнение Бернулли

Уравнение Бернулли для струйки жидкости формулируется следующим образом: для элементарной струйки идеальной жидкости полная удельная энергия, т.е. сумма удельной энергии положения, удельной энергии давления и кинетической удельной энергии – есть величина постоянная во всех сечениях струйки.

Уравнение Бернулли выглядит так:

Подробное описание всех входящих в состав уравнения параметров уже описан в этой статье.

Содержание статьи

Смысл уравнения Бернулли

По существу вывода уравнение Бернулли для струйки идеальной жидкости представляет собой закон сохранения механической энергии, составленный применительно к единице массового расхода жидкости. Это следует из того, что в процессе вывода значения работы сил, приложенных к выделенному объему струйки и значения кинетической энергии этого объема были поделены на величину ρqΔT.

Отсюда вытекает, что поскольку член υ 2 /2 является мерой кинетической энергии единицы массы движущейся жидкости, то сумма членов gz+p/ρ будет мерилом ее потенциальной энергии.

В отношении величины gz это очевидно, ведь если частица жидкости массы m расположена на высоте z относительно некоторой плоскости и находится под действием сил тяжести, то способность ее совершить работу, т.е. её потенциальная энергия относительно этой плоскости равняется mgz. Но если её поделить на массу частиц m, то эта часть потенциальной энергии даст величину gz.

Для более ясного физического представления о том, что потенциальная энергия измеряется величиной p/ρ рассмотрим такую схему: пусть к трубе, заполненной жидкостью с избыточным давлением p, присоединен пьезометр, снабженный на входе в него краном.

Кран сначала закрыт, т.е. пьезометр свободен от жидкости, а элементарный объем жидкости ΔV массой ρ*ΔV перед краном находится под давлением p.

Если затем открыть кран, то жидкость в пьезометре поднимется на некоторую высоту, равную

Таким образом, единица массы, находящейся под давлением p, как бы несет в себе ещё заряд потенциальной энергии, определяемой величиной p/ρ.

В гидравлике для характеристики удельной энергии обычно используется понятие напор, под которым понимают энергию жидкости, отнесенную к единице силы тяжести, а не её массы. В соответствии с этим уравнение Бернулли записанное в начале этой статьи примет вид

Такое уравнение Бернулли для элементарной струйки идеальной жидкости в другой форме, весьма удобно для гидравлических расчетов и может быть сформулировано следующим образом.

Для элементарной струйки идеальной жидкости полный напор, т.е. сумма геометрического, пьезометрического и скоростного напоров, есть величина постоянная во всех её сечениях.

Отсюда следует, что между напором и удельной энергией существует очень простая зависимость

где э – удельная энергия

Уравнение Бернулли для элементарной струйки реальной жидкости

Если вместо идеальной жидкости рассматривать жидкость реальную, то уравнение Бернулли для реальной жидкости должно принять несколько другой вид.

При движении идеальной жидкости её полная удельная энергия или напор сохраняет постоянное значение по длине струйки, а при движении реальной жидкости эта энергия будет убывать по направлению движения. Причиной этого являются затраты энергии на преодоление сопротивлений движению, обусловленные внутренним трением в вязкой жидкости.

Если же мы рассмотрим два сечения для струйки идеальной жидкости: 1-1 в начале и 2-2 в конце струйки, то полная удельная энергия будет

Полная удельная энергия для сечения 1-1 всегда будет больше, чем полная удельная энергия для сечения 2-2 на некоторую величину потерь, и уравнение Бернулли в этом случае получается

Величина Э_1-2 представляет собой меру энергии, потерянную единицей массы жидкости на преодоление сопротивлений при её движениями между указанными сечениями.

Соответствующий этой потере удельной энергии напор называют потерей напора между сечениями 1-1 и 2-2 и обозначают h_1-2 . Поэтому уравнение Бернулли для элементарной струйки реальной жидкости можно представить в виде

Уравнение Бернулли для потока реальной жидкости

Уравнение Бернулли для струйки реальной жидкости это еще только половина дела, ведь в при решении различных практических вопросов о движении жидкостей приходится иметь дело с потоками конечных размеров. Уравнение Бернулли в этом случае может быть получено, исходя из рассмотрения потока как совокупности множества элементарных струек.

Учитывая, что все струйки движутся с одной и той же средней скоростью форма записи уравнения Бернулли для потока идеальной жидкости становится идентичной его записи для элементарной струйки.

В таком виде уравнение Бернулли обычно и применяется при решении практических задач для потоков однородной несжимаемой жидкости при установившемся движении, происходящем под действием одной силы тяжести.

Такое уравнение составляется для различных живых сечений потока, вблизи которых движение жидкости должно удовлетворять условиям медленно изменяющегося движения, хотя на пути между этими сечениями движение может и не удовлетворять указанным условиям.

Слагаемое h_1-2 в этом уравнении показывает потери напора на преодоление сопротивлений движению жидкости. При этом в гидравлике различают два основных вида сопротивлений:
— h_лп — линейные потери — сопротивления, проявляющиеся по всей длине потока, обусловленные силами трения частиц жидкости друг о друга и о стенки, ограничивающие поток.
— h_мп — местные потери – местные сопротивления, обусловленные различного рода препятствиями, устанавливаемыми в потоке (задвижка, кран, колено), приводящими к изменениям величины или направления скорости течения жидкости

Поэтому полная потеря напора между двумя сечениями потока при наличии сопротивлений обоих видов будет

Видео по теме

Уравнение Бернулли подходит и для газов. Явление уменьшения давления при повышении скорости потока является основой работы различных приборов для измерения расхода. Закон Бернулли справедлив и для жидкостей вязкость которых равна нулю. При описании течения таких жидкостей используют уравнение Бернулли с добавлением слагаемых учитывающих потери на местные сопротивления.

Уравнение Д. Бернулли для элементарной струйки установившегося движения жидкости

Уравнение Д. Бернулли для элементарной струйки установившегося движения жидкости

Уравнение Д. Бернулли для элементарной струйки установившегося движения жидкости. Рассмотрим уравнения Эйлера (4.15) для движения невязкой жидкости. 1 dr + x =канава Р ДХ Людмила Фирмаль

• В рассматриваемом случае действует только сила тяжести, ускорение свободного падения которой равно q и может быть записано в принятом направлении оси координат X = 0, Y = 0 и 2 = e、 Таким образом, три условия Xdh + Udu + Mg = Oyh + + Опи §ДГ= §ДГ. Преобразуем правую часть уравнения(4.51), зная, что перемещения равны друг другу. г (1х + ^АУ + ^ АИ = =^э-э + ^и U + 4-СГ& = ihiyih + juiyu + идигу = Здесь и находится локальная скорость живого участка струйки. Подставляя значение тернарного выражения, соответствующего формуле (4.51).

Если разделить все члены уравнения (4.52) на§(ускорение свободного падения), то получится уравнение, связанное с единицей веса. Но… ^ + 2)=0.(4.53） После интеграции напишите следующее (4.54） Формула (4.54) получена ученым Российской академии наук в 1738 г. Бернулли, Д для основного потока установившегося движения невязкой капельной жидкости. Уравнение Бернулли называется уравнением Бернулли. Таким образом, вы знаете, что удельный вес равен y =D. Вы можете написать уравнение Бернулли в виде: = С (4.55） D. уравнение Бернулли D.

• Заметим, что его можно получить из интеграла Бернулли (4.26). Элементарный поток рассматривается как поток с потенциальным движением. 62. В этом случае возможность применения силы можно объяснить следующим образом: Икс= * Вверх dh. О, y = ^ = 0、 4/7 г-ДГ-йо Тогда EP = gdg или= = gg +C. И после некоторых преобразований D. интегралы Бернулли принимают вид: Или 2 -) + = C Нет? ^ 2 ^ г D. приложенный к основной струйке вязкостного fluids. To выведем уравнение Бернулли, рассмотрим значение (интерпретацию) его энергии.

По этой причине мы рассчитываем механическую энергию небольшой частицы массы dm, центрированной в точке A в элементарном потоке (рис. 4.13) для горизонтальной опорной плоскости 01-Ox. Потенциальная энергия по гл. 3. Энергия： ми= _0Е._ (4.57） Таким образом, зависимость(4.57)обозначается через D. It является уравнением Бернулли и математически выражает закон сохранения энергии, найденный М. В. Ломоносовым: сумма потенциальной и кинетической энергий вдоль основного потока невязкой жидкости постоянна (см. рис. 4.13).）： OEP. (4.58） Кинетическая энергия, как физика、 Известно, что От Людмила Фирмаль

• Полная механическая энергия состоит из суммы потенциальной энергии и кинетической энергии §o1EK де = ЛЕП + ДТ(Р + 1 + гоу 2-2〜 (4.56） Ч. 3, энергия на единицу веса(вес Жидкость) называется специфической сумма G +это Часть определенной энергии это определенная потенциальная энергия, которая состоит из определенной энергии определенного положения r и определенной потенциальной энергии давления. (См. Главу 3).Формула-sh-называется удельной кинетической энергией.

Смотрите также:

Возможно эти страницы вам будут полезны:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Уравнение Бернулли для элементарной струйки идеальной жидкости при установившемся движении

Для вывода уравнения Бернулли используем известную из механики теорему, касающуюся изменения кинетической энергии. Напомним, что эта теорема читается так: изменение кинетической энергии 2 рассматриваемого тела на некотором его перемещении равно сумме работ всех сил (внешних и внутренних), приложенных к данному телу, на том же перемещении.

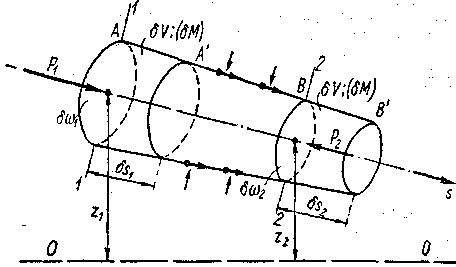
Возьмем элементарную струйку потока (рис. 3-20). Выделим сечениями 1—1 и 2—2 некоторый отсек струйки АВ. Обозначим через z₁и z₂ превыше­ния сечений 1—1 и 2—2 над плоскостью сравнения OO, через 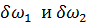— площади живых сечений струйки в сечениях 1—1и 2—2.

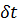
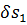
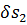
Будем считать, что за время отсек АВ струйки переместится в положе­ние А’В’ при этом сечение 1—1 струйки переместится на расстояние и сечение 2—2 струйки — на расстояние . Заметим, что

Рассуждая, как и в § 3-9, можем показать, что объемы элементарных отсеков струйки АА’ и ВВ’ равны, т. е.

объем (АА’) = объему (ВВ’) = 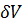(обозначение),

причем

где 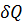— расход жидкости для струйки.

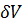
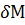
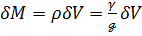
Обозначим массу элементарного объема через :

(3-55)

где 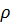— плотность жидкости.

Найдем теперь изменение кинетической энергии отсека АВ при переме­щении его в положение А’В’ и работу сил, приложенных к этому отсеку, на указанном перемещении.

1°. Изменение кинетической энергии отсека АВ при перемещении его в положение А’В’. Обозначим упомянутое изменение кинетической энергии (КЭ) через б (КЭ). Тогда можно написать (см. рис. 3-20):

(КЭ) = КЭ (А’В’) — КЭ (АВ) = КЭ (А’В -f ВВ’) —

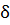
— КЭ (АА’ + А’В) = КЭ (ВВ’) — КЭ (АА’),

или, учитывая (3-55),

( 3-56)

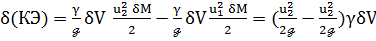
Рис. 3-20. К выводу уравнения (3-60)

2°. Работа сил при перемещении отсека АВ в поло­жение А’В’.При указанном перемещении получаем работу следующих сил.

1. Работа силы тяжести. Как видно, эффект действия силы тяжести проявился как бы в том, что отсек АА’ переместился в положение ВВ’ (а отсек А ‘В остался на месте). Пользуясь такой условной схемой работу силы тяжести (РСТ) получаем в виде

(3-57)

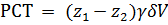
Справедливость (3-57) может быть обоснована и более строго. Разбиваем отсек А’В на элементарные отсеки объемом 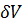. Тогда иско­мая работа силы тяжести может быть представлена в виде:

где z’, z», z», . . ., z ( n ) — возвышения над плоскостью 00 граничных сече­ний, выделяющих элементарные объемы .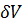

2. Работа сил гидродинамического давления,
действующего на торцовые сечения1—1 и 2—2 отсека
АВ (со стороны окружающей его жидкости). Эта работа

(3-58)

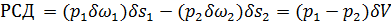
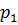
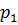
где и — гидродинамические давления соответственно в сечениях 1—1 и 2—2.

3. Работа внешних сил давления окружающей ж ид кости на боковую поверхность отсека АВ. Эта работа равна нулю, так как силы направлены перпендикулярно к перемещениям жидких частиц, движущихся вдоль боковой поверхности отсека АВ.

4. Работа внутренних сил давления (нормальных сил взаимодействия отдельных частиц жидкости, составляющих объем АВ).

Эти силы являются парными (противоположно направленными) с одинако­выми перемещениями. Сумма работ их равна нулю.

5. Работа внешних и внутренних сил трения равна нулю (силы трения в рассматриваемой нами идеальной жидкости отсут­ствуют).

3°. Окончательный вывод. Используя теорему изменения кинетической энергии, можем написать:

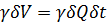
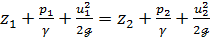
Разделим это выражение на , т. е. отнесем его к еди­нице в е с а того объема жидкости, который проходит за время б/ через живое сечение струйки. При этом полученное уравнение представим в виде

(3-59)

Так как сечения 1—1 и 2—2 были намечены произвольно, то (3-59) можно переписать также в виде:

(3-60)

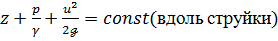
Уравнение (3-59) или (3-60) называется уравнением Бернулли. Оно было получено Даниилом Бернулли в 1738 г. Это уравнение относится только к элементарной струйке идеальной жидкости.

Обратим внимание еще на следующее:

1) уравнение Бернулли связывает величины z, р, и;

2) как видно из (3-60), в случае идеальной жидкости сумма трех слагае мых z, , является постоянной величиной вдоль рассматриваемой струйки;

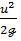
3) если указанная постоянная величина для данной струйки равна A_lt то для соседней струйки сумма приведенных трех слагаемых равняется А₂, причем в’ общем случае А₁ ≠ A₂;

4) зная для данной струйки постоянную величину А, а также зная для данного сечения струйки из трех величин (z, и, р) какие-либо две величины, мы можем, пользуясь уравнением Бернулли, найти третью неизвестную величину для рассматриваемого сечения струйки.

Уравнение (3-60) можно получить также путем интегрирования дифференциальных урав­нений Эйлера (см. § 3-3) для любой системы объемных сил, действующих на жид­кость и имеющих потенциал (см. § 9-2). Уравнение (3-60) относится к определенной линии тока (точнее: к элементарной струйке, намеченной вдоль определенной линии тока). Это уравнение часто называют интегралом Бернулли.

Более подробное рассмотрение данного вопроса показывает, что уравнение Бернулли (интеграл Бернулли) оказывается справедливым как для безвихревого (потенциального) уста­новившегося движения, так и для вихревого установившегося движения идеальной жидкости, при условии, однако, что на жидкость действуют объемные силы, имеющие потенциал (в част­ности, сила тяжести, которую мы имели в виду выше). При рассмотрении установившегося вихревого движения идеальной жидкости под скоростью и, входящей в уравнение Бернулли, следует понимать (так же как и в случае безвихревого движения) скорость, относящуюся к дей­ствительному векторному полю, отражающему рассматриваемое движение жидкости (к разло­жению движения на три его вида, поясненных в § 3-4, здесь обращаться не следует).

Можно также показать, что в случае: а) без вихревого (потенциального) движения идеальной жидкости и б) объемных сил, действующих на жидкость, имеющих потен­циал, величина А, о которой говорили выше, является одинаковой для всех линий тока, образующих поток: А₁= А₂= А₃ = — В этом случае уравнение (3-60) оказывается справед­ливым для всей области, занятой жидкостью, а не только для определенной линии тока.

Дата добавления: 2015-12-29 ; просмотров: 529 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ