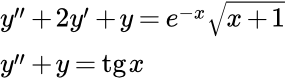Уравнение в вариациях второго порядка

Примеры решений дифференциальных уравнений второго порядка методом Лагранжа

Здесь мы применим метод вариации постоянных Лагранжа для решения линейных неоднородных дифференциальных уравнений второго порядка. Подробное описание этого метода для решения уравнений произвольного порядка изложено на странице
Решение линейных неоднородных дифференциальных уравнений высших порядков методом Лагранжа >>> .

Пример 1

Решить дифференциальное уравнение второго порядка с постоянными коэффициентами методом вариации постоянных Лагранжа:
(1)

Шаг 1. Решение однородного уравнения

Вначале мы решаем однородное дифференциальное уравнение:
(2)
Ищем решение в виде . Составляем характеристическое уравнение:

Это уравнение второго порядка.

Решаем квадратное уравнение:
.
Корни кратные: . Фундаментальная система решений уравнения (2) имеет вид:
(3) .
Отсюда получаем общее решение однородного уравнения (2):
(4) .

Шаг 2. Вариация постоянных – замена постоянных функциями

Варьируем постоянные C ₁ и C ₂ . То есть заменим в (4) постоянные и на функции:
.
Ищем решение исходного уравнения (1) в виде:
(5) .

Находим вторую производную:
.
Подставляем в исходное уравнение (1):
(1) ;

.
Поскольку и удовлетворяют однородному уравнению (2), то сумма членов в каждом столбце последних трех строк дает нуль и предыдущее уравнение приобретает вид:
(7) .
Здесь .

Вместе с уравнением (6) мы получаем систему уравнений для определения функций и :
(6) :
(7) .

Решение системы уравнений

Решаем систему уравнений (6-7). Выпишем выражения для функций и :
.
Находим их производные:
;
.

Решаем систему уравнений (6-7) методом Крамера. Вычисляем определитель матрицы системы:

.
По формулам Крамера находим:
;
.

Итак, мы нашли производные функций:
;
.
Интегрируем (см. Методы интегрирования корней). Делаем подстановку
; ; ; .

Общее решение исходного уравнения:

;
.

Пример 2

Решить дифференциальное уравнение методом вариации постоянных Лагранжа:
(8)

Шаг 1. Решение однородного уравнения

Решаем однородное дифференциальное уравнение:

(9)
Ищем решение в виде . Составляем характеристическое уравнение:

Это уравнение имеет комплексные корни:
.
Фундаментальная система решений, соответствующая этим корням, имеет вид:
(10) .
Общее решение однородного уравнения (9):
(11) .

Шаг 2. Вариация постоянных – замена постоянных функциями

Теперь варьируем постоянные C ₁ и C ₂ . То есть заменим в (11) постоянные на функции:
.
Ищем решение исходного уравнения (8) в виде:
(12) .

Далее ход решения получается таким же, как в примере 1. Мы приходим к следующей системе уравнений для определения функций и :
(13) :
(14) .
Здесь .

Решение системы уравнений

Решаем эту систему. Выпишем выражения функций и :
.
Из таблицы производных находим:
;
.

Решаем систему уравнений (13-14) методом Крамера. Определитель матрицы системы:

.
По формулам Крамера находим:
;
.

Первый интеграл немного сложней (см. Интегрирование тригонометрических рациональных функций). Делаем подстановку :

.
Поскольку , то знак модуля под знаком логарифма можно опустить. Умножим числитель и знаменатель на :
.
Тогда
.

Общее решение исходного уравнения:

.

Автор: Олег Одинцов . Опубликовано: 05-08-2013 Изменено: 19-06-2017

Решение уравнения в вариациях второго порядка нелинейных управляемых систем Текст научной статьи по специальности « Математика»

Аннотация научной статьи по математике, автор научной работы — Огородников Юрий Иннокентьевич

Для исходных уравнений движения управляемого объекта в виде системы нелинейных обыкновенных дифференциальных уравнений в нормальной форме Коши получены уравнение в вариациях второго порядка и решение этого уравнения. Уравнение в вариациях определяет связь между вариацией вектора состояния управляемой системы и вариацией вектора управления, когда малое возмущение управления в управляемой системе приводит к соответствующему малому возмущению фазовой траектории. Широко известны уравнение в вариациях первого порядка , представляющее собой систему линейных дифференциальных уравнений, и аналитическое решение этого уравнения. Уравнение в вариациях второго порядка записывается в виде системы нелинейных дифференциальных уравнений, аналитическое решение которых неизвестно. При выводе уравнения в вариациях второго порядка для упрощения записи используется скалярное произведение векторов. В статье используется подход, при котором решение нелинейного уравнения в вариациях второго порядка осуществляется методом итераций. Вариации вектора состояния и вектора управления являются малыми величинами. Это обстоятельство позволяет найти решение нелинейного уравнения в вариациях второго порядка в две итерации: решение линейного уравнения в вариациях первого порядка подставляется в квадратичные члены уравнения в вариациях второго порядка и решается соответствующая система линейных дифференциальных уравнений. Дальнейших итераций можно не проводить, поскольку они дают поправки к вариации вектора состояния, имеющие формально третий порядок малости.

Похожие темы научных работ по математике , автор научной работы — Огородников Юрий Иннокентьевич

SOLUTION OF EQUATION IN THE SECOND ORDER VARIATIONS FOR NON-LINEAR CONTROLLABLE SYSTEMS

An equation in the second order variations and solution of this equation have been obtained for initial equations of motion of a controllable object in the form of a system of common non-linear differential equations in the normal Cauchy form. An equation in variations impacts the relations between variation of the system’s state vector and variation of the control selection when a small disturbance of control in the controlled system results in the corresponding small disturbance of a phase trajectory. An equation in the first-order variations representing a system of linear differential equation and an analytical solution of this equation are well-known. An equation in the second-order variations, is presented as a system of non-linear differential equations whose solution is unknown. When deriving the equation in the second-order variations the scalar product of vectors is used for simplifying its representation. The paper uses the approach when a non-linear equation in the second order variations is solved using the iterative method. The state vector and control vector variations are small values. This fact allows us to find a solution of non-linear equation in the second-order variations into two iterations: solution of a non-linear equation in the first-order variations is introduced into the quadratic members of the equation in the second-order variations and the corresponding system of linear differential equations is solved. Further iterations can be omitted as their corrections of the state vector variations formally have the third order of smallness.

Текст научной работы на тему «Решение уравнения в вариациях второго порядка нелинейных управляемых систем»

Современные технологии. Математика. Механика и машиностроение

в том, что здесь пытаемся управлять более высокочастотным элементом через медленный упругий элемент, что, в соответствии с теорией автоматического управления, приводит к значительным фазовым задержкам при передаче управляющего воздействия на второй упругий элемент. Устранить этот недостаток здесь можно, например, путем фазовой коррекции сигнала Д—, что в условиях априорной неопределенности налагает дополнительные трудности.

Более простым и эффективным решением для этого случая является построение управления через второй более быстродействующий упругий элемент: сигнал Д— переместить между массами т и т2. При этом система уравнений (1) будет незначительно изменена — Д— перейдет из первого уравнения в правые части второго (со знаком минус) и третьего (плюс) уравнений этой системы. Исследования при таком решении показали также высокое качество гашения упругих колебаний, близкое рассмотренному выше.

Представленные результаты показали достаточно высокую эффективность активной системы гашения упругих колебаний в трехмассовом упругом исполнительном механизме, построенной на основе адаптивного управления с указанным принципом функционирования.

Необходимо отметить, что качество управления можно повысить путем использования априорной информации об объекте, применения более точных датчиков, уменьшения временного шага алгоритма идентификации и др. Также в ка-

честве вывода можно рекомендовать строить активную систему гашения упругих колебаний с подачей управляющего воздействия через более быстродействующий упругий элемент.

1. Динамический синтез в обобщенных задачах виброзащиты и виброизоляции технических объектов / Елисеев С.В. и др. Иркутск : Изд-во Иркут. гос. ун-та, 2008. 523 с.

2. Кузнецов Н.К. Динамика управляемых машин с дополнительными связями. Иркутск: Изд-во ИрГТУ, 2009. 288 с.

3. Кузнецов Н. К., Перелыгина А.Ю. Динамическое гашение колебаний упругой трехмассовой системы // Современные технологии. Системный анализ. Моделирование. 2008. №3. С. 1419.

4. Кузнецов Н.К. Активное гашение упругих колебаний исполнительных механизмов мехатрон-ных систем // Современные технологии. Системный анализ. Моделирование. 2011. Спецвып. С.101-110.

5. Круглов С.П. Условия адаптируемости систем управления с идентификатором и эталоном // LAP LAMBERT Academic Publishing GmbH & Co. KG, Saarbucken, Deutschland, 2012. 125 c.

6. Льюнг Л. Идентификация систем. Теория для пользователя : пер. с англ. / под ред. Я.З. Цып-кина. М. : Наука, 1991. 432 с.

УДК 62-501.12 Огородников Юрий Иннокентьевич,

к. т. н, ИДСТУ СО РАН, тел. 89834011463, e-mail: ogor23@yandex.ru

РЕШЕНИЕ УРАВНЕНИЯ В ВАРИАЦИЯХ ВТОРОГО ПОРЯДКА НЕЛИНЕЙНЫХ УПРАВЛЯЕМЫХ СИСТЕМ

Yu. I. Ogorodnikov

SOLUTION OF EQUATION IN THE SECOND ORDER VARIATIONS FOR NON-LINEAR CONTROLLABLE SYSTEMS

Аннотация. Для исходных уравнений движения управляемого объекта в виде системы нелинейных обыкновенных дифференциальных уравнений в нормальной форме Коши получены уравнение в вариациях второго порядка и решение этого уравнения. Уравнение в вариациях определяет связь между вариацией вектора состояния управляемой системы и вариацией вектора управления, когда малое возмущение управления в управляемой системе приводит к соответствующему малому возмущению фазовой траектории. Широко известны уравнение в вариациях первого порядка, представляющее собой систему линейных дифференциальных уравнений, и аналитическое решение этого уравнения. Уравнение в вариациях второго порядка записывается в виде системы нелинейных дифференциальных уравнений, аналитическое решение которых неизвестно. При выводе уравнения в вариациях второго порядка для упрощения записи используется скалярное произведение векторов. В статье используется подход, при котором решение нелинейного уравнения в вариациях второго порядка осуществляется методом итераций. Вариации вектора состояния и вектора управления являются малыми величинами. Это обстоятельство позволяет найти решение нелинейного уравнения в вариациях второго порядка в две итерации: решение линейного уравнения

в вариациях первого порядка подставляется в квадратичные члены уравнения в вариациях второго порядка и решается соответствующая система линейных дифференциальных уравнений. Дальнейших итераций можно не проводить, поскольку они дают поправки к вариации вектора состояния, имеющие формально третий порядок малости.

Ключевые слова: нелинейная управляемая система, уравнение в вариациях первого порядка, уравнение в вариациях второго порядка.

Abstract. An equation in the second order variations and solution of this equation have been obtained for initial equations of motion of a controllable object in the form of a system of common non-linear differential equations in the normal Cauchy form. An equation in variations impacts the relations between variation of the system’s state vector and variation of the control selection when a small disturbance of control in the controlled system results in the corresponding small disturbance of a phase trajectory. An equation in the first-order variations representing a system of linear differential equation and an analytical solution of this equation are well-known. An equation in the second-order variations, is presented as a system of non-linear differential equations whose solution is unknown. When deriving the equation in the second-order variations the scalar product of vectors is used for simplifying its representation. The paper uses the approach when a non-linear equation in the second order variations is solved using the iterative method. The state vector and control vector variations are small values. This fact allows us to find a solution of non-linear equation in the second-order variations into two iterations: solution of a non-linear equation in the first-order variations is introduced into the quadratic members of the equation in the second-order variations and the corresponding system of linear differential equations is solved. Further iterations can be omitted as their corrections of the state vector variations formally have the third order of smallness.

Keywords: non-linear controllable system, equation in the first order variations, equation in the second order variations.

Рассматривается движение управляемого объекта во времени, описываемое векторным дифференциальным уравнением x(t) = f (x(t), u(t)), x(t0) = x0, t e T = [t0, ti ] с R ,(1)

где x(t) e R n — n-мерный вектор состояния системы;

u(t) e R m — m-мерный вектор управления; x(-) e D(T), D(T) — пространство абсолютно непрерывных на T функций;

u (•) e L (T), L (T) — пространство кусочно-непрерывных на T функций с нормой

llu Mil = max max\u. (t)|; (2)

II v ‘llo> i=1,2. m teT 1 V /l

f (x, u) — известная нелинейная n-мерная вектор-функция, непрерывная и непрерывно дифференцируемая по (x, u) дважды;

u(-), x(-) — символы функций, рассматриваемых как точки функциональных пространств.

Использование в качестве основного функционального класса, из которого разрешается выбирать u(t), класса кусочно-непрерывных на T функций обосновывается тем фактом, что решения содержательных задач оптимального управления в подавляющем большинстве — сравнительно просто устроенные функции, имеющие разрывы первого рода, а между точками разрывов — достаточно гладкие.

Допустим, что все требования существования и единственности решения уравнения (1) при заданных начальных условиях выполнены [1].

Пусть известно некоторое управление м0(-), которому соответствует «невозмущённая» траектория системы х0(-). Пусть управление и0(•) возмущено малой функцией 5ш(^)еЬ(Т), следствием чего будет малое возмущение фазовой траектории: хо(0 ^ хо(0 + 5х(-).

Связь между 5х(0 и 5и(^ определяет известное уравнение в вариациях. В теории первого порядка оно имеет вид [2]

5х(?) = (г )5х(0+/и (ОЦг), 5х(^) = 0,1 е Т = ^ ].(3)

В (3) элементами на пересечении 7-й строки и /-го столбца матриц и /и(?) служат частные производные 8//8х/ и д[/ды/ соответственно, вычисленные в точке (и0, х0).

Уравнение (3) является точным для систем вида (1), линейных относительно х и и. В общем случае 5х(0 отличается от точной разности между возмущённой и невозмущённой траекториями на величину более высокого порядка малости, чем норма от 55и.

Решение уравнения в вариациях (3) имеет

5х(г) = |т)/и (т)5и(тУс, г е Т = [г0, ^ ], (4)

где 0(, т) — матрица Коши уравнения в вариациях (3);

/и (г) — якобиан для дифференциальной системы (1), связывающей вектор состояния х(0

Современные технологии. Математика. Механика и машиностроение

размерности п и вектор управления п(р) размерности т.

Уравнение в вариациях первого порядка в виде (3) и его решение в виде (4) широко известны. Поставим задачу вывести уравнение в вариациях второго порядка и выписать для него решение.

Вывод уравнения в вариациях второго порядка

Разложим в ряд Тейлора нелинейные правые части системы (1) в окрестности невозмущённого движения, ограничивая ряд членами второго порядка включительно.