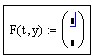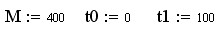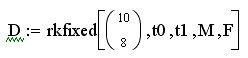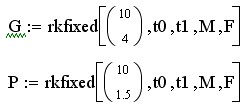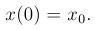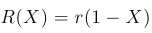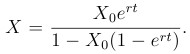Уравнение ван дер поля mathcad

Уравнение ван дер поля mathcad

Государственное образовательное учреждение

высшего профессионального образования

Глазовский государственный педагогический институт

ЗАДАЧ С ПОМОЩЬЮ

Майер, Р.В. Решение физических задач с помощью пакета MathCAD [Электронный ресурс] / Р.В.Майер. — Глазов: ГГПИ, 2006. — 37 c.

Рецензент: В.А.Саранин, доктор физико-математических наук, профессор кафедры физики и дидактики физики ГГПИ.

В краткой форме рассмотрены некоторые способы решения физических задач с помощью математического пакета MathCAD. Показаны методы рассчета электрических цепей постоянного тока, однофазных и трехфазных цепей переменного тока, колебательных систем, переходных процессов, способы разложения функций в ряд Фурье и проведения спектрального анализа. Приведены примеры использования комплексных чисел, решения дифференциальных уравнений, построения графиков. Для студентов высших учебных заведений.

Компьютерное моделирование, проведение вычислительного эксперимента является одним из современных методов исследования физических явлений. Он имеет свои особенности, преимущества и недостатки по сравнению с другими методами изучения физических систем. Совершенно очевидно, что студенты высших учебных заведений должны иметь представления о компьютерных моделях, численных методах изучения различных объектов познания, достаточно свободно ориентироваться в современных программных продуктах. Современный персональный компьютер позволяет за несколько секунд решить сложную систему уравнений, построить график изучаемой зависимости, промоделировать трудновоспроизводимый эксперимент.

Важным уровнем овладения методами вычислительной математики и физики является самостоятельное написание студентами различных компьютерных программ на алгоритмических языках программирования Basic, Pascal, Visual Basic, Delphi. Создавая подобные компьютерные модели «с нуля», работая с исходным кодом программы, студент глубже понимает конкретные способы обработки информации, методы программирования.

С другой стороны необходимо уметь работать с современными математическими пакетами, различными системами компьютерной математики. К ним относится пакет MathCAD — достаточно распространенная система автоматического проектирования (САПР), в которой объединены редактор документов, системный интегратор, центр ресурсов, электронные книги, справочная система, броузер Интернета. Пакет MathCAD имеет мощный математический аппарат, позволяющий выполнять символьные вычисления, решать системы алгебраических и дифференциальных уравнений, операции с векторами и матрицами, писать программы, строить графики и поверхности, и т.д.

Основы работы в MathCAD подробно изложены в соответствующей литературе и в настоящей работе не рассматриваются. В предлагаемом пособии проанализированы некоторые типы задач общего курса физики, которые могут быть решены средствами MathCAD и позволяют сформировать представления о возможностях использования этого математического пакета при изучении физики.

1. ДВИЖЕНИЕ ТОЧКИ В ОДНОРОДНОМ ПОЛЕ

С УЧЕТОМ СИЛЫ СОПРОТИВЛЕНИЯ

Задача 1. Тело бросили под углом к горизонту в однородном поле тяжести. Начальные координаты и скорость тела, коэффициент сопротивления воздуха известны. Напишите дифференциальные уравнения и построить траекторию движения тела.

Из второго закона Ньютона:

Решение этой системы уравнений — в документе 01.mcd.

Задача 2. Исследуйте движение тела в поле тяжести при других начальных условиях. Докажите, что из—за силы сопротивления воздуха время подъема меньше времени спуска на тот же уровень. Для этого достаточно проанализировать график y=y(t).

Задача 3. Вычислите скорость и ее проекции на оси в данный момент времени времени. Найдите нормальное и тангенциальное ускорение, радиус кривизны траектории. Когда ускорение тела больше g?

2. ЦЕПИ ПОСТОЯННОГО ТОКА

Задача 5. Цепь состоит из нескольких ветвей, в каждой из которых находится источник ЭДС и резистор (рис.1). Необходимо рассчитать цепь, то есть определить токи во всех ее ветвях.

Из законов Кирхгофа получаем систему уравнений:

Для решения этой системы уравнений запишем матрицу:

Левую часть матрицы, содержащую коэффициенты при токах I_i, обозначим через A, а правую — через B. Чтобы получить матрицу токов в MathCAD используется оператор TOK:=A -1 · B. Решение задачи представлено в документе 03.mcd.

Задача 6. Рассчитайте цепь, состоящую из нескольких источников ЭДС и резисторов, и составьте баланс мощностей.

3. ОДНОФАЗНЫЕ ЦЕПИ ПЕРЕМЕННОГО ТОКА

Задача 7. Цепь состоит из источника переменной ЭДС и трех ветвей, в каждой из которых резистор, конденсатор и катушка индуктивности. Вторая и третья ветви соединены параллельно между собой, последовательно с ними включена первая ветвь. Рассчитайте все токи и напряжения, полную, активную и реактивную мощности. Постройте векторную диаграмму. Определите действующие значения всех токов и напряжений.

Импеданс k—ой ветви, содержащей последовательно соединенные резистор r_k, конденсатор C_k и катушку индуктивности L_k, равен:

Если ветви 2 и 3 соединены параллельно, а ветвь 1 — последовательно с ними, то импеданс цепи:

Неизвестные токи и напряжения найдем из закона Ома:

Это позволяет построить векторную диаграмму цепи, рассчитать комплекс полной мощности. Решение задачи представлено в файле 04.mcd.

Задача 8. Добавьте к предыдущей цепи четвертую ветвь параллельно источнику. Величины сопротивления, емкости и индуктивности подберите сами. Рассчитайте цепь, постройте векторную диаграмму.

Задача 9. Решите задачу 7 для случая, когда первая и третья ветви состоят их резистора, конденсатора и катушки индуктивности, соединенных параллельно. Постройте векторную диаграмму.

4. ТРЕХФАЗНЫЕ ЦЕПИ

Задача 10. Имеется четырехпроводная трехфазная цепь с несимметричной нагрузкой. Определите комплексы токов во всех линейных и нейтральном проводах, их модули, вычислите мощность, постройте векторные диаграммы.

Из законов Кирхгофа получаем систему:

Для ее решения создают две матрицы A и B, затем получают третью матрицу TOK:=A -1 · B, элементами которой являются комплексы токов (документ 05.mcd). Их модули равны действующим значениям токов.

Задача 11. Рассчитайте четырехпроводную трехфазную цепь с несимметричной нагрузкой, каждая фаза которой содержит резистор, конденсатор, катушку индуктивности, соединенные смешанно.

Задача 12. Рассчитайте трехфазную цепь с несимметричной нагрузкой, соединенной треугольником. Каждая фаза нагрузки содержит резистор, конденсатор, катушку индуктивности, соединенные смешанно.

Задача 13. Фазоуказатель состоит из конденсатора и двух одинаковых лампочек, соединенных звездой без нейтрали. Какая из лампочек будет гореть ярче, если конденсатор находится в фазе A?

5. КОЛЕБАТЕЛЬНОЕ ДВИЖЕНИЕ

Задача 14. Имеется идеальная колебательная система. Ее вывели из состояния равновесия и предоставили самой себе. Получите график колебательного движения и фазовую кривую.

Решение дифференциального уравнения незатухающих колебаний:

представлено в документе 06.mcd.

Задача 15. Тело, подвешенное на пружине, совершает гармонические колебания x(t)=Asin(ωt+φ). Средствами MathCAD продифференцируйте эту зависимость, постройте графики зависимости кинетической и потенциальной энергии от времени (07.mcd).

Задача 16. Двойной маятник состоит из подвешенной на нити длиной L₁ материальной точки m₁, к которой с помощью нити длиной L₂ подвешена материальная точка m₂. Изучите зависимость потенциальной энергии от углов α и β, которые образуют нити с вертикалью.

Маятник движется в одной вертикальной плоскости, система имеет две степени свободы. Ее потенциальная энергия равна:

В файле 08.mcd построена поверхность U=U(α,β), характеризующая зависимость потенциальной энергии от координат маятника. Видно, что значениям α=π и β=0 соответствует седлообразное положение равновесия: потенциальная энергия по координате α достигает максимума, а по координате β — минимума.

Задача 17. Последовательный колебательный контур, состоящий из резистора, конденсатора и катушки индуктивности, подключен к источнику переменного напряжения регулируемой частоты. Постройте график зависимости тока, напряжения на конденсаторе и катушке индуктивности, сдвига колебаниями тока и напряжения питания от частоты.

Полное сопротивление колебательного контура и сдвиг фаз между колебаниями тока и напряжения:

Ток в контуре равен I=U/z. Решение задачи — в документе 09.mcd.

6. АВТОКОЛЕБАТЕЛЬНЫЕ ПРОЦЕССЫ

Задача 18. Исследуйте автоколебательную систему, в которой один раз за период осциллятору сообщается энергия (действует постоянная сила). Постройте график колебаний и фазовую траекторию.

Рассмотрим колебательную систему, на которую при смещениях x в интервале [-a; a] и движении в положительном направлении действует постоянная сила, равная F_m:

Силу запишем через heaviside step function:

В этом случае уравнение автоколебаний принимает вид:

Соответствующий документ MathCAD представлен в файле 10.mcd. На фазовой кривой хорошо виден скачок, соответствующий увеличению амплитуды колебаний при передаче колебательной системе очередной порции энергии. Множество точек, к которому стремится фазовая кривая называется аттрактором.

Задача 19. Промоделируйте движение автоколебательной системы, в которой каждый раз при прохождении положения равновесия (дважды за период) осциллятору сообщается энергия (действует постоянная сила).

Пусть система подталкивает осциллятор вблизи положения равновесия, действуя на него с постоянной силой b:

Из второго закона Ньютона получаем дифференциальное уравнение:

Решение этого уравнения представлено в файле 11.mcd.

Задача 20. Промоделируйте автоколебательную систему, описывающуюся уравнением Ван-дер-Поля:

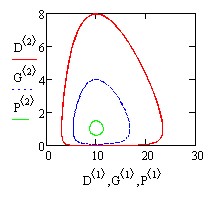
Решение задачи приведено в документе 12.mcd. Колебательная система воздействует посредством положительной обратной связи на клапан, регулирующий поступление энергии от источника, в результате чего возникают автоколебания. Их амплитуда растет до тех пор, пока энергия потерь за период не будет равна энергии от источника.

Задача 21. Фрикционный маятник Фроуда состоит из физического маятника, расположенного на вращающемся валу. Сила трения между валом и маятником с увеличением их относительной скорости убывает. Исследуйте колебания маятника.

Проекцию вращающего момента, действующего со стороны вала на маятник, будем считать равной

Если маятник движется в направлении вращения и его скорость меньше скорости вала, то со стороны вала на него действует достаточно большой момент силы трения в направлении вращения вала. Когда маятник движется в противоположном направлении, его скорость относительно вала велика, поэтому момент силы трения мал. Так автоколебательная система регулирует поступление энергии к осциллятору.

Запишем второй закон Ньютона в проекциях:

Для решения этого дифференциального уравнения используется документ 13.mcd. Из графиков x=x(t) и v=v(t) видно, что маятник Фроуда колеблется относительно нового положения равновесия, смещенного в сторону вращения вала, причем его скорость в установившемся режиме не превышает скорость вала ω. Замкнутая кривая на фазовой плоскости, при t стремящемся к бесконечности является аттрактором.

Задача 22. Промоделируйте движения маятника Фроуда для случая, когда начальная скорость маятника превышает скорость вращения вала. Убедитесь, что через достаточно большой промежуток времени система переходит в установившееся состояние, фазовая кривая стремиться к аттрактору.

7. РЕЛАКСАЦИОННЫЕ ПРОЦЕССЫ

Задача 23. Цепь состоит из резистора и катушки индуктивности, подключаемых к источнику постоянного напряжения. В начальный момент ток через катушку равен 0. Определите значение тока и напряжения на катушке в последующие моменты времени.

Решение дифференциального уравнения переходного процесса

представлено в документе 14.mcd.

Задача 24. Колебательный контур содержит резистор, конденсатор, катушку индуктивности. Конденсатор зарядили и подключили к цепи. Исследуйте получающиеся затухающие колебания.

Дифференциальное уравнение затухающих колебаний выглядит так:

Его решение представлено в документе 15.mcd.

Задача 25. Исследуйте цепь из резистора, конденсатора и катушки индуктивности, подключаемых к источнику переменного напряжения. В начальный момент конденсатор разряжен, ток через катушку индуктивности равен 0.

Запишем дифференциальное уравнение переходного процесса:

Начальные условия: q(0)=Cu(0)=0, i(0)=q'(0)=0. Решение этого уравнения представлено в документе 16.mcd.

8. РАЗЛОЖЕНИЕ В РЯД ФУРЬЕ. СПЕКТРАЛЬНЫЙ АНАЛИЗ

Задача 26. Разложите пилообразные импульсы напряжения u(t) в ряд Фурье. Восстановите сигнал по 3, 7, 15, 30 и 50 первым гармоникам. Сравните получившуюся функцию с исходной.

Решение задачи предложено в документе 17.mcd.

Задача 27. Разложите импульсы, получающиеся в результате однополупериодного и двухполупериодного выпрямления, в ряд Фурье. Восстановите сигнал по 3, 7, 15, 30 и 50 первым гармоникам.

Задача 28. Получите спектр последовательности радиоимпульсов, представляющих собой обрывки синусоидальных колебаний.

Решение — в документе 18.mcd.

Задача 29. Получите спектр амплитудно—модулированного сигнала

Видно, что спектр содержит колебания на основной частоте и на двух зеркальных частотах (документ 19.mcd).

Задача 30. Доработайте программу так, чтобы промоделировать детектирование амплитудно—модулированного сигнала. Детектором является диод, обрезающий нижнюю часть синусоиды, а сглаживание пульсаций осуществляется за счет емкостного фильтра (документ 20.mcd).

Задача 31. Характеристика нелинейного элемента может быть аппроксимирована полиномом второй степени i(u)=au 2 +bu+c. Изучите спектральный состав отклика системы (силы тока) на оказываемое гармоническое воздействие (напряжение) (документ 21.mcd).

9. ВЛИЯНИЕ ЕМКОСТИ И ИНДУКТИВНОСТИ НА КРИВУЮ ТОКА

Задача 32. К источнику периодической негармонической ЭДС подключена активно—емкостная (активно—индуктивная) нагрузка. Используя разложение в ряд Фурье, получите кривые тока и изучите их спектр.

При активно—индуктивной нагрузке кривая тока в большей степени похожа на синусоиду, чем кривая напряжения, а в случае активно—емкостной — наоборот (документ 22.mcd). Это объясняется тем, что гармоникам тока высокого порядка конденсатор оказывает меньшее сопротивление, а катушка индуктивности — большее.

10. РАСЧЕТ ЦЕПЕЙ, СОДЕРЖАЩИХ ИСТОЧНИК НЕГАРМОНИЧЕСКОЙ ЭДС

Задача 33. Цепь состоит из параллельно соединенных резистора и конденсатора, к которым последовательно подключена катушка индуктивности и источник негармонического напряжения

Найдите токи в ветвях, их действующие значения, мощности.

Заменим этот источник источником постоянной ЭДС U₀ и тремя источниками переменной ЭДС U_m1sin(ωt+φ₁), U_m2sin(2ωt+φ₂), U_m3sin(3ωt+φ₃).

Найдем импеданс цепи для k-ой гармоники:

где tg(φ_k) равен отношению мнимой и действительной частей импеданса. Комплексная амплитуда k—ой гармоники тока определяется как отношение комплексной амплитуды напряжения к импедансу для k—ой гармоники. В представленном ниже документе MathCAD (23.mcd) построен график u(t), рассчитаны импедансы и амплитуды токов для различных гармоник, найдены действующие значения тока и напряжения, определена зависимость i(t), построен график.

11. ЭЛЕКТРИЧЕСКОЕ И МАГНИТНОЕ ПОЛЕ

Задача 34. Два точечных электрических заряда q₁, q₂ имеют координаты (X₁,Y₁) и (X₂,Y₂). Рассчитайте распределение потенциала электрического поля, постройте эквипотенциальные линии и поверхность φ=φ(x,y).

Потенциал электрического поля, создаваемого зарядами q_i с координатами (X_i,Y_i), i=1, 2, . в точке (x,y) равен:

Результаты расчета эквипотенциальных линий и поверхности φ=φ(x,y) — в документе 24.mcd. Заряды положительные, поэтому по мере приближения к каждому из них потенциал возрастает.

Задача 35. Рядом с заряженной пластиной расположены два точечных заряда. Изучите распределение потенциала и постройте силовые линии напряженности электрического поля.

Зависимость φ=φ(x,y) определяется как в предыдущей задаче, напряженность электрического поля в двумерном случае равна:

Для построения силовых линий вычисляются проекции вектора напряженности на оси координат и создается матрица E_i,j:=Ex(x_i,y_j)+ 1i· Ey(x_i,y_j) и нормированная матрица A_i,j, используемая для построения векторного поля (25.mcd).

Задача 36. Рассчитайте индукцию магнитного поля, создаваемого двумя витками с током, и постройте силовые линии в случаях, когда токи сонаправлены и противоположно направлены.

Рассмотрим виток с током, лежащий в плоскости XOY, с центром в точке O. Разобъем его на элементы dl_s, определим элементарный магнитный момент, создаваемый каждым элементом в точке наблюдения, и просуммируем их.

Элемент витка и точка наблюдения имеют координаты (r·cosφ_s, r·sinφ_s, 0), и (x, y, z) соответственно. Для расчета индукции магнитного поля используется закон Био—Савара—Лапласа:

где μ₀ — магнитная постоянная, I — сила тока. Решение приведено в документе 26.mcd. Витки расположены параллельно плоскости XOY, на экране получаются силовые линии магнитного поля в плоскости YOZ.

Задача 37. В рассмотренном случае постройте график зависимости модуля индукции магнитного поля от координаты вдоль оси витков с током и перпендикулярно ей.

Задача 38. Получите проекции вектора индукции магнитного поля на плоскость перпендикулярную оси соленоида (витка) с током.

Задача 39. Рассчитайте магнитное поле, создаваемое двумя (тремя) параллельными проводниками, по которым текут токи в различных направлениях.

Задача 40. Изучите магнитное поле, создаваемое соленоидом и прямолинейным проводником с током. Получите проекции индукции магнитного поля на плоскость, содержащую проводник с током.

Задача 41. Имеется два соленоида, расположенных соосно по отношению друг к другу. Постройте силовые линии магнитного поля в случаях, когда токи текут в одном направлении и в противоположных направлениях (27.mcd).

12. ИНТЕРФЕРЕНЦИЯ ВОЛН

Задача 42. Две волны с равными частотами распространяются навстречу друг другу. В результате их наложения возникает стоячая волна. Постройте смещения частиц среды в различные моменты времени (28.mcd).

Задача 43. Рассчитайте интерференционную картину, создаваемую двумя когерентными источниками, работающими в противофазе, в плоскости, содержащей эти источники.

Расстояние от источников до точки наблюдения равно:

Задача 44. Рассчитайте интерференционную картину от двух источников, на плоскости, расположенной параллельно прямой, содержащей эти источники. Длина волны и расположение источников известны.

Геометрическая разность хода и интенсивность равны:

13. МОДЕЛИРОВАНИЕ ЯВЛЕНИЙ ПЕРЕНОСА

Задача 45. Однородный стержень с известным коэффициентом температуропроводности нагревают в середине. Правый конец поддерживается при постоянной температуре, левый — теплоизолирован. Начальное распределение температуры и мощность источника известны. Определите температуру в последующие моменты времени.

Уравнение теплопроводности для стержня:

Решение задачи в документе 31.mcd. В результате вычислений получаются кривые T=T(t,x) зависимости температуры от координаты x в заданные моменты времени t. Видно, что температура средней части стержня за счет источников тепла повышается.

Моделирование диффузии осуществляется аналогично.

Задача 46. Стержень разрезали на две половины и одну из них нагрели, после чего половинки стержня соединили. Рассчитайте распределение температуры вдоль стержня в последующие моменты времени.

Задача 47. Часть сосуда заполнена водным раствором соли, а другая часть — чистой водой. Изучите самопроизвольное перемешивание жидкостей за счет диффузии.

14. ДИНАМИЧЕСКИЙ ХАОС

Задача 48. Промоделируйте хаотическое движение броуновской частицы.

На броуновскую частицу со стороны окружающих ее молекул действует сила, хаотическим образом изменяющая свою величину и направление. Чтобы промоделировать ее движение необходимо прибавлять к координатам частицы случайные величины (документ 32.mcd). Траектория частицы является фракталом, то есть объектом, любая часть которого после увеличения подобна целому.

Задача 49. Колебательная система состоит из шарика, находящегося внутри потенциальной ямы с двумя углублениями, задаваемой функцией: U(x)=0.25x 4 -0.5x 2 . На шарик действует вынуждающая сила F(t)=F_mcos(ω t). Исследуйте поведение системы.

Потенциальное поле создает возвращающую силу

Два варианта решения представлены в документах 33.mcd и 34.mcd. Видно, что система совершает хаотические колебания относительно двух положений равновесия.

Задача 50. Конвекционные потоки в атмосфере описываются системой дифференциальных уравнений dx/dt=a(-x+y), dy/dt=bx-y-xz, dz/dt=-cz+xy. Изучите поведение этой системы, получите странный аттрактор Лоренца. В чем состоит эффект бабочки?

Решение задачи — в документе 35.mcd. Видно, что аттрактор Лоренца похож на закрученную восьмерку, и захватывает две большие области фазового пространства. При этом малые изменения состояния атмосферы могут привести к существенным изменениям ее состояния в будущем. Например, бабочка, взмахнув крыльями в Австралии, при определенных метеорологических условиях может вызвать торнадо в Америке.

Внедрение в учебный процесс компьютерной техники позволяет существенным образом изменить методику изучения некоторых вопросов курса физики, связанных с осуществлением громоздких, многократно повторяющихся вычислительных процедур, решением систем дифференциальных уравнений, построением графиков и поверхностей, наглядным представлением результатов решения задачи. Если раньше поведение физической системы анализировалось исключительно аналитически, то теперь появилась возможность применения численных методов компьютерного моделирования, что имеет определенные преимущества.

Рассмотренные выше задачи создают лишь общее представление о возможностях пакета MathCAD. Более глубокое изучение вопроса требует привлечения специальных руководств и пособий, некоторые из которых перечислены в списке литературы. Настоящее электронное пособие может быть использовано студентами и преподавателями при изучении основ компьютерного моделирования, методов математической физики, а также при решении задач курсов общей физики, электротехники и т.д.

1. Дьяконов, В. MathCAD 2000 [Текст]: учебный курс / В.Дьяконов — СПб.: Питер, 2001. — 592 с.
2. Кирьянов, Д.В. MathCAD 12 [Текст]: наиболее полное руководство / Д.В.Кирьянов. — Спб. БХВ — Петербург, 2005. — 562.
3. Майер, Р.В. Информационные технологии и физическое образование [Текст] / Р.В.Майер. — Глазов: ГГПИ, 2006. — 64 с.
4. Поршнев, С.В. Компьютерное моделирование физических процессов с использованием пакета MathCAD [Текст]: учебное пособие / С.В.Поршнев. — М.: Горячая линия—Телеком, 2002. — 252 c.
5. Физическая энциклопедия / Гл. ред. А.М.Прохоров. Ред. кол. Д.М.Алексеев, А.М.Балдин, А.М.Бонч-Бруевич, А.С.Боровик—Романов и др. — М.: Большая Российская энциклопедия. — 1992—1995. (в 6 томах).

ПРИЛОЖЕНИЕ

МАЙЕР Роберт Валерьевич, доктор педагогических наук, профессор кафедры информационных технологий в физическом образовании физического факультета Глазовского государственного педагогического института.

Издательская лицензия ИД N06035 от 12.10.2001.

Формат 60 x 90 1/16. Усл. печ. л. 2,15.

Глазовский государственный педагогический институт.

427621, Удмуртия, г. Глазов, ул. Первомайская, 25.

решение физических задач в MathCAD решение физических задач в MathCAD решение физических задач в MathCAD решение физических задач в MathCAD решение физических задач в MathCAD решение физических задач в MathCAD решение физических задач в MathCAD решение физических задач в MathCAD решение физических задач в MathCAD решение физических задач в MathCAD решение физических задач в MathCAD решение физических задач в MathCAD решение физических задач в MathCAD решение физических задач в MathCAD решение физических задач в MathCAD решение физических задач в MathCAD решение физических задач в MathCAD решение физических задач в MathCAD решение физических задач в MathCAD решение физических задач в MathCAD решение физических задач в MathCAD решение физических задач в MathCAD решение физических задач в MathCAD решение физических задач в MathCAD решение физических задач в MathCAD решение физических задач в MathCAD решение физических задач в MathCAD решение физических задач в MathCAD решение физических задач в MathCAD решение физических задач в MathCAD решение физических задач в MathCAD решение физических задач в MathCAD

Уравнение ван дер поля mathcad

Примечание
Допустимо, и даже часто предпочтительнее, задание функцииOdesolve (t, tl, step) с тремя параметрами, где step- внутренний параметрчисленного метода, определяющий количество шагов, в которых метод Рунге-Кутты, будет рассчитывать решение дифференциального уравнения. Чембольше step, тем с лучшей точностью будет получен результат, но тем большевремени будет затрачено на его поиск. Помните, что подбором этого параметраможно заметно (в несколько раз) ускорить расчеты без существенного ухудшения их точности.

Совет
В листинге 11.2 приведен пример не лучшего стиля MathCAD-программиро-вания. Сначала переменной у присвоено значение скаляра у=0.1, а затем этойже переменной присвоено матричное значение (результат решения ОДУ). Старайтесь избегать такого стиля, который ухудшает читаемость программы и может приводить, в более сложных случаях, к трудно опознаваемым ошибкам.Неплохим решением было бы назвать результат по-другому, например и.

График решения рассматриваемого уравнения показан на рис. 11.1. Обратите внимание, что он соответствует получению решения в матричном виде (листинг 11.2), поэтому по осям отложены соответствующие столбцы, выделенные из матрицы у оператором <>.

Примечание
Пример, решенный в листингах 11.1-11.2, взят из области математическойэкологии и описывает динамику популяций с внутривидовой конкуренцией.Сначала происходит рост численности популяции, близкий к экспоненциальному, а затем выход на стационарное состояние.

Рис. 11.2. Решение уравнения осциллятора(листинг 11.3)

Примечание
В листинге 11.3 решено уравнение затухающего гармонического осциллятора,которое описывает, например, колебания маятника. Для модели маятника y(t)описывает изменения угла его отклонения от вертикали, у 1 (t) — угловую скорость маятника, у» (t) — ускорение, а начальные условия, соответственно,начальное отклонение маятника у (0) =0.1 и начальную скорость у’ (0) = 0.

Примечание
Как вы заметили, задача сформулирована для систем ОДУ первого порядка.Однако если в систему входят и уравнения высших порядков, то ее можно свести к системе большего числа уравнений первого порядка подобно тому, какэто было сделано на примере уравнения осциллятора (см. разд. 11.2).

Рис. 11.3. Матрица решений системы уравнений(листинг 11.4)
Обратите внимание на некоторое разночтение в обозначении индексов вектораначальных условий и матрицы решения. В ее первом столбце собраны значения нулевой компоненты искомого вектора, во втором столбце — первой компоненты и т. д.
Чтобы построить график решения, надо отложить соответствующие компоненты матрицы решения по координатным осям: значения аргумента и — вдоль оси х, а и и и — вдоль оси Y (рис. 11.4). Как известно, решенияобыкновенных дифференциальных уравнений часто удобнее изображать нев таком виде, а в фазовом пространстве, по каждой из осей которого откладываются значения каждой из найденных функций. При этом аргумент входит в них лишь параметрически. В рассматриваемом случае двух ОДУ такойграфик — фазовый портрет системы — является кривой на фазовой плоскости и поэтому особенно нагляден. Он изображен на рис. 11.5 (слева), иможно заметить, что для его построения потребовалось лишь поменять метки осей на u и и соответственно.

Примечание
Фазовый портрет типа, изображенного на рис. 11.5, имеет одну стационарнуюточку (аттрактор), на которую «накручивается» решение. В теории динамических систем аттрактор такого типа называется фокусом.

Рис. 11.4. График решения системы ОДУ (11.2-1) (листинг 11.4)

5 )и верный результат на конце интервала, левый график мало напоминает правильный фазовый портрет (см. рис. 11.5 или правый график на рис. 11.6), начиная быть приемлемым только при предельно допустимом для обсуждаемыхфункций значении асс=10

Рис. 11.6. Фазовый портрет, полученный bulstoer (слева) и rkadapt (справа) (листинг 11.5)
В заключение остановимся на влиянии выбора параметра асе на расчеты.Для этого воспользуемся простой программой, представленной на листинге 11.6. В ней из матрицы решения все той же задачи Коши взято лишь полученное значение одной из функции на правой границе интервала. Но затоэтот результат оформлен в виде функции пользователя у(е), в качестве аргумента которой выбран параметр асе функции bulstoer.
Листинг 11,6. Использование решения ОДУ для определенияфункции пользователя

Вычисленный вид у(е) показан на рис. 11.7 вместе с аналогичным результатом для функции rkadapt. Как видно, в данном примере численные методыработают несколько по-разному. Метод Рунге-Кутты дает результат темближе к истинному, чем меньше выбирается е=асс. Метод Булирша-Штерадемонстрирует менее естественную зависимость у (е): даже при относительно больших е реальная точность остается хорошей (намного лучше методаРунге-Кутты). Поэтому для экономии времени расчетов (подчеркнем ещераз: для данной конкретной задачи) в функции bulstoer можно выбирать ибольшие асе.

Рис. 11.7. Зависимостьрасчетного значения одногоиз уравнений системы ОДУна конце интервалаот параметра асе(листинг 11.6)
Чтобы обеспечить заданную точность, алгоритмы, реализованные во встроенных функциях, могут изменять как количество шагов, разбивающих интервал (tO,tl), так и их расположение вдоль интервала. Чтобы выяснить, насколько шагов разбивался интервал при расчетах у(е)на рис. 11.7 для каждого е, следует вычислить размер получающейся матрицы. Для этого можно,например, определить подобные функции:

Рис. 11.8. Зависимостьчисла шагов от параметраасе численных методов
Сравнив два результата применения rkadapt для k=30 и k=ioo, обратитевнимание (рис. 11.8), как еще один параметр — максимальное число шагов k,

Примечание
В большинстве примеров, изложенных ниже, для построения фазового портрета рассчитывается несколько решений для разных начальных условий.

Рис. 11.9. График решения (слева) и фазовый портрет (справа) системы «хищник-жертва» (листинг 11.7)
Автоколебания
Рассмотрим решение уравнения Ван дер Поля, описывающего электрические колебания в замкнутом контуре, состоящем из соединенных последо вательно конденсатора, индуктивности, нелинейного сопротивления и элементов, обеспечивающих подкачку энергии извне (листинг 11.8). Неизвестная функция времени y(t) имеет смысл электрического тока, а в параметре ц заложены количественные соотношения между составляющими электрической цепи, в том числе и нелинейной компонентой сопротивления.
Листинг 11.8. Модель Ван дер Поля (р=1)

Рис. 11.10. График решения (слева) и фазовый портрет (справа) уравнения Ван дер Поля (листинг 11.8)
Решением уравнения Ван дер Поля являются колебания, вид которых дляц=1 показан на рис. 11.10. Они называются автоколебаниями и принципиально отличаются от рассмотренных нами ранее (например, колебаний маятника в разд. П.3.2) тем, что их характеристики (амплитуда, частота, спектр)не зависят от начальных условий, а определяются исключительно свойства ми самой динамической системы. Через некоторое время расчетов послевыхода из начальной точки решение выходит на один и тот же цикл колебаний, называемый предельным циклом. Аттрактор типа предельного цикла является замкнутой кривой на фазовой плоскости. К нему асимптотическипритягиваются все окрестные траектории, выходящие из различных начальных точек, как изнутри (рис. 11.10), так и снаружи (рис. 11.11) предельногоцикла.

Рис. 11.11. Решение уравнения Ван дер Поля при других начальных условиях у=-2,у’=-3

Примечание
Если компьютер у вас не самый мощный, то расчет фазового портрета срис. 11.10-11.11 в MathCAD может занять относительно продолжительноевремя, что связано с численным определением сначала решения у (t), а потомего производной. Время расчетов можно было бы существенно сократить, еслииспользовать вместо вычислительного блока Given/Odesolve одну из встроенных функций, которые выдают решение в виде матрицы, например, rkf ixed.

Аттрактор Лоренца
Одна из самых знаменитых динамических систем предложена в 1963 г. Лоренцем в качестве упрощенной модели конвективных турбулентных движений жидкости в нагреваемом сосуде тороидальной формы. Система состоитиз трех ОДУ и имеет три параметра модели (листинг 11.9). Поскольку неизвестных функций три, то фазовый портрет системы должен определяться нена плоскости, а в трехмерном пространстве.
Листинг 11.9. Модель Лоренца

Решением системы Лоренца при определенном сочетании параметров(рис. 11.12) является странный аттрактор (или аттрактор Лоренца) — притягивающее множество траекторий на фазовом пространстве, которое повиду идентично случайному процессу. В некотором смысле, аттрактор Лоренца является стохастическими автоколебаниями, которые поддерживаютсяв динамической системе за счет внешнего источника.

Рис. 11.12. Аттрактор Лоренца (листинг 11.9)
Решение в виде странного аттрактора появляется только при некоторых сочетаниях параметров. В качестве примера на рис. 11.12 приведен результат для г=10 и тех же значений остальных параметров. Как видно, аттрактором вэтом случае является фокус. Перестройка типа фазового портрета происходит в области промежуточных г. Критическое сочетание параметров, прикоторых фазовый портрет системы качественно меняется, называется в теории динамических систем точкой бифуркации. Физический смысл бифуркации в модели Лоренца, согласно современным представлениям, описываетпереход ламинарного движения жидкости к турбулентному.

Рис. 11.14. Фазовый портрет брюсселятора при В=0.5 (листинг 11.10)
Как видно из рис. 11.14, все траектории, вышедшие из разных точек, асимптотически стремятся к одному и тому же аттрактору (1,0.5). Из теории динамических систем нам известно, что такой аттрактор называется узлом(с узлом мы уже встречались в примерах разд. 11.1). Конечно, в общем случаепри анализе фазового портрета желательно «прощупать» большее число траекторий, задавая более широкий диапазон начальных условий. Не исключено, что в других областях фазовой плоскости траектории будут сходитьсяк другим аттракторам.
Эволюцию фазового портрета брюсселятора можно наблюдать, проводя расчеты с различным параметром в. При его увеличении узел будет сначалапостепенно смещаться в точку с координатами (1,в), пока не достигнетбифуркационного значения в=2. В этой точке происходит качественная перестройка портрета, выражающаяся в рождении предельного цикла. Придальнейшем увеличении в происходит лишь количественное изменениепараметров этого цикла. Решение, полученное при в=2.5, показано нарис. 11.15.

Примечание
Чтобы найти аттракторы динамической системы, как известно, нужно решитьсистему алгебраических уравнений, получающуюся из системы ОДУ заменой
нулями их левых частей. Эти задачи также удобно решать средствамиMathCAD (см. гл. 8). В частности, исследование зависимости фазового портрета от параметров системы ОДУ и поиск бифуркаций можно проводить методами продолжения (см. разд. «Метод продолжения по параметру» гл. 8).

Рис. 11.16. Решение нежестких ОДУ методом Рунге-Кутты(листинг 11.11)
На рис. 11.17 показано решение того же ОДУ с коэффициентом -50. Вас,несомненно, должен насторожить результат, выданный MathCAD. Характерная «разболтка» решения говорит о неустойчивости алгоритма. Первое,что можно сделать, — увеличить количество шагов в методе Рунге-Кутты. Для этого достаточно добавить третий параметр step в функциюodesoive(t,i,step). После нескольких экспериментов можно подобрать такое значение step, которое будет обеспечивать устойчивость решения. Читатель может самостоятельно убедиться, что при step>20 «разболтка» пропадает, и решение становится похожим на графики, показанные на рис. 11.16.

Рис. 11.17. Неверное решение более жесткого ОДУ методом Рунге-Кутты
Таким образом, во-первых, мы выяснили, что одни и те же уравнения сразными параметрами могут быть как жесткими, так и нежесткими. Во-вторых, чем жестче уравнение, тем больше шагов в обычных численных методах требуется для его устойчивого решения. С классическим примеромОДУ из листинга 11.11 все получилось хорошо, т. к. оно было не очень жестким, и небольшое увеличение числа шагов разрешило все проблемы. Длярешения обычными методами более жестких уравнений требуются миллионы, миллиарды и даже большее число шагов.

Примечание
Некоторые ученые замечают, что в последние годы методы Рунге-Кутты сталиуступать свое главенствующее положение среди алгоритмов решения ОДУ методам, способным решать жесткие задачи.

Исторически, интерес к жестким системам возник в середине XX века приизучении уравнений химической кинетики с одновременным присутствиемочень медленно и очень быстро протекающих химических реакций. Тогданеожиданно оказалось, что считавшиеся исключительно надежными методыРунге-Кутты стали давать сбой при расчете этих задач. Рассмотрим классическую модель взаимодействия трех веществ (Робертсон, 1966), которая какнельзя лучше передает смысл понятия жесткости ОДУ.
Пусть вещество «О» медленно превращается в «1»: «0»->»1″ (со скоростьюo.l), вещество «1» при каталитическом воздействии самого себя превращается очень быстро в вещество «2»: «i»+»i»-»»2″+»i» (ю 3 ). И, наконец, подобным образом (но со средней скоростью) реагируют вещества «2» и «1»:
» 1 » + .. 2 «_^»0»+»2» (ю 2 ). Система ОДУ, описывающая динамику концентрацииреагентов, с попыткой решения методом Рунге-Кутты, приведена в листинге 11.12.
Листинг 11.12. Жесткая система ОДУ химической кинетики

Бросается в глаза сильно различающийся порядок коэффициентов при разных слагаемых. Именно степень этого различия чаще всего и определяетжесткость системы ОДУ. В качестве соответствующей характеристики выбирают матрицу Якоби (якобиан) векторной функции F(t,y), т.е. функциональную матрицу, составленную из производных F(t,y) (см. разд. «Частныепроизводные» гл. 7). Чем вырожденнее матрица Якоби, тем жестче системауравнений. В приведенном примере определитель якобиана и вовсе равеннулю при любых значениях у 0 , YI и у 2 (листинг 11.13, вторая строка). В первой строке листинга 11.13 приведено напоминание способа вычисленияякобиана средствами MathCAD на примере определения элементов его первой строки.
Листинг 11.13. Якобиан рассматриваемой системы ОДУ химической кинетики

Для примера, приведенного в листинге 11.12, стандартным методом Рунге-Кутты все-таки удается найти решение (оно показано на рис. 11.18). Однакодля этого требуется очень большое число шагов, м=20000, что делает расчетыочень медленными. При меньшем числе шагов численному алгоритму неудается найти решение. В процессе работы алгоритма оно расходится, и
MathCAD вместо результата выдает ошибку о превышении предельно большого числа.
Еще один факт, на который стоит обратить внимание, — это различие в порядке величины получающегося решения. Как видно из рис. 11.18, концентрация первого реагента yi существенно (в тысячи раз) превышает концентрацию остальных. Это свойство также очень характерно для жесткихсистем.

Примечание
В принципе, можно было бы снизить жесткость системы «вручную», применяямасштабирование. Для этого нужно искусственно уменьшить искомую функциюyi, к примеру, в тысячу раз, разделив все слагаемые в системе ОДУ, содержащие yi, на 1000. После масштабирования для решения полученной системыметодом Рунге-Кутты будет достаточно взять всего м=20 шагов.

Рис. 11.19. Решение более жесткой системы ОДУ химической кинетики методом Розенброка
Обратите внимание, что порядки величины решений для концентраций различных веществ на рис. 11.19 различаются еще сильнее, чем в предыдущем(менее жестком) примере.

Примечание
Это еще раз доказывает, что одна и та же система ОДУ с различными коэффициентами может быть жесткой в разной степени. В частности, приведенныйвыше пример генератора Ван дер Поля с параметром ц=5000 — это уже пример жесткой задачи.

В заключение приведем встроенные функции, которые применяются длярешения жестких систем ОДУ не на всем интервале, а только в одной заданной точке ti.
— stiffb(yO,to,ti,acc,F, j, k, s) — метод Булирша-Штера- stiffr (yO,to,ti,acc,F, J,k,s) — метод Розенброка
Имена этих функций пишутся с маленькой буквы, а их действие и наборпараметров полностью аналогичны рассмотренным нами ранее для функций, относящихся к решению в заданной точке нежестких систем (см. разд. 11.3.2). Отличие заключается в специфике применяемого алгоритма и необходимости задания матричной функции якобиана J(t,y).

Создание моделей в программе Mathcad

МИНИСТЕРСТВО ЗДРАВООХРАНЕНИЯ РЕСПУБЛИКА УЗБЕКИСТАН

ФЕРГАНСКИЙ ФИЛИАЛ ТАШКЕНТСКОЙ МЕДИЦИНСКОЙ АКАДЕМИИ

КАФЕДРА «БИОФИЗИКИ, БИОХИМИИ И ИНФОРМАЦИОННЫХ

ТЕХНОЛОГИИ»

«Создание моделей в программе Mathcad»

(учебное методическое пособие)

Фергана 2020

Это методическое пособие предназначено для студентов в области лечебное дело, медико-профилактическое дело, биомедицинское инженерия по предмету информационные технологии в медицине для моделирования медицинских задач и их решение в области информационных технологий в медицине.

— старший преподаватель кафедры «Биофизики, биохимии и информационных технологий»

Ферганского филиала ТМА

— Профессор Ферганского филиала Ташкентского университета информационных технологий имени Мухаммеда Аль Хорезми.

— Профессор кафедры «Биофизики, биохимии и информационные технологии» Ферганского филиала ТМА.

Данное пособие обсуждалось на заседании кафедры «Биофизики, биохимии и информационных технологий» и рекомендовано к рассмотрению не УМС Ферганского филиала ТМА.

Протокол №______ “____” ________ 2020 г.

Данное пособие было рассмотрено и одобрено Советом Ферганского филиала TМA.

Протокол №_______ “____” _______ 2020 г.

Модель Ло́тки — Вольтерра́ (Хищник-Жертва). 7

Алгоритм выполнения работы. 8

Варианты заданий. 14

Модель спроса-предложения. 15

Содержательная постановка задачи. 15

Концептуальная постановка. 15

Математическая постановка. 16

Решение задачи. 16

Решения задачи на MathCAD. 17

Варианты заданий. 18

Модель динамики численности популяции. 19

Содержательная постановка задачи. 20

Концептуальная постановка задачи. 20

Математическая постановка задачи для модели Мальтуса. 20

Решение задачи. 21

Математическая постановка задачи для модели Ферхюльста. 21

Решение задачи. 22

Реализации задачи на MathCAD. 22

Варианты заданий. 24

Метод Эйлера. 24

Реализация метода на MathCAD. 25

Варианты заданий. 26

Нелинейный осциллятор Ван дер Поля. 27

Реализация уравнения на MathCAD. 29

Вычислительный блок Given/Odesolve. 30

Варианты заданий. 31

Аттрактор Лоренца. 31

Реализация аттрактора на MathCAD. 32

Варианты заданий. 36

Список использованной литературы. 37

Введение

В данной работе рассмотрены реализации математических методов и моделей в пакете MathCAD. В конце каждой главы даётся по 20 однотипных заданий для самостоятельного решения. Характерной особенностью пакета MathCAD является использование привычных стандартных математических обозначений, то есть документ на экране выглядит точно так же обычный математический расчет. Для использования пакета не требуется изучать какую-либо систему команд, как, например, в случае пакетов Mathematica или Maple. Пакет ориентирован в первую очередь на проведение численных расчетов, но имеет встроенный символический процессор Maple, что позволяет выполнять аналитические преобразования. В последних версиях предусмотрена возможность создавать связки документов Mathcad с документами Mathlab. В отличие от упомянутых выше пакетов, Mathcad является средой визуального программирования, то есть не требует знания специфического набора команд.

Для начала вычислений в среде MathCAD необходимо познакомится с элементами управления. Как и в аналогичных windows приложениях, имеется возможность сохранить результат вычислений, либо открыть предыдущий проект, в разделе Файл (File), выбрав соответствующие команды. Интерфейс приложения крайне прост в освоении. Но для более удобной работы в MathCAD необходимо настроить панель инструментов, выбрав оттуда все необходимые для работы панели, и расположив их на экране наиболее удобным образом (в последствии программа запомнит расположение этих элементов, и при старте они будут появляться там, где вы их определите). Для этого откроем вкладку Вид-> Панель инструментов и установим флажки напротив необходимых компонентов:

Далее в процессе работы мы познакомимся с ними подробнее.

Модель Ло́тки — Вольтерра́ (Хищник-Жертва)

Модель Лотки — Вольтерра (более правильным является произношение Вольте́рры, однако этот вариант мало распространён в русском языке) — модель межвидовой конкуренции, названная в честь её авторов — (Лотка, 1925; Вольтерра 1926), которые предложили модельные уравнения независимо друг от друга.

Такие уравнения можно использовать для моделирования систем «хищник-жертва», «паразит-хозяин», конкуренции и других видов взаимодействия между двумя видами (Одум, 1986)

В математической форме предложенная система имеет следующий вид:

где: — количество жертв,

, , , — коэффициенты, отражающие взаимодействия между видами.

Два дифференциальных уравнения моделируют временную динамику численности двух биологических популяций жертвы Y0 и хищника Y1. Предполагается, что жертвы размножаются с постоянной скоростью C, а их численность убывает вследствие поедания хищниками. Хищники же размножаются со скоростью, пропорциональной количеству пищи (с коэффициентом r), и умирают естественным образом (смертность определяется константой D). Рассчитаем три решения D, G, P для разных начальных условий.

Алгоритм выполнения работы:

1. Создаём новый файл MathCAD’ a: — меню Файл->Создать-

> в появившимся окне выбираем первый параметр — Чистый рабочий лист, и нажимаем кнопку ОК.

2. Наводим курсор на то место, где собираемся объявить начальные значения параметров:

3. Нажимаем клавишу C, затем вводим двоеточие : и знак равно = , на экране появится следующее:

Это значит что MathCAD ожидает ввода значения переменной С, вводим значение 0.1, выводим курсор с области рамки, и нажимаем левую кнопку мыши. Значение задано.

Примечание: Иногда пользовательские переменные предопределяют встроенные константы в MathCAD (появляется зеленая волнистая линия подчеркивания), на результате вычислений это не сказывается, но если вы собирались использовать их в программе, вам следует задать другое имя переменной.

4. Аналогичным образом задаём значения параметрам D и r:

5. Далее задаём функцию F c аргументами t и y: нажимаем клавишу F, открываем круглые скобки клавишей (, нажимаем клавишу t, затем ставим запятую , и вводим аргумент y нажатием соответствующей клавиши, закрываем скобку кнопкой ), ставим двоеточие :

5. Открываем вкладку Вид->Панель инструментов>Матрицы появится окошко с соответствующими методами для работы:

6. Нажимаем на кнопку «Матрица или вектор»:

7. В появившимся окне задаём количество строк равным двум, и один столбец, нажимаем клавишу ОК.

8. В появившихся скобках записываем первое уравнение:

9. Нажимаем клавишу С, затем умножить * вводим y с индексом ноль, для этого после того как вы ввели y, нажмите на иконку «Нижний индекс» в окошке «Матрица»:

Нажмите стрелку «вправо», для того чтобы продолжить запись уравнения вне рамках нижнего индекса. Далее введите: — r * y с индексом

0 умноженное на y с индексом 1, проделанным ранее способом.

10. Нажмите левой кнопкой мыши по черному квадрату расположенному чуть нижу первого уравнения:

Появится синий курсор, это означает, что вы можете продолжать ввод второго уравнения.

11. Уже известным вам способом запишите второе уравнение, чтобы функция выглядела следующим образом:

12. Далее зададим значения параметрам:

Примечание: Здесь t0 и t1 не имеют нижних индексов, а просто 1 и 0 просто разные обозначения двух переменных.

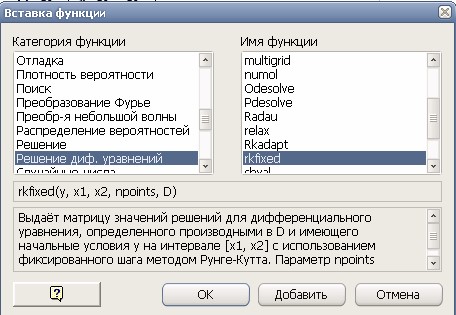
13. Затем, внутри переменной D вызовем функцию rkfixed, производящую вычисление дифференциального уравнения по методу Ренге-Кутта. Для этого во вкладке Добавить, выберем строку Функцию, в появившемся окне Вставка функций выберем Решение диф. уравнений в разделе Категория функции и rkfixed в разделе Имя функции, нажмём кнопку ОК:

14. Появится следующая строка:

Далее в окошке Матрица нажимаем на кнопку Матрица или векторы, задаём количество строк равным двум, а столбцов равным единице:

15. Приводим строку к следующему виду:

16. Аналогичным образом создаём переменные G и P со следующими значениями:

17. Для того чтобы MathCAD численно решил дифференциальные уравнения с параметрами из переменной D, необходимо ввести имя переменной D и знак равно, и щелкнуть кнопкой мыши на пустой рабочей области. Решение будет выглядеть так:

18. Далее нам нужно построить график функции. Для этого, во вкладке Вид выберем Панели инструментов > Графики. В появившемся окошке нажмём на кнопку Х-У график:

Появится следующая заготовка:

19. По оси х, введём переменную D, затем нажмём в окошке Матрица кнопку столбец матрицы:

В появившиеся сверху скобки внесём значение единица 1:

20. Далее поставим синий курсор справа перед D, нажмём пробел и введём следующие значения, аналогичным образом заполним пустующие поля по оси y, график должен иметь вид:

Нажав левой кнопкой мыши на пустую рабочую область, и немного подождав, получим следующий фазовый портрет (справа) системы «хищник—жертва»:

21. Для получения графика решения, проделаем описанные выше операции, но уже с другими параметрами, по оси х, введём D c нулевым столбцом матрицы, а по оси у – D с первым и вторым столбцами матрицы. Получим следующий график:

Модель замечательна тем, что в такой системе наблюдаются циклическое увеличение и уменьшение численности и хищника, и жертвы, так часто наблюдаемое в природе. Фазовый портрет системы представляет собой концентрические замкнутые кривые, окружающие одну стационарную точку, называемую центром. Как видно, модельные колебания численности обеих популяций существенно зависят от начальных условий — после каждого периода колебаний система возвращается в ту же точку. Динамические системы с таким поведением называют негрубыми.

Варианты заданий:

Произвести вычисление модели Хищник-Жертва на MathCAD’е в соответствие с вышеуказанным способом, используя нижеследующие параметры получить график решения и фазовый портрет модели:

Модель спроса-предложения

Содержательная постановка задачи

Представим себя на месте некоего фермера, который каждый год выращивает на своем поле пшеницу на продажу. Запасов, которые хранились бы больше года, он не делает. То есть живет если и не одним днем, то одним годом.

Решение о том, сколько пшеницы сеять, принимается простейшим образом, с учетом цен предыдущего года, а именно: если цены были высокие – в этом году надо сеять пшеницы больше, а если низкие – меньше. Спрос на пшеницу в течение года зависит прежде всего от ее цены в момент продажи. Когда цена растет, спрос, естественно, падает. И наоборот. Необходимо описать поведение цен в ближайшие годы как функцию от первоначальной цены.

Концептуальная постановка

• pn – цена за единицу веса пшеницы в n-м году

• sn – предложение (объем выращенной фермером пшеницы)

пшеницы в n-й год (в единицах веса);

• dn – спрос на пшеницу в n-й год (в единицах веса). Примем следующие предпосылки.

• Объектом исследования является зависимость цены pn на пшеницу от ее первоначальной цены p0.

• Предположим, что предложение sn+1 будущего года зависит линейно от цены pn в этом году: чем выше pn, тем больше sn+1 . Очевидно, что цена на пшеницу не должна быть меньше некоторой минимальной величины, покрывающей затраты на ее производство, лишь в этом случае величина предложения sn+1 будет больше нуля.

• Предположим, что спрос будущего года dn+1 зависит линейно от цены pn+1 в том же году: чем выше цена pn+1, тем меньше спрос dn+1.

Очевидно, что самый большой спрос на пшеницу должен существовать при pn+1=0.

• Предположим, что рыночная цена pn+1определяется равновесием между спросом dn+1и предложением sn+1. Требуется описать поведение цен в последующие годы p1, p2, p3, . в зависимости от значения цены p0.

Математическая постановка

Здесь a, b, c, g — положительные вещественные числа. Значения этих величин характеризуют динамику цены на рынке и специфичны для каждого продукта, например, отношение b/a характеризует минимально допустимую цену, а величина g — максимально возможный спрос; p0 задано.

Решение задачи

Подставляя (1) и (2) в (3), получим:

Введем новые положительные константы:

A = a/c>0, B = (b/c + g/c) > 0

Приходим к соотношению:

Это уравнение представляет некоторое линейное рекуррентное соотношение, которое позволяет построить последовательность интересующих нас решений p1, p2, p3, . .

Попробуем вывести общую формулу pn = f(p0). Пусть p0 задано.

Некоторая зависимость проглядывается, но вряд ли она очевидна. Но стоит умножить и разделить первое слагаемое на (1+А) – и все встает на свои места. Теперь общая формула очевидна:

Проведем расчеты для некоторых значений A и B. Предварительное изучение уравнения показывает, что основное влияние на динамику цены оказывает параметр А. Какое именно – выясним, положив В=1.

Вычислим для различных значений А изменение цены из года в год в течение 12 лет:

Решения задачи на MathCAD:

Далее уже известным вам из предыдущей лабораторной работы, способом, построим график решения задачи:

Из полученного графика видно, что не смотря на различные начальные условия цен на пшеницу х0, х1, х2, по прошествии нескольких лет цена на неё приходит к оптимальному значению в

0.66 у.е. когда спрос равен предложению.

Варианты заданий:

Произвести вычисление на MathCAD’е в соответствии вышеуказанному решению модели спроса-предложения, узнать оптимальную цену на пшеницу за определенное время, изменяя параметры:

Модель динамики численности популяции

Одним из важнейших разделов современной биологии и экологии является биология популяций. Популяцией в биологии называют сообщество особей одного вида, занимающих некоторую область пространства на нашей планете. Вопросы, которые приходится решать биологии популяций, разнообразны. Например, что получится, если поместить тысячу карасей в пруд с ограниченными пищевыми ресурсами? Что изменится, если выпустить туда еще пятьдесят щук, поедающих в среднем по два карася в день? Какая судьба постигнет вирус, вызывающий гибель определенного вида животных и распространяющийся с известной скоростью, зависящей от плотности популяции? Какими темпами будет увеличиваться численность людей на Земле? Список подобных вопросов можно продолжать и продолжать.

Характерной особенностью биологии как науки является то, что одним из основных методов исследования данной дисциплины все еще остается наблюдение. Объяснить это можно множеством причин, одной из которых является сложность формализации параметров, описывающих различные виды живых существ. В то же время отличительной чертой биологии популяций является то, что для исследования динамики популяций достаточно интенсивно используется математическое моделирование.

В природе встречаются популяции организмов как с дискретным, так и с непрерывным периодом размножения. К первым можно отнести многие виды насекомых (бабочки, майские жуки, саранча), рыб, птиц и млекопитающих с привязкой периода размножения к определенным временам года. Ко вторым относятся живые организмы, процесс размножения которых не привязан ко временам года (в первую очередь это домашние животные и человек). Модели для динамики популяций с дискретным и непрерывным периодом размножения существенно отличаются. В частности, для популяций с непрерывным периодом размножения применим аппарат дифференциального исчисления. Далее будут рассматриваться только популяции с непрерывным периодом размножения.

Первая модель динамики популяций была предложена священником Томасом Мальтусом еще в 1778 г. в опубликованной им работе “Трактат о народонаселении”. Хотя модель, предложенная Мальтусом, касалась народонаселения Земли, ее можно распространить на любую популяцию живых организмов. Рассмотрим эту модель более подробно.

Содержательная постановка задачи

Как будет изменяться численность популяции, если сдерживающие факторы (болезни, хищники, конкурирующие виды, ограниченность питания и т.п.) отсутствуют?

Концептуальная постановка задачи

Исследование популяции провести при следующих допущениях:

(1) объектом исследования является некоторая популяция организмов;

(2) сдерживающие факторы роста популяции отсутствуют;

(3) скорость прироста численности популяции прямо пропорциональна величине численности популяции.

Последние два предположения являются относительно грубыми. Их применение оправдано на довольно коротком начальном этапе развития популяции (например, при начальном развитии колонии бактерий в автоклаве при достаточно интенсивном перемешивании биомассы).

Математическая постановка задачи для модели Мальтуса

Пусть x(t) – численность популяции в момент времени t. Функцией прироста R(t) называют относительное изменение численности за время

Если эта величина – некоторая константа r, то закон, управляющий динамикой численности популяции в модели Мальтуса, имеет вид:

Переходя к пределу при ∆t → 0, получим следующее обыкновенное дифференциаль-ное уравнение (1):

Итак, для решения поставленной задачи необходимо найти решение уравнения (1) при начальном условии (2):

Решение задачи

Для решения уравнения (1) можно воспользоваться методом разделения переменных:

Окончательно имеем (1):

Полученное по модели Мальтуса решение (1) предсказывает неограниченный рост численности популяции по экспоненциальному закону. В действительности неограниченный рост невозможен, так как сдерживающие факторы присутствуют всегда. Численность популяции, как правило, испытывает небольшие колебания относительно некоторой величины.

Одним из первых обратил на это внимание П.Ф. Ферхюльст, сформулировав в 1845 г. закон, содержащий ограничение на рост популяции. Он объяснил это тем, что любая экологическая ниша можетобеспечить существование популяции только определенного максимального размера xmax и что коэффициент прироста должен сни- жаться, когда размеры популяции приближаются к xmax. Будем

измерять численность популяции в относительных единицах:

Тогда функцию прироста по Ферхюльсту можно записать следующим образом (2):

С учетом (1) запишем математическую постановку задачи для модели Ферхюльста.

Математическая постановка задачи для модели Ферхюльста

Найти решение задачи Коши (3):

при начальных условиях:

Решение задачи

Уравнение (3) можно проинтегрировать методом разделения переменных:

в результате чего получим решение:

Реализации задачи на MathCAD:

Примечание: Для установки переменного значения t, следует открыть вкладку Вид, Панель управления, Матрица и нажать на кнопку «Область переменной»:

Параметр e, в функции X(t, N) – экспонента, для её вставки необходимо открыть вкладку Вид, Панель инструментов, Калькулятор, и нажать кнопку «Экспонента»:

Далее создаём график, следующего вида:

На созданном нами выше, графике, показано изменение относительной численности популяции во времени при различных начальных значениях N0 и r (условие N0 > 1 возможно, если в период времени до начала рассмотрения изменения популяции окружающие условия были более благоприятны для нее).

Варианты заданий:

Произвести вычисление на MathCAD’е, в соответствии с вышеуказанной моделью изменяя начальные параметры: