Ван дер Ваальса закон калькулятор
| Решите для | Уравнения |
|---|---|
| P | 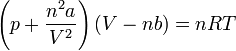 |
| T | 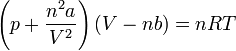 |
| n | 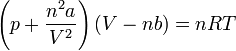 |
| V | 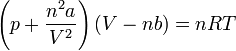 |
Ван дер Ваальса закон калькулятор представляет собой мощный онлайновый инструмент для решения задач с использованием Ван дер Ваальса закона уравнением. Выберите количество, чтобы решить для и одна из Ван дер Ваальса закона уравнениями в использовании. Форма для ввода всех известных газа и агрегатов будет представлена. Введите значение и нажмите вычисления, чтобы увидеть шаг за шагом Ван дер Ваальса закона раствором.
Feel free to ask for help with your Ван дер Ваальса закона problem in chemistry forum.
Van der Waals Calculator
Easily calculate the pressure, volume, temperature or quantity in moles of a gas using this Van der Waals equation calculator. Supports a variety of input metrics such as Celsius, Fahrenheit, Kelvin, Pascals, bars, atmospheres, and volume in both metric and imperial units cubed.
Related calculators
This is a gas law calculator which incorporates the van der Waals equation into one easy to use tool you can use as a:
- gas pressure calculator
- gas volume calculator
- gas quantity calculator
- gas temperature calculator
The van der Waals equation is a better approximation to a real gas than the ideal gas law (see «Applicability» below). To use the Van der Waals calculator, enter the three known measures and the two substance-specific constants to calculate the fourth measure. The calculator uses the combined gas law formula discussed below to perform the computations. The Van der Waals equation calculator also supports both imperial and metric units for volume and pressure and 5 different temperature scales: Kelvin, Celsius, Fahrenheit, Rankine and Reamur, both as input and as output.
The units supported by the gas law calculator for volume are: mm 3 , cm 3 , m 3 , ml, L (litre), gallons, fluid ounces, cubic inches, cubic feet and cubic yards. Units supported for pressure are Pascals, kiloPascals, MegaPascals, GigaPascals, milibars, bars, atmospheres, millimeters of Hg liquid, millimeters of H2O liquid, and pound-force per squared inches (psi).
The Van der Waals equation is an expansion of the ideal gas law formula used for ideal gas law calculation which accounts for the volume of real gas molecules and for the molecular attraction forces which make real gases more compressible than an ideal gas. This first is achieved by replacing V with (Vm — b) in the ideal gas formula where b is the volume occupied by one mole of the particular molecule (a.k.a. repulsion parameter) and Vm is the molar volume. The second is achieved by adding to the observed pressure a a / Vm 2 term in which a is a constant which depends on the particular gas and is sometimes referred to as an «attraction parameter».
The above substitutions in the PV = nRT formula lead to the formula (P + a / Vm 2 )(Vm — b) = RT which through simple transformation can be expressed in the more familiar form of the Van der Waals equation:
where P is the pressure in Pascals, V is the volume in m 3 , n is the quantity in moles, T is the absolute temperature in Kelvins and finally R is the universal gas constant, a is the aforementioned substance-specific constant. R is equivalent to the Boltzmann constant, but expressed in units of energy per temperature increment per mole (the pressure–volume product). In SI based units it is 8.3144598(48) kg⋅m 2 ⋅mol −1 ⋅K −1 ⋅s −2 . A mole is the amount of substance which contains as many elementary entities as there are atoms in 12 g of carbon-12.
This is the formula used in our Van de Waals equation calculator, so make sure you understand all inputs correctly.
Understanding the applicability of the formula will help you determine when using a Van der Waals calculator is appropriate. The van der Waals equation is considered reasonable for liquid and low-pressure gaseous states below the critical temperature of the gas or liquid in question. It is an even more significant improvement over the ideal gas law for temperatures above the critical (The critical temperature of a substance is such that at and above it vapor of the substance cannot be liquefied, regardless of the amount of pressure being applied).
The equation diverges from experimental behavior when the liquid phase and a gas phase would be in equilibrium (vapor–liquid equilibrium). Such «metastable» states are qualitatively (though likely not quantitatively) predicted by the van der Waals equation of state. Empirically-based corrections can be used such as the Maxwell’s correction, at the cost of simplicity. The van der Waals equation is still used in textbooks as a pedagogic tool for understanding vapor–liquid behavior and equations of state. Some other, more accurate equations of state such as the Redlich–Kwong and Peng–Robinson equation of state are simply modifications of the van der Waals equation.
[1] NIST Special Publication 330 (2008) — «The International System of Units (SI)», edited by Barry N.Taylor and Ambler Thompson, p. 52
[2] «The International System of Units» (SI) (2006, 8th ed.). Bureau international des poids et mesures pp. 142–143. ISBN 92-822-2213-6
2.5. Уравнение Ван-дер-Ваальса
Уравнение Клапейрона — Менделеева следует из молекулярно-кинетической теории в предположении идеальности газа. Если мы хотим описывать поведение реальных систем, надо учесть взаимодействие молекул между собой. Точный учет межмолекулярных сил — задача чрезвычайно трудная. Поэтому было предложено несколько модификаций уравнения состояния идеального газа, которые могли бы учесть основные особенности реальных систем. Наиболее удачной попыткой стало уравнение Ван-дер-Ваальса, при получении которого вносились поправки в уравнение состояния идеального газа
В подходе Ван-дер-Ваальса, во-первых, принимается во внимание, что молекулы имеют конечные размеры. Если обозначить собственный объем всех молекул в моле вещества буквой b, то для движения молекул остается свободный объем
и именно он должен фигурировать в уравнении состояния. Во-вторых, учитывается, что молекула, подлетающая к стенке сосуда, «чувствует» притяжение других молекул, которое уравновешивалось, когда молекула была внутри сосуда. Дополнительная сила, направленная внутрь сосуда, эквивалентна дополнительному давлению pi, (его называют «внутренним» давлением газа). Поэтому вместо давления р газа на стенки сосуда уравнение состояния должно содержать сумму р+рi.
Как зависит внутреннее давление pi от параметров системы? Сила, действующая на каждую молекулу, пропорциональна концентрации п молекул в системе. Число подлетающих к стенке молекул также пропорционально п, и потому внутреннее давление пропорционально квадрату концентрации частиц:
Обозначая коэффициент пропорциональности буквой а, приходим к уравнению Ван-дер-Ваальса
Для одного моля вещества это уравнение упрощается:
http://www.gigacalculator.com/calculators/van-der-waals-equation-calculator.php
http://online.mephi.ru/courses/physics/molecular_physics/data/course/2/2.5.1.html




