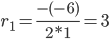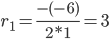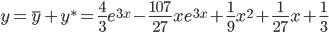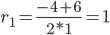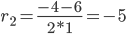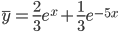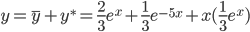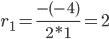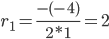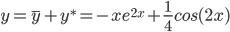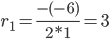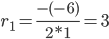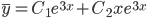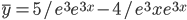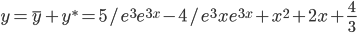Уравнение вида y py qy 0

Пример решения дифференциального уравнения

Решение находим с помощью сервиса линейные дифференциальные уравнения с постоянными коэффициентами.
Данное дифференциальное уравнение относится к линейным дифференциальным уравнениям с постоянными коэффициентами.
Решение уравнения будем искать в виде y = e rx . Для этого составляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами:
r 2 -6 r + 9 = 0
D = (-6) 2 — 4·1·9 = 0


Корни характеристического уравнения:
Корень характеристического уравнения r₁ = 3 кратности 2.
Следовательно, фундаментальную систему решений составляют функции:
y₁ = e 3x , y₂ = xe 3x
Общее решение однородного уравнения имеет вид: y = C₁·e 3x +C₂·x·e 3x
Найдем частное решение при условии:y(0) = 4/3, y'(0) = 1/27
Поскольку y(0) = c1, то получаем первое уравнение:
c1 = 4/3
Находим первую производную:
y’ = 3·c1·e 3·x +3·c2·x·e 3·x +c2·e 3·x
Поскольку y'(0) = 3·c1+c2, то получаем второе уравнение:
3·c1+c2 = 1/27
В итоге получаем систему из двух уравнений:
c1 = 4/3
3·c1+c2 = 1/27
т.е.:
c₁ = 4 /₃, c₂ = -107 /₂₇
Тогда частное решение при заданных начальных условиях можно записать в виде:

Рассмотрим правую часть:
f(x) = x 2 -x+3
Поиск частного решения.
Линейное дифференциальное уравнение с постоянными коэффициентами и правой частью вида:
R(x) = e αx (P(x)cos(βx) + Q(x)sin(βx)), где P(x), Q(x) — некоторые полиномы
имеет частное решение
y(x) = x k e αx (R(x)cos(βx) + S(x)sin(βx))
где k — кратность корня α+βi характеристического полинома соответствующего однородного уравнения, R(x), S(x) — полиномы, подлежащие определению, степень которых равна максимальной степени полиномов P(x), Q(x).
Здесь P(x) = x 2 -x+3, Q(x) = 0, α = 0, β = 0.
Следовательно, число α + βi = 0 + 0i не является корнем характеристического уравнения.
Уравнение имеет частное решение вида: y*=A·x 2 +B·x+C
Вычисляем производные:
y’ = 2·A·x+B
y″ = 2·A
которые подставляем в исходное дифференциальное уравнение:
y″ -6y’ + 9y = (2·A) -6(2·A·x+B) + 9(Ax 2 + Bx + C) = x 2 -x+3
или
9·A·x 2 -12·A·x+2·A+9·B·x-6·B+9·C = x 2 -x+3
Приравнивая коэффициенты при одинаковых степенях х, получаем систему уравнений:
9A = 1
-12A + 9B = -1
2A -6B + 9C = 3
Решая ее, находим:
A = 1 /₉;B = 1 /₂₇;C = 1 /₃;
Частное решение имеет вид:
y * = 1 /₉x 2 + 1 /₂₇x + 1 /₃
Таким образом, общее решение дифференциального уравнения имеет вид:

Пример №2. y″ +4y’ — 5y = 2·e x

Решение:
Данное дифференциальное уравнение относится к линейным дифференциальным уравнениям с постоянными коэффициентами.
Решение уравнения будем искать в виде y = e rx . Для этого составляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами:
r 2 +4 r — 5 = 0
D = 4 2 — 4·1·(-5) = 36


Корни характеристического уравнения:
r₁ = 1
r₂ = -5
Следовательно, фундаментальную систему решений составляют функции:
y₁ = e x
y₂ = e -5x
Общее решение однородного уравнения имеет вид: y = C₁·e 3x +C₂·e -5x
Найдем частное решение при условии:y(0) = 1, y'(0) = -1
Поскольку y(0) = c1+c2, то получаем первое уравнение:
c1+c2 = 1
Находим первую производную:
y’ = c1·e x -5·c2·e -5·x
Поскольку y'(0) = c1-5·c2, то получаем второе уравнение:
c1-5·c2 = -1
В итоге получаем систему из двух уравнений:
c1+c2 = 1
c1-5·c2 = -1
которую решаем или методом матриц или методом исключения переменных.
c₁ = 2 /₃, c₂ = 1 /₃
Тогда частное решение при заданных начальных условиях можно записать в виде:

Рассмотрим правую часть:
f(x) = 2·e x
Поиск частного решения.
Линейное дифференциальное уравнение с постоянными коэффициентами и правой частью вида:
R(x) = e αx (P(x)cos(βx) + Q(x)sin(βx)), где P(x), Q(x) — некоторые полиномы
имеет частное решение
y(x) = x k e αx (R(x)cos(βx) + S(x)sin(βx))
где k — кратность корня α+βi характеристического полинома соответствующего однородного уравнения, R(x), S(x) — полиномы, подлежащие определению, степень которых равна максимальной степени полиномов P(x), Q(x).
Здесь P(x) = 2, Q(x) = 0, α = 1, β = 0.
Следовательно, число α + βi = 1 + 0i является корнем характеристического уравнения кратности k = 1(r₁).
Уравнение имеет частное решение вида: y*=A·x 2 +B·x+C
Вычисляем производные: y’ = A·e x (x+1)
y″ = A·e x (x+2)
которые подставляем в исходное дифференциальное уравнение:
y″ + 4y’ -5y = (A·e x (x+2)) + 4(A·e x (x+1)) -5(x (Ae x )) = 2·e x
или
6·A·e x = 2·e x
Приравнивая коэффициенты при одинаковых степенях х, получаем систему уравнений:
6A = 2
Решая ее, находим:
A = 1 /₃;
Частное решение имеет вид:
y * = x ( 1 /₃e x )
Таким образом, общее решение дифференциального уравнения имеет вид:

Пример №3. y″ — 4y’ + 4y = 2sin(2x), y(0) = 0. y'(0) = -1

Решение:
Решение уравнения будем искать в виде y = e rx . Для этого составляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами:
r 2 -4 r + 4 = 0
D = (-4) 2 — 4·1·4 = 0


Корни характеристического уравнения:
Корень характеристического уравнения r₁ = 2 кратности 2.
Следовательно, фундаментальную систему решений составляют функции:
y₁ = e 2x
y₂ = xe 2x
Общее решение однородного уравнения имеет вид: y = C₁·e 2x +C₂·x·e 2x
Найдем частное решение при условии:y(0) = 0, y'(0) = -1
Поскольку y(0) = c1, то получаем первое уравнение:
c1 = 0
Находим первую производную:
y’ = 2·c1·e 2·x +2·c2·x·e 2·x +c2·e 2·x
Поскольку y'(0) = 2·c1+c2, то получаем второе уравнение:
2·c1+c2 = -1
В итоге получаем систему из двух уравнений:
c1 = 0
2·c1+c2 = -1
т.е.:
c₁ = 0, c₂ = -1
Тогда частное решение при заданных начальных условиях можно записать в виде:
y =-x·e 2x
Рассмотрим правую часть: f(x) = 2·sin(2·x)
Поиск частного решения.
Здесь P(x) = 0, Q(x) = 2, α = 0, β = 2.
Следовательно, число α + βi = 0 + 2i не является корнем характеристического уравнения .
Уравнение имеет частное решение вида: y * = Acos(2x) + Bsin(2x)
Вычисляем производные:
y’ = 2·B·cos(2x)-2·A·sin(2x)
y″ = -4(A·cos(2x)+B·sin(2x))
которые подставляем в исходное дифференциальное уравнение:
y″ -4y’ + 4y = (-4(A·cos(2x)+B·sin(2x))) -4(2·B·cos(2x)-2·A·sin(2x)) + 4(Acos(2x) + Bsin(2x)) = 2·sin(2·x)
или
8·A·sin(2x)-8·B·cos(2x) = 2·sin(2·x)
Приравнивая коэффициенты при одинаковых степенях х, получаем систему уравнений:
8A = 2
0A -8B = 0
Решая ее, находим:
A = 1 /₄;B = 0;
Частное решение имеет вид:
y * = 1 /₄cos(2x) + 0sin(2x)
или
y * = 1 /₄cos(2x)
Таким образом, общее решение дифференциального уравнения имеет вид:

Пример №4. Найти частное решение, общее решение и решение задачи Коши уравнения: y″ — 6y’ + 9y = 9x 2 +6x + 2, y(1) = 1, y'(1) = -1

Решение:
Решение уравнения будем искать в виде y = e rx . Для этого составляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами:
r 2 -6 r + 9 = 0
D = (-6) 2 — 4·1·9 = 0


Корни характеристического уравнения:
Корень характеристического уравнения r₁ = 3 кратности 2.
Следовательно, фундаментальную систему решений составляют функции:
y₁ = e 3x
y₂ = xe 3x
Общее решение однородного уравнения имеет вид:

Найдем частное решение при условии:y(1) = 1, y'(1) = -1
Поскольку y(1) = c1·e 3 +c2·e 3 , то получаем первое уравнение:
c1·e 3 +c2·e 3 = 1
Находим первую производную:
y’ = 3·c1·e 3·x +3·c2·x·e 3·x +c2·e 3·x
Поскольку y'(1) = 3·c1·e 3 +4·c2·e 3 , то получаем второе уравнение:
3·c1·e 3 +4·c2·e 3 = -1
В итоге получаем систему из двух уравнений:
c1·e 3 +c2·e 3 = 1
3·c1·e 3 +4·c2·e 3 = -1
которую решаем или методом матриц или методом исключения переменных.
c₁ = 5/e 3 , c₂ = -4/e 3
Тогда частное решение при заданных начальных условиях можно записать в виде:

Рассмотрим правую часть:
f(x) = 9·x 2 +6·x+2
Поиск частного решения.
Здесь P(x) = 9·x 2 +6·x+2, Q(x) = 0, α = 0, β = 0.
Следовательно, число α + βi = 0 + 0i не является корнем характеристического уравнения .
Уравнение имеет частное решение вида: y*=A·x 2 +B·x+C
Вычисляем производные:
y’ = 2·A·x+B
y″ = 2·A
которые подставляем в исходное дифференциальное уравнение:
y″ -6y’ + 9y = (2·A) -6(2·A·x+B) + 9(Ax 2 + Bx + C) = 9·x 2 +6·x+2
или
9·A·x 2 -12·A·x+2·A+9·B·x-6·B+9·C = 9·x 2 +6·x+2
Приравнивая коэффициенты при одинаковых степенях х, получаем систему уравнений:
9A = 9
-12A + 9B = 6
2A -6B + 9C = 2
Решая ее, находим:
A = 1;B = 2;C = 4 /₃;
Частное решение имеет вид:
y * = x 2 + 2x + 4 /₃
Таким образом, общее решение дифференциального уравнения имеет вид:

Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами

Данная статья рассматривает способы решения линейных дифференциальных однородных уравнений второго порядка с постоянными коэффициентами вида y » + p y ‘ + q y = 0 с p и q являющимися действительными числами. Будет рассмотрена теория с приведением примеров с подробным решением.

Перейдем к формулировке теоремы, которая показывает, какого вида должно быть уравнение, чтобы можно было искать общее решение ЛОДУ.

Теорема общего решения линейного однородного дифференциального уравнения

Общим решением линейного однородного дифференциального уравнения вида y ( n ) + f n — 1 ( x ) · y ( n — 1 ) + . . . + f 0 ( x ) · y = 0 с непрерывными на интервале интегрирования x коэффициентами f 0 ( x ) , f 1 ( x ) , . . . , f n — 1 ( x ) определяют линейную комбинацию вида y 0 = ∑ j = 1 n C j · y j , где y j , j = 1 , 2 , . . . , n являются линейно независимыми частными решениями ЛОДУ на интервале x , где C j , j = 1 , 2 , . . . , n берут за произвольные постоянные.

Отсюда получаем, что общее решение такого уравнения y » + p y ‘ + q y = 0 может быть записано как y 0 = C 1 ⋅ y 1 + C 2 ⋅ y 2 , где y 1 и y 2 выражаются линейно независимыми решениями, а С 1 и C 2 – произвольными постоянными. Необходимо поработать с нахождением частных решений y 1 и y 2 .

Существует формула по Эйлеру для поиска частных решений вида y = e k · x .

Если взять y = e k · x за частное решение ЛОДУ второго порядка с постоянными коэффициентами y » + p y ‘ + q y = 0 , тогда, используя подстановку, получим тождество вида:

e k · x » + p · e k · x ‘ + q · e k · x = 0 k 2 · e k · x + p · e k · x + q · e k · x = 0 e k · x · ( k 2 + p · k + q ) = 0 k 2 + p · k + q = 0

Данное тождество называют характеристическим уравнением с постоянными коэффициентами k 1 и k 2 , которые и являются его решениями и определяют частые решения вида y 1 = e k 1 · x и y 2 = e k 2 · x заданного ЛОДУ.

При различных значениях p и q можно получить характеристические уравнения с корнами такого вида:

1. Действительные и различные k 1 ≠ k 2 , k 1 , k 2 ∈ R .
2. Действительные и совпадающие k 1 = k 2 , = k 0 , k 0 ∈ R .
3. Комплексно сопряженную пару k 1 = α + i · β , k 2 = α — i · β .

Первый случай показывает, что решениями такого уравнения могут быть y 1 = e k 1 · x и y 2 = e k 2 · x , а общее решение принимает вид y 0 = C 1 · e k 1 · x + C 2 · e k 2 · x с постоянными коэффициентами. Функции y 1 = e k 1 · x и y 2 = e k 2 · x рассматриваются, как линейно независимыми по причине отличного от нуля определителя Вронского W ( x ) = y 1 y 2 y 1 ‘ y 2 ‘ = e k 1 · x e k 2 · x k 1 · e k 1 · x k 2 · e k 2 · x = e k 1 · x · e k 2 · x · k 2 — k 1 с действительными k 1 ≠ k 2 , k 1 , k 2 ∈ R .

Второй случай объясняет, что первым частным решением функции – это выражение y 1 = e k 0 · x . Вторым частным решением можно брать y 2 = x · e k 0 · x . Определим, что y 2 = x · e k 0 · x может являться частным решением ЛОДУ второго порядка с постоянными коэффициентами y » + p y ‘ + q y = 0 и докажем линейную независимость y 1 и y 2 .

Имеем, что k 1 = k 0 и k 2 = k 0 являются совпадающими корнями характеристического уравнения. Тогда оно примет вид k — k 0 2 = 0 ⇔ k 2 — 2 k 0 · k + k 0 2 = 0 . Отсюда следует, что y » — 2 k 0 · y ‘ + k 0 2 · y = 0 является линейным однородным дифференциальным уравнением. Необходимо подставить выражение y 2 = x · e k 0 · x для того, чтобы убедиться в тождественности:

y 2 » — 2 k 0 · y ‘ 2 + k 0 2 · y 2 = 0 x · e k 0 · x » — 2 k 0 · x · e k 0 x ‘ + k 0 2 · x · e k 0 · x = 0 e k 0 · x + k 0 · x · e k 0 x ‘ — 2 k 0 · e k 0 · x + k 0 · x · e k 0 x + k 0 2 · x · e k 0 · x = 0 ( k 0 · e k 0 · x + k 0 · e k 0 · x + k 0 2 · x · e k 0 · x — — 2 k 0 · e k 0 · x — k 0 2 · x · e k 0 · x + k 0 2 · x · e k 0 · x ) = 0 0 ≡ 0

Отсюда следует, что y 2 = x · e k 0 · x — это частное решение данного уравнения. Необходимо рассмотреть линейную независимость y 1 = e k 0 · x и y 2 = x · e k 0 · x . Чтобы убедиться в этом, следует прибегнуть к вычислению определителя Вронского. Он не должен быть равен нулю.

W ( x ) = y 1 y 2 y 1 ‘ y 2 ‘ = e k 0 · x x · e k 0 · x e k 0 · x ‘ x · e k 0 · x ‘ = = e k 0 · x x · e k 0 · x k 0 · e k 0 · x e k 0 · x · ( 1 + k 0 · x ) = = e k 0 · x · e k 0 · x · 1 + k 0 · x — k 0 · x · e k 0 · x · e k 0 · x = e 2 k 0 · x ≠ 0 ∀ x ∈ R

Можно сделать вывод, что линейно независимые частные решения ЛОДУ второго порядка с постоянными коэффициентами y » + p y ‘ + q y = 0 считаются y 1 = e k 0 · x и y 2 = x · e k 0 · x . Это подразумевает то, что решением будет являться выражение y 0 = C 1 · e k 0 · x + C 2 · x · e k 0 · x при k 1 = k 2 = k 0 , k 0 ∈ R .

Третий случай говорит о том, что имеем дело с парой комплексных частных решений ЛОДУ вида y 1 = e α + i · β · x и y 2 = e α — i · β · x .

Запись общего решения примет вид y 0 = C 1 · e α + i · β · x + C 2 · e α — i · β · x .

Функции y 1 = e a · x · cos β x и y 2 = e a · x · sin β x могут быть записаны вместо частных решений уравнения, причем с соответствующими действительной и мнимой частями. Это понятно при преобразовании общего решения y 0 = C 1 · e α + i · β · x + C 2 · e α — i · β · x . Для этого необходимо воспользоваться формулами из теории функции комплексного переменного вида. Тогда получим, что

y 0 = C 1 · e α + i · β · x + C 2 · e α — i · β · x = = C 1 · e α · x · cos β x + i · sin β x + C 2 · e α · x · cos β x — i · sin β x = = ( C 1 + C 2 ) · e α · x · cos β x + i · ( C 1 — C 2 ) · e α · x · sin β x = = C 3 · e α · x · cos β x + C 4 · e α · x · sin β x

Отчетливо видно, что С 3 и С 4 используются в качестве произвольных постоянных.

Алгоритм нахождения общего решения линейного однородного дифференциального уравнения

Алгоритм нахождения общего решения линейного однородного дифференциального уравнения 2 порядка с постоянными переменными вида y » + p y ‘ + q y = 0 :

1. Запись характеристического уравнения k 2 + p ⋅ k + q = 0 .
2. Нахождение корней характеристического уравнения k 1 и k 2 .
3. Производим запись ЛОДУ, исходя из полученных значений с постоянными коэффициентами:

• y 0 = C 1 · e k 1 · x + C 2 · e k 2 · x при k 1 ≠ k 2 , k 1 , k 2 ∈ R ;
• y 0 = C 1 · e k 0 · x + C 2 · x · e k 0 · x при k 1 = k 2 = k 0 , k 0 ∈ R ;
• y 0 = e α · x · ( C 1 · cos β x + C 2 · sin β x ) при k 1 = α + i · β , k 2 = α — i · β .

Найти общее решение заданного уравнения с постоянными коэффициентами y » + 4 y ‘ + 4 y = 0 .

Решение

Следуя алгоритму, необходимо записать характеристическое уравнение k 2 + 4 ⋅ k + 4 = 0 , после чего обозначить его корни. Получаем, что

k 2 + 4 k + 4 = 0 ( k + 2 ) 2 = 0 k 1 = k 2 = k 0 = — 2

Очевидно, что полученные корни являются совпадающими.

Ответ: Запись общего решения: y 0 = C 1 · e k 0 x + C 2 · x · e k 0 x = C 1 · e — 2 x + C 2 · x · e — 2 x .

Найти решение заданного уравнения вида y » — 5 y ‘ + 6 y = 0 .

Решение

По условию имеется ЛОДУ 2 порядка с постоянными коэффициентами. Это указывает на то, что необходимо записать характеристическое уравнение и обозначить его корни. Получим:

k 2 — 5 k + 6 = 0 D = 5 2 — 4 · 6 = 1 k 1 = 5 — 1 2 = 2 k 2 = 5 + 1 2 = 3

Видно, что корни различные и действительные. Это говорит о том, что уравнение общего вида запишется как y 0 = C 1 · e k 1 x + C 2 e k 2 x = C 1 · e 2 x + C 2 · e 3 x .

Ответ: y 0 = C 1 · e k 1 x + C 2 e k 2 x = C 1 · e 2 x + C 2 · e 3 x .

Найти общее решение дифференциального уравнения вида y » — y ‘ + 3 y = 0 .

Решение

Необходимо перейти к характеристическому уравнению ЛОДУ 2 порядка, что соответствует записи k 2 — k + 3 = 0 , после чего обозначить его корни. Тогда получим, что

D = 1 2 — 4 · 3 = — 11 k 1 = 1 + i 11 2 = 1 2 + i · 11 2 k 2 = 1 — i 11 2 = 1 2 — i · 11 2 ⇒ α = 1 2 , β = 11 2

На выходе имеем пару комплексно сопряженных корней характеристического уравнения. Отсюда следует, что общим решением является запись уравнения вида

y 0 = e a · x · ( C 1 · cos β x + C 2 · sin β x ) = = e x 2 · C 1 · cos 11 x 2 + C 2 · sin 11 2

Ответ: y 0 = e x 2 · C 1 · cos 11 x 2 + C 2 · sin 11 2 .

Линейные неоднородные дифференциальные уравнения

Линейные неоднородные дифференциальные уравнения (ЛНДУ) второго порядка с постоянными коэффициентами — это уравнения вида

Общее решение линейного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами можно записать как сумму

где \(\) — это общее решение линейного однородного уравнения с постоянными коэффициентами

Y- частное решение ЛНДУ.

В некоторых специальных случаях частное решение ЛНДУ может быть найдено методом неопределенных коэффициентов, в общем случае используют метод вариации произвольных постоянных. В данном пункте мы рассмотрим неоднородные дифференциальные уравнения с правой частью специального вида и применим метод неопределенных коэффициентов, а метод вариации произвольных постоянных будет изложен позже.

Общее решение неоднородного дифференциального уравнения второго порядка ищем в зависимости от вида правой части, то есть от функции f(x).

где \((x)\) — многочлен степени n.

Ia. Если a не является корнем характеристического уравнения, то есть

то частное решение ЛНДУ ищем в виде

где \((x)\) — многочлен степени n с постоянными коэффициентами.

(Подробно. Это значит, что если степень Р равна 0 (то есть f(x) — произведение е в какой-либо степени и некоторого числа, либо f(x) — только число (в этом случае степень e равна нулю)), то и Q — многочлен нулевой степени, то есть число. В этом случае Q=A. А — неопределенный коэффициент, который будем искать.

Если степень P равна 1 (то есть, f(x) равна произведению е в какой-либо степени и mx, где m — некоторое число, либо f(x) — только mx (если e в нулевой степени)), то и Q — многочлен первой степени, значит, его будем искать в виде Q=Ax+B, где A и B — неопределенные коэффициенты.

Если степень P — вторая (то есть, f(x) есть произведение e в какой-либо степени и mx², или f(x) — только mx² (если e в нулевой степени)), то и Q — многочлен второй степени, его будем искать в виде Q=Ax²+Bx+C, где A,B,C — неопределенные коэффициенты. И т.п.)

Iб. Если a — один из корней характеристического уравнения, то если верно только одно из равенств

, то частное решение ЛНДУ ищем в виде

Iв. Если a — кратный корень характеристического уравнения, то есть

(например, при дискриминанте, равном 0), то частное решение неоднородного дифференциального уравнения второго порядка в этом случае есть

IIa. Если a+bi не является корнем характеристического уравнения, то есть

\[a \pm bi \ne \alpha \pm \beta i,\]

то частное решение неоднородного дифференциального уравнения ищем как

где \((x),(x) — \) многочлены степени N, N — больная из степеней n и m.

IIб. Если a+bi является корнем характеристического уравнения, то есть

\[a \pm bi = \alpha \pm \beta i,\]

то для этого случая частное решение неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами ищем в виде

Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!