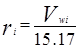Уравнение вильсона непригодно для описания

Разработка энергосберегающих технологий процесса ректификации продуктов синтеза хлорбензола

Трейдинг криптовалют на полном автомате по криптосигналам. Сигналы из первых рук от мощного торгового робота и команды из реальных профессиональных трейдеров с опытом трейдинга более 7 лет. Удобная система мгновенных уведомлений о новых сигналах в Телеграмм. Сопровождение сделок и индивидуальная помощь каждому. Сигналы просты для понимания как для начинающих, так и для опытных трейдеров. Акция. Посетителям нашего сайта первый месяц абсолютно бесплатно .

4. Моделирование парожидкостного равновесия

Выбор модели, адекватно описывающей фазовое равновесие системы, является важным и необходимым шагом при решении массообменного процесса. На сегодняшний день разработано достаточно большое число методов математического моделирования различных типов парожидкостного равновесия.

В настоящей работе на основании общих р

екомендаций по применению были выбраны три группы математических моделей, имеющих различное представление о структуре раствора и межмолекулярных взаимодействиях:

· Модели локальных составов (Wilson, NRTL, UNIQUAC);

· Уравнения состояния (SRK, Peng Robinson);

· Групповая модель (UNIFAC).

4.1. Модели локальных составов

Концепция локальных составов позволяет учитывать структуру раствора, свойства чистых веществ и межмолекулярные взаимодействия разных типов (слабые неспецифические и сильные специфические).

Согласно этой теории раствор рассматривается как упорядоченная структура.

Для бинарной смеси можно выделить молекулы двух сортов, при этом молекула одного вида находится в окружении молекул другого вида. Зависимость между концентрациями компонентов внутри такого образования с общей молярной концентрацией компонентов в растворе описывается соотношением, учитывающим вероятность возникновения связей между разноименными молекулами.

4.2. Модель Вильсона 33

Уравнение Вильсона было первым уравнением, в котором была применена концепция локального состава. Основная идея ее состоит в том, что из-за разницы в межмолекулярных взаимодействиях локальный состав вблизи конкретной молекулы в растворе будет отличаться от состава жидкости. Для бинарной пары два параметра связаны со степенью, в которой каждая молекула влияет на состав своего локального окружения. Выражение для коэффициента активности представлено ниже:

(4.2.1.)

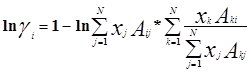
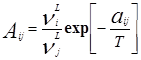
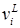
где:, (aij, °K); (4.2.2.)

– мольный объем жидкости компонента i.

Параметры aij представляет энергию взаимодействия между молекулами i и j.

Уравнение Вильсона может быть использовано в довольно широком интервале температур, несмотря на то, что его параметры в явном виде не включают температурную зависимость. Эта модель также дает хорошие результаты для смесей, содержащих полярные компоненты.

К недостаткам модели можно отнести то, что уравнение Вильсона не может описывать локальные максимумы или минимумы коэффициента активности, а также не подходит для описания равновесия с частично смешивающимися жидкими фазами.

4.3. Модель NRTL 37

Уравнение NRTL (non-random two-liquid – неслучайное двужидкостное) было разработано Реноном и Праузницем с целью использовать концепцию локального состава в тех случаях, когда уравнение Вильсона неспособно к предсказанию разделения фаз жидкость – жидкость. Модель NRTL дает хорошие результаты для широкого круга систем, в частности для смесей в высокой степени неидеальных и для частично несмешивающихся систем.

Выражение для коэффициента активности имеет вид:

(4.3.1.)

, (когда единицей измерения является °K); (4.3.2.)

(4.3.3.)

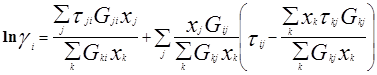
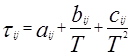
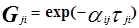
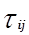
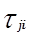
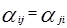
Для каждой бинарной пары требуется три параметра (, , ), которые могут быть расширены включением в них температурной зависимости.

4.4. Модель UNIQUAC 39

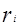
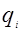
Уравнение UNIQUAC (universal quasi-chemical – универсальное квазихимическое) было развито Абрамсом и Праусницем на основании статистически-механических положений и решеточной квазихимической модели Гуггенхайма. Каждую молекулу характеризует два параметра: объем и площадь (поверхность) .

Избыточная энергия Гиббса (и соответственно логарифм коэффициента активности) делится на комбинаторную и остаточную части. Комбинаторная часть зависит только от размеров и форм отдельных молекул, она не содержит бинарных параметров. Остаточная часть, которая учитывает энергетические взаимодействия, имеет два регулируемых бинарных параметра. Выражение для коэффициента активности имеет следующий вид:

(4.4.1.)

(4.4.2.)

(4.4.3.)

(4.4.4.) (4.4.5.)

(4.4.6.) (4.4.7.)

(4.4.8.) (4.4.9.) (4.4.10.)

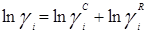
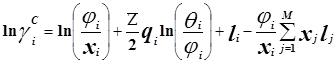
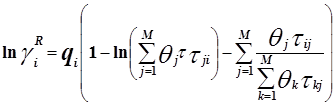
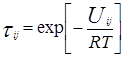
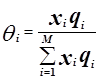
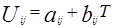
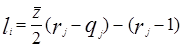
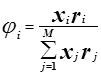
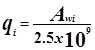
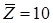
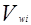
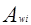
где , – объем и площадь Ван-дер-Ваальса молекулы i

С и R – комбинаторный и остаточный вклады в коэффициент активности жидкости.

Для каждой бинарной пары необходимы два параметра: Uij и Uji, которые используются в вычислениях остаточной части коэффициента активности. По желанию параметры могут быть расширены включением температурной зависимости.

Уравнение UNIQUAC адекватно описывает широкий ряд систем, оно применяется для неэлектролитических смесей, содержащих полярные или неполярные компоненты, также подходит для частично смешивающихся систем.

4.5. Уравнения состояния 42

Уравнения состояния применимы для широкого диапазона температур и давлений. Они могут быть использованы для расчетов всех термодинамических свойств, таких как К-значения, энтальпия, энтропия и плотность. Стандартным состоянием, как для жидкости, так и для пара является идеальный газ, а отклонения от идеального поведения определяются расчетом коэффициентов фугитивности для обеих фаз.

В 1972 г. для улучшения предсказания парового давления чистых компонентов и парожидкостного равновесия многокомпонентных смесей Соав предложил следующую температурную зависимость:

(4.6.1.)

(4.6.2.)

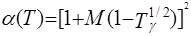
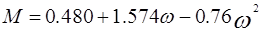
Chemicals-el.ru

» Сайт о химических элементах

Математическое моделирование фазовых равновесий

Уравнение Вильсона было предложено в 1964 году. При его разработке Вильсон исходил из того, что межмолекулярные взаимодействия зависят от «локальных концентраций», которые он выражал в объемных долях. Эти концентрации входят в вероятностные члены энергетического распределения Больцмана.

Теория локальных составов рассматривает раствор как упорядоченную структуру, в которой можно выделить для бинарной системы два вида молекулярных микроансамблей с определенным координационным числом. Один тип микроансамблей имеет в центре молекулу первого компонента, другой – молекулу второго компонента.

Согласно уравнению Вильсона избыточную энергию Гиббса можно представить следующим образом:

, (1.49)

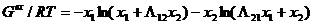
где 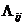– приведенные значения параметров.

Применяя уравнение (1.50):

, (1.50)

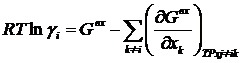
можно найти коэффициенты активности:

(1.51)

(1.52)

(1.53)

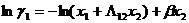
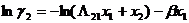
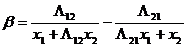
Было предпринято несколько попыток придать выводу уравнения Вильсона более строгое теоретическое обоснование и в некотором отношении улучшить его. Так, Моулрап вывел это и ряд других уравнений, используя одну из модификаций уравнения Ван-дер-Ваальса, в которой учитывается локальный состав, при этом он исходил в каждом случае из различных допущений. Нитта и Катаяма рассматривают уравнение Вильсона как вывод теории ассоциированных растворов. Цубока и Катаяма считают его частым случаем своих выкладок, предполагающим равенство молярных объемов компонентов.

Уравнение Вильсона позволяет точно представить равновесие жидкость–пар в двух- и многокомпонентных системах с использованием только параметров бинарного взаимодействия. К тому же оно отличается простотой. Еще одна положительная особенность этого уравнения состоит в том, что в нем заранее учтен температурный эффект [42].

Для представления равновесия жидкость–жидкость нельзя непосредственно применить уравнение Вильсона [4]; использование в этих целях его модификации, уравнения Цубоки–Катаямы, дает удовлетворительные результаты, хотя последнее не было подвергнуто такой тщательной экспериментальной проверке, как другие уравнения. Уравнение Вильсона положено в основу метода групповых вкладов ASOG, используемого для получения коэффициентов активности.

В [43] авторы определяли число корней уравнения Вильсона по данным о единственной бинарной точке. Термодинамический анализ этой модели с использованием парциальных избыточных функций был проведен в [44].

Уравнение NRTL (nonrandom two-liquid) для избыточной энергии Гиббса выводят, основываясь на теории, согласно которой жидкость в двухкомпонентной системы имеет ячеистую структуру, причем эти ячейки (кластеры) состоят из молекул типа 1 и 2, каждая из которых окружена такими же молекулами, которые в свою очередь имеют аналогичное окружение, и т.д.

Итоговое уравнение для избыточной энергии Гиббса имеет вид:

(1.54)

(1.55)

(1.56)

(1.57)

, (1.58)

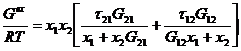
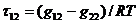
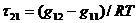
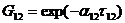
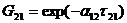
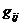
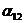
где – Гиббсовы энергии взаимодействий между молекулами, причем подстрочным индексом j указывают центральную молекулу;

– константа, принимаемая за характеристику заданности системы.

Коэффициенты активности получают дифференцированием:

(1.59)

(1.60)

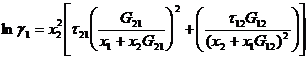
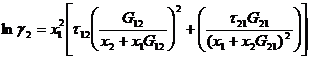
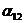
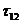
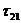
Эти уравнения содержат три независимых параметра , и .

При помощи трехпараметрического уравнения NRTL можно, как правило, достаточно хорошо представить данные о равновесии в бинарных системах. Преимущество уравнения NRTL по сравнению с уравнениями Маргулеса и ван Лаара состоит в том, что его можно применять к многокомпонентным системам, основываясь только на бинарных параметрах, а по сравнению с уравнением Вильсона – в том, что его можно использовать для представления равновесия жидкость–жидкость. Кроме того, применительно к водным системам уравнение NRTL часто превосходит другие уравнения. Однако его недостаток состоит в том, что для каждой пары составляющих необходимы три параметра.

Смотрите также

Очистка воды на ионитных фильтрах
Вода — это великая ценность, которую человек получил в дар от природы. Ее надо оберегать и уметь рационально использовать. Потребление некачественной воды может нанести непоправимый вред здо .

Кремний
Коробецкая Анастасия 10А класс КРЕМНИЙ Научный руководитель: Сукачева Т.А. Ядро: возможна большая доля силикатов Земная кора: глины, граниты, базальты, полевые шпаты. .

теорема вильсона

Рассмотрим утверждение, которое является критерием простоты числа, т. е. устанавливает необходимое и достаточное условие для того, чтобы данное натуральное число было простым. Эта теорема носит имя Вильсона, но впервые была доказана Жозефом Луи Лагранжем (Joseph Louis Lagrange). Теорема Вильсона насколько красива, настолько и бесполезна практически — факториалы растут чрезвычайно быстро*.

Теорема 1.1. (Вильсон) Если $p$ — простое число, то выполняется сравнение \begin \label (p — 1)! + 1 \equiv 0 \quad (\mathrm

а если $p$ — составное, то соотношение ($\ref$) не выполняется.

Для доказательства нам потребуется вспомогательное утверждение, которое интересно также и само по себе.

Лемма 1.1. Если $\textrm<НОД>(a, b) = 1$, то существуют целые числа $u$, $v$, такие что \begin \label au + bv = 1. \end

Доказательство. Очевидно, достаточно доказать утверждение для случая, когда $a$, $b$ — натуральные числа. Нетривиальной частью доказательства является идея индукции по сумме $a + b$. При $a + b = 2$ имеем $a = b = 1$ и (\ref) выполняется с $u = 1$, $v = 0$. Пусть теорема верна для всех $a$, $b$, таких что $\textrm<НОД>(a,b) = 1$, $a + b 2$. Тогда, так как $a + b > 2$, $\textrm<НОД>(a,b) = 1$, то $a \ne b$. Не теряя общности можно считать, что $a > b$. Поскольку, очевидно, $\textrm<НОД>(a — b, b) = 1$ и $(a — b) + b = a 1$, $b > 1$, $НОД(a, b) = 1$, то для каждого $k = 0, 1, \ldots$ существуют единственные целые числа $u$, $v$, такие, что выполняется \begin \label au — bv = 1, \end где $kb + 1 3$ (для случаев $p = 2$, $p = 3$ утверждение теоремы не трудно проверить непосредственным вычислением). Докажем, что все числа \begin \label 2, 3, \ldots , p — 2 \end

распадаются на пары** чисел, произведение которых даёт при делении на $p$ остаток$

1$. Пусть $q$ пробегает ряд (\ref), тогда по следствию из леммы 1.1 найдутся единственные целые $u$, $v$, такие что $$ qu — pv = 1, \qquad 1 < u < p $$ Следовательно, множество чисел (\ref) можно разбить на такие пары $(q_i, \overline)$, $i = 1, 2, \ldots, (p — 3)/2$, для которых \begin \label q_i\overline = pv_i + 1, \end где $i = 1, 2, \ldots, (p — 3)/2. $ Перемножая (\ref) по всевозможным значениям $i$ получим $$ (p — 2)! = pV + 1, $$ где $V$ — некоторое натуральное число. После умножения обеих частей последнего равенства на $p — 1$ имеем $$ (p — 1)! = p(p — 1)V + p — 1, $$ или $$ (p — 1)! + 1 = p\big((p — 1)V + 1\big), $$ то есть, фактически, соотношение (\ref).