Коническая винтовая линия.
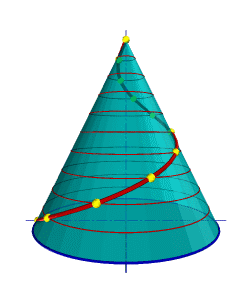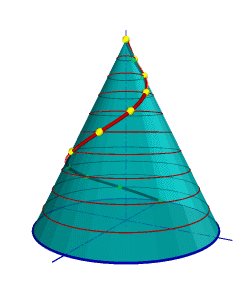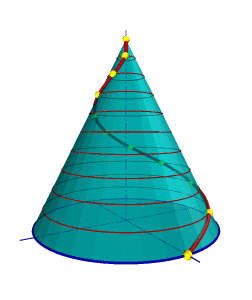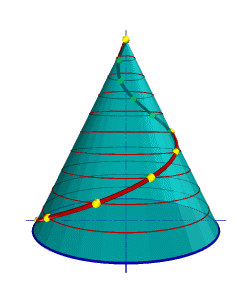
Такую линию описывает точка, которая движется по какой-либо образующей прямого кругового конуса, вращающегося вокруг своей оси так, что путь пройденный точкой по образующей все время равен углу поворота конуса (рис.7.10).
| Проекция на ось конуса смещения точки вдоль образующей за один оборот называется шагом конической винтовой линии. Горизонтальной проекцией конической винтовой линии является спираль Архимеда — одна из замечательных плоских кривых линий. | 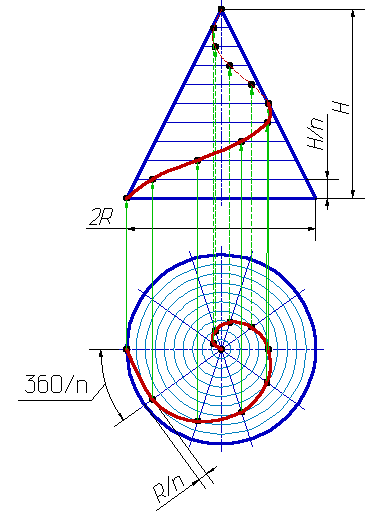 |
 | |
| а) модель | б) эпюр |
| Рисунок 7.10 Коническая винтовая линия |
Поверхность. Формообразование поверхностей. Поверхности вращения. Винтовые поверхности. Линейчатые поверхности с плоскостью параллелизма (Поверхности Каталана). Поверхности параллельного переноса.
| Поверхность |
«Поверхность, одно из основных геометрических понятий. При логическом уточнении этого понятия в разных отделах геометрии ему придаётся различный смысл.
1) В школьном курсе геометрии рассматриваются плоскости, многогранники, а также некоторые кривые поверхности. Каждая из кривых П. определяется специальным способом, чаще всего как множество точек, удовлетворяющих некоторым условиям. Например, поверхность шара — множество точек, отстоящих на заданном расстоянии от данной точки. Понятие «Поверхность» лишь поясняется, а не определяется. Например, говорят, что поверхность есть граница тела или след движущейся линии.
2) Математически строгое определение поверхности основывается на понятиях топологии. При этом основным является понятие простой поверхности, которую можно представить как кусок плоскости, подвергнутый непрерывным деформациям (растяжениям, сжатиям и изгибаниям). . «
*Большая советская энциклопедия.
Поверхности составляют широкое многообразие нелинейных фигур трехмерного пространства. Инженерная деятельность человека связана непосредственно с конструированием, расчетом и, изготовлением различных поверхностей. Большинство задач прикладной геометрии сводится к автоматизации конструирования, расчета и воспроизведения сложных технических поверхностей. Способы формообразования и отображения поверхностей, начертательной геометрии составляют основу инструментальной базы трехмерного моделирования современных графических редакторов.
Рассматривая поверхности как непрерывное множество точек, между координатами которых может быть установлена зависимость, определяемая уравнением вида F(x,y,z)=0, можно выделить алгебраические поверхности (F(x,y,z)— многочлен n-ой степени) и трансцендентные (F(x,y,z)— трансцендентная функция).
Если алгебраическая поверхность описывается уравнением n-й степени, то поверхность считается поверхностью n-го порядка. Произвольно расположенная секущая плоскость пересекает поверхность по кривой того же порядка ( иногда распадающейся или мнимой), какой имеет исследуемая поверхность. Порядок поверхности может быть определен также числом точек ее пересечения с произвольной прямой, не принадлежащей целиком поверхности, считая все точки (действительные и мнимые).
В начертательной геометрии фигуры задаются графически, поэтому целесообразно поверхность рассматривать как совокупность всех последовательных положений некоторой перемещающейся в пространстве линии.
| образование и задание поверхности на чертеже. |
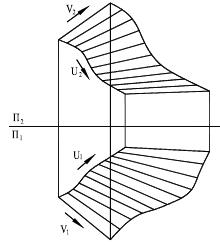
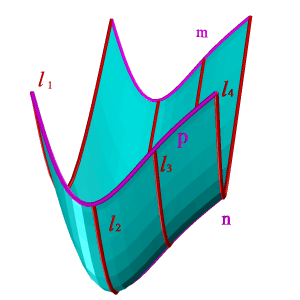
Поверхность можно рассматривать, как совокупность последовательных положений l1,l2… линии l, перемещающейся в пространстве по определенному закону (рис.8.1). В процессе образования поверхности линия l может оставаться неизменной или менять свою форму — изгибаться или деформироваться. Для наглядности изображения поверхности на эпюре Монжа закон перемещения линии l целесообразно задавать графически в одной линии или целого семейства линий (m, n, p. ). Подвижную линию принято называть образующей, неподвижные — направляющими. Такой способ образования поверхности принято называть кинематическим.
 | Примером такого способа могут служить все технологические процессы обработки металлов режущей кромкой, когда поверхность изделия несет на себе «отпечаток» режущей кромки резца, т.е. её поверхность можно рассматривать как множество, линий конгруэнтных профилю резца. По виду образующей различают поверхности линейчатые и нелинейчатые, образующая первых – прямая линия, вторых – кривая. Линейчатые поверхности в свою очередь разделяют на так называемые развертывающие, которые можно без складок и разрывов развернуть на плоскость и неразвертывающиеся. Значительный класс поверхностей формируется движением окружности постоянного или переменного радиуса. Это так называемые циклические поверхности (рис.8.2). Если же группировать поверхности по закону движения образующей линии и производящей поверхности, то большинство встречающихся в технике поверхностей можно разделить на: ·Поверхности вращения; ·Винтовые поверхности; ·Поверхности с плоскостью параллелизма; ·Поверхности переноса. Особое место занимают такие нелинейные поверхности, образование которых, не подчинено ни какому закону. Оптимальную форму таких поверхностей определяют теми физическими условиями, в которых они работают и устанавливают ее форму экспериментально (поверхности лопастей турбин, обшивка каркасов морских судов и самолетов). Множество линий, заполняющих поверхность так, что через каждую точку поверхности проходит в общем случае одна линия этого множества, называется каркасом поверхности. Поверхность может быть задана и конечным множеством точек, которое принято называть точечным каркасом. Проекции каркаса могут быть построены, если задан определитель поверхности – совокупность условий, задающих поверхность в пространстве и на чертеже. Различают две части определителя: геометрическую и алгоритмическую. Геометрическая часть определителя представляет собой набор постоянных геометрических элементов (точек, прямых, плоскостей и т.п.), которые могут и не входить в состав поверхности. Вторая часть – алгоритмическая (описательная) – содержит перечень операций, позволяющий реализовать переход от фигуры постоянных элементов к непрерывному каркасу. Например, циклическая поверхность, каркас которой состоит из окружностей (рис.8.3), может быть задан следующим образом: ·Геометрическая часть определителя: три направляющих l, m, n, ось iпучка плоскостей ·Алгоритмическая часть: выделяем из пучка плоскостей с осью iплоскость α; находим точки А, В, С, в которых αпересекает соответственно направляющие l, m, n. Строим окружность, определяемую тремя найденными точками. Переходим к следующей плоскости пучка и повторяем построение. |
| Рисунок 8.1. Поверхность, образованная движением линии | |
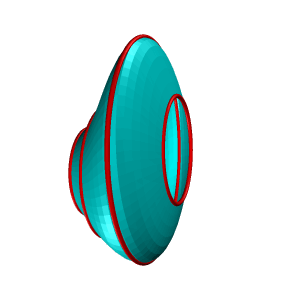 | |
| Рисунок 8.2. Циклическая поверхность | |
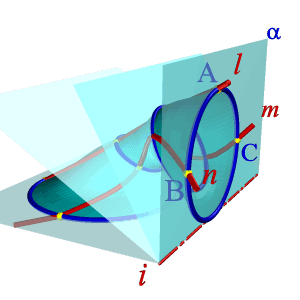 | |
| Рисунок 8.3. Образование циклической поверхности |
| // Поверхности вращения. |
Поверхности вращения – это поверхности созданные при вращении образующей mвокруг оси i (рис.8.4).
Геометрическая часть определителя состоит из двух линий: образующей m и оси i (рис 8.4.а).
Алгоритмическая часть включает две операции:
2. Каждую точку вращают вокруг оси i.
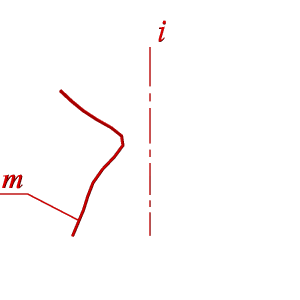 | 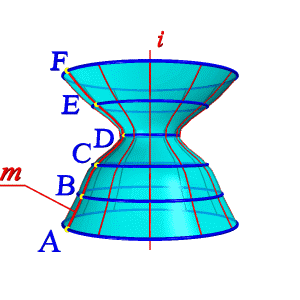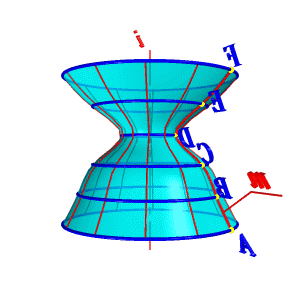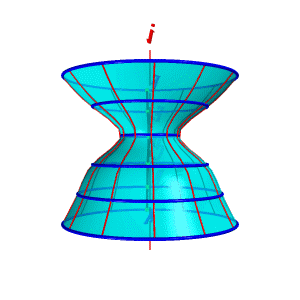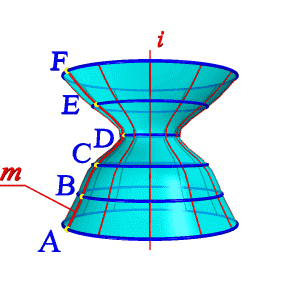 |
| а) эпюр | б) модель |
| Рисунок 8.4. Образование поверхности вращения |
 | Так создается каркас поверхности, состоящей из множества окружностей (рис.8.5), плоскости которых расположены перпендикулярно оси i. Эти окружности называются параллелями; наименьшая параллель называется горлом, наибольшая – экватором. Из закона образования поверхности вращения вытекают два основных свойства: 1. Плоскость перпендикулярная оси вращения, пересекает поверхность по окружности – параллели. 2. Плоскость, проходящая через ось вращения, пересекает поверхность по двум симметричным относительно оси линиям – меридианам. Плоскость проходящая через ось параллельно фронтальной плоскости проекций называется плоскостью главного меридиана, а линия, полученная в сечении, – главным меридианом. |
| Рисунок 8.5 Поверхность вращения |
 | 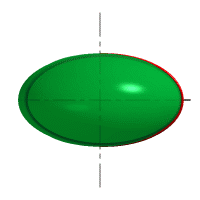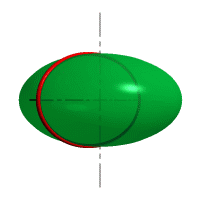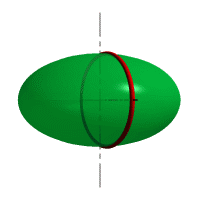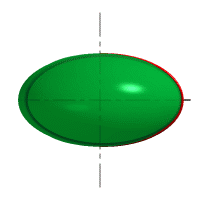 |
| Рисунок 8.6. Образование сферы | Рисунок 8.7. Образование сфероида |
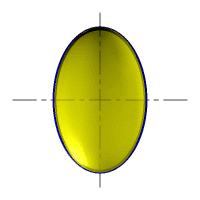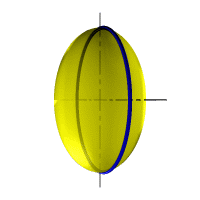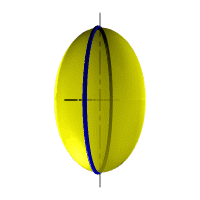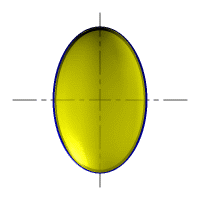 | Рассмотрим наиболее распространенные поверхности вращения с криволинейными образующими: Сфера – образуется вращением окружности вокруг её диаметра (рис.8.6). При сжатии или растяжении сферы она преобразуется в эллипсоиды, которые могут быть получены вращением эллипса вокруг одной из осей: если вращение вокруг большой оси то эллипсоид называется вытянутым (рис.8.8), если вокруг малой – сжатым или сфероидом (рис.8.7). Тор– поверхность тора формируется при вращении окружности вокруг оси, не проходящей через центр окружности (рис.8.9). Параболоид вращения– образуется при вращении параболы вокруг своей оси (рис.8.10). |
| Рисунок 8.8. Образование вытянутого эллипсоида |
 | 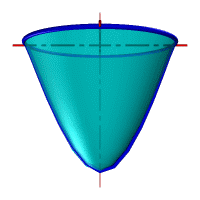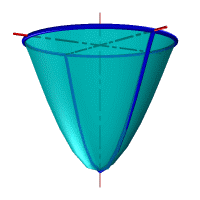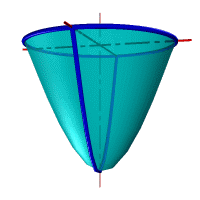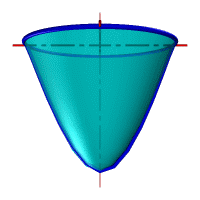 |
| Рисунок 8.8. Тор | Рисунок 8.10. Параболоид вращения |
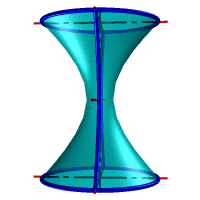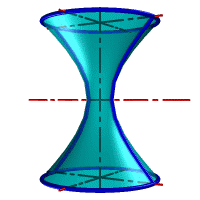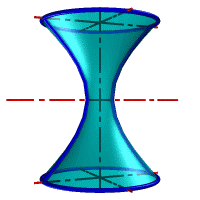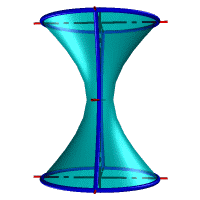 | 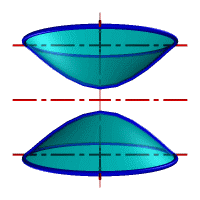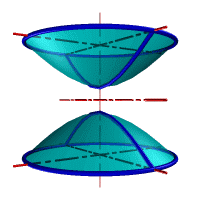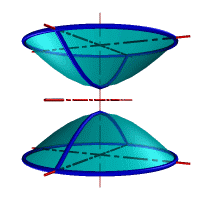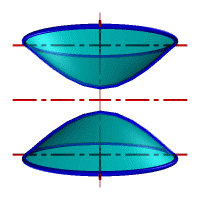 |
| а) однополостной | б) двуполостной |
| Рисунок 8.11. Гиперболоид вращения |
Гиперболоид вращения– различают одно (рис.8.11а) и двух (рис.8.11б) полостной гиперболоиды вращения. Первый получается при вращении вокруг мнимой оси, а второй – вращением гиперболы вокруг действительной оси.
| // Винтовые поверхности. |
Винтовые поверхности образуются винтовым движением некоторой линии – образующей.
Под винтовым движением понимается совокупность двух движений: поступательного параллельно некоторой оси, и вращательного, вокруг той же оси.
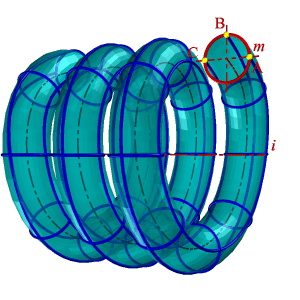 | При этом поступательное и угловое перемещение находятся в определенной зависимости ∆h=k∆v, где ∆h – линейное перемещение за время ∆t, ∆v– угловое перемещение за то же время, k – коэффициент пропорциональности. Если k=Const, то шаг поверхности постоянный. Геометрическая часть определителя винтовой поверхности ни чем не отличается от поверхности вращения и состоит из двух линий: образующей m, и оси i(рис.8.12). Алгоритмическая часть: 1. На образующей m выделяют ряд точек А, В, С, … 2. Строят винтовые линии заданного шага и направления, по которым перемещаются заданные точки. |
| Рисунок 8.12. Винтовая поверхность |
| Линейчатые поверхности с плоскостью параллелизма (поверхности каталана). |
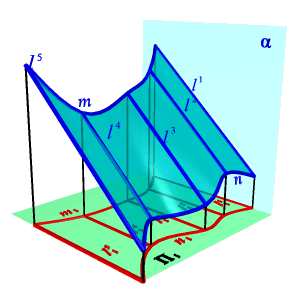 | Поверхность с плоскостью параллелизма представляет собой множество прямых линий l (образующих), параллельных некоторой плоскости α (плоскости параллелизма) и пересекающих две данные направляющие m, n (рис. 8.13). В зависимости от формы направляющих образуются три частных вида поверхностей. Цилиндроид. Цилиндроидом называется поверхность, образованная движением прямолинейной образующей по двум направляющим кривым линиям, при этом образующая во всех положениях параллельна плоскости параллелизма (рис.8.13). Коноид.Коноидом называется поверхность, образованная движением прямолинейной образующей по двум направляющим, одна из которых кривая линия, а другая прямая, при этом образующая во всех положениях параллельна плоскости параллелизма (рис.8.14). |
| Рисунок 8.13. Цилиндроид |
Гиперболический параболоид. Гиперболическим параболоидом или косой плоскостью называется поверхность, образованная движением прямолинейной образующей, параллельной плоскости параллелизма, по двум направляющим линиям – скрещивающимся прямым (рис.8.15).
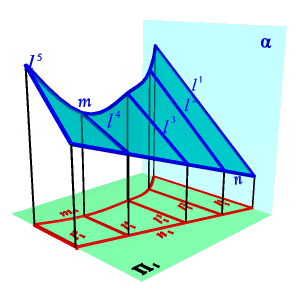 | 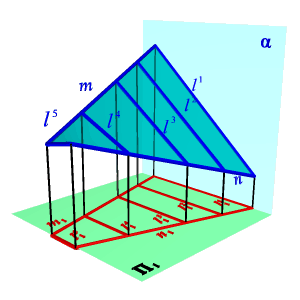 |
| Рисунок 8.14. Коноид | Рисунок. 8.15. Гиперболический параболоид |
| Поверхности параллельного переноса. |
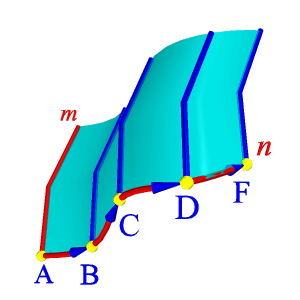 | Поверхностью параллельного переноса называется поверхность, образованная поступательным плоскопараллельным перемещением образующей — плоской кривой линии m по криволинейной направляющей n (рис.8.16). Геометрическая часть определителя состоит из двух кривых линий образующей — m и направляющей – n. Алгоритмическая часть определителя содержит перечень операций: 1. На направляющей п выбираем ряд точек А, В, С,… 2. Строим векторы АВ , ВС,… 3. Осуществляем параллельный перенос линии т по векторам АВ, ВС , … Наглядным примером плоскости параллельного переноса может служить скользящая опалубка, применяемая в строительстве. |
| Рисунок 8.16. Поверхность параллельного переноса |
8.2 Задание поверхности на чертеже
Для изображения поверхности на чертеже необходимо выяснить проекции каких элементов поверхности необходимо задать для того, чтобы получитьобратимый чертеж. Поверхность считается заданной, если относительно любой точки (на чертеже), можно дать однозначный ответ на вопрос: «Принадлежит ли эта точка рассматриваемой поверхности?». Другими словами, если по одной проекции точки, принадлежащей поверхности, можно построить ее вторую проекцию.
Возможны два способа задания: аналитический и графический.При аналитическом задании, в общем случае, поверхность может быть определена уравнением в неявном виде F(x,y,z) = 0, в явном виде z =f(x,y), или параметрической форме x = X(u,v), y= Y(u,v), z = Z(u,v). Параметры u и v получили название криволинейных координат.
Графическое задание поверхностей также предусматривает несколько вариантов. Один из них непосредственно вытекает из аналитического способа.Табулирование уравнений, задающих поверхность, позволяет получить либо двухпараметрическое множество точек, либо два однопараметрических семейства линий. Эти семейства определяют, так называемый каркас поверхности (точечный или линейчатый). Изображение этих каркасов на чертеже позволяет говорить о каркасном задании поверхности (рисунок 8.2).
Рисунок 8.17 – Линейчатый каркас
Еще один, самый распространенный, графический способ — задание поверхности очерками. При проецировании произвольной поверхности на плоскость проекций
некоторые из проецирующих прямых будут касаться этой поверхности и обра-
зовывать некоторую проецирующую (цилиндрическую для параллельного про-
Линия касания этих поверхностей называется контурной линией, а ее
проекция на соответствующую плоскость очерком.
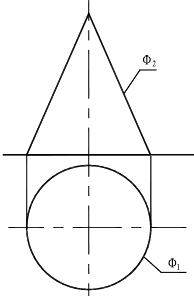
В соответствии с рисунком 8.3 поверхность прямого кругового конуса на
комплексном чертеже задана своими очерками (горизонтальным очерком Φ1 и,
соответственно, фронтальным Φ2). Очерки дают более наглядное представле-
ние об изображаемом объекте.
Рисунок 8.3 – Прямой круговой конус Рисунок 8.4 — Сфера
Пользуются при задании кинематических поверхностей и понятием оп-
ределителя. Под определителем кинематической поверхности понимают со-
вокупность независимых условий, однозначно определяющих эту поверхность.
Условиями могут быть: задание образующей поверхности, закон ее изменения
(в случае переменной образующей), закон движения образующей и др. Некото-
рые из них могут быть выражены графически. Например, сфера Ф может быть
представлена как поверхность вращения: Ф[i,l] (рисунок 8.4).
Условиями, включенными в определитель поверхности и определяющи-
ми ее форму, могут быть также параметры формы.
Одна и та же поверхность может быть образована несколькими способа-
ми. Поэтому она может иметь разные определители.
Все рассмотренные способы задания поверхности связаны между собой и
при решении многих задач приходится переходить от одного способа задания к
8.2 Точка и линия на поверхности
Обобщение определений на принадлежность точки и линии плоскости позволяет утверждать, что: точка лежит на поверхности, если она лежит на линии, лежащей наповерхности; линия лежит на поверхности в том случае, если все ее точки лежат наповерхности.
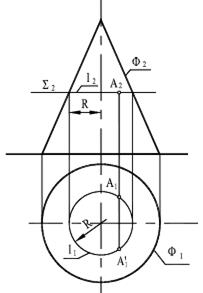
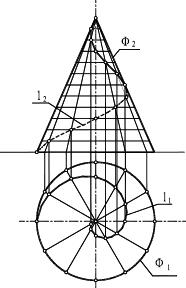
Рисунок 8.17 — Точка на конусе Рисунок 8.18 – Винтовая коническая линия
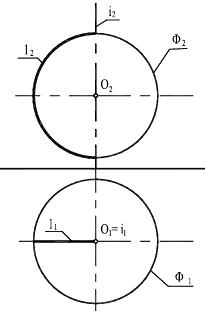
В соответствии с рисунком 8.17 и данным выше определением точка А лежит на поверхности конуса, заданного очерками Ф2 и Ф2. Точка А лежит наокружности l, полученной пересечением конической поверхности с горизонтальной плоскостью уровня Σ. Здесь одной фронтальной проекции точки А2 соответствуют две горизонтальные А1 и А’1. Рисунок 8.18 иллюстрирует винтовую линию l на поверхности конуса Ф,построенную по точкам. При построении точек, принадлежащих поверхностям, выбирают такие линии, лежащие на них, которые легко могут быть построены (прямые, окружности).
Дата добавления: 2015-10-26 ; просмотров: 3220 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Цилиндрические и конические винтовые линии
Цилиндрические и конические винтовые линии
Из пространственных кривых в технике находят широкое применение винтовые линии и поверхности. Винтовую линию можно рассматривать как результат перемещения точки по поверхности вращения.
Гелисой называют винтовую линию, которая образуется в результате равномерного вращения точки вокруг оси и одновременного перемещения с постоянной скоростью вдоль нее.
Величину 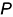
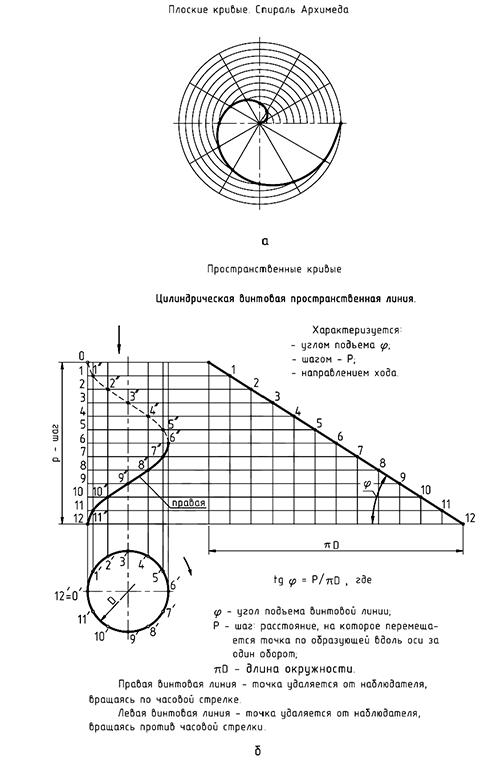
Для построения проекции винтовой линии, в частности гелисы, предварительно строят проекции прямого кругового цилиндра (рис. 11.7, б).
Окружность основания цилиндра (горизонтальная проекция гелисы) делят на равное количество равных частей (например, на 12, так как это можно сделать тем же раствором циркуля, которым была вычерчена окружность). На такое же количество частей делят цилиндр по высоте, равной шагу винтовой линии, на фронтальной проекции. Из точек, отмеченных на окружности, проводят вертикальные линии связи до их пересечения с горизонтальными линиями, проведенными из соответствующих точек деления шага. Соединив полученные точки плавной кривой линией, получают фронтальную проекцию винтовой линии (линия изображена с учетом ее видимости на поверхности цилиндра, рис. 11.7, б).
Различают правые и левые винтовые линии. Изображенная на рис. 11.7, б цилиндрическая винтовая линия является правой. Она характеризуется тем, что при вращении по часовой стрелке точка удаляется от наблюдателя, а при вращении против часовой стрелки — приближается. Если эти условия не соблюдаются, винтовая линия называется левой.
На рис. 11.7, б справа показано построение развертки винтовой линии. Там же приведена формула для определения крутизны винтовой линии.
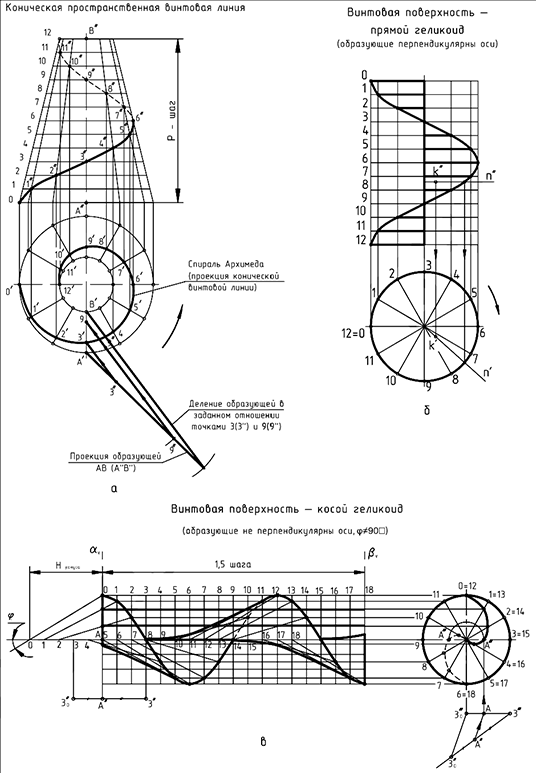
На рис. 11.8, а приведена коническая винтовая линия, которая образуется в результате движения точки по поверхности конуса при условии, что она равномерно вращается вокруг оси конуса и движется вдоль нее с постоянной скоростью. Судя по направлениям этих ее движений — это также правая винтовая линия. Для построения ее проекций горизонтальные проекцию окружностей оснований приведенного усеченного конуса делят на 12 равных частей и, соединяя их, строят горизонтальные проекции образующих конуса.
Определив фронтальные проекции полученных точек посредством линий связей, строят фронтальные проекции образующих. Затем делят конус по высоте (равна шагу винтовой линии) на то же количество частей горизонтальными линиями и отмечают точки их пересечения с фронтальными проекциями образующих.
Соединив найденные точки плавной кривой линией, получают фронтальную проекцию конической винтовой линии (линия изображена с учетом видимости ее на поверхности конуса, рис. 11.8, а). Далее, опуская из этих точек линии связи, отмечают на пересечениях с горизонтальными проекциями соответствующих образующих точки, через которые пройдет горизонтальная проекция конической винтовой линии.
По форме она представляет собой спираль Архимеда. Там же, на рис. 11.8, а, показаны дополнительные построения по определению горизонтальных проекций 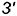
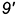
Графически показано, как поделены горизонтальные проекции этих образующих на отрезки в том же отношении, в котором поделены их фронтальные проекции винтовой линией (для уменьшения количества построений указанное деление обоих отрезков совмещено в одном построении).
Винтовые поверхности — прямой и косой геликоиды
При винтовом движении отрезка линии образуются винтовые поверхности. В зависимости от формы образующей линии, винтовые поверхности могут быть линейчатыми и нелинейчатыми. Они находят большое применение в технике, особенно в машиностроении и поэтому заслуживают отдельного внимания.
Все точки образующей при винтовом движении описывают винтовые линии (за исключением точки, находящейся на оси вращения поверхности), каждая из которых может служить направляющей поверхности. Линейчатые винтовые поверхности называют геликоидами. В зависимости от положения образующей относительно оси вращения геликоиды могут быть прямыми (образующая перпендикулярна оси) и косыми (образующая наклонена к оси).
Чертеж прямого геликоида приведен на рис. 11.8,6. Построение его проекций вначале повторяет построения цилиндрической винтовой линии, приведенные на рис. 11.7, б. Но вместо фронтального очерка цилиндра необходимо показать фронтальные проекции образующих винтовой поверхности. Эти проекции представляют собой горизонтальные отрезки, расположенные между осью вращения поверхности и фронтальной проекцией винтовой линии. Фронтальный очерк прямого геликоида образуют указанная винтовая линия, являющаяся проекцией траектории движения внешнего конца образующей, и проекция траектории движения ее внутреннего конца, совпадающая с фронтальной проекцией оси вращения образующей. Направление геликоида определяют так же, как и винтовой линии.
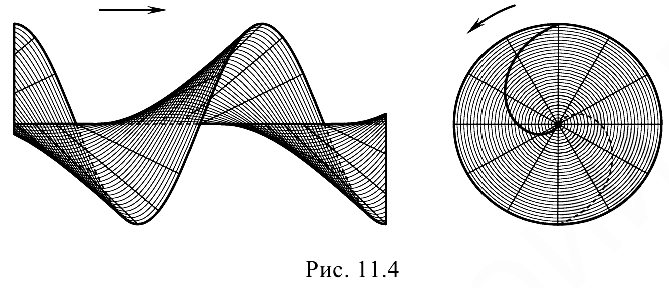
При построении проекций косого геликоида необходимо знать угол наклона его образующей к оси вращения. Эта поверхность имеет более сложный очерк (рис. 11.4).
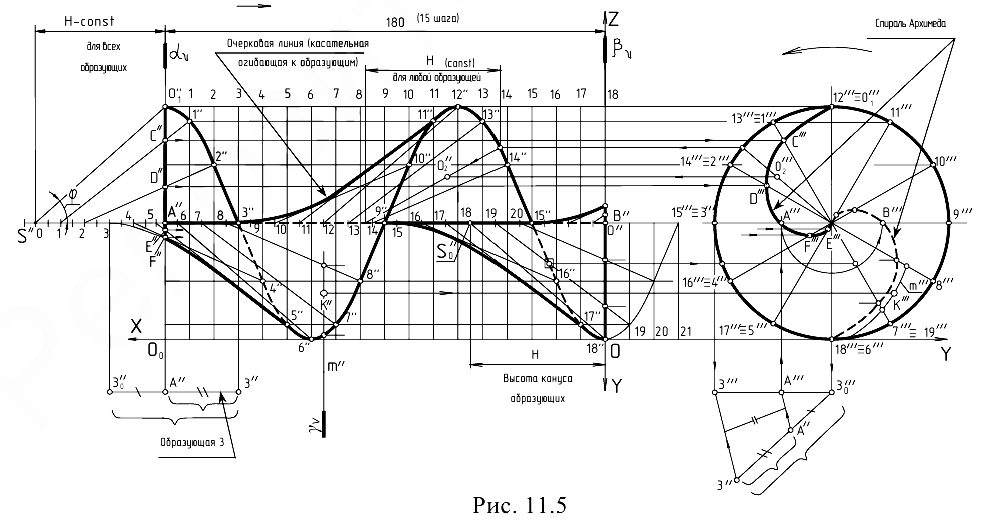
Чертеж косого геликоида, образованного наклонной прямолинейной образующей за 1,5 оборота винтового движения, приведен на рис. 11.5 и повторен на рис. 11.8, в.
Исходным условием для построений его чертежа является шаг винтового движения образующей и ее начальное положение под углом 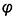
Построение недостающей профильной проекции 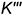
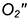
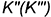
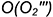
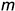
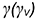
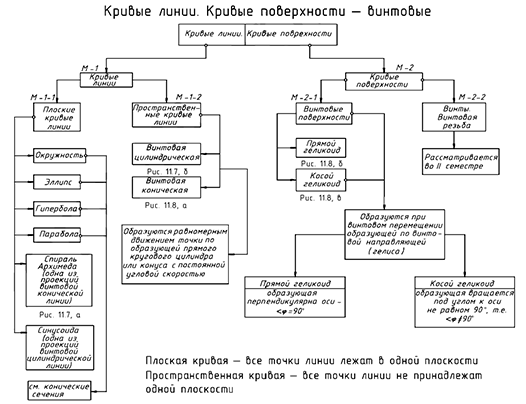
Структуризация материала данной лекции схематически представлена на рис. 11.6 (лист 1). На последующих листах 2 и 3 (рис. 11.7 и 11.8) компактно приведены иллюстрации к этой схеме для визуального закрепления основной части изученного материала при повторении.
Эта теория взята со страницы лекций для 1 курса по предмету «начертательная геометрия»:
Возможно эти страницы вам будут полезны:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Винтовая линия
Винтовая линия относится к пространственным кривым. Различают цилиндрические, конические, сферические и другие винтовые линии.
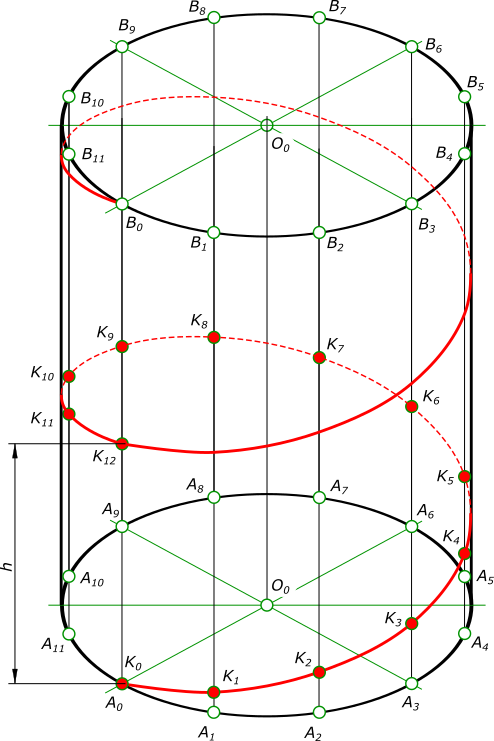
Цилиндрическая винтовая линия описывается точкой, которая совершает равномерное движение вдоль образующей кругового цилиндра, а образующая вращается с постоянной угловой скоростью вокруг оси цилиндра.
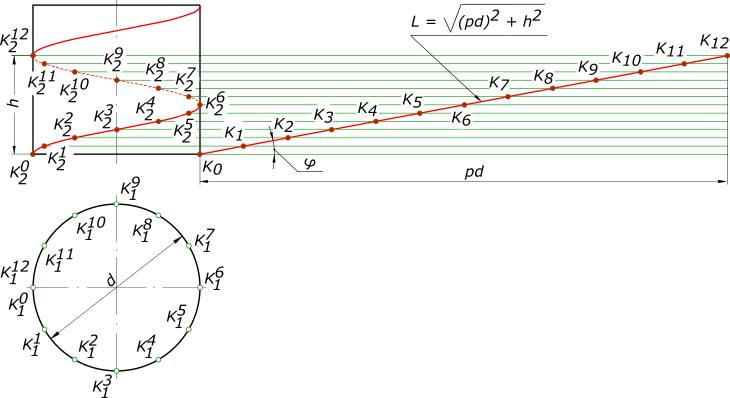
Образующая занимает 12 последовательных положений: A 0 B 0 . Дуги A 0 A 1 , A 1 A 2 A 2 A 3 и т. д. равны между собой и каждая равна pd/n, где d — диаметр цилиндра, p = 3,14 и n — число положений образующей цилиндра, принятое для построения. Пусть образующая занимает 12 последовательных положений: A 0 B 0 , A 1 B 1 , A 2 B 2 и т. д. Начальному положению образующей AB соответствует A 0 B 0 , а точки K — K 0 . При перемещении образующей AB в положение A 1 B 1 точка K займет положение K 1 , и поднимется по образующей на величину отрезка A 1 K 1 = h/12. При последующем перемещении образующая займет положение A 2 B 2 , а точка K положение K 2 и поднимется на высоту равную A 2 B 2 = 2A 1 B 1 = 2(h/12), и т. д. Когда образующая совершит полный оборот и снова займет начальное положение, точка K будет находится на ней на высоте A 12 B 12 = 12(h/12) = h, величине шага винтовой линии. При этом точка описывает кривую K 0 K 6 K 12 , длина которой равна длине одного витка. На практике эти движения достигаются на токарном станке, где острие резца соответствует данной точке.
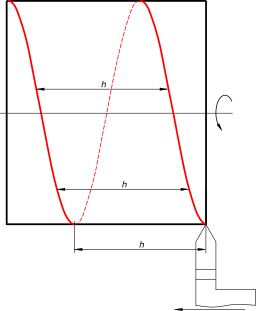
Резец оставит на цилиндрической поверхности след — винтовую линию. Винтовая линия может быть правой или левой. Правой винтовой линией называют линию, совершающую подъем вокруг своей оси против часовой стрелки, а левой — винтовую линию, совершающую подъем по часовой стрелке. Правая цилиндрическая винтовая линия
может быть построена, когда заданы ее элементы. Винтовая линия характеризуется следующими элементами: шаг, виток и угол подъема. Шагом винтовой линии называется расстояние между смежными витками, измеренное вдоль образующей кругового цилиндра. Витком называют винтовую линию, описанную точкой за один оборот образующей вокруг оси кругового цилиндра. Длина витка равна L. Углом подъема винтовой линии называют отношение tg(φ)= h/(pd), тогда φ = arctg(φ), где d — диаметр цилиндра, p=3,14.
Винтовая линия может быть получена на конической поверхности
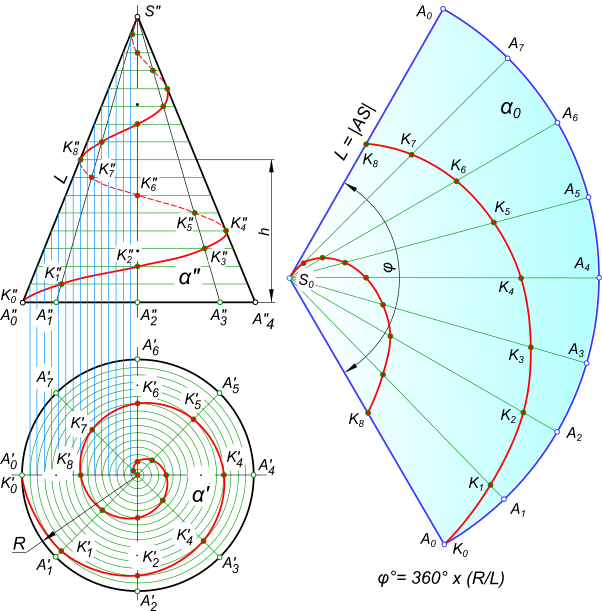
В этом случае, точка совершает равномерно-поступательное движение вдоль образующей прямого кругового конуса, а сама образующая SA вращается вокруг его оси с постоянной угловой скорости. Расстояние между точками смежных витков, измеренное параллельно оси конуса (например между точками A0K8), является шагом h конической винтовой линии. Проекция винтовой линии на фронтальной плоскости проекций представляет собой синусоиду с затухающим колебанием (затухающей волной), а на горизонтальной — спираль Архимеда. При построении развертки боковой поверхности конуса винтовая линия развернется в спираль, а конус — в сектор, угол при вершине которого равен φ= 360°×(h/L), а длина дуги радиуса R, соответствующая углу φ, равна 2πR.
http://lfirmal.com/tsilindricheskie-i-konicheskie-vintovyie-linii/
http://ngeo.fxyz.ru/%D0%BE%D1%80%D1%82%D0%BE%D0%B3%D0%BE%D0%BD%D0%B0%D0%BB%D1%8C%D0%BD%D1%8B%D0%B5_%D0%BF%D1%80%D0%BE%D0%B5%D0%BA%D1%86%D0%B8%D0%B8/%D0%BB%D0%B8%D0%BD%D0%B8%D1%8F/%D0%B2%D0%B8%D0%BD%D1%82%D0%BE%D0%B2%D0%B0%D1%8F_%D0%BB%D0%B8%D0%BD%D0%B8%D1%8F/