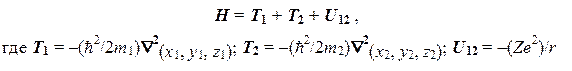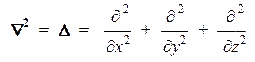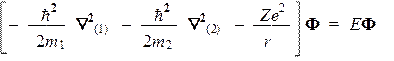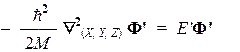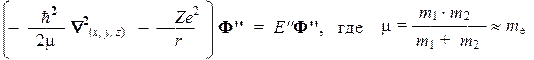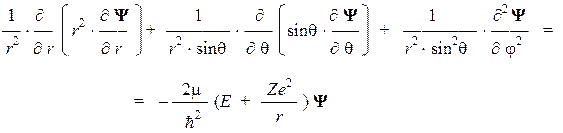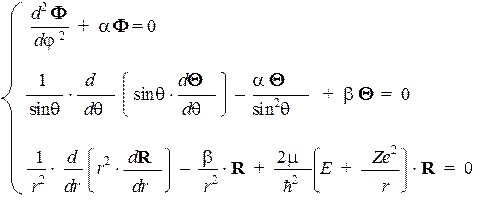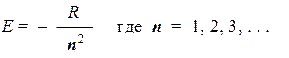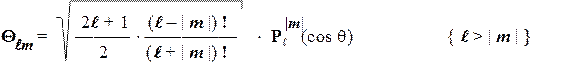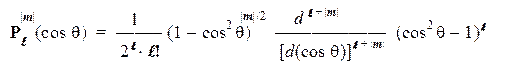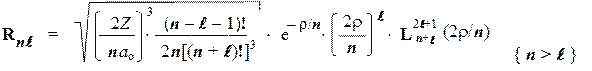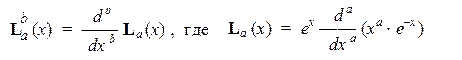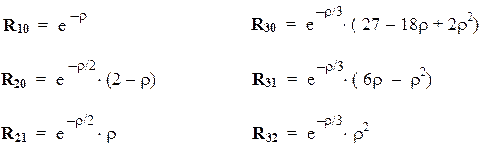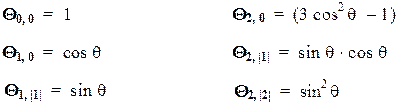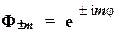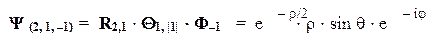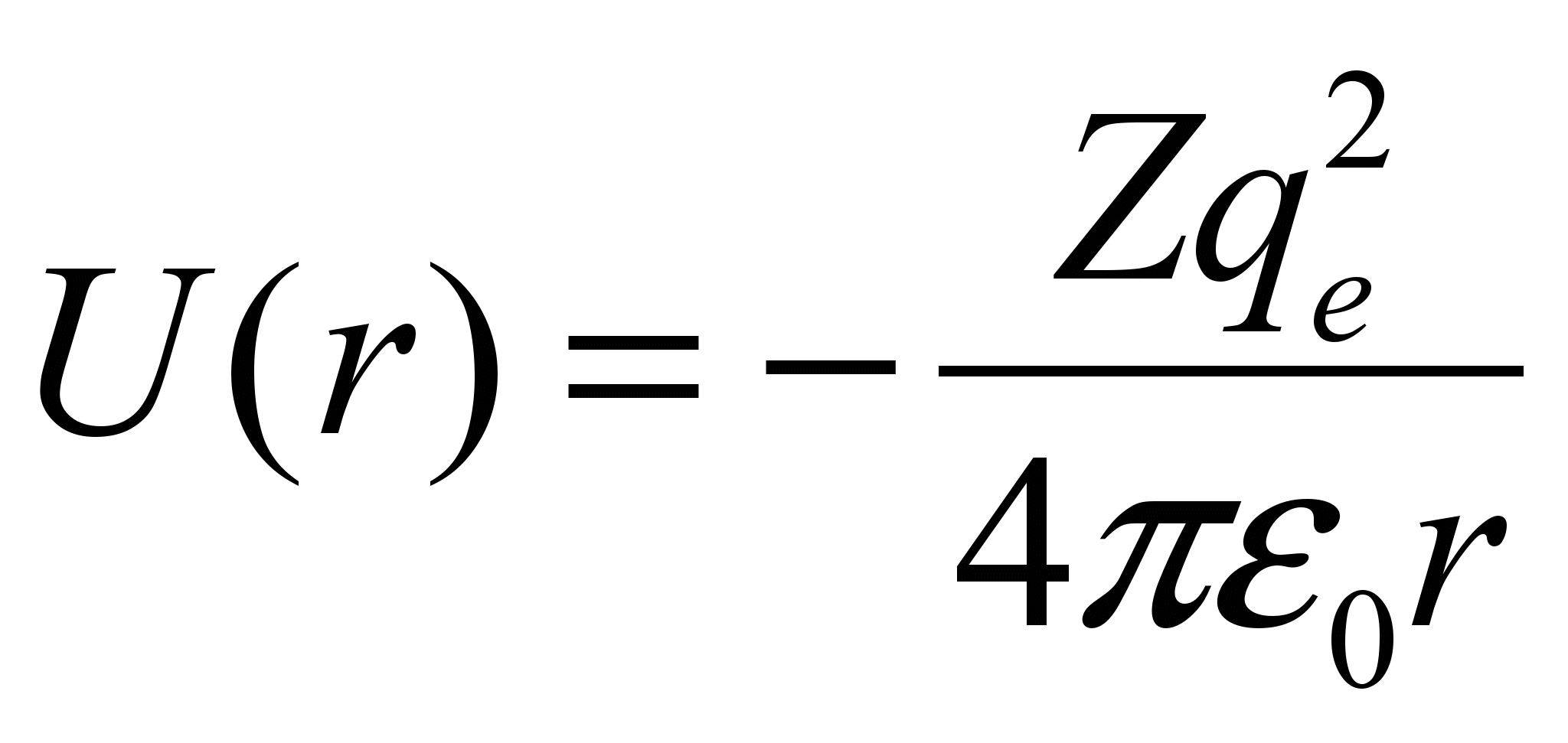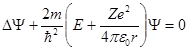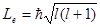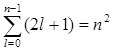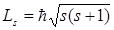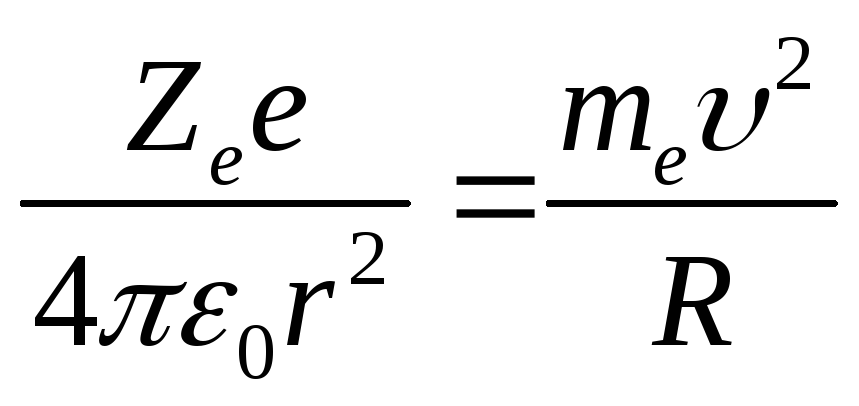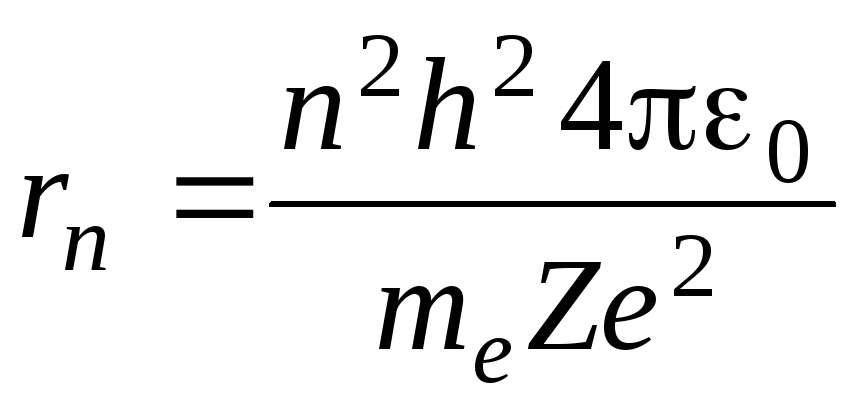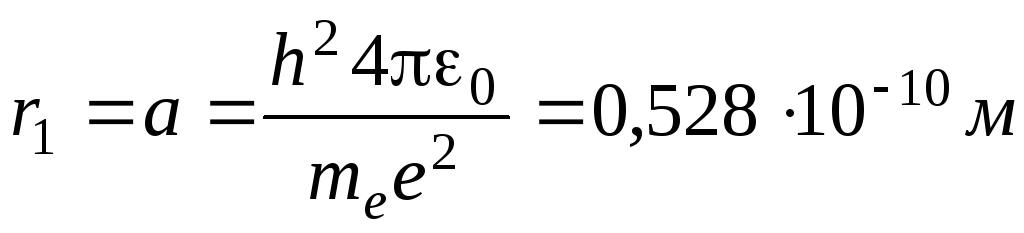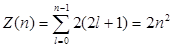Уравнение волновой функции для атома водорода

Волновые функции атома водорода

Векторы состояния атома водорода удобно представлять в пространственном базисе:

| F ñ = C₁| 1 ñ + C₂| 2 ñ + • • • = SC_i| i ñ ,

где каждое базисное состояние | i ñ отличается тем, что для него точно известны положения обеих частиц в пространстве относительно фиксированной лабораторной системы координат, т.е. известны 6 чисел-координат (x₁, y₁, z₁, x₂, y₂, z₂)_i. Ясно, что с таким бесконечномерным вектором состояния можно практически работать только после его перевода в функциональное представление — волновую функцию. Эти волновые функции, описывающие любые состояния атома, допустимые законами квантовой механики, должны, в общем случае, зависеть от шести пространственных координат и от времени: Ф = Ф(x₁, y₁, z₁, x₂, y₂, z₂; t). В дальнейшем ограничимся рассмотрением только стационарных состояний (нестационарные состояния не представляют интереса для химической проблематики, поскольку время их жизни, как правило, не превышает 10 –8 с), для которых волновую функцию можно представить в виде произведения пространственного и временного множителей:

В результате задача сводится к установлению вида пространственного множителя Ф(x₁, y₁, z₁, x₂, y₂, z₂) и значения энергии Е, которые можно найти из уравнения на собственные значения: НФ = ЕФ.Оператор Гамильтона для данной системы включает в себя три слагаемых: два одночастичных оператора кинетической энергии (Т₁ и Т₂) и двухчастичный оператор потенциальной энергии (U₁₂):

Здесь символ Ñ 2 (иногда вместо него употребляется эквивалентный символ D) обозначает одночастичный оператор «набла-квадрат», представляющий собой сумму вторых частных производных по декартовым координатам некоторой частицы:

Таким образом, интересующее нас уравнение на собственные значения (т.н. «стационарное уравнение Шредингера») имеет вид:

Решениями этого уравнения являются волновые функции, описывающие все возможные стационарные состояния атома водорода, а также соответствующие им энергии (в нерелятивистском приближении, т.е. без учета магнитных эффектов). Если атом изолирован от окружающих тел, то движения частиц в нем можно разделить на два типа:

1) глобальное движение атома как материальной точки (центра масс) в лабораторной системе координат (X, Y, Z).

2) локальные движения частиц во внутренней системе координат (x, y, z), начало которой расположено в центре масс.

Первый тип движения можно исследовать, смотря на атом «издалека», т.е. полагая его просто материальной точкой без внутренней структуры. Второй тип движения можно исследовать, смотря на атом «изнутри» и полагая, что атом как целое является неподвижным. В этом случае наблюдатель находится в центре масс и видит лишь относительное движение электрона и ядра. Независимость внешнего и внутреннего движений позволяет представить шестимерную волновую функцию в виде произведения двух трехмерных функций:

Первый сомножитель представляет собой глобальную функцию, описывающую движение атома как целого (т.е. как одной бесструктурной частицы с массой M = m₁ + m₂) и удовлетворяет трехмерному уравнению:

Это стандартное уравнение для свободной частицы с массой М. Его решения известны из модельных квантовомеханических задач «свободная частица» и «частица в трехмерном потенциальном ящике» (см. [3]).

Второй сомножитель представляет собой «внутреннюю» функцию, описывающую движение электрона и ядра относительно неподвижного центра масс. Согласованный характер движения электрона и ядра дает возможность заменить их единственной «квазичастицей», обладающей массой m и движущейся вокруг неподвижного центра масс. Вследствие большого различия в массах электрона и ядра эта квазичастица по своим свойствам практически совпадает с электроном. Поэтому в дальнейшем будем рассматривать ее как обычный электрон с незначительно уменьшенной массой. Внутренняя функция, описывающая движение электрона (квазичастицы), удовлетворяет трехмерному уравнению вида:

В декартовой системе координат это уравнение невозможно сделать более простым, так как входящая в него переменная r зависит от всех трех декартовых координат электрона: r 2 = x 2 + y 2 + z 2 . Поэтому целесообразно перейти к сферической системекоординат, в которой переменная r является независимой координатой. Замена производится по правилам:

x = r × sinq × cosj ; y = r × sinq × sinj ; z = r × cosq

где угол q отсчитывается в вертикальной плоскости от оси z и изменяется в интервале от 0 до p, а угол j отсчитывается в горизонтальной плоскости от оси x и изменяется в интервале от 0 до 2p. После замены переменных волновая функция изменяет свой вид: Ф»(x, y, z) ¾® Y(r, q, j), а стационарное уравнение Шредингера приобретает такую форму:

Сделанная замена переменных позволяет представить трехмерную функцию в виде произведения трех одномерных функций-сомножителей:

Y(r, q, j) = R(r) × Q(q) × F(j)

которые являются решениями системы из трех одномерных уравнений:

Необходимо отметить, что в результате процедуры разделения в уравнениях появились две новые константы — a и b, которые учитывают существующие взаимосвязи между уравнениями и их решениями. Эти параметры должны иметь одни и те же значения во всех уравнениях, куда они входят. Данное условие выполняется только для некоторых «разрешенных» значений, образующих дискретный набор, а именно:

a = 0, 1, 4, 9, 16, 25, … и b = 0, 2, 6, 12, 20, 30, 42, …

С целью упрощения этих рядов удобно ввести два новых вспомогательных параметра — l и m, для которых выполняются более простые условия:

b = l(l+ 1) , где l = 0, 1, 2, . . .

a = m × m , где m = 0, ±1, ±2, . . .

Дискретность в решениях R-, Q— и F-уравнений, вызываемая приведенными ограничениями для параметров a и b, приводит, в свою очередь, к дискретности допустимых значений энергии атома (она входит в R‑уравнение), связанной с внутренним движением:

Целые числа, входящие в приведенные формулы, называются квантовыми числамиатома водорода: n — главное, l — орбитальное, m — магнитное. Они выступают в роли параметров, нумерующих возможные решения уравнения Шредингера, или, что то же самое, волновые функции стационарных состояний:

Y(r, q, j) = R(r) • Q(q) • F(j) = Y(n, l, m) =

= R(n, l) • Q(l, m) • F(m) = R(n, l) • Y(l, m)

Произведения Q(l, m) • F(m) = Y(l, m)называются шаровыми функциями.

Приведем явный вид Q-иF-функций (в сферических координатах):

В этом уравнении символом Р обозначен т.н. «присоединенный полином Лежандра» степени l и порядка |m|, представляющий собой некоторую степенную функцию от (cos q). Явный вид этих полиномов можно найти в справочниках или вычислить по следующей формуле:

Для R-уравнения решения имеют вид:

Здесь символом Lобозначен т.н. «присоединенный полином Лаггера» степени (n + l) и порядка (2l + 1) — степенная функция от новой переменной r = (Z/a_o)×r, которая представляет собой шкалу расстояний: прокалиброванную с помощью т.н. «атомных единиц длины» а_о = 4pe_oh 2 /me 2 » 0,053 нм (здесь константа e_o = 8,84×10 – 12 ф/м — диэлектрическая постоянная).

Явный вид присоединенных полиномов Лаггера можно найти в справочниках или вычислить по формуле:

Стоящие впереди полиномов Лежандра и Лаггера сложные выражения являются нормировочными множителями, которые при задании конкретных величин квантовых чисел приобретают простой вид.

Следует обратить внимание на важное обстоятельство. В формулы входят некоторые величины, являющиеся факториалами типа х!. Эта функция определена только для целых неотрицательных чисел х. В результате, на допустимые совместные (т.е. относящиеся к одному состоянию атома) значения квантовых чисел накладываются ограничения, указанные выше в фигурных скобках.

Для иллюстрации можно привести конкретные выражения для волновых функций с небольшими номерами.

R-функции (нормировочные множители опущены):

(В обозначениях функций первый числовой индекс равен главному квантовому числу n, а второй — орбитальному квантовому числу l.)

Q-функции(нормировочные множители опущены):

(В обозначениях функций первый числовой индекс равен орбитальному квантовому числу l, а второй — модулю магнитного числа |m|.)

Ф-функции(нормировочные множители опущены):

Располагая таблицами таких функций, можно легко построить явный вид волновой функции для любого стационарного состояния атома водорода. Пусть, например, состояние характеризуется набором квантовых чисел <n, l, m> = <2, 1, –1>. Тогда волновая функция будет иметь вид (нормировочный множитель опущен):

Полный вид волновой функции можно получить при умножении этой пространственной части на временной экспоненциальный множитель:

где Е₂ — энергия, соответствующая значению n = 2.

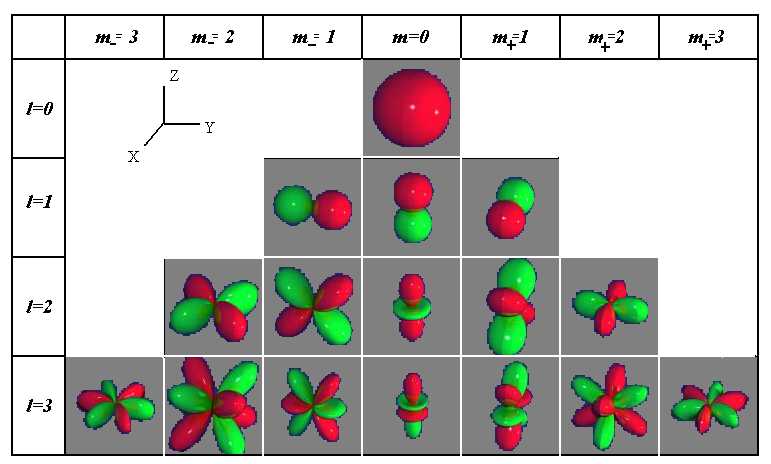
Обозначаемые тремя индексами функцииY_n,l,m часто называют водородными атомными орбиталями или Н-АО. Заметим, что в большинстве случаев они содержат комплексную экспоненту и, следовательно, являются комплекснозначными функциями. Это обстоятельство часто отмечается и в названии — комплексные атомные орбитали (КАО).

Существует еще одна, более удобная, номенклатура Н-АО. Каждый тип АО обозначается определенным символом — латинской буквой — указывающим на значение орбитального квантового числа:

Впереди буквы-символа указывается значение главного квантового числа, а магнитное квантовое число обозначается цифровым подстрочным индексом, следующим за буквой-символом. Например:

Y ₁₀₀ = 1s_o

Y ₂₀₀ = 2s_o Y ₂₁₀ = 2p_o Y _21–1 = 2p_–1 Y ₂₁₁ = 2p₁

Y ₃₀₀ = 3s_o Y ₃₁₀ = 3p_o Y _31–1 = 3p_–1 Y ₃₁₁ = 3p₁

Y ₃₂₀ = 3d_o Y ₃₂₁ = 3d₁ Y _32–1 = 3d_–1 . . . и т.д.

В ряде случаев бывает более удобным использование не самих волновых функций, а некоторых линейных комбинаций, построенных из этих функций, с целью получить чисто действительные функции. Такие линейные комбинации строятся в виде суммы или разности двух КАО, у которых все квантовые числа одинаковы по величине, но магнитные числа противоположны по знаку. У таких пар КАО R— и Q-сомножители в точности одинаковы, поскольку они не зависят от знака магнитного числа. В результате получаются суммы и разности комплексно сопряженных экспонент, которые сводятся к действительным тригонометрическим функциям (здесь нормировочные множители опущены):

Y_{(n, l, m)} + Y_{(n, l, –m)} = RQ(eimj +e–imj )= RQ• cos (mj) = Y + _{( n, l, |m|)}

Y_{(n, l, m)} – Y_{(n, l, –m)} = RQ(eimj – e–imj )= RQ• sin (mj) = Y – _{( n, l, |m|)}

Такие линейные комбинации называются действительными атомными орбиталями (ДАО). В их обозначениях нижний индекс заменяется на буквенный. Например, для АО p-типа имеем:

или для АО d-типа:

3d(x 2 – y 2 ) (3d₂ – 3d_–2)

3dxy 3d₀

3dz 2

ДАО удобны в том отношении, что их можно изображать графически, анализировать различные пространственные характеристики и симметрию. Подчеркнем, что наборы КАО и ДАО полностью эквивалентны в математическом отношении и представляют собой два базисных набора в одном и том же пространстве состояний (см. модель «плоский ротатор» в [3]).

Состояния, описываемые волновыми функциями типа Y_n,l,m, обычно называются чистыми. Кроме них существует множество состояний смешанных (или суперпозиционных), для которых одно или несколько квантовых чисел являются неопределенными:

Все такие функции, составленные из слагаемых с разными значениями квантовых чисел n и/или l, описывают нестационарные состояния, которые в течение короткого времени (порядка 10 –8 с) редуцируют к одному из стационарных состояний типа Y_n,l,m, в которых все три квантовые числа точно определены. Исключением из этого общего правила являются суперпозиционные функции типа Y_n,l. Редукция таких состояний может быть вызвана только действием внешних причин (например, магнитного поля).

Дата добавления: 2015-06-10 ; просмотров: 3439 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Уравнение Шредингера

Вы будете перенаправлены на Автор24

Предпосылки вывода уравнения Шредингера

Основная идея волновой механики заключается в том, что для таких малых тел, как электрон, нельзя с определенностью сказать, где оно находится в данное время и куда направляется. Можно установить только относительную вероятность его нахождения в том или ином месте и наличие определенного количества движения в определенный момент времени.

В соответствии с волновой механикой какая-либо система – атом, молекула, электрон и т.д. – описывается функцией состояния или волновой функцией, обозначаемой $\psi$ («пси»), которая является функцией координат всех частиц, образующих эту систему. Следовательно, величина $\psi$ зависит только от положения всех частиц в пространстве.

В 1924 г. де Бройль предположил, что точно также, как свет, который, как обычно считают, имеет волновую природу, на самом деле при определенных обстоятельствах ведет себя, как будто он состоит из частиц – квантов, — так и очень малые частицы, такие, как электроны, также могут обладать волновыми свойствами. Де Бройль предположил, что с пучком электронов следует связывать длину волны, определяемую уравнением

где $\hbar$ – постоянная Планка ($6,626\cdot 1034 Дж\cdot с$ или $6,626\cdot 10-27 эрг\cdot с$), а $p$ – количество движения (импульс) электрона в пучке, т.е. его масса, умноженная на его скорость.

Физическое подтверждение волновой природы электрона было продемонстрировано в 1927 – 1928 гг. Дейвиссоном, Джермером и Томсоном, которые показали, что пучок электронов может испытывать дифракцию на подходящей решетке (атомы в кристалле золота), аналогичную дифракции пучка света.

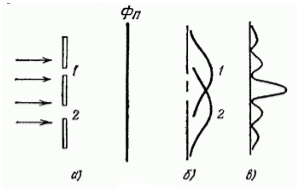
Рисунок 1. Дифракция пучка электронов

На преграду с двумя узкими щелями направлен параллельный пучок моноэнергетических (т.е. обладающих одинаковой кинетической энергией) электронов (рис. 1. а). За преградой находится фотопластина $Фn$. При закрытии щели номер $2$ и экспонировании в течение времени $t$ почернение на проявленной фотопластине будет характеризоваться кривой $1$ (рис. 1. б). При закрытии щели номер $1$, соответственно, почернение на фотопластине будет соответствовать кривой $2$. Однако в случае, когда открыты обе щели картина почернения фотопластины (рис. 1. в) отнюдь не эквивалентна наложению двух первых картин. Зато она аналогична картине, получающейся при интерференции двух когерентных световых волн.

Готовые работы на аналогичную тему

Тот факт, что системы малых частиц проявляют, по крайней мере, при определенных условиях, волновые свойства, предполагает возможность описания таких систем уравнениями, подобными те, которые описывают другие виды волнового движения, например, волны, которые распространяются вдоль колеблющейся струны, или волновое движение, приписываемое электромагнитному излучению. Действительно, можно начать с волнового уравнения, соответствующего электромагнитным волнам, и путем определенных замен, превратить его в уравнение, соответствующее нашему случаю. Хотя эти замены диктуются физическими причинами, они в основном произвольны и могут быть приняты только потому, что приводят к уравнению, которое, как показывает опыт, позволяет получить правильное решение физических задач. Поэтому следует принять волновое уравнение как постулат, так как у химиков основной интерес вызывает применение волнового уравнения к атомным и молекулярным системам, а не физические и математические соображения, которыми руководствовался Шредингер, впервые его предложивший в 1925 г.

Общий вид уравнения Шредингера

Рисунок 2. Эрвин Шрёдингер (1887 — 1961)

Волновое уравнение, применяемое для расчета стационарных состояний системы, можно записать в символическом виде:

где $H$ представляет собой определенный способ выражения общей энергии системы, а $E$ – числовое значение этой энергии. Для всех систем, которые обычно интересуют химиков, общая энергия представляет собой сумму кинетической энергии $Т$ и потенциальной энергии $V$:

Это соотношение было широко использовано физиком-теоретиком Гамильтоном, поэтому $H$ часто называют функцией Гамильтона, а $\mathcal H$ гамильтонианом системы.

Уравнение Шредингера на примере атома водорода

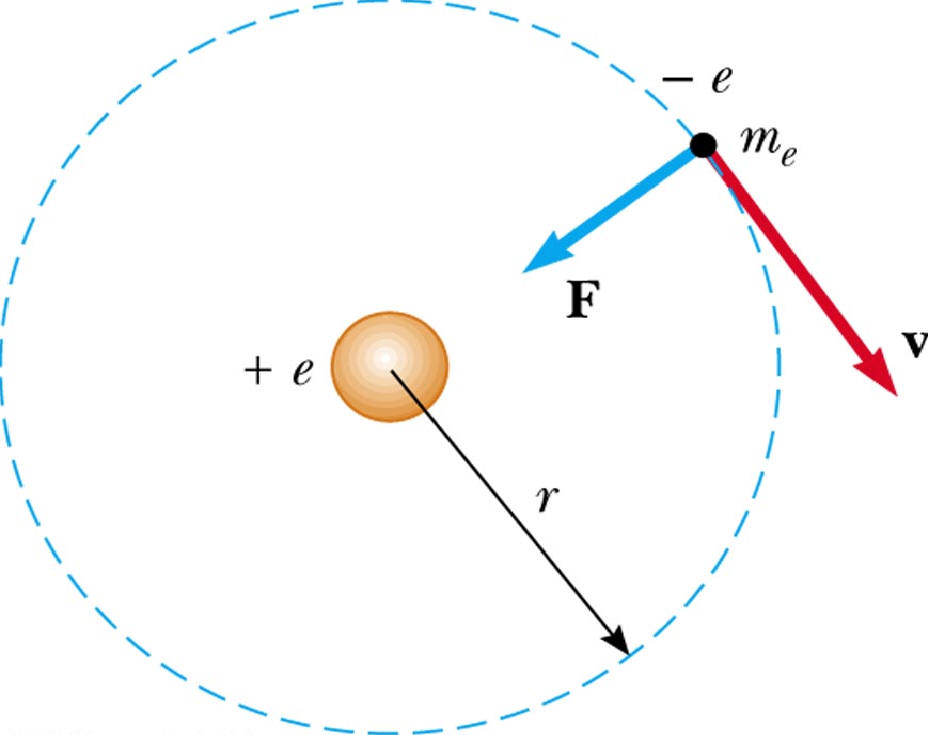
Рассмотрим модель атома водорода, предложенную Бором. Для простоты предположим, что тяжелое ядро закреплено (оно почти, но не совершенно неподвижно, когда электрон движется вокруг него). Тогда полная кинетическая энергия $Т$ системы представляет собой просто кинетическую энергию электрона

где $m$ – масса электрона и $\nu$ – его скорость. Потенциальная энергия системы есть просто энергия, возникающая вследствие электростатического взаимодействия (гравитационные силы приблизительно в $10^<18>$ раз меньше), и ее можно выразить как

где $e$ — заряд электрона, $r$ — радиус орбиты, знак минус появляется вследствие того, что заряд одной из частиц положителен $(+)$, а другой отрицателен $(-)$. Поэтому для атома водорода функция Гамильтона в классической (т.е. доквантовомеханической) физике равна:

Если использовать понятие количества движения электрона $p=m\nu$, данное уравнение запишется в следующем виде:

Теперь для перехода от классического описания этой или какой-либо другой системы к описанию при помощи волновой механики, необходимо взять функцию Гамильтона (уравнение 6) и произвести в ней определенные замены: в функции Гамильтона количество движения следует заменить выражением

Таким образом, гамильтониан для атома водорода в его квантовомеханической форме $<\mathcal H>$ следует записать в виде

Если теперь это выражение гамильтониана подставить в общее волновое уравнение (уравнение 1), то получим:

Это и есть волновое уравнение для атома водорода. Из уравнения 9 следует, что нужно вторые производные функции $\psi $ сложить и умножить на $-<<\hbar >^2>/<8<\pi >^2m>$, затем к этому добавить $\left(-/\right)\psi $, тогда получим величину, тождественную Е$\psi $. Если найдена функция $\psi $, то говорят, что она является решением волнового уравнения, и ее называют волновой функцией. Вообще, может быть несколько различных функций $\psi_1$, $\psi_2$, . , $\psi_n$, которые являются решениями уравнения 9, причем каждой соответствует свое значение энергии $Е_1$, $Е_2$, . , $Е_n$.

Уравнение волновой функции для атома водорода

Атом водорода и водородоподобные системы – это системы, состоящие из ядра с зарядом Ze и одного электрона (например, ионы He + , Li 2+ ).

Решение задачи об энергетических уровнях электрона для атома водорода (а также водородоподобных систем: иона гелия Не + , двукратно ионизованного лития Li + + и др.) сводится к задаче о движении электрона в кулоновском поле ядра.

Потенциальная энергия взаимодействия электрона с ядром, обладающим зарядом Zе (для атома водорода Z =1):

Состояние электрона в атоме водорода описывается волновой функцией Ψ, удовлетворяющей стационарному уравнению Шредингера

Его решения позволяют определить характеристики ВДПА:

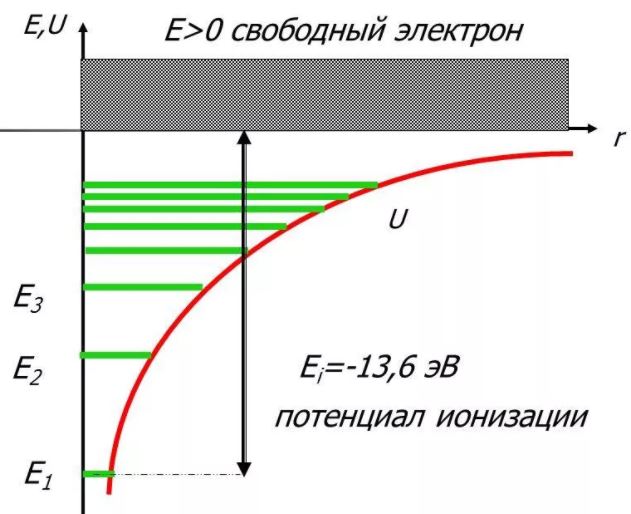
Энергия . В теории дифференциальных уравнений доказывается, что такие уравнения имеют решения, удовлетворяющие требованиям однозначности, конечности и непрерывности волновой функции Ψ, только при собственных значениях энергии

при n = 1, 2, 3.

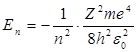
т. е. для дискретного набора отрицательных значений энергии.

Таким образом, как и в случае «потенциальной ямы» с бесконечно высокими «стенками», решение уравнения Шредингера для атома водорода приводит к появлению дискретных энергетических уровней. Самый нижний уровень Е₁, отвечающий минимальной возможной энергии, – основной, все остальные (Е_n>E₁, n = 2, 3,…) – возбужденные. При Е 0 движение электрона является свободным; область непрерывного спектра Е >0 соответствует ионизованному атому.

Энергия ионизации атома водорода равна

Квантовые числа . В квантовой механике доказывается, что уравнению Шредингера удовлетворяют собственные функции Ψ, определяемые тремя квантовыми числами: главным п, орбитальным l и магнитным m_l.

Главное квантовое число n, определяет энергетические уровни электрона в атоме и может принимать любые целочисленные значения, начиная с единицы:

Из решения уравнения Шредингера вытекает, что момент импульса (механический и орбитальный момент) электрона квантуется, т. е. не может быть произвольным, а принимает дискретные значения, определяемые формулой

где l – орбитальное квантовое число,которое при заданном n принимает значения

т. е. всего п значений, и определяет момент импульса электрона в атоме.

Из решения уравнений Шредингера следует также, что вектор L_e момента импульса электрона может иметь лишь такие ориентации в пространстве, при которых его проекция L_еz а направление z внешнего магнитного поля принимает квантованные значения, кратные ħ

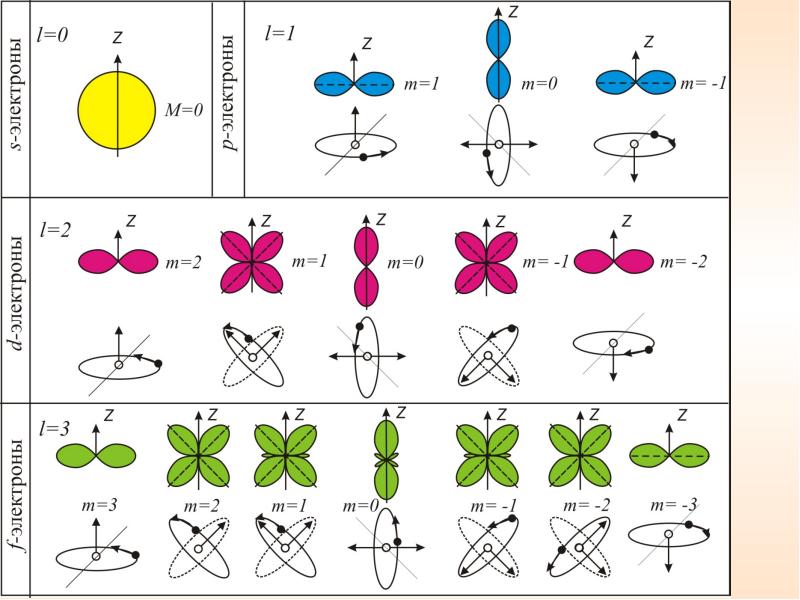
где т_l – магнитное квантовое число,которое при заданном l может принимать значения

т.е. всего 2l+1 значений. Таким образом, магнитное квантовое число т_l определяет проекцию момента импульса электрона на заданное направление, причем вектор момента импульса электрона в атоме может иметь в пространстве 2l + 1 ориентаций.

Так как при данном п орбитальное квантовое число l может изменяться от 0 до n – 1, а каждому значению l соответствует 2l + 1 различных значений т_l, то число различных состояний, соответствующих данному n, равно

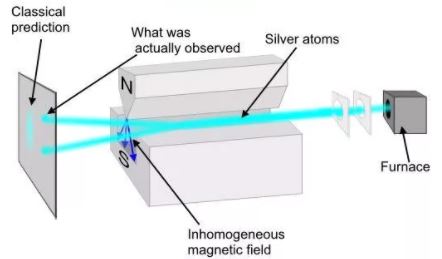
Опыт Штерна и Герлаха

О. Штерном и В. Герлахом были поставлены опыты (1921), целью которых являлось измерение магнитных моментов р _m атомов различных химических элементов. Для определения орбитального момента импульса L _l и р _m одного электрона опыты должны быть поставлены с атомами, у которых орбитальные механические (и магнитные) моменты всех электронов, кроме одного, взаимно компенсируют друг друга. Такими атомами являются атомы химических элементов, образующие первую группу периодической системы Менделеева и имеющие один валентный электрон на внешней оболочке.

Идея опытов Штерна и Герлаха заключалась в измерении силы, действующей на атом в неоднородном магнитном поле. Опыты Штерна и Герлаха обнаружили ошибочность классического предположения отом, что магнитный момент р_m и механический момент импульса L_l атома произвольно ориентируются относительно направления внешнего поля, и подтвердили наличие пространcтвенного квантования.

В трубке, где был создан вакуум порядка 10 -5 мм рт. ст., помещался источник пучка атомов — нагреваемый до высокой температуры серебряный шарик К. Атомы серебра вылетали с его поверхности со средней тепловой скоростью порядка 100 м/с, соответствующей температуре испарения серебра. Из этих атомов при помощи щелевых диафрагм В вырезался узкий пучок, проходящий через сильное и неоднородное магнитное поле, направленное перпендикулярно пучку. Основная трудность опыта состояла в том, чтобы достигнуть такой большой неоднородности магнитного поля, которая сказывалась бы на расстояниях порядка размеров атома. При такой величине неоднородности поля можно было рассчитывать получить значительную отклоняющую силу F, действующую на атом в магнитном поле. Необходимая неоднородность поля была достигнута в результате применения сильного электромагнита SN с полюсными наконечниками специальной формы. Приемником атомов серебра служила фотопластинка А.

Если бы момент импульса L_l атома (и его магнитный момент р_m ) мог принимать произвольные ориентации в магнитном поле, то можно было бы ожидать непрерывного распределения попаданий атомов на пластинку с большей плотностью попаданий в середине пластинки и меньшей плотностью к ее краям. Опыты, проведенные с серебром и атомами других элементов периодической системы, привели к совершенно другому результату. На рисунке показана фотография результата опыта Штерна и Герлаха с литием. Из рисунка видно, что на фотопластинке получились две резкие полосы — все атомы отклонялись в магнитном поле двояко, что соответствовало лишь двум возможным ориентациям магнитного момента во внешнем поле. Момент импульса атома (и его магнитный момент) равен суммарным моментам электронов, поскольку магнитные моменты ядер имеют значительно меньшее значение, чем магнитные моменты электронов. Последние совпадают с суммарными моментами валентных электронов, так как моменты электронов замкнутых оболочек компенсируются.

Для объяснения этого американские физики Д. Уленбек (1900- 1974) и С. Гаудсмит (1902-1979) предположили, что электрон обладает собственным неуничтожимым механическим моментом импульса, не связанным с движением электрона в пространстве — спином.

Спин электрона (и всех других микрочастиц) — квантовая величина, у нее нет классического аналога; это внутреннее неотъемлемое свойство электрона, подобное его заряду и массе.

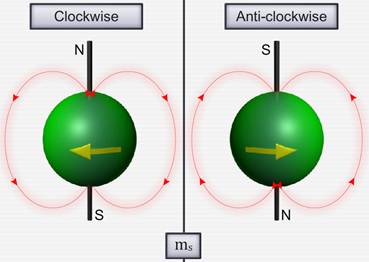
Если электрону приписывается собственный механический момент импульса (спин) L_s, то ему соответствует собственный (спиновый) магнитный момент р_ms,. Согласно общим выводам квантовой механики, спин квантуется по закону

где s – спиновое квантовое число.

По аналогии с орбитальным моментом импульса, проекция L_sz, спина квантуется так, что вектор L_s, может принимать 2s + 1 ориентаций. Так как в опытах Штерна и Герлаха наблюдались только две ориентации, то 2s + 1 = 2, откуда s = 1 / 2. Проекция спина на направление внешнего магнитного поля, являясь квантованной величиной, определяется выражением

где m_s – магнитное спиновое квантовое число; оно может иметь только два значения: m_s = ± ½.

Таким образом, опытные данные привели к необходимости характеризовать электроны (и микрочастицы вообще) добавочной внутренней степенью свободы. Поэтому для полного описания состоянии электрона в атоме необходимо наряду с главным, орбитальным и магнитным квантовыми числами задавать еще магнитное спиновое квантовое число.

Движение электрона в атоме водорода по круговой орбите радиусом r описывается уравнением:

Найдем радиус n-орбиты:

Для атома водорода радиус первой орбиты электрона (первый боровский радиус) равен

Принцип запрета Паули

Если перейти от рассмотрения движения одной микрочастицы (одного электрона) к многоэлектронным системам, то проявляются особые свойства, не имеющие аналога в классической физике. Пусть квантово-механическая система состоит из одинаковых частиц, например электронов. Все электроны имеют одинаковые физические свойства – массу, электрический заряд, спин и др. внутренние характеристики (например, квантовые числа). Такие частицы называют тождественными, которые невозможно экспериментально различить тождественные частицы.

В классической механике даже одинаковые частицы можно различить но положению в пространстве и импульсам. Если частицы в какой-то момент времени пронумеровать, то в следующие моменты времени можно проследить за траекторией любой из них. Классические частицы, таким образом, обладают индивидуальностью.

В квантовой механике положение иное. Из соотношения неопределенностей вытекает, что для микрочастиц вообще неприменимо понятие траектории; состояние микрочастицы описывается волновой функцией, позволяющей вычислять лишь вероятность (|Ψ| 2 ) нахождения микрочастицы в окрестностях той или иной точки пространства. Если же волновые функции двух тождественных частиц в пространстве перекрываются, то разговор о том, какая частица находится в данной области, лишен смысла: можно лишь говорить о вероятности нахождения в данной области одной из тождественных частиц. Таким образом, в квантовой механике тождественные частицы полностью теряют свою индивидуальность и становятся неразличимыми.

Принцип неразличимости тождественных частиц ведет к определенному свойству симметрии волновой функции. Если при перемене частиц местами волновая функция не меняет знака, то она называется симметричной,если меняет антисимметричной.Изменение знака волновой функции не означает изменения состояния, так как физический смысл имеет лишь квадрат модуля волновой функции. В квантовой механике доказывается, что характер симметрии волновой функции не меняется со временем.

Установлено, что симметрия или антисимметрия волновых функций определяется спином частиц. В зависимости от характера симметрии все элементарные частицы и построенные из них системы (атомы, молекулы) делятся на два класса.

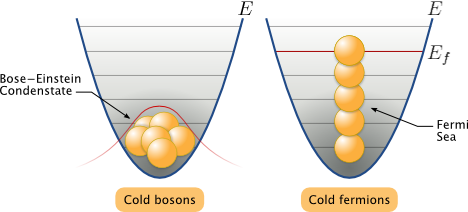
Частицы с полуцелым спином (например, электроны, протоны, нейтроны) описываются антисимметричными волновыми функциями и подчиняются статистике Ферми – Дирака; эти частицы называются фермионами.

Частицы с нулевым или целочисленным спином (например, π-мезоны, фотоны) описываются симметричными волновыми функциями и подчиняются статистике Бозе – Эйнштейна; эти частицы называются бозонами.

Сложные частицы (например, атомные ядра), составленные из нечетного числа фермионов, являются фермионами (суммарный спин – полуцелый), а из четного бозонами (суммарный спин целый).

Зависимость характера симметрии волновых функций системы тождественных частиц от спина частиц теоретически обоснована швейцарским физиком В. Паули (1900—1958), что явилось еще одним доказательством того, что спин является фундаментальной характеристикой микрочастиц.

Квантово-механическая формулировка принципа Паули:

Два одинаковых фермиона, входящих в одну систему, не могут находиться в одинаковых состояниях, так как для фермионов волновая функция должна быть антисимметричной.

Отметим, что число однотипных бозонов, находящихся в одном и том же состоянии, не лимитируется.

Таким образом, принцип Паули утверждает, что два электрона, связанные в одном и том же атоме, различаются значениями по крайней мере одного квантового числа.

Согласно принципу, данному п соответствует п 2 различных состояний электронов, отличающихся значениями l и т_l. Квантовое число m_s, может принимать лишь два значения (±1/2). Поэтому максимальное число электронов, находящихся в состояниях, определяемых данным главным квантовым числом, равно

Совокупность электронов в многоэлектронном атоме, имеющих одно и то же главное квантовое число n, называют электронной оболочкой.

В каждой из оболочек электроны распределяются по подоболочкам, соответствующим данному l. Поскольку орбитальное квантовое число принимает значения от 0 до п – 1, число подоболочек равно порядковому номеру п оболочки. Количество электронов в подоболочке определяется магнитным и магнитным спиновым квантовыми числами: максимальное число электронов в под оболочке с данным l равно 2 (2l+ 1).

Многоэлектронный атом

В многоэлектронном атоме, заряд которого равен Ze, электроны будут занимать различные «орбиты» (оболочки). При движении вокруг ядра Z‑электроны располагаются в соответствии с квантово‑механическим законом, который называется принципом Паули (1925 г.). Он формулируется так:

1. В любом атоме не может быть двух одинаковых электронов, определяемых набором четырех квантовых чисел: главного n, орбитального /, магнитногоm и магнитного спиновогоm_s.

2. В состояниях с определенным значением могут находиться в атоме не более 2n 2 электронов.

Значит, на первой оболочке («орбите») могут находиться только 2 электрона, на второй – 8, на третьей – 18 и т. д.

Таким образом, совокупность электронов в многоэлектронном атоме, имеющих одно и то же главное квантовое число n, называют электронной оболочкой . В каждой из оболочек электроны располагаются по подоболочкам, которые соответствуют определенному значению /. Так как орбитальное квантовое число l принимает значения от 0 до (n – 1), число подоболочек равно порядковому номеру оболочки п. Количество электронов в подоболочке определяется магнитным квантовым числом m_l и магнитным спиновым числом m_s.