Волновое уравнение. Плоская и сферическая волны. Представление волн в комплексной форме
Электромагнитная природа света, уравнения Максвелла.
Свет — электромагнитное излучение, испускаемое нагретым или находящимся в возбуждённом состоянии веществом, воспринимаемое человеческим глазом. Нередко, под светом понимают не только видимый свет, но и примыкающие к нему широкие области спектра. В физике свет изучается в разделе Оптика. Свет может рассматриваться либо как электромагнитная волна, скорость распространения в вакууме которой постоянна, либо как поток фотонов: частиц, обладающих определённой энергией и нулевой массой покоя.
Видимый свет — электромагнитное излучение с длинами волн ≈ 380—760 нм (от фиолетового до красного). rot E = -∂B/∂t — закон Джоуля-Ленца . rot H = j+dD/∂t — закон Био-Савара-Лапласа . 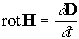
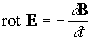
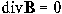
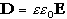
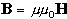
√ᵋᵋ0 Е=√µµ0 Н- уравнение связи
Волновое уравнение. Плоская и сферическая волны. Представление волн в комплексной форме.
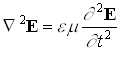
E=E0 cos (wt-(k,r)); k-волновое число. H= H0 cos(wt-(k,r)); c— скор света
Позволяет предположить что свет — электромагнитные волны распространяющиеся в пространстве со скоростью С и имеет определенную длину волны и частоту. Уравнением волны называется выражение, которое дает смещение колеблющейся точки как функцию ее координат (x, y, z) и времени t. Введем волновое число , или в векторной форме:
где 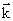
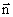
Так как 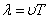
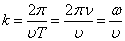
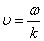
В случае, когда скорость волны υ во всех направлениях постоянна, а источник точечный, волна будет сферической. 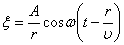
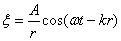
Плоская волна
Определение и основные понятия плоской волны
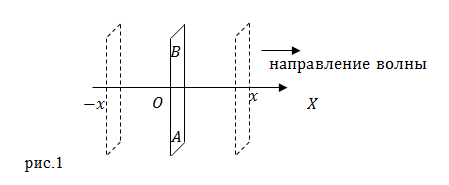
Пусть источником волн в бесконечной упругой среде является бесконечно большая пластина. Она совершает колебания вдоль оси X, плоскость пластины перпендикулярна оси X (рис.1).
Пластина совершает гармонические колебания. Введем следующие обозначения: $s_0$ — смещение точек пластины AB и примыкающих к ней частиц среды от положения равновесия; $A_0$ — амплитуда колебаний пластины; $\varphi $ — фаза колебаний; $\omega $ — циклическая частота колебаний. Уравнение колебаний пластины имеет вид:
В таком случае в среде распространяется гармоническая волна такой же частоты. Если среда является однородной и изотропной, то колебания всех частиц вещества на одинаковых расстояниях от пластины идентичны (совпадают амплитуды и начальные фазы колебаний). То есть волновые поверхности имеют вид параллельных плоскостей, которые перпендикулярны оси X (направлению волны). Данные волны называют плоскими.
Волны, волновые поверхности которых представляют собой плоскости, называют плоскими.
Уравнение плоской волны
Колебания в точках среды, находящихся на расстоянии $x$ от плоскости AB отстают по фазе от колебаний источника на величину $kx$:
при отсутствии рассеяния энергии волны в веществе $A$=$A_0$. $k=\frac<2\pi ><\lambda >\ $- волновое число.
Для точек пространства находящихся правее плоскости AB $x>0$, для точек находящихся левее этой плоскости $x Пример 1
Задание: Плоская гармоническая волна распространяется по прямой, которая совпадает с осью X, в положительном направлении оси. Среда энергию не поглощает. Скорость распространения волны равна $v$. Амплитуда волны $A.$ Две точки, которые находятся на расстояниях $x_1\ и\ x_2$ от источника волны совершают колебания с разностью фаз $\Delta \varphi =\frac<3\pi ><5>$. Какова длина волны? Запишите уравнение волны.
Решение: Запишем уравнение плоской волны:
Фазы колебаний двух точек в этой волне равны:
\[<\varphi >_1=\omega t-kx_1+\varphi ;;\ <\varphi >_2=\omega t-kx_2+\varphi \left(1.3\right).\]
Найдем их разность:
\[\Delta \varphi =\omega t-kx_2+\varphi -\left(\omega t-kx_1+\varphi \right)=k\left(x_2-x_1\right)=\frac<2\pi ><\lambda >\left(x_2-x_1\right)\left(1.4\right).\]
Выразим длину волны ($\lambda $) из (1.4):
Для написания уравнения волны через известные из условий задачи величины используем формулу:
Можем записать уравнение волны:
Задание: В однородном упругом веществе имеется плоская стоячая волна вида: $s=A<\cos (\omega t)\ ><\cos (kx)\ >$. Нарисуйте графики зависимости $s\left(x\right)$ при $t=0$ и $t=\frac
Уравнение волны в комплексной форме
| Уравнения плоской и сферической волн |   |
Уравнением волны называется выражение, которое дает смещение колеблющейся точки как функцию ее координат (x, y, z) и времени t.
Эта функция должна быть периодической как относительно времени, так и координат (волна – это распространяющееся колебание, следовательно периодически повторяющееся движение). Кроме того, точки, отстоящие друг от друга на расстоянии l, колеблются одинаковым образом. Уравнение плоской волны Найдем вид функции x в случае плоской волны, предполагая, что колебания носят гармонический характер. Направим оси координат так, чтобы ось x совпадала с направлением распространения волны. Тогда волновая поверхность будет перпендикулярна оси x. Так как все точки волновой поверхности колеблются одинаково, смещение x будет зависеть только от х и t:
Найдем вид колебания частиц в плоскости, соответствующей произвольному значению x. Чтобы пройти путь x, необходимо время Следовательно, колебания частиц в плоскости x будут отставать по времени на t от колебаний частиц в плоскости
– это уравнение плоской волны. Таким образом, x есть смещение любой из точек с координатой x в момент времени t. При выводе мы предполагали, что амплитуда колебания Такой же вид уравнение (5.2.3) будет иметь, если колебания распространяются вдоль оси y или z. В общем виде уравнение плоской волны записывается так:
Выражения (5.2.3) и (5.2.4) есть уравнения бегущей волны. Уравнение (5.2.3) описывает волну, распространяющуюся в сторону увеличения x. Волна, распространяющаяся в противоположном направлении, имеет вид: Уравнение волны можно записать и в другом виде. Введем волновое число
где Так как
Уравнение сферической волны В случае, когда скорость волны υ во всех направлениях постоянна, а источник точечный, волна будет сферической. Предположим, что фаза колебаний источника равна wt (т.е.
где А равна амплитуде на расстоянии от источника равном единице. Уравнение (5.2.7) неприменимо для малых r, т.к. при источники: http://www.webmath.ru/poleznoe/fizika/fizika_82_ploskaja_volna.php http://ens.tpu.ru/POSOBIE_FIS_KUSN/%D0%9A%D0%BE%D0%BB%D0%B5%D0%B1%D0%B0%D0%BD%D0%B8%D1%8F%20%D0%B8%20%D0%B2%D0%BE%D0%BB%D0%BD%D1%8B.%20%D0%93%D0%B5%D0%BE%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B0%D1%8F%20%D0%B8%20%D0%B2%D0%BE%D0%BB%D0%BD%D0%BE%D0%B2%D0%B0%D1%8F%20%D0%BE%D0%BF%D1%82%D0%B8%D0%BA%D0%B0/05-2.htm |
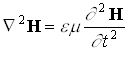
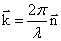
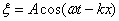

 .
. . Пусть колебание точек, лежащих в плоскости
. Пусть колебание точек, лежащих в плоскости  , имеет вид (при начальной фазе
, имеет вид (при начальной фазе  )
)

 .
. ,
, . Это будет, если энергия волны не поглощается средой.
. Это будет, если энергия волны не поглощается средой. , или
, или  .
. .
. , или в векторной форме:
, или в векторной форме: ,
, – волновой вектор,
– волновой вектор,  – нормаль к волновой поверхности.
– нормаль к волновой поверхности. , то
, то  . Отсюда
. Отсюда  . Тогда уравнение плоской волны запишется так:
. Тогда уравнение плоской волны запишется так: .
. ). Тогда точки, лежащие на волновой поверхности радиуса r, будут иметь фазу
). Тогда точки, лежащие на волновой поверхности радиуса r, будут иметь фазу  . Амплитуда колебаний здесь, даже если волна не поглощается средой, не будет постоянной, она убывает по закону
. Амплитуда колебаний здесь, даже если волна не поглощается средой, не будет постоянной, она убывает по закону  . Следовательно, уравнение сферической волны:
. Следовательно, уравнение сферической волны: , или
, или  ,
, , амплитуда стремится к бесконечности. То, что амплитуда колебаний
, амплитуда стремится к бесконечности. То, что амплитуда колебаний  , следует из рассмотрения энергии, переносимой волной.
, следует из рассмотрения энергии, переносимой волной.