Уравнение вращательного движения маятника обербека

Отчет по работе №1.04 «Изучение законов механики на маятнике обербека»

Псковский политехнический институт

Филиал Санкт — Петербургского государственного университета.

Отчет по работе №1.04

«Изучение законов механики

на маятнике обербека».

Цель работы: Изучить законы механики вращательного движения тел.

Механическое движение — это изменение взаимного расположения тел (или частей одного тела), происходящее в пространстве с течением времени.

Движение тел характеризуется траекторией, перемещением, путём, скоростью и ускорением.

Траектория — геометрическое место точек пространства через которое проходит в своём движении тело. В зависимости от траектории движения делятся на прямолинейные и криволинейные.

Положение тела в пространстве характеризует радиус-вектор,(рис.1). Перемещение — вектор, проведённый из начальной в конечную точку

участка траектории и определяющий изменение радиуса — вектора

Путь — длина отрезка траектории отсчитанного вдоль неё

Скорость — векторная физическая величина, характеризующая быстроту перемещения тел (материальной точки)

Ускорение — векторная физическая величина, характеризующая быстро ту изменения скорости

Кинематика — раздел механики, изучающий законы механического движения без анализа причин, его вызывающих. Закон движения материальной точки

динамика — раздел механики, изучающий механическое движение с выяснением причины вызывающей это движение. В основе динамики лежат за коны Ньютона, которые утверждают, что причиной изменения скорости тел является взаимодействие тел.

Сила — векторная физическая величина, являющаяся мерой механического взаимодействия тел.

Инертность — свойство тел сохранять свое механическое состояние. Мерой инертности в поступательном движении является масса, во вращательном — момент инерции.

Второй закон Ньютона утверждает, что ускорение тела пропорционально равнодействующей силе и обратно пропорционально массе этого тела

Мерами движения тел служат: импульс и кинетическая энергия. Соответственно, мерами действия силы во времени является импульс силы, а в пространстве — работа.

Механическая работа равна скалярному произведению силы на перемещение

Основные теоремы динамики:

Изменение импульса тела равно импульсу всех приложенных к телу внеш них сил

Если силы обладают таким свойством, что работа их сил не зависит от формы траектории, то силы называются потенциальными. Примером потенциальной силы является сила тяжести, а силы непотенциальной — сила трения.

В курсе механики доказывается, что работа потенциальных сил равна убыли потенциальной энергии

Потенциальной энергией называется энергия которой обладают тела при их взаимодействии, например тело, поднятое над Землей на высоту h, обладает потенциальной энергией взаимодействия равной

Полная механическая энергия равна сумме кинетической и потенциальной энергий

Теорема об изменении полной механической энергии утверждает, что изменение этой энергии равно работе непотенциальных сил

Вращательное движение как частный случай криволинейного движения возникает тогда, когда вектор силы действующей на тело перпендикулярен вектору скорости. Траекторией движения тела является окружность.. Кинематическими характеристиками движения являются: угол поворота радиус-вектора, угловая скорость и угловое ускорение. Направление вектора W определяется правилом правого винта (рис.2).

Основное уравнение кинематики вращательного движения

Основное уравнение динамики вращательного движения твёрдого тела относительно неподвижной оси имеет вид

Это уравнение аналогично уравнению Ньютона для движения материальной точки (4): роль силы играет момент силы, роль массы — момент инерции, а роль ускорения — угловое ускорение.

С помощью маятника Обербека (рис. 3) можно экспериментально проверить уравнение (11) что является одновременно и проверкой основных положений механики по вращению твёрдого тела.

В маятнике Обербека вращающий момент М создаётся силой натяже ния нити Т

где 1 — радиус шкива (Р = Р. или Р.

Величину силу Т легко найти из уравнения движения платформы с перегруз ком

Ускорение а можно найти, если измерить время, в течение которого нагруженная платформа из состояния покоя опускается на расстояние h.

Момент инерции всей системы можно вычислить по формуле

Таким образом, используя уравнения (12, 13, 14, 15, 16) и проведя соответствующие измерения, можно проверить закон вращательного движения (11).

На практике значительное влияние может оказать момент сил трения, приложенный к осям маятника. Неучёт его может сильно исказить результаты опыта. Преобразуем уравнение (11) выделив момент сил трения в явном виде

Экспериментальная работа делится на три части:

в первой — исследуется вращательное движение маятника под действием раз личных перегрузков при постоянном моменте инерции системы. Из данных этого опыта определяют момент инерции системы 1 и момент сил трения. Во второй части — изучается вращение маятника при различных значениях момента инерции грузов относительно оси вращения, те. при различных положениях грузов, на спинах маятника Обербека;

в третьей части проверяется преобразование механической энергии при вращательном движении.

Энергия маятника Обербека складывается из собственно энергии маятника и энергии платформы. В начальный момент времени кинетическая энергия маятника и платформы равна нулю. Потенциальная энергия платформы:

После того как платформа опустилась с высоты h, кинетическая энергия маятника станет равной

Тогда согласно теореме об изменении полной механической энергии (9)

где А, — работа сил трения в системе.

Работа силы тяжести равна изменению потенциальной энергии

На рис.1 показан маятник Обербека — прибор для исследования законов вращательного движения. Каждый груз, имеет свой момент инерции относительно своего центра масс:

Лабораторные работы по физике

ИЗУЧЕНИЕ ЗАКОНОВ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ НА МАЯТНИКЕ ОБЕРБЕКА

Цель работы: 1) изучение кинематических и динамических характеристик вращательного движения;

2) экспериментальное определение момента инерции крестовины маятника Обербека и момента сил трения;

3) проверка справедливости закона сохранения (превращения) энергии механической системы.

Схема экспериментальной установки

1 – ось вращения;

Основным элементом маятника Обербека (рис. 1) является крестовина, способная свободно вращаться вокруг неподвижной горизонтальной оси 1. Крестовина состоит из четырех стержней 2 с грузами-насадками 3, расположенными симметрично относительно оси вращения. С крестовиной жестко скреплен шкив 4 радиусом R. На шкив намотана нить 5, перекинутая через легкий блок 6. К свободному концу нити привязан груз 7, массу которого m можно изменять в процессе опытов. Для измерения высоты h расположения груза над полом служит линейка 8, а для измерения времени его падения – секундомер 9.

Если поднятый на высоту h груз отпустить, то он начнет падать с ускорением , которое определяется вторым законом Ньютона. На груз действуют две силы: сила тяжести и сила натяжения нити (сопротивлением воздуха в данном случае можно пренебречь). Уравнение основного закона динамики:

в проекциях на направление движения груза имеет вид:

Пренебрегая массами нити 5 и блока 6, можно считать, что нить действует на поверхность шкива касательной силой , равной по модулю силе : | | = | | = Fн . Касательная сила создает вращающий момент , по модулю равный произведению модуля силы на ее плечо, т.е. на радиус шкива R: Мн = Fн R. С учетом (1) вращающий момент силы натяжения нити равен

Под действием момента крестовина начинает вращаться с угловым ускорением . При этом на оси вращения возникают, хотя и незначительные, силы трения. Эти силы создают тормозящий момент , направленный противоположно угловому ускорению. С учетом направления моментов сил натяжения и трения алгебраическая запись уравнения основного закона динамики вращательного движения имеет вид

J e = Мн – Мтр , (3)

где J – момент инерции крестовины маятника Обербека относительно оси вращения.

Известно, что момент инерции зависит только от распределения массы тела относительно оси. Для крестовины маятника величина J определяется в основном положением грузов-насадок 3 на стержнях 2. Если их положение в ходе опытов не изменяется, то и момент инерции остается постоянным. Момент сил трения также можно считать практически неизменным. Поэтому зависимость углового ускорения e от момента силы натяжения Мн , согласно уравнению (3), имеет линейный характер. Определив опытным путем значения e при различных Мн и обработав соответствующим образом полученную экспериментальную зависимость e (Мн), с помощью этого уравнения можно найти неизвестные величины J и Мтр . Рассмотрим теперь методику измерения углового ускорения e и момента силы натяжения Мн .

Так как нить 5 практически нерастяжима, все ее точки, включая точки на поверхности шкива, движутся с одинаковым ускорением , равным по модулю ускорению падающего груза : | | = | | = a. Груз падает с высоты h равноускоренно; при этом за время t он проходит путь

Измерив высоту h и время падения груза t, можем найти ускорение

Если известны масса груза т и радиус шкива R, то по формуле (2) можно рассчитать момент силы натяжения нити Мн .

Угловое ускорение вращения шкива, а следовательно, и крестовины и тангенциальное (касательное) ускорение точек на поверхности шкива связаны известным соотношением

Таким образом, зная массу груза т, радиус шкива R и высоту h, с которой падает груз, а также измерив время его падения t, можно экспериментально определить величины e и Мн .

Рассмотрим теперь превращение энергии в вышеописанном опыте. Поднятый на высоту h груз обладает потенциальной энергией

кинетическая энергия системы «груз + крестовина» при этом равна нулю. В момент падения груза на пол его потенциальная энергия обращается в ноль, но за счет ее уменьшения груз приобретает кинетическую энергию

а крестовина – кинетическую энергию вращения

где v – скорость груза в момент падения; w – угловая скорость вращения крестовины к этому моменту.

Итак, начальное значение полной механической энергии рассматриваемой системы равно W0 = Wp , а конечное W = Wk1 + Wk2 . Изменение энергии:

Как известно, изменение полной механической энергии консервативной системы равно нулю, а при наличии неконсервативных сил – их работе. В данной системе действуют неконсервативные силы трения, работа которых равна

где j – угол поворота крестовины за время падения груза. Знак « – » отражает тот факт, что работа сил трения и сопротивления всегда отрицательна (угол между направлениями силы и перемещения равен 180 ° ). Итак, закон сохранения (превращения) энергии в данном случае можно записать как

С учетом соотношений (6)-(9) уравнение (10) примет вид:

Для экспериментальной проверки справедливости уравнения (11) необходимо знать все входящие в него величины. К ним относятся, во-первых, заранее известные ускорение свободного падения g, масса груза т и высота h; во-вторых, определяемые путем обработки экспериментальной зависимости момент инерции крестовины J и момент сил трения Мтр ; в-третьих, кинематические характеристики системы v, w и j . Остановимся на определении последних.

Скорость груза в момент его падения на пол найдем исходя из закономерностей равноускоренного движения:

Такую же по величине скорость имеют и точки на поверхности шкива. Используя связь между линейной и угловой скоростями, получим

Так как линейное расстояние, пройденное точками на поверхности шкива, равно перемещению груза за тот же промежуток времени, угол j (в радианах) может быть рассчитан как

Порядок измерений и обработки результатов

1. Запишите радиус шкива R , выразив его в метрах, в тетрадь (R=17мм).

2. Занесите во второй столбец таблицы 1 значение массы груза т (в кг).

3. Вращая крестовину, намотайте нить на шкив так, чтобы нижняя поверхность груза 7 оказалась на заданной высоте h над полом, запишите значение высоты в тетрадь (значение h задает преподаватель или спишите с экрана монитора).

4. Отпустив крестовину, одновременно включите секундомер, а в момент касания грузом пола – выключите. Запишите время падения в третий столбец таблицы 1.

5. Повторите пп. 3 и 4 с тем же грузом еще два раза. Рассчитайте и занесите в таблицу среднее из трех значений времени t.

6. Увеличивая массу груза согласно рекомендациям, выполните пп. 2-5 еще пять раз.

7. Для каждого из шести проделанных опытов рассчитайте ускорение а по формуле (4), подставляя в нее среднее из трех измеренных значений времени падения t. Величину а (с точностью не менее чем до трех значащих цифр) запишите в четвертый столбец таблицы 1.

8. По формулам (2) и (5) вычислите значения момента силы натяжения нити Мн и углового ускорения e . Результаты занесите в соответствующие столбцы табл. 1.

9. Руководствуясь правилами [1], постройте график зависимости углового ускорения от момента силы натяжения (в данной работе необходимо, чтобы начало координат совпадало с нулевыми значениями откладываемых величин e и Мн). Нанесите на график экспериментально полученные точки.

10. Одним из описанных ниже способов* обработайте линейную экспериментальную зависимость e (Мн) и найдите значения момента инерции крестовины J и момента сил трения Мтр. Запишите эти значения в тетрадь.

11. Для одного из проделанных опытов рассчитайте по формулам (12)-(14) скорость груза v, угловую скорость вращения w и угол поворота j крестовины маятника Обербека в момент падения груза на пол.

12. Вычислите значения левой и правой частей уравнения закона сохранения энергии (11). Сравнив эти значения между собой, сделайте выводы.

Обработка зависимости e (Мн)

Угловое ускорение крестовины e и момент силы натяжения нити Мн связаны уравнением основного закона динамики вращательного движения (3). Зависимость e (Мн) можно представить в виде

где . Таким образом, определив коэффициенты линейной зависимости (15) K и b, легко найти момент инерции J и момент сил трения Мтр :

Обработку экспериментальной зависимости e (Мн) можно провести либо графически, либо методом наименьших квадратов.

Графический способ. По экспериментальным точкам проведите сглаживающую прямую. Из уравнения (3) следует, что угловое ускорение e обращается в нуль при Мн = Мтр . Таким образом, момент сил трения Мтр определяется (с учетом масштаба!) отрезком, отсекаемым проведенной прямой на оси абсцисс (рис. 2).

Величина K в уравнении (15) представляет собой угловой коэффициент прямой, т.е. тангенс угла ее наклона к оси абсцисс. Согласно (16), момент инерции J есть величина, обратная K, – значит, его можно найти как котангенс этого угла. Выбрав на сглаживающей прямой две достаточно удаленные друг от друга точки, рассчитайте значение J как отношение отрезков

причем величины отрезков D Мн и D e должны быть взяты с учетом масштаба графика и выражены в соответствующих единицах измерения: D Мн – в Н × м, а D e – в рад/с2 или в с – 2. Только в этом случае результат будет правильным, и момент инерции будет иметь размерность кг × м2.

Метод наименьших квадратов. (Подробно этот метод рассмотрен в [1]). Изучив данный материал, заполните два последних столбца табл. 1. Найдите суммы значений величин в последних четырех столбцах и занесите их в строку « S = ». Вычислите коэффициенты K и b зависимости (15); результаты расчетов запишите в тетрадь. Для определения момента инерции крестовины J и момента сил трения Мтр воспользуйтесь соотношениями (16). На графике зависимости e (Мн) проведите прямую по двум точкам, координаты которых рассчитайте по найденным значениям коэффициентов. Убедитесь в правильности проведенных расчетов (прямая должна «наилучшим» образом пройти через экспериментальные точки).

Какие величины характеризуют вращательное движение?

Что характеризует момент инерции твердого тела относительно оси вращения? Как он рассчитывается?

Сформулируйте и докажите теорему Штейнера.

Как изменится кинетика опускания гири, если грузы на крестовине передвинуть ближе (дальше) к оси вращения.

Дайте определение момента силы. Какие моменты сил действуют на крестовину маятника Обербека в этой работе.

Запишите математически и сформулируйте главный закон динамики вращательного движения.

Покажите, что в пренебрежении трением, расчетная формула для момента инерции маятника Обербека будет иметь вид:
.

Запишите и поясните закон сохранения (превращения) механической энергии в этой работе.

НА МАЯТНИКЕ ОБЕРБЕКА

Цели и задачи работы: изучение законов вращательного движения твердого тела; определение момента инерции маятника Обербека.

Твердое тело можно рассматривать как систему материальных точек, расстояние между которыми неизменно. Вращательным движением твердого тела называется такое движение, при котором траектории всех точек тела являются концентрическими окружностями с центром на одной прямой, называемой осью вращения. 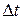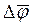Пусть твердое тело, вращаясь вокруг неподвижной в данной системе отсчета оси 00 / , совершило за время бесконечно малый поворот (рис. 1).

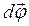
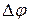
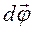
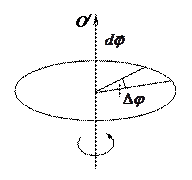
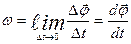
Соответствующий угол поворота характеризуется вектором , модуль которого равен углу поворота , а направление совпадает с осью 00 / , причем так, что направления вращения и вектора отвечают правилу правого винта. Величина

(1),

характеризующая быстроту изменения угла поворота, называется угловой скоростью. Направление вектора угловой скорости совпадает с направлением вектора 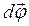. Единица угловой скорости – радиан в секунду (рад/с).

При вращательном движении все точки тела имеют одинаковую угловую скорость и угловое ускорение, но линейная скорость различна. Линейная скорость любой точки твердого тела равна векторному произведению угловой скорости на радиус-вектор, соединяющий эту точку с произвольной точкой О оси вращения (рис. 2)

(2)

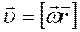
Модуль вектора линейной скорости равен

(3)

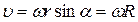
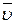
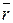
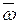
где R — радиус окружности, которую описывает рассматриваемая точка. Вектор направлен в сторону вращения по касательной к траектории и перпендикулярен плоскости, в которой лежат и .

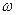
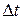
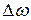
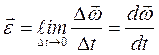
При неравномерном вращении величина меняется со временем и за промежуток времени получает приращение . Величина

(4),

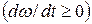
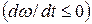
характеризующая быстроту изменения во времени угловой скорости, называется угловым ускорением вращающегося тела. Если тела вращается вокруг неподвижной оси, то вектор углового ускорения направлен вдоль этой же оси; в ту же сторону, что и вектор угловой скорости, при ускоренном вращении и в противоположную – при замедленном вращении . Единица углового ускорения – радиан на секунду в квадрате (рад/с 2 ).

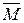
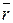
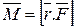
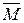
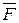
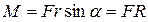
При вращательном движении тела изменение его кинематических и динамических величин зависит от действующего на тело вращательного момента сил и момента инерции тела. Моментом силы называется векторная величина , равная векторному произведению радиус–вектора , проведенного из точки О в точку приложения силы А, на вектор силы

(5)

Вектор перпендикулярен плоскости, в которой расположен вектор силы и радиус – вектор и образует с ними правовинтовую пару (рис. 3) Модуль вектора равен

(6)

где R — плечо вектора 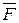относительно т. О.

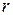
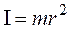
Моментом инерции материальной точки относительно какой-либо оси называется произведение ее массы на квадрат расстояния от оси вращения:

(7)

Момент инерции тела равен сумме моментов инерции всех материальных точек

(8)

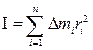
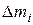
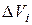
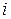
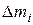
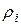
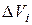
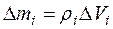
где — элементарная масса, заключенная в объеме — й частицы. Элементарная масса равен произведению плотности тела в данной точке на соответствующий элементарный объем :

(9)

Следовательно, момент инерции можно представить в виде:

(10)

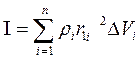
Если плотность тела постоянная, ее можно вынести за знак суммы:

(11)

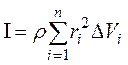
Соотношения (10) и (11) являются приближенными, причем тем более точными, чем меньше элементарные объемы и соответствующие им элементарные массы. Следовательно, задача нахождения моментов инерции сводится к интегрированию:

(12)

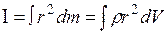
Момент инерции является физической величиной, характеризующей инертность тела при изменении им угловой скорости под действием вращающего момента.

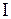
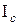
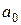
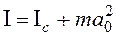
В случаях, когда ось вращения тела произвольна, то вычисление момента инерции значительно упрощается, если воспользоваться теоремой Штейнера: момент инерции относительно произвольной оси равен сумме момента инерции относительно геометрической оси и произведения масса тела на квадрат расстояния между осями:

(13)

Основной закон динамики вращательного движения твердого тела относительно неподвижной оси z записывается следующим образом:

(14)

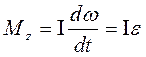
где М_z — суммарный момент всех внешних сил относительно оси вращения.

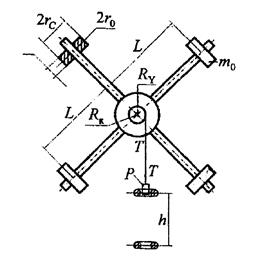
Экспериментальная установка (рис. 4, маятник Обербека) состоит из четырех стержней, укрепленных на втулке под прямым углом друг к другу. На ту же втулку насажены два шкива с радиусами R_м и R_б . Эта система может вращаться свободно вокруг горизонтальной оси. Момент инерции системы можно изменять, передвигая цилиндрические грузы вдоль стержней.

Момент силы создается грузом Р, привязанным к нити, которая навита на один из шкивов. Груз Р удерживается на высоте h и обладает потенциальной энергией mgh, где m — масса груза; g — ускорение свободного потения. Если предоставить грузу возможность падать, то это падение будет происходить с ускорением 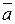. При этом шкив со стержнями и расположенными на нем грузами будет вращаться с угловым ускорением .

Измеряя время t, в течение которого груз Р из состояния покоя опустится на расстояние h, можно найти ускорение груза:

(15),

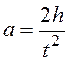
которое связано с угловым ускорением соотношением

(16)

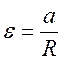
где R — радиус шкива.

Если через Т обозначить силу натяжения нити, то вращающий момент сил будет определяться по формуле:

(17).

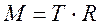
Силу Т можно найти из уравнения движения груза Р:

(18)

(19)

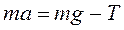
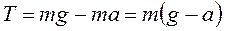
Подставляя (19) в (17), получим формулу для момента сил:

(20)

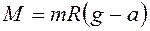
Момент инерции всей системы можно вычислить по следующей формуле:

(21)

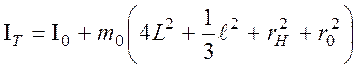
где L, , r_{H ,} r₀ – параметры, указанные на рис. 4.

Оборудование, технические и инструментальные средства: маятник Обербека, грузы, штангенциркуль, счетчик-секундомер.

Порядок выполнения работы:

1. Установить цилиндрические грузы массой m₀ на некотором расстоянии L от оси маятника так, чтобы маятник находился в безразличном равновесии, для чего рекомендуется несколько раз привести маятник во вращение, каждый раз давая ему возможность остановиться. После этого окончательно определить расстояние L по формуле

(22)

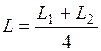
где L₁ и L₂ — расстояния между центрами цилиндрических грузов на стержнях.

2. Измерить размеры цилиндрического груза и радиусы R_M малого и R_б большего шкивов, внешний r_H, внутренний r₀ радиусы и длину образующей 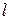цилиндрического груза.

3. Измерить высоту h — расстояние между двумя датчиками.

4. Прикрепить к нити, намотанной на шкив радиуса R_M , груз массой m .

5. Включить счетчик – секундомер.

6. Отпустить груз и определить время его падения t с высоты h.

7. Вычислить линейное ускорение по формуле (15) и угловое ускорение по формуле (16)

8. Вычислить момент сил по формуле (20).

9. Повторить пункты 4-8 для двух-трех грузов других масс.

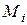
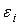
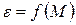
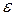
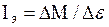
10. По вычисленным значениям и построить график зависимости , по оси ординат которого откладывают величину , по оси абсцисс – момент силы М. Полученная зависимость должна быть линейная.

11. Из графика определите экспериментальный момент инерции системы и момент силы трения М_тр на оси вращения, способы нахождения которых показаны на рис. 5

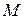
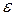
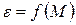
12. Повторить пункты 4-11 для шкива радиуса R_б. Выбирая масштаб для значений и , можно построить графики зависимости от малого и большего шкивов в одной системе координат и убедиться, что они лежат на одной прямой.

13. Определить теоретический момент инерции системы расчетным путем по формуле (21). Значение момента инерции 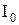маятника без цилиндрических грузов указано на установке.

14. Проверить сходимость экспериментально и теоретически полученных значений моментов инерции системы по формуле:

(23)

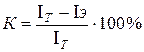
1. Результаты измерений и вычислений занести в таблицу:

Контрольные вопросы

1. Что такое вращательное движение?

2. Сформулируйте определения и напишите формулы для угловой скорости и углового ускорения. Укажите их направления и единицы измерения.

3. Какова связь между линейной и угловой скоростью?

4. Как направлена линейная скорость?

5. Что называется моментом инерции? Что характеризует эта величина?

6. Сформулируйте теорему Штейнера и запишите формулу закона.

7. Что такое момент сил? Как направлен вектор момента сил?

8. Основной закон динамики вращательного движения.