Уравнение вращательного движения прямоугольной пластины с заданными размерами

Сложное движение точки. Пример решения задачи

Теория, применяемая для решения приведенной ниже задачи, излагается на странице “Сложное движение точки, теорема Кориолиса”.

Условие задачи

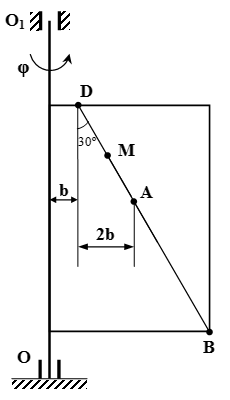
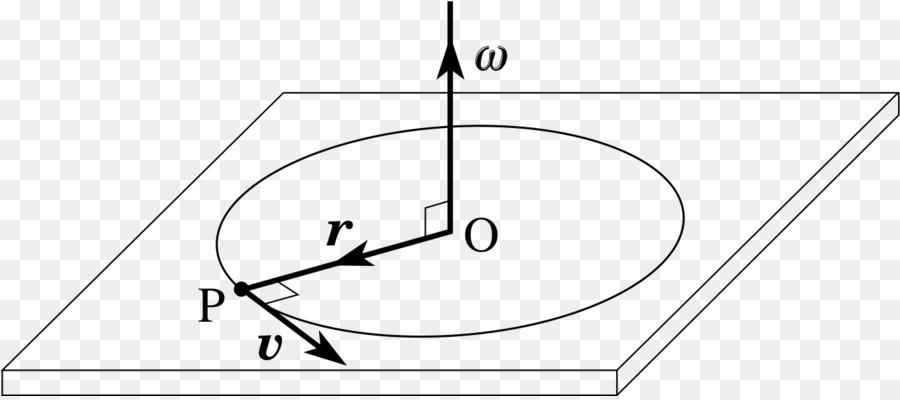
Прямоугольная пластина вращается вокруг неподвижной оси по закону φ = 6 t 2 – 3 t 3 . Положительное направление отсчета угла φ показано на рисунках дуговой стрелкой. Ось вращения OO ₁ лежит в плоскости пластины (пластина вращается в пространстве).

По пластине вдоль прямой BD движется точка M . Задан закон ее относительного движения, т. е. зависимость s = AM = 40( t – 2 t 3 ) – 40 ( s — в сантиметрах, t — в секундах). Расстояние b = 20 см . На рисунке точка M показана в положении, при котором s = AM > 0 (при s 0 точка M находится по другую сторону от точки A ).

Найти абсолютную скорость и абсолютное ускорение точки M в момент времени t ₁ = 1 с .

Указания. Эта задача – на сложное движение точки. Для ее решения необходимо воспользоваться теоремами о сложении скоростей и о сложении ускорений (теорема Кориолиса). Прежде чем производить все расчеты, следует по условиям задачи определить, где находится точка M на пластине в момент времени t ₁ = 1 с , и изобразить точку именно в этом положении (а не в произвольном, показанном на рисунке к задаче).

Решение задачи

Дано: b = 20 см , φ = 6 t 2 – 3 t 3 , s = |AM| = 40( t – 2 t 3 ) – 40 , t ₁ = 1 c .

Определение положения точки

Определяем положение точки в момент времени t = t ₁ = 1 c .
s = 40( t ₁ – 2 t ₁ 3 ) – 40 = 40(1 – 2·1 3 ) – 40 = –80 см.
Поскольку s 0 , то точка M ближе к точке B, чем к D.
|AM| = |–80| = 80 см.
Делаем рисунок.

Определение абсолютной скорости точки

Согласно теореме о сложении скоростей, абсолютная скорость точки равна векторной сумме относительной и переносной скоростей:
.

Определение относительной скорости точки

Определяем относительную скорость . Для этого считаем, что пластина неподвижна, а точка M совершает заданное движение. То есть точка M движется по прямой BD . Дифференцируя s по времени t , находим проекцию скорости на направление BD :
.
В момент времени t = t ₁ = 1 с ,
см/с.
Поскольку , то вектор направлен в направлении, противоположном BD . То есть от точки M к точке B . Модуль относительной скорости
v_от = 200 см/с .
Изображаем вектор на рисунке.

Определение переносной скорости точки

Определяем переносную скорость . Для этого считаем, что точка M жестко связана с пластиной, а пластина совершает заданное движение. То есть пластина вращается вокруг оси OO₁. Дифференцируя φ по времени t , находим угловую скорость вращения пластины:
.
В момент времени t = t ₁ = 1 с ,
.
Поскольку 0″ style=»width:48px;height:18px;vertical-align:-10px;background-position:-583px -267px»> , то вектор угловой скорости направлен в сторону положительного угла поворота φ , то есть от точки O к точке O₁. Модуль угловой скорости:
ω = 3 с -1 .
Изображаем вектор угловой скорости пластины на рисунке.

Из точки M опустим перпендикуляр HM на ось OO₁.
При переносном движении точка M движется по окружности радиуса |HM| с центром в точке H .
|HM| = |HK| + |KM| = 3 b + |AM| sin 30° = 60 + 80·0,5 = 100 см ;
Переносная скорость:
v_пер = ω|HM| = 3·100 = 300 см/с .

Вектор направлен по касательной к окружности в сторону вращения.

Определение абсолютной скорости точки

Определяем абсолютную скорость . Абсолютная скорость точки равна векторной сумме относительной и переносной скоростей:
.
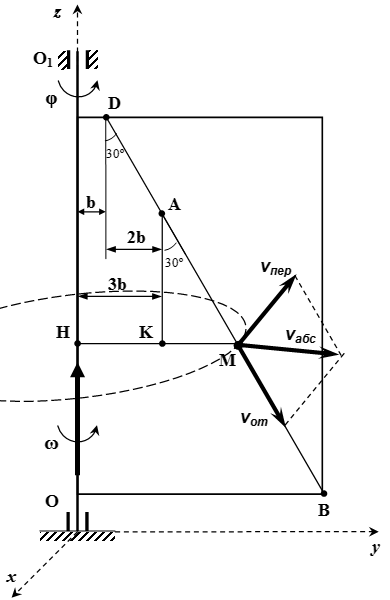
Проводим оси неподвижной системы координат Oxyz . Ось z направим вдоль оси вращения пластины. Пусть в рассматриваемый момент времени ось x перпендикулярна пластине, ось y лежит в плоскости пластины. Тогда вектор относительной скорости лежит в плоскости yz . Вектор переносной скорости направлен противоположно оси x . Поскольку вектор перпендикулярен вектору , то по теореме Пифагора, модуль абсолютной скорости:
.

Определение абсолютного ускорения точки

Согласно теореме о сложении ускорений (теорема Кориолиса), абсолютное ускорение точки равно векторной сумме относительного, переносного и кориолисова ускорений:
,
где
– кориолисово ускорение.

Определение относительного ускорения

Определяем относительное ускорение . Для этого считаем, что пластина неподвижна, а точка M совершает заданное движение. То есть точка M движется по прямой BD . Дважды дифференцируя s по времени t , находим проекцию ускорения на направление BD :
.
В момент времени t = t ₁ = 1 с ,
см/с 2 .
Поскольку , то вектор направлен в направлении, противоположном BD . То есть от точки M к точке B . Модуль относительного ускорения
a_от = 480 см/с 2 .
Изображаем вектор на рисунке.

Определение переносного ускорения

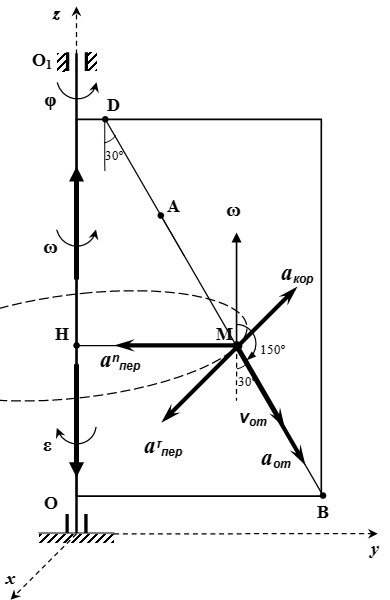
Определяем переносное ускорение . При переносном движении точка M жестко связана с пластиной, то есть движется по окружности радиуса |HM| с центром в точке H . Разложим переносное ускорение на касательное к окружности и нормальное ускорения:
.
Дважды дифференцируя φ по времени t , находим проекцию углового ускорения пластины на ось OO ₁ :
.
В момент времени t = t ₁ = 1 с ,
с –2 .
Поскольку , то вектор углового ускорения направлен в сторону, противоположную положительного угла поворота φ , то есть от точки O₁ к точке O. Модуль углового ускорения:
ε = 6 с -2 .
Изображаем вектор углового ускорения пластины на рисунке.

Переносное касательное ускорение:
a τ _пер = ε |HM| = 6·100 = 600 см/с 2 .
Вектор направлен по касательной к окружности. Поскольку вектор углового ускорения направлен в сторону, противоположную положительного угла поворота φ , то направлен в сторону, противоположную положительному направлению поворота φ . То есть направлен в сторону оси x .

Переносное нормальное ускорение:
a n _пер = ω 2 |HM| = 3 2 ·100 = 900 см/с 2 .
Вектор направлен к центру окружности. То есть в сторону, противоположную оси y .

Определение кориолисова ускорения

Кориолисово (поворотное) ускорение:
.
Вектор угловой скорости направлен вдоль оси z . Вектор относительной скорости направлен вдоль прямой |DB| . Угол между этими векторами равен 150° . По свойству векторного произведения,
.
Направление вектора определяется по правилу буравчика. Если ручку буравчика повернуть из положения в положение , то винт буравчика переместится в направлении, противоположном оси x .

Определение абсолютного ускорения

Абсолютное ускорение:
.
Спроектируем это векторное уравнение на оси xyz системы координат.

;

;

.
Модуль абсолютного ускорения:

.

Абсолютная скорость ;
абсолютное ускорение .

Автор: Олег Одинцов . Опубликовано: 10-01-2016

Вращательное движение твердого тела: уравнение, формулы

В природе и технике мы часто сталкиваемся с проявлением вращательного движения твердых тел, например, валов и шестерен. Как в физике описывают этот тип движения, какие формулы и уравнения для этого применяются, эти и другие вопросы освещаются в данной статье.

Что такое вращение?

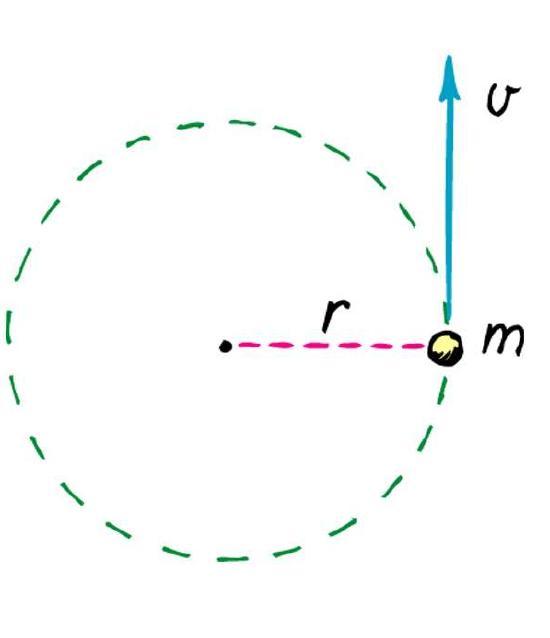
Каждый из нас интуитивно представляет, о каком движении пойдет речь. Вращение — это процесс, при котором тело или материальная точка движется по круговой траектории вокруг некоторой оси. С геометрической точки зрения ось вращения твердого тела — это прямая, расстояние до которой в процессе перемещения остается неизменным. Это расстояние называют радиусом вращения. Далее будем обозначать его буквой r. Если ось вращения проходит через центр масс тела, то ее называют собственной осью. Примером вращения вокруг собственной оси является соответствующее движение планет Солнечной системы.

Вам будет интересно: Афронт — это ситуация, в которой не хочется оказаться

Чтобы вращение происходило, должно существовать центростремительное ускорение, которое возникает за счет центростремительной силы. Эта сила направлена от центра масс тела к оси вращения. Природа центростремительной силы может быть самой разной. Так, в космическом масштабе ее роль выполняет гравитация, если тело закреплено нитью, то сила натяжения последней будет центростремительной. Когда тело вращается вокруг собственной оси, роль центростремительной силы играет внутреннее электрохимическое взаимодействие между составляющими тело элементами (молекулами, атомами).

Вам будет интересно: Декабрист Оболенский Евгений Петрович: биография. Декабристские организации

Необходимо понимать, что без присутствия центростремительной силы тело будет двигаться прямолинейно.

Описывающие вращение физические величины

Во-первых, это динамические характеристики. К ним относятся:

• момент импульса L;
• момент инерции I;
• момент силы M.

Во-вторых, это кинематические характеристики. Перечислим их:

• угол поворота θ;
• скорость угловая ω;
• ускорение угловое α.

Кратко опишем каждую из названных величин.

Момент импульса определяется по формуле:

Где p — линейный импульс, m — масса материальной точки, v — ее линейная скорость.

Момент инерции материальной точки рассчитывается с помощью выражения:

Для любого тела сложной формы величина I рассчитывается, как интегральная сумма моментов инерции материальных точек.

Момент силы M вычисляется так:

Здесь F — внешняя сила, d — расстояние от точки ее приложения до оси вращения.

Физический смысл всех величин, в названии которых присутствует слово «момент», аналогично смыслу соответствующих линейных величин. Например, момент силы показывает возможность приложенной силы сообщить угловое ускорение системе вращающихся тел.

Кинематические характеристики математически определяются следующими формулами:

Как видно из этих выражений, угловые характеристики аналогичны по своему смыслу линейным (скорости v и ускорению a), только они применимы для круговой траектории.

Динамика вращения

В физике изучение вращательного движения твердого тела осуществляется с помощью двух разделов механики: динамики и кинематики. Начнем с динамики.

Динамика изучает внешние силы, действующие на систему вращающихся тел. Сразу запишем уравнение вращательного движения твердого тела, а затем, разберем его составные части. Итак, это уравнение имеет вид:

Момент силы, который действует на систему, обладающую моментом инерции I, вызывает появление углового ускорения α. Чем меньше величина I, тем легче с помощью определенного момента M раскрутить систему до больших скоростей за малые промежутки времени. Например, металлический стержень легче вращать вдоль его оси, чем перпендикулярно ей. Однако, тот же стержень легче вращать вокруг оси, перпендикулярной ему, и проходящей через центр масс, чем через его конец.

Закон сохранения величины L

Выше была введена эта величина, она называется моментом импульса. Уравнение вращательного движения твердого тела, представленное в предыдущем пункте, часто записывают в иной форме:

Если момент внешних сил M действует на систему в течение времени dt, то он вызывает изменение момента импульса системы на величину dL. Соответственно, если момент сил равен нулю, тогда L = const. Это и есть закон сохранения величины L. Для нее, используя связь между линейной и угловой скоростью, можно записать:

L = m*v*r = m*ω*r2 = I*ω.

Таким образом, при отсутствии момента сил произведение угловой скорости и момента инерции является постоянной величиной. Этот физический закон используют фигуристы в своих выступлениях или искусственные спутники, которые необходимо повернуть вокруг собственной оси в открытом космосе.

Центростремительное ускорение

Выше, при изучении вращательного движения твердого тела, уже была описана эта величина. Также была отмечена природа центростремительных сил. Здесь лишь дополним эту информацию и приведем соответствующие формулы для расчета этого ускорения. Обозначим его ac.

Поскольку центростремительная сила направлена перпендикулярно оси и проходит через нее, то момента она не создает. То есть эта сила не оказывает совершенно никакого влияния на кинематические характеристики вращения. Тем не менее, она создает центростремительное ускорение. Приведем две формулы для его определения:

Таким образом, чем больше угловая скорость и радиус, тем большую силу следует приложить, чтобы удержать тело на круговой траектории. Ярким примером этого физического процесса является занос автомобиля во время поворота. Занос возникает, если центростремительная сила, роль которой играет сила трения, становится меньше, чем центробежная сила (инерционная характеристика).

Кинематика вращения

Три основные кинематические характеристики были перечислены выше в статье. Кинематика вращательного движения твердого тела формулами следующими описывается:

θ = ω*t => ω = const., α = 0;

θ = ω0*t + α*t2/2 => ω = ω0 + α*t, α = const.

В первой строке приведены формулы для равномерного вращения, которое предполагает отсутствие внешнего момента сил, действующего на систему. Во второй строке записаны формулы для равноускоренного движения по окружности.

Отметим, что вращение может происходить не только с положительным ускорением, но и с отрицательным. В этом случае в формулах второй строки следует перед вторым слагаемым поставить знак минус.

Пример решения задачи

На металлический вал в течение 10 секунд действовал момент силы 1000 Н*м. Зная, что момент инерции вала равен 50 кг*м2, необходимо определить угловую скорость, которую придал валу упомянутый момент силы.

Применяя основное уравнение вращения, вычислим ускорение вала:

Поскольку это угловое ускорение действовало на вал в течение времени t = 10 секунд, то для вычисления угловой скорости применяем формулу равноускоренного движения:

Здесь ω0 = 0 (вал не вращался до действия момента сил M).

Подставляем в равенство численные значения величин, получаем:

ω = 1000/50*10 = 200 рад/с.

Чтобы это число перевести в привычные обороты в секунду, необходимо его поделить на 2*pi. Выполнив это действие, получаем, что вал будет вращаться с частотой 31,8 об./с.

Уравнение вращательного движения прямоугольной пластины с заданными размерами

2017-05-21
Тонкая прямоугольная пластина может свободно вращаться вокруг горизонтальной оси $aa^< \prime>$, совпадающей с одной из ее коротких сторон (рис.). Длинная сторона $b = 0,6 м$. В точку, находящуюся ниже оси вращения на расстоянии $x = 0,5 м$, ударяет пуля массы $m_ <1>= 10 г$, летевшая горизонтально перпендикулярно пластине со скоростью $v = 200 м/с$. Масса пластины $m_ <2>= 8 кг$, момент инерции относительно заданной оси $J = \frac<1> <3>m_ <2>b^<2>$. Какую угловую скорость приобретает пластина, если удар абсолютно упругий? При каком значении х в момент удара не возникнет горизонтальная сила реакции оси, действующая на пластину?

Пластина приобретает скорость в результате удара пули, поэтому целесообразно рассматривать систему тел пластина — пуля. Внешними по отношению к этой системе являются сила тяжести и вертикальная сила реакции оси, не изменяющие импульса системы. Однако во время взаимодействия пули с пластиной возникает еще горизонтальная сила реакции оси, очевидно тем большая, чем больше сила удара.

Следовательно, импульс системы не постоянен, и изменение импульса системы $\Delta \vec

_$ определяется действием только этой горизонтальной внешней силы:

$\Delta \vec

_ = \langle \vec \rangle \Delta t$, (1)

где $\langle \vec \rangle$ — среднее за время удара $\Delta t$ значение горизонтальной силы реакции оси.

Так как время удара очень мало, то можно считать, что пластина не успеет отклониться от вертикального положения и импульс системы как до удара, так и сразу после удара направлен горизонтально.

Однако моменты всех внешних сил относительно заданной оси равны нулю и момент импульса системы остается постоянным:

Момент импульса системы до удара равен моменту импульса пули $\vec_ <1>= \vec \times m_ <1>\vec$. Момент импульса системы после удара $\vec_ = J \vec < \omega>+ \vec \times m_ <1>\vec$, где $\vec< \omega>$ — искомая угловая скорость пластины; $\vec$ — скорость пули после удара, направленная в сторону, противоположную первоначальному движению пули (удар упругий, а масса пластины велика по сравнению с массой пули). Подставляя выражения $\vec_<1>$ и $\vec_$ в уравнение (2), получаем

$\vec \times m_ <1>\vec = J \vec < \omega>+ \vec \times m_ <1>\vec$. (3)

При абсолютно упругом ударе кинетическая энергия системы остается постоянной:

Уравнения (3) и (4) позволяют найти угловую скорость пластины сразу после удара. Тогда из уравнения (1) можно определить, при каком значении х горизонтальная сила реакции оси равна нулю.

Чтобы от векторного равенства (3) перейти к скалярным соотношениям, введем оси координат. Проекции векторов $\vec_ <1>= \vec \times m_ <1>\vec$ и $J \vec< \omega>$ на ось 2, совпадающую с осью вращения, положительны; причем, как видно из рисунка,

$rv \sin ( \hat< \vec, \vec> ) = rv \sin \alpha = xv$

и $L_ = xm_<1>v$. Проекция вектора $\vec \times m_ <1>\vec$ на эту же ось отрицательна и равна $- xm_ <1>u$. Тогда [см. (3)]

$xm_<1>v = J \omega — xm_ <1>u$. (5)

Уравнения (4) и (5) образуют систему, совместное решение которой позволяет найти искомую угловую скорость:

Совместное решение уравнений (5) и (4) часто вызывает затруднения, поэтому приводим краткое пояснение к решению. Перепишем оба уравнения так, чтобы в левой части оказались только члены, относящиеся к телу $m_<1>$:

$m_ <1>(v^ <2>— u^<2>) = J \omega^<2>, xm_ <1>(v + u) = J \omega$. (7)

Разделив почленно первое из уравнений (7) на второе и умножив на х, получим

$v — u = \omega x$. (8)

Домножим уравнение (8) на $m_<1>x$ и сложим это уравнение со вторым из уравнений (7):

$m_<1>vx — m_<1>ux = m_ <1>\omega x^<2>$
+
$m_<1>vx + m_ <1>ux = J \omega$
————-
$2m_<1>vx = \omega ( J + m_ <1>x^<2>)$

Очевидно, при расчете величиной $m_<1>x^<2>$ по сравнению с $J$ можно пренебречь. Тогда, учитывая, что $J = m_<2>b^<2>/3$, по формуле (6) находим

Чтобы определить, при каком условии не возникает горизонтальная сила реакции оси, следует перейти от векторного равенства (1) к скалярным соотношениям, определив импульсы системы до и после удара.
До удара $\vec

_ = m_ <1>\vec$. Проекции на горизонтальные оси ОY и 0Z:

После удара $\vec

_ = m_ <2>\vec_ <0>+ m_ <1>\vec$, где $\vec_<0>$ — скорость центра масс пластины. Проекции на те же оси

Тогда векторному равенству (1) соответствует одно скалярное

$p_ — p_ = \langle F_ \rangle \Delta t$.

Очевидно, $\langle F_ \rangle$ (а следовательно, и $\langle \vec \rangle$ равна нулю, если $p_ =p_$. Переписывая это условие в явном виде, получаем

$m_ <2>\omega b/2 — m_<1>u = m_<1>v$.

Это равенство и есть условие, при котором не возникает горизонтальной реакции оси и импульс системы не изменяется. Перепишем его в виде

$m_ <2>\omega b/2 = m_<1>v + m_<1>u$. (9)

Правую часть этого равенства можно выразить из уравнения (5), согласно которому

$m_<1>v + m_<1>u = J \omega /x$. (10)

Подставив выражение момента инерции пластины в (10), получим $m_<1>v + m_<1>u = m \omega b^<2>/(3x)$. Тогда условие (9) примет вид $m \omega b/2 = m \omega b^ <2>/(3x)$, откуда

Если пуля попадает в точку, лежащую на расстоянии $x = 2b/3$ от оси вращения, то горизонтальная сила реакции оси не возникает.

Если $x > 2b/3$, то $p_ <2y>> p_<1y>$. Следовательно, $\langle F_ \rangle \Delta t > 0$, т. е. возникающая горизонтальная сила реакции оси будет направлена по оси ОY — по движению пули.

Как видно из решения, длина стороны пластины, с которой совпадает ось вращения, не влияет на результат.