Уравнение вращательного движения вокруг точки

Вращательное движение тела. Закон вращательного движения

В этой статье описывается важный раздел физики — «Кинематика и динамика вращательного движения».

Основные понятия кинематики вращательного движения

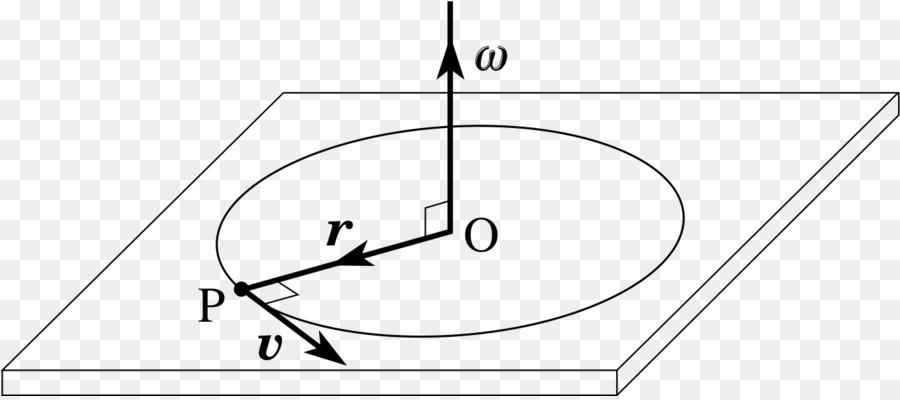
Вращательным движением материальной точки вокруг неподвижной оси называют такое движение, траекторией которого является окружность, находящаяся в плоскости перпендикулярной к оси, а центр ее лежит на оси вращения.

Вращательное движение твердого тела — это движение, при котором по концентрическим (центры которых лежат на одной оси) окружностям движутся все точки тела в соответствии с правилом для вращательного движения материальной точки.

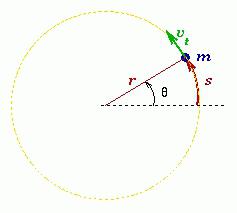
Пусть произвольное твердое тело T совершает вращения вокруг оси O, которая перпендикулярна плоскости рисунка. Выберем на данном теле точку M. При вращении эта точка будет описывать вокруг оси O круг радиусом r.

Через некоторое время радиус повернется относительно исходного положения на угол Δφ.

За положительное направление поворота принято направление правого винта (по часовой стрелке). Изменение угла поворота со временем называется уравнением вращательного движения твердого тела:

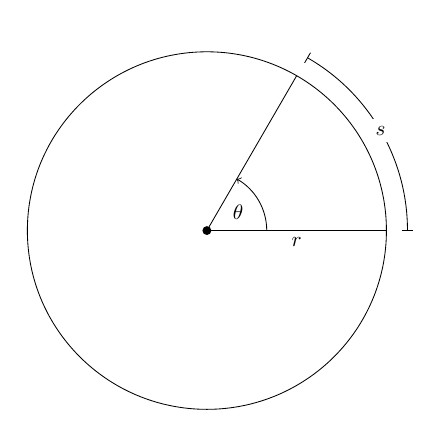
Если φ измерять в радианах (1 рад — это угол, соответствующий дуге, длиной равной ее радиусу), то длина дуги окружности ΔS, которую пройдет материальная точка M за время Δt, равна:

Основные элементы кинематики равномерного вращательного движения

Мерой перемещения материальной точки за небольшой промежуток времени dt служит вектор элементарного поворота dφ.

Угловая скорость материальной точки или тела — это физическая величина, которая определяется отношением вектора элементарного поворота к продолжительности этого поворота. Направление вектора можно определить правилом правого винта вдоль оси О. В скалярном виде:

Если ω = dφ/dt = const, то такое движение называется равномерное вращательное движение. При нем угловую скорость определяют по формуле

Согласно предварительной формуле размерность угловой скорости

Равномерное вращательное движение тела можно описать периодом вращения. Период вращения T — физическая величина, определяющая время, за которое тело вокруг оси вращения выполняет один полный оборот ([T] = 1 с). Если в формуле для угловой скорости принять t = T, φ = 2 π (полный один оборот радиуса r), то

поэтому период вращения определим следующим образом:

Число оборотов, которое за единицу времени совершает тело, называется частотой вращения ν, которая равна:

Единицы измерения частоты: [ν]= 1/c = 1 c -1 = 1 Гц.

Сравнивая формулы для угловой скорости и частоты вращения, получим выражение, связывающее эти величины:

Основные элементы кинематики неравномерного вращательного движения

Неравномерное вращательное движение твердого тела или материальной точки вокруг неподвижной оси характеризует его угловая скорость, которая изменяется со временем.

Вектор ε, характеризующий скорость изменения угловой скорости, называется вектором углового ускорения:

Если тело вращается, ускоряясь, то есть dω/dt > 0, вектор имеет направление вдоль оси в ту же сторону, что и ω.

Если вращательное движение замедлено — dω/dt 2 /r = ω 2 r 2 /r.

Итак, в скалярном виде

Тангенциальное ускоренной материальной точки, которая выполняет вращательное движение

Момент импульса материальной точки

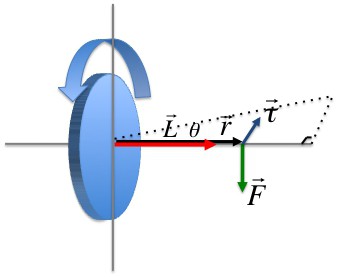
Векторное произведение радиуса-вектора траектории материальной точки массой m_i на ее импульс называется моментом импульса этой точки касательно оси вращения. Направление вектора можно определить, воспользовавшись правилом правого винта.

Момент импульса материальной точки (L_i) направлен перпендикулярно плоскости, проведенной через r_i и υ_i, и образует с ними правую тройку векторов (то есть при движении с конца вектора r_i к υ_i правый винт покажет направление вектора L_i).

В скалярной форме

Учитывая, что при движении по кругу радиус-вектор и вектор линейной скорости для i-й материальной точки взаимно перпендикулярные,

Так что момент импульса материальной точки для вращательного движения примет вид

Момент силы, которая действует на i-ю материальную точку

Векторное произведение радиуса-вектора, который проведен в точку приложения силы, на эту силу называется моментом силы, действующей на i-ю материальную точку относительно оси вращения.

В скалярной форме

Величина l_i, равная длине перпендикуляра, опущенного из точки вращения на направление действия силы, называется плечом силы F_i.

Динамика вращательного движения

Уравнение динамики вращательного движения записывается так:

Формулировка закона следующая: скорость изменения момента импульса тела, которое совершает вращение вокруг неподвижной оси, равна результирующему моменту относительно этой оси всех внешних сил, приложенных к телу.

Момент импульса и момент инерции

Известно, что для i-й материальной точки момент импульса в скалярной форме задается формулой

Если вместо линейной скорости подставить ее выражение через угловую:

то выражение для момента импульса примет вид

Величина I_i = m_ir_i 2 называется моментом инерции относительно оси i-й материальной точки абсолютно твердого тела, проходящей через его центр масс. Тогда момент импульса материальной точки запишем:

Момент импульса абсолютно твердого тела запишем как сумму моментов импульса материальных точек, составляющих данное тело:

Момент силы и момент инерции

Закон вращательного движения гласит:

Известно, что представить момент импульса тела можно через момент инерции:

Учитывая, что угловое ускорение определяется выражением

получим формулу для момента силы, представленного через момент инерции:

Замечание. Момент силы считается положительным, если угловое ускорение, которым он вызван, больше нуля, и наоборот.

Теорема Штейнера. Закон сложения моментов инерции

Если ось вращения тела через центр масс его не проходит, то относительно этой оси можно найти его момент инерции по теореме Штейнера:
I = I₀ + ma 2 ,

где I₀ — начальный момент инерции тела; m — масса тела; a — расстояние между осями.

Если система, которая совершает обороты округ неподвижной оси, состоит из n тел, то суммарный момент инерции такого типа системы будет равен сумме моментов, ее составляющих (закон сложения моментов инерции).

Вращения твердого тела вокруг неподвижной точки

Содержание:

Вращением твердого тела вокруг неподвижной оси называется такое движение твердого тела, при котором хотя бы две его точки остаются неподвижными. Прямая, проходящая через эти неподвижные точки называется осью вращения. Траекториями движения точек твердого тела являются окружности с радиусами равными расстояниям от заданных точек тела до оси вращения.

На странице -> решение задач по теоретической механике собраны решения задач и заданий с решёнными примерами по всем темам теоретической механики.

Вращения твердого тела вокруг неподвижной точки (сферическое движение)

Движение тела вокруг неподвижной точки (центра) называется сферическим движением. Сформулируем определение сферического движения.

Вращением твердого тела вокруг неподвижной точки называют такое движение, при котором одна точка тела остается все время неподвижной, а все остальные точки движутся по кругам, которые расположены на поверхностях сфер, описанных с неподвижной точки.

Одной из главных задач при изучении сферического движения является нахождение величин, характеризующих это движение: положение тела, угловые скорость и ускорение тела, вычисления скоростей и ускорений точек тела.

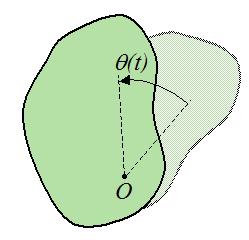
Рассмотрим движение тела вокруг неподвижного центра О (рис. 2.39). Выберем неподвижную систему отсчета Ox₁y₁z₁, относительно которой будем изучать движение тела, и подвижную — Oxyz, которую жестко свяжем с телом, что движется. Начало обеих систем координат расположим в неподвижном центре.

Для определения положения вращающегося тела относительно неподвижной системы координат Ox₁y₁z₁ необходимо задать относительно этой системы координат положения другой, подвижной системы координат Oxyz, скрепленной с движущимся телом. Для этого Эйлер предложил следующую теорему:

«Произвольное перемещение твердого тела вокруг неподвижной точки можно выполнить тремя последовательными поворотами тела вокруг трех осей, проходящих через неподвижную точку».

Согласно этой теореме положения тела, вращающегося вокруг неподвижной точки, определяется тремя углами. Линия ОК, вдоль которой пересекаются плоскости Oxy и Ox₁y₁ называется линией узлов. Тогда положения подвижных осей координат x, y, z (рис. 2.39) по отношению к неподвижной системе отсчета Ox₁y₁z₁ можно определить тремя углами:

,

,

.

Эти углы носят название углов Эйлера и имеют следующие наименования:

1. — угол прецессии, изменение которого означает вращение тела вокруг оси Oz₁, которая называется осью прецессии;

2. — угол нутации, изменение которого характеризует вращение тела вокруг линии узлов ОК, которая является осью нутации;

3. φ — угол собственного вращения, изменение которого означает вращение тела вокруг оси Oz, которая является осью собственного вращения.

Первый угол y, угол прецессии, который определяет положение линии узлов ОК относительно неподвижной координатной оси Ox₁, считается положительным, если он отсчитывается при повороте линии узлов ОК против часовой стрелки, если смотреть навстречу оси Oz₁.

Вторым углом Эйлера является угол нутации , угол между координатными плоскостями x₁Oy₁ и xOy, который можно измерять между перпендикулярами к указанным плоскостям — Oz₁ и Oz. Положительное направление угла — поворот против часовой стрелки оси Oz вокруг точки О, если смотреть навстречу линии узлов ОК. Угол отсчитывается от оси Oz₁.

Для полного определения положения данного тела относительно неподвижной системы Ox₁y₁z₁ необходимо задать угол между подвижной осью Ох и положительным направлением линии узлов ОК — угол собственного вращения φ. Этот угол считается положительным, если он меняется против часовой стрелки, смотря навстречу оси Oz.

При изменении угла φ тело вращается вокруг оси собственного вращения Oz, перпендикулярной плоскости, где расположены прямые ОК и O_x, образующих этот угол. Таким образом, угол φ определяет положение подвижной координатной оси Ox относительно линии узлов ОК.

Углы Эйлера широко применяются в теории гироскопа. Движение гироскопа, симметричного тела с неподвижной точкой на оси симметрии, которое очень быстро (30-40 тысяч об/мин.) вращается вокруг этой оси, можно представить составленным из трех движений, которые определяются углами , , φ . Изменение углов и имеет скорость на 1-2 порядка ниже, чем угла собственного вращения φ.

При вращении тела вокруг неподвижной точки в общем случае изменяются все три угла Эйлера: , , φ. Эти углы являются независимыми параметрами, которые определяют положение тела при сферическом движении относительно неподвижной системы координат. Задание трех углов Эйлера, как функции времени, являются необходимыми и достаточными условиями для полного описания сферического движения.

Следовательно, для определения положения тела с одной неподвижной точкой в ​​любой момент времени необходимо задать углы Эйлера как однозначные и непрерывные функции времени:

,

,

.

Уравнение является кинематическими уравнениями вращения твердого тела вокруг неподвижной точки. Если эти уравнения заданы, то в любой момент времени может быть определено положение твердого тела относительно неподвижной системы координат.

Действительно, отложим сначала в плоскости x₁Oy₁ от оси Ox₁ угол прецессии y против часовой стрелки, если он положительный, и определим положение линии узлов ОК. Далее отложим угол q от оси Oz₁, плоскость которого перпендикулярна линии узлов ОК, и определим положение оси z собственного вращения. И наконец, отложим в плоскости xOy угол φ от линии узлов против часовой стрелки, если он положительный, и определим положение оси Ox. Положение тела определено однозначно.

Теорема Эйлера – Даламбера

Произвольное элементарное перемещение тела, имеющего одну неподвижную точку, может осуществляться по одному элементарному повороту вокруг некоторой специально выбранной мгновенной оси вращения, проходящей через эту неподвижную точку.

Предположим, что положение тела, которое вращается вокруг точки О, определяется углами , , φ (как это показано на рис. 2.39).

Тогда его перемещения за элементарный промежуток времени можно представить как совокупность поворотов на углы d, d, dφ, вокруг оси Oz₁, линии узлов ОК и оси Oz соответственно. Прибавляясь, эти три поворота создадут одно действительное элементарное перемещение тела.

Сначала рассмотрим, каким будет результат сложения поворотов вокруг осей Oz и Oz₁, (рис. 2.40). При повороте на угол dφ любая точка тела, лежащего в плоскости Ozz₁ (внутри угла zOz₁), получит элементарное перемещение, которое перпендикулярно этой плоскости и численно равна , — расстояние от точки до оси Oz. Одновременно, при повороте вокруг оси Oz₁ та же точка получит обратное перемещение, которое численно равна .

Внутри угла обязательно найдется такая точка В, для которой = . Это означает, что перемещение этой точки равно нулю, и точка B будет неподвижной. Таким образом, имеем две неподвижные точки O и В, следовательно, неподвижную ось ОВ, вокруг которой происходит то самое элементарное вращение, которое составляет сумму вращений вокруг осей Oz и Oz₁.

Если теперь рассматривать вращения вокруг оси ОВ и линии узлов ОК, после аналогичных соображений придем к выводу, что элементарные повороты вокруг осей ОВ и ОК эквивалентны элементарному повороту вокруг некоторой оси ОР, проходящей через точку О.

Таким образом, ось ОР, элементарным поворотом вокруг которой тело перемещается из данного положения в соседнее, бесконечно близкое данному называется мгновенной осью вращения.

Следует заметить, что от неподвижной мгновенная ось вращения отличается тем, что ее положение меняется как в отношении системы отсчета Ox₁y₁z₁, так и в отношении подвижной системы координат Oxyz. Каждое последующее вращение происходит вокруг своей мгновенной оси вращения, которая, безусловно, всегда пересекает неподвижную точку О.

То есть, движение твердого тела вокруг неподвижной точки состоит из серии последовательных элементарных поворотов вокруг мгновенных осей вращения, которые пересекают неподвижную точку.

Геометрическое место мгновенных осей вращения относительно неподвижной системы отсчета называется недвижимым аксоидом. Неподвижный аксоид является конической поверхностью с вершиной в неподвижной точке тела, потому что все мгновенные оси пересекают неподвижную точку.

Геометрическое место мгновенных осей во вращающемся теле называют подвижным аксоидом, который также является конической поверхностью. Для каждого движения твердого тела вокруг неподвижной точки имеем пару аксоидов. Таким образом, во вреся сферического движения подвижной аксоид катится по неподвижному без скольжения, поскольку общая образующая этих аксоидов в каждый момент времени служит мгновенной осью, вокруг которой вращается тело, поэтому все точки оси неподвижные. Если подвижный аксоид катится без скольжения по неподвижному аксоиду, то происходит движение тела вокруг неподвижной точки.

Кинематические характеристики движения тела вокруг неподвижной точки

Угловая скорость:

Сделаем сначала определения угловой скорости тела, вращающегося вокруг неподвижной точки.

Угловая скорость, с которой происходит элементарный поворот тела вокруг мгновенной оси вращения, называется угловой скоростью тела в данный момент времени или мгновенной угловой скоростью тела.

Согласно этому определению, если тело вернется вокруг мгновенной оси на некоторое бесконечно малый угол dφ, то мгновенной угловой скоростью будет:

.

Угловую скорость можно изобразить в виде вектора , направленного вдоль мгновенной оси ОР (рис. 2.41).

Если учесть, что положение мгновенной оси ОР непрерывно меняется, то вектор угловой скорости будет меняться в течении времени как по модулю, так и по направлению, а конец вектора будет описывать некоторую произвольную кривую AB, которая является годографом вектора . На рис. 2.41 показаны различные положения мгновенной оси вращения OP, OP₁, OP₂ и соответственно расположенные на них векторы угловой скорости , и .

Угловое ускорение:

Второй кинематической характеристикой тела, вращающегося вокруг неподвижной точки является угловое ускорение.

Угловое ускорение тела в данный момент времени, или мгновенное угловое ускорение , которое характеризует изменение в течении времени угловой скорости по модулю и по направлению, является векторной величиной и численно равна:

.

Для нахождения расположения вектора углового ускорения можно использовать такую ​​аналогию. Как известно, вектор скорости произвольной точки равен производной от радиус-вектора этой точки по времени t и направлен вдоль касательной к траектории движения точки. В этом случае траектория точки является годографом концов радиус-векторов .

По аналогии с этим, вектор углового ускорения направлен по касательной к кривой AB в соответствующей точке. То есть, угловое ускорение можно считать, как скорость движения конца вектора .

Таким образом, вектор мгновенного углового ускорения имеет направление производной по времени от вектора мгновенной угловой скорости , он параллельный касательной к годографу векторной функции (t). Изображать угловое ускорение необходимо вектором, параллельный касательно к годографу векторов угловой скорости в данной точке, но приложенный к неподвижной точке O (рис. 2.40).

Скорости и ускорения точек тела в сферическом движении

Векторная формула Эйлера (2.54), полученная для вращательного движения тела вокруг неподвижной оси, справедлива и для сферического движения тела.

В сферическом движении в каждый момент времени тело вращается вокруг мгновенной оси OP, которая пересекает неподвижную точку O, с угловой скоростью , вектор которой расположен на мгновенной оси. Точки тела, которые принадлежат мгновенной оси OP, имеют скорости , равны нулю, как и в случае неподвижной оси вращения.

Следовательно, скорость произвольной точки М тела (рис. 2.42) определяется как векторное произведение и . А именно:

,

где — радиус-вектор точки M относительно неподвижной точки О.

Модуль скорости при этом будет равен:

,

где h — кратчайшее расстояние точки к мгновенной оси OP.

Таким образом, скорости точек тела в сферическом движении пропорциональны расстояниям от этих точек к мгновенной оси. Направление вектора скорости перпендикулярно плоскости, в которой расположены векторы и , то есть расстоянию h и направлен в сторону вращения.

Как известно, скорость точки является первой производной от радиус-вектора этой точки по времени (2.4):

.

В то же время, по векторной формуле (2.54) скорость равна , откуда:

Длина радиус-вектора , как расстояние между двумя точками твердого тела, является постоянной величиной при движении этого тела. Следовательно, уравнение (2.77) можно рассматривать как формулу для вычисления производной по времени от вектора, модуль которого устойчивый, а изменение его происходит только вследствие вращения с угловой скоростью вместе с телом вокруг неподвижной точки.

Если жестко скрепить подвижную систему координат Oxyz с телом, вращающимся вокруг неподвижной точки с угловой скоростью , так для единичных векторов , , , направленных по этим осям, модули которых постоянные, на основании (2.77) имеем:

,

,

.

Выражения называют формулами Пуассона.

Для определения ускорения точки тела, которое осуществляет сферическое движение, возьмем производную по скалярному аргументу t (время) от векторной функции скорости :

.

,

.

тогда окончательно имеем:

В отличии от вышеупомянутой формулы, здесь и — угловые скорость и ускорение вокруг мгновенных осей, первое слагаемое — вращательное ускорение:

,

второе слагаемое — осевое ускорение:

.

Движение свободного твердого тела

Рассмотрим наиболее общий случай движения твердого тела — свободное движение тела, когда оно может как угодно перемешиваться относительно неподвижной системы отсчета Oxyz (рис. 2.43).

Как известно из аналитической геометрии, положения твердого тела в пространстве можно определить тремя точками, которые не расположены на одной прямой и неизменно связаны с телом.

На девять координат этих точек наложено три ограничения, которые выражают неизменность расстояний между точками, потому что они принадлежат твердому телу. Итак, независимых параметров или степеней свободы тела будет шесть.

Смотря с другой стороны, при определении положения твердого тела можно задать три координаты одной его точки, например, точки A, которую назовем полюсом с координатами , , , и выбрать еще три параметра, характеризующих вращения тела вокруг полюса. Остальные параметры могут быть углами Эйлера , , φ (на рис. 2.43 не показаны). Совокупность шести скалярных функций времени, которые однозначно определяют положение свободного твердого тела в любой момент времени, является законом его движения:

,

,

,

,

,

.

Три первые уравнения определяют движение полюса и вместе с ним поступательное движение твердого тела. Последние три уравнения определяют движение тела относительно системы координат (то есть относительно точки A, как неподвижной).

Таким образом, с геометрической точки зрения элементарное перемещение свободного тела состоит из поступательного перемещения вместе с полюсом, при котором полюс переходит в соседнее положение , и с некоторого перемещения по отношению к осям .

Последнее перемещения по теореме Эйлера-Даламбера является поворотом вокруг мгновенной оси вращения , которая проходит через точку A.

Поскольку движением тела является совокупность элементарных перемещений, то можно его обозначить следующим образом:

«Свободное движение тела в общем случае состоит из поступательного движения, при котором все точки тела движутся как произвольно выбранный полюс A со скоростью полюса , и ряда элементарных поворотов с угловой скоростью ω вокруг мгновенных осей вращения, которые проходят через полюс» (рис. 2.44).

Свободно движутся брошенный камень, снаряд, неуправляемая ракета тому подобное.

Основными кинематическими характеристиками движения является скорость и ускорение полюса, которые определяют скорость и ускорение поступательной части движения, а также угловая скорость ω и угловое ускорение ε вращения вокруг полюса. Значения величин этих характеристик можно определить по уравнениям.

В отдельном случае движение свободного тела может быть плоскопараллельным. Тогда вектор угловой скорости будет всегда перпендикулярен плоскости движения. При этом, как в общем случае, так и в отдельном, вращающаяся часть движения, как и значение угловой скорости ω, от выбора полюса не зависит.

Определим скорости и ускорения точек свободного тела.

Как и в случае плоскопараллельного движения, можно предположить, что скорость и ускорение точки свободного тела состоит геометрически со скорости ускорения векторов полюса и относительной скорости (ускорение) точки вокруг полюса (последние получает точка M при движении вместе с телом вокруг полюса A)

,

,

где ; ; — радиус-вектор точки M относительно полюса A; — скорость точки M относительно полюса A; — ускорение точки M относительно полюса A; ε — угловое ускорение тела.

Услуги по теоретической механике:

Учебные лекции:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Вращательное движение твердого тела: уравнение, формулы

В природе и технике мы часто сталкиваемся с проявлением вращательного движения твердых тел, например, валов и шестерен. Как в физике описывают этот тип движения, какие формулы и уравнения для этого применяются, эти и другие вопросы освещаются в данной статье.

Что такое вращение?

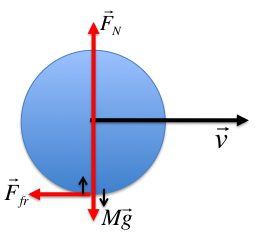
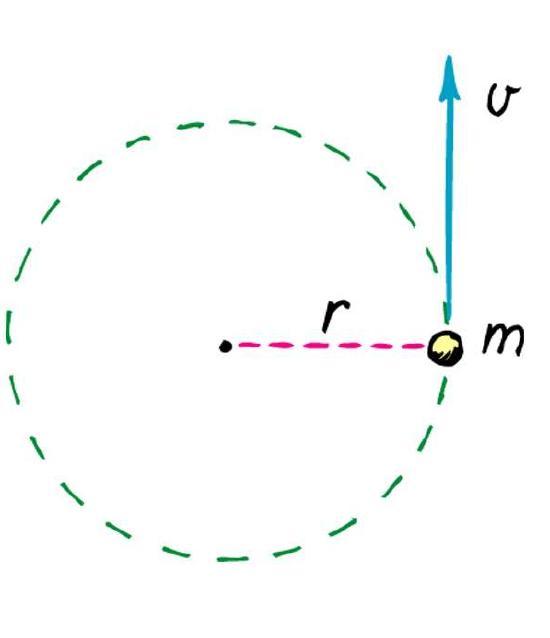
Каждый из нас интуитивно представляет, о каком движении пойдет речь. Вращение — это процесс, при котором тело или материальная точка движется по круговой траектории вокруг некоторой оси. С геометрической точки зрения ось вращения твердого тела — это прямая, расстояние до которой в процессе перемещения остается неизменным. Это расстояние называют радиусом вращения. Далее будем обозначать его буквой r. Если ось вращения проходит через центр масс тела, то ее называют собственной осью. Примером вращения вокруг собственной оси является соответствующее движение планет Солнечной системы.

Вам будет интересно: Афронт — это ситуация, в которой не хочется оказаться

Чтобы вращение происходило, должно существовать центростремительное ускорение, которое возникает за счет центростремительной силы. Эта сила направлена от центра масс тела к оси вращения. Природа центростремительной силы может быть самой разной. Так, в космическом масштабе ее роль выполняет гравитация, если тело закреплено нитью, то сила натяжения последней будет центростремительной. Когда тело вращается вокруг собственной оси, роль центростремительной силы играет внутреннее электрохимическое взаимодействие между составляющими тело элементами (молекулами, атомами).

Вам будет интересно: Декабрист Оболенский Евгений Петрович: биография. Декабристские организации

Необходимо понимать, что без присутствия центростремительной силы тело будет двигаться прямолинейно.

Описывающие вращение физические величины

Во-первых, это динамические характеристики. К ним относятся:

• момент импульса L;
• момент инерции I;
• момент силы M.

Во-вторых, это кинематические характеристики. Перечислим их:

• угол поворота θ;
• скорость угловая ω;
• ускорение угловое α.

Кратко опишем каждую из названных величин.

Момент импульса определяется по формуле:

Где p — линейный импульс, m — масса материальной точки, v — ее линейная скорость.

Момент инерции материальной точки рассчитывается с помощью выражения:

Для любого тела сложной формы величина I рассчитывается, как интегральная сумма моментов инерции материальных точек.

Момент силы M вычисляется так:

Здесь F — внешняя сила, d — расстояние от точки ее приложения до оси вращения.

Физический смысл всех величин, в названии которых присутствует слово «момент», аналогично смыслу соответствующих линейных величин. Например, момент силы показывает возможность приложенной силы сообщить угловое ускорение системе вращающихся тел.

Кинематические характеристики математически определяются следующими формулами:

Как видно из этих выражений, угловые характеристики аналогичны по своему смыслу линейным (скорости v и ускорению a), только они применимы для круговой траектории.

Динамика вращения

В физике изучение вращательного движения твердого тела осуществляется с помощью двух разделов механики: динамики и кинематики. Начнем с динамики.

Динамика изучает внешние силы, действующие на систему вращающихся тел. Сразу запишем уравнение вращательного движения твердого тела, а затем, разберем его составные части. Итак, это уравнение имеет вид:

Момент силы, который действует на систему, обладающую моментом инерции I, вызывает появление углового ускорения α. Чем меньше величина I, тем легче с помощью определенного момента M раскрутить систему до больших скоростей за малые промежутки времени. Например, металлический стержень легче вращать вдоль его оси, чем перпендикулярно ей. Однако, тот же стержень легче вращать вокруг оси, перпендикулярной ему, и проходящей через центр масс, чем через его конец.

Закон сохранения величины L

Выше была введена эта величина, она называется моментом импульса. Уравнение вращательного движения твердого тела, представленное в предыдущем пункте, часто записывают в иной форме:

Если момент внешних сил M действует на систему в течение времени dt, то он вызывает изменение момента импульса системы на величину dL. Соответственно, если момент сил равен нулю, тогда L = const. Это и есть закон сохранения величины L. Для нее, используя связь между линейной и угловой скоростью, можно записать:

L = m*v*r = m*ω*r2 = I*ω.

Таким образом, при отсутствии момента сил произведение угловой скорости и момента инерции является постоянной величиной. Этот физический закон используют фигуристы в своих выступлениях или искусственные спутники, которые необходимо повернуть вокруг собственной оси в открытом космосе.

Центростремительное ускорение

Выше, при изучении вращательного движения твердого тела, уже была описана эта величина. Также была отмечена природа центростремительных сил. Здесь лишь дополним эту информацию и приведем соответствующие формулы для расчета этого ускорения. Обозначим его ac.

Поскольку центростремительная сила направлена перпендикулярно оси и проходит через нее, то момента она не создает. То есть эта сила не оказывает совершенно никакого влияния на кинематические характеристики вращения. Тем не менее, она создает центростремительное ускорение. Приведем две формулы для его определения:

Таким образом, чем больше угловая скорость и радиус, тем большую силу следует приложить, чтобы удержать тело на круговой траектории. Ярким примером этого физического процесса является занос автомобиля во время поворота. Занос возникает, если центростремительная сила, роль которой играет сила трения, становится меньше, чем центробежная сила (инерционная характеристика).

Кинематика вращения

Три основные кинематические характеристики были перечислены выше в статье. Кинематика вращательного движения твердого тела формулами следующими описывается:

θ = ω*t => ω = const., α = 0;

θ = ω0*t + α*t2/2 => ω = ω0 + α*t, α = const.

В первой строке приведены формулы для равномерного вращения, которое предполагает отсутствие внешнего момента сил, действующего на систему. Во второй строке записаны формулы для равноускоренного движения по окружности.

Отметим, что вращение может происходить не только с положительным ускорением, но и с отрицательным. В этом случае в формулах второй строки следует перед вторым слагаемым поставить знак минус.

Пример решения задачи

На металлический вал в течение 10 секунд действовал момент силы 1000 Н*м. Зная, что момент инерции вала равен 50 кг*м2, необходимо определить угловую скорость, которую придал валу упомянутый момент силы.

Применяя основное уравнение вращения, вычислим ускорение вала:

Поскольку это угловое ускорение действовало на вал в течение времени t = 10 секунд, то для вычисления угловой скорости применяем формулу равноускоренного движения:

Здесь ω0 = 0 (вал не вращался до действия момента сил M).

Подставляем в равенство численные значения величин, получаем:

ω = 1000/50*10 = 200 рад/с.

Чтобы это число перевести в привычные обороты в секунду, необходимо его поделить на 2*pi. Выполнив это действие, получаем, что вал будет вращаться с частотой 31,8 об./с.