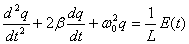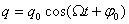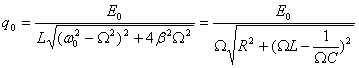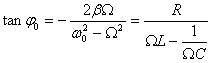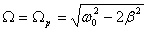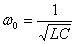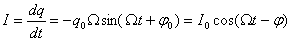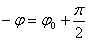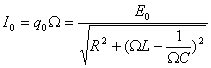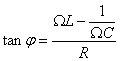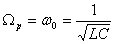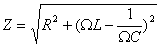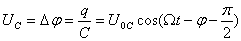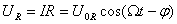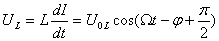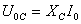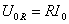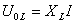Уравнение вынужденных колебаний для заряда конденсатора

Вынужденные электрические колебания

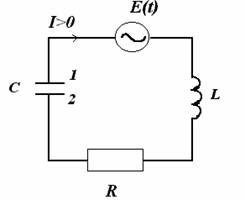
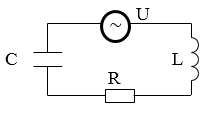
Рассмотрим электромагнитный колебательный контур, в котором помимо ёмкости, индуктивности, сопротивления есть ещё и генератор переменного напряжения, то есть источник электрической энергии. Очевидно, что в таком контуре со временем (это время обычно мало) установятся вынужденные колебания тока с частотой генератора и с постоянной амплитудой; подвод энергии от генератора будет в точности компенсировать потери энергии на сопротивлении.

Не будем учитывать внутреннее сопротивление генератора (будем считать, что у нас хороший, «идеальный» генератор). Получим уравнение для колебаний заряда на обкладках конденсатора. Для этого нам необходимо в закон Ома , который мы писали для затухающих колебаний, добавить в левую часть э.д.с. генератора E(t).

Дифференциальное уравнение вынужденных колебаний заряда в электромагнитном контуре в стандартном (каноническом) виде получается следующим:

или

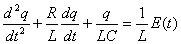
которое полностью аналогично уравнению вынужденных колебаний пружинного маятника . Э.д.с. генератора 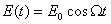. Поэтому сразу можем написать решение:

Резонансная частота колебаний заряда на обкладках конденсатора запишется также по аналогии с резонансной частотой механических колебаний маятника:

Напомню, что в электрическом контуре:

и

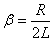
Обратите внимание, что резонансная частота для заряда зависит от коэффициента затухания, а, следовательно, от сопротивления.

Чаще нас интересуют не колебания заряда на конденсаторе, а колебания тока в цепи контура. Найдем эти колебания, продифференцировав заряд по времени:

В этом уравнении сделана подстановка —

Напомню, что — j является сдвигом фазы между напряжением генератора 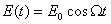и током в цепи. В такой записи знак минус показывает, что напряжение первично, а ток отстает по фазе.

Формулы для амплитуды тока и сдвига фаз выглядят так:

Существенное отличие колебаний тока от колебаний заряда состоит в том, что резонансная частота для тока не зависит от сопротивления; она просто равна собственной частоте свободных колебаний в контуре:

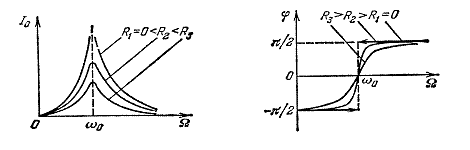
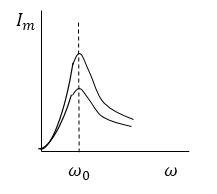
Колебания тока в цепи имеют аналогом не колебания механического маятника, а колебания его скорости. Резонансные кривые для амплитуды тока и зависимость сдвига фаз от частоты для различных сопротивлений — на графиках. Обратите внимание, что при резонансе сдвиг фаз между током и напряжением на генераторе отсутствует.

Посмотрим ещё раз на формулу для амплитуды колебаний тока. В числителе стоит амплитудное напряжение на генераторе (мы пренебрегаем внутренним сопротивлением генератора, поэтому его э.д.с. равна напряжению на его клеммах); в знаменателе — величина, имеющая размерность сопротивления. Она включает в себя не только активное сопротивление R, но и составляющую, зависящую от ёмкости и индуктивности контура и от частоты генератора. Эта величина носит название полного сопротивления контура, или импеданса контура Z:

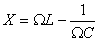
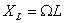
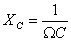
Величина носит название реактивного сопротивления, а её составляющие: — индуктивным сопротивлением; — ёмкостным сопротивлением.

Посмотрим, как ведут себя колебания тока и напряжения на различных участках контура.

Ток в цепи устанавливается со скоростью распространения электрического поля, то есть со скоростью света с. Время установления тока в цепи

l/c, где l — длина контура. Это время в реальных контурах много-много меньше, чем период колебаний. Поэтому мы считаем, что в каждый момент времени значения тока на всех участках цепи одинаково; колебания тока на сопротивлении, индуктивности и ёмкости происходят синхронно.

Иначе обстоит дело с колебаниями напряжения. Вычислим напряжение на каждом элементе контура и посмотрим, как они отличаются по амплитуде и фазе.

Видно, что напряжение на конденсаторе отстает на четверть периода от напряжения на сопротивлении, а напряжение на индуктивности на столько же по фазе опережает его. Напряжение на ёмкости и индуктивности всегда отличаются по фазе на полпериода. Наглядно сдвиг фаз на элементах цепи можно посмотреть на векторной диаграмме; из неё, в частности, ясно, почему импеданс вычисляется таким образом.

Общее падение напряжения на всех трех элементах цепи равно напряжению на клеммах генератора; поэтому угол j на диаграмме дает сдвиг по фазе между током и напряжением на генераторе.

Вынужденные колебания в контуре. Резонанс

Вы будете перенаправлены на Автор24

Уравнение вынужденных колебаний

Вынужденными колебаниями называют периодические изменения параметров, которые описывают систему под влиянием внешней силы. Для реализации вынужденных электрических колебаний в $RLC$ контуре в него включают переменную ЭДС (рис.1).

В общем случае вынужденные колебания в таком контуре можно записать как:

где $L$ — индуктивность, $R$ — сопротивление, $C$ — емкость, $U\left(t\right)$ — внешнее воздействие.

Рассмотрим случай, когда в контур подается переменное напряжение ($U$) изменяющееся по гармоническому закону:

Тогда уравнение колебаний запишется в виде:

где $<\omega >_0=\frac<1><\sqrt>$- собственная частота колебаний контура, $\beta =\frac<2L>.$ По аналогии с механическими колебаниями можно записать частное решение данного уравнения как:

Как известно, общее решение неоднородного уравнения получают как сумму частного решения данного уравнения (в нашем случае это (4)) и общего решения соответствующего однородного уравнения. Так для уравнения:

общим решением является выражение:

Так как выражение (6) содержит множитель $e^<\left(-\beta t\right)>$, то при $t\to \infty ,\ $ $e^<\left(-\beta t\right)>\to 0,$ поэтому для установившихся колебаний решением уравнения (3) считают функцию (4).

Сила тока для установившихся вынужденных колебаний может быть записана как:

где $I_m=<\omega q>_m$, $\varphi =\Psi-\frac<\pi ><2>$ — сдвиг фаз между тока и приложенного напряжения. Соответственно:

Готовые работы на аналогичную тему

Надо отметить, что выполняется равенство:

Выражение (9) означает, что сумма напряжений на каждом из элементов цепи в момент времени $t$ равна приложенному напряжению.

Резонанс

Появление сильных колебаний при частоте внешней силы равной (или почти равной) собственной частоте колебательного контура, называют резонансом. Суть явления заключается в том, что как бы одиночные «толчки» усиливают друг друга. В таком случае получается, что энергия, которая вкладывается в систему, является максимальной. Амплитуда колебаний нарастает до тех пор, пока увеличивающиеся силы трения (в среднем) за период толчка не станут компенсировать действие каждого «толчка». В этот момент устанавливается максимум энергии и максимум амплитуды.

Резонансной частотой для заряда ($<\omega >_$) и напряжения ($<\omega >_$) на конденсаторе являются частоты, заданные уравнениями:

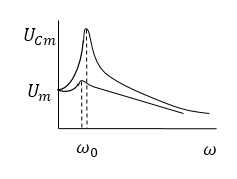
Резонансные кривые для заряда и напряжения на конденсаторе имеют одинаковый вид (рис.2).

Если $\omega =0$ кривые (рис.2) сходятся в одной точке, при этом напряжение на конденсаторе равно напряжению, которое возникает на нем при подключении источника:

Максимум резонансной кривой выше и острее, чем меньше коэффициент затухания (меньше $R$, больше $L$).

Кривые для силы тока изображены на рис. 3. Амплитудное значение силы тока максимально, если $\omega L-\frac<1><\omega C>=0.\ $Частота силы тока при резонансе ($<\omega >_$):

Задание: Получите функции $U_R(t),U_C(t),U_L(t)$ в $RCL$ контуре, если приложенное напряжение задано уравнением: $U=U_m.$

Решение:

В качестве основы для решения задачи используем выражение:

\[I\left(t\right)=\left(\omega t-\varphi \right)\left(1.1\right).\]

Исходя из (1.1) для напряжения на сопротивлении ($U_R$) в соответствии с законом Ома для участка цепи можно записать, что:

\[U_R\left(t\right)=RI\left(t\right)=<_m cos\ >\left(\omega t-\varphi \right)\left(1.2\right).\]

Используя закон изменения заряда в контуре, заданном в условии:

найдем $U_C\left(t\right)$ как:

где $U_=\frac=\frac<С\omega >.$ Напряжение на катушке индуктивности найдем как:

Задание: Определите, во сколько раз напряжение на конденсаторе может превышать напряжение, которое приложено к $RLC$ контуру, если добротность контура равна $O$. Считать, что внешнее напряжение подчиняется гармоническому закону, затухание в контуре мало.

Решение:

Условие малости затухания для контура означает, что:

и резонансную частоту можно считать равной собственной частоте.

Напряжение на конденсаторе можно выразить как:

где $q_m=\frac<\omega \sqrt<^2>>$. Если при резонансе в нашем случае $\omega \approx <\omega >_0$, то максимальное напряжение на конденсаторе при резонансе равно ($U_$):

где при малом затухании можно считать, что $<\omega >_0L-\frac<1><<\omega >_0C>\approx 0$

Найдем отношение $\frac>$, получим:

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 26 04 2021

Вынужденные колебания. Переменный ток

Дадим определение понятию вынужденных колебаний.

Вынужденные колебания – это процессы, которые происходят в электрических цепях под воздействием периодического источника тока.

Основным отличием вынужденных колебаний по сравнению с собственными колебаниями в электрических цепях является то, что они являются незатухающими. Неизбежные потери энергии компенсируются за счет внешнего источника периодического воздействия, который не позволяет колебаниям затухать.

Что такое переменный ток?

Переменный ток — электрический ток, который с течением времени изменяется по величине и направлению или, в частном случае, изменяется по величине, сохраняя своё направление в электрической цепи неизменным.

Рассмотрим случай, когда электрическая цепь способна совершать собственные свободные колебания с некоторой частотой ω 0 . Предположим, что к этой цепи подключен внешний источник, напряжение которого изменяется по гармоническому закону с частотой ω .

Частота свободных колебаний в электрической сети ω 0 будет определяться параметрами этой сети. Вынужденные колебания, которые установятся при подключении внешнего источника ω , будут происходить на частоте этого внешнего источника.

Частота вынужденных колебаний устанавливается не сразу после включения внешнего источника, а спустя некоторое время Δ t . По порядку величины это время будет равно времени затухания свободных колебаний в сети τ .

Цепи переменного тока

Цепи переменного тока – это такие электрические цепи, в которых под воздействием периодического источника тока происходят установившиеся вынужденные колебания.

Рассмотрим устройство колебательного контура, в который включен источник тока с напряжением, изменяющимся по периодическому закону:

e ( t ) = ε 0 cos ω t,

где ε 0 – амплитуда, ω – круговая частота.

Фактически, это будет R L C -цепь.

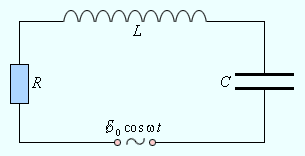
Рисунок 2 . 3 . 1 . Вынужденные колебания в контуре.

Будем считать, что для изображенной на этом рисунке электрической цепи выполняется условие квазистационарности. Это позволит нам записать закон Ома для мгновенных значений токов и напряжений:

R J + q C + L d J d t = ε 0 c o c ω t.

Величину L d J d t принято называть напряжением на катушке индуктивности. Фактически, это ЭДС самоиндукции катушки, которую мы для простоты вычислений перенесли с противоположным знаком в левую часть уравнения из правой.

Уравнение вынужденных колебаний можно записать в виде:

u R + u C + u L = e ( t ) = ε 0 cos ω t.

где u R ( t ) , u C ( t ) и u L ( t ) – мгновенные значения напряжений на резисторе, конденсаторе и катушке соответственно. Амплитуды этих напряжений будем обозначать буквами U R , U C и U L . Напряжения при установившихся вынужденных колебаниях изменяются с частотой внешнего источника переменного тока ω .

Векторная диаграмма токов и напряжений

Для решения уравнения вынужденных колебаний мы можем использовать достаточно наглядный метод векторных диаграмм. Для этого используем векторную диаграмму, на которой с помощью векторов изобразим колебания определенной заданной частоты ω .

Давайте посмотрим, как построить векторную диаграмму токов и напряжений.

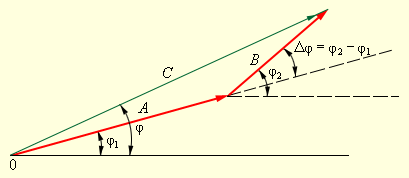
Рисунок 2 . 3 . 2 . Векторная диаграмма, на которой с помощью векторов изображены гармонические колебания A cos ( ω t + φ 1 ) , B cos ( ω t + φ 2 ) и их суммы C cos ( ω t + φ ) .

Наклон векторов к горизонтальной оси определяется фазой колебаний φ 1 и φ 2 , а длины векторов соответствуют амплитудам колебаний A и B . Относительный фазовый сдвиг определяет взаимную ориентацию векторов: ∆ φ = φ 1 — φ 2 . Для того, чтобы построить вектор, изображающий суммарное колебание, нам необходимо использовать правило сложения векторов: C → = A → + B → .

При вынужденных колебаниях в электрической цепи для построения векторной диаграммы напряжений и токов нам необходимо знать соотношения между амплитудами токов и напряжений и фазовый сдвиг между ними для любого участка цепи.

Источник переменного тока может быть подключен к:

• катушке индуктивности L ;
• резистору с сопротивлением R ;
• конденсатору с емкостью С .

Рассмотрим эти три примера подробнее. Будем считать, что напряжение на резисторе, катушке и конденсаторе во всех трех случаях равно напряжению внешнего источника переменного тока.

Резистор в цепи переменного тока

J R R = u R = U R cos ω t ; J R = U R R cos ω t = I R cos ω t

Мы обозначили амплитуду тока, который протекает через резистор, через I R . Соотношение R I R = U R выражает связь между амплитудами тока и напряжения на резисторе. Фазовый сдвиг в этом случае равен нулю. Физическая величина R – это активное сопротивление на резисторе.

Конденсатор в цепи переменного тока

u C = q C = U C cos ω t

J C = d q d t = C d u C d t = C U C ( — ω sin ω t ) = ω C U C cos ω t + π 2 = I C cos ω t + π 2 .

Соотношение между амплитудами тока I C и напряжения U C : 1 ω C I C = U C .

Ток опережает по фазе напряжение на угол π 2 .

Физическая величина X C = 1 ω C — это емкостное сопротивление конденсатора.