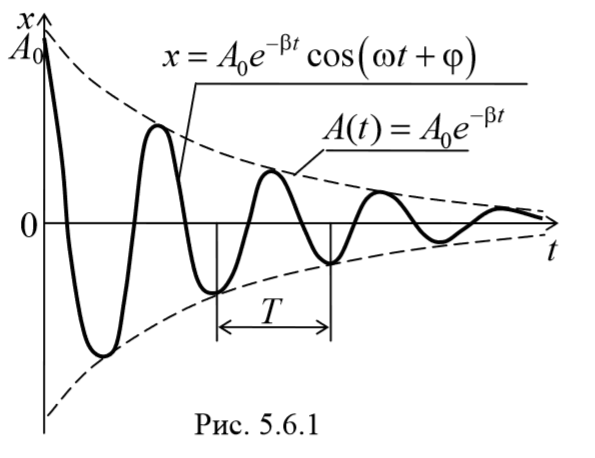
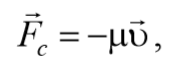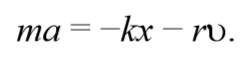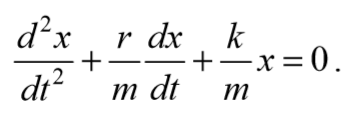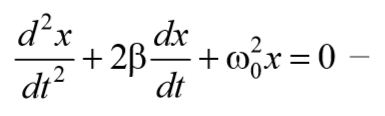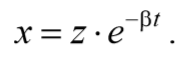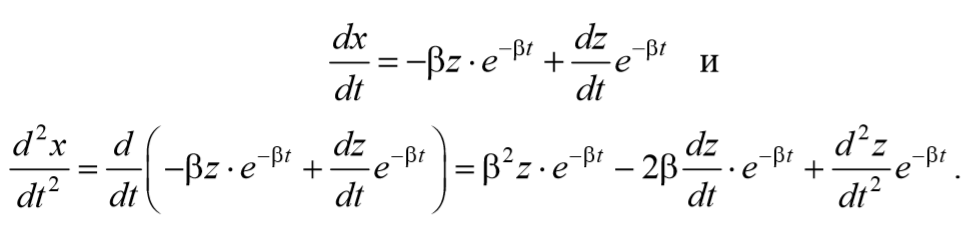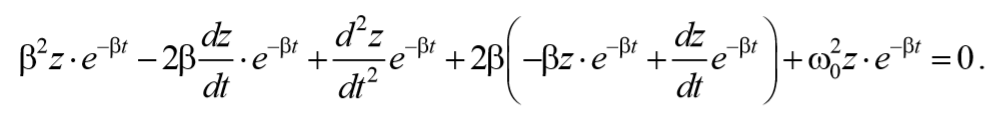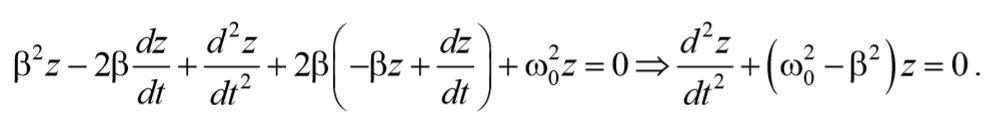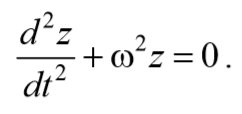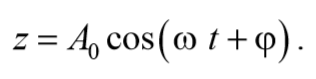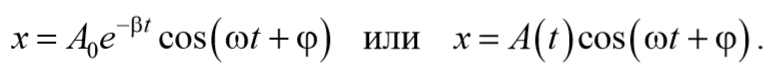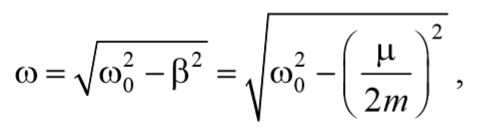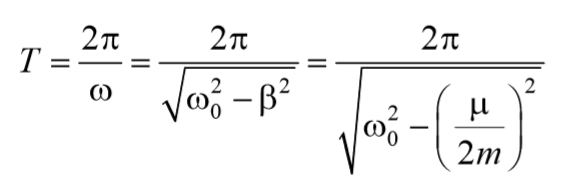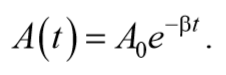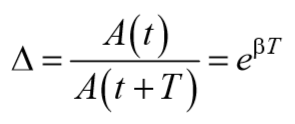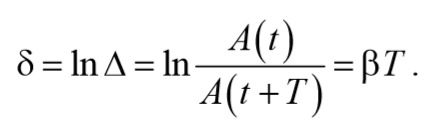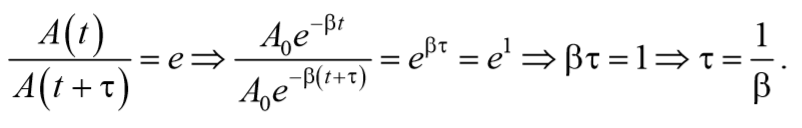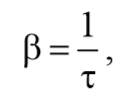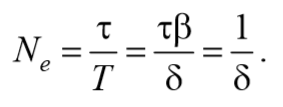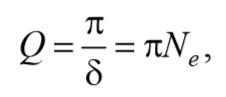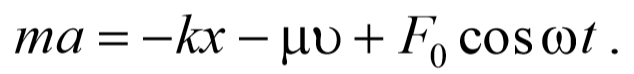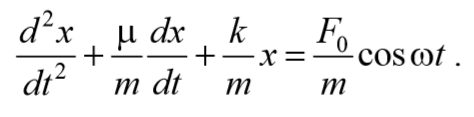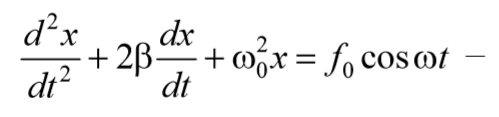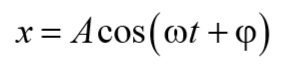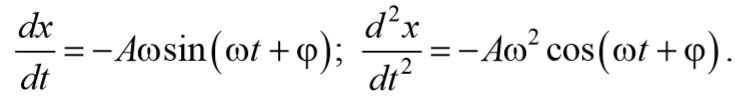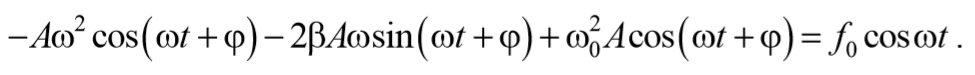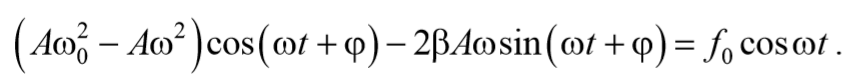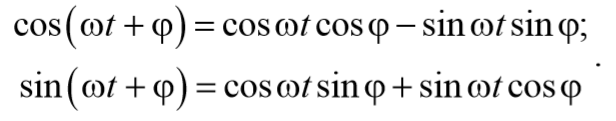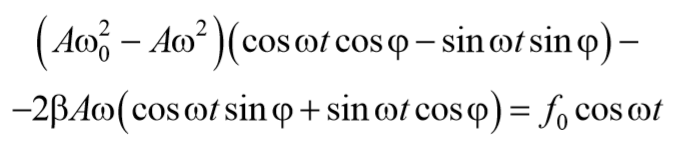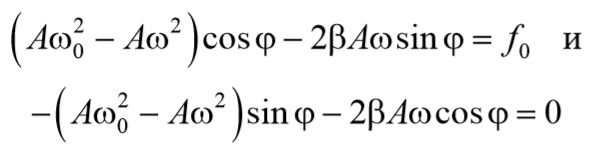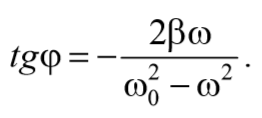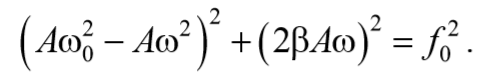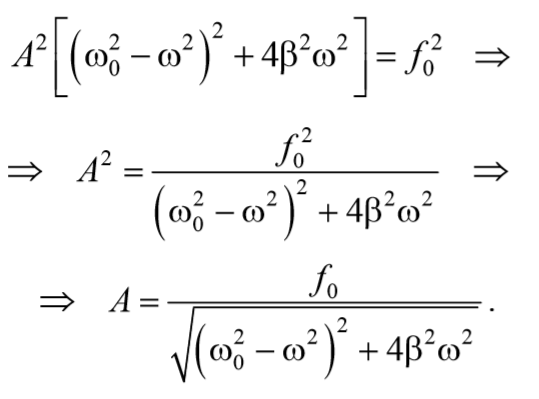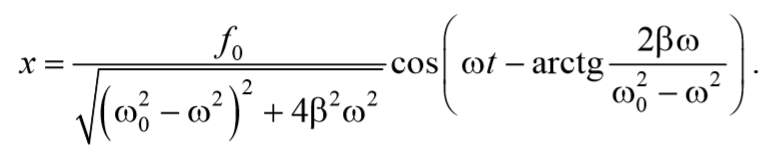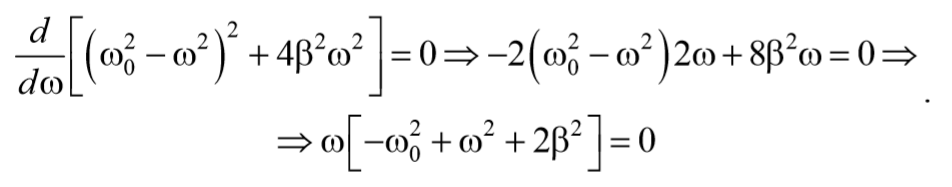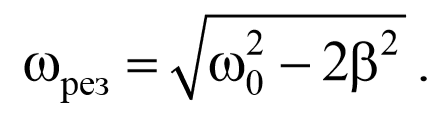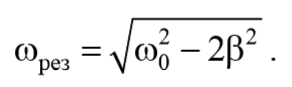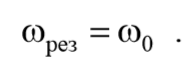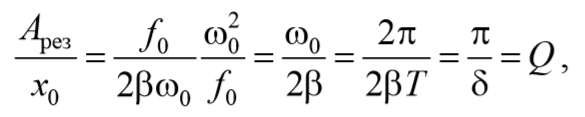Уравнение вынужденных колебаний с затуханием

Уравнение вынужденных колебаний с затуханием

§6 Затухающие колебания

Декремент затухания. Логарифмический декремент затухания.

Добротность

Свободные колебания технических систем в реальных условиях протекают, когда на них действуют силы сопротивления. Действие этих сил приводит к уменьшению амплитуды колеблющейся величины.

Колебания, амплитуда которых из-за потерь энергии реальной колебательной системы уменьшается с течением времени, называются затухающими.

Наиболее часто встречается случаи, когда сила сопротивления пропорциональна скорости движения

где r — коэффициент сопротивления среды. Знак минус показывает, что F_C направлена в сторону противоположную скорости.

Запишем уравнение колебаний в точке, колеблющийся в среде, коэффициент сопротивлений которой r . По второму закону Ньютона

где β — коэффициент затухания. Этот коэффициент характеризует скорость затухания колебаний, При наличии сил сопротивления энергия колеблющейся системы будет постепенно убывать, колебания будут затухать.

— дифференциальное уравнение затухающих колебаний.

— у равнение затухающих колебаний.

ω – частота затухающих колебаний:

Период затухающих колебаний:

Затухающие колебания при строгом рассмотрении не являются периодическими. Поэтому о периоде затухаюших колебаний можно гово­рить, когда β мало.

Если затухания выражены слабо (β→0), то . Затухающие колебания можно

рассматривать как гармонические колебания, амплитуда которых меняется по экспоненциальному закону

В уравнении (1) А₀ и φ₀ — произвольные константы, зависящие от выбора момента времени, начиная е которого мы рассматриваем колебания

Рассмотрим колебание в течение, некоторого времени τ, за которое амплитуда уменьшится в е раз

τ — время релаксации.

Коэффициент затихания β обратно пропорционален времени, в течение которого амплитуда уменьшается в е раз. Однако коэффициента затухания недостаточна для характеристики затуханий колебаний. Поэтому необходимо ввести такую характеристику для затухания колебаний, в которую входит время одного колебаний. Такой характеристикой является декремент (по-русски: уменьшение) затухания D , который равен отношению амплитуд, отстоящих по времени на период:

Логарифмический декремент затухания равен логарифму D :

Логарифмический декремент затухания обратно пропорционален числу колебаний, в результате которых амплитуда колебаний умень­шилась в е раз. Логарифмический декремент затухания — постоянная для данной системы величина.

Еще одной характеристикой колебательной система является добротность Q .

Добротность пропорциональна числу колебаний, совершаемых системой, за время релаксации τ.

Добротность Q колебательной системы является мерой относительной диссипации (рассеивания) энергии.

Добротность Q колебательной системы называется число, показывающее во сколько раз сила упругости больше силы сопротивления.

Чем больше добротность, тем медленнее происходит затухание, тем затухающие колебания ближе к свободным гармоническим.

§7 Вынужденные колебания.

Резонанс

В целом ряде случаев возникает необходимость создания систем, совершающих незатухающие колебания. Получить незатухающие колебания в системе можно, если компенсировать потери энергии, воздействуя на систему периодически изменяющейся силой.

Запишем выражение для уравнения движения материальной точки, совершающей гармоническое колебательное движение под действием вынуждающей силы.

По второму закону Ньютона:

(1)

— дифференциальное уравнение вынуж­денных колебаний.

Это дифференциальное уравнение является линейным неоднородным.

Его решение равно сумме общего решения однородного уравнения и частного решения неоднородного уравнения:

Найдем частное решение неоднородного уравнения. Для этого перепишем уравнение (1) в следующем виде:

(2)

Частное решение этого уравнения будем искать в виде:

т.к. выполняется для любого t , то должно выполняться равенство γ = ω , следовательно,

Это комплексное число удобно представить в виде

где А определяется по формуле (3 ниже), а φ — по формуле (4), следовательно, решение (2),в комплексной форме имеет вид

Его вещественная часть, являвшаяся решением уравнения (1) равна:

(3)

(4)

Слагаемое Х_о.о. играет существенную роль только в начальной стадии при установлении колебаний до тех пор, пока амплитуда вынужденных колебаний не достигнет значения определяемого равенством (3). В установившемся режиме вынужденные колебания происходят с частотой ω и являются гармоническими. Амплитуда (3) и фаза (4) вынужденных колебаний зависят от частоты вынуждающей силы. При определенной частоте вынуждающей силы амплитуда может достигнуть очень больших значений. Резкое возрастание амплитуды вынужденных колебаний при приближении частоты вынуждающей силы к собственной частоте механи­ческой системы, называется резонансом.

Частота ω вынуждающей силы, при которой наблюдается резонанс, называется резонансной. Для того чтобы найти значение ω_рез, необходимо найти условие максимума амплитуды. Для этого нужно определить условие минимума знаменателя в (3) (т.е. исследовать (3) на экстремум).

Зависимость амплитуды колеблющейся величины от частоты вынуждающей силы называется резонансной кривой. Резонансная кривая будет тем выше, чем меньше коэффициент затухания β и с уменьшением β, максимум резонансных кривых смешается вправо. Если β = 0, то

При ω→0 все кривые приходят к значению — статическое отклонение.

Параметрический резонанс возникает в том случае, когда периодическое изменение одного из параметров система приводит к резкому увеличению амплитуды колеблющейся системы. Например, кабины, делающие «солнышко» за счет изменения положения центра тяжести система.(То же в «лодочках».) См. §61 .т. 1 Савельев И.В.

Лекция №8. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ

5.6. Затухающие гармонические колебания.

Во всякой реальной колебательной системе имеются силы сопротивления, действие которых приводит к уменьшению энергии системы. Если убыль энергии не восполняется за счет работы внешних сил, то колебания будут затухать. Затухающие колебания − это колебания, амплитуда которых из-за потерь энергии реальной колебательной системой с течением времени уменьшается. В простейшем, и вместе с тем наиболее часто встречающемся случае, сила сопротивления, вызывающая затухание, зависит от скорости колебательного движения, т. е. ее можно считать прямо пропорциональной скорости

где μ − постоянная, называемая коэффициентом сопротивления.

Знак «минус» обусловлен тем, что сила и скорость имеют противоположные направления. Тогда второй закон Ньютона для гармонических колебаний при наличии сил сопротивления имеет вид

Учитывая , что a= $$d^2x\over dt^2$$ , а υ= $$dx\over dt$$ и разделив на массу m , получим

Применив обозначения $$ = ω_0<^2>$$ , $$ <μ\over m>= 2β$$ и $$ = f_0$$ получим

дифференциальное уравнение затухающих колебаний . Отметим, что ω₀ представляет собой ту частоту, с которой совершались бы свободные колебания системы в отсутствие сопротивления среды. Эта частота называется собственной частотой .

Для решения уравнения (5.6.4) сделаем подстановку

Проведем замену переменных

Подставим (5.6.5 и 5.6.6) в выражение (5.6.4)

Преобразуем , сократив на e -βt

Рассмотрим случай, когда сопротивление среды настолько мало, что ω₀ 2 -β 2 >0 есть величина положи мы можем ввести тельная, и обозначение ω₀ 2 -β 2 =ω 2 , после чего уравнение (5.6.8) примает вид

В случае большого сопротивления среды ω₀ 2 -β 2 , движение становится непериодическим.

Решение уравнения (5.6.8) можно записать в виде

Окончательно, подставляя последнее уравнение в выражение (5.6.5), получаем общее решение дифференциального уравнения затухающих колебаний (5.6.4)

В соответствии с видом полученной функции движение можно рассматривать как гармоническое колебание с частотой

и амплитудой, изменяющейся по закону

На рисунке показан график данной функции. Пунктирными линиями показаны пределы, в которых находится смещение колеблющейся точки. Верхняя из пунктирных кривых дает график функции A(t) , причем величина A₀ представляет собой амплитуду в начальный момент времени. Начальное смещение зависит от A₀ и также от начальной фазы φ , т.е. x₀=A₀cosφ .

5.7. Коэффициент затухания и логарифмический декремент затухания.

Отношение значений амплитуд, соответствующих моментам времени, отличающимся на период, равно

и называется декрементом затухания .

Для характеристики системы обычно используется колебательной логарифмический декремент затухания , т.е. логарифм декремента затухания

Скорость затухания колебаний определяется величиной называем коэффициентом затухания $$β=<μ\over 2m>$$ .

Найдем время, называемое временем релаксации τ , за которое амплитуда уменьшается в e раз

т. е. коэффициент затухания обратен по величине промежутку времени, за который амплитуда колебаний уменьшается в e раз.

За время релаксации τ система успевает совершить $$N_e=<τ\over T>$$ колебаний

Следовательно, $$δ=<1\over N_e>$$ логарифмический декремент затухания обратно пропорционален по величине числу колебаний, за которые амплитуда колебаний уменьшается в e раз.

Для характеристики колебательной системы используется величина

которая называется добротностью колебательной системы.

Величина Q , пропорциональная числу колебаний, совершаемых системой за время, в течение которого амплитуда колебаний уменьшается в e раз.

5.8. Вынужденные колебания.

До сих пор мы рассматривали свободные колебания, когда выведенная из положения равновесия система совершает колебания будучи предоставленной самой себе. Рассмотрим колебательную систему, которая подвергается действию внешней силы, изменяющейся по гармоническому закону F=F₀cosωt . Колебания, возникающие под действием внешней периодически изменяющейся силы, называются вынужденными колебаниями . В этом случае уравнение второго закона Ньютона имеет вид

Учитывая , что a= $$d^2x\over dt^2$$ , а υ= $$dx\over dt$$ и разделив на массу m , получим

Применив обозначения $$ = ω_0<^2>$$ , $$ <μ\over m>= 2β$$ и $$ = f_0$$ получим

дифференциальное уравнение вынужденных колебаний.

Будем искать решение уравнения (5.8.3) в виде

предполагая, что результирующее колебание будет совершаться с частотой внешней вынуждающей силы.

Подставим (5.8.4) и (5.8.5) в уравнение (5.8.3)

Чтобы уравнение (69) обратилось в тождество необходимо, чтобы коэффициенты при cosωt и sinωt были равны нулю.

Из выражения (71) получаем

Возведем в квадрат уравнения (70) и сложим

Подставив полученные выражения (71) и (73) в выражение (64) получим уравнение вынужденных колебаний

5.9. Резонанс.

Зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы приводит к тому, что при некоторой частоте амплитуда колебаний достигает максимального значения.

Явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающей силы к частоте, равной или близкой собственной частоте колебательной системы называется резонансом , а соответствующая частота − резонансной частотой.

Найдем резонансную частоту. Амплитуда вынужденных колебаний будет max, когда выражение $$(ω_0<^2>-ω^2)^2 + 4β^2ω^2$$ в уравнении $$A=-ω^2)^2 + 4β^2ω^2>>$$ (5.8.13) будет минимальным.

Продифференцируем это выражение по ω и приравняем к нулю

Полученное уравнение имеет три решения: ω=0 и ω=± $$\sqrt <ω_0<^2>-2β^2>$$ . 2 . Первое решение соответствует максимуму знаменателя. Из остальных двух решений отрицательное не имеет физического смысла (частота не может быть отрицательной). Таким образом, резонансная циклическая частота

Подставив это значение в выражение для амплитуды (5.8.13), получим выражение для амплитуды при резонансе

Из последнего уравнения (5.9.3) следует, что при отсутствии сопротивления среды амплитуда при резонансе обращалась бы в бесконечность, а резонансная частота, согласно (5.9.2), при тех же условиях (при β=0 ), совпадала бы с собственной частотой колебаний системы ω₀

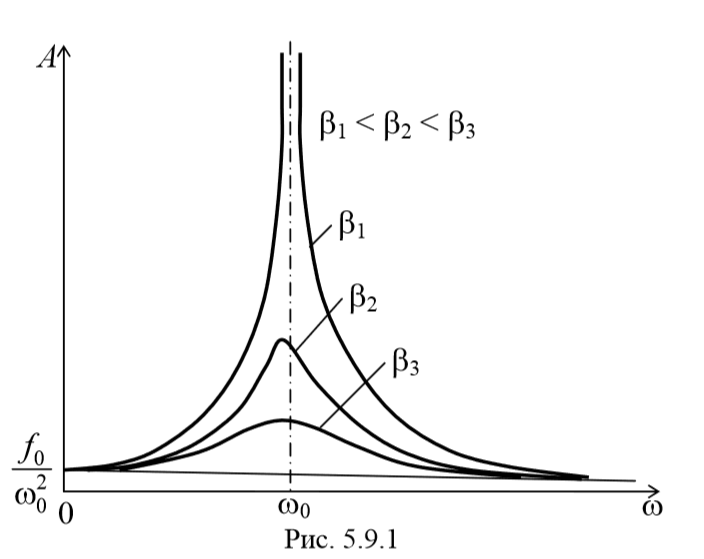
Зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы показана графически на рис. 5.9.1. В соответствии с (5.9.2) и (5.9.3), чем меньше параметр β , тем выше и правее лежит максимум данной кривой. Изображенная на рис. 5.9.1 совокупность графиков функций (5.8.13), соответствующих различным значениям параметра β , называется резонансными кривыми .

При стремлении ω к нулю все кривые приходят к одному и тому же, отличному от нуля, предельному значению, равному f₀ω₀ 2 . Это значение представляет собой смещение из положения равновесия, которое получает система под действием постоянной силы величины F₀

При стремлении ω к бесконечности все кривые асимптотически стремятся к нулю, так как при большой частоте сила так быстро изменяет свое направление, что система не успевает заметно сместиться из положения равновесия.

Наконец, отметим, что чем меньше β , тем сильнее изменяется с частотой амплитуда вблизи резонанса, тем «острее» получается максимум. При малом затухании (т. е. β ) амплитуда при резонансе приближенно равна A_pes≈f₀/2βω₀ . Разделим это выражение на смещение x₀ из положения равновесия под действием постоянной силы F₀ , равное x₀=f₀/ω_p 2 . В результате получим

где δ = βТ – логарифмический декремент затухания (5.7.2); Q – добротность колебательной системы (5.7.6).

Таким образом, добротность Q показывает, во сколько раз амплитуда в момент резонанса превышает смещение системы из положения равновесия под действием постоянной силы той же величины, что и амплитуда вынуждающей силы. Следует отметить, что это справедливо лишь при небольшом затухании.

Уравнение вынужденных колебаний

Если маятник отвести от положения устойчивого равновесия и отпустить, то он начнет совершать собственные затухающие колебания под действием упругой силы и силы сопротивления. Будем считать, что упругая сила пропорциональна смещению F_упр = −kx, а сила сопротивления пропорциональна скорости движения . Здесь и r – коэффициенты упругости и сопротивления. Если кроме этого приложить к маятнику еще внешнюю периодическую силу , то он будет совершать вынужденные колебания.

Получим формулу для амплитуды вынужденных колебаний маятника, решив уравнение второго закона Ньютона

. (16.1)

Разделив на массу, приведем уравнение к канонической форме

, (16.2)

Это дифференциальное уравнение вынужденных колебаний. В нем введены обозначения: – коэффициент затухания, – циклическая частота собственных свободных колебаний.

Как показывает опыт, если на маятник начать действовать периодической силой, то вынужденные колебания устанавливаются не сразу. В течение некоторого времени на вынужденные колебания накладываются собственные колебания. Но так как собственные колебания являются затухающими, то со временем они исчезают и маятник совершает только вынужденные колебания. Их частота равна частоте внешней периодической силы. Поэтому частное решение уравнения (16.2) будем искать для установившихся вынужденных колебаний в виде

, (16.3)

где – амплитуда колебаний, наибольшее смещение маятника от положения равновесия. Чтобы убедиться, что функция (16.3) является решением, следует подставить ее и первую, вторую производные в уравнение (16.2)

. (16.4)

Это уравнение содержит две неизвестные величины: амплитуду колебаний А и сдвиг фаз между силой и смещением . Для их определения воспользуемся заменой тригонометрического уравнения его геометрическим представлением в виде векторной диаграммы (рис. 16.1).

Для этого из полюса О следует провести векторы, длины которых равны амплитудам, а углы относительно полярной оси равны начальным фазам. Теперь, если вращать векторы вокруг полюса О против часовой стрелки с угловой скоростью, равной частоте ω, то их проекции будут равны членами уравнения (16.4).

На векторной диаграмме сумма векторов, изображающих слагаемые в левой части уравнения должна быть равна вектору, изображающему правую часть уравнения (16.4). Запишем теорему Пифагора для заштрихованного треугольник

. (16.5)

Отсюда получим уравнение для амплитуды вынужденных колебаний

. (16.6)

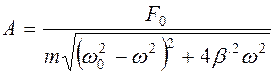
С ростом частоты амплитуда сначала возрастает от величины статического смещения , достигает наибольшего значения и затем снова уменьшается (рис. 16.2). Сильное увеличение амплитуды вынужденных колебаний при некоторой частоте называется резонансом. Чтобы получить условие резонанса, следует, как при поиске максимума функции, приравнять производную от подкоренного выражения (16.6) к нулю. Откуда получим . Как видно, резонанс наступает при частоте вынуждающей силы, близкой к частоте свободных колебаний. Подставив частоту резонансав формулу (16.6), получим для амплитуды резонанса

. (16.7)

Резонанс обусловлен тем, что направление скорости тела и направление силы совпадают в течение всего периода колебания. Поэтому отбор мощности от источника (N=F∙V)оказывается наибольший. Чем меньше сопротивление среды (β → 0), тем выше амплитуда при резонансе.

По резонансной кривой можно определить коэффициент затухания. Проведем на уровне горизонтальную линию (рис. 16.2). Абсциссы точек пересечения определим, подставив в левую часть уравнения (16.6) амплитуду при резонансе (16.7), деленную на . Решив квадратное уравнение относительно корней ω₁ и ω₂, получим, что полуширина резонансной кривой Δω = ω₁– ω₂ равна коэффициенту затухания: .

Сдвиг фаз между силой и смещением можно определить из треугольника векторной диаграммы (рис. 16.1)

. (16.8)

При малых частотах вынуждающей силы (ω

Определим центробежную силу инерции. Якорь – не болванка, а сложная конструкция и изготовить ее идеально точно крайне затруднительно. Центр масс якоря может быть смещен относительно оси вала на некоторое расстояние r₀. Уменьшают этот разбаланс методом статической балансировки, добиваясь при строго горизонтальной оси якоря безразличного равновесия в любом положении. Однако, возможно, что у одной части якоря ее центр масс находится по одну сторону оси вала, а у другой – по другую, хотя общий может быть на оси. Тогда при вращении возникает переменный момент сил. Его устраняют методом динамической балансировки, уравновешивая каждую часть якоря дополнительными грузами.

Ограничимся действием только центробежной силы инерции. Ее равнодействующая приложена к центру масс. Величина центробежной силы равна 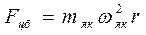, где m_як – масса якоря, ω_як – угловая скорость вращения якоря, r – расстояние от оси вращения до центра масс якоря. Вектор силы вращается вместе с якорем. В проекции на вертикальное направление, вдоль которого происходят колебания двигателя, центробежная сила становится периодической силой, вызывающей вынужденные колебания двигателя с циклической частотой, равной скорости вращения якоря:

. (16.9)

Амплитуда колебаний двигателя относительно вагона рассчитывается по формуле (6), при подстановке амплитуды центробежной силы

. (16.10)

Проблема в приведенных расчетах заключается в том, что вал при вращении под действием центробежной силы изгибается, и расстояние от оси вращения до центра масс r не постоянно, оно зависит от скорости вращения. При малой скорости вращения центробежная сила увеличивает изгиб вала. Если частота вращения оказывается равна частоте собственных колебаний якоря на валу, наступает резонанс и расстояние центра масс от оси вращения наибольшее. А при очень большой скорости вращения сила и смещение оказываются в противофазе, как это должно быть при вынужденных колебаниях якоря на валу, и смещение стремится к нулю. Вибрации при этом почти исчезают.

Таким образом, тяговый электродвигатель может иметь даже две резонансных частоты: при колебаниях двигателя как целого в подвеске и при колебаниях якоря относительно корпуса двигателя. Если же резонанс наступил, то следует быстрее увеличить скорость вращения и пройти опасный диапазон.

Задачи

1. Определить, при какой скорости вагон начнет сильно раскачиваться в вертикальном направлении из-за ударов о стыки рельсов. Масса вагона 60 т, коэффициент упругости восьми пружин подвески 2·10 7 Н/м, длина рельса 25 м.

2. Центр масс ротора массой 400 кг тягового двигателя массой 800 кг смещен относительно оси вращения на 0,01 мм. Двигатель подвешен к раме вагона, коэффициент упругости подвески 8·10 5 Н/м. При какой частоте вращения наступит резонанс. Определить амплитуду колебаний при резонансе, если коэффициент затухания амортизаторов 0,8 1/с.

3. Определить амплитуду вынуждающей силы вибростенда по графику зависимости амплитуды от частоты вынужденных колебаний (рис.16.4) колесной пары массой 1200 кг, установленной с пружинами подвески на вибростенде. Коэффициент затухания колебаний 0,3 1/с

4. Колесная пара массой 1300 кг с подвеской установлена на вибростенде. Определить приближенно по графику (рис.16.4) коэффициент затухания амортизаторов как полуширину резонансного пика на уровне . Определить коэффициент упругости пружин подвески.

5. На вагон массой 40 т со стороны рельсов действует вертикальная переменная сила F = 300 sin 31,4 t Н. При каком значении коэффициента упругости подвески вагона наступит резонанс. Чему равна при этом амплитуда колебаний, если коэффициент затухания 0,4 1/с.

6. Определить, при какой скорости начнет сильно раскачиваться вагон, совершая галопирующие колебания из-за ударов о стыки рельсов. Масса вагона 60 т, расстояние между осями 12 м, длина вагона 15м, коэффициент упругости передней и задней подвесок 1·10 7 Н/м. Длина рельса 25 м.

7. Определить, при какой амплитуде колебаний вагона при вибрации с частотой 20 Гц незакрепленные предметы будут подпрыгивать относительно пола вагона.

17. ВОЛНЫ В УПРУГИХ СРЕДАХ

Волны – это процесс распространения колебаний в пространстве. Существует большое многообразие видов механических волн в упругих средах. Наиболее известны объемные волны. В объеме газа, жидких и твердых сред могут распространяться продольные волны, в которых частицы совершают колебания вдоль направления распространения волны. В твердых средах могут распространяться поперечные волны, в которых частицы совершают колебания перпендикулярно направлению распространения волны. Различные виды волн распространяются вдоль поверхности жидкости, твердых тел, по земной коре. Распространяются волны в стержнях, шнурах, проводах и так далее. Всегда, когда среда обладает упругостью и массой, в ней могут распространяться упругие волны.

Уравнение волны.

Получим уравнение волны. Это уравнение изменения параметра колебаний частиц средыв любой точке пространства в зависимости от времени и расстояния до источника колебаний. Параметром, который периодически изменяется в упругой волне, может быть смещение частиц от положения равновесия, скорость частиц, или плотность и давление в жидкости и газе, механические напряжения, т.д. Под частицей понимается сравнительно небольшой объем вещества, но содержащий огромное число молекул, которые движутся совместно.

Пусть, например, смещение источника происходят по уравнению 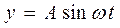, где А – амплитуда колебаний, ω – циклическая частота колебаний. Источник действует на ближайшие частицы окружающей среды, вынуждая их совершать колебания около их положений равновесия с частотой колебаний источника. Те, в свою очередь, заставляют совершать колебания следующие частицы. Происходит процесс распространения вынужденных колебаний в пространстве, который называется волной.

Поверхность среды, до которой дошло возбуждение от источника колебаний, называется фронтом волны. Форма фронта волны может быть различной. В однородной среде фронт от точечного источника (пульсирующий шарик) является сферическим. Фронт можно считать плоским на большом расстоянии от точечного источника или при излучении большой колеблющейся плоскостью, или при колебаниях поршня в цилиндрической трубе.

Пусть от источника распространяется вдоль оси x волна с плоским фронтом. Если можно пренебречь затуханием колебаний, то амплитуда колебаний частиц среды одинакова. Частицы среды начинают колебания позже, чем источник. Время запаздывания равно времени распространения волны , где V – скорость распространения фронта волны, x – расстояние от источника колебаний до частиц на фронте. Уравнение вынужденных колебаний частиц на оси x будет отличаться от уравнения колебаний источника только временем запаздывания

. (17.1)

Это уравнение является уравнением бегущей гармонической (синусоидальной) волны. Его можно изобразить графиком синусоиды, который вместе с волной перемещается вдоль оси x со скоростью фронта (рис. 17.1). За время одного периода колебаний фронт перемещается на расстояние, называемое длиной волны . Длина волны также равна расстоянию между ближайшими точками на линии распространения, разность фаз которых равна 2π радиан.

Перепишем уравнение волны, введя в него длину волны. Подставив при , получим

. (17.2)

Здесь называется волновым вектором. В общем случае это вектор, показывающий направление распространения фронта волны. Если волна распространяется в направлении против оси x, то волновой вектор в уравнении (17.2) отрицателен.

Функция (17.2) описывает распространение монохроматической бесконечной волны. Аргумент функции называется фазой. Поверхность среды, для частиц которой фаза постоянна, , называется волновой поверхностью. Для частиц на фронте фаза равна нулю. Фронт и волновые поверхности перемещаются с так называемой фазовой скоростью. Продифференцировав формулу фазы, получим .

Если волна излучается конечное время, то её описывают как группу монохроматических волн разных близких частот и скорость перемещения группы называют групповой скоростью.

При распространении волны частицы вещества, то есть масса вещества, волной не переносится. Переносится кинетическая и потенциальная энергия колебаний и импульс вследствие взаимодействия частиц.

Интерференция волн

Интерференция – это явление наложения волн, в результате которого в пространстве возникают области усиления и ослабления колебаний. Согласно принципу суперпозиции, волны при встрече не искажают друг друга, проходят друг через друга, не изменяясь. В области наложения волн происходит перераспределение энергии колебаний. Устойчивое во времени и в пространстве интерференционное распределение энергии возможно только при наложении когерентных волн. Волны являются когерентными, если разность фаз в точке наблюдения постоянна по времени и частоты одинаковы. Для поперечных волн дополнительно должно соблюдаться условие параллельности направления колебаний. Усиление колебаний будет, если в точке наблюдения разность фаз равна четному числу π радиан, (горб на горб). Волны ослабляют друг друга, если разность фаз равна нечетному числу π радиан, (горб на впадину).

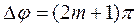
Рассмотрим частный случай интерференции – образование стоячих волн. Например, в струне, концы которой закреплены в стенках. Если перпендикулярно струне действует периодическая сила, то от места возбуждения в обоих направлениях распространяются поперечные волны. Достигнув места закрепления у стенки, волны отражаются. По закону сохранения энергии амплитуда отраженной волны должна быть равна амплитуде бегущей волны. Отраженная и бегущая волны интерферируют. Около самой стенки струна закреплена, и её конец совершать колебания не может. Значит, в этой точке отраженная волна должна быть в противофазе с бегущей волной. Уравнения для бегущей и отраженной волны примут вид

;(17.3)

. (17.4)

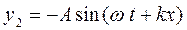
Здесь А – амплитуда колебаний w – циклическая частота, x– координата от начала струны. Бегущая и отраженная волны накладываются. Сложив уравнения волн по формулам тригонометрии, получим уравнение для результата интерференции

. (17.5)

Как видно, частицы струны совершают колебания с частотой бегущей волны, но фазовая скорость отсутствует. Собственно говоря, это не волна, а колебательное состояние среды. Его называют стоячей волной. Выражение имеет смысл амплитуды. Точки среды, где амплитуда равна нулю, называются узлами смещения. Расстояние между двумя соседними узлами равно половине длины волны. Узлы отделяют друг от друга изолированные зоны, называемые пучностями, в которых частицы совершают колебания (рис.17.2). Направления колебаний в соседних пучностях противоположны. Максимальная амплитуда в два раза больше амплитуды бегущих волн. Стоячая волна в струне может возникнуть при условии, что на её закрепленных концах будут узлы смещения. Для этого длина струны должна быть равна целому числу полуволн (рис.17.3).