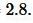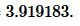Уравнение высоты опущенной на плоскость онлайн калькулятор

Высота треугольника онлайн

С помощю этого онлайн калькулятора можно найти высоту треугольника. Для нахождения высоты треугольника введите известные элементы треугольника и нажмите на кнопку «Вычислить». Теоретическую часть смотрите ниже.

Открыть онлайн калькулятор

Высота треугольника. Определение

Определение 1. Отрезок, проведенный из вершины треугольника к прямой, содержащей противоположную сторону, называется высотой треугольника.

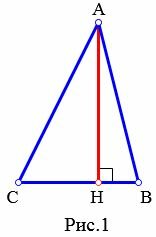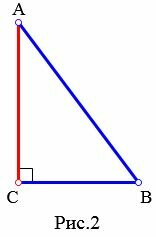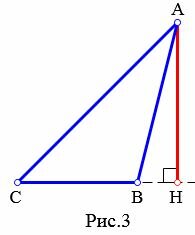Высота треугольника может содержаться внутри треугольника (Рис.1), совпадать со стороной треугольника (при прямоугольном треугольнике высота совпадает с катетом (Рис.2) ), проходить вне треугольника (при тупоугольном треугольнике(Рис.3)).

Теорема о пересечении высот треугольника

Теорема 1. Все три высоты треугольника (или их продолжения) пересекаются в одной точке.

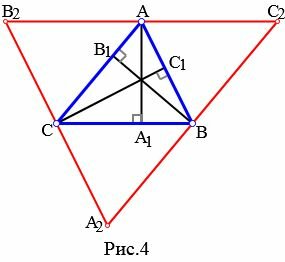Доказательство. Рассмотрим произвольный треугольник ABC (Рис.4). Докажем, что высоты $ \small AA_1 ,$ $ \small BB_1 ,$ $ \small CC_1 $ пересекаются в одной точке. Из каждой вершины треугольника проведем прямую, параллельно противоположной стороне. Получим треугольник $ \small A_2B_2C_2. $ Покажем, что точки $ \small A, \ B, \ C $ являются серединами сторон треугольника $ \small A_2B_2C_2. $ $ \small AB=A_2C $ так как они являются противоположными сторонами параллелограмма $ \small ABA_2C. $ $ \small AB=CB_2 $ так как они являются противоположными сторонами параллелограмма $ \small ABCB_2. $ Тогда $ \small CB_2=CA_2, $ то есть точка $ \small C $ является серединой стороны $ \small A_2B_2 $ треугольника $ \small A_2B_2C_2. $ Аналогично доказывается, что точки $ \small A $ и $ \small B $ являются серединами сторон $ \small B_2C_2 $ и $ \small A_2C_2, $ соответственно.

Далее из $ \small AA_1⊥BC $ следует, что $ \small AA_1⊥B_2C_2 $ поскольку $ \small BC \ ǁ \ B_2C_2 $. Аналогично, $ \small BB_1⊥A_2C_2, $ $ \small CC_1⊥A_2B_2. $ Получили, что $ \small AA_1,$ $ \small BB_1, $ $ \small CC_1$ являются серединными перпендикулярами сторон $ \small B_2C_2, $ $ \small A_2C_2, $ $ \small A_2B_2, $ соответственно. Но серединные перпендикуляры треугольника пересекаются в одной точке (см. статью Серединные перпендикуляры к сторонам треугольника). Следовательно высоты треугольника или их продолжения пересекаются в одной точке.

Точка пересечения высот треугольника называется ортоцентром.

Высота треугольника по основанию и площади

Пусть известны сторона треугольника и площадь. Найти высоту треугольника, отпущенная на известную сторону (Рис.5).

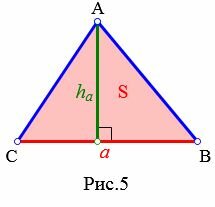Решение. Площадь треугольника по основанию и высоте вычисляется из формулы:

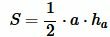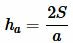(1)

Пример 1. Сторона треугольника равна $ \small a=5 $ а площадь $ \small S=7. $ Найти высоту треугольника.

Применим формулу (1). Подставляя значения $ \small a $ и $ \small S $ в (1), получим:

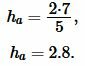Ответ:

Высота треугольника по трем сторонам

Формула площади треугольника по трем сторонам имеет следующий вид (см. статью на странице Площадь треугольника онлайн):

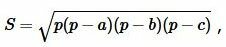(2)

где $ \small a, \ b, \ c $ стороны треугольника а полупериод $ \small p $ вычисляется из формулы:

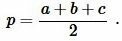(3)

Высота треугольника, отпущенная на сторону $ \small a$ вычисляется из формулы (1). Подставляя (2) в (1), получим формулу вычисления высоты треугольника по трем сторонам:

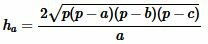(4)

Пример 2. Известны стороны треугольника: $ \small a=5, $ $ \small b= 4, $ $ \small c=7. $ Найти высоту треугольника, отпущенная на сторону $ \small a. $

Решение: Найдем, сначала полупериод $ \small p $ треугольника из формулы (3):

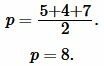Подставляя значения $ \small a , \ b, \ c $ и $ \small p $ в (4), получим:

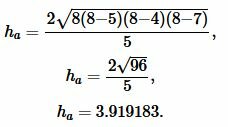Ответ:

Высота треугольника по двум сторонам и радиусу описанной окружности

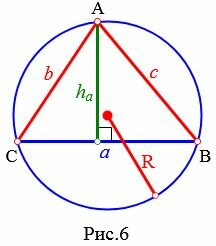Рассмотрим треугольник на рисунке 6. Из теоремы синусов имеем:

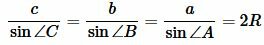(5)

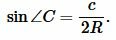(6)

Далее, из теоремы синусов имеем:

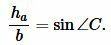(7)

Подставляя (6) в (7), получим:

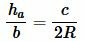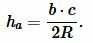(8)

Отметим, что радиус описанной окружности должен удовлетворять следующему неравенству:

$\small \max (b,c) ≤2R Пример 3. Известны стороны треугольника: \( \small b=7, $ $ \small c= 3 $ и радиус описанной окружности $ \small R=4. $ Найти высоту треугольника, отпущенная на сторону $ \small a. $

Решение: Проверим сначала условие (9):

$\small \max (7,3) ≤2 \cdot 4 Ответ: \( \small 2\frac<5><8>. $

Высота треугольника по стороне и прилежащему к ней углу

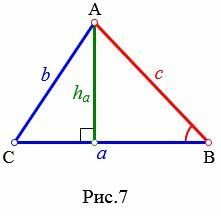Найдем высоту $ \small h_a $ треугольника на рисунке 7. Из теоремы синусов имеем:

$ \small \frac<\large h_a><\large \sin \angle B>=\frac<\large c><\large \sin 90°>, $

$ \small h_a=c \cdot \sin \angle B. $

(11)

Пример 4. Известны сторона $ \small c=12 $ треугольника и прилежащий угол $ \small \angle B=30°. $ Найти высоту треугольника, отпущенная на сторону $ \small a. $

Решение: Для нахождения высоты треугольника подставим значения $ \small c=12 $ и $ \small \angle B=30° $ в (11). Имеем:

Онлайн калькулятор. Расстояние от точки до плоскости

Предлагаю вам воспользоваться онлайн калькулятором для вычисления расстояния от точки до плоскости.

Воспользовавшись онлайн калькулятором, вы получите детальное пошаговое решение вашей задачи, которое позволит понять алгоритм решения задач на вычисление расстояния от точки до плоскости и закрепить пройденный материал.

Найти расстояние от точки до плоскости

Ввод данных в калькулятор для вычисления расстояния от точки до плоскости

В онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел.

Дополнительные возможности калькулятора для вычисления расстояния от точки до плоскости

Используйте кнопки и на клавиатуре, для перемещения между полями калькулятора.

Теория: Расстояние от точки до плоскости

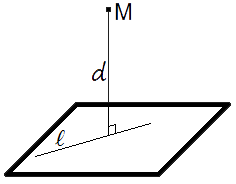
Расстояние от точки до плоскости — равно длине перпендикуляра, опущенного из точки на плоскость.

Если задано уравнение плоскости A x + B y + C z + D = 0, то расстояние от точки M(M _x , M _y , M _z ) до плоскости можно найти используя следующую формулу

d =	\|A·M _x + B·M _y + C·M _z + D\|
	√ A 2 + B 2 + C 2

Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Решение задач по математике онлайн

//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘

Калькулятор онлайн.
Составить уравнение плоскости

Этот калькулятор онлайн составляет (находит) уравнение плоскости по трем точкам, лежащим на плоскости или по нормали и одной точке лежащей на плоскости.

Онлайн калькулятор для нахождения уравнения плоскости не просто даёт ответ задачи, он приводит подробное решение с пояснениями, т.е. отображает процесс решения для того чтобы проконтролировать знания по математике и/или алгебре.

Этот калькулятор онлайн может быть полезен учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.

Если вы не знакомы с правилами ввода чисел, рекомендуем с ними ознакомиться.

Числа можно вводить целые или дробные.
Причём, дробные числа можно вводить не только в виде десятичной, но и в виде обыкновенной дроби.

Правила ввода десятичных дробей.
В десятичных дробях дробная часть от целой может отделяться как точкой так и запятой.
Например, можно вводить десятичные дроби так: 2.5 или так 1,3

Правила ввода обыкновенных дробей.
В качестве числителя, знаменателя и целой части дроби может выступать только целое число.

Знаменатель не может быть отрицательным.

При вводе числовой дроби числитель отделяется от знаменателя знаком деления: /
Ввод: -2/3
Результат: $ -\frac<2> <3>$

Целая часть отделяется от дроби знаком амперсанд: &
Ввод: -1&5/7
Результат: $ -1\frac<5> <7>$

Составить уравнение плоскости

Немного теории.

Общее уравнение плоскости

Пусть заданы:
прямоугольная система координат Oxyz,
произвольная плоскость $ \pi $;
точка $ M_0(x_0;y_0;z_0) \in \pi $;
вектор $ \vec(A;B;C) $, перпендикулярный плоскости $ \pi $ (смотри рисунок).

Рассмотрим произвольную точку М(х; у; z). Точка М лежит на плоскости $ \pi $ тогда и только тогда, когда векторы $ \vec $ и $ \vec $ взаимно перпендикулярны. Так как координаты вектора $ \vec $ равны $ x-x_0, \; y-y_0, \; z-z_0 $ , то в силу условия перпендикулярности двух векторов (скалярное произведение должно быть равно нулю) получаем, что точка М (х; у; z) лежит на плоскости $ \pi $ тогда и только тогда, когда

Раскрывая скобки, приведем уравнение (1) к виду
$ Ax+By+Cz+(-Ax_0-By_0-Cz_0)=0 $
Далее, обозначая число $ -Ax_0-By_0-Cz_0 $ через $ D $, получаем

Верно и обратное: всякое уравнение первой степени вида (2) определяет в заданной прямоугольной системе координат плоскость. Действительно, пусть заданы прямоугольная система координат Oxyz и уравнение $ Ax+By+Cz+D=0 $ с произвольными коэффициентами А, В, С и D, причем из коэффициентов А, В и С хотя бы один отличен от нуля. Данное уравнение заведомо имеет хотя бы одно решение $ x_0, \; y_0, \; z_0 $ ( если, например, $ C \neq 0 $, то, взяв произвольные х₀, и y₀, из уравнения получим: $ z_0 = -\fracx_0 — \fracy_0-\frac $ ).

Таким образом, существует хотя бы одна точка M₀(x₀; y₀; z₀), координаты которой удовлетворяют уравнению, т.е. Ax₀+By₀+Cz₀+D=0. Вычитая это числовое равенство из уравнения Ax+By+Cz+D=0, получаем уравнение
A(x-x₀) + B(y-y₀) + C(z-z₀) + D=0,
эквивалентное данному. Полученное уравнение (а стало быть, и уравнение Ax+By+Cz+D=0 ) совпадает с уравнением (1) и, значит, определяет плоскость $ \pi $, проходящую через точку M₀(x₀ и перпендикулярную вектору $ \vec(A;B;C) $.

Вектор $ \vec(A;B;C) $, перпендикулярный плоскости, называется нормальным вектором или нормалью этой плоскости.

Теорема
Если два уравнения $ A_1x+B_1y+C_1z+D_1=0 $ и $ A_2x+B_2y+C_2z+D_2=0 $ определяют одну и ту же плоскость, то их коэффициенты пропорциональны, т.е. $$ \frac = \frac = \frac = \frac $$

Угол между двумя плоскостями

Рассмотрим две плоскости $ \pi_1 $, и $ \pi_2 $, заданные соответственно уравнениями

При любом расположении плоскостей $ \pi_1 $, и $ \pi_2 $ в пространстве один из углов $ \varphi $ между ними равен углу между их нормалями $ \vec(A_1;B_1;C_1) $ и $ \vec(A_2;B_2;C_2) $ и вычисляется по следующей формуле:
$$ \cos \varphi = \frac < \vec\cdot \vec>< |\vec| |\vec| > = \frac <\sqrt\; \sqrt > \tag <3>$$

Второй угол равен $ 180^\circ -\cos \varphi $

Условие параллельности плоскостей

Если плоскости $ \pi_1 $ и $ \pi_2 $ параллельны, то коллинеарны их нормали $ \vec $ и $ \vec $, и наоборот. Но тогда
$$ \frac = \frac = \frac \tag <4>$$
Условие (4) является условием параллельности плоскостей $ \pi_1 $ и $ \pi_2 $

Условие перпендикулярности плоскостей

Если плоскости $ \pi_1 $ и $ \pi_2 $ взаимно перпендикулярны, то их нормали $ \vec $ и $ \vec $ также перпендикулярны, и наоборот. Поэтому из формулы (3) непосредственно получаем условие перпендикулярности плоскостей $ \pi_1 $ и $ \pi_2 $:
$ A_1 A_2 + B_1 B_2 + C_1 C_2 = 0 $

источники:

http://ru.onlinemschool.com/math/assistance/cartesian_coordinate/p_plane/

http://www.math-solution.ru/math-task/lp-eqplain