Построение переходных и частотных характеристик линейных САУ: Методическое пособие для подготовки и выполнения лабораторной работы № 3
Страницы работы
Фрагмент текста работы
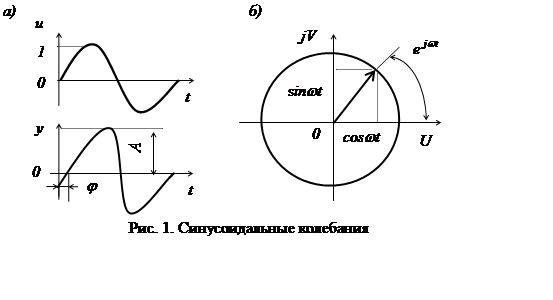
Принимается также символическая запись синосоидальных колебаний в виде:
Строго говоря, e j w t = cos(wt) + sin(wt), что геометрически изображается вращающимся единичным вектором (рис. 1, б). Проекции последнего на прямоугольные оси дают cos(wt) и sin(wt). Поэтому для суждения о вынужденных синусоидальных колебаниях звена достаточно формально исследовать реакцию звена на символический сигнал e j w t .
 |
Для получения частотных характеристик пользуются принципом суперпозиции. Его сущность заключается в следующем: реакция системы на несколько одновременно действующих входных воздействий равна сумме реакций на каждое воздействие в отдельности. Это позволяет ограничиться изучением систем только с одним воздействием (входом).
В общем случае уравнение линейной стационарной системы с одним входом можно записать так:
Ее передаточная функция:
называют частотной передаточной функцией.
Частотную передаточную функцию (ЧПФ) называют комплекснозначной функцией от действительной переменной w(частоты). ЧПФ можно представить, как комплексную функцию, в алгебраической форме записи:
Показательная форма записи:
Модуль вычисляется по формуле:
А(w) = |W(jw)| = 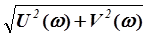
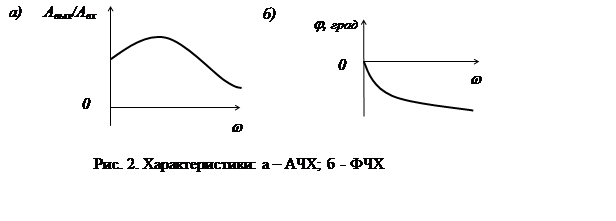
где А(w) – амплитудно-частотная функция, ее график называют амплитудно-частотной характеристикой (рис. 2, а), которая выражает отношение амплитуды колебаний на выходе звена к амплитуде колебаний на его входе в зависимости от частоты выходного сигнала.
 |
Аргумент равен:
j(w) = 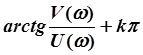
где j(w) – фазочастотная функция, ее график называют фазочастотной характеристикой (рис. 2, б). Она выражает зависимость разности фаз между входными и выходными колебаниями звена от частоты входного сигнала. Опережению фазы соответствует j > 0, а отставанию j
ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ. КАЧЕСТВО ПРОЦЕССА УПРАВЛЕНИЯ
6. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ. КАЧЕСТВО ПРОЦЕССА УПРАВЛЕНИЯ
Комплексную (амплитудно-фазовую) частотную характеристику (КЧХ, АФХ) W(jw) аналитически легко получить по соответствующей передаточной функции, если положить Р = jw.
Путём выделения в выражении КЧХ вещественной U(w) и мнимой V(w) частей, получаются соответственно вещественная (ВЧХ) и мнимая (МЧХ) частотные характеристики
Модуль А(w) и аргумент j(w) КЧХ определяют соответственно амплитудную (АЧХ) и фазовую (ФЧХ) частотные характеристики
Между всеми частотными характеристиками имеют место очевидные соотношения:
W(jw) = А(w) e j j ( w ) ;
А(w) = ÖU 2 (w) + V 2 (w) ;
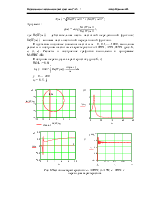
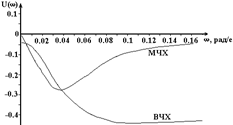
Применительно к САУ рис.3.1 при входном воздействии Df(t) частотные характеристики приведены на рис.6.1 и 6.2.
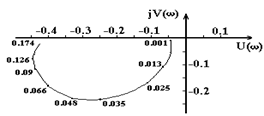
| U(w) | -0.03 | -0.04 | -0.06 | -0.08 | -0.11 | -0.17 | -0.25 | -0.33 | -0.4 | -0.44 | -0.44 |
| V(w) | -0.01 | -0.05 | -0.1 | -0.13 | -0.17 | -0.21 | -0.29 | -0.23 | -0.18 | -0.11 | -0.06 |
| w,рад/с | 0.001 | 0.005 | 0.01 | 0.013 | 0.018 | 0.025 | 0.035 | 0.48 | 0.066 | 0.09 | 0.13 |
Рис.6.1. Комплексная (а), вещественная (б) и мнимая (б) частотные характеристики САУ рис.3.1 при входном воздействии Df(t) и Ку = 20
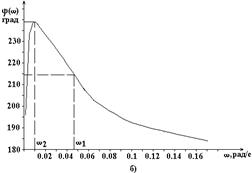
| w,рад/с | 0.001 | 0.005 | 0.01 | 0.013 | 0.018 | 0.025 | 0.035 | 0.048 | 0.066 | 0.09 | 0.13 |
| A(w) | 0.04 | 0.071 | 0.117 | 0.153 | 0.202 | 0.27 | 0.34 | 0.402 | 0.439 | 0.454 | 0.444 |
| j(w),град | 196 | 232 | 239 | 238 | 237 | 231 | 223 | 215 | 204 | 194 | 188 |
Рис.6.2. Амплитудная (а) и фазовая (б) частотные характеристики САУ рис.3.1 при входном воздействии Df(t) и Ку = 20, Кос = 20.
Из частотных характеристик следует, что при гармоническом характере возмущающего воздействия Df(t) влияние его на отклонение управляемой величины Dx(t) очень сильно возрастает с увеличением частоты. Например, при w1 = 0.047 рад/с и Df = 1.0sinw1t Dx(t) = 0.4sin(w1t + 215 0 ), т. е. амплитуда колебаний Dxm = 0.4 имеет такое же значение, как и при отсутствии регулирования. Действительно, если в САУ рис.3.1 разорвать главную обратную связь, то будет
Частотные характеристики
Министерство образования Российской Федерации
Балтийский государственный технический университет “Военмех”
Кафедра систем обработки информации и управления
В. Ю. ЕМЕЛЬЯНОВ
Конспект лекций
Санкт-Петербург
Математический аппарат частотных характеристик вместе с преобразованием Лапласа является основой аппарата классической теории автоматического управления. Формальной основой методов получения частотных характеристик является теория комплексных функций. Однако ряд известных общих результатов последней при их применении к математическим моделям реальных объектов, рассматриваемым в рамках теории управления, нуждается в уточнении или в устранении неоднозначности.
При получении всех частотных характеристик входной сигнал звена или системы считается гармоническим. При последующем анализе систем частотные характеристики применяются и при наличии произвольных входных сигналов. Такой прием основан на возможности представления сигнала произвольного вида в виде суммы гармоник (ряд Фурье или интеграл Фурье).
Определения и правила получения частотных характеристик рассмотрим сначала применительно к динамическим звеньям.
Входной сигнал звена (рис. 1) рассматривается в форме x1(t)=sinwt, то есть считается изменяющимся по синусоидальному закону с амплитудой А=1, фазой j=0 и частотой w. Значение частоты рассматриваются в диапазоне от -¥ до +¥. Отрицательные частоты здесь вводятся для удобства построения математического аппарата анализа систем. На практике характеристики получают для частот в диапазоне от 0 до +¥. В область отрицательных частот их распространяют в соответствии со свойствами частоты или погрешности. Следует помнить, что аналитические выражения для частотных характеристик принято также записывать, подразумевая значение аргумента w³0.

1. Амплитудно-частотная и фазо-частотная характеристики
Амплитудно-частотная характеристика (АЧХ) A(w) показывает степень усиления или ослабления звеном амплитуды пропускаемого гармонического сигнала в зависимости от его частоты.
Фазо-частотная характеристика (ФЧХ) j(w) показывает зависимость от частоты фазового сдвига, вносимого звеном в пропускаемый гармонический сигнал.
Формально АЧХ и ФЧХ могут быть получены на основе частотной передаточной функции (ЧПФ) звена W(jw).
ЧПФ может быть получена из обычной передаточной функции заменой оператора Лапласа s на jw:
ЧПФ представляет собой комплексную функцию, то есть каждому фиксированному значению w=w1, соответствует значение ЧПФ W1=W(jw1), в общем случае являющееся комплексным числом W1=a+jb=rejj, где а–вещественная часть, b–мнимая часть, 

Если рассматривать частоту как аргумент и изменять в пределах от -¥ до +¥ или от 0 до +¥, будет изменяться и значение ЧПФ, и всех ее характеристик.
Аналогично комплексному числу ЧПФ может быть представлена в алгебраической (через вещественную и мнимую части) и показательной (через модуль и аргумент) формах:
где U(w) и V(w) – соответственно вещественная и мнимая части ЧПФ, A(w) и j(w) – соответственно модуль и аргумент ЧПФ.
АЧХ может быть определена как модуль ЧПФ: A(w)=|W(jw)|.
ФЧХ определяется как аргумент ЧПФ: j(w)=argW(jw).
По аналогии с комплексным числом для АЧХ и ФЧХ можно записать соотношения:

но пользоваться этими соотношениями для получения характеристик динамических звеньев и систем не рекомендуется.
Причины этого состоят в следующем:
1. Передаточные функции динамических звеньев и особенно систем могут представлять собой достаточно сложные выражения – отношения полиномов относительно s или jw, степень которых может достигать 4-5. Преобразование такой дроби к виду U(w)+jV(w) весьма трудоемко, а результат будет довольно громоздким. Итоговое выражение вида (1) получается неоправданно сложным и явно неудобно для дальнейшего использования.
2. При получении j(w) в форме (2) следует помнить, что математическая функция arctg x имеет бесконечное множество значений:
где Аrctg x – главное значение, лежащее в диапазоне от — p/2 до +p/2; n=0,1,2,… С формальной точки зрения все эти значения равноценны. Такая трактовка результата неприемлема при получении ФЧХ, так как последняя должна однозначно характеризовать свойства реального объекта, моделью которого является передаточная функция.
Для устранения неоднозначности и значительного упрощения процедуры получения АЧХ и ФЧХ необходимо использовать следующий способ.
Передаточная функция должна быть представлена в форме дроби вида

где zi — вещественные константы или полиномы относительно s первой или второй степени.
При отсутствии комплексных корней относительно s у числителя и знаменателя W(s) они должны быть разложены на сомножители, содержащие s в первой степени. Один из сомножителей в числителе окажется вещественной константой (коэффициент передачи звена k).
Только при наличии комплексных корней относительно s у числителя или знаменателя W(s) сомножитель zi оставляют в форме полинома второй степени относительно s, соответствующего такой паре корней.
При выполнении указанных требований ЧПФ будет иметь аналогичный вид:
Теперь АЧХ и ФЧХ можно определить на основе правил умножения и деления комплексных чисел:
1. Модуль произведения равен произведению модулей сомножителей.
2. Модуль отношения равен отношению модулей числителя и знаменателя.
3. Аргумент произведения равен сумме аргументов сомножителей.
4. Аргумент отношения равен разности аргументов числителя и знаменателя.
Соответственно для ЧПФ вида (3) получим:
A(w)=|W(jw)|=
где 
Рассмотрим подробнее модули и аргументы сомножителей ЧПФ.

Расстояние до точки 1 от начала координат равно k, вектор, проведенный из начала координат в точку 1, совпадает с положительной вещественной полуосью, следовательно,
Результаты очевидны, так как звено с передаточной функцией W(s)=k масштабирует (усиливает или ослабляет) сигнал, не внося фазового сдвига.
2. z2= jw — на рис.3 такому выражению соответствует изображающая точка 2 на вертикальной (мнимой) оси с координатой w. При w>0 получаем:
3. z3=1+ jw T – в соответствии с рис. 3 (точка 3) получаем:

Далее везде, как принято в литературе по теории управления, будет использоваться только главное значение арктангенса и записываться с маленькой буквы. Окончательно: arg z3 =arctg wT.

5. z5= —1+ jwT — на рис. 4 такому выражению соответствует изображающая точка 5. Расстояние от начала координат до точки 5 находится аналогично случаям 3 и 4:

Угол наклона вектора, направленного в точку 5 из начала координат, j5 лежит в пределах от 
Перейдем к сомножителям второго порядка относительно s.

принято записывать таким образом, чтобы под знаком арктангенса содержалось положительное выражение:

В итоге для всего диапазона положительных частот получим:
Модуль рассматриваемого сомножителя определяется для любых частей одинаково – через его вещественную и мнимую части:

Рассмотрим ряд примеров получения АЧХ и ФЧХ динамических звеньев.
Пример 1. Апериодическое звено 1 порядка.


Представим ЧПФ в виде отношения
Выражение для АЧХ примет вид:

Для построения примерного графика АЧХ отметим следующее:
— при w = 0 
— при 

— при увеличении w от 0 до 
— модуль является четной функцией, следовательно при рассмотрении частот от — 

Примерный график АЧХ для рассматриваемого звена представлен на рисунке 6.
Выражение для ФЧХ примет вид:
Для построения примерного графика ФЧХ отметим следующее:
— при w = 0 j(0) = – arctg 0 = 0;
— арктангенс является монотонно возрастающей функцией, причем для главного значения арктангенса 

— арктангенс является нечетной функцией, следовательно ФЧХ, определяемая в общем случае на основе выражения (2) – также нечетная функция, и график ФЧХ при рассмотрении частот от — 

Примерный график ФЧХ для рассматриваемого примера представлен на рисунке 7.
Пример 2. Колебательное звено.

Получим ЧПФ и представим ее в виде дроби, состоящей из простейших сомножителей:
Выражение для АЧХ примет вид:

— при w=0 
— 
При достаточно малых значениях T2 по сравнению с T1 полученная функция A(w) может иметь максимум (резонансный пик). Соответствующее максимуму значение аргумента (частоты) найдем из условия равенства нулю производной:
Экстремумы имеют место на частотах:
w1 = 0,
Проанализировав знаки 


Выражение для ФЧХ рассматриваемого звена примет вид:

— при w = 0 
— при 


— при 



Характеристики на рисунках 8 и 9, как и во всех подобных задачах, построены с учетом четности АЧХ и нечетности ФЧХ.

Получим ЧПФ и представим ее в виде дроби, состоящих из простейших сомножителей:

Выражение для АЧХ примет вид:
Проанализируем полученное выражение:
— при w=0 







— все сомножители выражения для A(w) изменяются монотонно, следовательно, значения A(w) при увеличении частоты от 0 до 

Примерный график представлен на рисунке 10.
Выражение для ФЧХ примет вид:
— при w = 0 
— при 


— при T1>T2 на любой конечной положительной частоте 




— при w > 0 V(w) 0 

3. Амплитудно-фазовая частотная характеристика
Амплитудно-фазовой частотной характеристикой (амплитудно-фазовой характеристикой, АФХ) называется годограф частотной передаточной функции.
Годограф комплексной функции одного вещественного аргумента строится на комплексной плоскости, показанной на рис. 2. Любому значению аргумента на комплексной плоскости соответствует точка. Множество точек, соответствующее плавному изменению аргумента от — ¥ до ¥, образует кривую, которая и называется годографом.
 |
Пусть задана ЧПФ W(jw). Для некоторой частоты w1 (для определенности w1 > 0) соответствующая точка на комплексной плоскости может быть построена в декартовых координатах (рис. 22) на основе представления ЧПФ в алгебраической форме: W(jw1 ) = U(w1 ) +jV(w1 ), где U(w1) – значение ВЧХ, V(w1) – значение МЧХ на частоте w1 .
Представление ЧПФ в показательной форме даёт полярные координаты такой точки:

где А(w1) — значение АЧХ, j(w1) — значение ФЧХ частоте w1.
При плавном изменении частоты от 0 до ¥ множество соответствующих точек образуют кривую, например, как показано на рис. 22.
Для получения второй половины годографа, соответствующей отрицательным частотам, определим положение изображающей точки для w = — w1 на основе свойств четности и нечетности частотных характеристик.
ВЧХ является четной функцией, следовательно, при изменении знака аргумента w горизонтальная координата изображающей точки сохраняет свое значение U(-w1) = U(w1). МЧХ – нечетная функция, следовательно, при изменении знака w изменяется знак вертикальной координаты изображающей точки V(-w1) = — V(w1).
Таким образом, точки годографа, соответствующие частотам w1 и — w1, симметричны относительно горизонтальной оси. Поскольку значение w1 выбиралось произвольным, можно сделать вывод о том, что участки АФХ, соответствующие w > 0 и w 0 значения ФЧХ лежат в пределах от 0 до 
— при w = 0 точка АФХ имеет декартовы координаты (U(0); V(0)) = (k; 0);
— при 
Представленная на рис. 23 АФХ полностью соответствует указанным результатам.
Пример 10. Идеальное дифференцирующее звено.

 |
Графики частотных характеристик показаны на рис. 24.
По АЧХ и ФЧХ можно установить следующее:


— при w = 0 A(w) = 0, при 
Аналогичные выводы можно сделать, анализируя ВЧХ и МЧХ.
АФХ представлена на рис. 25. Характеристика совпадает с вертикальной осью.
Следующий пример требует особого внимания. Он показывает, что в ряде случаев только одна пара характеристик (АЧХ и ФЧХ или ВЧХ и МЧХ) не дает всей необходимой информации для приближенного построения АФХ.
Пример 11. Интегрирующее звено с замедлением.


Выражения для АЧХ и ФЧХ имеют вид:


Их графики показаны на рис. 26.
По АЧХ и ФЧХ можно установить следующее:


— при 

— при 
— длина вектора направленного в точки АФХ, и угол его наклона изменяются монотонно.
Варианты АФХ, соответствующие полученным результатам (с учетом неопределенности при 
Дополнительную информацию, позволяющую уточнить поведение АФХ на малых частотах, можно получить по ВЧХ и МЧХ. Получим выражения для этих характеристик и построим примерные графики (рис. 28):



По графику и из соответствующего выражения нетрудно установить, что горизонтальная координата точек АФХ при 


Отметим, что попытка выполнить приближенное построение АФХ по ВЧХ и МЧХ также вызовет затруднения: по графикам, показанным на рис. 28, не удается установить асимптотический характер АФХ при 
Таким образом, при построении АФХ целесообразно использовать обе пары частотных характеристик: АЧХ и ФЧХ, ВЧХ и МЧХ – для получения полной информации или, по крайней мере, для проверки результата.
Пример 12. Апериодическое звено 2 порядка.


Выражения для АЧХ и ФЧХ имеют вид:


Их графики показаны на рис. 29.
По графикам на рис. 29 можно установить следующее:
— при w > 0 значения ФЧХ отрицательны и монотонно изменяются от 0 до — p, следовательно, АФХ при w > 0 начинается в четвертом и заканчивается в третьем квадранте, смене квадрантов соответствует точка пересечения АФХ с осью координат (вертикальной) на некоторой ненулевой частоте;
— при w = 0 A(w) = k, соответствующая точка АФХ лежит на положительной горизонтальной полуоси;
— при увеличении частоты длина вектора, направленного в точку АФХ, монотонно уменьшается (кривая АФХ приближается к началу координат);
— при 
— вторая половина АФХ, соответствующая отрицательным частотам, может быть получена отражением относительно горизонтальной оси.



Очевидно, при 



Построить графики ВЧХ и МЧХ и сопоставить их с АФХ предлагается самостоятельно.
Уравнение для определения частоты w1 примет вид: 


или в выражение для АЧХ (в этом случае получим расстояние до искомой точки от начала координат):

Для отрицательных частот точка пересечения АФХ с вертикальной осью будет соответствовать частоте — w1 и иметь вертикальную координату 
http://kazedu.com/referat/159865/2
http://pandia.ru/text/79/190/31860.php