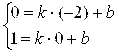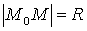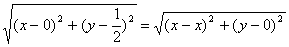Уравнение задано графически точка r 1 4

Графический метод решения задач с параметрами

Теперь вы узнали, что такое параметр, и увидели решение самых простых задач.

Но подождите — рано успокаиваться и говорить, что вы все знаете. Есть множество типов задач с параметрами и приемов их решения. Чтобы чувствовать себя уверенно, мало посмотреть решения трех незатейливых задач.

Вот список тем, которые стоит повторить:

1. Элементарные функции и их графики. Парабола, синус, логарифм, арктангенс и все остальные — всех их надо знать «в лицо».

Только после этого можно переходить к самому простому и наглядному способу решения задач с параметрами — графическому. Конечно, он не единственный. Но начинать лучше всего именно с него.

Мы разберем несколько самых простых задач, решаемых графическим методом. Больше задач — в видеокурсе «Графический метод решения задач с параметрами» (бесплатно).

1. При каких значениях параметра a уравнение имеет ровно 2 различных решения?

Дробь равна нулю тогда и только тогда, когда ее числитель равен нулю, а знаменатель не равен нулю.

В первом уравнении выделим полный квадрат:

Это уравнение окружности с центром в точке и радиусом равным 2. Обратите внимание — графики будем строить в координатах х; а.

Уравнение задает прямую, проходящую через начало координат. Нам нужны ординаты точек, лежащих на окружности и не лежащих на этой прямой.

Для того чтобы точка лежала на окружности, ее ордината а должна быть не меньше 0 и не больше 4.

Кроме того, точка не должна лежать на прямой , которая пересекает окружность в точках и Координаты этих точек легко найти, подставим в уравнение окружности.

Точка С также не подходит нам, поскольку при мы получим единственную точку, лежащую на окружности, и единственное решение уравнения.

2. Найдите все значения a, при которых уравнение имеет единственное решение.

Уравнение равносильно системе:

Мы возвели обе части уравнения в квадрат при условии, что (смотри тему «Иррациональные уравнения»).

Раскроем скобки в правой части уравнения, применяя формулу квадрата трехчлена. Получаем систему.

Приводим подобные слагаемые в уравнении.

Заметим, что при прибавлении к правой и левой части числа 49 можно выделить полные квадраты:

Решим систему графически:

Уравнение задает окружность с центром в точке , где радиус

Неравенство задает полуплоскость, которая расположена выше прямой , вместе с самой этой прямой.

Исходное уравнение имеет единственное решение, если окружность имеет единственную общую точку с полуплоскостью. Другими словами, окружность касается прямой, заданной уравнением

Пусть С — точка касания.

На координатной плоскости отметим точки и , в которых прямая пересекает оси Y и Х.

Рассмотрим треугольник ABP. Он прямоугольный, и радиус окружности PC является медианой этого треугольника. Значит по свойству медианы прямоугольного треугольника, проведенной к гипотенузе.

Из треугольника ABP найдем длину гипотенузы AB по теореме Пифагора.

Решая это уравнение, получаем, что

3. Найдите все положительные значения параметра а, при каждом из которых система имеет единственное решение.

График уравнения — окружность с центром и радиусом равным 2.

График уравнения — две симметричные окружности и радиуса 2 c центрами в точках и

Второе уравнение при задает окружность с центром в точке и радиусом a.

Вот такая картинка, похожая на злую птицу. Или на хрюшку. Кому что нравится.

Система имеет единственное решение в случаях, когда окружность , задаваемая вторым уравнением, касается только левой окружности или только правой

Если a — радиус окружности , то это значит, что (только правая) или (только левая).

Пусть А — точка касания окружности и окружности

, (как гипотенуза прямоугольного треугольника МNР с катетами 3 и 4),

В — точка касания окружности и окружности

длину MQ найдем как гипотенузу прямоугольного треугольника KMQ с катетами 7 и 4; Тогда для точки В получим:

Есть еще точки С и D, в которых окружность касается окружности или окружности соответственно. Однако эти точки нам не подходят. В самом деле, для точки С:

, но и это значит, что окружность с центром в точке М, проходящая через точку С, будет пересекать левую окружность и система будет иметь не одно, а три решения.

Аналогично, для точки D:

и значит, окружность с центром М, проходящая через точку D, будет пересекать правую окружность и система будет иметь три решения.

4. При каких значениях a система уравнений имеет 4 решения?

Конечно же, решаем графически. Только непуганый безумец возьмется решать такую систему аналитически : -)

И в первом, и во втором уравнении системы уже можно разглядеть известные «базовые элементы» (ссылка) — в первом ромбик, во втором окружность. Видите их? Как, еще нет? — Сейчас увидите!

Просто выделили полный квадрат во втором уравнении.

Сделаем замену Система примет вид:

Вот теперь все видно! Рисовать будем в координатах

Графиком первого уравнения является ромб, проходящий через точки с координатами и

Графиком второго уравнения является окружность с радиусом и центром в начале координат.

Когда же система имеет ровно 4 решения?

1) В случае, когда окружность вписана в ромб, то есть касается всех сторон ромба.

Запишем площадь ромба двумя способами — как произведение диагоналей пополам и как произведение стороны на высоту, проведенную к этой стороне.

Диагонали нашего ромба равны 8 и 6. Значит,

Сторону ромба найдем по теореме Пифагора. Видите на рисунке прямоугольный треугольник со катетами 3 и 4? Да, это египетский треугольник, и его гипотенуза, то есть сторона ромба, равна 5. Если h — высота ромба, то

При этом Мы помним, что если окружность вписана в ромб, то диаметр этой окружности равен высоте ромба. Отсюда

Мы получили ответ:

2) Есть второй случай, и мы его найдем.

Давайте посмотрим — если уменьшить радиус окружности, сделав , окружность будет лежать внутри ромба, не касаясь его сторон. Система не будет иметь решений, и нам это не подходит.

Пусть радиус окружности больше, чем , но меньше 3. Окружность дважды пересекает каждую из четырех сторон ромба, и система имеет целых 8 решений. Опять не то.

Пусть радиус окружности равен 3. Тогда система имеет 6 решений.

А что, если ? Окружность пересекает каждую сторону ромба ровно 1 раз, всего 4 решения. Подходит!

Значит, Объединим случаи и запишем ответ:

Больше задач и методов решения — на онлайн-курсе Анны Малковой. И на интенсивах ЕГЭ-Студии в Москве.

Решение системы уравнений графическим методом средствами MS Excel

Цели и задачи.

1. Развитие приемов умственной деятельности, формирование и развитие функционального мышления учащихся, развитие познавательных потребностей учащихся, создание условий для приобретения опыта работы учащихся в среде ИКТ.
2. Достижение сознательного усвоения учебного материала учащимися, работа над повышением грамотности устной речи, правильного использования компьютерных терминов.
3. Научить применять возможности MS Excel в повседневной жизни, в познавательной деятельности.
4. Закрепить навыки создания таблиц и диаграмм.
5. Научить решать систему уравнений графическим методом, исследовать график функции.

Оборудование урока: компьютеры, мультимедиа проектор.

Программное обеспечение: Windows XP, пакет программ MS Office 2003.

Тема нашего урока тесно связана с математикой разделы “Графики функций” и “Решение систем уравнений”. Поэтому нам понадобятся ранее полученные навыки. Но мы постараемся упростить нашу задачу с помощью применения современных вычислительных средств.

Запишите в тетради тему урока и укажите дату.

Назовите мне кого из класса сегодня нет.

Давайте вспомним, что такое уравнение, и как его можно решить графически.

Назовите, пожалуйста, что в математике называют уравнением, решением уравнения и системой уравнений.

(Учащиеся приводят определения)

Уравнение – это математическое выражение, содержащее неизвестную величину (переменную) и 0 с правой стороны от знака =.

Система уравнений – несколько связанных уравнений, имеющих одинаковые обозначения неизвестных величин (переменных).

Решением уравнения – называют такое значение неизвестной величины, при подстановке которого левая часть выражения принимает значение 0. И мы получаем верное равенство.

Но, с другой стороны, подобное выражение можно представить как функцию с зависимой и независимой величинами. Если мы слева от знака = поставим Y, а справа заданное выражение. Y – зависимая величина, Х – независимая величина. В этом случае Решением уравнения является точка пересечения графика функции с осью ОХ.

Для решения уравнения графическим методом необходимо рассчитать значения функции в ключевых точках с координатой Х (Х меняется в диапазоне допустимых значений), нанести эти точки на систему координат, построить график функции и определить координаты точки пересечения графика с осью ОХ.

Это достаточно сложная задача. Нужно достаточно много вычислений и аккуратное построение графика функции. Также мы заранее не можем сказать, из какого диапазона чисел необходимо брать значения Х.

Но эту задачу может взять на себя ЭВМ.

Мы воспользуемся возможностями программы MS Excel.

Основная часть

Давайте разобьемся на 2 группы. Сильные ученики, которые уже хорошо владеют средствами MS Excel, попытаются самостоятельно разработать таблицу. А остальные ребята будут вместе со мной последовательно выполнять действия.

Сильные ученики пересаживаются за дальние компьютеры и самостоятельно разрабатывают таблицу для решения системы уравнений. Они должны получить примерно такую картинку на экране.

С остальными мы работаем в режиме “Делай как Я”. Я демонстрирую действия на экране проектора и комментирую, вы стараетесь выполнять эти действия у себя на ЭВМ.

И так. Мы запустили программу MS Excel.

Мы хотим разработать таблицу для решения системы уравнений:

Нам необходимо задать диапазон изменения величины Х и рассчитать соответствующее значение Y.

Сформируем начальные данные.

В ячейку A1 запишем – нач Х =. В ячейку D1 запишем – шаг Х =. В ячейках B1, E1 их соответствующие значения – (-2,5) и 0,15.

В ячейках C4, F4 запишем общий вид наших уравнений. В строке 5 сформируем заголовки будущих таблиц значений заданных функций.

Теперь в столбиках B, E мы должны сформировать значения для величины Х. А в столбиках C, E значения величин Y. У нас должна получиться вот такая картинка. Столбики со значением величины X мы должны сформировать так, чтобы было удобно менять начальное его значение и шаг X, которые мы создали в заголовке.

Формулы, которые нам нужно ввести приведены на рисунке.

Заметьте, что большинство формул повторяются, и их можно ввести методом копирования.

Заполните, пожалуйста, в каждой таблице 20-25 строчек.

Символ $ в формуле обозначает, что данный адрес ячейки является абсолютным и он не будет изменяться при копировании формулы.

Проверьте, чтобы ваши расчётные данные совпадали с рисунком 2.

Нам осталось красиво оформить таблицы. Для этого нужно указать, какие границы отображать в ячейках расположения расчётных таблиц. Выделите их указателем мышки и задайте режим “Все границы”.

Теперь нам необходимо построить графики заданных функций. Для этого воспользуемся инструментом “Диаграммы”.

Выберем тип диаграммы Точечная-Сглаженная и на следующем экране укажем необходимые нам диапазоны данных, как указано на рисунке. Незабудем указать название для каждого графика. Легенду расположим снизу. А саму диаграмму “На текущем листе”, поместив её справа от расчётных таблиц.

Если вы всё сделали правильно, то у вас на экране должна получиться вот такая картинка.

У кого не получилось, давайте вместе разберёмся в ошибках и добъёмся требуемого результата.

Теперь изменяя значения в ячейках B1, D1 можно смещать графики функций вдоль оси ОХ и изменять их масштаб.

Мы видим, что одно из решений нашей системы уравнений равно -1,5.

Изменяя начальное значение Х, найдите на графике второе решение системы уравнений.

Сколько у вас получилось?

Великолепно. У нас получилось. Мы легко решили такую сложную систему уравнений.

Но можно немного изменить нашу таблицу и усовершенствовать для решения множества подобных систем уравнений или для исследования графиков заданных функций.

Для этого нужно внести изменения в таблицу и расчётные формулы.

Можно сделать следующим образом, как показано на рисунке. Формулы в ячейках показаны на следующем рисунке.

Самостоятельно внесите все необходимые изменения.

Попробуйте изменять коофициенты A, B, C, D и посмотрите, как меняется форма и положение графиков соответствующих формул.

Заключительный этап урока

Ребята, как вы думаете, что удобней самостоятельно строить график функции на бумаге или поручить эту задачу ЭВМ?

А что легче для вас?

Конечно же, на данном этапе вам удобней самостоятельно на бумаге построить график функции. Но в конце урока мы получили универсальную таблицу, которая позволяет решать множество подобных заданий.

Мы ещё раз убедились, что компьютер это мощный инструмент, который позволяет не только приятно проводить время за играми, но и решать серьёзные задачи.

Надеюсь, что вам понравилось сегодняшняя работа. И вы Довольны достигнутыми результатами.

1.6. Первая основная задача аналитической геометрии на плоскости

Основных задач аналитической геометрии на плоскости две. Первая из них: Для заданной линии найти ее уравнение. Вторая задача – обратная: По заданному уравнению линии построить линию.

Начнем с рассмотрения первой, более трудной, задачи. Трудность решения этой задачи очевидна: ведь нужно найти математическое уравнение, которому будут удовлетворять координаты любой точки данной линии, и только они. Для достаточно сложных линий (например, для линии, образованной свободным движением руки) точное решение этой задачи вообще оказывается невозможным – только приближенное. Однако для не слишком сложных и, главное, четко описанных линий их уравнения найти можно. Мы, например, без труда сделали это в предыдущем параграфе для линий, изображенных на рис. 1.12 и 1.13. Рассмотрим еще несколько примеров.

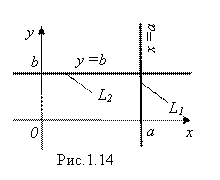
Пример 1. Найти уравнения вертикальной прямой L1 и горизонтальной прямой L2, изображенных на рис. 1.14.

Решение. Уравнения этих прямых очевидны: X= A – уравнение прямой L1, Y = B – уравнение прямой L2. Действительно, этим уравнениям удовлетворяют координаты любой точки соответствующих прямых, и только они. В частности, Y = 0 – это уравнение оси Ox, а X = 0 – уравнение оси Oy.

Пример 2. Найти уравнение прямой L, изображенной на рис. 1.15.

Решение. Как известно из школьного курса математики, наклонная прямая – это график линейной функции вида Y = Kx + B. Значит, уравнение данной прямой L имеет вид Y = Kx + B. Нам только нужно найти параметры K и B этого уравнения.

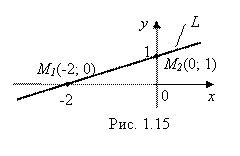
Используем рис. 1.15. Так как точки М1(-2; 0) и М2 (0; 1) лежат на прямой L, то их координаты (X; Y) должны удовлетворять уравнению прямой. Подставляя эти координаты в уравнение прямой Y = Kx + B, получим систему из двух равенств:

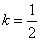
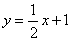
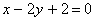
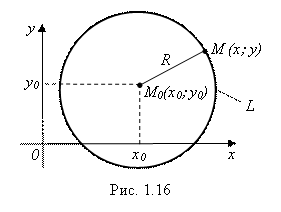
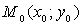
Решая ее, находим: ; B = 1. Следовательно, уравнение данной прямой L таково: . Или, в неявной форме, .

Пример 3. Найти уравнение окружности L с центром в заданной точке и заданным радиусом R (рис. 1.16).

Решение. Для любой точки М(X; Y) окружности L, и только для точек этой окружности, имеет место равенство:

Реализуя это равенство с помощью формулы (3.1) расстояния между двумя точками, получим:

.

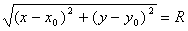
Возводя обе части этого равенства в квадрат, получим равносильное равенство:

. (5.1)

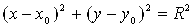
Это и есть искомое уравнение указанной окружности L.

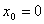
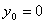
В частности, если центр окружности совпадает с началом координат (; ), то ее уравнение примет вид:

Это уравнение, кстати, совпадает с уравнением (4.11), полученным ранее другим путем.

Пример 4. Найти уравнение линии, состоящей из точек, равноудаленных от оси Ох и от точки .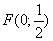

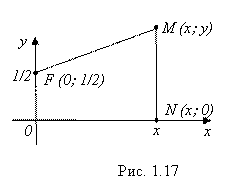
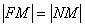
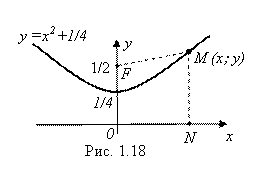
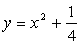
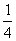
Решение. Пусть М(X; Y) – произвольная точка указанной линии, а N (x; 0) – проекция точки М(X; Y) на ось Ох (рис. 1.17). По условию задачи для любой точки М(X; Y) линии и только для точек этой линии. Если использовать формулу (3.1) расстояния между двумя точками, то это равенство примет вид:

После возведения в квадрат обеих частей и очевидных упрощений оно примет вид: . Это и есть уравнение указанной в задаче линии. Судя по этому уравнению, эта линия – парабола Y = X2, поднятая на вдоль оси Оу (рис. 1.18).

А теперь рассмотрим вопрос о Приближенных уравнениях линий. Чаще всего этот вопрос возникает, когда речь идет о линиях, полученных в результате экспериментов.

А именно, пусть экспериментальным путем изучается зависимость Y = F(X) между двумя величинами. Например, зависимость урожайности культуры Y от количества внесенных под нее удобрений X; пройденного пути Y от времени движения X; прибыли предприятия Y от величины затрат X и т. д. В ходе эксперимента для ряда значений X определяются соответствующие значения Y, что приводит к экспериментальной таблице вида

Данные этой таблицы можно изобразить и графически в виде системы экспериментальных точек М1 (X1; Y1), М2 (X2; Y2), … МN (Xn; Yn) (рис. 1.19). По этим экспериментальным данным нужно получить искомое уравнение Y = F(X), связывающее Y с X. Такое уравнение называется Эмпирической формулой, а сама задача получения такой формулы называется Задачей построения эмпирической формулы.

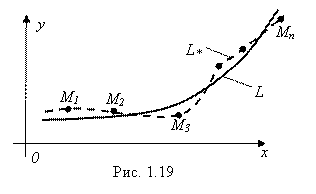
В этой задаче фактически идет речь о нахождении уравнения Y = F(X) линии L по точкам М1, М2, … МN, которые, вообще говоря, на этой линии не лежат, так как они содержат в себе неизбежные погрешности эксперимента и, кроме того, содержат результат влияния различных неучтенных факторов (помех). Поэтому искомая линия L может отличаться от линии L*, непосредственно соединяющей экспериментальные точки. В частности, линия L* может иметь весьма причудливую форму, в то время как сама линия L будет простой и гладкой (например, прямой). Линия L должна как бы сглаживать линию L*, устраняя ее незначительные перепады, связанные с неточным положением экспериментальных точек.

При нахождении эмпирической формулы Y = F(X), а значит, и соответствующей ей линии L, приходится решать две частные задачи.

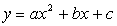
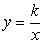
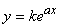
Первая из них – выбор Типа эмпирической формулы. То есть выбор того класса функций, к которому принадлежит искомая функция Y = F(X). Во многих случаях класс функций, из которого подбирается эмпирическая формула, подсказывается теоретическими представлениями о характере изучаемой зависимости (зависимость линейная вида Y = Kx или Y = Kx + B, квадратичная вида , обратно пропорциональная вида , показательная вида и т. д.). Или, если указанные теоретические представления отсутствуют, то класс функций для эмпирической формулы подбирают по характеру расположения экспериментальных точек.

После того, как вид эмпирической формулы выбран, то есть первая частная задача решена, остается определить Наилучшие значения входящих в эту формулу числовых коэффициентов. Эта задача (вторая частная задача) уже более легкая, ибо решается стандартным методом – Методом наименьших квадратов. В соответствии с этим методом наилучшими значениями параметров эмпирической формулы считаются те, при которых сумма квадратов отклонений экспериментальных точек от эмпирической кривой Y = F(X) была бы минимальной.

Вручную реализовывать метод наименьших квадратов трудоемко, но это и не требуется – это обычно делается по стандартным программам на ЭВМ.

Впрочем, в простейшем (и наиболее часто встречающимся на практике) случае, когда экспериментальные точки располагаются приблизительно по прямой, можно обойтись и без метода наименьших квадратов – можно все сделать вручную, графическим путем.

В этом случае эмпирическая формула Y = F(X) строится, естественно, в виде уравнения прямой Y = Kx + B. Параметры и B этого уравнения имеют наглядный геометрический смысл (рис.1.20), поэтому могут быть найдены из чертежа. Сама прямая L, сглаживающая экспериментальные точки, строится на глаз, вручную. Этот графический путь почти исключает вычисления, он нагляден, и при достаточном навыке дает результаты ненамного худшие, чем метод наименьших квадратов.

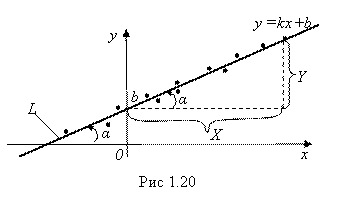
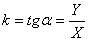
Кстати, этим путем можно построить и достаточно хорошие эмпирические формулы для ряда экспериментальных кривых – параболы, гиперболы и т. д., но на этом останавливаться не будем.

1. Написать уравнение прямой, проходящей через начало координат и точку .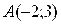

2. Написать уравнение линии, по которой движется точка М(x; y), равноудаленная от начала координат и от точки A(-4; 2). Лежат ли на этой линии точки B(-2;1), C(2;3), D(1;7)?

3. Найти уравнение линии, по которой движется точка, оставаясь постоянно вдвое ближе к оси Ох, чем к оси Оу. Построить линию по ее уравнению.

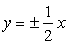
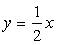
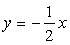
Ответ: – крест из прямых и .

4. Найти уравнение линии, состоящей из таких точек, что разность расстояний от каждой из них до точек F1(-2;-2) и F2(2;2) равна 4. Построить линию по ее уравнению.

Ответ: 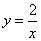– гипербола.

5. По данным эксперимента, представленным в таблице, графическим путем подобрать эмпирическую формулу вида Y = Kx + B.