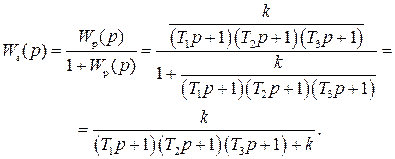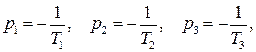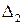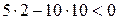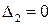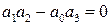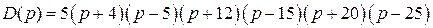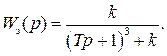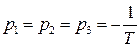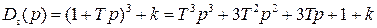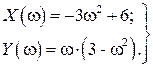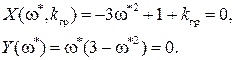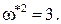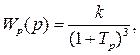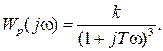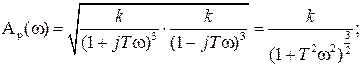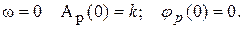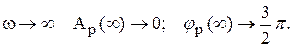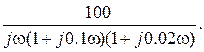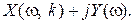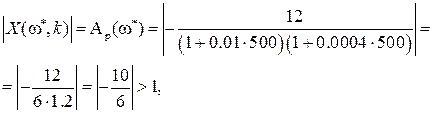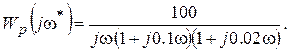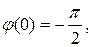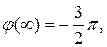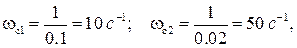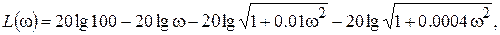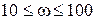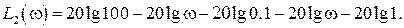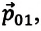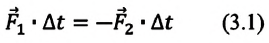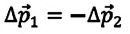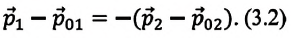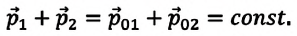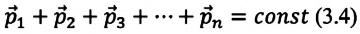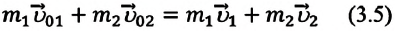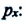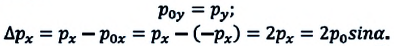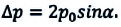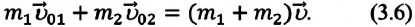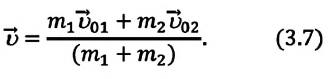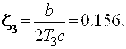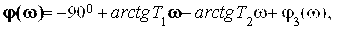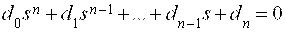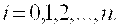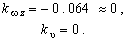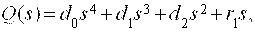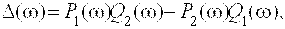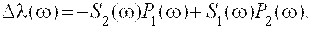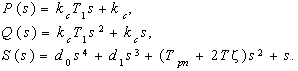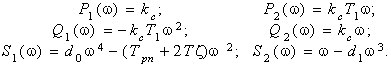Определение устойчивости САР
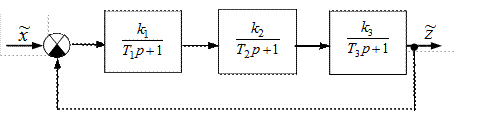
В замкнутой САР (рис. IV. 27) заданы (в числовом выражении)
Рис. IV. 27. Функциональная схема замкнутой САР
Определить устойчивость разомкнутой и замкнутой САР и найти kгр.
Для решения поставленной задачи воспользуемся критерием Гурвица. Найдем передаточные функции, а затем и характеристические уравнения разомкнутой и замкнутой систем.
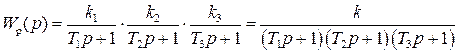
где 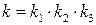
Для разомкнутой системы характеристическое уравнение имеет вид
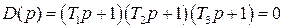
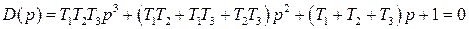
а для замкнутой САР получается
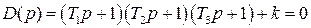
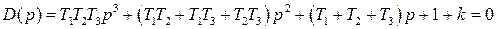
Нетрудно понять, что для исследования устойчивости разомкнутой САР применять критерий устойчивости Гурвица излишне, ибо непосредственно из вида характеристического уравнения разомкнутой системы (IV. 3. 11) легко найти, что все корни левые
т. е. разомкнутая САР при всегда положительных Т1, Т2, Т3 устойчива.
Вот по виду характеристического уравнения замкнутой САР (IV. 3. 12) так просто, как в предыдущем случае, определить соответствующие корни не удается, поэтому приходится применить критерий устойчивости Гурвица . При введении обозначений
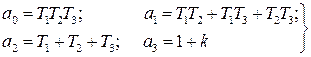
характеристическое уравнение замкнутой САР (IV. 3. 13) примет вид
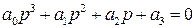
В разделе IV. 2. 2 было выяснено, что для САР с характеристическим уравнением третьего порядка для устойчивости необходимо и достаточно при положительных коэффициентах ai( i =0, 1, 2,3) выполнение условия ( IV. 2. 3)
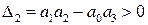
Из (IV. 3. 14) видно, условия ai>0 при положительных Т1, Т2, Т3 и k всегда выполняются, а для проверки условия (IV. 2.3) надо в него подставить заданные значения параметров Т1, Т2, Т3 и k и определить знак минора
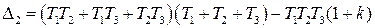
Если этот минор больше нуля, то заданная замкнутая САР устойчива.
Граничный коэффициент усиления kгр найдется из предпоследнего минора, приравненного к нулю
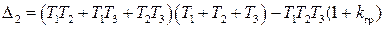
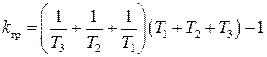
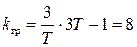
Характеристическое уравнение САР имеет вид
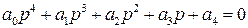
Определить устойчивость САР.
Так как заданное характеристическое уравнение 4-го порядка имеет один неположительный коэффициент (а4=0), то, согласно условию Стодолы (что в данном случае совпадает с критерием Гурвица) САР не сожжет быть устойчивой, а только либо нейтральной либо неустойчивой.
Запишем заданное характеристическое уравнение в другом виде
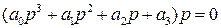
Видно, что один из корней – нулевой. САР будет находиться на границе устойчивости, если все остальные корни характеристического уравнения левые (при наличии хотя бы одного правого корня САР будет неустойчивой). Эти остальные корни будут левыми, если выполняются условия устойчивости для уравнения
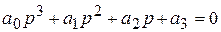
а именно (согласно разделу IV. 2. 2)
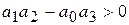
После подстановки значений коэффициентов последнее неравенство
не выполняется, следовательно САР неустойчива.
Передаточная функция разомкнутой САР имеет вид
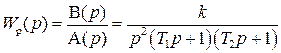
Определить устойчивость замкнутой САР.
Характеристическое уравнение замкнутой САР определяется выражением
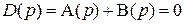
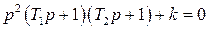
После простого преобразования получим
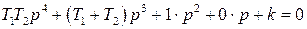
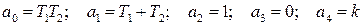
Согласно критерию Гурвица для устойчивости системы необходимо, чтобы все ai( i=0, 1, 2, 3, 4) > 0. В нашем же случае 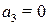
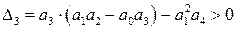
Учитывая что 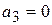
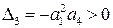
Поскольку 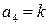
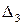
Переходная функция разомкнутой САР имеет вид
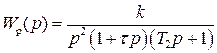
где 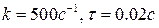
Определить постоянную времени Тгр, при которой замкнутая САР находиться на границе устойчивости.
Получим характеристическое уравнение замкнутой САР
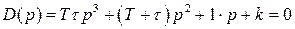
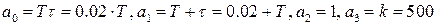
Граница устойчивости определяется из равенства нулю второго минора
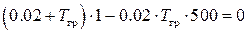
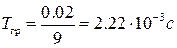
Характеристический полином САР 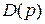
Каково изменение аргумента 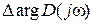
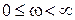
Характеристическое уравнение 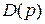
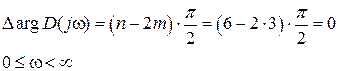
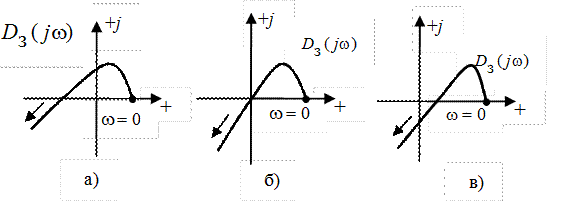
Какой из указанных годографов Михайлова замкнутой системы
Рис. IV. 28. Годографы Михайлова для устойчивой, нейтральной и неустойчивой замкнутой систем.
соответствует САР с передаточной функцией
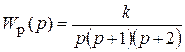
Характеристический полином замкнутой системы имеет вид
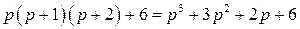
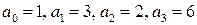
Для этого полинома второй минор оказывается равный нулю
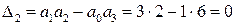
т.е. замкнутая САР находится на границе устойчивости, что соответствует годографу Михайлова, имеющему вид рис. IV. 28, б.
Определить устойчивость разомкнутой и замкнутой САР и найти kгр.
Запишем передаточные функции разомкнутой
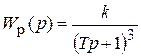
а замкнутой САР
Поскольку из характеристического уравнения разомкнутой САР
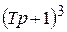
следует, что все три его корня
при положительном Т есть левые, то, значит, разомкнутая САР устойчива.
Для определения устойчивости замкнутой САР применим критерий Михайлова.
Характеристический полином замкнутой системы, имеющий третий порядок,
после замены 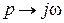
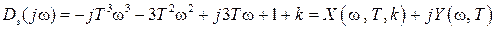
В этом выражении мы выделили действительную часть 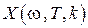
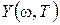
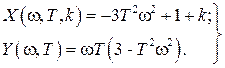
Ответ на вопрос – устойчива ли замкнутая САР можно получить по виду годографа Михайлова, зависящего от конкретных значений параметров k и T. Пусть для определенности k =5, T =1 с. Тогда соотношения (IV. 3. 15) примут
Задаваясь численными значениями 
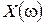
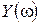

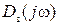
 | 1.42 | 1.5 | 1.73 | ∞ |
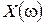 | -0.75 | -3 | -6 | ∞ |
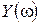 | 1.42 | 1.125 | -2 | ∞ |
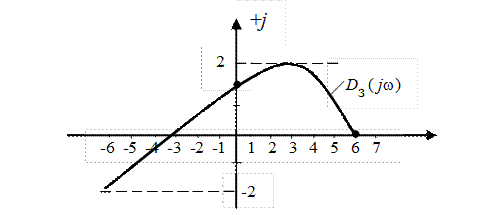
Рис. IV. 29. Годограф Михайлова.
Поскольку годограф Михайлова, начинается на положительном отрезке действительной оси, с ростом частоты от 0 до 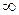
Определим теперь kгр. В разделе IV. 3. 2 было показано, что на границе устойчивости годограф Михайлова проходит через начало координат, т.е. выполняются условия (IV. 3. 4) .
В нашем случае при k = kгр, 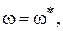
Из второго из этих уравнений, отбрасывая неверное решение 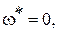
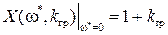
Подставляя это значение граничной частоты в выражение для 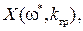
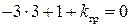
т.е. kгр = 8, как и в примере П. IV. 1.
П. IV. 8. Предыдущую задачу П. IV. 7. решить с помощью критерия Найквиста.
Передаточную функцию разомкнутой системы мы получили в виде
откуда ясно, что все корни характеристического уравнения левые и, значит, разомкнутая система устойчива.
Если провести замену 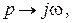
Построим эту характеристику. Найдем сначала 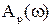
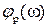
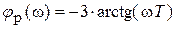
При
При
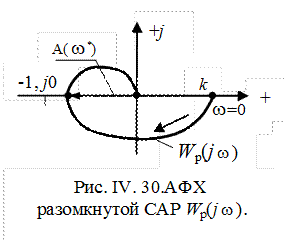
Следовательно, качественно АФХ разомкнутой системы Wp(j 
Устойчивость системы в замкнутом состоянии зависит от того, охватывает ли 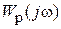




Из заданной операторной формы управления системы получим
Wp(j 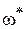
В отличии от предыдущего примера для разнообразия АФХ разомкнутой САР Ap( 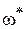
Wp(j 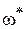
Для этого нужно освободиться от мнимости в знаменателе выражения для
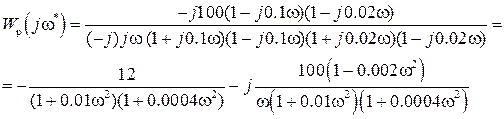
Определим величину 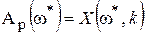
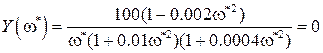
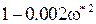
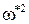
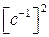
При подстановке этого значения частоты в X( 
отсюда следует, что замкнутая САР неустойчива.
kгр 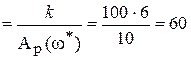
П. IV. 10. Предыдущий пример решить с помощью логарифмического критерия устойчивости.
В предыдущем примере мы нашли, что АФХ разомкнутой системы имеет вид
Получим отсюда выражение для АЧХ Ap( 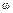
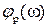
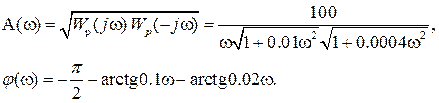
Имея в виду, что
а сопрягающие частоты
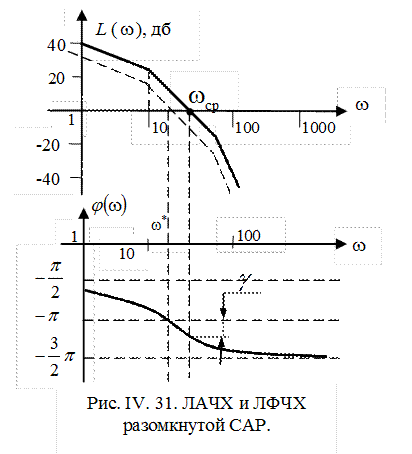
Построим асимптотическую ЛАЧХ и качественный вид ФЧХ разомкнутой системы.
Найдем частоту среза 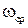
запишем выражение для ЛАЧХ на втором участке
На частоте среза 
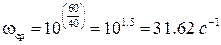
Значение фазочастотной характеристики 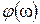
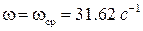
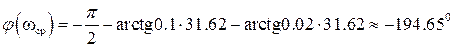
Следовательно, запас устойчивости по фазе для данной системы будет отрицательным
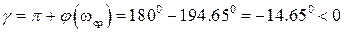
а сама система в замкнутом состоянии неустойчива.
Граничный коэффициент усиления 
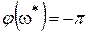

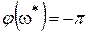
Из (IV. 3. 19) получим
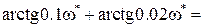
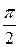
Из тригонометрии известно, что
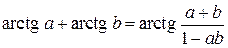
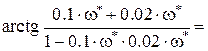
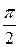
Величине 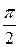
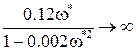
а это для 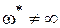
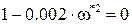
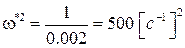
а сама частота 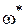
Величину 
Подставим сюда 
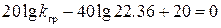
Отсюда 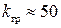
В предыдущем примере для той же задачи мы получили 

Вопросы для самопроверки.
1. Что понимается под устойчивостью системы?
2. Каковы признаки устойчивости САР?
3. Сформулируйте условие Стодолы.
4. Как найти граничное значение параметра по критерию устойчивости Гурвица.
5. Расскажите о принципе аргумента.
6. Что такое годограф Михайлова? Как он проходит в случае границы устойчивости системы?
7. Сформулируйте критерий устойчивости Найквиста для всех трех видов устойчивости разомкнутой САР.
8. Прокомментируйте связь логарифмического критерия устойчивости с критерием Найквиста.
9. Какие запасы устойчивости Вы знаете?
Дата добавления: 2016-04-14 ; просмотров: 4896 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Замкнутая система в физике — формулы и определения с примерами
Содержание:
Замкнутая система:
Как вы уже знаете, все изменения, происходящие в природе, есть результат взаимодействия между телами. Существуют разные виды взаимодействия — гравитационное, электромагнитное, ядерное и слабое. Характер этих взаимодействий зависит не только от их природы, но и от расстояния между взаимодействующими телами и свойств этих тел. в каждом явлении один из видов взаимодействия является более решающим по сравнению с другими. Например, если гравитационное взаимодействие на больших расстояниях является решающим, то на расстояниях, сравнимых с размерами атомного ядра, можно говорить только о действии ядерных сил. Исследуя определенные явления, ученые не учитывают второстепенные (не являющиеся решающими в данном явлении) взаимодействия. Например, при вычислении силы тяги вертолета необходимо учитывать силу притяжения Земли. в то же время действие притяжения Луны и электромагнитное взаимодействие между вертолетом и облаками не учитываются.
В общей научной картине природы группа объектов, связанных общими свойствами и условно изолированных от внешней среды, рассматривается как замкнутая система.
Что такое замкнутая система
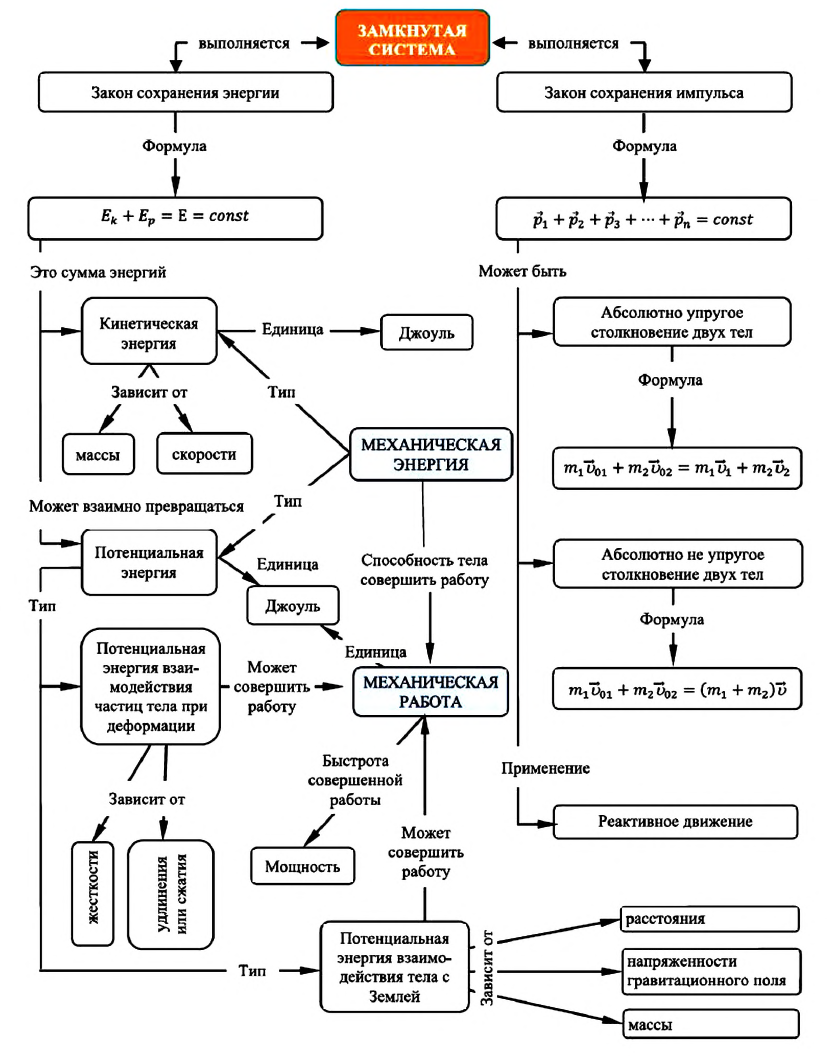
Замкнутая система — это система тел, при данных условиях взаимодействующих только друг с другом и не взаимодействующих с другими телами (равнодействующая внешних сил равна нулю). В замкнутых системах выполняются законы сохранения.
Карта замкнутой системы:
Закон сохранения импульса. Импульс является одной из физических величин, обладающих свойством сохранения. Это свойство состоит в том, что при взаимодействии тел только друг с другом сумма их импульсов не меняется, полный импульс системы остается постоянным.
Полным импульсом системы называется геометрическая сумма импульсов всех тел, из которых состоит система.
В результате взаимодействия тел их импульсы меняются. Как образец исследуем взаимодействие двух тел.
Обозначим импульс первого тела до взаимодействия
Учитывая, что 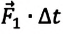
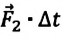
Изменения импульсов двух тел, произошедшие в результате их взаимодействия, равны по модулю и противоположны по направлению.
После преобразований получается, что векторная (геометрическая) сумма импульсов двух тел, взаимодействующих между собой, остается неизменной:
Обобщая последнее выражение для замкнутой системы, состоящей из 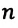
Векторная сумма импульсов тел, составляющих замкнутую систему, остается постоянной:
Столкновение двух тел
Результатом столкновения двух тел является деформация и изменение их импульсов вследствие действия возникающих сил упругости. Различают два идеализированных вида столкновения: абсолютно упругое и абсолютно неупругое столкновение.
Абсолютно упругое столкновение
При абсолютно упругом столкновении происходит упругая деформация — тело восстанавливает форму и размеры. Как пример упругой деформации можно привести столкновение бильярдных или стальных шаров. При таких столкновениях механическая энергия не превращается во внутреннюю энергию — полная механическая энергия системы не уменьшается: кинетическая энергия полностью или частично превращается в потенциальную энергию упругой деформации, а эта энергия в свою очередь заново превращается в кинетическую энергию шаров. Для абсолютно упругого столкновения выполняется закон сохранения импульса (3.3): Геометрическая сумма импульсов двух тел до абсолютно упругого столкновения равна геометрической сумме их импульсов после столкновения:
Где 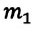
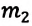
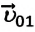
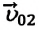
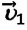
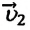
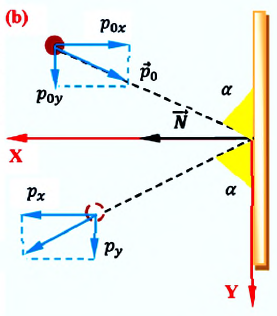
Частный случай: абсолютно упругое столкновение шарика со стеной. Предположим, что шарик сталкивается со стеной под углом 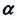
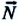
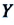
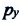
Где 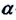
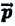
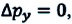
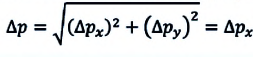
Абсолютно неупругое столкновение
Возникающая при абсолютно неупругом столкновении деформация полностью сохраняется. В это время полная механическая энергия не сохраняется, некоторая её часть превращается во внутреннюю энергию системы. После абсолютно неупругого столкновения двух тел оба эти тела, «прилипнув» друг к другу, или движутся с общей скоростью, или покоятся.
Таким образом, закон сохранения импульса при абсолютно неупругом столкновении двух тел, образующих замкнутую систему, можно записать:
Где 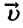
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Реактивное движение в физике
- Освоение космоса — история, этапы и достижения с фотографиями
- Закон сохранения механической энергии в физике
- Релятивистская механика в физике
- Законы Ньютона в физике
- Гравитационные силы в физике
- Центр тяжести в физике (центр масс)
- Импульс тела в физике
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Оценка устойчивости по ЛЧХ
АФЧХ разомкнутой системы подразделяются на два типа:
АФЧХ первого рода, все точки, пересечения которых с вещественной осью расположены справа от критической точки (кривая 1, рис. 3.14);
АФЧХ второго рода, точки, пересечения которых с вещественной осью расположены как справа, так и слева от критической точки (кривая 2, рис. 3.14).
В системах первого рода увеличение коэффициента усиления ведет к сдвигу ветви кривой влево и приближению ее к критической точке. Запасы устойчивости при этом уменьшаются и при k=kкр система попадает на границу устойчивости. Уменьшение коэффициента усиления стабилизирует систему. В системах 2-го рода переход системы на границу устойчивости может происходить как при увеличении коэффициента усиления, так и при его уменьшении. Из критерия Найквиста следует, что замкнутая система, имеющая в разомкнутом состоянии АФЧХ 1-го рода устойчива, если всем точкам АФЧХ, вплоть до точки пересечения ее с окружностью единичного радиуса (w=wс) , соответствуют значения фазы j(w), большие, чем -p, т.е. должно выполняться неравенство wс 6дб, что соответствует значениям h>2.
Для того, чтобы САУ неустойчивая в разомкнутом состоянии и имеющая АФЧХ 2-го рода, была устойчивой в замкнутом состоянии, необходимо и достаточно, чтобы разность между числом положительных и отрицательных переходов фазовой характеристикой через линию -p была равна р/2, где р- число корней характеристического уравнения разомкнутой системы, лежащих в правой полуплоскости, при всех частотах когда L(w)>0.
Необходимо подчеркнуть, что показанные способы оценки устойчивости по ЛЧХ и определения запасов устойчивости справедливы при таком расположении оси ординат относительно фазовой характеристики, когда с началом координат совмещена точка j(w)=-180 0 .
По ЛЧХ можно определить и критический коэффициент усиления. Для этого необходимо сместить ЛАХ вдоль линий сопряжения параллельно самой себе так, чтобы выполнить условие wс = wp и вычислить коэффициент усиления для вновь полученной ЛАХ.
Определение критического коэффициента усиления для статической и астатической систем иллюстрируется рис. 3.17 а и 3.17б.
Некоторые особенности возникают при определении критического коэффициента усиления, если в состав передаточной функции разомкнутой системы входит колебательное звено с малым показателем затухания, причем начало асимптоты, соответствующей этому звену лежит ниже оси частот. В этом случае критический коэффициент усиления определяется в момент касания резонансного пика оси частот.
Пример. Построить ЛЧХ системы стабилизации угла тангажа и оценить ее устойчивость. Определить запасы устойчивости и рассчитать критическое значение передаточного числа по углу тангажа.
Передаточную функцию разомкнутой системы можно привести к виду
Корни характеристического уравнения разомкнутой системы имеют значения:
Следовательно, 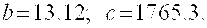
где 
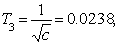
Определим частоты сопряжения и разобьем сетку координат.
Построим ЛАХ системы, учитывая, что коэффициент усиления разомкнутой системы равен 
Это можно сделать как по специальным графикам, так и расчетным путем по известной амплитудной частотной характеристике. АЧХ данной системы определяется выражением
Подставив несколько значений частоты в окрестности частоты сопряжения w03, получим значения АЧХ, рассчитаем значения ЛЧХ и построим уточняющую кривую. Фазовая частотная характеристика строится как сумма фазовых характеристик типовых звеньев, входящих в состав передаточной функции
где
Из графиков ЛЧХ следует, что wс 0 . Для систем, в которые входят колебательные звенья с малым относительным коэффициентом затухания, запас устойчивости по модулю определяется в точке резонанса и в данном случае он равен » 10дб, что соответствует значению h=3.16. Полученные значения запасов устойчивости незначительно отличаются от значений рассчитанных в соответствии с критериями Гурвица и Михайлова.
В исследуемом случае критический коэффициент усиления определяется при касании L(wр) оси частот. Перенесем ЛАХ параллельно самой себе так, чтобы в точке w=wр она касалась оси частот и продлим первую асимптоту до пересечения с осью частот. В этой точке k=w=7.244, что соответствует значению (ku)кр=16.74.
Выделение областей устойчивости
Среди физических параметров, характеризующих САУ, всегда имеется несколько, легко поддающихся изменению и использующихся для определенной настройки системы. При конструировании системы весьма важно знать диапазоны значений изменяемых параметров, допустимые с точки зрения сохранения устойчивости САУ. Об этих диапазонах можно судить, если в пространстве изменяемых параметров построить область устойчивости, т.е. выделить область значений параметров, при которых система сохраняет устойчивость.
Область устойчивости в теории автоматического управления принято называть D – областью, а представление области параметров в виде областей устойчивости и неустойчивости называют D – разбиением.
Построение области устойчивости по алгебраическим критериям
Допустим, что коэффициенты характеристического уравнения
зависят от двух изменяемых параметров m и l. Для построения области устойчивости прежде всего нужно, в соответствии с необходимым условием устойчивости, выделить область изменяемых параметров при нахождении в которой, коэффициенты характеристического уравнения положительны. Это можно сделать, решив систему уравнений

Для построения границы положительности коэффициентов аi необходимо из решений уравнений (3.26) выбрать те, которые обеспечивают положительность всех коэффициентов. Из всех границ положительности только две одновременно могут быть и границами устойчивости. Такими являются границы, уравнениями которых являются

Доказано, что если d0 и dn приблизятся к нулю, то характеристическое уравнение будет иметь два действительных корня

При дальнейшем уменьшении коэффициенты d0 и dn перейдут через ноль, станут отрицательными, а корни (3.28) окажутся положительными. Так как вещественные корни определяют апериодические составляющие решения дифференциального уравнения, то границы (3.27) называют апериодическими границами устойчивости. На самих границах устойчивости корни (3.28) равны соответственно ±¥ и 0. Стороны кривых, di(m,l)=0, примыкающие к области положительности соответствующих коэффициентов, штрихуются в сторону положительности. Может случиться так, что какой либо из коэффициентов, d0 или dn не зависит от изменяемых параметров. Это означает отсутствие соответствующей апериодической границы устойчивости.
Колебательной границей устойчивости называется кривая в плоскости изменяемых параметров, при переходе через которую пара комплексно – сопряженных корней изменяет знак своей вещественной части на обратный. Доказано, что колебательная граница устойчивости определяется выражением

В этом выражении Dn-1 – (n-1) – й определитель Гурвица. Колебательная граница устойчивости штрихуется в сторону положительности Dn-1.
Пример. Построить область устойчивости в плоскости параметров ku и kwz системы стабилизации угла тангажа.
Характеристическое уравнение замкнутой системы имеет вид
Исследуем неравенства d2>0, d3>0, d4>0 . Из первого неравенства следует, что для положительности коэффициента d2 необходимо, чтобы выполнялось условие
Неравенство d4>0 определяет, что для положительности этого коэффициента необходимо, чтобы ku>0. Для выполнения неравенства d3>0 требуется, чтобы
При любых значениях передаточного числа по углу больших нуля, правая часть последнего выражения по модулю будет больше единицы. Таким образом, границами положительности коэффициентов будут
От изменяемых параметров зависит коэффициент dn=d4 и не зависит коэффициент d0. Поэтому уравнение ku=0 одновременно является и апериодической границей устойчивости.
Составив определитель Гурвица, для его Dn-1 минора получим
Подставим в это выражение значения коэффициентов d2, d3, d4, как функций параметров ku и kw , после преобразований получим квадратное уравнение, определяющее передаточное число по угловой скорости как функцию от передаточного числа по углу тангажа
По этому выражению строится колебательная граница устойчивости. График деления области исследуемых параметров на области устойчивости и неустойчивости показан на рис. 3.19.
Граница колебательной неустойчивости штрихуется в сторону положительности Dn-1- го определителя Гурвица, а прямая kwz=0 в сторону положительности этого коэффициента.
Для проверки полученных результатов выберем какие – либо значения параметров внутри заштрихованной области, например ku=5, kwz=0.6, вычислим значения коэффициентов характеристического уравнения и оценим устойчивость замкнутой системы по критерию Гурвица.
Получим, что при выбранных значениях передаточных чисел система устойчива. Это означает, что и вся область, внутрь которой обращены штрихи, является областью устойчивости.
D – разбиение в плоскости одного параметра
Пусть нас интересует влияние какого – либо одного параметра на устойчивость САУ и этот параметр входит в характеристическое уравнение линейно, так что это уравнение можно представить в виде

Сделав замену s= jw , получим

Задавая значения частоты от -¥ до +¥, можно построить кривую m(w), отображающую мнимую ось плоскости корней на плоскость m. Эта граница D – разбиения симметрична относительно вещественной оси. Поэтому вычисления можно вести в диапазоне частот от 0 до +¥, а затем дополнить полученную кривую ее зеркальным отображением на диапазон частот от -¥ до нуля. При движении по мнимой оси от -¥ до +¥ на плоскости корней область устойчивости остается слева. Поэтому при движении по кривой D – разбиения в сторону увеличения частоты ее штрихуют слева. Область, внутрь которой обращены штрихи, является предполагаемой областью устойчивости. Для окончательного решения, необходимо взять какое – либо вещественное значение параметра m в исследуемой области и воспользоваться каким – либо критерием устойчивости. Если при избранном значении параметра система устойчива, то рассматриваемая область является областью устойчивости.
Пример. Построить область устойчивости системы стабилизации угла тангажа в плоскости передаточного числа ku.
Характеристическое уравнение исследуемой системы можно записать в виде
где
В полученных выражения сделаем замену s=jw и получим
В этих выражениях
Построенная по этим выражениям кривая D – разбиения показана на рис. 3.20.
Так как необходимым условием устойчивости рассматриваемой системы является ku>0, то мнимая ось также является границей устойчивости и штрихуется в сторону положительности ku. Значение этого коэффициента, равное 5, находится внутри заштрихованной области и мы знаем, что при этом значении система устойчива. Значит и весь отрезок вещественной оси, расположенный внутри заштрихованной области, дает значения передаточного числа по углу, при которых система устойчива. Можно показать, что окончание этого отрезка находиться в точке, равной критическому значению коэффициента ku=16.56.
D – разбиение в плоскости двух параметров
Пусть коэффициенты характеристического уравнения линейно зависят от двух параметров m и l так, что его можно записать в виде

После замены s=jw получим
Так как равенство нулю всего преобразованного характеристического уравнения может выполняться только, если одновременно равны нулю его вещественная и мнимая части, то получим систему уравнений относительно изменяемых параметров

Разрешив систему (3.33) относительно m и l, получим
где
Задавая значения частоты от -¥ до +¥, определим совокупность точек на плоскости m — l, образующих кривую D – разбиения. Функции m(w) и l(w) являются четными, и поэтому, при изменении частоты в указанных выше пределах, кривая D – разбиения пробегается дважды. При построении кривой D – разбиения в плоскости двух параметров необходимо руководствоваться следующими правилами [8,14]:
1) если в системе (3.33) первое уравнение получено из вещественных частей, а второе – из мнимых частей функций P(jw), Q(jw) и S(jw) и если параметр m по написанию стоит первым, а l — вторым, то система координат должна быть правой, т.е. ось m является осью абсцисс с отсчетом положительных значений вправо, а ось l — осью ординат с отсчетом положительных значений вверх;
2)двигаясь по кривой D – разбиения при изменении частоты в сторону увеличения, ее штрихуют слева, если D(w)>0, и справа, если D(w) * ¹ 0,¥ одновременно D(w * )= =Dm(w * )=Dl(w * )=0. Тогда система (3.33) становится линейно – зависимой и ее уравнения отличаются друг от друга только на постоянный множитель. В этом случае эта система сводится к одному уравнению, определяющему на плоскости m — l прямую линию, которая называется особой прямой.
Если особая прямая пересекает кривую D – разбиения в точке w=w * и в этой точке определитель D(w) меняет знак, то эта прямая также является границей устойчивости и в указанной точке изменяется направление штриховки кривой и особой прямой. Если при w=w * изменение знака главного определителя не происходит, то штриховка на особую прямую не наносится. Если свободный член характеристического уравнения dn=dn(m,l), то это соответствует существованию особой прямой для w=0 и ее уравнение будет

Уравнение особой прямой для w=¥ определяется выражением
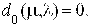
Прямые (3.34) и (3.35) называются концевыми. Они штрихуются одинарной штриховкой, согласованной в точках w=0 и w=¥ с направлением штриховки основной линии. Предполагаемая область устойчивости находится внутри заштрихованного участка и проверяется аналогично предыдущему. Переход через кривую D – разбиения, заштрихованную дважды, соответствует переходу через границу устойчивости двух корней, а переход через особую концевую с одинарной штриховкой – переходу одного корня. Если концевые прямые не имеют общих точек с основной кривой, то штриховка на них наносится в сторону положительности параметров.
Пример. Построить область устойчивости системы стабилизации угла тангажа в плоскости параметров ku и kwz.
Характеристическое уравнение замкнутой системы может быть представлено в виде (3.32), где
После подстановки s=jw и выделения вещественных и мнимых частей, получим
Составив систему уравнений (3.33) и решив ее, получим
Определив корни этих уравнений, можно сделать вывод, что общих корней, кроме нулевого корня, не существует.
Значит особых прямых нет, существует только концевая прямая, соответствующая уравнению dn=kcku=0. Руководствуясь выше приведенными правилами, построим кривую D – разбиения и заштрихуем ее и концевую прямую. Проверку осуществим в точке ku=5, kwz=0.6.
уже ранее установили, что в этой точке система устойчива, а значит и заштрихованная область является областью устойчивости.
Практическая пригодность САУ, определяется ее устойчивостью и приемлемым качеством процесса управления (регулирования). На любую САУ действуют различные внешние возмущения, которые могут нарушать ее нормальную работу. Правильно спроектированная система должна устойчиво работать при всех внешних возмущениях.
В простейшем случае, понятие устойчивость системы связана со способностью ее возвращения к исходному состоянию после кратковременного внешнего воздействия. Если система неустойчивая, она не возвращается к состоянию равновесия, из которого по каким-то причинам вышла.
Только устойчивая система автоматического управления может выполнять возложенные на нее функции. Поэтому одной из основных задач САУ является обеспечение ее устойчивости.
Устойчивость считается важнейшим и обязательным понятием, так как только в устойчивой системе могут быть удовлетворены другие требования к качеству.
В своей работе я исследовал устойчивость системы стабилизации угла тангажа самолета и определял критическое значение передаточного числа автопилота по углу тангажа, используя различные критериями устойчивости. А именно:
ü Критерием устойчивости Рауса-Гурвица;
ü Критерием устойчивости Михайлова;
ü Критерием устойчивости Найквиста.
http://www.evkova.org/zamknutaya-sistema-v-fizike
http://poisk-ru.ru/s16373t3.html