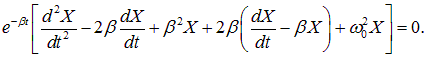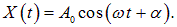Уравнение затухающих колебаний для заряда

Затухающие колебания в контуре и их уравнение

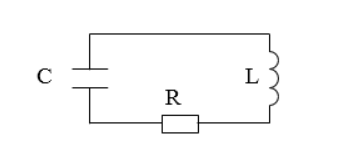
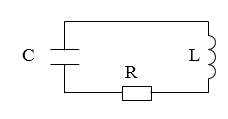
Существуют колебания в системе без источника энергии, называемые затухающими. Рассмотрим реальный контур с сопротивлением не равным нулю. Для примера используют контур с включенным сопротивлением R , с емкостью конденсатора C , с катушкой индуктивности L , изображенный на рисунке 1 . Колебания, происходящие в нем, — затухающие.

Именно наличие сопротивления становится главной причиной их затухания. Данный процесс возможен посредствам потерь энергии на выделение джоулева тепла. Аналог сопротивления в механике – действие сил трения.

Характеристики затухающих колебаний

Затухающие колебания характеризуют коэффициентом затухания β . Применив второй закон Ньютона, получим:

m a = — k x — y v , d 2 x d t 2 + r m d x d t + k m x = 0 , ω 0 2 = k m , β = r 2 m .

Из записи видно, что β действительно является характеристикой контура. Реже вместо β применяют декремент затухания δ ,

Значение a ( t ) является амплитудой заряда, силы тока и так далее, δ равняется количеству колебаний, а N e — период времени уменьшения амплитуды в e раз.

Для R L C контура применима формула с ω частотой.

При небольшой δ ≪ 1 говорят, что β ≪ ω 0 ω 0 = 1 L C — собственная частота, отсюда ω ≈ ω 0 .

При рассмотрении затухающих колебаний последовательного контура колебательный контур характеризуется добротностью Q :

Q = 1 R L C = ω 0 L R , где R , L и C — сопротивление, индуктивность, емкость, а ω 0 — частота резонанса. Выражение L C называют характеристическим или волновым сопротивлением. Для параллельного контура формула примет вид:

Q = R L C = R ω 0 L .

R является входным сопротивлением параллельного контура.

Эквивалентное определение добротности применяется при слабых затуханиях. Его выражают через отношение энергий:

Q = ω 0 W P d = 2 π f 0 W P d , называемое общей формулой.

Уравнения затухающих колебаний

Рассмотрим рисунок 1 . Изменение заряда q на конденсаторе в таком контуре описывается дифференциальным уравнением:

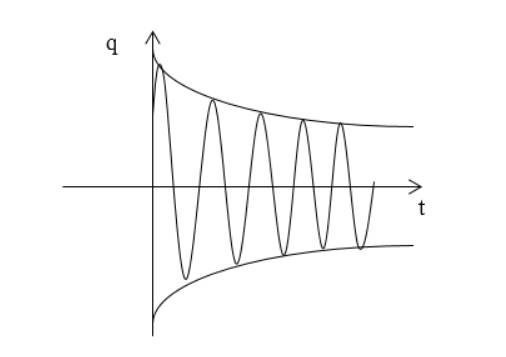
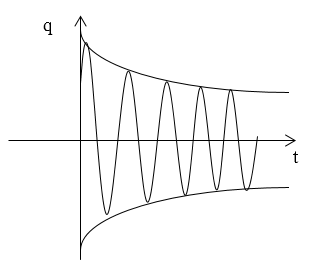
q ( t ) = q 0 e ( — β t ) cos ω t + a ‘ 0 = q 0 e — β t cos ( ω t ) .

Если t = 0 , то заряд конденсатора становится равным q 0 , и ток в цепи отсутствует.

Если R > 2 L C изменения заряда не относят к колебаниям, разряд называют апериодическим.

Значение сопротивления, при котором колебания превращаются в апериодический разряд конденсатора, критическое R k .

Функция изображается аналогично рисунку 2 .

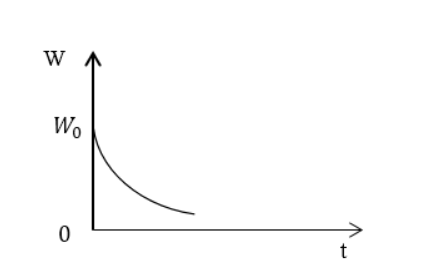
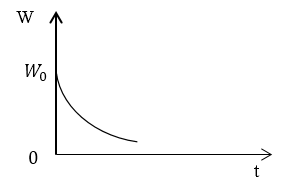
Записать закон убывания энергии, запасенной в контуре W ( t ) при W ( t = 0 ) = W 0 с затухающими колебаниями. Обозначить коэффициент затухания в контуре β , а собственную частоту — ω 0 .

Решение

Отправная точка решения – это применение формулы изменения заряда на конденсаторе в R L C — контуре:

q ( t ) = q 0 e ( — β t ) cos ω t + a ‘ 0 = q 0 e — β t cos ( ω t ) .

Предположим, что при t = 0 , a ‘ 0 = 0 . Тогда применим выражение

Для нахождения I ( t ) :

I ( t ) = — ω 0 q 0 e ( — 2 β t ) sin ( ω t + α ) , где t g α = β ω .

Очевидно, что электрическая энергия W q запишется как:

W q = q 2 2 C = q 0 2 2 C e ( — 2 β t ) cos 2 ( ω t ) = W 0 e ( — 2 β t ) cos 2 ( ω t ) .

Тогда значение магнитной энергии контура W m равняется:

W m = L 2 ω 0 2 q 0 2 e ( — 2 β t ) sin 2 ω t + a = W 0 e — 2 β t sin 2 ω t + a .

Запись полной энергии будет иметь вид:

W = W q + W m = W 0 e ( — 2 β t ) ( cos 2 ( ω t ) + sin 2 ( ω t + a ) ) = = W 0 e ( — 2 β t ) 1 + β ω 0 sin ( 2 ω t + α ) .

Где sin α = β ω 0 .

Ответ: W ( t ) = W 0 e ( — 2 β t ) 1 + β ω 0 sin ( 2 ω t + a ) .

Применив результат предыдущего примера, записать выражение для энергии, запасенной в контуре W ( t ) , при медленно затухающих колебаниях. Начертить график убывания энергии.

Решение

Если колебания в контуре затухают медленно, то:

Очевидно, выражение энергии, запасенной в контуре, вычислим из

W ( t ) = W 0 e ( — 2 β t ) 1 + β ω 0 sin ( 2 ω t + a ) , предварительно преобразовав до W ( t ) = W 0 e ( — 2 β t ) .

Такое упрощение возможно по причине выполнения условия β ω 0 ≪ 1 , sin ( 2 ω t + a ) ≤ 1 , что означает β ω 0 sin ( 2 ω t + a ) ≪ 1 .

Ответ: W ( t ) = W 0 e ( — 2 β t ) . Энергия в контуре убывает по экспоненте.

Затухающие колебания в контуре и их уравнение

Вы будете перенаправлены на Автор24

Определение, характеристики затухающих колебаний

В реальном мире любые колебания в системе, где нет источника энергии, являются затухающими. Рассмотрим реальный контур, сопротивление которого отлично от нуля. Примером простейшей системы, которую рассматривают в таком случае может служить контур включают сопротивление $(R)$, конденсатор емкостью $C$, катушку индуктивности $L$, тогда такой контур имеет вид указанный на рис.1. Колебания в таком контуре являются затухающими.

Причиной затухания колебаний в таком контуре является наличие сопротивления. Его существование ведет к тому, что в контуре происходят потери энергии на выделение джоулева тепла. В механике аналогом сопротивления являются силы трения.

Затухающие колебания характеризуют коэффициентом затухания ($\beta $), равным:

Из выражения (1) видно, что $\beta $ является характеристикой контура. Иногда для характеристики затухания используют логарифмический декремент затухания ($\delta $), который равен:

где $a\left(t\right)$- амплитуда какой — либо величины (заряда, силы тока и т.д.). $\delta $ равен количеству колебаний ($N_e$) за время, в течение которого амплитуда уменьшается в e раз:

Для $RLC$ контура:

где $\omega $ — частота.

Если затухание небольшое ($\delta \ll 1$), то полагают, что $\beta \ll <\omega >_0$ ($<\omega >_0=\sqrt<\frac<1>>-собственнная\ частота$), тогда $\omega \approx <\omega >_0$. В таком случае:

Рассматривая затухающие колебания, колебательный контур характеризуют его добротностью ($O$). Он равен:

Для слабого затухания добротность можно выразить как:

Также при слабом затухании электрических колебаний добротность можно выразить через отношение энергий:

где $W$ — энергия контура, $\triangle W$- уменьшение энергии контура за одно колебание.

Готовые работы на аналогичную тему

Уравнение затухающих колебаний

Обратимся вновь к контуру, который изображен на рис.1. Изменение заряда ($q$) на конденсаторе в таком контуре описывается дифференциальным уравнением вида:

где $\omega =\sqrt<\frac<1>-\frac<4L^2>> \cdot \beta =\frac<2L>$. Амплитуда равна:

В том случае, если при $t=0$ заряд на конденсаторе равен $q_0$, тока в цепи нет, то для $A_0$ можно записать:

Начальная фаза колебаний ($<\alpha >_0$) равна:

При $R >2\sqrt<\frac>$ изменение заряда не является колебаниями, разряд конденсатора называют апериодическим.

Сопротивление, при котором колебания превращаются в апериодический разряд конденсатора называется критическим ($R_k$). Величина $R_k$ определяют условием:

График функции (10) изображают как на рис.2.

Задание: Запишите закон убывания энергии, запасенной в контуре $(W(t))$, если $W(t=0)=W_0,$ колебания являются затухающими. Коэффициент затухания колебаний в контуре равен $\beta $. Собственная частота $<\omega >_0.\ $

Решение:

В качестве отправной точки для решения задачи используем уравнение изменения заряда на конденсаторе в $RLC$ -контуре в виде:

в выражении (1.1) мы предположили, что при $t=0,\ <<\alpha >‘>_0=0$. Используя выражение:

Найдем $I(t)$, получим:

Следовательно, электрическая энергия контура ($W_q$) имеет вид:

Магнитная энергия контура ($W_m$) равна:

Полная энергия равна:

Задание: Используя результат Примера 1, запишите выражение для энергии, запасенной в контуре ($W(t)$), если колебания затухают в контуре очень медленно. Изобразите график убывания энергии запасенной в контуре.

Решение:

Если колебания в контуре затухают медленно, то это значит:

Следовательно, выражение для энергии, запасенной в контуре:

можно преобразовать к виду:

Ответ: $W\left(t\right)=W_0e^<\left(-2\beta t\right)>$. Энергия контура убывает по экспоненте.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 26 04 2021

1.6. Свободные затухающие колебания

Гармонические колебания, существующие вечно, являются одной из физических абстракций. В реальных системах колебания по прошествии некоторого времени затухают из-за диссипации энергии. Таким образом, представлением о гармонических колебаниях можно пользоваться лишь для времен, малых по сравнению с характерным временем затухания. Затухание колебаний всегда будет наблюдаться в системах с трением.

Уравнение затухающих колебаний

Рассмотрим в качестве примера пружинный маятник, помещенный в вязкую среду. Помимо силы упругости на тело будет действовать сила сопротивления, пропорциональная скорости

где r — соответствующий коэффициент, зависящий от вязкости среды, размеров и формы тела. Поэтому уравнение движения примет вид:

Здесь новый, дополнительный параметр системы, называемый коэффициентом затухания. Колебания незатухающие, если .

Другой пример — электромагнитный контур. Если помимо конденсатора С и индуктивности L в контуре имеется еще и активное сопротивление R, то ЭДС самоиндукции равна сумме напряжения на конденсаторе и падения напряжения на сопротивлении. Поэтому уравнения (1.15) примут теперь вид:

Подставляем первое уравнение во второе:

Напомним, что комбинация L/R уже встречалась нам в теории электромагнетизма, где она характеризовала характерное время затухания (появления) экстратоков замыкания-размыкания. Таким образом, величина b имеет размерность обратного времени, совпадающую с размерностью циклической частоты.

Анализ решений

Итак, в обоих рассмотренных случаях дифференциальное уравнение свободных затухающих колебаний линейной системы имеет вид:

Дифференцируя функцию x(t), получаем:

Подставляем эти выражения в (1.67):

Выражение в квадратных скобках должно быть равно нулю. Замечаем, что в этом выражении сокращаются члены с первой производной . Получаем в итоге дифференциальное уравнение для функции X(t):

Здесь возможны два случая. Пусть сначала . Тогда можно ввести параметр

так что уравнение (1.71) примет вид:

Но это — стандартное уравнение гармонических колебаний, общее решение которого мы знаем:

Значит, мы нашли общее решение уравнения затухающих колебаний (1.67):

Во многих системах коэффициент затухания мал по сравнению с собственной частотой колебаний: . Тогда движение системы можно рассматривать как почти гармоническое колебание с частотой и с амплитудой, изменяющейся по закону (рис. 1.22)

Рис. 1.22. Свободные затухающие колебания

Коэффициент затухания определяет скорость уменьшения амплитуды колебаний: он обратен по величине промежутку времени, за который амплитуда уменьшается в e раз.

Период затухающих колебаний равен:

Пусть первое наибольшее положительное отклонение достигается в момент времени . Последующие наибольшие отклонения того же знака (A’, A», A»’ и т.д. — см. рис. 1.22) образуют геометрическую прогрессию:

Отношение значений амплитуд, соответствующих моментам времени, отличающимся на период, равно:

Это соотношение называется декрементом затухания. Логарифм этого отношения называется логарифмическим декрементом затухания:

Определим количество колебаний, которое совершит система за время . За это время амплитуда уменьшается в е раз, а число колебаний равно:

Следовательно, логарифмический декремент затухания обратен по величине числу колебаний, совершаемых за то время, за которое амплитуда уменьшается в е раз.

Для характеристики колебательной системы часто употребляется величина, называемая добротностью:

которая пропорциональна числу колебаний N_е, совершаемых системой за то время , за которое амплитуда колебаний уменьшается в е раз. Например, для электромагнитного контура при находим:

Мы видели, что полная энергия в колеблющейся системе пропорциональна квадрату амплитуды. При малом затухании (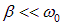) имеем:

где E₀ — значение полной энергии колеблющейся системы в начальный момент времени. Можно определить убыль энергии за период Т:

то есть при слабом затухании добротность, с точностью до множителя , равна отношению полной энергии, запасенной в колебательной системе в данный момент времени, к убыли энергии за один период колебаний.

При увеличении затухания частота колебаний

стремится к нулю, а период колебаний растет. В предельном случае

период обращается в бесконечность, то есть движение перестает быть периодическим. Соответствующий математический анализ показывает, что при движение носит апериодический характер — выведенная из положения равновесия система возвращается в положение равновесия, не совершая колебаний.