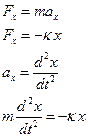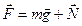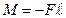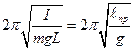Уравнение затухающих колебаний физического маятника

Теория метода и описание установки

Изучение затухающих колебаний физического маятника

Методические указания к лабораторной работе №5 по дисциплине

Механика. Молекулярная физика и термодинамика»

для студентов специальностей 150106, 150105, 150201, 150404, 2005030.

Составитель: Мигранова С.Г.

Методические указания к лабораторной работе №5 по дисциплине «Общая физика. Механика. Молекулярная физика и термодинамика» для студентов специальностей 150106, 150105, 150201, 150404, 2005030. Магнитогорск: МГТУ, 2012.

Рецензент: Дубосарская Ю.М.

Лабораторная работа № 5

Изучение затухающих колебаний физического маятника

Цель работы: изучение затухающих колебаний, определение основных характеристик затухающих колебаний.

Приборы и принадлежности: физический маятник, постоянный магнит, секундомер, весы.

Краткая теория

Затухающие колебания.Затуханием колебаний называется постепенное ослабление колебаний с течением времени, обусловленной потерей энергии колебательной системой. Затухание колебаний в механических системах вызывается в основном трением, сопротивлением среды и возбуждением в ней волн.

Найдем дифференциальное уравнение, описывающее свободные затухающие колебания физического маятника. Если колеблющееся тело нельзя представить как материальную точку, маятник называют физическим. Движение маятника описывается уравнением динамики вращательного движения , где — результирующий момент сил, действующих на систему, — момент инерции системы, — угловое ускорение: . На физический маятник действует момент силы тяжести и момент сил сопротивления, при малых отклонениях пропорциональный угловой скорости .

При малых колебаниях , тогда

(1) — дифференциальное уравнение затухающих колебаний физического маятника.

Введем обозначения физических характеристик:

— циклическая частота свободных незатухающих колебаний маятника,

— циклическая частота затухающих колебаний, — период затухающих колебаний.

(2) -уравнение затухающих колебаний, полученное при выполнении условий: отклонения маятника малы, момент сил сопротивления пропорционален скорости, выполняется неравенство .

Решение дифференциального уравнения затухающих колебаний имеет следующий вид:

, (3)

где (4) — амплитуда затухающих колебаний, (5) — коэффициент затухания.

График зависимости при начальной фазе имеет вид экспоненты, причем, чем меньше коэффициент β, тем амплитуда убывает слабее.

Затухающие колебания — непериодические, т.к. в начальный момент никогда не повторяется. Однако обращается в ноль и достигает max и min через один и тот же промежуток времени .

Промежуток времени , в течение которого амплитуда затухающих колебаний уменьшается в е раз, называется временем релаксации.

(6)

Логарифмическим декрементом затухания называется безразмерная величина , равная логарифму отношения амплитуды в момент времени к амплитуде через период:

, (7), где — число колебаний, в течение которых амплитуда уменьшается в е раз.

Добротностью колебательной системы называется безразмерная величина , равная , умноженным на отношение энергии в момент времени к разности энергий через период:

Т.к. полная энергия пропорциональна квадрату амплитуды, т.е. , то

При малых значениях логарифмического декремента затухания (

колебаний. График зависимости от будет иметь вид прямой, проходящей через начало координат. На графике легко определяются по точке пересечения с горизонтальной прямой, соответствующей значению . Если график не пресекается с ординатой, равной единице, то можно заменить 1 на 0,5, но тогда полученное значение нужно умножить на 2.

Затухания и приведенной длины физического маятника

Литература

1. Детлаф А.А., Яворский Б.М. Курс физики. ‑ М., 1989. С. 298 – 314.

2. Методические указания к выполнению лабораторных работ по физике. Раздел «Механика материальной точки». / МТИПП. ‑ М., 1990. С 18 – 31.

Введение

Всякое движение, в котором наблюдается повторяемость во времени значений физических величин, определяющих это движение, называется колебательным движением.

Гармоническим колебательным движением называется такое движение, при котором величина, характеризующая состояние системы, изменяется со временем по закону синуса или косинуса, т.е. уравнение гармонических колебаний имеет вид:

, (1)

где x – смещение от положения равновесия;

A – амплитуда колебаний – наибольшее смещение от положения равновесия;

– фаза колебаний;

j_о – начальная фаза колебаний;

w_о – собственная циклическая частота колебаний – это число колебаний за 2p секунд.

Время одного полного колебания Т называется периодом колебаний. Количество колебаний в единицу времени называется частотой колебаний . Между периодом, частотой и циклической частотой существует связь:

(2)

Если выражение (1) продифференцировать по времени, то получим закон изменения скорости от времени

(3)

Продифференцировав (3) еще раз по времени, найдем закон зависимости ускорения от времени:

(4)

учитывая, что 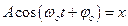, получим

(5)

Последнее уравнение показывает, что при гармонических колебаниях ускорение пропорционально величине смещения и всегда направлено противоположно смещению.

Примерами систем, в которых могут возникать гармонические колебания, могут служить мятники: пружинный, математический и физический.

Рассмотрим пружинный маятник – грузик на идеально упругой пружине при отсутствии трения. На примере его движения получим дифференциальное уравнение гармонических колебаний.

Чтобы система (маятник) совершала гармонические колебания, необходимо воздействие на нее упругой или квазиупругой силы, изменяющейся при смещении системы от положения равновесия по закону:

(6)

Эта сила, пропорциональна смещению и всегда направлена к положению равновесия. Применим второй закон Ньютона к пружинному маятнику.

Возвращающая сила 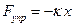, действуя на тело массой m, создает ускорение а. Согласно второму закону Ньютона

Колебания происходят вдоль оси х (рис.1), поэтому спроецируем векторное уравнение на ось ОХ :

Поделив все члены на m, перенеся их в одну часть равенства, обозначив , получим окончательный вид дифференциального уравнения гармонических колебаний пружинного маятника:

или , (7)

где – собственная частота колебаний пружинного маятника;

– период колебаний (8)

Решением уравнения (7) является уравнение (1).

Рассмотрим математический маятник – это материальная точка, подвешенная на невесомой и нерастяжимой нити длиною (рис. 2). На грузик m действуют сила тяжести и сила натяжения нити . Равнодействующая этих сил «похожа» на силу упругости тем, что она пропорциональна величине смещения и направлена к положению равновесия, но сила не имеет упругой природы. Силу называют квазиупругой силой. Колебательные движения математического маятника можно рассматривать как часть вращательного. Для его описания применим основной закон вращательного движения

, (9)

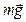
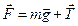
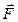
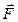
где M – момент возвращающей силы;

I – момент инерции материальной точки;

e

– угловое ускорение.

При условии малых колебаний заменим ; , x – смещение точки от положения равновесия.

Подставим полученные выражения в формулу

Знак « – » имеет то же значение, что и в случае (6)

или

Поделив все члены на , перенеся их в одну сторону, обозначив , получим окончательный вид дифференциального уравнения гармонических колебаний математического маятника:

или , (10)

где – собственная частота колебаний;

– период колебаний. (11)

Из формулы (11) видно, что период колебаний математического маятника не зависит от его массы, а определяется лишь его длиной и ускорением свободного падения.

Решением уравнения (10) является уравнение (1).

Рассмотрим физический маятник – это абсолютно твердое тело, которое может свободно вращаться вокруг оси О, не проходящей через его центр масс (рис. 3).

На физический маятник действует сила тяжести 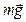и сила реакции опоры . При отклонении физического маятника от положения равновесия на угол j, равнодействующая этих сил является квазиупругой возвращающей силой

Колебания физического маятника рассматриваем как часть вращательного движения вокруг оси О и для его описания применяем основное уравнение динамики вращательного движения

,

где М – момент возвращающей силы;

I – момент инерции твердого тела, относительно оси О;

e – угловое ускорение.

Знак « – » имеет тот же смысл, что и в случае (6)

В случае малых колебаний заменим , , х – смещение маятника от положения равновесия.

Сделав подстановку, получили

или

Поделив все члены равенства на , перенесем в одну сторону и обозначим , получим

или (12)

дифференциальное уравнение гармонических колебаний физического маятника.

– собственная частота колебаний

Период колебаний физического маятника выражается формулой

(13)

Приведенной длиной физического маятника называется длина такого математического маятника, у которого его период колебаний совпадает с периодом колебаний данного физического маятника.

(14)

Решением уравнения (12) является уравнение (1).

Итак, гармонические колебания, возникающие в идеальных колебательных системах, не зависимо от вида маятника, описываются одинаковыми уравнениями (7), (10), (12), которые имеют решение (1).

В реальных колебательных системах всегда присутствуют силы трения, на преодоление которых будет тратиться собственная энергия системы. Если энергия не будет восполняться за счет работы внешних сил, то колебания будут затухать, т.е. амплитуда их будет уменьшаться с течением времени.

При малых смещениях от положения равновесия на систему будут действовать:

1) квазиупругая возвращающая сила ;

2) сила сопротивления, пропорциональная скорости и направленная противоположно ее направлению ,

где r – коэффициент сопротивления.

Применим второй закон Ньютона к описанию движения колеблющейся системы

В проекции на ось ОХ, это уравнение будет выглядеть как , если подставить и , получим

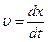
Поделив все члены равенства на m, перенеся их в одну сторону, обозначив , , получим дифференциальное уравнение затухающих колебаний.

или (15)

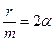
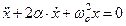
Решением уравнения (15) будет периодическая функция с убывающей амплитудой

, (16)

где A_o – наибольшее отклонение системы от положения равновесия;

– коэффициент затухания;

– закон убывания амплитуды;

– частота затухающих колебаний.

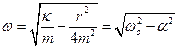
Уменьшение амплитуды колебаний за один период характеризует декремент затухания

В качестве меры затухания берут величину натурального логарифма декремента затухания

(17)

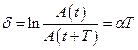
d называют логарифмическим декрементом затухания.

Для получения незатухающих колебаний необходимо воздействовать на систему дополнительной переменной внешней силой, работа которой непрерывно восполняла бы убыль энергии из-за наличия сил трения. Эта переменная сила называется вынуждающей, а колебания – вынужденными.

Пусть вынуждающая сила меняется по гармоническому закону

При этом условии уравнение второго закона Ньютона в случае вынужденных колебаний будет иметь вид

Поделим все члены равенства на m, обозначим ; , , получим дифференциальное уравнение вынужденных колебаний

или (18)

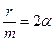
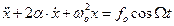
Решением этого уравнения является уравнение вида:

, (19)

где амплитуда установившихся колебаний имеет вид

,

а начальная фаза может быть определена из условия

Амплитуда колебаний зависит от частоты вынуждающей силы. Если затухание существует , то амплитуда колебаний достигнет наибольшего значения при частоте вынуждающей силы, совпадающей с частотой незатухающих колебаний w_о:

Явление возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающей силы к значению называется резонансом. Соответственно величина называется резонансной циклической частотой, а кривые зависимости – резонансными кривыми (рис. 5).

Форма резонансных кривых зависит от величины коэффициента затухания a. С увеличением a резонансные кривые становятся более пологими, уменьшается значение максимума амплитуды

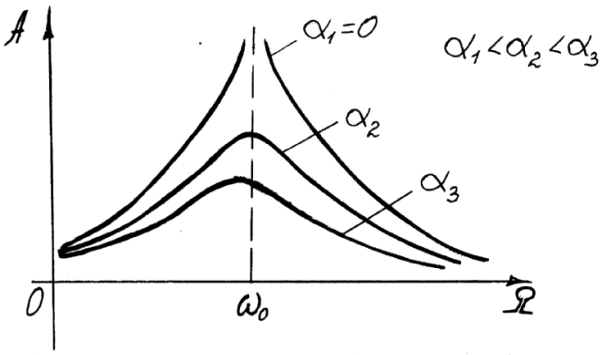Рис. 5

Описание установки и метода измерений

Прибор для изучения законов колебательного движения представляет собой комбинацию двух связанных маятников: физического 1 и математического 2 (рис.6). Связь маятников осуществляется при помощи вилки 3, жестко связанной с физическим маятником, в ушко которого продернута нить математического маятника. Длина математического маятника может быть измерена на требуемую величину путем перемещения нити с помощью фиксируемого ползунка 4, закрепленного на линейке 5. Положение ползунка на

этой линейке позволяет задать необходимую длину математического маятника. Амплитуда колебаний обоих маятников определяется по шкале 6.

Для увеличения затухания на физическом маятнике может быть закреплена тормозящая пластина 7.

Порядок выполнения и обработка результатов измерений

1. Определение логарифмического декремента затухания

1. Убирают математический маятник (для этого можно поднять шарик или отвести его в сторону).

2. На физическом маятнике закрепляют тормозящую пластину 7.

3. Отклоняют физический маятник до заданной начальной амплитуды A_o, отпускают его и одновременно включают секундомер. Фиксируют число полных колебаний n и промежуток времени t, по прошествии которого амплитуда принимает значение A_n.

4. Полученные результаты заносят в табл. 1.

5. Определяют период T физического маятника по формуле ,

где t – время, n – число полных колебаний.

6. Вычисляют логарифмический декремент затухания по формуле:

и коэффициент затухания по формуле:

7. Вычисляются относительные и абсолютные погрешности при определении d и a. Все результаты заносятся в табл. 1.

№ п/п

Ao, дел

An, дел

n,

t, с

T, с

Tср, с

DT, с

d

dср

Dd

a, с -1

aср, с -1

Da, с -1

A_o – начальная амплитуда; A_n – конечная амплитуда;

n – число колебаний; t – время колебаний;

Т – период колебаний; a – коэффициент затухания;

d – логарифмический декремент затухания.

2. Снятие резонансной кривой

1. Выводят из зацепления математический маятник.

2. Устанавливают начальную длину математического маятника (максимальную или минимальную).

3. Отводят физический маятник на 5 – 6 делений от положения равновесия и дают ему свободно качаться.

Наблюдая возникновение колебаний математического маятника, фиксируют по шкале 6 максимальное значение угла отклонения при заданной длине маятника и заносят в табл. 2 результаты.

4. Изменяя длину маятника последовательно на 10 см, повторяют опыт, проходя весь интервал возможных длин. На участке, где начинает обнаруживаться явление резонанса, изменение длины уменьшают до 5 см. Заносят показания в табл. 2.

5. Строят график зависимости угла отклонения математического маятника от его длины . По графику определяют резонансное значение и сравнивают его величину с – приведенной длиной физического маятника, определяемой по формуле:

с использованием численного значения T по результатам предыдущего опыта.

Делаются соответствующие выводы.

, м.

, дел.

1. Что мы называем математическим, физическим маятником?

2. Напишите уравнение гармонических колебаний.

3. Выведите дифференциальное уравнение затухающих колебаний.

4. Выведите период колебаний математического и физического маятников.

5. Дайте определение логарифмического декремента затухания. Что характеризует логарифмический декремент затухания?

6. Выведите дифференциальное уравнение вынужденных колебаний.

7. Дайте объяснение явления механического резонанса.

Затухающие колебания

Определение затухающих колебаний

Механическое движение всегда сопровождается трением. Трение приводит к рассеянию (диссипации) механической энергии. Диссипация энергии имеется в любых не идеализированных колебательных системах, она вызывает затухание собственных колебаний.

Затухающими колебаниями называют колебания, амплитуда которых постепенно уменьшается со временем из-за потерь энергии колебательной системой.

Уравнение колебаний пружинного маятника с затуханием

Иногда, если тело движется в веществе, силу сопротивления ($<\overline>_

$), которая действует на рассматриваемое тело, при маленьких скоростях его движения, считают прямо пропорциональной скорости ($\overline$):

\[<\overline>_

=-\beta \overline\left(1\right),\]

где $\beta $ — коэффициент сопротивления.

Данную силу учитывают в уравнении второго закона Ньютона при описании движения. Так, уравнение, которое описывает линейные колебания по вертикали (колебания по оси X) пружинного маятника, учитывающее силу трения принимает вид:

где $\dot=v_x.$ Принимая во внимание равенства:

(где $<\omega >_0$- циклическая частота свободных незатухающих колебаний (собственная частота колебаний при $\gamma $=0) той же колебательной системы; $\gamma $ — коэффициент затухания) уравнение колебаний пружинного маятника с затуханием (2) преобразуем к виду:

Малые собственные колебания, затухающие вследствие сопротивления среды в любой физической системе (математический маятник, физический маятник, электрические колебания . ) описывают при помощи уравнения формы (4).

Уравнение затухающих колебаний имеет точное решение:

где $\omega =\sqrt<<\omega >^2_0-<\gamma >^2>$; $A_0$ — начальная амплитуда колебаний, задаваемая начальными условиями; $\varphi $ — постоянная из начальных условий. При $\gamma \ll <\omega >_0$, $\omega \approx <\omega >_0$, параметр $A_0e^<-\gamma t>$ можно считать медленно изменяющейся во времени амплитудой колебаний.

Затухание колебаний по экспоненте связано с тем, что силу сопротивления мы приняли пропорциональной скорости. Если использовать другую зависимость силы трения от скорости, то закон затухания изменится.

Диссипация энергии при затухающих колебаниях

Пусть затухание мало, при этом потеря энергии колебательной системой за один период много меньше, чем энергия колебаний.

Рассеяние энергии за период колебаний происходит не равномерно, ввиду осцилляции кинетической энергии ($E_k$). Уравнение убывания энергии при затухающих колебаниях будет иметь вид:

\[\frac

=-\frac<2\beta >\left\langle E_k\right\rangle \left(6\right),\]

где $\frac

$ — скорость изменения энергии колебаний; $\left\langle E_k\right\rangle $ — средняя величина кинетической энергии за период колебаний. Уравнение (6) не применяют для промежутков времени, которые меньше периода колебаний.

Так как мы считаем затухание малым, то $\left\langle E_k\right\rangle $ можно принять равным (как при свободных колебаниях) половине полной энергии осциллятора:

\[\left\langle E_k\right\rangle =\frac<2>\left(7\right).\]

В таком случае уравнение (6) можно записать в виде:

Выражение (8) отображает «сглаженное» поведение энергии колебаний (в случае, если детали изменения энергии за один период колебаний не интересны). Оно показывает, что скорость изменения энергии пропорциональна самой энергии. Решением уравнения (8) является функция:

где $E_0$ — величина энергии колебательной системы в начальный момент времени.

Так как энергия колебаний пропорциональна квадрату амплитуды ($E\sim A^2$), изменение амплитуды колебаний за большие отрезки времени (в сравнении с периодом колебаний) запишем в виде функции:

$A_0$ — начальная амплитуда колебаний.

Время жизни колебаний. Период затухающих колебаний. Декремент затухания

Из формулы (10) видно, что амплитуда затухающих колебаний убывает по экспоненте. За время $\tau =\frac<1><\gamma >$ амплитуда убывает в $e$ раз и это не зависит от $A_0$. Время $\tau $ в этом случае называют временем жизни колебаний (или временем релаксации) (не смотря на то, что в соответствии с выражением (9) колебания должны длиться бесконечно). Тезис о малости затухания означает, что время жизни колебаний не бесконечно, а много больше, чем их период ($\tau \gg T$). За время жизни происходит много колебательных движений.

Строго говоря, затухающие колебания не являются строго периодическими движениями. Периодом в данном случае считают промежуток времени между двумя последовательными максимальными отклонениями от положения равновесия.

Период затухающих колебаний считают равным:

Пусть $A\left(t\right)\ и\ A(t+T)$ — амплитуды двух последовательных колебаний, моменты времени которых отличаются на период. Отношение этих амплитуд, следуя (10) равно:

называют декрементом затухания. Натуральный логарифм декремента затухания ($\theta $):

называют логарифмическим декрементом затухания. Для колебательной системы $\theta $ постоянная величина.

Примеры задач с решением

Задание. Каков коэффициент затухания маятника ($\gamma $), если за $\Delta t$ амплитуда его колебаний уменьшилась в $n$ раз?

Решение. За основу решения задачи примем уравнение затухающих колебаний в виде:

По условию задачи имеем:

С другой стороны:

где $t_2-t_1=\Delta t$. Найдем натуральный логарифм от правой и левой части выражения (1.2), получим:

Выразим $\gamma $ из (1.3) учтем, что $\frac=n$:

Ответ. $\gamma =\frac<<\ln n\ >><\Delta t>$

Задание. Что представляет собой фазовая траектория затухающего колебания?

Решение. Фазовой траекторией называют траекторию движения в плоскости $\left(x;;v\right).$ По оси абсцисс откладывается отклонение $x$, по оси ординат откладывают скорость $v$. Каждому движению в момент времени $t$ соответствует изображающая точка, на указанной плоскости координаты ее $\left(x,v\right),$ они однозначно определены мгновенными значениями отклонения и скорости. Точка со временем движется и описывает траекторию (рис.1). В данном случае время выступает как параметр, уравнение фазовой траектории задет функция:

Фазовая траектория затухающего колебания, если

\[<\overline>_

=-\beta \overline\left(2.2\right),\]

представляет собой незамкнутую спираль, которая закручивается вокруг начала координат (рис.1). Если затухание колебаний малое, то есть за время жизни колебательная система совершает множество колебаний, количество витков спирали в фазовой плоскости будет таким же.

источники:

http://lektsii.org/12-53098.html

http://www.webmath.ru/poleznoe/fizika_46_zatuhajushhie_kolebanija.php