Уравнение затухающих колебаний в контуре для заряда

Затухающие колебания в контуре и их уравнение

Вы будете перенаправлены на Автор24

Определение, характеристики затухающих колебаний

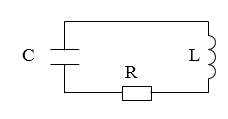
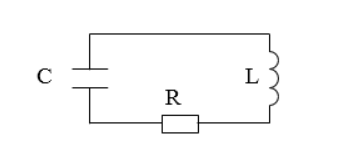
В реальном мире любые колебания в системе, где нет источника энергии, являются затухающими. Рассмотрим реальный контур, сопротивление которого отлично от нуля. Примером простейшей системы, которую рассматривают в таком случае может служить контур включают сопротивление $(R)$, конденсатор емкостью $C$, катушку индуктивности $L$, тогда такой контур имеет вид указанный на рис.1. Колебания в таком контуре являются затухающими.

Причиной затухания колебаний в таком контуре является наличие сопротивления. Его существование ведет к тому, что в контуре происходят потери энергии на выделение джоулева тепла. В механике аналогом сопротивления являются силы трения.

Затухающие колебания характеризуют коэффициентом затухания ($\beta $), равным:

Из выражения (1) видно, что $\beta $ является характеристикой контура. Иногда для характеристики затухания используют логарифмический декремент затухания ($\delta $), который равен:

где $a\left(t\right)$- амплитуда какой — либо величины (заряда, силы тока и т.д.). $\delta $ равен количеству колебаний ($N_e$) за время, в течение которого амплитуда уменьшается в e раз:

Для $RLC$ контура:

где $\omega $ — частота.

Если затухание небольшое ($\delta \ll 1$), то полагают, что $\beta \ll <\omega >_0$ ($<\omega >_0=\sqrt<\frac<1>>-собственнная\ частота$), тогда $\omega \approx <\omega >_0$. В таком случае:

Рассматривая затухающие колебания, колебательный контур характеризуют его добротностью ($O$). Он равен:

Для слабого затухания добротность можно выразить как:

Также при слабом затухании электрических колебаний добротность можно выразить через отношение энергий:

где $W$ — энергия контура, $\triangle W$- уменьшение энергии контура за одно колебание.

Готовые работы на аналогичную тему

Уравнение затухающих колебаний

Обратимся вновь к контуру, который изображен на рис.1. Изменение заряда ($q$) на конденсаторе в таком контуре описывается дифференциальным уравнением вида:

где $\omega =\sqrt<\frac<1>-\frac<4L^2>> \cdot \beta =\frac<2L>$. Амплитуда равна:

В том случае, если при $t=0$ заряд на конденсаторе равен $q_0$, тока в цепи нет, то для $A_0$ можно записать:

Начальная фаза колебаний ($<\alpha >_0$) равна:

При $R >2\sqrt<\frac>$ изменение заряда не является колебаниями, разряд конденсатора называют апериодическим.

Сопротивление, при котором колебания превращаются в апериодический разряд конденсатора называется критическим ($R_k$). Величина $R_k$ определяют условием:

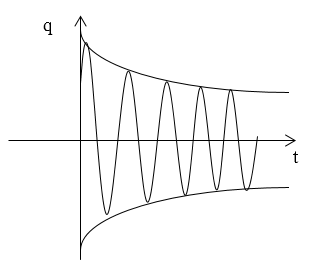
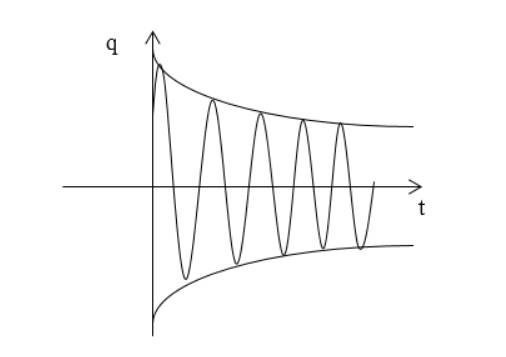
График функции (10) изображают как на рис.2.

Задание: Запишите закон убывания энергии, запасенной в контуре $(W(t))$, если $W(t=0)=W_0,$ колебания являются затухающими. Коэффициент затухания колебаний в контуре равен $\beta $. Собственная частота $<\omega >_0.\ $

Решение:

В качестве отправной точки для решения задачи используем уравнение изменения заряда на конденсаторе в $RLC$ -контуре в виде:

в выражении (1.1) мы предположили, что при $t=0,\ <<\alpha >‘>_0=0$. Используя выражение:

Найдем $I(t)$, получим:

Следовательно, электрическая энергия контура ($W_q$) имеет вид:

Магнитная энергия контура ($W_m$) равна:

Полная энергия равна:

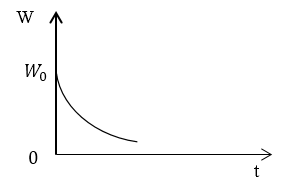
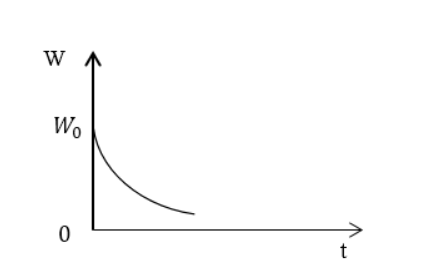
Задание: Используя результат Примера 1, запишите выражение для энергии, запасенной в контуре ($W(t)$), если колебания затухают в контуре очень медленно. Изобразите график убывания энергии запасенной в контуре.

Решение:

Если колебания в контуре затухают медленно, то это значит:

Следовательно, выражение для энергии, запасенной в контуре:

можно преобразовать к виду:

Ответ: $W\left(t\right)=W_0e^<\left(-2\beta t\right)>$. Энергия контура убывает по экспоненте.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 26 04 2021

Затухающие колебания в контуре и их уравнение

Существуют колебания в системе без источника энергии, называемые затухающими. Рассмотрим реальный контур с сопротивлением не равным нулю. Для примера используют контур с включенным сопротивлением R , с емкостью конденсатора C , с катушкой индуктивности L , изображенный на рисунке 1 . Колебания, происходящие в нем, — затухающие.

Именно наличие сопротивления становится главной причиной их затухания. Данный процесс возможен посредствам потерь энергии на выделение джоулева тепла. Аналог сопротивления в механике – действие сил трения.

Характеристики затухающих колебаний

Затухающие колебания характеризуют коэффициентом затухания β . Применив второй закон Ньютона, получим:

m a = — k x — y v , d 2 x d t 2 + r m d x d t + k m x = 0 , ω 0 2 = k m , β = r 2 m .

Из записи видно, что β действительно является характеристикой контура. Реже вместо β применяют декремент затухания δ ,

Значение a ( t ) является амплитудой заряда, силы тока и так далее, δ равняется количеству колебаний, а N e — период времени уменьшения амплитуды в e раз.

Для R L C контура применима формула с ω частотой.

При небольшой δ ≪ 1 говорят, что β ≪ ω 0 ω 0 = 1 L C — собственная частота, отсюда ω ≈ ω 0 .

При рассмотрении затухающих колебаний последовательного контура колебательный контур характеризуется добротностью Q :

Q = 1 R L C = ω 0 L R , где R , L и C — сопротивление, индуктивность, емкость, а ω 0 — частота резонанса. Выражение L C называют характеристическим или волновым сопротивлением. Для параллельного контура формула примет вид:

Q = R L C = R ω 0 L .

R является входным сопротивлением параллельного контура.

Эквивалентное определение добротности применяется при слабых затуханиях. Его выражают через отношение энергий:

Q = ω 0 W P d = 2 π f 0 W P d , называемое общей формулой.

Уравнения затухающих колебаний

Рассмотрим рисунок 1 . Изменение заряда q на конденсаторе в таком контуре описывается дифференциальным уравнением:

q ( t ) = q 0 e ( — β t ) cos ω t + a ‘ 0 = q 0 e — β t cos ( ω t ) .

Если t = 0 , то заряд конденсатора становится равным q 0 , и ток в цепи отсутствует.

Если R > 2 L C изменения заряда не относят к колебаниям, разряд называют апериодическим.

Значение сопротивления, при котором колебания превращаются в апериодический разряд конденсатора, критическое R k .

Функция изображается аналогично рисунку 2 .

Записать закон убывания энергии, запасенной в контуре W ( t ) при W ( t = 0 ) = W 0 с затухающими колебаниями. Обозначить коэффициент затухания в контуре β , а собственную частоту — ω 0 .

Решение

Отправная точка решения – это применение формулы изменения заряда на конденсаторе в R L C — контуре:

q ( t ) = q 0 e ( — β t ) cos ω t + a ‘ 0 = q 0 e — β t cos ( ω t ) .

Предположим, что при t = 0 , a ‘ 0 = 0 . Тогда применим выражение

Для нахождения I ( t ) :

I ( t ) = — ω 0 q 0 e ( — 2 β t ) sin ( ω t + α ) , где t g α = β ω .

Очевидно, что электрическая энергия W q запишется как:

W q = q 2 2 C = q 0 2 2 C e ( — 2 β t ) cos 2 ( ω t ) = W 0 e ( — 2 β t ) cos 2 ( ω t ) .

Тогда значение магнитной энергии контура W m равняется:

W m = L 2 ω 0 2 q 0 2 e ( — 2 β t ) sin 2 ω t + a = W 0 e — 2 β t sin 2 ω t + a .

Запись полной энергии будет иметь вид:

W = W q + W m = W 0 e ( — 2 β t ) ( cos 2 ( ω t ) + sin 2 ( ω t + a ) ) = = W 0 e ( — 2 β t ) 1 + β ω 0 sin ( 2 ω t + α ) .

Где sin α = β ω 0 .

Ответ: W ( t ) = W 0 e ( — 2 β t ) 1 + β ω 0 sin ( 2 ω t + a ) .

Применив результат предыдущего примера, записать выражение для энергии, запасенной в контуре W ( t ) , при медленно затухающих колебаниях. Начертить график убывания энергии.

Решение

Если колебания в контуре затухают медленно, то:

Очевидно, выражение энергии, запасенной в контуре, вычислим из

W ( t ) = W 0 e ( — 2 β t ) 1 + β ω 0 sin ( 2 ω t + a ) , предварительно преобразовав до W ( t ) = W 0 e ( — 2 β t ) .

Такое упрощение возможно по причине выполнения условия β ω 0 ≪ 1 , sin ( 2 ω t + a ) ≤ 1 , что означает β ω 0 sin ( 2 ω t + a ) ≪ 1 .

Ответ: W ( t ) = W 0 e ( — 2 β t ) . Энергия в контуре убывает по экспоненте.

III. ЗАТУХАЮЩИЕ КОЛЕБАНИЯ В ЭЛЕКТРИЧЕСКОМ КОЛЕБАТЕЛЬНОМ КОНТУРЕ

Затухающие электромагнитные колебания возникают при разряде конденсатора в электрическом контуре, содержащем индуктивность , и активное сопротивление . Электрический колебательный контур изображён на рис. 4.

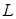
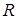
Для данного колебательного контура второе уравнение Кирхгоффа запишется:

(17)

где — падение напряжения на активном сопротивлении, падение напряжения на конденсаторе, — ЭДС самоиндукции, возникающая в катушке индуктивности.

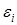
Очевидно, возникающий в цепи электрический ток, связан с разрядом конденсатора соотношением:

, . (18)

С учетом (18) уравнение (17) запишется:

. (19)

Если ввести обозначение и , уравнение (19) совпадает с уравнением(1) -дифференциальным уравнением затухающих колебаний:

. (20)

Следовательно, изменение заряда на пластинах конденсатора будет происходить по закону:

, (21)

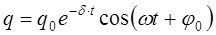
где q₀ — начальное значение заряда на конденсаторе.

Так как напряжение на конденсаторе связано с зарядом, то

. (22)

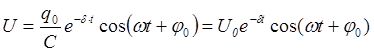
Кривую зависимости U(t) можно наблюдать при помощи электронного осциллографа.

Учитывая определение силы тока (18), зависимость переменного, возникающего в цепи, тока от временизапишется:

, (23)

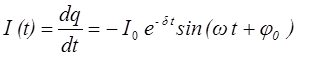
где — начальная амплитуда силы тока.

Уравнения (21), (22) и (23) называются уравнениями электромагнитных колебаний.

Из выражений (8) ,(19) и (20) следует, что период затухающих колебаний в зависимости от параметров колебательной системы определится:

(24)

Период незатухающих (гармонических) колебаний тоже зависит от параметров колебательной системы:

(25)

Как следует из формул (24) и (25), T отличается от T₀ тем сильнее, чем больше величина δ (при δ 0, а I(t) = I₀(t=0) – δ t в процессе колебаний уменьшается за счет выделения теплоты на активном сопротивлении колебательного контураR. Амплитуда затухающих колебаний уменьшается со временем тем быстрее, чем больше коэффициент затухания δ.

Из определения добротности колебательной системы (11) и зависимости коэффициента затухания и собственной частоты колебаний от параметров колебательного контура, получим выражение для добротности колебательного контура .

. (28)

Добротность электрического колебательного контура равна отношению волнового сопротивления контура к его электрическому сопротивлению R.