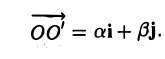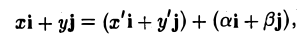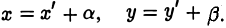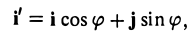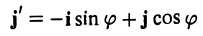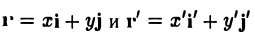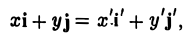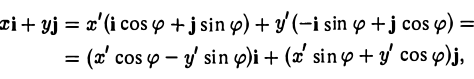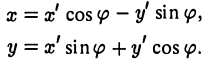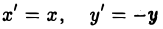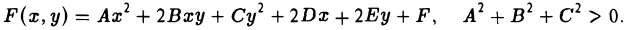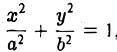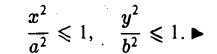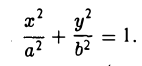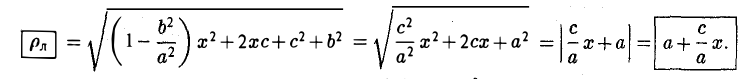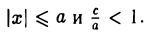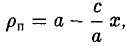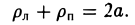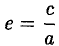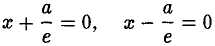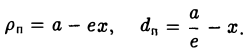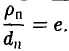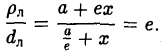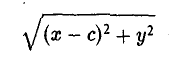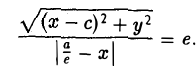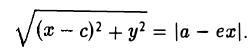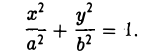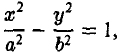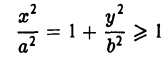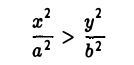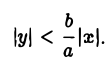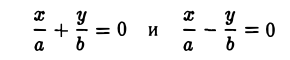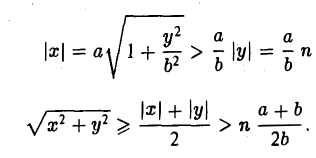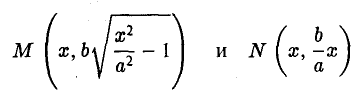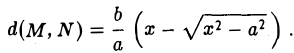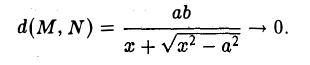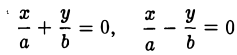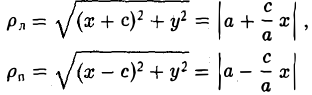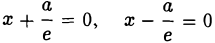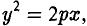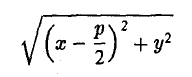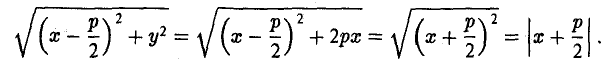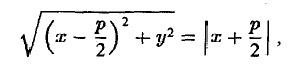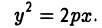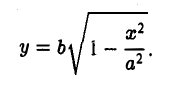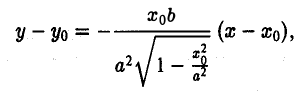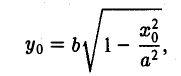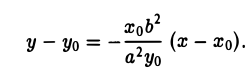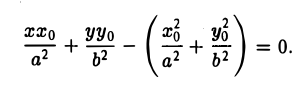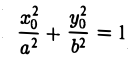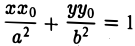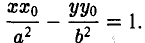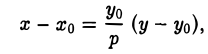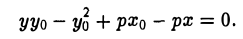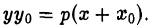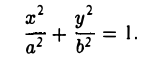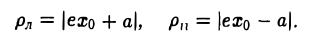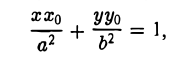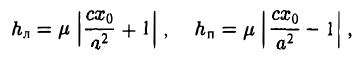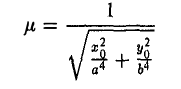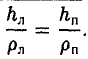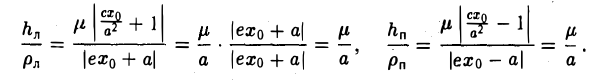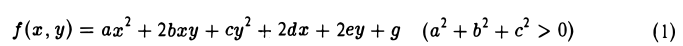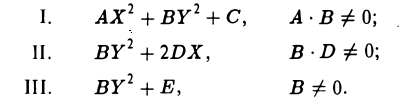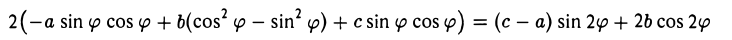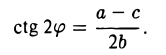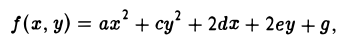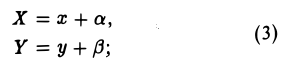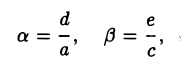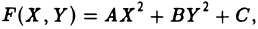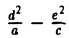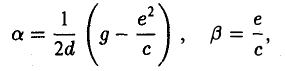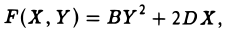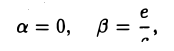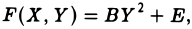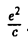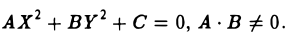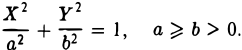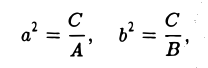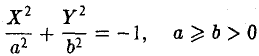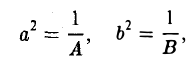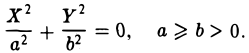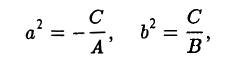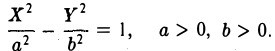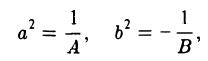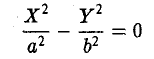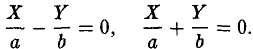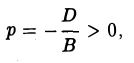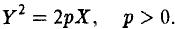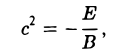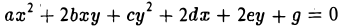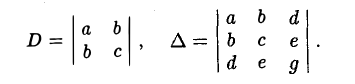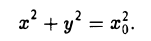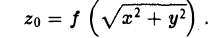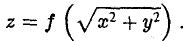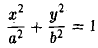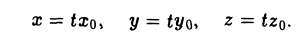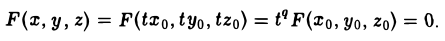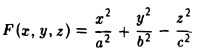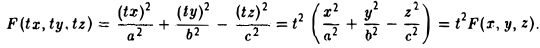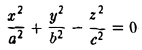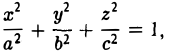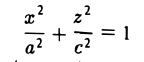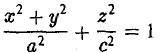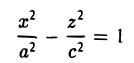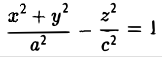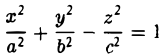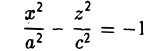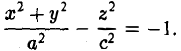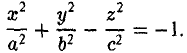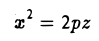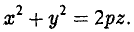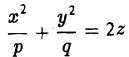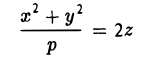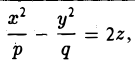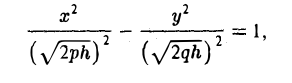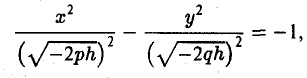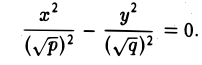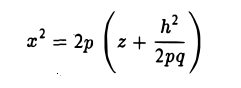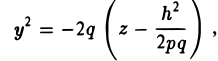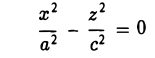Уравнение зеркального отражения на плоскости

Законы отражения света

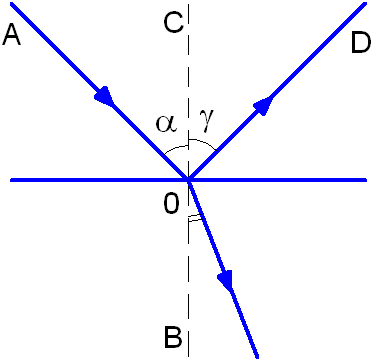
На границе раздела двух различных сред, если эта граница раздела значительно превышает длину волны, происходит изменение направления распространения света: часть световой энергии возвращается в первую среду, то есть отражается, а часть проникает во вторую среду и при этом преломляется. Луч АО носит название падающий луч, а луч OD – отраженный луч (см. рис. 1.3). Взаимное расположение этих лучей определяют законы отражения и преломления света.

Рис. 1.3. Отражение и преломление света.

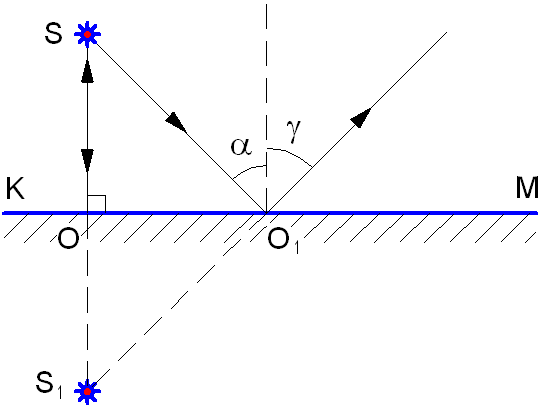
Угол α между падающим лучом и перпендикуляром к границе раздела, восстановленным к поверхности в точке падения луча, носит название угол падения.

Угол γ между отражённым лучом и тем же перпендикуляром, носит название угол отражения.

Каждая среда в определённой степени (то есть по своему) отражает и поглощает световое излучение. Величина, которая характеризует отражательную способность поверхности вещества, называется коэффициент отражения. Коэффициент отражения показывает, какую часть принесённой излучением на поверхность тела энергии составляет энергия, унесённая от этой поверхности отражённым излучением. Этот коэффициент зависит от многих причин, например, от состава излучения и от угла падения. Свет полностью отражается от тонкой плёнки серебра или жидкой ртути, нанесённой на лист стекла.

Законы отражения света

Законы отражения света были найдены экспериментально ещё в 3 веке до нашей эры древнегреческим учёным Евклидом. Также эти законы могут быть получены как следствие принципа Гюйгенса, согласно которому каждая точка среды, до которой дошло возмущение, является источником вторичных волн. Волновая поверхность (фронт волны) в следующий момент представляет собой касательную поверхность ко всем вторичным волнам. Принцип Гюйгенса является чисто геометрическим.

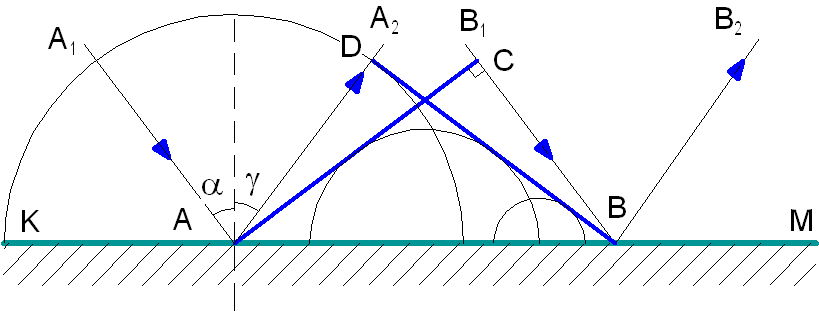
На гладкую отражательную поверхность КМ (рис. 1.4) падает плоская волна, то есть волна, волновые поверхности которой представляют собой полоски.

Рис. 1.4. Построение Гюйгенса.

А₁А и В₁В – лучи падающей волны, АС – волновая поверхность этой волны (или фронт волны).

Пока фронт волны из точки С переместится за время t в точку В, из точки А распространится вторичная волна по полусфере на расстояние AD = CB, так как AD = vt и CB = vt, где v – скорость распространения волны.

Волновая поверхность отражённой волны – это прямая BD, касательная к полусферам. Дальше волновая поверхность будет двигаться параллельно самой себе по направлению отражённых лучей АА₂ и ВВ₂.

Прямоугольные треугольники ΔАСВ и ΔADB имеют общую гипотенузу АВ и равные катеты AD = CB. Следовательно, они равны.

Углы САВ = = α и DBA = = γ равны, потому что это углы со взаимно перпендикулярными сторонами. А из равенства треугольников следует, что α = γ .

Из построения Гюйгенса также следует, что падающий и отражённый лучи лежат в одной плоскости с перпендикуляром к поверхности, восстановленным в точке падения луча.

Законы отражения справедливы при обратном направлении хода световых лучей. В следствие обратимости хода световых лучей имеем, что луч, распространяющийся по пути отражённого, отражается по пути падающего.

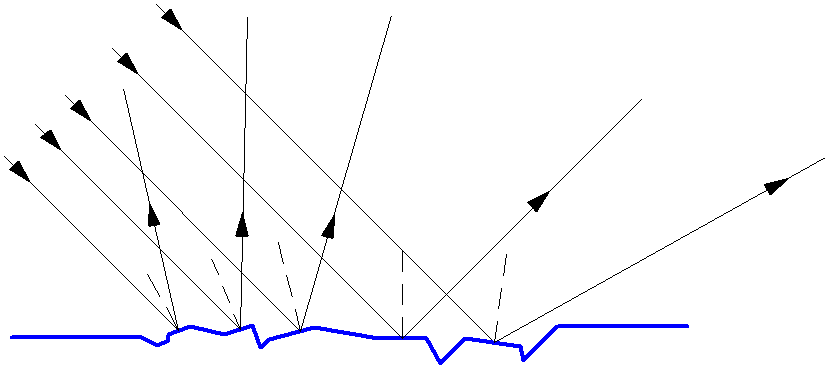
Большинство тел лишь отражают падающее на них излучение, не являясь при этом источником света. Освещённые предметы видны со всех сторон, так как от их поверхности свет отражается в разных направлениях, рассеиваясь. Это явление называется диффузное отражение или рассеянное отражение. Диффузное отражение света (рис. 1.5) происходит от всех шероховатых поверхностей. Для определения хода отражённого луча такой поверхности в точке падения луча проводится плоскость, касательная к поверхности, и по отношению к этой плоскости строятся углы падения и отражения.

Рис. 1.5. Диффузное отражение света.

Например, 85% белого света отражается от поверхности снега, 75% — от белой бумаги, 0,5% — от чёрного бархата. Диффузное отражение света не вызывает неприятных ощущений в глазу человека, в отличие от зеркального.

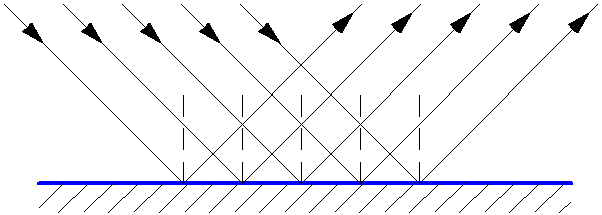
Зеркальное отражение света – это когда падающие на гладкую поверхность под определённым углом лучи света отражаются преимущественно в одном направлении (рис. 1.6). Отражающая поверхность в этом случае называется зеркало (или зеркальная поверхность). Зеркальные поверхности можно считать оптически гладкими, если размеры неровностей и неоднородностей на них не превышают длины световой волны (меньше 1 мкм). Для таких поверхностей выполняется закон отражения света.

Рис. 1.6. Зеркальное отражение света.

Плоское зеркало – это зеркало, отражающая поверхность которого представляет собой плоскость. Плоское зеркало даёт возможность видеть предметы, находящиеся перед ним, причём эти предметы кажутся расположенными за зеркальной плоскостью. В геометрической оптике каждая точка источника света S считается центром расходящегося пучка лучей (рис. 1.7). Такой пучок лучей называется гомоцентрическим. Изображением точки S в оптическом устройстве называется центр S’ гомоцентрического отражённого и преломлённого пучка лучей в различных средах. Если свет, рассеянный поверхностями различных тел, попадает на плоское зеркало, а затем, отражаясь от него, падает в глаз наблюдателя, то в зеркале видны изображения этих тел.

Рис. 1.7. Изображение, возникающее с помощью плоского зеркала.

Изображение S’ называется действительным, если в точке S’ пересекаются сами отражённые (преломлённые) лучи пучка. Изображение S’ называется мнимым, если в ней пересекаются не сами отражённые (преломлённые) лучи, а их продолжения. Световая энергия в эту точку не поступает. На рис. 1.7 представлено изображение светящейся точки S, возникающее с помощью плоского зеркала.

Луч SO падает на зеркало КМ под углом 0°, следовательно, угол отражения равен 0°, и данный луч после отражения идёт по пути OS. Из всего множества попадающих из точки S лучей на плоское зеркало выделим луч SO₁.

Луч SO₁ падает на зеркало под углом α и отражается под углом γ ( α = γ ). Если продолжить отражённые лучи за зеркало, то они сойдутся в точке S₁, которая является мнимым изображением точки S в плоском зеркале. Таким образом, человеку кажется, что лучи выходят из точки S₁, хотя на самом деле лучей, выходящих их этой точки и попадающих в глаз, не существует. Изображение точки S₁расположено симметрично самой светящейся точке S относительно зеркала КМ. Докажем это.

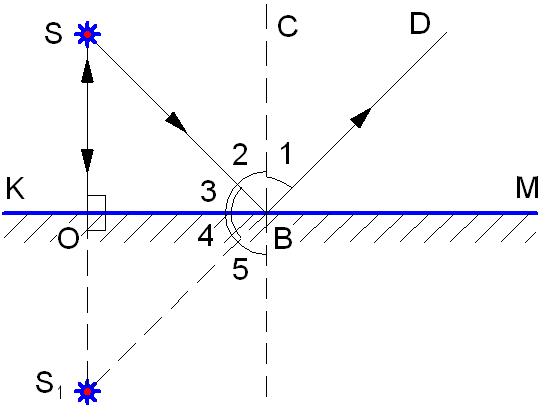
Луч SB, падающий на зеркало под углом 2 (рис. 1.8), согласно закону отражения света отражается под углом 1 = 2.

Рис. 1.8. Отражение от плоского зеркала.

Из рис. 1.8 видно, что углы 1 и 5 равны – как вертикальные. Суммы углов 2 + 3 = 5 + 4 = 90°. Следовательно, углы 3 = 4 и 2 = 5.

Прямоугольные треугольники ΔSOB и ΔS₁OB имеют общий катет ОВ и равные острые углы 3 и 4, следовательно, эти треугольники равны по стороне и двум прилежащим к катету углам. Это означает, что SO = OS₁, то есть точка S₁ расположена симметрично точке S относительно зеркала.

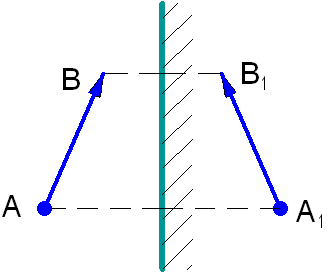
Для того чтобы найти изображение предмета АВ в плоском зеркале, достаточно опустить перпендикуляры из крайних точек предмета на зеркало и, продолжив их за пределы зеркала, отложить за ним расстояние, равное расстоянию от зеркала до крайней точки предмета (рис. 1.9). Это изображение будет мнимым и в натуральную величину. Размеры и взаимное расположение предметов сохраняются, но при этом в зеркале левая и правая стороны у изображения меняются местами по сравнению с самим предметом. Параллельность падающих на плоское зеркало световых лучей после отражения также не нарушается.

Рис. 1.9. Изображение предмета в плоском зеркале.

В технике часто применяют зеркала со сложной кривой отражающей поверхностью, например, сферические зеркала. Сферическое зеркало – это поверхность тела, имеющая форму сферического сегмента и зеркально отражающая свет. Параллельность лучей при отражении от таких поверхностей нарушается. Зеркало называют вогнутым, если лучи отражаются от внутренней поверхности сферического сегмента. Параллельные световые лучи после отражения от такой поверхности собираются в одну точку, поэтому вогнутое зеркало называют собирающим. Если лучи отражаются от наружной поверхности зеркала, то оно будет выпуклым. Параллельные световые лучи рассеиваются в разные стороны, поэтому выпуклое зеркало называют рассеивающим.

Кривые и поверхности второго порядка в математике с примерами решения и образцами выполнения

Кривая второго порядка — геометрическое место точек плоскости, прямоугольные координаты которых удовлетворяют уравнению вида.

Кривые второго порядка используются при решении задач по аналитической геометрии, кривые других порядков используются при решении задач математического анализа в разделе вычисления кратных, криволинейных и поверхностных интегралов.

Кривые и поверхности второго порядка

Преобразование координат на плоскости

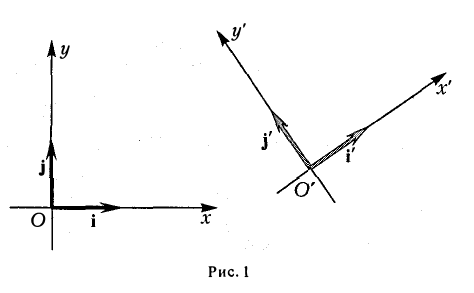
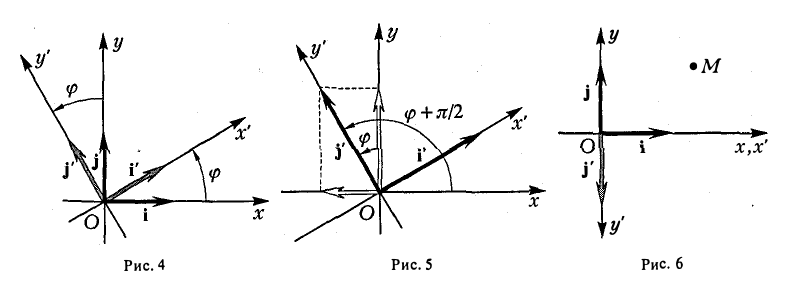
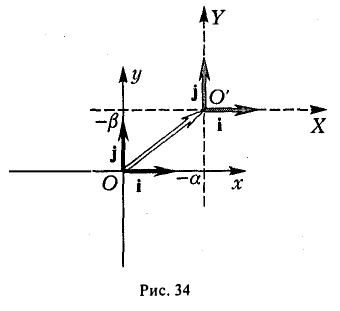
Пусть на плоскости заданы две прямоугольные декартовы системы координат, Оху и О’х’у’ (рис. 1). Произвольная точка М относительно одной из этих координатных систем определяется парой чисел х и у, а относительно другой — парой чисел x’ и у’. Ясно, что между парами (х,у) и (x’, у’) имеется связь. Найдем ее.

Параллельный перенос

Предположим, что соответствующие координатные оси параллельны и сонаправлены, а точки начала отсчета различны. Это означает, что орты координатных осей соответственно равны (рис. 2).

Пусть г и г’ — радиусы-векторы точки М, т.е.

и а, β — координаты точки О’ относительно системы координат Оху, т. е.

Поворот

Предположим, что координатные оси одной системы координат получаются из координатных осей другой системы поворотом на угол φ, а начальные точки совпадают (рис.4). Координатами единичного вектора i’ являются косинусы углов φ и 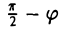, образованных этим вектором с осями Ох и Оу:

а координатами единичного вектора j’ служат косинусы углов 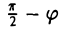и φ:

(рис. 5). Так как радиус-векторы

произвольной точки М в рассматриваемом случае равны,

то, заменяя векторы i’ и j’ их выражениями, получаем, что

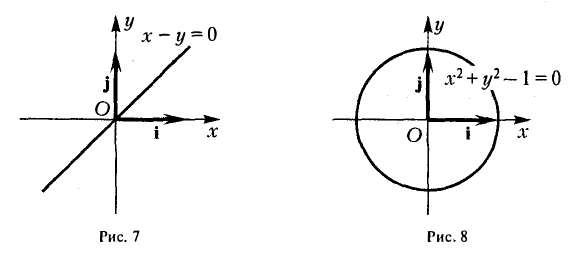
Зеркальное отражение

В случае, когда оси абсцисс Ох и Ох’ координатных систем совпадают, а оси ординат Оу и Оу’ направлены противоположно, координаты (х, у) и (х’,у’) произвольной точки М связаны равенствами

Справедливо следующее утверждение.

Любое преобразование прямоугольных декартовых координат (с сохранением масштаба) можно представить в виде последовательного выполнения переноса, поворота и <если необходимо) зеркального отражения.

Кривые второго порядка

Пусть на плоскости задана прямоугольная декартова система координат Оху. Множество точек плоскости, координаты х и у которых удовлетворяют равенству

F(x, у) = 0,

где F(x, у) — некоторая функция двух переменных, называется плоской кривой, или плоской линией само равенство называется уравнением данной линии (кривой).

Например, равенство х — у = 0 есть уравнение прямой — биссектрисы первого и третьего координатных углов (рис. 7). Равенство x 2 + y 2 — 1 = 0 — уравнение окружности единичного радиуса с центром в начале координат (рис. 8).

Рассмотрим многочлен второй степени от двух переменных х и у:

F(x,y) = 0

будем называть уравнением линии (кривой) второго порядка.

Если линиями первого порядка являются именно прямые и только они, то множество кривых второго порядка заметно разнообразней. Поэтому исследованию общего уравнения кривой второго порядка естественно предпослать изучение некоторых частных, но важных случаев.

Эллипс

Эллипсом называется кривая, уравнение которой в некоторой прямоугольной декартовой системе координат Оху имеет вид (1)

Система координат Оху, в которой уравнение эллипса имеет вид (1), называется канонической (для данного эллипса); само уравнение (!) называется каноническим уравнением эллипса. Окружность

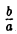
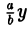
является частным случаем эллипса (при а = b). Это позволяет несложным способом определить форму эллипса: эллипс (1) получается из окружности (2) путем ее равномерного сжатия» к оси Ох (с коэффициентом), т.е. заменой в уравнении x 2 + y 2 = a 2 координаты у на (рис.9).

Свойства эллипса

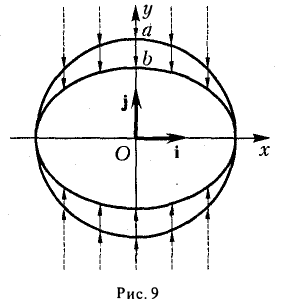
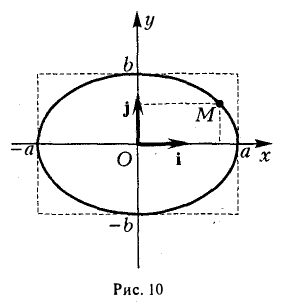
1. Эллипс (I) содержится в прямоугольнике

В этом легко убедиться, заметив, что, если точка М(х, у) принадлежит эллипсу (1), то (рис. 10)

Точки (±а, 0), (0, ±b) называются вершинами эллипса.

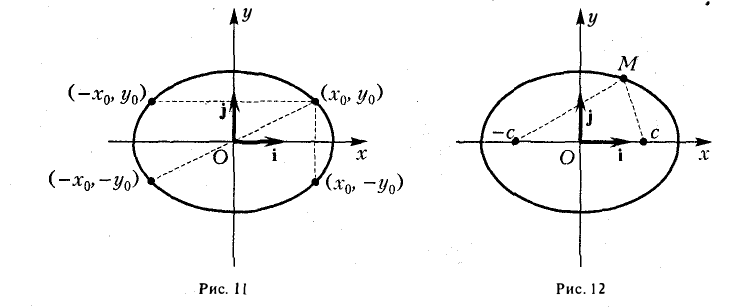
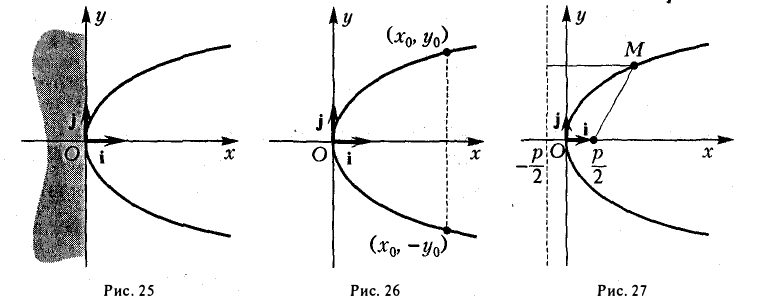
2. Координатные оси Ох и Оу канонической системы являются осями симметрии эллипса, а начало координат О — его центром симметрии. Это означает, что если точка Мо(хo, yо) принадлежит эллипсу, то точки (-хо, yо), (-xо, -yо) и (хо, -yо) также ему принадлежат (рис. 11).

3. Если эллипс не является окружностью, то координатные оси канонической системы — единственные оси симметрии.

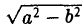
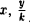
Положим с = . Ясно, что с 0 называется преобразование, переводящее произвольную точку М(х, у) окружности в точку М’ ().

Пусть сначала М(х, у) — произвольная точка эллипса

Вычислим ее расстояния от фокусов эллипса (рис. 12). Имеем

Заменяя y 2 его выражением

после несложных преобразований получаем, что

Последнее равенство вытекает из того, что

Легко убедиться в том, что

Доказательство того, что точки, обладающие указанным свойством, принадлежат эллипсу, было проведено ранее (см. раздел «Простейшие задачи аналитической геометрии» Введения, задача 2).

называется эксцентриситетом эллипса (I). Ясно, что 0

называются директрисами эллипса. У каждого эллипса две директрисы — левая и правая (рис. 13).

5. Эллипс есть множество точек плоскости, отношение расстояний от которых до данной точки (фокуса эллипса) и доданной прямой (одноименной с фокусом директрисы эллипса) постоянно (равно эксцентриситету эллипса).

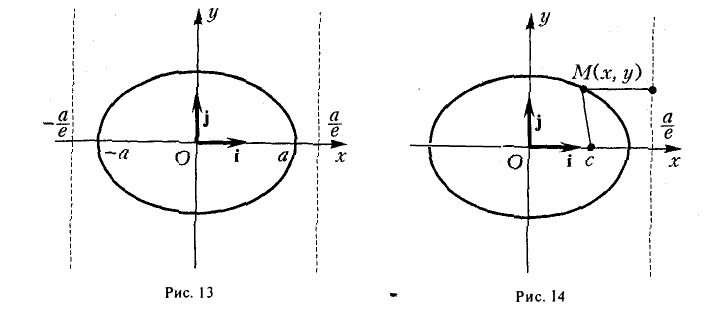
Пусть сначала М(х,у) — произвольная точка эллипса (1). Вычислим расстояния от нее до правого фокуса и до правой директрисы (рис. 14). Имеем соответственно

Откуда легко получаем требуемое

Аналогично проверяется, что

Рассмотрим теперь на плоскости точку (с, 0) и прямую х =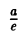(с = ае). Возьмем произвольную точку М(х, у) и вычислим расстояния от нее до выбранной точки (с, 0) —

— и до выбранной прямой —

Возведем обе части последнего соотношения в квадрат и, положив 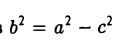и учтя равенство с = ае, после простых преобразований получим

Тем самым, точка М(х,у) лежит на эллипсе (1).

Гипербола

Гиперболой называется кривая, уравнение которой в некоторой прямоугольной системе координат Оху имеет вид (1)

Система координат Оху, в которой уравнение гиперболы имеет вид (1), называется канонической (для данной гиперболы); само уравнение (1) называется каноническим уравнением гиперболы.

Свойства гиперболы

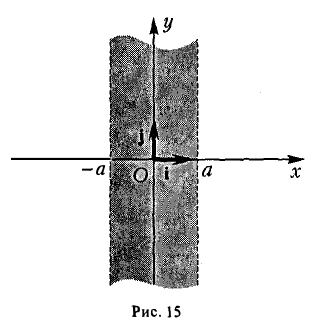
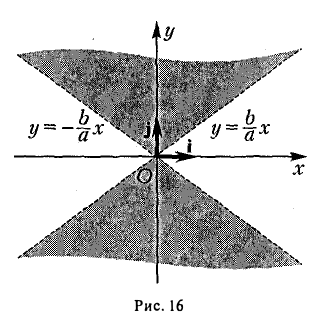
1. Гипербола (1) лежит вне полосы |x|

и, значит, |x| ≥ а (рис. 15).

Точки (±а, 0) называются вершинами гиперболы.

2. Гипербола (1) лежит в вертикальных углах, образованных прямыми у = ±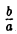х и содержащих точки оси Ох (рис. 16).

вытекает, что если точка М(х, у) лежит на гиперболе (1), то

Таким образом, гипербола состоит из двух частей — ветвей гиперболы, левой и правой. Прямые

называются асимптотами гиперболы.

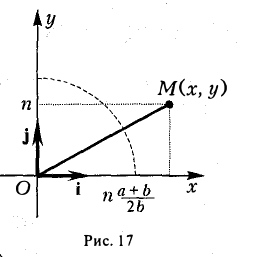
3, На гиперболе лежат точки, сколь угодно далекие от начала координат O(0, 0).

Пусть, например, точка М(х, у) лежит на гиперболе (1) и \у\ = n, где n — произвольное положительное число (рис. 17).

Возьмем в первой четверти две точки: точку гиперболы (1) и точку ее асимптоты 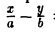= 0 с одинаковой абсциссой х > а —

соответственно — и вычислим расстояние между ними. Имеем

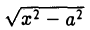
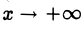
Умножив и разделив полученное выражение на сумму х +и перейдя затем к пределу при получим

Тем самым, установлен следующий факт.

4. Если текущая точка асимптоты неограниченно удаляется от начала координат, т.е. \х\ —» + ∞, то на гиперболе можно указать соответствующую ей точку так, чтобы расстояние между ними стремилось к нулю (рис. 18).

Верно и обратное.

стремится к нулю.

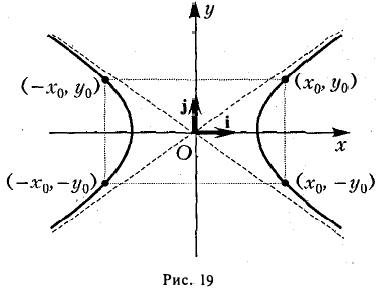
6. Оси канонической координатной системы являются осями симметрии гиперболы, а начало координат — ее центром симметрии (рис. 19).

Координатные оси канонической системы — единственные оси симметрии гиперболы.

Положим с = 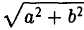. Ясно, что с > 0. .Точки (-с, 0) и (с, 0) называются фокусами гиперболы, 2с — фокусное расстояние.

Гипербола есть множество точек, абсолютная величина разности расстояний от которых до двух данных точек (фокусов гиперболы) постоянна (равна заданному числу).

Доказательство этого свойства проводится так же, как и доказательство свойства 4 эллипса. Покажем, например, что каждая точка гиперболы обладает указанным свойством. Если М(х, у) — точка гиперболы (1), то расстояния от нее до фокусов соответственно равны

(рис. 20). Так как 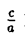> 1, то

Отсюда нетрудно вычислить, что

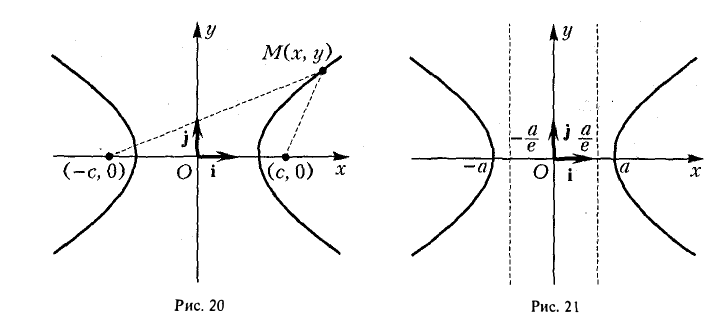
называется эксцентриситетом гиперболы (1). Ясно, что е > 1. Прямые

называются директрисами гиперболы (рис. 21). У каждой гиперболы две директрисы — левая и правая.

Практически также, как и для эллипса, доказывается следующий факт.

8. Гипербола есть множество точек, отношение расстояний от которых до данной точки (фокуса гиперболы) и доданной прямой (одноименной с фокусом директрисы) постоянно (равно эксцентриситету гиперболы) (рис. 22).
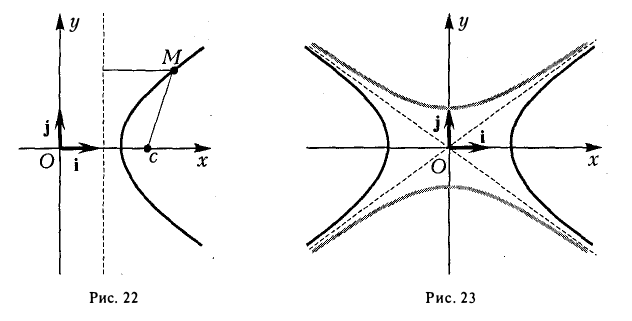
Гипербола (2)

называется сопряженной гиперболе (1). Взаимное расположение гипербол (1) и (2) указано на рис. 23.

Парабола

Параболой называется кривая, уравнение которой в некоторой прямоугольной декартовой системе координат Оху имеет вид (1)

Система координат Оху, в которой уравнение параболы имеет вид (1), называется канонической (для данной параболы); уравнение (]) называется каноническим уравнением параболы.

Свойства параболы

1. Все точки параболы лежат в правой полуплоскости: х ≥ 0 (рис. 25). Точка 0(0, 0) лежит на параболе и называется ее вершиной.
2. На параболе лежат точки, сколь угодно далеко расположенные от начала координат О(0, 0).
3. Ось абсцисс канонической координатной системы является (единственной) осью симметрии параболы (рис. 26).

Ось симметрии параболы называется осью параболы. Число р называется фокальным параметром параболы; точка (; 0) — фокус параболы; прямая х = — директриса параболы.

4. Парабола есть множество точек, равноудаленных отданной точки (фокуса параболы) и от данной прямой (директрисы параболы) (рис. 27).

Пусть точка М(х, у) лежит на параболе (1). Вычислим расстояния от нее до фокуса (;0)

и до директрисы х = —

Заменяя у 2 его выражением 2рх, легко убеждаемся в том, что

Верно и обратное. Если для некоторой точки М(х, у) расстояния от нее до точки (; 0) и до прямой х = — равны —

то, возводя в квадрат, после простых преобразований получаем, что эта точка лежит на параболе:

Оптическое свойство кривых второго порядка

Касательные к эллипсу и гиперболе

Если кривая задана уравнением

y = f(x)

то уравнение касательной к ней, проходящей через точку (хо,у0)> где Уо = f(xо), можно записать в следующем виде

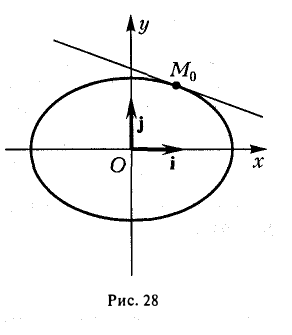
Пусть Мо(хо, yо) — точка эллипса

Предположим для определенности, что точка М0 лежит в первой четверти, т. е. хо > 0, yо > 0. Тогда часть эллипса, лежащую в первой четверти, можно описать уравнением

Пользуясь формулой (1), получаем уравнение касательной к эллипсу в точке Мо

а так как точка (х0, у о) лежит на эллипсе, то

Полученное соотношение после несложных преобразований можно записать так:

Отсюда с учетом тождества

приходим к уравнению

(рис. 28). Полученное соотношение является уравнением касательной к эллипсу, проходящей через его точку (х0, yо), и в общем случае ее произвольного расположения, т. е. при любых знаках хо и уо.

Уравнение касательной к гиперболе выводится аналогично и имеет следующий вид

Подчеркнем, что точка (хо, yо) лежит на гиперболе.

Касательные к параболе

Если кривая задана уравнением

х = g(у),

то уравнение касательной к ней, проходящей через точку (хo,уo), где х0 = g (уо), можно записать в следующем виде

Пусть М0(х0, у0) — точка параболы. Пользуясь формулой (I), получаем уравнение касательной к параболе

Отсюда в силу равенства 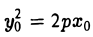приходим к уравнению касательной вида

Замечание:

Сопоставляя канонические уравнения эллипса, гиперболы и параболы с уравнениями касательных к этим кривым, нетрудно заметить, что для получения последних не требуется специальных вычислений. В самом деле, заменяя у 2 на уу ₀ , а х 2 на хх ₀ (в случае параболы 2х нужно заменить на x + х ₀ ). приходим к уравнению соответствующей касательной. Еще раз отметим, что сказанное справедливо лишь в том случае, когда точка (x ₀ . y ₀ ) лежит на кривой.

Оптическое свойство эллипса

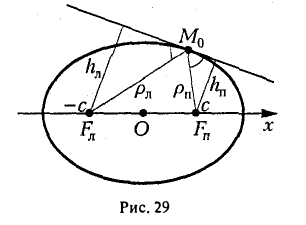
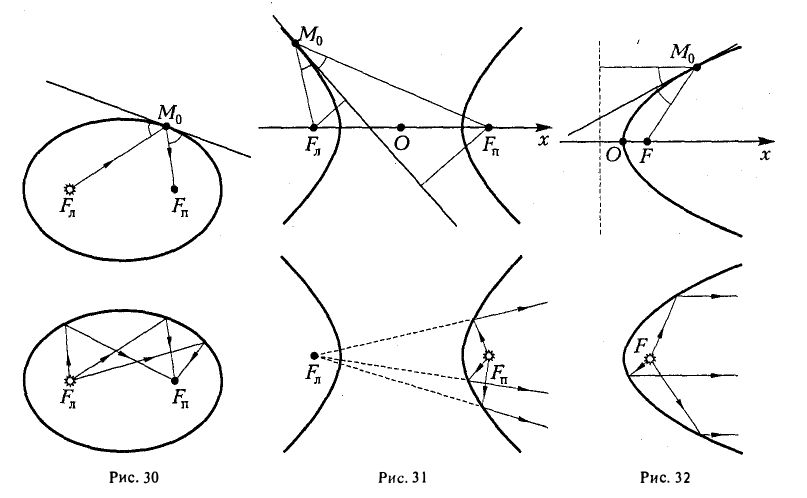
Пусть М ₀ — произвольная точка эллипса

Как уже отмечалось, расстояния от нее до фокусов F_л и F _n — фокальные радиусы — равны соответственно

Проведем через точку М ₀ касательную к эллипсу,

и вычислим, на каком расстоянии от этой касательной лежат фокусы F_л (-c, 0) и F_n (c; 0) (напомним, что для этого следует воспользоваться формулой (10).

— нормирующий множитель (рис. 29). Нетрудно проверить, что

Обратившись к рис.29, заметим, что вычисленные отношения равны синусам углов, образованных касательной и фокальными радиусами точки касания. Из того, что синусы этих углов равны, вытекает равенство и самих углов. Тем самым доказано оптическое свойство эллипса: касательная к эллипсу образует равные углы с фокальными радиусами точки касания.

Это свойство называется оптическим по следующей причине: если поместить в один из фокусов эллипса с зеркальной «поверхностью» точечный источник света, то все лучи после отражения от «поверхности» эллипса сойдутся в другом его фокусе (рис. 30).

Оптическое свойство гиперболы

Устанавливается аналогичными выкладками и заключается в следующем.

Если поместить в один из фокусов гиперболы точечный источник света, то каждый луч после отражения от зеркальной «поверхности» гиперболы видится исходящим из другого фокуса (рис. 31).

Оптическое свойство параболы

Если в фокус параболы помещен точечный источник света, то все лучи, отраженные от зеркальной «поверхности» параболы, будут направлены параллельно оси параболы (рис. 32).

Классификация кривых второго порядка

Многочлены второй степени на плоскости

Теорема:

Пусть на плоскости введена прямоугольная декартова система координат Оху и пусть

— многочлен второй степени от переменных х и у.

Тогда на плоскости можно построить прямоугольную дека ртов у систему координат O’XY так, что после замены переменных х и у на переменные X и Y исходный многочлен f(x, у) приведется к многочлену F(X, Y) одного из следующих трех видов:

1-й шаг. Поворотом координатных осей на подходящим образом выбранный угол всегда можно добиться того, чтобы коэффициент при произведении разноименных координат обратился в нуль.

Пусть b ≠ 0 (при 6 = 0 этот шаг не нужен). Повернем оси координат вокруг точки О. Эта операция описывается следующими формулами

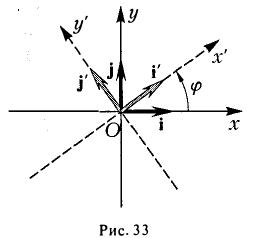
При этом координатные оси исходной системы Оху поворачиваются на угол φ (рис.33).

Заменим переменные х и у в формуле (1) их выражениями (2) через x’ и у’ и вычислим коэффициент 2b’ при произведении х’у’. Он равен

и обращается в нуль, если

Так как полученное уравнение разрешимо относительно φ, то указанным преобразованием всегда можно добиться обращения в нуль нужного коэффициента.

Приступая ко второму этапу преобразования, будем считать, что исходный многочлен f(x,у) уже имеет вид

где а 2 + с 2 >0. Для определенности положим с ≠ 0 (это не ограничивает общности наших рассуждений, так как заменой х, у в случае необходимости этого всегда можно добиться).

2-й шаг. Переносом начала координат можно достичь дальнейшего упрощения вида многочлена f(x,y). Эта операция описывается следующими формулами:

координатные оси новой системы O’XY получаются из координатных осей исходной системы Оху параллельным переносом в точку (-а, — β) (рис. 34).

Укажем конкретные значения а и β. Возможны три случая

I. а ≠ 0, с ≠ 0. Тогда, полагая

где А = а, В = с, С = g —

II. а = 0, d ≠ 0. Тогда, полагая

III. а = d = 0. Тогда, полагая

где В = с, Е = g —

Канонические уравнения кривых второго порядка

Если многочлен второй степени F(X, У) приравнять к нулю, то получим уравнение линии второго порядка

F(X, У) = 0.

Рассмотрим каждый из трех полученных выше случаев I, II, III отдельно.

I.

Э. А • В > 0. Домножением обеих частей уравнения на — 1 и заменой X на У, а У на X (в случае необходимости) всегда можно добиться того, чтобы В ≥ А > 0.

С

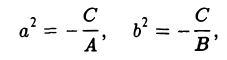
(мнимый эллипс)2). На действительной плоскости нет ни одной точки (X, Y), координаты которой обращали бы это уравнение в тождество.

Точка (0, 0) является единственной точкой плоскости, координаты которой удовлетворяют этому уравнению; точку (0,0) можно мыслить как действительную точку пересечения двух мнимых пересекающихся прямых 3).

Г. А • В 0, В

— пару пересекающихся прямых:

2) Название можно объяснить некоторым сходством этого уравнения с уравнением эллипса.
3) Название можно объяснить некоторым сходством этого уравнения с уравнением пары пересекающихся
прямых.

II. BY 2 + 2DX = О, В • D ≠ 0.

Всегда можно добиться того, чтобы В • D

III. BY 2 + Е = 0, В ≠ 0. Можно считать, что В > 0.

1. Е

Y 2 — с 2 = 0, с > 0

— пару параллельных прямых.

Y 2 — с 2 = 0, с 2 = 0

— пара совпадающих прямых.

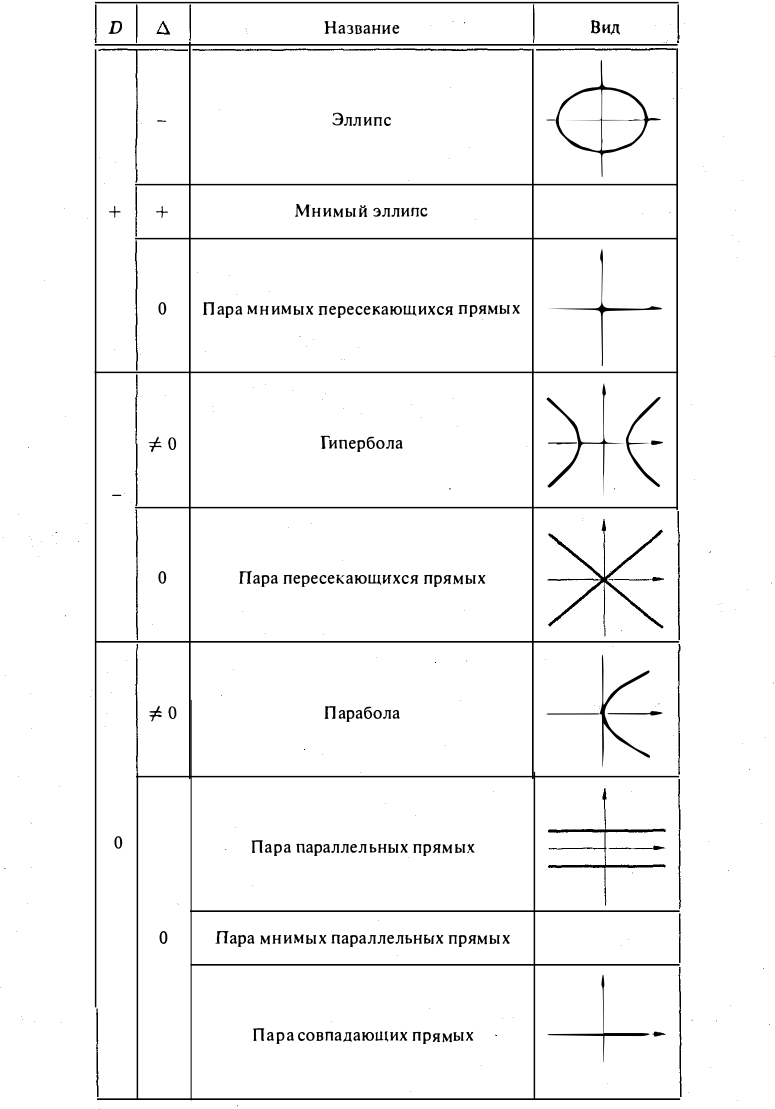
Чтобы определить тип кривой второго порядка, не обязательно проводить все указанные выше преобразования. Достаточно вычислить знаки некоторых выражений, составленных из коэффициентов уравнения.

— уравнение линии второго порядка. Введем следующие обозначения

Числа D и ∆ не зависят от выбора системы координат на плоскости и называются инвариантами. Из приводимой таблицы видно, какому сочетанию знаков определителей D и ∆ соответствует та или иная линия второго порядка.

Задача:

Убедитесь в том, что D и ∆ при рассмотренных преобразованиях системы координат действительно остаются неизменными.
4) Название можно объяснить некоторым сходством этого уравнения с уравнением пары параллельных прямых.

Поверхности второго порядка

Пусть в пространстве задана прямоугольная декартова система координат Oxyz. Множество точек пространства, координаты х, у и z которых удовлетворяют равенству

F(x, у, z) = О,

называется поверхностью; равенство (*) называется уравнением этой поверхности.

Пример:

— уравнение сферы радиуса о с центром в точке (0,0,0) (рис. 35).

Рассмотрим многочлен второй степени от трех переменных х, у и z

Уравнение

F(x, y, z) = 0

будем называть уравнением поверхности второго порядка.

Исследование общего уравнения поверхностей второго порядка оказывается зна-чительноболее сложным, чем исследование общего уравнения кривых второго порядка, требует разработки соответствующего математического аппарата и будет проведено в конце главы VI.

В оставшихся параграфах этой главы мы сначала остановимся на изучении геометрических свойств некоторых важных классов общих поверхностей; затем используем их для рассмотрения канонических уравнений основных поверхностей второго порядка и исследования структуры этих поверхностей.

Некоторые классы поверхностей

Поверхности вращения

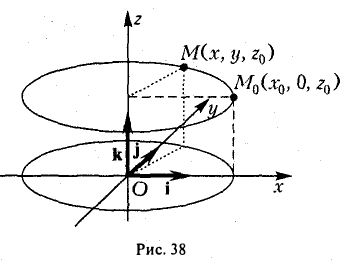
Рассмотрим на плоскости Oxz кривую γ, заданную уравнением

г = f(x), х ≥ 0

(рис. 36). При вращении кривой γ вокруг оси Oz она будет заметать некоторую поверхность, называемую поверхностью вращения (рис. 37). Найдем уравнение этой поверхности, т. е. равенство, которому должны удовлетворять координаты точек построенной поверхности и только они.

Тем самым, координаты х, у и z0 любой точки М этой окружности связаны следующим равенством

В силу произвольности выбора точки М0 на кривой γ искомое уравнение полученной поверхности вращения имеет вид

Цилиндрические поверхности

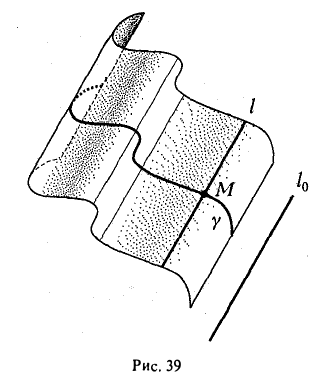
Через каждую точку некоторой заданной кривой γ проведем прямую l параллельно заданной прямой l0. Множество точек, лежащих на так построенных прямых, назовем цилиндрической поверхностью (рис. 39); кривая γ называется направляющей цилиндрической поверхности, а прямая l — ее образующей.

Найдем уравнение, описывающее цилиндрическую поверхность.

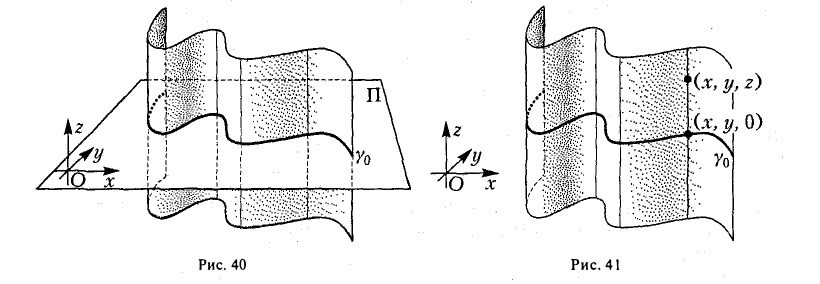
Возьмем произвольную точку О и проведем через нее плоскость П, перпендикулярную образующей I. Построим в пространстве прямоугольную координатную систему Oxyz, взяв за ось Oz прямую, перпендикулярную плоскости П. Тогда плоскость П будет координатной плоскостью Оху (рис.40). Плоскость П пересекает цилиндрическую поверхность по направляющей γ0.

F(x,y) = 0

— уравнение этой направляющей. Убедимся в том, что последнее соотношение можно считать уравнением искомой цилиндрической поверхности.

самом деле, пусть (х, у, z) — точка цилиндрической поверхности (рис. 41). Тогда точка (х, у, 0) лежит на γ0 и, значит, удовлетворяет уравнению

F(x,y)=0.

Но координаты точки (х, у, z) также обращают это уравнение в тождество. Последнее обстоятельство и позволяет считать соотношение F(x,y) = 0 искомым уравнением.

Пример:

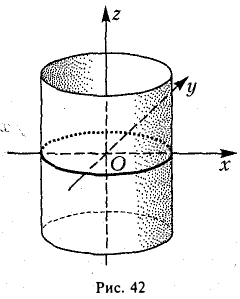
Введем в пространстве прямоугольные декартовы координаты Охуz. Соотношение

является уравнением цилиндрической поверхности (эллиптического цилиндра) (рис. 42).

Замечание:

F(y, z) = 0

описывает цилиндрическую поверхность с образующей, параллельной координатной оси Оx, а уравнение

F(x,z) = 0

— цилиндрическую поверхность с образующей, параллельной оси Oy.

Конические поверхности

Пусть γ — произвольная кривая и О — точка вне eе. Через каждую точку кривой γ и точку О проведем прямую l. Множество точек, лежащих на построенных таким образом прямых, называется конической поверхностью (рис.43); кривая γ — направляющая конической поверхности, l — ее образующая, точка О — вершина. Рассмотрим функцию

F (x, у, z)

переменных х, у и z. Функция F(x, у, z) называется однородной функцией степени q, если для любого t > 0 выполняется равенство

Покажем, что если F(x, у, z) однородная функция, то F
является уравнением конической поверхности.

В самом деле, пусть

т.е. точка М0(xo, уо, zо) лежит на этой поверхности. Будем считать, что 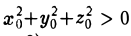. Проведем через эту точку и точку 0(0,0, 0) (считая, что F(0,0, 0) = 0) прямую I (рис. 44). Ее параметрические уравнения имеют вид

Подставляя полученные выражения для х, у и z в функцию F(x, у, z), видим, что

Это означает, что вся прямая l лежит на поверхности, определяемой уравнением F(x,y,z) = 0, которое, следовательно, и описывает коническую поверхность.

Пример:

является однородной функцией второй степени:

— уравнение конической поверхности (конуса второго порядка) (рис.45).

Воспользуемся теперь полученными выше результатами для исследования геометрической формы поверхностей второго порядка.

Эллипсоид. Гиперболоиды. Параболоиды. Цилиндры и конус второго порядка

Эллипсоид

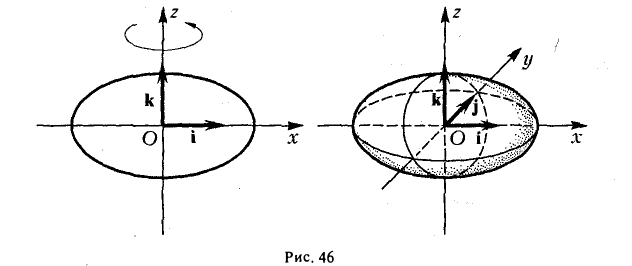
Эллипсоидом называется поверхность, уравнение которой в некоторой прямоугольной декартовой системе координат Oxyz имеет вид

где а ≥ b ≥ с > 0. Для того, чтобы выяснить, как выглядит эллипсоид, поступим следующим образом. Возьмем на плоскости Oxz эллипс

и будем вращать его вокруг оси Oz (рис. 46).

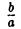
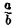
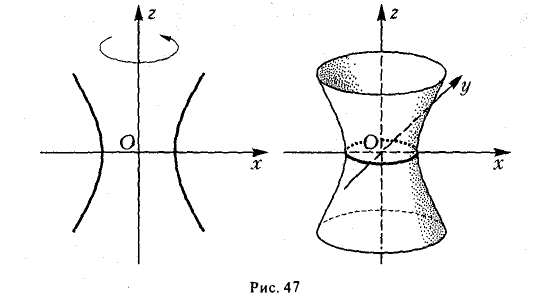
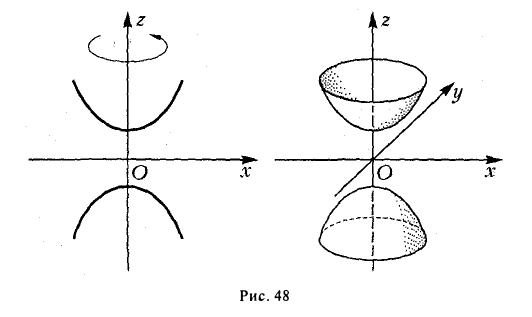
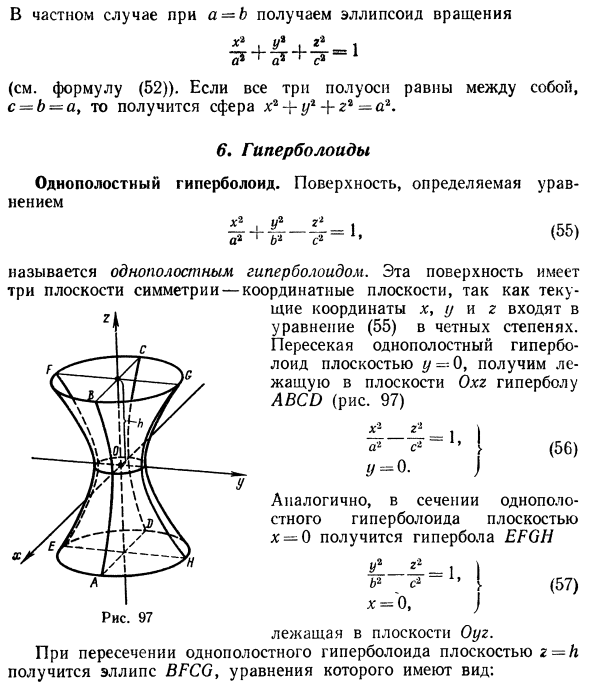
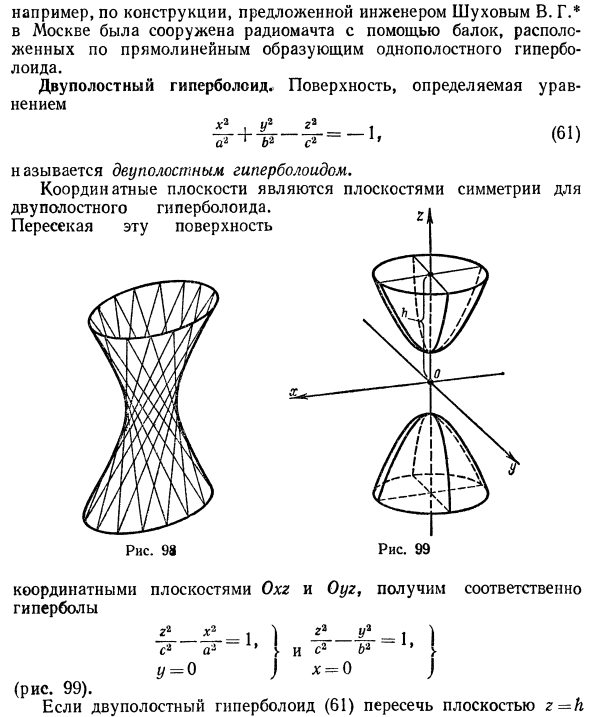
— эллипсоид вращения — уже дает представление о том, как устроен эллипсоид общего вида. Чтобы получить его уравнение, достаточно равномерно сжать эллипсоид вращения . вдоль оси Оу с коэффициентом — ≤ 1, т. с. заменить в его уравнении у на y 5).

Гиперболоиды

вокруг оси Oz (рис. 47), получим поверхность, называемую однополостным гиперболоидом вращения. Его уравнение имеет вид

получается тем же способом, что и в случае эллипсоида вращения.

5) Эллипсоид вращения («) можно получить равномерным сжатием сферы х 2 + у 2 + z 2 = а 2 вдоль оси Оz с коэффициентом — 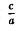≤ 1.

Путем равномерного сжатия этой поверхности вдоль оси Оу с коэффициентом 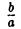≤ 1 получим однополостный гиперболоид общего вида. Его уравнение

получается тем же способом, что и в разобранном выше случае эллипсоида. Путем вращения вокруг оси Oz сопряженной гиперболы

получим двуполостный гиперболоид вращения (рис.48). Его уравнение

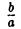
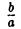
Путем равномерного сжатия этой поверхности вдоль оси Оу с коэффициентом ≤ 1 приходим к двуполостному гиперболоиду общего вида. Заменой у на у получаем его уравнение

Эллиптический параболоид

вокруг оси Oz (рис.49), получаем параболоид вращения. Его уравнение имеет вид

Путем сжатия параболоида вращения вдоль оси Оу с коэффициентом 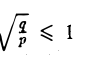получаем эллиптический параболоид. Его уравнение

получается из уравнения параболоида вращения

путем замены у на 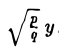. Если р Гиперболический параболоид

Гиперболическим параболоидом называется поверхность, уравнение которой в некоторой прямоугольной декартовой системе координат Oxyz имеет вид

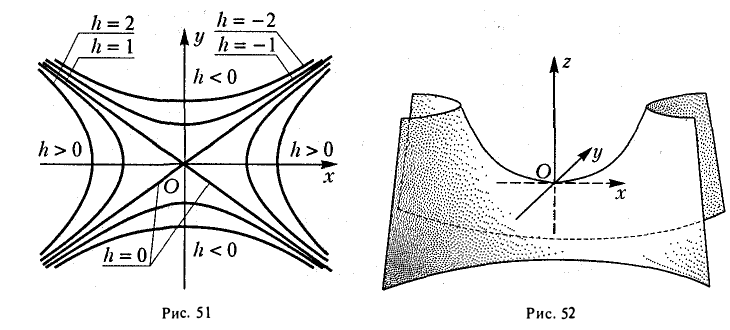
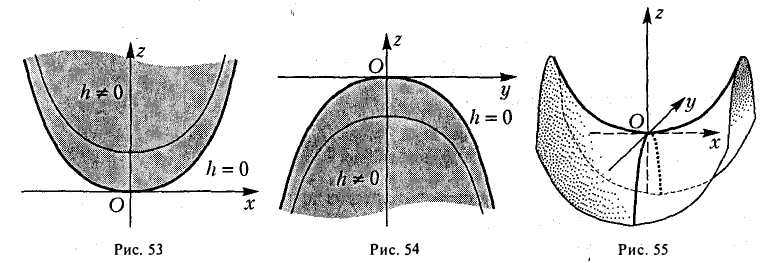
где р > 0, q > 0. Вид этой поверхности определим, применив так называемый метод сечений, который заключается в следующем: параллельно координатным плоскостям проводятся плоскости, пересекающие исследуемую поверхность, и по изменению конфигурации возникающих в результате плоских кривых делается вывод о структуре самой поверхности.

Начнем с сечений плоскостями z = h = const, параллельными координатной плоскости Оху. При h > 0 получаем гиперболы

при h

при h = 0 — пару пересекающихся прямых

Заметим, что эти прямые являются асимптотами для всех гипербол (т. е. при любом h ≠ 0). Спроектируем получаемые кривые на плоскость Ох у. Получим следующую картину (рис. 51). Уже это рассмотрение позволяет сделать заключение о седлообразном строении рассматриваемой поверхности (рис. 52).

Рассмотрим теперь сечения плоскостями

у = h.

Заменяя в уравнении поверхности у на h, получаем уравнения парабол (рис.53).

Аналогичная картина возникает при рассечении заданной поверхности плоскостями

х = h.

В этом случае также получаются параболы

ветви которых направлены вниз (а не вверх, как для сечения плоскостями у = h) (рис. 54).

Используя последние два типа сечений, приходим к заключению, что гиперболический параболоид можно получить путем параллельного переноса параболы х2 = 2pz вдоль параболы у2 = -2qz, или наоборот (рис. 55).

Замечание:

Методом сeчeний можно разобраться в строении и всех ранее рассмотренных поверхностей второго порядка. Однако путем вращения кривых второго порядка и последующего равномерного сжатия к пониманию их структуры можно прийти проще и значительно быстрее.

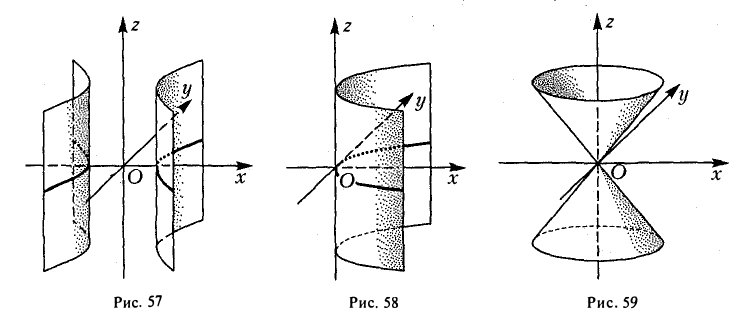
Оставшиеся поверхности второго порядка по существу уже рассмотрены ранее. Это цилиндры:

представление о котором можно получить либо путем вращения пары пересекающихся прямых

вокруг оси Oz и последующего сжатия, либо методом сечений. Конечно, в обоих случаях получим, что исследуемая поверхность имеет вид, указанный на рис. 59.

Дополнение к поверхностям второго порядка

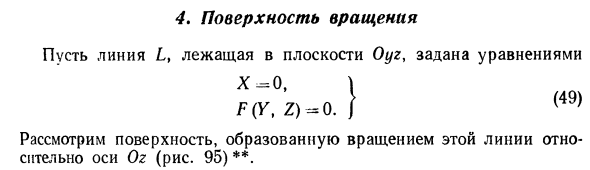
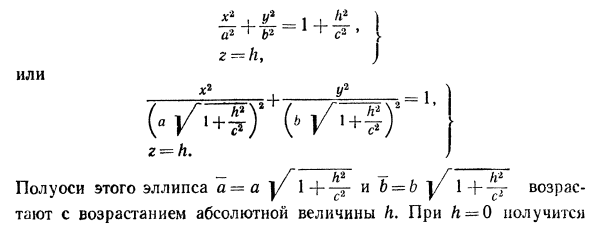
Решение заданий и задач по предметам:

Дополнительные лекции по высшей математике:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Урок №43. IBL. Зеркальная облученность

Обновл. 5 Фев 2022 |

На предыдущем уроке мы настроили работу PBR в сочетании с освещением на основе изображений (IBL), предварительно рассчитав для карты освещенности диффузную часть непрямого освещения. На этом уроке мы сосредоточимся на зеркальной части уравнения отражения.

Зеркальная часть уравнения отражения

Вспомним наше уравнение отражения:

Вы увидите, что зеркальная часть Кука-Торренса (слагаемое в скобках, которое умножается на k_S ) не является для интеграла константой и зависит не только от направления входящего света, но и от направления (входящего) обзора. Попытка решить интеграл для всех входящих световых направлений, включая всевозможные направления обзора, приведет к слишком большим затратам ресурсов компьютера и времени, особенно учитывая то, что этот расчет должен проводиться в режиме реального времени. Компания Epic Games предложила решение — методику под названием аппроксимация разделенной суммы, которая позволяет предварительно провести (правда с некоторыми оговорками) свертку зеркальной части уравнения.

Аппроксимация разделенной суммы разделяет зеркальную часть уравнения отражения на две отдельные части, к которым мы можем по отдельности применить операцию свертки и позже объединить их в PBR-шейдере для реализации зеркального непрямого освещения на основе изображений. Подобно тому, как мы предварительно свернули карту облученности, аппроксимация разделенной суммы требует передать ей HDR-карту окружения в качестве входных данных свертки. Чтобы понять алгоритм аппроксимации разделенной суммы, мы снова рассмотрим уравнение отражения, но на этот раз сосредоточимся на его зеркальной части:

По тем же причинам (производительности), как и в случае с операцией свертки облученности, мы не можем в режиме реального времени рассчитать зеркальную часть интеграла и надеяться при этом на разумную производительность. Поэтому более рационально будет сначала предварительно вычислить этот интеграл для получения чего-то вроде зеркальной IBL-карты, а затем при помощи нормали фрагмента произвести выборку из этой карты. Однако именно здесь всё становится немного сложнее. На предыдущем уроке мы смогли предварительно вычислить карту облученности благодаря тому, что интеграл зависел только от ω_i , и у нас была возможность вынести постоянные члены диффузного альбедо из-под знака интеграла. На этот раз, как видно из BRDF, интеграл зависит не только от ω_i :

Он также зависит и от ω₀ , поэтому мы не можем производить выборки из предварительно вычисленной кубической карты. Положение точки p здесь не играет никакой роли. Попытка выполнить предварительные вычисления данного интеграла для каждой возможной комбинации ω_i и ω₀ в режиме реального времени — это, мягко говоря, непрактичный подход.

Идея аппроксимации разделенной суммы, выдвинутая компанией Epic Games, решает эту проблему, разбивая предварительное вычисление на 2 отдельные части, которые мы позже можем объединить для получения итогового предварительно вычисленного результата, который нам нужен. Аппроксимация разделенной суммы разбивает интеграл зеркальной составляющей на два отдельных интеграла:

Свертка первой части известна как предварительно отфильтрованная карта окружения, которая (аналогично карте облученности) является предварительно вычисленной картой свертки окружения, но на этот раз с учетом шероховатости поверхности. Для увеличения уровня шероховатости карта окружения свернута с рассредоточенными векторами выборки, что создает более размытые отражения. Результаты последовательного размытия для каждого уровня шероховатости, который мы подвергаем свертке, сохраняются в предварительно отфильтрованных мипмап-уровнях карты. Например, предварительно отфильтрованная карта окружения, хранящая предварительно рассчитанный результат свертки 5 различных значений шероховатости для 5 своих мипмап-уровней, выглядит следующим образом:

Далее, мы генерируем векторы выборки и величину их разброса, используя функцию нормального распределения (NDF) BRDF Кука-Торренса, которая принимает в качестве входных данных вектор нормали и вектор направления обзора. Поскольку при свертке карты окружения направление обзора заранее не известно, то по методу Epic Games последующая аппроксимация выполняется, предполагая, что направление обзора (и, следовательно, направление зеркального отражения) совпадает с исходящим направлением выборки ω₀ . Это приводит к следующему коду:

Таким образом, предварительно отфильтрованной карте окружения при применении к ней операции свертки, не нужно будет знать о направлении обзора. Это означает, что мы не получим хороших зеркальных отражений, когда будем смотреть на отражающую поверхность под острым углом (углом скольжения), изображенным на следующей картинке; однако на практике это часто считается приемлемым компромиссом:

Вторая часть уравнения разделенной суммы эквивалентна BRDF-части зеркального интеграла. Если мы представим, что входящая энергетическая яркость для всех направлений представлена полностью белым светом ( L(p, x) = 1.0 ), то мы можем предварительно рассчитать значение BRDF с учетом параметра шероховатости и угла между нормалью n и направлением света ω_i (или их скалярного произведения n ⋅ ω_i ). По методу Epic Games, предварительно вычисленный результат BRDF для каждой комбинации вектора нормали и направления света при различных значениях шероховатости сохраняется в виде 2D LUT-текстуры (сокр. «LUT» от англ. «Look Up Table» = «Таблица поиска»), известной как карта интегрирования BRDF. 2D LUT-текстура отображает масштаб (красный) и значение смещения (зеленый) для расчета коэффициента Френеля поверхности, в результате чего мы получаем решение для второй части разделенного интеграла:

Мы генерируем LUT-текстуру путем обработки горизонтальной координаты текстуры (в диапазоне [0.0, 1.0] ) в качестве входного значения n ⋅ ω_i BRDF, а вертикальной координаты — в качестве входного значения шероховатости. Объединяя данную карту интегрирования BRDF и предварительно отфильтрованную карту окружения, мы получаем значение зеркального интеграла:

Эта теория даст нам немного общего представления о том, каким образом при помощи аппроксимации разделенной суммы (по методу Epic Games) находится приближенное значение зеркальной части непрямого освещения уравнения отражения.

Предварительная фильтрация HDR-карты окружения

Предварительная фильтрация карты окружения очень похожа на то, как мы свернули карту облучения. Разница заключается в том, что теперь мы учитываем показатель шероховатости и храним последовательность более грубых отражений в предварительно отфильтрованных мипмап-уровнях карты.

Во-первых, нам нужно создать новую кубическую карту для хранения данных предварительно отфильтрованной карты окружения. Используя функцию glGenerateMipmap(), можно быть уверенными, что у нас будет достаточный объем памяти для мипмап-уровней карты окружения:

Обратите внимание, что поскольку мы планируем производить выборку из мипмап-карт переменной prefilterMap , то нам нужно будет убедиться, что фильтр уменьшения задан как GL_LINEAR_MIPMAP_LINEAR , благодаря чему задействуется трилинейная фильтрация. Мы храним предварительно отфильтрованные зеркальные отражения c разрешением 128×128 точек (каждой грани) базового мипмап-уровня. Этого будет достаточно для большинства материалов и их отражений, но если у вас есть большое количество гладких материалов (например, автомобильные отражения), то вы можете увеличить разрешение.

На предыдущем уроке мы свернули карту окружения при помощи сферических координат, генерируя векторы выборки, равномерно распределенные по полусфере Ω . Хотя это и прекрасно работает для облучения, но для зеркальных отражений данный подход менее эффективен. Когда речь заходит о зеркальных отражениях, зависящих от шероховатости поверхности, то важно понимать одну деталь, а именно: отражения света могут совпадать с вектором отражения r поверхности или быть (если поверхность не очень шероховатая) разбросанными относительно вектора отражения:

Общая форма возможных исходящих отражений света известна как зеркальный лепесток. С увеличением значения шероховатости размер зеркального лепестка увеличивается; очертание зеркального лепестка изменяется при изменении направления входящего света. Таким образом, форма зеркального лепестка сильно зависит от материала поверхности.

Когда речь заходит о модели микроповерхности, мы можем представить себе зеркальный лепесток как ориентацию отражения относительно срединных векторов микроповерхностей при заданном направлении падающего света. Видя, что большинство световых лучей лежит внутри области зеркального лепестка, ориентированного вдоль срединных векторов микрограней, то и векторы выборки имеет смысл генерировать подобным образом, поскольку в противном случае большинство из них окажутся бесполезными. Этот процесс известен как выборка по значимости.

Интегрирование по методу Монте Карло и выборка по значимости

Чтобы полностью понять важность процесса выборки по значимости, мы сначала углубимся в математическую конструкцию, известную как интегрирование по методу Монте-Карло. Интегрирование по методу Монте-Карло тесно связано с такими математическими дисциплинами, как статистика и теория вероятностей. Метод Монте-Карло помогает нам дискретно решить задачу вычисления некоторой статистики или значения популяции, не принимая во внимание всей популяции.

Допустим, вы хотите подсчитать средний рост всех граждан страны. Можно конечно измерить рост каждого гражданина и затем усреднить итоговое значение, получив тем самым точный ответ. Однако, поскольку большинство стран имеют довольно значительное население, произвести подсчет среднего роста подобным методом будет просто нереально: потребуется слишком много усилий и времени.

Другой подход состоит в том, чтобы провести измерения на небольшом подмножестве людей, элементами которого являются выбранные случайным образом (несмещенные) элементы исходного множества (всей популяции), измерить их рост и усреднить результат. Причем в этой популяции может быть всего лишь 100 человек. Хотя итоговый результат будет не так точен, как при прямом подходе, но вы получите близкий к истине ответ. Описанный метод подсчета известен как закон больших чисел. Его идея заключается в том, что если вы измеряете некоторое меньшее подмножество (размера N ) случайных элементов выборки из общей совокупности, то результат будет приближен с некоторой погрешностью к истинному ответу и становится еще ближе к нему по мере увеличения числа элементов в выборке N .

Интегрирование по методу Монте-Карло основывается на законе больших чисел и использует тот же принцип при решении интеграла. Вместо того, чтобы решать интеграл для всех возможных (теоретически, их может быть бесконечно много) элементов (выборки) x , просто сгенерируйте N элементов выборки, случайным образом отобранных из общей совокупности, и усредните их. По мере увеличения N мы будем получать результат, приближающийся к точному ответу при решении интеграла:

Чтобы решить интеграл, мы берем N случайных элементов выборки в интервале от a до b , складываем их значения и делим на общее число этих элементов, находя тем самым их среднее значение. pdf — это функция плотности вероятности, которая сообщает нам о вероятности появления конкретного значения элемента в объеме выборки. Например, данная pdf функция роста людей некоторой популяции будет выглядеть примерно так:

Как видно из графика, если мы возьмем любой случайный элемент (человека) из нашего совокупного множества (населения), то вероятность, что выбранный человек будет иметь рост 1.70 — больше, по сравнению с вероятностью того, что выбранный человек будет иметь рост 1.50.

Когда речь заходит об интегрировании по методу Монте-Карло, некоторые элементы выборки могут иметь более высокую вероятность быть сгенерированными, чем другие. Вот почему для любой оценки по методу Монте-Карло мы делим или умножаем значение элемента выборки на вероятность его появления в соответствии с функцией плотности вероятности. До сих пор в каждом из случаев оценки интеграла, полученные нами элементы выборки были равномерно распределенными, имея одинаковый шанс быть сгенерированными. Наши оценки являлись несмещенными, т.е. при постоянно увеличивающемся количестве элементов выборки оценка в конечном итоге сойдется к точному решению интеграла.

Однако некоторые оценки по методу Монте-Карло являются смещенными, т.е. генерируемые элементы выборки не являются полностью случайными, а фокусируются на определенном значении или направлении. Эти смещенные оценки по методу Монте-Карло имеют более высокую скорость сходимости, следовательно, они могут сходиться к точному решению интеграла гораздо быстрее, но из-за их «смещенной природы» вполне вероятно, что они никогда окончательно к нему не сойдутся. Это, как правило, является приемлемым компромиссом, в особенности для компьютерной графики, поскольку там гораздо более важно получить визуально приемлемые результаты, нежели точное решение. Как мы вскоре увидим, с помощью выборки по значимости (которая использует смещенную оценку), сгенерированные значения элементов выборки будут смещены в определенных направлениях, что учитывается умножением или делением значения каждого элемента на соответствующее значение функции плотности вероятности.

Интегрирование по методу Монте-Карло довольно распространено в компьютерной графике, поскольку является интуитивно понятным и достаточно эффективным способом дискретной аппроксимации непрерывных интегралов: возьмите любую область/объем (например, полусферу Ω ), сгенерируйте N случайных элементов выборки в пределах этой области/объема и просуммируйте их, взвешивая вклад каждого значения элемента в конечный результат.

Интегрирование по методу Монте-Карло — это большой раздел математики, и я не хочу углубляться в его подробности. Упомяну только один момент — существует несколько способов генерации случайных выборок. По умолчанию, каждая выборка полностью (псевдо)случайна, как мы и привыкли, но, используя определенные свойства квазислучайных последовательностей, мы можем генерировать векторы выборки, которые все еще являются случайными, но при этом имеют интересные свойства. Например, мы можем выполнить интегрирование по методу Монте-Карло на так называемых последовательностях с низким расхождением, которые также генерируют случайные значения выборки, но каждое значение распределяется более равномерно:

Метод Монте-Карло, в котором для генерации векторов выборки используется последовательность с низким расхождением, называется интегрированием квази Монте-Карло. Метод интегрирования квази Монте-Карло имеет более высокую скорость сходимости, что делает его привлекательным для использования в приложениях с высокой производительностью.

Учитывая вышеописанную теорию об интегрировании по методу Монте-Карло и интегрирование квази Монте-Карло, можно выделить еще одно интересное свойство, позволяющее обеспечить еще более быструю скорость сходимости, а именно: применить выборку по значимости. Когда речь заходит о зеркальных отражениях света, векторы отраженного света ограничены областью зеркального лепестка, размер которой определяется шероховатостью поверхности. Поскольку любая (квази)случайно сгенерированная выборка, лежащая вне области зеркального лепестка, не имеет отношения к зеркальному интегралу, то имеет смысл, за счет смещения оценки по методу Монте-Карло, сосредоточить генерацию значений выборки именно внутри зеркального лепестка.

В этом и есть суть метода выборки по значимости: генерировать векторы выборки в некоторой области, ограниченной значением шероховатости и ориентированной относительно срединного вектора микрограни. Комбинируя процесс выборки интегрирования квази Монте-Карло с последовательностью с низким расхождением и смещая векторы выборки с помощью выборки по значимости, мы получаем высокую скорость сходимости. Поскольку в таком случае сходимость к решению происходит с более высокой скоростью, то нам потребуется значительно меньшее количество элементов выборки для достижения достаточного уровня аппроксимации.

Последовательность с низким расхождением

На данном уроке мы произведем предварительный расчет зеркальной части уравнения непрямого отражения, используя метод интегрирования квази Монте-Карло и выборку по значимости для случайной последовательности с низким расхождением. Последовательность, которую мы будем использовать, известна как последовательность Хэммерсли, подробно описанная Holger Dammertz. В основе последовательности Хэммерсли лежит последовательность Ван дер Корпута, которая отзеркаливает двоичное представление десятичной дроби относительно её десятичной точки.

Учитывая некоторые хитрые побитовые трюки, мы можем довольно эффективно генерировать последовательность Ван дер Корпута в шейдерной программе, которую используем для получения i-го элемента последовательности Хэммерсли из выборки с объёмом N :