Прямые на координатной плоскости
 Линейная функция Линейная функция |
 График линейной функции График линейной функции |
 Прямые, параллельные оси ординат Прямые, параллельные оси ординат |
 Уравнения вида px + qy = r . Параллельные прямые. Перпендикулярные прямые Уравнения вида px + qy = r . Параллельные прямые. Перпендикулярные прямые |
Линейная функция
Линейной функцией называют функцию, заданную формулой
| y = kx + b, | (1) |
где k и b – произвольные (вещественные) числа.
При любых значениях k и b графиком линейной функции является прямая линия .
Число k называют угловым коэффициентом прямой линии (1), а число b – свободным членом .
График линейной функции
При k > 0 линейная функция (1) возрастает на всей числовой прямой, а её график ( прямая линия ) имеет вид, изображенный на рис. 1, 2 и 3.
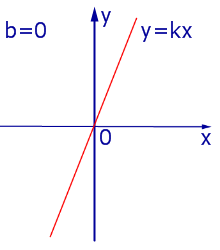 |
| Рис.1 |
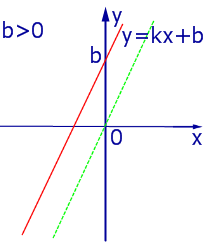 |
| Рис.2 |
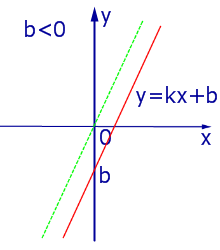 |
| Рис.3 |
При k = 0 линейная функция (1) принимает одно и тоже значение y = b при всех значениях x , а её график представляет собой прямую линию, параллельную оси абсцисс, и изображен на рис. 4, 5 и 6.
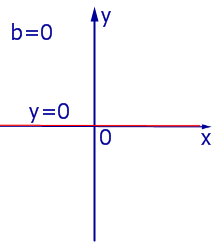 |
| Рис.4 |
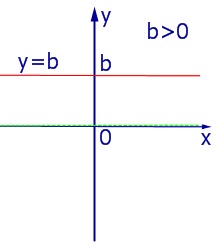 |
| Рис.5 |
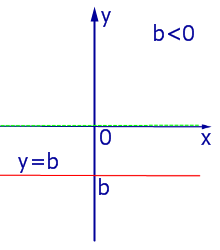 |
| Рис.6 |
При k линейная функция (1) убывает на всей числовой прямой, а её график ( прямая линия ) имеет вид, изображенный на рис. 7, 8 и 9.
| k y = kx + b1 и y = kx + b2 , имеющие одинаковые угловые коэффициенты и разные свободные члены имеющие разные угловые коэффициенты y = kx + b1 и перпендикулярны при любых значениях свободных членов. Угловой коэффициент прямой линии
равен тангенсу угла φ , образованному (рис. 10) при повороте положительной полуоси абсцисс против часовой стрелки вокруг начала координат до прямой (2).
Прямая (1) пересекает ось Oy в точке, ордината которой (рис. 11) равна b . При Прямые, параллельные оси ординатПрямые, параллельные оси Oy , задаются формулой
где c – произвольное число, и изображены на рис. 13, 14, 15.
Замечание 1 . Из рис. 13, 14, 15 вытекает, что зависимость, заданная формулой (3), функцией не является, поскольку значению аргумента x = c соответствует бесконечное множество значений y .; Уравнение вида px + qy = r . Параллельные прямые. Перпендикулярные прямые
где p, q, r – произвольные числа. В случае, когда что и требовалось. В случае, когда откуда вытекает, что уравнение (4) задает прямую линию вида (3). В случае, когда q = 0, p = 0, уравнение (4) имеет вид
и при r = 0 его решением являются точки всей плоскости: В случае, когда Замечание 2 . При любом значении r1 , не совпадающем с r прямая линия, заданная уравнением
параллельна прямой, заданной уравнением (4) . Замечание 3 . При любом значении r2 прямая линия, заданная уравнением
перпендикулярна прямой, заданной уравнением (4) . Пример . Составить уравнение прямой, проходящей через точку с координатами (2; – 3) и
В соответствии с формулой (6), будем искать уравнение прямой, параллельной прямой (8), в виде
где r1 – некоторое число. Поскольку прямая (9) проходит через точку с координатами (2; – 3), то справедливо равенство Итак, уравнение прямой, параллельной к прямой В соответствии с формулой (7), будем искать уравнение прямой, перпендикулярной прямой (8), в виде
где r2 – некоторое число. Поскольку прямая (10) проходит через точку с координатами (2; – 3), то справедливо равенство Love SoftИнструменты пользователяИнструменты сайтаБоковая панельНавигация СвязьСодержаниеУравнение прямойПрямая — ГМТ, равноудаленных от двух точек. (I) Общее уравнение прямой на плоскостиУравнение прямой имеет вид $Ax + By + C = 0$, где $A$, $B$ и $C$ — некоторые числа, причем $A$ и $B$ не равны 0 одновременно. При $A=0$ прямая параллельна оси oX, при $B=0$ — параллельна оси oY. При $C=0$ прямая проходит через начало координат. Вектор с координатами $(A;B)$ называется нормальным вектором, он перпендикулярен прямой. Также уравнение можно переписать в виде $$A(x-x_0) + B(y-y_0) = 0$$ (II) Уравнение прямой с угловым коэффициентомУравнением вида $y = kx + b$ можно задать не любую прямую — а именно, нельзя задать прямую, перпендикулярную оси абсцисс. (III) Уравнение прямой в отрезках на осяхЕсли прямая пересекает оси OX и OY в точках с координатами (a, 0) и (0, b), то она может быть найдена используя формулу уравнения прямой в отрезках $$\frac x a + \frac В этом виде невозможно представить прямую, проходящую через начало координат. (IV) Уравнение прямой, проходящей через две точкиПусть даны две несовпадающие точки A(x1;y1) и B(x2;y2). Уравнение прямой, проходящей через точки A(x1;y1) и B(x2;y2) имеет вид: (V) Каноническое уравнение прямойЕсли известны координаты точки $P(x_0, y_0)$ лежащей на прямой и направляющего вектора $ \vec v = (a; b)$, то уравнение прямой можно записать в каноническом виде, используя следующую формулу: (VI) Параметрическое уравнение прямойПараметрические уравнения прямой могут быть записаны следующим образом $$ x = a t + x_0, y = b t + y_0$$ где $(x_0, y_0)$ — координаты точки лежащей на прямой, $(a, b)$ — координаты направляющего вектора прямой. (VII) Уравнение прямой в полярных координатахУравнение прямой с углом наклона $\alpha$ в полярных координатах $r$ и $\phi$: $$r \cos(\phi-\alpha)=p$$ Калькулятор Переход к другой форме записиОт общего уравнения к уравнению с угловым коэффициентомВыразить переменную y: $Ax + By + C = 0$ $y = -\frac A B x- \frac C B$ От уравнения с угловым коэффициентом к общему уравнениюПеренести все члены в левую часть уравнения Угловой коэффициент прямойУгловой коэффициент прямой $k$ = численно равен тангенсу угла между прямой и положительным направлением оси абсцисс. Тангенс угла может рассчитываться как отношение противолежащего катета к прилежащему. Slope — угловой коэффициент — наклон, склон холма, показатель насколько крутой холм или гора. Чтобы найти наклон между двумя точками на плоскости используется формула: Иногда горизонтальное изменение называют «пробег», а вертикальное изменение — «подъем» или «снижение, спад». Наклон биссектрисы первого координатного угла равен 1, так как скорость изменения по оси X и по оси Y одинаковы. Например, найдем наклон между точками (2, 1) и (-9, 7) Найдем наклон между точками (-1, -3) и (1, 1) Чем больше модуль числа, чем круче склон. Положительное число означает, что наклон идет вверх при движении слева направо (прямая возрастает). Отрицательное число означает, что наклон идет вниз при движении слева направо (прямая убывает). Угол между двумя прямымиПусть две неперпендикулярные прямые представляются уравнениями $$y= a_1 x+ b_1 \\ y= a_2 x+ b_2$$ Тогда угол между двумя прямыми найдется по формуле $$tg(θ)=\frac Условие параллельности двух прямыхДве прямые параллельны (или совпадают), если равны их угловые коэффициенты. Теорема. Прямые $y = k_1 x + b_1$ и $y = k_2 x + b_2$ параллельны тогда и только тогда, когда $k_1 = k_2$ и $b_1 \ne b_2$. ЗадачаПроверить, выполняется ли условие параллельности прямых $2x-3y+1=0$ и $4x-6y-5=0$. ЗадачаСоставить уравнение прямой линии, проходящей через точку $(1;2)$ параллельно прямой $2x-3y+1=0$. Условие перпендикулярности двух прямыхУсловие перпендикулярности прямых заключается в том, что произведение их угловых коэффициентов равно –1: $$k_1 \cdot k_2=-1$$ ЗадачаПри каком значении $k$ уравнение $y=kx+1$ определяет прямую, перпендикулярную к прямой $y=2x-1$? ЗадачаСоставить уравнение прямой линии, проходящей через точку $(-1;1)$ перпендикулярно к прямой $3x-y+2=0$. Сводная таблица
Задачи — угловой коэффициент на бумаге в клеткуОпределить угловой коэффициент прямой: Расстояние от точки до прямойКогда прямая на плоскости задана уравнением $ax + by + c = 0$, где a, b и c — такие вещественные константы, что a и b не равны нулю одновременно, и расстояние от прямой до точки $(x_0,y_0)$ равно Точка на прямой, наиболее близкая к $(x_0,y_0)$, имеет координаты Прямая линия. Уравнение прямой.Свойства прямой в евклидовой геометрии. Через любую точку можно провести бесконечно много прямых. Через любые две несовпадающие точки можно провести единственную прямую. Две несовпадающие прямые на плоскости или пересекаются в единственной точке, или являются параллельными (следует из предыдущего). В трёхмерном пространстве существуют три варианта взаимного расположения двух прямых:
Прямая линия — алгебраическая кривая первого порядка: в декартовой системе координат прямая линия задается на плоскости уравнением первой степени (линейное уравнение). Общее уравнение прямой. Определение. Любая прямая на плоскости может быть задана уравнением первого порядка причем постоянные А, В не равны нулю одновременно. Это уравнение первого порядка называют общим уравнением прямой. В зависимости от значений постоянных А, В и С возможны следующие частные случаи: • C = 0, А ≠0, В ≠ 0 – прямая проходит через начало координат • А = 0, В ≠0, С ≠0 — прямая параллельна оси Ох • В = 0, А ≠0, С ≠ 0 – прямая параллельна оси Оу • В = С = 0, А ≠0 – прямая совпадает с осью Оу • А = С = 0, В ≠0 – прямая совпадает с осью Ох Уравнение прямой может быть представлено в различном виде в зависимости от каких – либо заданных Уравнение прямой по точке и вектору нормали. Определение. В декартовой прямоугольной системе координат вектор с компонентами (А, В) перпендикулярен прямой , заданной уравнением Пример. Найти уравнение прямой, проходящей через точку А(1, 2) перпендикулярно вектору (3, -1). Решение. Составим при А = 3 и В = -1 уравнение прямой: 3х – у + С = 0. Для нахождения коэффициента С подставим в полученное выражение координаты заданной точки А. Получаем: 3 – 2 + C = 0, следовательно С = -1. Итого: искомое уравнение: 3х – у – 1 = 0. Уравнение прямой, проходящей через две точки. Пусть в пространстве заданы две точки M 1 ( x 1 , y 1 , z 1 ) и M2 ( x 2, y 2 , z 2 ), тогда уравнение прямой, проходящей через эти точки: Если какой-либо из знаменателей равен нулю, следует приравнять нулю соответствующий числитель. На плоскости записанное выше уравнение прямой упрощается: Дробь Пример. Найти уравнение прямой, проходящей через точки А(1, 2) и В(3, 4). Решение. Применяя записанную выше формулу, получаем: Уравнение прямой по точке и угловому коэффициенту. Если общее уравнение прямой Ах + Ву + С = 0 привести к виду: и обозначить уравнением прямой с угловым коэффициентом k. Уравнение прямой по точке и направляющему вектору. По аналогии с пунктом, рассматривающим уравнение прямой через вектор нормали можно ввести задание прямой через точку и направляющий вектор прямой. Определение. Каждый ненулевой вектор Аα1 + Вα2 = 0 называется направляющим вектором прямой. Пример. Найти уравнение прямой с направляющим вектором Решение. Уравнение искомой прямой будем искать в виде: Ax + By + C = 0. В соответствии с определением, коэффициенты должны удовлетворять условиям: 1 * A + (-1) * B = 0, т.е. А = В. Тогда уравнение прямой имеет вид: Ax + Ay + C = 0, или x + y + C / A = 0. при х = 1, у = 2 получаем С/ A = -3, т.е. искомое уравнение: Уравнение прямой в отрезках. Если в общем уравнении прямой Ах + Ву + С = 0 С≠0, то, разделив на –С, получим: Геометрический смысл коэффициентов в том, что коэффициент а является координатой точки пересечения прямой с осью Ох, а b – координатой точки пересечения прямой с осью Оу. Пример. Задано общее уравнение прямой х – у + 1 = 0. Найти уравнение этой прямой в отрезках. С = 1, Нормальное уравнение прямой. Если обе части уравнения Ах + Ву + С = 0 разделить на число нормирующем множителем, то получим xcosφ + ysinφ — p = 0 – нормальное уравнение прямой. Знак ± нормирующего множителя надо выбирать так, чтобы μ * С Что-то не нашли? Ошибка? Предложения? Сообщите нам источники: http://xlench.bget.ru/doku.php/mat/algebra/eq-line http://www.calc.ru/1437.html |

 , параллельны .
, параллельны . , пересекаются при любых значениях свободных членов.
, пересекаются при любых значениях свободных членов.



 прямая (1) пересекает ось Ox в точке, абсцисса которой (рис. 12) вычисляется по формуле
прямая (1) пересекает ось Ox в точке, абсцисса которой (рис. 12) вычисляется по формуле



 уравнение (4) можно переписать в виде (1), откуда вытекает, что оно задаёт прямую линию .
уравнение (4) можно переписать в виде (1), откуда вытекает, что оно задаёт прямую линию .

 получаем:
получаем:

 уравнение (5) решений вообще не имеет.
уравнение (5) решений вообще не имеет.
 Загрузки всякие
Загрузки всякие
 Калькулятор для составления уравнения прямой — показывает ход решения
Калькулятор для составления уравнения прямой — показывает ход решения












 = k называется угловым коэффициентом прямой.
= k называется угловым коэффициентом прямой.

 , то полученное уравнение называется
, то полученное уравнение называется (α1, α2), компоненты которого удовлетворяют условию
(α1, α2), компоненты которого удовлетворяют условию (1, -1) и проходящей через точку А(1, 2).
(1, -1) и проходящей через точку А(1, 2). или
или  , где
, где
 , а = -1, b = 1.
, а = -1, b = 1. , которое называется
, которое называется