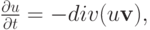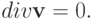Уравнении в частных производных по численным методам

Аналитические методы решения уравнений в частных производных

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

К курсовой работе по дисциплине

«ЧИСЛЕННЫЕ МЕТОДЫ»

Рецензент – доцент В.В. Луценко

Составитель Бондаренко А.И.

Методические указания к курсовой работе по дисциплине «Численные методы»/ Сост. А.И. Бондаренко; Шахтинский ин-т (филиал) ЮРГТУ (НПИ). – Новочеркасск: ЮРГТУ, 2008. — 12 с.

Методические указания содержат теоретический материал, примеры выполнения и требования к оформлению курсовой работы по дисциплине «Численные методы».

Предназначены для студентов второго курса специальностей 230201«Информационные системы и технологии» и 0808001 «Прикладная информатика».

© Шахтинский институт ЮРГТУ, 2008

© Бондаренко А.И., 2008

ВВЕДЕНИЕ

Изучение различных процессов требует наряду с глубоким пониманием физики происходящих явлений совершенного владения современными методами вычислительной математики.

Обычно математическая модель записывается в форме как угодно сложных математических структур и, как правило, получить аналитическое решение такой задачи не удаётся. Приходится использовать численные методы вычислительной математики, реализация которых на ЭВМ требует соответствующего программного обеспечения. Результаты моделирования объекта на ЭВМ позволяют “проиграть” его поведение в самых разных, под­час экстремальных условиях. Значение такого вычислительного экспери­мента трудно переоценить, особенно если натурный эксперимент опасен, дорог или просто невозможен.

Большинство физических процессов можно сформулировать на языке дифференциальных уравнений с частными производными. Производные в этих уравнениях описывают важнейшие физические величины: скорость, ускорение, силу, температуру, трение, ток, потенциал и т.д.). Многие из таких уравнений не имеют аналитического решения и, чтобы их решить, приходится прибегать к численным методам.

В курсовой работе рассматривается одно из самых важных уравнений математической физики — уравнение Лапласа на примере решения задачи Дирихле в заданной плоской области. Отсутствие аналитического решения поставленной задачи требует выбора численного метода и его реализации на ЭВМ.

Курсовая работа является завершающим этапом изучения курса “Численные методы”. Цель курсовой работы:

· систематизация, закрепление и расширение теоретических и практических знаний по компьютерному моделированию типовых вычислительных алгоритмов и анализа полученной информации;

· выявление степени подготовленности студентов к самостоятельной работе в ходе решения поставленных задач.

Аналитические методы решения уравнений в частных производных

Существует целый арсенал методов для решения уравнений в частных производных. Перечислим некоторые аналитические методы решения таких уравнений.

Метод разделения переменных. Уравнение с частными производными с n независимыми переменными сводится к n обыкновенным дифференциальным уравнениям. Решение краевых задач для уравнения Лапласа может быть найдено методом разделения переменных (методом Фурье) лишь для простейших областей (круг, прямоугольник, шар цилиндр и др.).

Метод преобразования координат. Исходное уравнение с частными производными сводится к обыкновенному дифференциальному уравнению или к другому, более простому уравнению с частными производными с помощью соответствующего преобразования координат (например, поворота координатных осей и т.п.).

Введение новых переменных. Исходное уравнение с частными производными преобразуется к такому уравнению с частными производными для другой неизвестной функции, которое решается легче, чем исходное.

Метод интегральных уравнений. Уравнение с частными производными сводится к интегральному уравнению (уравнение, в котором неизвестная функция стоит под знаком интеграла).

Вариационные методы. Вместо уравнения с частными производными решается некоторая задача минимизации. Оказывается, что функция, доставляющая минимум некоторому выражению, является решением исходного уравнения.

Метод разложения по собственным функциям. Эти собственные функции находятся как решения так называемой задачи на собственные значения, которые соответствуют исходной задаче для уравнения с частными производными.

Метод функций Грина. Начальные и граничные условия заменяются системой простейших источников, и задача решается для каждого простейшего источника. Полное решение исходной задачи получается в результате суммирования решений для элементарных источников.

Численные методы решения уравнений в частных производных гиперболического типа (на примере уравнения переноса)

3.1. Простейшее линейное уравнение переноса

Рассмотрим простейший пример уравнений в частных производных . Пусть в некотором объеме движущейся жидкости находится пассивная примесь, т.е. такая, наличие которой не меняет принципиально характер движения. Например, это может быть маркер — краска, чернила или мелкие частицы, которые специально добавлены в жидкость для визуализации течений. Тогда изменение концентрации примеси в любом сколь угодно малом объеме равно потоку примеси через границы объема в единицу времени (закон сохранения массы), и можно записать, устремляя рассматриваемый объем к нулю

где u — концентрация пассивной примеси, — скорость течения жидкости. Пусть жидкость несжимаема и

Тогда из двух предыдущих соотношений сразу следует уравнение

( 3.1)

Равенство (3.1) будем в дальнейшем называть уравнением переноса пассивной примеси или линейным уравнением переноса . Кроме (3.1), будем рассматривать и одномерное уравнение переноса

( 3.2)

а также неоднородное уравнение переноса

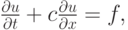( 3.3)

где f — заданная функция , играющая роль источника ( стока ).

Неоднородным уравнением переноса описываются системы, в которых пассивная примесь может вступать, например, в химические реакции. Если уравнения переноса описывают распространение планктона, то в правой части будет стоять функция , описывающая размножение планктона и его пассивную утечку (например, за счет его поедания рыбами). О неоднородных линейных моделях речь пойдет ниже.

Уравнения вида (3.1), (3.2), (3.3) традиционно рассматриваются в курсах обыкновенных дифференциальных уравнений [13.1], [13.2].

Причина этого кроется в следующем обстоятельстве. Рассмотрим систему ОДУ

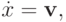( 3.4)

соответствующую (3.1). Это — уравнение характеристик для линейного уравнения переноса . Если функция u является первым интегралом (3.4), то она является решением (3.1). Иными словами, вдоль характеристики решение однородного уравнения переноса сохраняет постоянное значение .

Упражнение. Найти в явном виде уравнение характеристики для (3.2). В какое уравнение перейдет неоднородное уравнение переноса (3.3) вдоль характеристики ?

Для корректной постановки задач для линейного уравнения переноса начальные и граничные условия необходимо ставить на некоторой гиперповерхности. Так как решение уравнений переноса распространяется вдоль характеристик , то начальная гиперповерхность должна быть трансверсальной ко всем характеристикам (не иметь точек касания с характеристиками ). Кроме того, если для однородного уравнения переноса какая — либо характеристика имеет с начальной гиперповерхностью более одной общей точки, то значения начальной функции во всех этих точках должны быть равны между собой. Все эти условия достаточно очевидны, если вспомнить физический смысл уравнения переноса.

Отметим, что наличие характеристик можно считать условием того, что система имеет гиперболический тип. Так, если система уравнений произвольного порядка n имеет n действительных характеристик , будем называть ее гиперболической. Таким образом, линейное уравнение переноса имеет гиперболический тип.