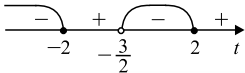Уравнений из егэ 14 задание

Задание 14. Неравенства — профильный ЕГЭ по математике

Задание 14 Профильного ЕГЭ по математике можно считать границей между «неплохо сдал ЕГЭ» и «поступил в вуз с профильной математикой». Здесь не обойтись без отличного знания алгебры. Потому что встретиться вам может любое неравенство: показательное, логарифмическое, комбинированное (например, логарифмы и тригонометрия). И еще бывают неравенства с модулем и иррациональные неравенства. Некоторые из них мы разберем в этой статье.

Хотите получить на Профильном ЕГЭ не менее 70 баллов? Учитесь решать неравенства!

Темы для повторения:

Разберем неравенства разных типов из вариантов ЕГЭ по математике.

Дробно-рациональные неравенства

1. Решите неравенство:

Решим неравенство относительно t методом интервалов:

Вернемся к переменной x:

Показательные неравенства

2. Решите неравенство

Сделаем замену Получим:

Умножим неравенство на

Дискриминант квадратного уравнения

Значит, корни этого уравнения:

Разложим квадратный трехчлен на множители.

. Вернемся к переменной x.

Внимание. Сначала решаем неравенство относительно переменной t. Только после этого возвращаемся к переменной x. Запомнили?

Следующая задача — с секретом. Да, такие тоже встречаются в вариантах ЕГЭ,

3. Решите неравенство

Сделаем замену Получим:

Вернемся к переменной

Первое неравенство решим легко: С неравенством тоже все просто. Но что делать с неравенством ? Ведь Представляете, как трудно будет выразить х?

Оценим Для этого рассмотрим функцию

Сначала оценим показатель степени. Пусть Это парабола с ветвями вниз, и наибольшее значение этой функции достигается в вершине параболы, при х = 1. При этом

Мы получили, что

Тогда , и это значит, что Значение не достигается ни при каких х.

Логарифмические неравенства

4. Решите неравенство

Запишем решение как цепочку равносильных переходов. Лучше всего оформлять решение неравенства именно так.

Следующее неравенство — комбинированное. И логарифмы, и тригонометрия!

5. Решите неравенство

А вот и метод замены множителя (рационализации). Смотрите, как он применяется. А на ЕГЭ не забудьте доказать формулы, по которым мы заменяем логарифмический множитель на алгебраический.

6. Решите неравенство:

Мы объединили в систему и область допустимых значений, и само неравенство. Применим формулу логарифма частного, учитывая, что . Используем также условия

Обратите внимание, как мы применили формулу для логарифма степени. Строго говоря,

Согласно методу замены множителя, выражение заменим на

Решить ее легко.

Разберем какое-нибудь нестандартное неравенство. Такое, что не решается обычными способами.

7. Решите неравенство:

Привести обе части к одному основанию не получается. Ищем другой способ.

Заметим, что при x = 9 оба слагаемых равны 2 и их сумма равна 4.

Функции и — монотонно возрастающие, следовательно, их сумма также является монотонно возрастающей функцией и каждое свое значение принимает только один раз.

Поскольку при x=9 значение монотонно возрастающей функции равно 4, при значения этой функции меньше 4. Конечно, при этом , то есть x принадлежит ОДЗ.

Метод координат

Для решения задачи по стереометрии координатным методом нужно выбрать декартову систему координат. Ее можно выбрать как угодно, главное, чтобы она была удобной. Приведем примеры выбора системы координат в кубе, пирамиде и конусе:

Далее необходимо найти координаты основных точек в выбранной системе координат. Это могут быть вершины объемной фигуры, середины ребер или любые другие точки, указанные в условии задачи. Найдем координаты куба и правильной пирамиды (предположим, что все ребра равны \(4\)):

Куб: Очевидно, что координаты точки \(A\) в начале координат — \((0;0;0)\). т. \(B\) — \((4;0;0)\), т. \(G\) — \((4;4;4)\) и т.д. (Рис. 1).

С кубом все просто, но в других фигурах могут возникнуть трудности с нахождением координат.

Давайте рассмотрим правильную пирамиду \(ABCD\):

У \(т. A\) координаты \((0;0;0)\), потому что она лежит в начале координат.

Координату \(x\) точки \(С\) можно получить, опустив перпендикуляр \(CE\) из \(т.С\) на ось \(OX\). (см. Рис. 2). Получится \(т.E\), указывающая на искомую координату по \(x\) – 2.

Координату \(y\) точки \(С\) тоже получаем, опустив перпендикуляр \(CF\) на ось \(OY\). Координата \(y\) \(т.С\) будет равна длине отрезка \(AF=CE\). Найдем его по теореме Пифагора из треугольника \(AFC\): $$ ^2=^2+^2,$$ $$ 4^2=2^2+^2,$$ $$ CE=\sqrt<12>. $$ Координата \(z\) точки \(C\), очевидно, равна \(0\), потому что \(т.С\) лежит в плоскости \(XOY\). $$ C (2;\sqrt<12>; 0). $$

И найдем координаты вершины пирамиды (\(т.D\)). (Рис. 3) Координаты \(X\) и \(Y\) у точки \(D\) совпадают с координатами \(X\) и \(Y\) у точки \(H\). Напомню, что высота правильной треугольной пирамиды падает в точку пересечения медиан, биссектрис и высот. Отрезок \(EH=\frac<1><3>*CE=\frac<1><3>*\sqrt<12>\) (медианы в треугольнике точкой пересечения делятся в отношении как \(\frac<1><3>\)) и равен координате точки \(D\) по \(Y\). Длина отрезка \(IH=2\) будет равна координате точки \(D\) по \(X\). А координата по оси \(Z\) равна высоте пирамиде: $$ ^2=^2+^2, $$ $$ =\sqrt<4^2-<\frac<2><3>*AF>^2>, $$ $$ =\frac<32><3>. $$ $$ D (2, \frac<1><3>*\sqrt<12>, \frac<32><3>). $$

Координаты вектора

Вектор – отрезок, имеющий длину и указывающий направление.

На самом деле, понимать, что такое вектор для решения задач методом координат необязательно. Можно просто использовать это понятие, как необходимый инструмент для решения задач по стереометрии. Любое ребро или отрезок на нашей фигуре мы будем называть вектором.

Для того, чтобы определить координаты вектора, нужно из координат конечной точки вычесть координаты начальной точки. Пусть у нас есть две точки (Рис. 4) : $$ т.А(x_A,y_A,z_A); $$ $$ т.B(x_B,y_B,z_B); $$ Тогда координаты вектора \(\vec\) можно определить по формуле: $$ \vec=. $$

Скрещивающиеся прямые

И так, мы научились находить координаты точек, и при помощи них определять координаты векторов. Теперь познакомимся с формулой нахождения косинуса угла между скрещивающимися прямыми (векторами). Пусть даны два вектора: $$ a=;$$ $$ b=; $$ тогда угол \(\alpha\) между ними находится по формуле: $$ \cos<\alpha>=\frac<\sqrt<^2+^2+^2>*\sqrt<^2+^2+^2>>. $$

Уравнение плоскости

В задачах №14 (С2) ЕГЭ по профильной математике часто требуется найти угол между прямой и плоскостью и расстояние между скрещивающимися прямыми. Но для этого вы должны уметь выводить уравнение плоскости. В общем виде уравнение плоскости задается формулой: $$ A*x+B*y+C*z+D=0,$$ где \(A,B,C,D\) – какие-то числа.

Если найти \(A,B,C,D\), то мы мы найдем уравнений плоскости. Плоскость однозначно задается тремя точками в пространстве, значит нужно найти координаты трех точек, лежащий в данной плоскости, а потом подставить их в общее уравнение плоскости.

Например, пусть даны три точки:

Подставим координаты точек в общее уравнение плоскости:

$$\begin A*x_K+B*y_K+C*z_K+D=0,\\ A*x_L+B*y_L+C*z_L+D=0, \\ A*x_P+B*y_P+C*z_P+D=0.\end$$

Получилась система из трех уравнений, но неизвестных 4: \(A,B,C,D\). Если наша плоскость не проходит через начало координат, то мы можем \(D\) приравнять \(1\), если же проходит, то \(D=0\). Объяснение этому простое: вы можете поделить каждое ваше уравнения на \(D\), от этого уравнение не изменится, но вместо \(D\) будет стоять \(1\), а остальные коэффициенты будут в \(D\) раз меньше.

Теперь у нас есть три уравнения и три неизвестные – можем решить систему:

Найти уравнение плоскости, проходящей через точки $$ K(1;2;3);\,P(0;1;0);\,L(1;1;1). $$ Подставим координаты точек в уравнение плоскости \(D=1\): $$\begin A*1+B*2+C*3+1=0,\\ A*0+B*1+C*0+1=0, \\ A*1+B*1+C*1+1=0.\end$$ $$\begin A+2*B+3*C+1=0,\\ B+1=0, \\ A+B+C+1=0.\end$$ $$\begin A-2+3*C+1=0,\\ B=-1, \\ A=-C.\end$$ $$\begin A=-0.5,\\ B=-1, \\ C=0.5.\end$$ Получаем искомое уравнение плоскости: $$ -0.5x-y+0.5z+1=0.$$

Расстояние от точки до плоскости

Зная координаты некоторой точки \(M(x_M;y_M;z_M)\), легко найти расстояние до плоскости \(Ax+By+Cz+D=0:\) $$ \rho=\frac<|A*x_M+B*y_M+C*z_M+D|><\sqrt>. $$

Найдите расстояние от т. \(H (1;2;0)\) до плоскости, заданной уравнением $$ 2*x+3*y-\sqrt<2>*z+4=0.$$

Из уравнения плоскости сразу находим коэффициенты: $$ A=2,\,B=3,\,C=-\sqrt<2>,\,D=4.$$ Подставим их в формулу для нахождения расстояния от точки до плоскости. $$ \rho=\frac<|2*1+3*2-\sqrt<2>*0+4|><\sqrt<2^2+3^2+<-\sqrt<2>>^2>>. $$ $$ \rho=\frac<12><\sqrt<16>>=3.$$

Расстояние между скрещивающимися прямыми

Расстояние между скрещивающимися прямыми – это расстояние от любой точки одной из прямых до параллельной ей плоскости, проходящей через вторую прямую.

Таким образом, если требуется найти расстояние между скрещивающимися прямыми, то нужно через одну из них провести плоскость параллельно второй прямой. Затем найти уравнение этой плоскости и по формуле расстояния от точки до плоскости найти расстояние между скрещивающимися прямыми. Точку на прямой можно выбрать произвольно (у которой легче всего найти координаты).

Рассмотрим задачу из досрочного ЕГЭ по математике 2018 года.

Дана правильная треугольная призма \(ABCFDE\), ребра которой равны 2. Точка \(G\) — середина ребра \(CE\).

• Докажите, что прямые \(AD\) и \(BG\) перпендикулярны.
• Найдите расстояние между прямыми \(AD\) и \(BG\).

Решим задачу полностью методом координат.

Нарисуем рисунок и выберем декартову систему координат. (Рис 5).

Задание 14. Неравенства. ЕГЭ 2022 по математике профильного уровня

Задачи для практики

Задача 1

Решите неравенство: $\log_7^2(9-x^2)-10\log_7(9-x^2)+21⩾ 0$.

Решение

$log_7^2(9 — x^2) — 10 log_7(9 — x^2) + 21 ≥ 0$.

Обозначим $log_7 (9 — x^2) = t$. Неравенство примет вид: $t^2 — 10t + 21 ≥ 0, (t — 3)(t — 7) ≥ 0$, отсюда $t ≤ 3, t ≥ 7$.

Числитель положительное число, либо равное нулю при $t = 4$, то есть $4^x = 4, x = 1$.

Знаменатель — положительное число при $t 16$.

А так как $t > 0$, то $t > 16$, то есть $4^x > 16, x > 2$.

Задача 3

Решение

ОДЗ: $x > 0, x ≠ 256, x ≠ 1$.

Обозначим $log_4 x = t$. Неравенство примет вид: $<(t - 3)^2>/≤ 0$.

Решим это неравенство методом интервалов.

Значит мы можем привести неравенство к следующему виду

$50(t^2 — 2t + 1) — 20(t + 1)^2 — 15(t — 1)(t + 1) ≤ 0$,

$50t^2 — 100t + 50 — 20t^2 — 40t — 20 — 15t^2 + 15 ≤ 0$,

$15t^2 — 140t + 45 ≤ 0, 3t^2 — 28t + 9 ≤ 0$.

$3t^2 — 28t + 9 = 0, D = 28^2 — 27 · 4 = 676 = 26^2$.

Решением неравенства $3t^2 — 28t + 9 ≤ 0$ будет $t ∈ [<1>/<3>; 9]$.

Переходя к переменной $x$, получаем $3^x ∈ [<1>/<3>; 9], x ∈ [-1; 2]$.

Задача 5

Решение

Выполним преобразования, обозначим $2^x=t$, $t>0$

Cледовательно, $45(t-1)^2-8(t^2-1)-21(t+1)^2⩽ 0$, $45t^2-90t+45-8t^2+8-21t^2-42t-21⩽ 0$, $16t^2-132t+32⩽ 0$, $16t^2-132t+32=0$, $4t^2-33t+8=0$, $D=33^2-32⋅ 4=961=31^2$. $t_<1, 2>= <33±31>/ <8>$, $t_1=8$; $t_2= <2>/ <8>= <1>/ <4>$

Решением неравенства $4t^2-33t+8⩽ 0$ будет $t∈ [ <1>/ <4>;8]$, то есть, переходя к переменной $x$, получаем $2^x∈ [ <1>/ <4>;8]$, $x∈ [-2;3]$.

Задача 6

Решение

Обозначим $log_9x = t$.

Тогда неравенство примет вид: $<3t + 1- (3-t)(2t+3)>/ <2t+3>≤ 0$.

Последнее неравенство решим методом интервалов.

$(t − 2)(t + 2) = 0, t = -2; t = 2.$

Вернёмся к исходной переменной.

Т.к. $<1>/=-<1>/=-log_2x$, а $log_<4x>2 = <1>/ <x> + 2>$, то неравенство примет вид $-log_<2>x + 6 ≥ <16>/<x> + 2>$. Пусть $log_2x = t$, тогда $<16>/+t-6 ≤ 0, <(t − 2)^2>/≤ 0, t = 2$ или $t 0; \9(x-1)≠1;$ то есть $x > 1, x ≠<10>/<9>$.

Неравенство примет вид $log_3(x − 1) ≤ 4 − <9>/$. Пусть $log_3(x − 1) = t$, тогда $t − 4 + <9>/≤ 0, <(t − 1)^2>/≤ 0, t = 1$ или $t 0, x ≠ <1>/<3>, x ≠ 1$.

Используя свойства логарифмов, преобразуем неравенство:

Пусть $log_<3>x = t$, тогда получим неравенство, которое удобно решить методом интервалов:

Получим два простых неравенства и одно двойное, решим их, возвращаясь к переменной $x$:

Применяя метод рационализации, получим, что на ОДЗ исходное неравенство равносильно неравенству:

$(x^2 + 2x − 3)(2x − 1 − 1)(4x^2 − 11x + 7 − 1) ≤ 0;$

$(x − 1)(x + 3)(2x − 2)(4x^2 − 11x + 6) ≤ 0;$

Из рисунка следует, что $<3>/<4>≤ x 0;\ x -2≠0;\ <|x -2|>≠ 1;$

$-6t^2 + 10t + 4 = -2(3t^2 — 5t — 2) = -2(t — 2)(3t + 1)$.

$t 2$. С учётом условия $t > 0, <3>/ <16>≤ t 2$. Возвращаясь к переменной $x$, получим, что $<3>/ <16>≤ 3^x 2$, откуда $log_3<3>/ <16>≤ x log_<3>2$.

Задача 16

Решение

Обозначим $2^x = t, t > 0$. Неравенство примет вид:

Полученное неравенство при условии $t > 0$ равносильно неравенству $t^2 + 7t — 6 ≤ 0$ (так как $t> 0, t + 2 > 0$ и $t + 6 > 0$),

$0 0$. Неравенство примет вид:

Так как при этом $t + 3 > 0$ и $t + 2> 0$, то неравенство верно при $t — 1 <7>/<3>$ выражение $3x — 7 > 0$, а при $x 1$, то есть при $x > 2.4$, выражение $log_<5x-11>(x^2 — 8x + 17) > 0$; при $0 2.4$.

Задача 19

Решите неравенство $(7x — 10) log_<4x-3>(x^ <2>— 4x + 9) ≥ 0$.

Решение

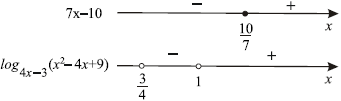
В правой части неравенства стоит $0$, в левой — произведение двух множителей. Определим знаки каждого из этих множителей.

При $x =<10>/<7>$ выражение $7x-10 = 0$, при $x > <10>/<7>$ выражение $7x-10 > 0$, а при $x 1$, то есть при $x > 1$, выражение $log_<4x-3>(x^2 — 4x + 9) >0$, при $0 ×

Для доступа к решениям необходимо включить уведомления от группы Турбо в вк — это займет буквально 10 секунд. Никакого спама, только самое важное и полезное для тебя. Ты всегда можешь запретить уведомления.