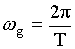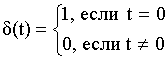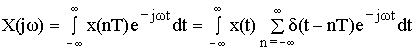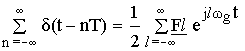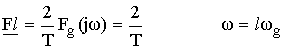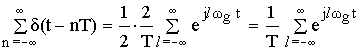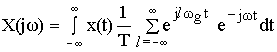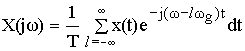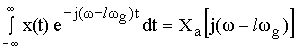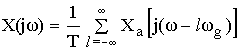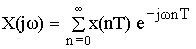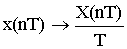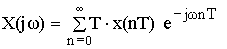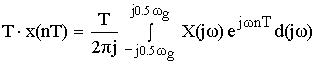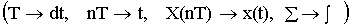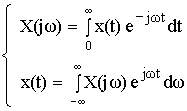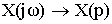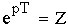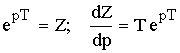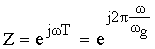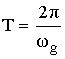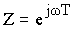Описание линейной дискретной системы во временной области
3.1.2.1. Импульсная и переходная характеристики ЛДС
Во временной области линейная дискретная система (ЛДС) описывается импульсной характеристикой.
Импульсной характеристикой 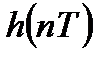
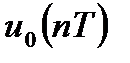
Рисунок 2.1 – определение импульсной характеристики ЛДС
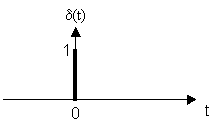
Единичный дискретный импульс описывается соотношением:
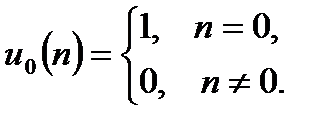
Импульсная характеристика 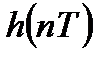
При описании ЛДС во временной области кроме импульсной характеристики используют переходную характеристику.
Переходной характеристикой 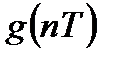
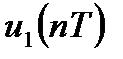
Рисунок 2.2 – определение переходной характеристики ЛДС
Единичный дискретный скачок описывается соотношением:
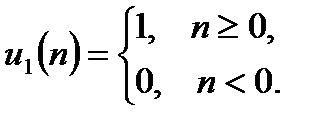
3.1.2.2. Связь выходного сигнала ЛДС с входным во временной области
Во временной области соотношение вход-выход ЛДС описывается линейными уравнениями:
— формулой свертки при использовании импульсной характеристики;
— разностным уравнением, если используются параметры ЛДС.
Формула линейной свертки
Для получения уравнения свертки представим любой дискретный сигнал 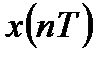
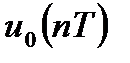
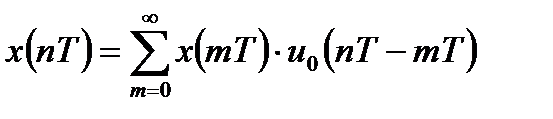
Воспользовавшись свойствами аддитивности и определением импульсной характеристики линейной дискретной системы, можно получить уравнение свертки:
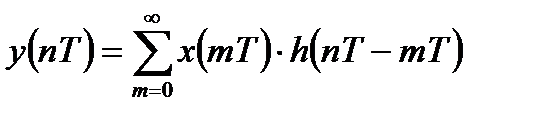
В результате замены переменных можно получить второй вариант записи формулы свертки:
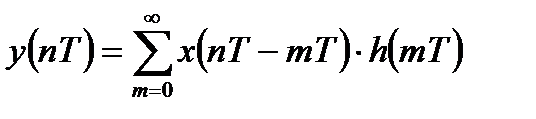
Стандартное условное обозначение операции свертки имеет следующий вид:
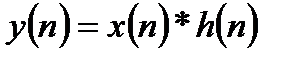
В общем случае ЛДС суммирует с некоторыми весовыми коэффициентами не только некоторое количество входных отсчетов, но и некоторое количество предшествующих выходных отсчетов:
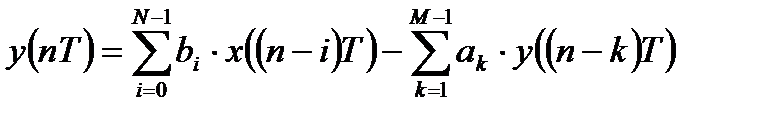
где 
Данная форма разностного уравнения иногда называется алгоритмом дискретной фильтрации. Если в левой части уравнения разместить только выходные отсчеты, а в правой части только входные, то получают форму записи, которую называют классическим разностным уравнением:
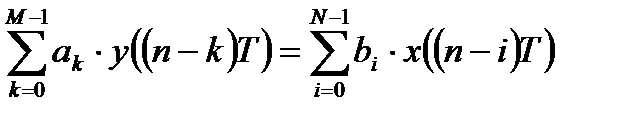
Разностное уравнение является аналогом дифференциального уравнения аналоговой линейной системы для линейных дискретных систем.
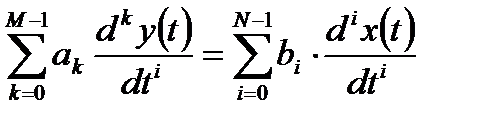
Переход дифференциального уравнения к дискретному аналогу в виде разностных уравнений может быть произведен путем замены производных конечными разностями:
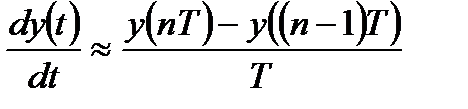
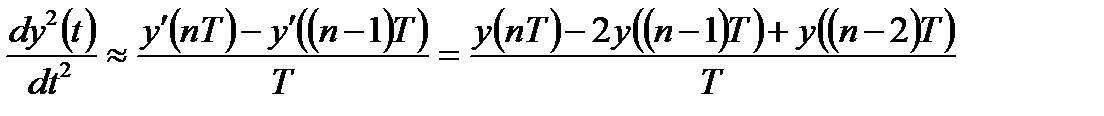
Вычисление выходного сигнала аналоговой системы может быть получено только приближенно путем замены операции интегрирования в интеграле Дюамеля одним из методов численного интегрирования. В то же время разностное уравнение или алгоритм дискретной фильтрации представляют собой алгоритм непосредственного вычисления выходного сигнала методом прямой подстановки при известном входном воздействии и предшествующих значениях выходного сигнала (реакции).
3.1.3. Описание линейной дискретной системы в Z – области
Математический аппарат z – преобразования, подобно преобразованию Лапласа в теории линейных аналоговых цепей, существенно упрощает анализ ЛДС.
Передаточная функция ЛДС
Применим z – преобразование к уравнению дискретной линейной свертки 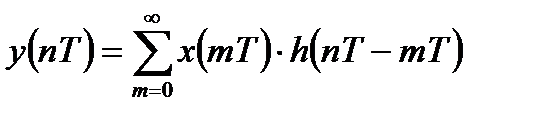
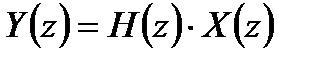
где 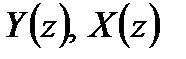
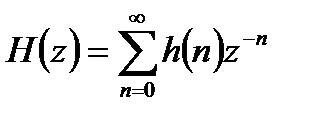
Функция, представляющая собой z – преобразование импульсной характеристики
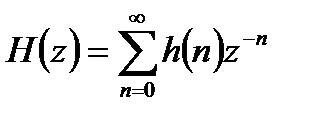
называется передаточной функцией (системной функцией) ЛДС.
Передаточная функция также может быть представлена и следующим образом:
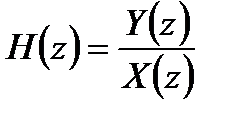
При известном изображении 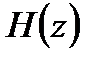
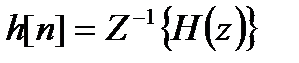
Таким образом, передаточная ЛДС – это отношение z – преобразования реакции к z – преобразованию воздействия.
Связь передаточной функции с разностным уравнением
Применим z – преобразование к разностному уравнению
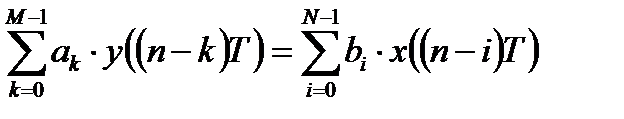
В этом случае, учитывая свойство z – преобразования по запаздыванию воздействия, можно получить передаточную функцию ЛДС общего вида:
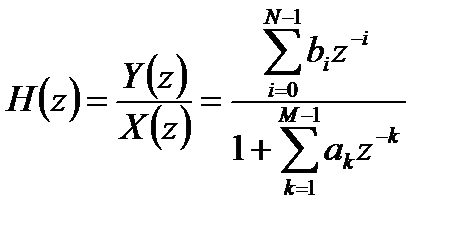
Таким образом, передаточная функция ЛДС представляет собой дробно-рациональную функцию, числитель и знаменатель которой дееются многочленами аргумента 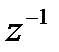
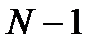
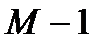
Как любая дробно-рациональная функция, передаточная функция ЛДС характеризуется полюсами и нулями.
Нулями называют значения 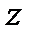
Полюсами называют значения 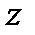
Разновидности передаточных функций
Кроме передаточной функции общего вида, существуют другие формы записи передаточной функции.
Одна из эквивалентных форм записи передаточной функции выглядит следующим образом
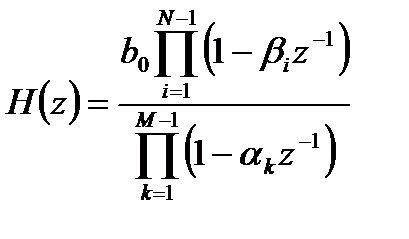
где 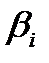
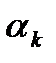
Нули и полюса передаточной функции могут быть либо вещественными, либо составлять комплексно-сопряженные пары. Коэффициент усиления 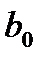
Возможен третий вариант представления передаточной функции в виде суммы простых дробей ( 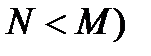
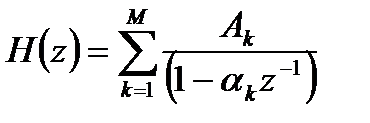
где 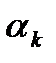
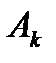
Оценка устойчивости ЛДС по ее передаточной функции
Представление функции передачи в виде суммы простых дробей позволяет найти импульсную характеристику системы через обратное z – преобразование, так как каждому слагаемому выражения (3.7) соответствует обратное преобразование вида 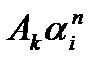
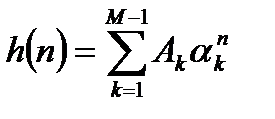
Таким образом, ряд будет сходиться и ЛДС будет устойчива, если выполняется условие:
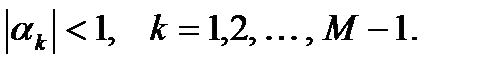
Таким образом, для того, чтобы ЛДС была устойчива, необходимо и достаточно, чтобы все полюса ее передаточной функции распределялись внутри единичного круга комплексной z-плоскости.
Уравнений систем по временной области
Название работы: Методы моделирования во временной области
Предметная область: Коммуникация, связь, радиоэлектроника и цифровые приборы
Описание: Методы моделирования во временной области. Модели во временной области наиболее удобны для анализа переходных процессов в ТУ моделирования статического режима и нелинейных устройств. Рассмотрим алгоритмы формирования системы уравнений математической модели ТУ
Дата добавления: 2013-03-19
Размер файла: 71 KB
Работу скачали: 13 чел.
Методы моделирования во временной области.
Модели во временной области наиболее удобны для анализа переходных процессов в ТУ, моделирования статического режима и нелинейных устройств.
Рассмотрим алгоритмы формирования системы уравнений математической модели ТУ во временной области
Рассмотренные методы автоматизированного формирования системы уравнений математикой мелели, несмотря на удобство алгоритмической реализации обладают тем существенным недостатком, что приводят к математическим моделям в виде систем дифференциально-алгебраических уравнений высокого порядка, решение которых зачастую связано, с большими вычислительными трудностями.
С середины 50-х годов в автоматизированном проектировании на чал широко применяться метод переменных состояний позволяющий получить систему уравнений математической модели в виде двух систем матричных уравнений:
где вектор фазовых переменных, называемых переменными состояния, Q — вектор, характеризующий входные воздействия, Fвектор выходных параметров, L, М постоянные действительные матрицы соответствующего размера.
Уравнения (1) представляют собой систему дифференциальных уравнений первого порядка, называемую системой уравнений для переменных состояния в нормальной форме, численное решение которой относительно вектора фазовых переменных V самое простое из всех методов моделирования. Кроме того, уравнений в (1), как правило, оказывается меньше, чем при использовании метода узловых потенциалов либо контурных токов, что также облегчает процесс моделирования, особенно нелинейных устройств.
Алгоритмическую реализацию метода во многом определяет выбор вектора переменных состояния V. За вектор переменных состояния могут быть, например, выбраны узловые потенциалы, при этом размерность системы (1) будет равна количеству узлов в электрической модели, контурные токи либо другие переменные. При моделировании переходных процессов в радиоэлектронных устройствах за переменные состояния рационально выбирать вектор, состоящий из напряжений на всех конденсаторах электрической модели устройства Uc и токов во всех индуктивностях позволяющий для динамических моделей получить систему дифференциальных уравнений первого порядка минимально возможной размерности.
2. Численный анализ во временной области.
При моделировании во временной области нелинейных ТУ нельзя использовать метод обратного преобразования Лапласа и приходится решать системы дифференциальных либо дифференциально-алгебраических уравнений численными методами. Алгоритмы интегрирования систем дифференциальных уравнений описаны во множестве учебников, мы рассмотрим здесь некоторые из них, наиболее удобные для моделирования ТУ. Для упрощения описания алгоритмов будем рассматривать их на примере одного уравнения с одной неизвестной, затем распространим результаты на системы уравнений.
Пусть требуется найти функцию и , удовлетворяющую уравнению
и придающую при t= t о заданное начальное значение и (t о )= u о
Выбор начального значения u о служит для выделения одной из кривых семейства, задаваемого уравнением (18), как покапано на рис. 3,а.
Эта задача в математике известна как задача Коши. Для ее решения широко используются разностные методы. В разностных методах решение задачи получают в дискретном ряде значений аргумента отличающихся на шаг интегрирования. В одношаговых разностных методах для нахождения следующего значения u k = u(t k ) требуется иyформация только об одном предыдущем шаге. Из одношаговых методов наибольшую известность получил метод РунгeКутта, который на самом деле является целым семейством методов, представляющих аппроксимацию методов, основанных на рядах Тейлора, но без явного вычисления производных, за исключением первой.
Для пояснения методов Рунге — Кутта представим значение искомого решения уравнения в точке t k , разложением в ряд Тейлора вокруг предыдущей точки t k-1 , u k-1
Если шаг интегрирования D t мал, то всеми членами разложения высокого порядка можно пренебречь и представить (19) в виде
где — первая производная в предыдущей точке t k-1 .
Если процесс продолжить, то для любой последующей точки задания аргумента получим итерационную формул
Полученные выражения (20) для определения переменной u k известны как явный метод Эйлера, а по своей сути он представляет метод Рунге — Кутта первого порядка. Графически выражение (20) проиллюстрировано на рис. 3,а, начиная с точки t 1 , u 1 , где видно, что на каждом новом шаге определения приближенного решения переходим на другую кривую ее семейства. Систематическая ошибка метода (ошибка дискретизации) имеет порядок D t 2 , так как члены разложения (19) содержащие степени D t выше второй, отбрасываются. Кроме систематической ошибки, в процессе вычисления появляется ошибка округления, величина которой определяется ЭВМ и программой, которая накапливается с ростом числа шагов.
Точность метода можно значительно повысить, если сохранить член с D t 2 , однако для этого необходимо знание второй производной.
Величину второй производной можно аппроксимировать конечно-разностным выражением
где для вычисления f(u k+1 , t k+1 ,) используется приближенное значение U k+1 = U k + D t f(u k ,t k ), вычисленное по методу Эйлера, подставив это выражение в ряд Тейлора и отбросив члены выше третьего порядка D t 3 , можно получить
Выражение (5.38) известно как модифицированный метод Эйлера и по своей сути представляет метод РунгеКутта второго порядка. Ошибка дискретизации для этого метода пропорциональна D t 3 .
Очевидно, что чем выше порядок вычисляемой конечно- разностным методом производной, тем больше дополнительных вычислений правой части уравнения (18) необходимо сделать. Метод Рунге — Кутта дает набор формул для расчета координат точек внутри интервала для реализации этой идей. Для примера приведем распространенную формулу метода Рунге — Кутта четвертого порядка
Заметим, что в методе Рунге — Кутта четвертого порядка вначале вычисляется величина для предыдущей точки.
Затем, используя это значение k o , аргумент смещают на пол шага вперед и получают значение k 1 . На основе k 1 из этой точки t k опять со смещением на половину интервала интегрирования вычисляют значение k 2 и, наконец, сделав полный шаг вперед от точки t k , вычисляют значение k 3 . Значения k 1 k 2 k 3 затем суммируются с весами 1/6, 1/3, 1/3, 1/6.
Шаг интегрирования выбирается из максимально допусти мой ошибки на каждом шаге интегрирования. Оценка ошибок в современных алгоритмах обычно оценивается автоматически, позволяя автоматически изменять длину шага. Недостатком методов Рунге Кутта высокого порядка является необходимость вычисления большого числа значений правой части уравнения (18) для каждого шага, причем эти вычисленные значения не используются на последующих шагах.
Одношаговые методы легко распространяются на системы обыкновенных дифференциальных уравнений. Если в результате работы программы моделирования система уравнений модели получилась более высокого порядка, то с помощью подстановок ее всегда можно свести к системе обыкновенных дифференциальных уравнений. Например в дифференциальном уравнении второго порядка можно воспользоваться подстановкой = v и получить систему двух обыкновенных дифференциальных уравнений.
Пусть после подобных подстановок система уравнений математической модели приведена к системе обыкновенных дифференциальных уравнений вида
где U вектор переменных, вектор правых частей уравнений системы. Воспользовавшись для простоты модифицированной формулой Эйлера (5.38), запишем итерационную формулу для решения системы обыкновенных дифференциальных уравнений одношаговым методом второго порядка:
где [1] единичная матрица.
Для сравнения различных одношаговых методов по эффективности рассмотрим решение этими методами уравнения
при следующих начальных условиях =0, u= 1
Аналитическое решение этого уравнения с учетом задания граничных условий имеет вид
Уравнений систем по временной области
Цифровая обработка сигналов
Часть1 §1 Дискретизация непрерывных сигналов
Возникновение ЦОС – пятидесятые годы. В это время ЭВМ впервые стали применяться для моделирования аналоговых (непрерывных) сигналов (моделирование может быть использовано для обработки реальных сигналов). Для этого сигнал записывался на магнитную ленту и потом обрабатывался на ЭВМ. Время обработки измерялось в часах, время записи – в секундах.
В шестидесятые годы изобретен алгоритм Фурье, быстрое преобразование Фурье. В результате свертку сигнала можно было заменить произведением спекторов этих сигналов, что ускоряло обработку сигналов на несколько порядков и в результате появляется возможность обработки сигналов в реальном масштабе времени.
В семидесятые и восьмидесятые годы развитие микроэлектроники позволило запараллеливать вычислительные операции (развернуть процесс в пространстве). В результате скорость обработки сигналов резко возросла и процесс обработки сигналов стали более широкополосным. ЦОС в настоящее время применяется в различных областях техники, где она нужна.
§1 Дискретизация непрерывных сигналов.
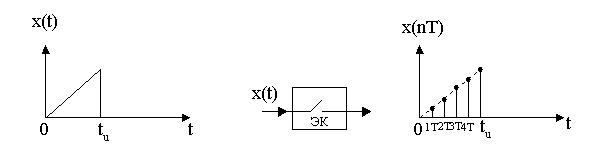
Цифровые системы связи вырабатывают дискретные сигналы, которые получаются из непрерывных путем дискретизации.
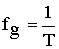
fg – частота дискретизации
Т – интервал дискретизации
X ( t ) – непрерывный (аналоговый) сигнал
X ( n Т) – дискретный сигнал
X ( n Т) = X ( n ) = Xn = < X 0; X 1; X 2; … > – обозначения дискретного сигнала.
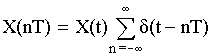
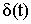
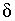
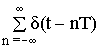
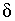
§2 Связь спектров дискретных и непрерывных сигналов.
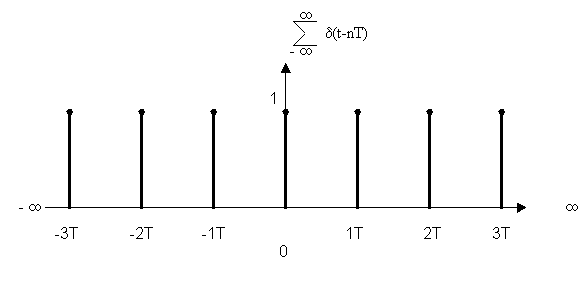
Пусть 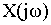
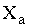
Для установления связи между спектрами воспользуемся прямым преобразованием Фурье:
Раскладываем в ряд Фурье:
Fl – амплитуда гармоник.
Определим Fl используя формулу связи между спектрами периодических и непериодических сигналов.
В силу линейности операции в этом выражении знаки 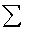
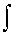
Воспользуемся теоремой смещения (теорема о спектрах).
Если 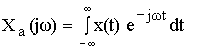
Формула связи спектров дискретного и аналогового сигналов имеет вид:
Вывод: спектр дискретного сигнала равен сумме равно-смещенных спектров аналогового сигнала, сдвинутых на величину кратных 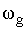
Полученный результат продемонстрируем на графиках.
Если 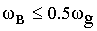
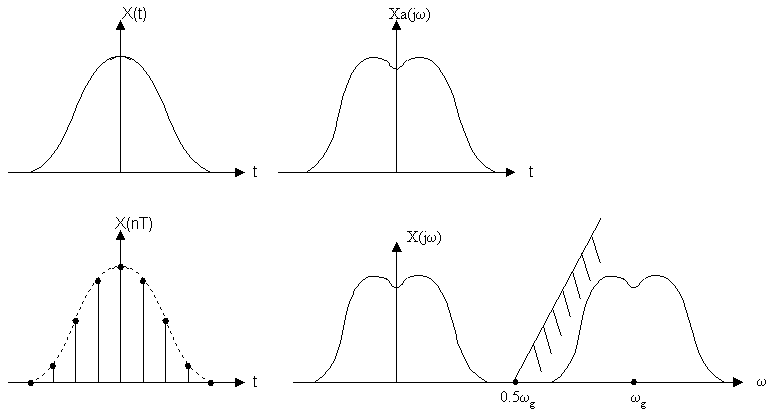
Если ωв>0.5ω g , то смежные спектры перекрываются и возникают ошибки наложения, погрешности (не устранимые), поэтому восстановить такой сигнал можно только с искажением (искажения могут оказаться значительными).
§3 Преобразования Фурье и Лапласа для дискретных сигналов.
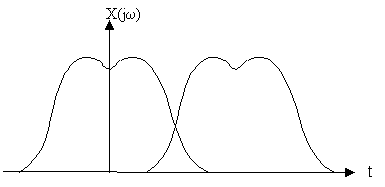
Формула Фурье для дискретного сигнала:

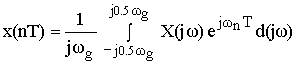
Сигнал x ( nT ) нормирован по отношению к X .
После денормирования сигнала формулу записываем в виде:
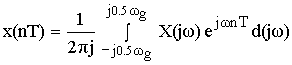
Устремляем T к нулю. Если 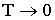
Денормированные формулы прямого и обратного преобразования Фурье для непрерывных сигналов:
Это доказывает справедливость формулы Фурье для дискретного сигнала. Переменную ω можно распространить на всю плоскость комплексного переменного: 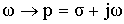
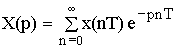
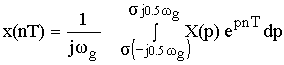
§4 Z – преобразования.
Изображение по Лапласу дискретных сигналов X ( p ) является функцией трансцендентной, что значительно затрудняет частотный анализ дискретных сигналов. Переменную p , находящуюся в показателе экспоненты, заменяют:
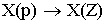
X ( Z ) – Z -изображение дискретного сигнала x ( nT ).
Если в формулах Лапласа сделать замену:
В результате получаем формулы Z -преобразования:
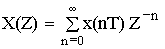
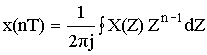
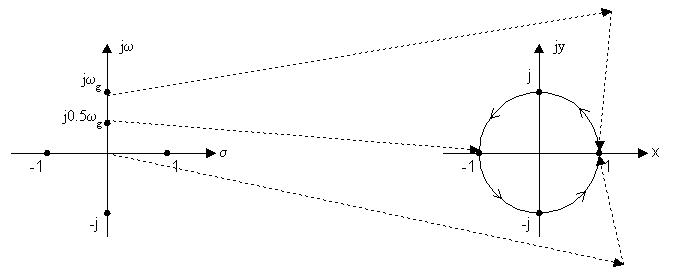
Рассмотрим особенности перехода от плоскости комплексного переменного p = σ + jω к плоскости комплексного переменного Z = x + jy .
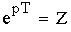
где
Если ω=0.5ω g , то 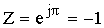
Если ω = ωg , то 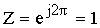
При увеличении переменной ω, переменная Z осуществляет многократное перемещение по единичной окружности.
По изображению X ( Z ) можно получить спектр дискретного сигнала, для этого вместо Z надо подставить:
Точкам в левой полуплоскости комплексного переменного p соответствуют значения переменной внутри единичного круга на плоскости Z .
http://5fan.ru/wievjob.php?id=9983
http://s1921687209.narod.ru/5sem/course112/lec1.htm