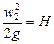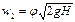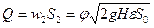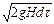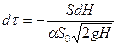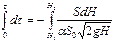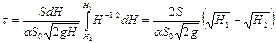Уравнения бернулли и его практические приложения

Некоторые практические приложения уравнения Бернулли

Рассмотрим применение уравнения Бернулли для определения ско­ростей и расходов и времени истечения жидкостей из резервуаров.

Принципы измерения скорости и расхода жидкости. Для определения скоростей и расходов жидкостей в промышленной практике обычно при­меняются дроссельные приборы и пневмометрические трубки.

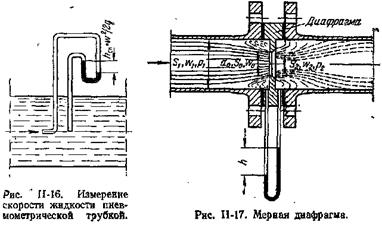
Принцип работы пневмометрических трубок, напри­мер трубки Пито-Прандтля, может быть пояснен с помощью рис. II-16. В каждом сечении разность уровней жидкости в трубках, изображенных на рисунке, выражает скоростной напор h_ск в точке сечения, лежащей на оси трубы.

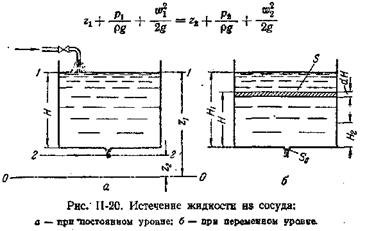
Разность уровней рабочей жидкости в трубках удобнее измерять не посредством пьезометрических трубок, как показано на рис. II-16, а при помощи дифференциального манометра (рис. II-17). Его U-образная трубка заполнена жидкостью, которая не смешивается с рабочей и имеет значительно большую плотность, чем последняя (например, вода или спирт – при работе с газами или ртуть – при работе с капельными жидкостями). Это позволяет измерять перепады давлений в случае значительного избыточного давления (или вакуума) в трубопроводе при относительно небольшой высоте прибора.

По результатам измерений 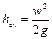находят максимальную скорость жидкости вдоль оси трубопровода. Для определения средней скорости жидкости либо снимают эпюру распределения скоростей по сечению трубопровода (рис. II-10), передвигая пневмометрическую трубку в различные точки сечения, либо используют соотношения между средней и максимальной скоростями при ламинарном и турбулентном режимах течения. Расход жидкости находят, умножая среднюю ско­рость на площадь поперечного сечения трубопровода.

Такой способ определения скорости и расхода жидкости прост, но недостаточно точен из-за трудности установки пневмометрических трубок строго вдоль оси трубопровода.

Более широко распространено определение скоростей и расходов жидкостей с помощью дроссельных приборов, принцип работы которых основан на измерении перепада давлений при изменении поперечного сечения трубопровода. При искусственном сужении сечения потока посредством дроссельного прибора скорость и, соответственно, кинетическая энергия потока в этом более узком сечении возрастают, что приводит к уменьшению потенциальной энергии давления в том же сече­нии. Поэтому, измерив дифференциальным манометром перепад давлений между сечением трубопровода до его сужения и сечением в самом сужении (или вблизи него), можно вычислить изменение скорости между сечениями, а по нему — скорость и расход жидкости.

В качестве дроссельных приборов используют мерные диафрагмы, сопла и трубы Вентури.

Мерная диафрагма (рис. II-17) представляет собой тонкий диск с отверстием круглого сечения, центр которого расположен на оси трубы. Мерное сопло (рис. II-18) является насадкой, имеющим плавно закругленный вход и цилиндрический выход. Дифманометры мерных сопел (а также диафрагм) присоединяют к трубопроводу через кольцевые камеры а, соединенные с внутренним пространством трубопровода отверстиями, равномерно расположенными по окружности, или двумя каналами b.

Труба Вентури (рис. II-19) имеет постепенно сужающееся сечение, которое затем расширяется до первоначального размера. Вслед­ствие такой формы трубы Вентури потеря давления в ней меньше, чем в диафрагмах или соплах. Вместе с тем длина трубы Вентури очень велика по сравнению с толщиной диафрагмы или сопла, которые могут быть уста­новлены между фланцами трубопровода.

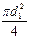
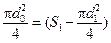
В трубе Вентури и в сопле площадь сечения сжатой струи S₂ = равна площади самого отверстия S₀ — — площадь сечения трубопровода, на котором установлен дроссельный прибор. В диа­фрагме S₂ S₂), а также потеря напора в диафрагме.

Коэффициент a называется коэффициентом расхода дроссельного прибора. Его значение зависит от значения критерия Рейнольдса для жидкости и от отношения диаметра отверстия дроссельного прибора к диаметру трубопровода:

(II,55)

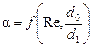
Значения a, определенные опытным путем, приводятся в специальной и справочной литературе.

Диаметр дроссельного устройства обычно в 3-4 раза меньше диаметра трубопровода, поэтому величиной (d₂/d₁) 2 в уравнении (II,54) можно в первом приближении пренебречь и находить расход жидкости по урав­нению

(II,56)

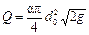
Среднюю скорость жидкости в трубопроводе определяют, разделив Q на площадь сечения трубопровода. Опуская индексы «1» у w₁ и d₁, получим

(II,57)

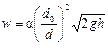
В случае работы со сжимаемыми жидкостями (газом или паром) при больших перепадах давлений в уравнения (II,56) и (II,57) вводят еще один поправочный коэффициент, учитывающий изменение плотности газа (пара).

Истечение жидкостей. Определим расход жидкости при ее истечении через круглое отверстие в тонком днище открытого сосуда, в котором поддерживается постоянный уро­вень H жидкости (рис. II-20, а).

Вытекающая из такого отверстия струя резко сжимается при выходе вследствие инерционного движения частиц жидкости, приближающихся внутри сосуда к отверстию по криволинейным траекториям (некоторые из них даже непосредственно перед выходом еще скользят почти парал­лельно днищу, то есть перпендикулярно оси струи). Расстояние от днища до сжатого сечения (вслед за которым дальнейшее сужение струи из-за увеличения скорости падающей жидкости выражено гораздо слабее) невелико и составляет около половины диаметра отверстия.

Выбрав плоскость сравнения 0—0 параллельной днищу сосуда, напи­шем уравнение Бернулли (считая жидкость идеальной) для сечения 1—1, соответствующего верхнему уровню жидкости в сосуде, и сечения 2—2, плоскость которого проходит через указанное сжатое сечение вытекающей струи:

Для открытого сосуда р₁ = р₂; кроме того, при постоянном уровне жидкости скорость ее w₁ = 0. Пренебрегая небольшим расстоянием от плоскости отверстия в днище сосуда до плоскости сжатого сечения струи, можно принять, что z_l — z₂ » H. Отсюда

(II,58)

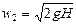
что соответствует известной формуле Торричелли.

При движении реальной жидкости часть напора H теряется на трение и преодоление сопротивления, обусловленного внезапным сужением потока в отверстии. Поэтому скорость реальной жидкости в сжатом сечении:

где j — поправочный коэффициент (j 3 /сек) жидкости равен произведению ее ско­рости w₂ на площадь сжатого сечения S₂ струи. Обозначим отношение S₂ площади поперечного сечения S₀ отверстия в днище через e. Это отно­шение e = S₂/S₀ называют коэффициентом сжатия струи.

(II,59)

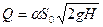
Коэффициент a представляет собой коэффициент расхода и выражается произведением коэффициентов скорости и сжатия струи:

Этот коэффициент определяют опытным путем, его значения зависят от значения критерия Re и могут быть найдены в справочниках в зависи­мости от свойств и скорости жидкости, а также от формы отверстия, его размера и удаленности от стенок сосуда.

Из уравнения (II,59) следует, что расход жидкости, вытекающей через отверстие в тонком днище, зависит от высоты постоянного уровня жидко­сти над отверстием и от размера отверстия, но не зависит от формы сосуда. Это уравнение применимо также для определения расхода жидко­сти, вытекающей через отверстие в тонкой боковой стенке сосуда, если считать Н расстоянием от верхнего уровня жидкости до оси отверстия.

Для жидкостей, по вязкости мало отличающихся от воды, можно при­нимать в первом приближении ее a » 0.62. При истечении жидкости через короткий цилиндрический патрубок (насадок) происходит дополнитель­ная потеря напора на входе и выходе жидкости, что приводит к сниже­нию j. Вместе с тем струя при входе в патрубок после некоторого сжатия снова расширяется и вытекает, заполняя все его сечение, т.е. можно счи­тать e = I. В итоге коэффициент расхода жидкости при истечении через насадок оказывается большим, чем при истечении через отверстие, и для воды может быть принят a » 0.82.

Если сосуд, из которого вытекает жидкость, закрыт и давление р₂ над жидкостью в нем отличается от наружного давления р₁, то при опре­делении расхода по формуле (II,59) вместо H в нее следует подставить 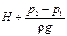, где r — плотность жидкости.

Теперь рассмотрим истечение при переменном уровне жидкости в сосуде с целью определения времени опорож­нения сосудов.

При таком истечении жидкости (рис. II-20,б) ее уровень H в сосуде снижается во времени и, согласно уравнению (II,58), уменьшается также скорость истечения w₀. Следовательно, процесс истечения носит неста­ционарный характер.

Определим время, за которое уровень жидкости в сосуде опустится от первоначальной высоты H₁ до некоторой высоты H₂. За бесконечно малый промежуток времени dt., в соответствии с уравнением (II,59), через отверстие в днище вытечет объем жидкости

dV = Qdt = aS₀

где S₀ — площадь поперечного сечения отверстия в днище сосуда.

За тот же промежуток времени dt уровень жидкости в сосуде пони­зится на бесконечно малую величину dH, и при постоянной площади поперечного сечения S сосуда убыль жидкости в нем составит

Знак минус в правой части указывает на уменьшение высоты жидкости в сосуде.

Приравнивая, согласно уравнению неразрывности потока, эти объемы, получим

aS₀ 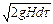= — SdH

Проинтегрируем это выражение, принимая, что коэффициент расхода a постоянен, т.е. не зависит от скорости истечения:

Таким образом, время опорожнения сосуда, имеющего постоянно поперечное сечение, от высоты H₁ до высоты H₂ составляет

(II,61)

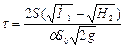
В случае полного опорожнения резервуара H₂ = 0 и уравнение (II,61) принимает вид

(II,61а)

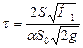
Решая задачу о времени опорожнения сосуда, площадь поперечного сечения которого изменяется по высоте (например, при истечении из конических резервуаров, горизонтальных цистерн и т.п.), следует при интегрировании выражения dt. учесть зависимость площади сечения S от уровня Н жидкости, т.е. учесть вид функции S = f(H).

Уравнение Бернулли и его применение

Разделы: Физика

Цели урока:

• Образовательные: знакомство с принципом Бернулли и его применением в технике и быту;
• Развивающие: развитие навыков проблемного подхода к решению поставленной задачи; развитие логического мышления учащихся; совершенствование умения наблюдать, сравнивать и сопоставлять изучаемые явления, выделять общие признаки и обобщать результаты экспериментов.
• Воспитательные: формирование научного мировоззрения, воспитание интереса и любознательности.

Оборудование: мультимедийный проектор, компьютер, интерактивная доска.

Демонстрационное оборудование: цилиндр Магнуса, по два бумажных листка на каждой парте учащихся, шарики для тенниса, фен, свеча и воронка, компьютерная модель (диск «Открытая физика 1.1»), рисунки.

1. Постановка учебной проблемы (просмотр видеосюжета, слайд 3).

Осенью 1912 г океанский пароход «Олимпик» плыл в открытом море, а почти параллельно ему, на расстоянии сотни метров, проходил с большой скоростью другой корабль, гораздо меньший, броненосный крейсер «Гаук». Когда оба судна заняли положение, изображенное на рисунке , произошло нечто неожиданное: меньшее судно стремительно свернуло с пути, словно повинуясь неведомой силе, повернулось носом к большому кораблю и, не слушаясь руля, двинулось почти прямо на него. «Гаук» врезался носом в бок «Олимпика».Удар был так силен, что «Гаук» проделал в борту «Олимпика» большую пробоину. Случай столкновения двух кораблей рассматривался в морском суде. Капитана корабля «Олимпик» обвинили в том, что он не дал команду пропустить броненосец. Как вы думаете, что произошло? Почему меньший корабль, не слушаясь руля, пошел наперерез «Олимпику»? Смоделируем это явление с помощью двух полосок бумаги.

Опыт 1. Между двумя полосками бумаги продуваем воздух, они сближаются. Скорость воздуха внутри полосок больше, значит давление между листами меньше, чем снаружи.

Парадоксальность результатов такого поведения тел можно объяснить, используя закон Берннули (уравнение Бернулли). Швейцарский ученый Даниил Бернулли длительное время жил в России, именно к этому времени относится создание его главного научного труда — теории гидромеханики. Основная теорема гидродинамики связывает давление жидкости с её скоростью. До сих пор вы рассматривали движение твердых тел. Сегодня мы перенесем знания законов сохранения на движение жидкостей и газов. Будем рассматривать закон Бернулли на качественном уровне.

2. Изучение нового материала.

Пусть жидкость течет без трения по трубе переменного сечения . Иначе говоря, через все сечения трубы проходят одинаковые объемы жидкости, иначе жидкости пришлось бы либо разорваться где-нибудь, либо сжаться, что невозможно. За время t через сечение S₁ пройдет объем

Делаем вывод: скорость течения жидкости в трубе переменного сечения обратно пропорциональна площади поперечного сечения.

Если площадь поперечного сечения увеличилась в 4 раза, то скорость уменьшилась во столько же раз и, наоборот, во сколько раз уменьшилось сечение трубы, во столько же раз увеличилась скорость течения жидкости или газа. Где наблюдается такое явление изменения скорости? Например, на реке, впадающей в море, наблюдается уменьшение скорости, вода из ванны — скорость увеличивается, мы наблюдаем турбулентное течение воды. Если скорость невелика, то жидкость течет как бы разделенная на слои («ламиниа» — слой). Течение называется ламинарным.

Итак, выяснили, что при течении жидкости из узкой части в широкую или наоборот, скорость изменяется, следовательно, жидкость движется с ускорением. А что является причиной возникновения ускорения? (Сила (второй закон Ньютона)). Какая же сила сообщает жидкости ускорение? Этой силой может быть только разность сил давления жидкости в широкой и узкой частях трубы.

К этому выводу впервые пришел академик Петербургской академии наук Даниил Бернулли в 1726 году, и закон теперь носит его имя. Принцип, впервые высказанный Д.Бернулли в 1726 г., гласит: в струе воды или воздуха давление велико, если скорость мала, и давление мало, если скорость велика. Существуют известные ограничения этого принципа, но здесь мы не будем на них останавливаться.

Опыт 2. Работа с интерактивной моделью [5].

Уравнение Бернулли показывает, что давление жидкости (или газа) больше там, где скорость её течения меньше и наоборот. Этот, казалось бы, парадоксальный вывод подтверждается опытами .

Даниил Бернулли (29.1.1700- 17.3.1782), сын Иоганна Бернулли (брат — Якоб Бернулли) . Занимался физиологией и медициной, но больше всего математикой и механикой. В 1725-33 он работал в Петербургской АН сначала на кафедре физиологии, а затем механики. Впоследствии он состоял почётным членом Петербургской АН, опубликовал (с 1728-78) в её изданиях 47 работ. В работах, завершенных написанным в Петербурге трудом «Гидродинамика» (1738), вывел основное уравнение стационарного движения идеальной жидкости, носящее его имя. Даниил Бернулли разрабатывал кинетические представления о газах.После рассмотрения принципа Бернулли можно объяснить причины столкновения двух кораблей .

Объяснение поведения двух листочков при продувании воздуха между ними . Давление воздуха в пространстве левее и правее листочков бумаги равно атмосферному давлению.Направив воздушный поток между листочками, мы тем самим в этом скоростном потоке воздуха создаем область пониженного давления в соответствии с законом Бернулли, в результате чего возникает разность давлений в пространстве между листками и с внешней стороны листков. Эта разность давлений является причиной «прилипания» листочков.

Опыт 3. Взять листок бумаги за короткую сторону и подуть вдоль листа. Лист поднимается вверх. Объяснение опыта: Скорость над листом больше, чем под листом, а давление меньше. Эта разность давлений и поднимает лист вверх .

Аэродинамический принцип создания подъемной силы был изложен Н. Е. Жуковским так: «. двигаясь под малым углом к горизонту с большой горизонтальной скоростью, наклонная плоскость сообщает громадному количеству последовательно прилегающего к ней воздуха малую скорость вниз и тем развивает большую подъемную силу вверх при незначительной затрате работы на горизонтальное перемещение». Следовательно, для создания подъемной силы по этому принципу необходимо перемещение тела относительно воздуха.
Аэродинамический принцип создания подъемной силы используется при подъеме аппарата тяжелее воздуха, к которым относятся планеры и дельтапланы, самолеты и сверхлегкие моторные летательные аппараты, вертолеты и автожиры, летательные аппараты с машущими крыльями (ортоптеры и орнитоптеры).

Подъемная сила у моторного сверхлегкого летательного аппарата создается неподвижно закрепленным крылом. При поступательном движении аппарата крыло обтекается потоком воздуха. Из-за особой формы сечения крыла (несимметричная форма) воздух, огибающий крыло сверху, движется быстрее, чем внизу, поэтому создается разность давлений под крылом и над ним, а в результате возникает подъемная сила. Для моторного аппарата перемещение в воздухе происходит под действием силы тяги, создаваемой силовой установкой.
Планеры, в том числе дельтапланы, создают подъемную силу так же, как моторные аппараты, неподвижно закрепленным крылом, но так как они не имеют силовой установки, то могут только планировать или летать на буксире. При планировании они снижаются за счет силы веса или набирают высоту за счет восходящих потоков воздуха. Подъемная сила появляется при обтекании не всех тел, а лишь тел с определенным профилем. Для крыльев дельтапланов должны применяться профили с хорошими летными характеристиками, создающими большую подъемную силу.

Жуковский Николай Егорович (5.I.1847-17.III.1921). Русский ученый в области механики, основоположник современной гидроаэродинамики. Жуковский является автором многочисленных оригинальных исследований в области механики твердого тела, астрономии, математики, гидродинамики и гидравлики, прикладной механики, теории регулирования машин и др.

Работы Жуковского в области аэродинамики явились источником основных идей, на которых строится авиационная наука. Он всесторонне исследовал динамику полёта птиц, теоретически предсказал ряд возможных траекторий полёта. В 1904 году Жуковский открыл закон, определяющий подъёмную силу крыла самолёта; определил основные профили крыльев и лопастей винта самолёта; разработал вихревую теорию воздушного винта. При его активном участии были созданы Центральный аэродинамический институт (ЦАГИ), Военно-воздушная инженерная академия (ныне носит имя Жуковского).

Проблема изучения подъемной силы имеет очень давнюю историю. Загадки полета птицы занимали умы ученых задолго до появления летательных аппаратов. Первая попытка исследования природы подъемной силы была сделана Леонардо да Винчи в 1505 году. Объясняя причину возникновения подъемной силы птицы, он считал, что из-за быстрых ударов крыльями воздух под ними уплотняется и поэтому поддерживает птицу. Эта гипотеза Леонардо да Винчи, основанная на сжимаемости воздуха, была ошибочной, так как применялась для полета с малыми скоростями, когда свойство сжимаемости воздуха практически не проявляется.

В 1852 году Магнус провел серию опытов для объяснения явления отклонения от вертикальной плоскости вращающихся артиллерийских снарядов. Он показал, что поперечная сила, вызывающая это отклонение, возникает из-за взаимодействия двух потоков воздуха: набегающего на снаряд и вращающегося вместе со снарядом. Это явление, получившее название эффекта Магнуса.

Опыт 4. Для опыта изготовим цилиндр из плотной, но не толстой бумаги диаметром 5 см, длиной 25-30 см. На цилиндр намотаем ленточку, один конец которой прикрепим к линейке. Резким движением вдоль горизонтальной поверхности стола сообщим цилиндру сложное движение (поступательное и вращательное) . При большой скорости цилиндр поднимается вверх и описывает небольшую вертикальную петлю. Объясните, почему это происходит.

Уравнение Бернулли объясняет такое поведение рулона (и закрученного мячика): вращение нарушает симметричность обтекания за счёт эффекта прилипания. С одной стороны бумажного цилиндра скорость потока больше (над цилиндром вектор скорости воздуха сонаправлен вектору скорости цилиндра), значит, давление там понижается, а под цилиндром вектор скорости воздуха антипараллелен вектору скорости цилиндра. В результате разности давлений возникает подъёмная сила, называемая силой Магнуса. Эта сила поднимает цилиндр вверх, а не по параболе.

Это явление носит название эффекта Магнуса, по имени ученого, открывшего и исследовавшего его экспериментально. Эффект Магнуса проявляется в таких природных явлениях, как образование смерчей над поверхностью океана. В месте встречи двух воздушных масс с разными температурами и скоростями возникает вращающийся вокруг вертикальной оси столб воздуха и несется вперед. В поперечнике такой столб может достигать сотен метров и несется со скоростью около 100м/с. Из-за быстрого вращения воздух отбрасывается к периферии вихря и давление внутри него понижается. Когда такой столб приближается к воде, то засасывает ее в себя, представляя огромную опасность для судов.

3. Закрепление нового материала.

По рисункам и демонстрациям объясните наблюдаемые явления (Слайд 12).

Опыт 5. «Демон» Бернулли.

Струя воздуха может поддерживать легкий шарик (например мяч для настольного тенниса). Воздушная струя ударяется о шарик и не дает ему падать. Когда шарик выскакивает из струи, окружающий воздух возвращает его обратно в струю, т.к. давление окружающего воздуха, имеющего малую скорость, велико, а давление воздуха в струе, имеющего большую скорость, мало. Дополнительная подъемная сила может возникать из-за вращения мяча вследствие эффекта Магнуса, который проявляется и при полете закрученного бейсбольного мяча. (Нередко подъемную силу, возникающую в рассматриваемом случае, ошибочно объясняют уменьшением давления в воздушной струе вследствие движения воздуха. Это неправильное истолкование смысла уравнения Бернулли. На самом деле давление в свободно движущейся воздушной струе равно атмосферному. Если насадка на шланг пылесоса сужается (как это обычно бывает), то скорость воздушного потока увеличивается, а давление уменьшается. Таким оно остается и в струе, пока в нее не будет «затянут» окружающий воздух. Тогда давление станет равным атмосферному. Поперечная устойчивость мяча объясняется уменьшением давления в струе, обтекающей мяч.)

Опыт 6. Воздух продувается между двумя воздушными шариками, подвешенными на нитях. Шарики сближаются и ударяются друг о друга.

Опыт 7. Напротив воронки зажигаем свечу. Через воронку продуваем воздух, пламя свечи отклоняется в сторону воронки.

Обсуждение рисунков (Слайд 14).

Ситуация 1. Ветер под зданием. В США был предложен проект жилого дома, в котором этажи, подобно мостам, «подвешиваются» между двумя мощными стенами, а пространство под домом остается открытым . Внешне такое здание выглядит весьма привлекательно, но оно абсолютно не пригодно для ветреных районов. Одно из таких зданий было выстроено на территории Массачусетского технологического института. И вот когда подули весенние ветры, скорость ветра под зданием достигла 160 км/ч. Чем вызвано столь сильное увеличение скорости ветра? (Ветер, попадающий на здание, частично прогоняется через нижний просвет. При этом скорость его возрастает).

Ситуация 2. Встречные поезда. Скоростные поезда . при встрече должны замедлить ход, иначе стекла в вагонах разобьются. Почему? В какую сторону при этом выпадают стекла: внутрь вагонов или наружу? Может ли случиться подобное, если поезда движутся в одном направлении? Будет ли вас притягивать к поезду или отталкивать от него, если вы окажетесь слишком близко от быстро идущего поезда?

(Впереди быстро идущего поезда создается фронт высокого давления, а за ним — область низкого давления. Когда встречные поезда разъезжаются, стекла в вагонах могут быть выдавлены наружу, поскольку между поездами возникает область пониженного давления).

Ситуация 3. Крылья и вентиляторы на гоночных автомобилях. Гоночные автомобили за время своего существования претерпели существенные изменения. К числу наиболее значительных усовершенствований можно отнести установку в задней части автомобиля горизонтального крыла. Когда автомобиль с таким крылом совершал поворот, водитель наклонял крыло вперед. При выходе из поворота, крыло снова принимало горизонтальное положение. Это устройство оказалось очень эффективным средством удержания машины на дороге во время поворотов и позволяло делать повороты с гораздо большей скоростью. Однако поломка таких крыльев на трассе делала машину неуправляемой, и поэтому пришлось установить неподвижные крылья. Каким образом крылья — подвижные или неподвижные — могут удерживать автомобиль на повороте?

Одна из самых странных гоночных машин «Чаппараль-2.1» была построена Джимом Холлом, который придумал и подвижное крыло. Почти 20 лет прошло с момента первых экспериментов легендарного Джима Холла с «машиной-крылом» Chapparal-Chevrolet до победы в Гран При «гоночного пылесоса», целиком и полностью обязанного своим преимуществом «граунд-эффекту». «Чаппараль» имел в задней части два больших вентилятора, которые засасывали воздух из-под днища и гнали его назад. Сбоку автомобиль был закрыт щитками почти до самой дороги, чтобы воздух проходил прямо под машиной. Благодаря этому Холлу удалось увеличить сцепление колес с дорогой и тем самым значительно повысить скорость автомобиля. Почему воздух, прогоняемый под машиной и выпускаемый позади, усиливает сцепление колес с дорогой? Можете ли вы оценить увеличение сцепления и скорости?

(Наклоненное вниз крыло создавало силу, направленную вниз; тем самым улучшалось сцепление колес с дорогой. Это позволяло машине быстрее проходить повороты. Аэродинамическая сила крыла здесь создавалась так же, как и на самолете, только в данном случае она была направлена вниз. Вентилятор в задней части автомобиля тоже создавал направленную вниз силу, увеличивающую сцепление колес с дорогой. Воздух, который засасывался под автомобиль, ускорялся, так как сечение воздушного потока уменьшалось. Согласно уравнению Бернулли, увеличение скорости потока сопровождается понижением давления. Таким образом, давление над автомобилем оказывалось выше, чем под ним, и автомобиль почти в полтора раза сильнее прижимался к дороге).

Ситуация 4. «Ветроход». Всегда находятся люди, способные увидеть то, чего не замечают другие, и обладающие неиссякаемой пытливостью — этим неотъемлемым качеством всех изобретателей. Таким человеком был немецкий инженер Антон Флеттнер (1885-1961). Однажды, наблюдая во время плавания на паруснике за усилиями матросов, работавших в шторм с парусами на высоте 40-50 м, он подумал: а нельзя ли чем-нибудь заменить классический парус, используя при этом все ту же силу ветра? Размышления заставили Флеттнера вспомнить о его соотечественнике физике Генрихе Густаве Магнусе. В качестве первого опытного судна для его испытания использовали видавшую виды трехмачтовую шхуну «Букау» водоизмещением 980 т. В 1924 году на ней вместо трех мачт поставили два ротора-цилиндра высотой 13,1 м и диаметром 1,5 м. Их приводили в движение два электромотора постоянного тока напряжением 220 В. Объясните принцип действия такого «ветрохода» . (Если на поверхность вращающегося ротора воздействует ветер, скорость последнего изменяется. Там, где поверхность движется навстречу ветру, его скорость уменьшается, а давление увеличивается. С противоположной же стороны ротора скорость воздушного потока, наоборот, увеличивается, а давление падает. Полученная разность давлений и создает движущую силу, которую можно использовать для перемещения судна).

Магнус в 1852 г доказал, возникающая поперечная сила, действующая на тело, вращающееся в обтекающем его потоке жидкости или газа, направлена в сторону, где скорость потока и вращение тела совпадают. Наличие такого эффекта Магнус подтвердил позже на опыте с весами. На одну из их чаш клали горизонтально цилиндр с подключенным к нему моторчиком, а на другую — уравновешивавшие гири. Цилиндр обдували воздухом, но, пока не включали моторчик, он оставался неподвижным, и равновесие весов не нарушалось. Однако стоило лишь запустить моторчик и тем самым заставить цилиндр вращаться, как чаша, где он находился, или поднималась, или опускалась — в зависимости от того, в каком направлении шло вращение. Этим опытом ученый установил: если на вращаемый цилиндр набегает поток воздуха, то скорости потока и вращения по одну сторону цилиндра складываются, по другую же — вычитаются. А поскольку большим скоростям соответствуют меньшие давления, на вращаемом цилиндре, помещенном в поток воздуха, возникает движущая сила, перпендикулярная потоку. Ее можно увеличивать или уменьшать, если крутить цилиндр быстрее или медленнее. Именно опыты Магнуса и навели Флеттнера на мысль заменить парус на судне вращающимся цилиндром. Но сразу же возникли сомнения. Ведь на большом судне такие роторы будут выглядеть огромными башнями высотой 20-25 м, которые в шторм создадут колоссальную опасность для судна. На эти вопросы требовалось ответить, и Флеттнер начал свои исследования, которые завершились созданием первого «ветрохода» — трехмачтовая шхуна «Букау».

Ситуация 5. В дождливую ветряную погоду, каждый из нас замечал, что раскрытые зонтики иногда «выворачиваются наизнанку» . Почему это происходит? Аналогичное действие производит на крыши домов сильный ураган. (Поток воздуха, набегающий на изогнутую поверхность зонта, движется по руслу своеобразной сужающейся трубы с большей скоростью, чем воздух в нижней части, следовательно, давление снизу больше, чем вверху, и зонт выворачивается)

Ситуация 6. В футболе одним из коварных ударов для вратаря считается так называемый «сухой лист» . Похожий подрезанный удар — «сплин» применяют в теннисе и других играх с мячом. Предвидеть, куда направится такой крученый мяч, неопытному спортсмену довольно трудно. Объясните, почему так происходит. («Виновата» во всем сила Магнуса, проявляющаяся при движении закрученного вдоль своей оси симметричного тела — мяча, цилиндра и т.п.).

Уравнение Бернулли просто объясняет множество явлений, происходящих в жидкости и газе. Это возникновение подъемной силы крыла, работа таких приборов как пульверизатор, карбюратор, газовой горелки и многое другое. Жизнь самого Даниила Бернулли похожа на его замечательное уравнение. Движение по разным городам и странам, взаимодействие со многими учеными, периодическое расширение и сжатие научных интересов в конечном итоге привели к результатам, которыми до сих пор пользуется человечество, находя все новые и новые применения.

Рефлексия. Конструирование бумажного самолетика. Чей самолет имеет большую дальность полета?

Домашнее задание. Применение закона Бернулли и эффекта Магнуса (рисунки, кроссворды, презентации, стихи)

Процессы и аппараты химической технологии. Гидромеханические процессы (стр. 2 )

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4

Таким образом, получаем:

или после сокращения на :

Система уравнений (1.21) представляет собой дифференциальные уравнения движения Эйлера для установившегося потока идеальной жидкости.

Решение уравнений Эйлера (1.21) для установившегося потока идеальной жидкости приводит к широко используемому уравнению гидродинамики: уравнению Бернулли, которое представляет собой частный случай закона сохранения энергии. При движении жидкости по трубопроводу без дополнительного подвода энергии или ее отвода удельная энергия жидкости, по закону сохранения энергии, остается неизменной. Согласно уравнению Бернулли, для установившегося потока идеальной капельной жидкости сумма удельных энергий положения (z), давления () и удельной кинетической энергии () одинакова для любого поперечного сечения потока:

Уравнение (1.22) представляет собой уравнение Бернулли для идеальной жидкости.

В частности для сечений 1-1 и 2-2:

.

Каждое слагаемое в уравнении Бернулли (1.22) выражается в метрах столба движущейся жидкости и называется, соответственно, геометрическим, пьезометрическим и скоростным (динамическим) напорами. Так

.

Сумма называется гидродинамическим напором. Согласно уравнению Бернулли, для всех поперечных сечений установившегося потока идеальной жидкости величина гидродинамического напора остаётся постоянной.

На рис.1.4 показано, что с помощью пьезометрической трубки энергия давления (напор) может быть измерена. Она равна высоте, на которую под действием давления поднимется жидкость ; Аналогично можно измерить геометрический и скоростной напоры. Для горизонтального трубопровода (рис. 1.4) при проведении плоскости сравнения по оси потока (z=0) уравнение Бернулли примет вид:

.

Рис.1.4 К выводу уравнения Бернулли для горизонтального потока:

1 — трубопровод; 2 – пьезометрическая трубка; 3 – трубка для измерения суммарного напора (статического и скоростного)

Реальная жидкость обладает вязкостью. Поэтому в правую часть уравнения Бернулли (1.23) вводится дополнительное слагаемое , учитывающее потерю энергии (напора), на преодоление гидравлического сопротивления между сечениями. Тем самым сохраняется равенство (баланс) напоров (или энергий) в любом сечении потока

.

Таким образом, при установившемся движении вязкой жидкости сумма геометрического, пьезометрического, скоростного и потерянного напоров в каждом сечении потока есть величина постоянная и равная общему гидродинамическому напору H (рис. 1.5).

Рис. 1.5. Графическая интерпретация уравнения Бернулли

Гидравлическое сопротивление обусловлено вязкостью жидкости, трением жидкости о шероховатые стенки трубы и местными сопротивлениями , возникающими при изменении скорости потока, или его направления. Таким образом, . Потеря напора на трение пропорциональна скоростному напору и определяется по уравнению Дарси-Вейсбаха:

,

где — коэффициент трения, зависящий от критерия Re и шероховатости труб (безразмерный); — длина трубы, м; — эквивалентный диаметр трубы, м.

Для потери давления (с учётом того, что )

.

Потеря напора на местные сопротивления:

,

где — сумма местных сопротивлений, находится в [1].

К местным сопротивлениям относятся вход и выход потока в трубу и из неё, внезапное сужение и расширение труб, отводы, колена, запорные и регулирующие устройства (краны, вентили, задвижки) и др.

Так как все напоры имеют размерность длины, то на рис. 1.5 (для трубопровода переменного сечения) они представлены вертикальными отрезками, а их сумма – гидродинамический напор, представлен отрезком H. Сумма геометрического, пьезометрического и скоростного напоров называется гидродинамическим напором.

Практическое приложение уравнения Бернулли

Уравнение Бернулли используется для расчёта скорости и расхода жидкости, а также времени истечения жидкости из отверстия в резервуаре. Для определения расхода жидкости и газа по сечению потока устанавливают специальные устройства (местные сопротивления) и замеряют разность давлений до и после устройства. Зная эту разность давлений, с помощью уравнения Бернулли находят искомый расход. Приборы, используемые для замеров перепадов давлений, называются дроссельными. К ним относятся мерные диафрагмы, сопла и трубы Вентури.

Определим скорость жидкости при её истечении из отверстия сосуда, в котором поддерживается постоянный уровень жидкости H (рис. 1.6). Истечение происходит из среды с атмосферным давлением в среду с таким же давлением. Составим уравнение Бернулли (1.23) для идеальной жидкости относительно сечений I –I и II –II. Сечение II –II, проходящее через отверстие в резервуаре примем за плоскость сравнения (нулевую плоскость)

.

Для сечения I –I напор z1=H, а для сечения II –II напор z2=0. Сосуд открыт, следовательно, р1=р2. При постоянном уровне жидкости в сечении I –I скорость ω1=0. Преобразовав уравнение Бернулли, получим: , откуда

.

Таким образом, теоретическая скорость истечения для идеальной жидкости ω2 зависит только от высоты столба жидкости в сосуде. Для реальной жидкости вводится ряд дополнительных поправок, которые учитывают изменение скорости жидкости при входе её в отверстие и сжатие струи жидкости при выходе из отверстия.

Рис. 1.6 Истечение жидкости через отверстие в днище сосуда

Режимы движения жидкости. Критерий Рейнольдса

Наиболее полно движение жидкости было исследовано Рейнольдсом в 1883 г. Им было замечено, что при малых скоростях рабочей жидкости потоки последней перемещаются прямолинейно, по параллельным траекториям, не перемешиваясь. Такое движение было названо ламинарным. При увеличении скорости течение жидкости становится волнообразным и, в конце концов, оно переходит в вихревое с интенсивным перемешиванием. Такое движение называется турбулентным. Опыт показывает, что переход от ламинарного режима к турбулентному происходит тем легче, чем больше массовая скорость жидкости (ω·ρ), диаметр трубы (d) и меньше вязкость жидкости (μ). Безразмерный комплекс величин , значение которого позволяет судить о режиме движения жидкости, называется критерием Рейнольдса (Re)

.

При режим движения жидкости будет ламинарным. При режим турбулентный. При переходный режим.

Если жидкость движется по трубе круглого сечения, то в формулу (1.29) подставляют внутренний диаметр трубы . Если жидкость движется по каналу некруглого сечения, то подставляют, так называемый, эквивалентный диаметр , равный отношению учетверённой площади сечения потока к смоченному периметру канала:

.

Рассмотрим движение жидкости по трубе постоянного поперечного сечения. Жидкость перемещается по трубопроводам и аппаратам вследствие перепада давления, создаваемого разностью уровней жидкости или работой насосов. Вследствие влияния сил вязкости (трения) скорость частиц жидкости в разных точках поперечного сечения потока неодинакова: по оси потока она максимальна, а у стенок трубы практически равна нулю. В инженерных расчётах обычно используют среднюю скорость.

Уравнения объёмного (V) и массового (М) расходов имеют вид:

м3/с,

, кг/с,

где — средняя скорость жидкости, м/с; F — площадь поперечного сечения потока, ; — плотность жидкости кг/м3.

Массовая скорость W – это количество жидкости, протекающей через единицу поперечного сечения в единицу времени:

.

Зависимость между массовой и линейной скоростями выражается равенством:

.

Для трубопровода круглого сечения (см. рис.) .

Диаметры труб, по которым течет жидкость или газ, указываются с учетом толщины стенки, например, d=25×2,5 мм. Внутренний диаметр трубы, по которой движется поток, будет равен dВ=25-2,5·2=20 мм.

Уравнение неразрывности (сплошности потока)

Если жидкость протекает по трубопроводу переменного сечения (без отводов и разветвлений), то приход ее массы в сечение 1 (рис. 1.7) , а в сечение 2:

При установившемся режиме . Следовательно: =. Если жидкость несжимаема (), то = или

Рис.1.7. К выводу уравнения неразрывности

В установившемся потоке жидкости средние по сечениям скорости обратно пропорциональны площадям этих сечений, а уравнение неразрывности потока (1.35) выражает закон сохранения массы.

Дифференциальные уравнения движения реальной жидкости (уравнения Навье-Стокса)

При движении реальной жидкости по трубопроводу или аппарату на нее действуют силы тяжести, давления и внутреннего трения (вязкости). В соответствии со вторым законом Ньютона сумма всех действующих в потоке сил равна произведению его массы на ускорение. Дифференциальные уравнения движения реальной (вязкой) жидкости по осям координат имеют вид:

, (1.36)

Здесь, например, для оси x:

— сумма вторых производных скорости по осям координат (оператор Лапласа).

— полная производная скорости по времени (субстанциональная производная).

Уравнения (1.36) представляют собой дифференциальные уравнения Навье-Стокса, описывающие движение вязкой жидкости в трубах, каналах и аппаратах.

При движении идеальной жидкости (), мы получим уравнения движения Эйлера (1.21), как частный случай уравнений Навье-Стокса. Если идеальная жидкость находится в состоянии покоя (), то получим уравнения равновесия Эйлера (1.17).

Если систему уравнений Навье-Стокса дополнить уравнением сплошности (неразрывности) потока, то получим полное описание движения вязкой жидкости. Уравнения Навье-Стокса (1.36) не могут быть решены в общем виде аналитически. Получены решения этой сложной системы уравнений только для некоторых простых частных случаев.

Теория подобия. Критерии гидродинамического подобия

Процессы химической технологии можно изучать теоретически, в результате чего составляются и решаются, чаще всего, дифференциальные уравнения, полностью описывающие процесс. Примерами, широко используемыми в инженерной практике, являются основное уравнение гидростатики и уравнение Бернулли, которые получены решением соответствующих дифференциальных уравнений равновесия и движения Эйлера для идеальной жидкости. Однако многие процессы настолько сложны и часто сопровождаются изменением большого числа параметров (давления, скорости, температуры, вязкости, плотности, геометрических параметров и др.), что полученные для них дифференциальные уравнения не могут быть решены известными в математике методами. Примером могут служит дифференциальные уравнения Навье-Стокса для реальной (вязкой) жидкости, решение которых возможно только в отдельных частных случаях. Поэтому возникает необходимость изучения процесса с помощью экспериментов (опытов), а это возможно только при наличии теории постановки опытов и обработки их результатов. Такой теорией является теория подобия. Она отвечает на вопрос, как нужно ставить опыт и обработать полученные результаты, чтобы их можно было распространить на подобные процессы, протекающие в условиях, отличных от условий опыта. Применение теории подобия позволяет вместо трудоёмких дорогостоящих опытов на промышленном аппарате (натуре) выполнять исследования на лабораторных установках (моделях) значительно меньшего размера. Кроме этого опыты можно проводить не с рабочими (часто вредными и опасными) веществами, а с модельными (например, водой, воздухом и т. д.) в условиях, отличающихся от промышленных. Всё это позволяет упрощать и удешевлять эксперименты, быстрее реализовывать результаты исследований. Согласно теории подобия между моделью и натурным объектом должны существовать геометрическое подобие, подобие физических величин и временное подобие.

Отношение однородных (одноимённых) сходственных величин у натуры и модели называется константой подобия k.

Так, константа геометрического подобия трубопроводов (натуры и модели) выразится: , где ; — длины и диаметры этих трубопроводов.

Константы подобия физических величин (плотности , вязкости , скорости , давления) натурного и модельного потоков в сходственных точках и в соответственные моменты времени выразятся так:

и т. д.

Если в рассматриваемом процессе свойства системы изменяются во времени, то константа временного подобия , указывает на то, что частицы жидкости в трубопроводах (натуре и модели) проходят геометрически подобные траектории за промежутки времени, находящиеся в постоянных соотношениях. Константы подобия или масштабные множители позволяют параметры натурного трубопровода выразить через одноимённые параметры модельного.

Подобие геометрических и физических параметров является необходимым, но недостаточным условием подобия модели и натурного объекта. Необходимо ещё, чтобы в сходственных точках геометрически подобных потоков отношение действующих сил были одинаковыми. Как известно, в потоке вязкой жидкости действуют силы веса (тяжести) и инерции, давления и трения. Соотношения сил давления и инерции, сил тяжести и инерции, сил инерции и трения (вязкости) выражают три безразмерных комплекса величин, являющихся критериями гидродинамического подобия потоков жидкости; они называются соответственно критериями Эйлера (), Фруда () и Рейнольдса (). Выражения этих безразмерных критериев и их физический смысл приводятся в табл. 1.1.

Равенство этих критериев в сходственных точках подобных потоков (натуры и модели) является необходимым условием их гидродинамического подобия (I теорема подобия):

.

Критерии подобия представляют собой отношения разнородных (разноимённых) физических величин и обозначаются начальными буквами имён учёных, внёсших большой вклад в данную область знаний.

Согласно II теореме подобия: решение любого дифференциального уравнения, связывающего между собой переменные, влияющие на процесс, может быть представлено в виде функциональной зависимости между критериями подобия, составленными из этих переменных.

Таким образом, зависимость между отдельными физическими величинами, входящими в уравнение Навье-Стокса (1.36), может быть заменена функциональной зависимостью между критериями подобия:

.

В ряде случае зависимость (1.37) может быть дополнена симплексом геометрического подобия (отношением двух однородных величин в одной и той же системе). При движении потока по трубам или каналам таким симплексом является отношение длины трубы к её диаметру : .

Конкретный вид зависимости (1.37) находится опытным путём.

При решении многих инженерных задач часто требуется определить перепад давления в трубопроводе, который входит в критерий , поэтому критерий Эйлера является определяемым. Остальные критерии (в них входят известные величины) – определяющие.

Т. е. критерий есть некая функция от определяющих критериев: .

В частности, при установившемся вынужденном движении (с помощью насосов и компрессоров) потоков в промышленном трубопроводе, когда определяющими являются силы инерции и трения, а роль силы тяжести (собственного веса потока) неизмеримо мала, критерием Фруда пренебрегают и ограничиваются зависимостью .

Согласно III теореме подобия: явления подобны, если их определяющие критерии равны. Следствием выполнения этого условия будет также равенство критериев Эйлера в сходственных точках подобных потоков.

В ряде случаев трудно вычислить ту или иную физическую величину, входящую в критерий подобия. Тогда эту величину исключают путём сочетания двух или более числа критериев. При этом получают производные критерии, составленные из основных критериев. Так, например, при естественной конвекции, возникающий под действием разности плотностей потока, обусловленной различием температур в разных точках объёма потока, очень трудно определить скорость конвекционных токов. Однако эта скорость входит в критерий Фруда, отражающий подобие таких процессов. Поэтому исключают скорость путём сочетания критериев Рейнольдса и Фруда:

.

Полученный безразмерный комплекс величин является производным критерием (состоит из основных критериев) и называется критерием Галилея (). Он является мерой отношения сил тяжести и трения (вязкости) в подобных потоках.

Если умножить критерий Галилея на дробь ( — плотности жидкости в разных точках), отражающую причину возникновения конвекционных токов, то получим новый производный критерий подобия – критерий Архимеда ().:

.

Основные критерии гидродинамического подобия