Даны уравнения боковых сторон равнобедренного треугольника : x + y − 2 = 0 и 7x − y + 4 = 0 и точка (3 ; 5) на его основании?
Алгебра | 10 — 11 классы
Даны уравнения боковых сторон равнобедренного треугольника : x + y − 2 = 0 и 7x − y + 4 = 0 и точка (3 ; 5) на его основании.
Найти уравнение прямой, на которой лежит основание.
На картинке можно изобразить все графики, хотя это и не столь нужно.
1. Найдем уравнение медианы / .
(2 — x + 7x + 4) / 2 = y ; y = 3 + 3x.
Чтобы было как — то графически было понятно, вы можете взять фиксированный x0 на графике, провести прямую, параллельную оси y через точку x0 и действительно увидеть, что «y» медианы задается как среднее между «y» сторон при неизменном x0.
2. Найдем перпендикулярк медиане.
Нужно найти его угол наклона.
У прямой угол тангенс угла наклона (y / x) равен 3, то тангенс угла перпендикуляра равен — 1 / 3.
Это можно объяснить, например, так.
Нарисуйте треугольник, образованный осью х, прямой 3x + 3 и перпендикуляром, проходящим через совершенно рандомную точку 3x + 3.
Получится прямоугольный треугольник, у которого известен тангенс одного угла tg(f) = 3.
Тогда тангенс второго — это tg(pi / 2 — f) = ctg(f).
Минус ввиду убывания графика перпендикуляра, что важно.
Тогда искомый график имеет вид : y = — 1 / 3(x) + m, где m — параметр, задающий положение графика основания.
Найти его можно, подставив точку (3 ; 5).
Таким образом, m = 6, а ответ : y + 1 / 3x — 6 = 0.
Боковая сторона равнобедренного треугольника в 4 раза больше его основания?
Боковая сторона равнобедренного треугольника в 4 раза больше его основания.
Найдите основание, если оно меньше боковой стороны на 6 см.
Основанием равнобедренного треугольника в два раза меньше его боковой стороны, а периметр треугольника 50дм?
Основанием равнобедренного треугольника в два раза меньше его боковой стороны, а периметр треугольника 50дм.
Найдите основание треугольника.
Периметр равнобедренного треугольника равен 10?
Периметр равнобедренного треугольника равен 10.
Основание равно 4.
Найти боковую сторону.
В равнобедренный треугольник вписана окружность, которая делит боковую сторону точкой касания в отношении 3 : 2, считая от основания?
В равнобедренный треугольник вписана окружность, которая делит боковую сторону точкой касания в отношении 3 : 2, считая от основания.
Найти боковую сторону треугольника, если его периметр равен 48 см.
В равнобедренном треугольнике, угол между боковыми сторонами в 3 раза больше угла при основании?
В равнобедренном треугольнике, угол между боковыми сторонами в 3 раза больше угла при основании.
Периметр равнобедренного треугольника равен 19 см, его боковая сторона на 1 см меньше основания?
Периметр равнобедренного треугольника равен 19 см, его боковая сторона на 1 см меньше основания.
Найдите стороны треугольника через систему уравнений.
Дан равнобедренный треугольник АВС с основанием АВ?
Дан равнобедренный треугольник АВС с основанием АВ.
Через точку А1 на стороне Ас треугольника проведена прямая параллельная его основанию, которая пересекает сторону Вс в точкеВ1.
Докажите что треугольника А1В1С1 тоже равнобедренный.
Периметр равнобедренного треугольника равен 120см ?
Периметр равнобедренного треугольника равен 120см .
Основание равно 50см .
Найти боковую сторону.
Даны уравнения боковых сторон равнобедренного треугольника 3х + у = 0 и х — 3у = 0 и точка М(5 ; 0) на его основании?
Даны уравнения боковых сторон равнобедренного треугольника 3х + у = 0 и х — 3у = 0 и точка М(5 ; 0) на его основании.
Найти периметр и площадь треугольника.
Помогите решить плиз.
Прямая, параллельная основанию равнобедренного треугольника abc , пересекает боковые стороны ab и ac в точках M и N?
Прямая, параллельная основанию равнобедренного треугольника abc , пересекает боковые стороны ab и ac в точках M и N.
Докажите , что треугольник AMN равнобедренный.
На этой странице находится вопрос Даны уравнения боковых сторон равнобедренного треугольника : x + y − 2 = 0 и 7x − y + 4 = 0 и точка (3 ; 5) на его основании?. Здесь же – ответы на него, и похожие вопросы в категории Алгебра, которые можно найти с помощью простой в использовании поисковой системы. Уровень сложности вопроса соответствует уровню подготовки учащихся 10 — 11 классов. В комментариях, оставленных ниже, ознакомьтесь с вариантами ответов посетителей страницы. С ними можно обсудить тему вопроса в режиме on-line. Если ни один из предложенных ответов не устраивает, сформулируйте новый вопрос в поисковой строке, расположенной вверху, и нажмите кнопку.
B ^ 2 + 3 _______ = (b — 1)(b — 3).
У квадрата площадь равна периметру. Например стораны 4 см. Площадь = 4 * 4 = 16. Периметр = 4 + 4 + 4 + 4 = 16.
Y = (x — 4) / (x + 1) y = 1 — 5 / (x + 1) Это гипербола у = — 5 / х во 2 и 4 четверти Строим у = — 5 / х х — 10 — 5 — 2 — 1 — 1 / 2 1 / 2 1 5 10 у 0, 5 1 2, 5 5 10 — 10 — 5 — 1 — 0, 5 Сдвигаем ось оу на 1 вправо, о ось ох на 1 вниз.
Y = √[(x — 4) / (x + 1)] (x — 4) / (x + 1)≥0 x≤ — 1 x≥4 x≠ — 1 корень x = 4 x→ + — ∞ y = 1 / 1 = 1 y’ = [(x — 4) / (x + 1]’ / 2√[(x — 4) / (x + 1)] [(x — 4) / (x + 1]’ = (u / v)’ = 1′ = 1 / v²[u’v — v’u] u = x — 4 u’ = 1 v = x + 1 v’ = 1 (u / v)’ = 1..
Равнобедренные треугольники
Равнобедренный треугольник — это такой треугольник, у которого две стороны равны. Равные стороны называются боковыми. Третья сторона называется основанием.
1. В равнобедренном треугольнике углы при основании равны.
2. В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
3. Высота равнобедренного треугольника, проведенная к основанию, является медианой и биссектрисой.
4. Медиана равнобедренного треугольника, проведенная к основанию, является высотой и биссектрисой.
5. Углы, противолежащие равным сторонам равнобедренного треугольника, всегда острые.
6. В равнобедренном треугольнике:
— биссектрисы, проведенные из вершин при основании, равны;
— высоты, проведенные из вершин при основании, равны;
— медианы, проведенные из вершин при основании, равны.
7. Центры вписанной и описанной окружностей лежат на высоте, биссектрисе и медиане, проведенных к основанию.
8. Вписанная окружность точкой касания делит основание пополам.
Внешним углом треугольника называется угол, смежный с каким-либо углом этого треугольника.
Внешний угол треугольника равен сумме двух углов, не смежных с ним.
$∠BCD$ — внешний угол треугольника $АВС$.
В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.
Соотношение между сторонами и углами в прямоугольном треугольнике:
В прямоугольном треугольнике $АВС$, с прямым углом $С$.
Для острого угла $В$: $АС$ — противолежащий катет; $ВС$ — прилежащий катет.
Для острого угла $А$: $ВС$ — противолежащий катет; $АС$ — прилежащий катет.
- Синусом ($sin$) острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
- Косинусом ($cos$) острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
- Тангенсом ($tg$) острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
- Котангенсом ($ctg$) острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему.
В прямоугольном треугольнике $АВС$ для острого угла $В$:
- В прямоугольном треугольнике синус одного острого угла равен косинусу другого острого угла.
- Синусы, косинусы, тангенсы и котангенсы острых равных углов равны.
- Синусы смежных углов равны, а косинусы, тангенсы и котангенсы отличаются знаками: для острых углов положительные значения, для тупых углов отрицательные значения.
$cos BOA= — cos BOC;$
$ctg BOA= — ctg BOC.$
В треугольнике $ABC$ $AB=BC, AH$ — высота, $AC=34, cos ∠BAC=0.15$. Найдите $CH$.
Так как треугольник $АВС$ равнобедренный, то $∠A=∠С$ (как углы при основании)
Косинусы равных углов равны, следовательно, $cos∠BAC=cos∠ВСА=0.15$
Рассмотрим прямоугольный треугольник $АНС$.
Косинусом ($cos$) острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
Распишем косинус $∠НСА$ (он же $∠ВСА$) по определению:
Из последнего равенства найдем $НС$, для этого $0.15$ представим в виде обыкновенной дроби и воспользуемся свойством пропорции:
Если на сторонах $ВС, АВ$ и продолжении стороны $АС$ треугольника $АВС$ за точку $С$ отмечены соответственно $А_1,С_1,В_1$, лежащие на одной прямой, то
Во всяком треугольнике стороны относятся как синусы противолежащих углов:
В треугольнике $АВС$ $ВС=16, sin∠A=<4>/<5>$. Найдите радиус окружности, описанной вокруг треугольника $АВС$.
Воспользуемся теоремой синусов:
Отношение стороны к синусу противолежащего угла равно двум радиусам описанной окружности
Далее подставим числовые данные и найдем $R$
Квадрат одной из сторон треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними:
Равнобедренный треугольник. Онлайн калькулятор
С помощю этого онлайн калькулятора можно найти неизвестные элементы (стороны, углы) а также периметр, площадь, высоты равнобедренного треугольника. Теоретическую часть и численные примеры смотрите ниже.
| Открыть онлайн калькулятор |
Определение равнобедренного треугольника
Определение 1 (Евклид). Треугольник, в котором длины двух сторон равны между собой называется равнобедренным треугольником.
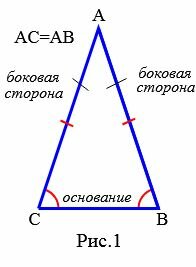
Равные стороны равнобедренного трекугольника называются боковыми сторонами. Третья сторона равнобедренного треугольника называется основанием треугольника (Рис.1).
Угол между боковыми сторонами равнобедненного треугольника (\( \small \angle A \) ) называется вершинным углом. Углы между основанием и боковыми сторонами (\( \small \angle B, \ \angle C \) ) называются углами при основании.
 |
Существует более общее определение равнобедненого треугольника:
Определение 2 (Современная трактовка). Треугольник, в котором длины хотя бы двух сторон равны между собой называется равнобедренным треугольником.
Из определения 2 следует, что равносторонний треугольник является частным случаем равнобедренного треугольника. Действительно, в качестве равных сторон можно взять любые две стороны равностороннего треугольника, а третья сторона будет основанием.
Теорема о равнобедренном треугольнике
Теорема 1. Углы, прилежащие к основанию равнобедренного треугольника равны.
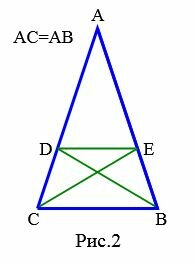 |
Доказательство (доказательство Прокла). Пусть задан равнобедренный треугольник ABC, где AB=AC (Рис.2). Докажем, что \( \small \angle B= \angle C. \) Возьмем любую точку D на стороне AC и точку E на стороне AB так, чтобы AD=AE. Проведем отрезки DE, CE, BD. Треугольники ABD и ACE равны по двум сторонам и углу между ними: AE=AD, AC=AB, угол \( \small \angle A \) общий (см. статью на странице Треугольники. Признаки равенства треугольников). Отсюда следует:
| \( \small CE=BD,\) | (1) |
| \( \small \angle ACE=\angle ABD.\) | (2) |
Из \( \small AB=AC\) и \( \small AD=AE \) следует:
| \( \small CD=BE.\) | (3) |
Рассмотрим треугольники CBE и BCD. Они равны по трем сторонам: \( \small CE=BD,\) \( \small CD=BE ,\) сторона \( \small BC \) общая. Отсюда следует, что
| \( \small \angle ECB= \angle DBC. \) | (4) |
Из (2) и (4) следует, что \( \small \angle B= \angle C. \)
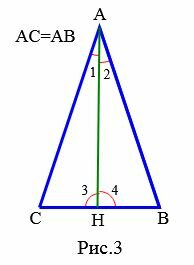 |
Доказательство (Вариант 2). Пусть задан равнобедренный треугольник ABC, где AB=AC (Рис.3). Проведем биссектрису \( \small AH \) треугольника. Тогда \( \small \angle CAH=\angle BAH. \) Докажем, что \( \small \angle B= \angle C. \) Треугольники AHB и AHC равны по двум сторонам и углу между ними: AC=AB, сторона \( \small AH \) общая, \( \small \angle CAH=\angle BAH. \) Отсюда следует: \( \small \angle B= \angle C. \)
Свойства равнобедренного треугольника
Теорема 2. В равнобедренном треугольнике биссектриса проведенная к основанию является медианой и высотой.
Доказательство. Рассмотрим равнобедренный треугольник ABC, где AB=AC, а AH− биссектриса треугольника (Рис.3). Треугольники AHB и AHC равны по двум сторонам и углу между ними: AC=AB, сторона \( \small AH \) общая, \( \small \angle 1=\angle 2. \) Тогда \( \small CH=HB, \) \( \small \angle 3=\angle 4. \) Равенство \( \small CH=HB \) означает, что \( \small AH \) является также медианой треугольника ABC. Углы \( \small \angle 3\) и \( \angle 4 \) смежные. Следовательно их сумма равна 180° и, поскольку эти углы равны, то каждый из этих углов равен 90°. Тогда \( \small AH \) является также высотой треугольника \( \small ABC. \) Поскольку высота \( \small AH \) перпендикулярна к \( \small BC \) и \( \small CH=HB, \) то \( \small AH \) является также серединным перпендикуляром к основанию равнобедренного треугольника.
Мы доказали, что биссектриса, медиана, высота и серединный перпендикуляр равнобедренного треугольника, проведенные к основанию совпадают.
Исходя из теоремы 2 можно сформулировать следующие теоремы, доказательство которых аналогично доказательству теоремы 2:
Теорема 3. В равнобедренном треугольнике медиана проведенная к основанию является биссектрисой и высотой.
Теорема 4. В равнобедренном треугольнике высота проведенная к основанию является биссектрисой и медианой.
Признаки равнобедренного треугольника
Признак 1. Если в треугольнике две стороны равны, то треугольник является равнобедренным.
Признак 1 следует из определения 1.
Признак 2. Если в треугольнике два угла равны, то треугольник является равнобедренным.
Доказательство признака 2 смотрите в статье Соотношения между сторонами и углами треугольника (Следствие 2. Признак равнобедренного треугольника).
Признак 3. Если в треугольнике высота проведенная к одной стороне совпадает с медианой проведенной к этой же стороне, то треугольник является равнобедренным.
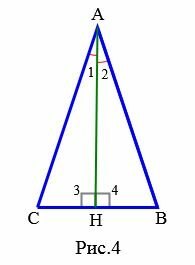
Доказательство. Пусть в треугольнике \( \small ABC \) \( \small AH \) является высотой и медианой (Рис.4). Тогда \( \small \angle 3=\angle4=90°, \) \( \small CH=HB. \) Треугольники \( \small AHC \) и \( \small AHB \) равны по двум сторонам и углу между ними (первый признак равенства треугольников): \( \small AH \) − общая сторона, \( \small CH=HB, \) \( \small \angle 3=\angle4. \) Следовательно \( \small AB=AC. \)
Признак 4. Если в треугольнике высота проведенная к одной стороне совпадает с биссектрисой проведенной к этой же стороне, то треугольник является равнобедренным.
Доказательство. Пусть в треугольнике \( \small ABC \) \( \small AH \) является высотой и биссектрисой (Рис.4). Тогда \( \small \angle 3=\angle4=90°, \) \( \small \angle 1=\angle2. \) Треугольники \( \small AHC \) и \( \small AHB \) равны по стороне и прилежащим двум углам (второй признак равенства треугольников): \( \small AH \) − общая сторона, \( \small \angle 1=\angle 2, \) \( \small \angle 3=\angle4. \) Следовательно \( \small AB=AC. \)
  |
Признак 5. Если в треугольнике биссектриса проведенная к одной стороне совпадает с медианой проведенной к этой же стороне, то треугольник является равнобедренным.
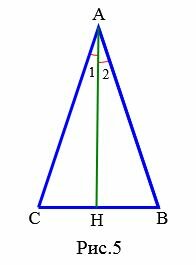
Доказательство (Вариант 1). Пусть в треугольнике \( \small ABC \) \( \small AH \) является биссектрисой и медианой (Рис.5). Тогда
| \( \small \angle 1=\angle2, \) \( \small CH=HB. \) | (5) |
Применим теорему синусов для треугольника \( \small AHC \):
| \( \small \frac <\large CH><\large \sin \angle 1>= \frac <\large AH><\large \sin \angle C>. \) | (6) |
Применим теорему синусов для треугольника \( \small AHB \):
| \( \small \frac <\large HB><\large \sin \angle 2>= \frac <\large AH><\large \sin \angle B>. \) | (7) |
тогда, из (5), (6), (7) получим:
| \( \small \frac <\large AH><\large \sin \angle C>= \frac <\large AH><\large \sin \angle B>. \) | (8) |
Следовательно \( \small \sin \angle C= \sin \angle B. \) Поскольку сумма всех углов треугольника равна 180°, то нам интересует синус углов от 0 до 180°. Учитывая это получим, что синусы углов равны в двух случаях: 1) \( \small \angle C= \angle B, \) 2) \( \small \angle C= 180° — \angle B. \) Поскольку сумма двух углов треугольника меньше 180°: \( \small \angle C + \angle B Доказательство (Вариант 2). Пусть в треугольнике \( \small ABC \) \( \small AH \) является биссектрисой и медианой, т.е. \( \small \angle 1=\angle 2, \) \( \small CH=HB \) (Рис.6). На луче \( \small AH \) отложим отрезок \( \small HD \) так, чтобы \( \small AH=HD. \) Соединим точки \( \small C \) и \( \small D. \)
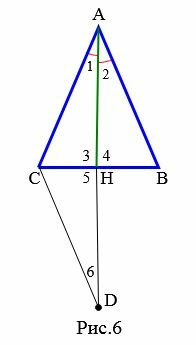 |
Треугольники \( \small AHB \) и \( \small DHC \) равны по двум сторонам и углу между ними (первый признак равенства треугольников). Действительно: \( \small AH=HD, \) \( \small CH=HB, \) \( \small \angle 4=\angle 5 \) (углы 4 и 5 вертикальные). Тогда \( \small AB=CD, \) \( \small \angle 6=\angle 2. \) Отсюда \( \small \angle 6=\angle 1. \) Получили, что треугольник \( \small CAD \) равнобедренный (признак 2). Тогда \( \small AC=CD. \) Но \( \small AB=CD \) и, следовательно \( \small AB=AC. \) Получили, что треугольник \( \small ABC \) равнобедренный.
1. Признак равенства равнобедренных треугольников по основанию и боковой стороне
Если основание и боковая сторона одного равнобедренного треугольника соответственно равны основанию и боковой стороне другого равнобедненного треугольника, то эти треугольники равны.
Действительно. Поскольку треугольник равнобедренный, то боковые стороны равны. То есть три стороны одного равнобедренного треугольника соответственно равны трем сторонам другого равнобедненного треугольника. А по третьему признаку равенства треугольников, эти треугольники равны.
2. Признак равенства равнобедренных треугольников по боковой стороне и углу при вершине
Если боковая сторона и угол при вершине одного равнобедренного треугольники соответственно равны боковой стороне и углу при вершине другого равнобедренного треугольника, то такие треугольники равны.
Действительно. Так как боковые стороны равнобедненного треугольника равны, то имеем: две стороны и угол между ними одного треугольника соотвественно равны двум сторонам и углу между ними другого треугольника. Тогда по первому признаку равенства треугольников, эти реугольники равны.
3. Признак равенства равнобедренных треугольников по основанию и углу при основании
Если основание и угол при основании равнобедренного треугольника соответственно равны основанию и углу при основании другого равнобедренного треугольника, то такие треугольники равны.
Доказательство. В равнобедренном треугольнике углы при основании равны. тогда имеем: основание и две углы одного равнобедненного треугольника равны основанию и двум углам другого равнобедненного треугольника. Тогда эти треугольники равны по второму признаку равенства треугольников.
Задачи и решения
Задача 1. Известны основание \( \small a=5 \) и высота \( \small h=6 \) равнобедренного треугольника. Найти углы, боковые стороны, периметр, площадь.
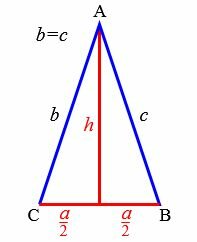 |
Решение. Найдем боковые стороны \( \small b \) и \( \small c \) равнобедренного треугольника. Воспользуемся теоремой Пифагора:
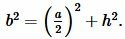 |
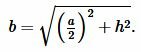 | (9) |
Подставляя значения \( \small a \) и \( \small h \) в (9), получим:
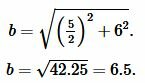 |
Боковая сторона \( \small c \) равнобедренного треугольника равна:
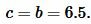 |
Найдем периметр треугольника. Периметр треугольника равен сумме длин его сторон:
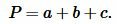 | (10) |
Подставляя значения \( \small a=5, \) \( \small b=6.5 \) и \( \small c=6.5 \) в (10), получим:
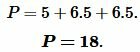 |
Найдем угол \( \small B \) равнобедренного треугольника:
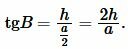 | (11) |
Подставляя значения \( \small a=5, \) \( \small h=6 \) в (11), получим:
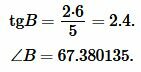 |
Тогда угол \( \small C \) равнобедренного треугольника равен:
 |
Поскольку сумма всех углов треугольника равна 180°, то имеем:
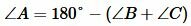 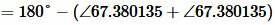 , , |
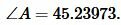 |
Площадь треугольника можно вычислить из формулы:
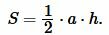 | (12) |
Подставляя значения \( \small a=5, \) \( \small h=6 \) в (12), получим:
http://examer.ru/ege_po_matematike/teoriya/ravnobedrennye_treugolniki
http://matworld.ru/geometry/ravnobedrennyj-treugolnik.php








