Уравнения де бройля и шредингера

Элементы квантовой механики

Корпускулярно-волновой дуализм свойств частиц вещества.

§1 Волны де Бройля

В 1924г. Луи де Бройль (французский физик) пришел к выводу, что двойственность света должна быть распространена и на частицы вещества — электроны. Гипотеза де Бройля заключалась в том, что электрон, корпускулярные свойства которого (заряд, масса) изучаются давно, имеет еще и волновые свойства, т.е. при определенных условиях ведет себя как волна.

Количественные соотношения, связывающие корпускулярные и волновые свойства частиц, такие же, как для фотонов.

Идея де Бройля состояла в том, что это соотношение имеет универсальный характер, справедливый для любых волновых процессов. Любой частице, обладающей импульсом р, соответствует волна, длина которой вычисляется по формуле де Бройля.

— волна де Бройля

p = mv — импульс частицы, h — постоянная Планка.

Волны де Бройля , которые иногда называют электронными волнами, не являются электромагнитными.

В 1927 году Дэвиссон и Джермер ( амер. физик ) подтвердили гипотезу де Бройля обнаружив дифракцию электронов на кристалле никеля. Дифракционные максимумы соответствовали формуле Вульфа — Брэггов 2 dsin j = n l , а брэгговская длина волны оказалась в точности равной .

Дальнейшее подтверждение гипотезы де Бройля в опытах Л.С. Тартаковского и Г. Томсона, наблюдавших дифракционную картину при прохождении пучка быстрых электронов (Е » 50 кэВ) через фольгу из различных металлов. Затем была обнаружена дифракция нейтронов, протонов, атомных пучков и молекулярных пучков. Появились новые методы исследования вещества — нейтронография и электронография и возникла электронная оптика.

Макротела также должны обладать всеми свойствами ( m = 1кг, следовательно, l = 6 . 6 2 · 1 0 — 3 1 м — невозможно обнаружить современными методами — поэтому макротела рассматриваются только как корпускулы).

§2 Свойства волн де Бройля

Пусть частица массы m движется со скоростью v . Тогда фазовая скорость волн де Бройля

Т.к. c > v , то фазовая скорость волн де Бройля больше скорости света в вакууме ( v _ф может быть больше и может быть менше с, в отличие от групповой ).

следовательно, групповая скорость волн де Бройля равна скорости движения частицы.

т.е. групповая скорость равная скорости света.

Волны де Бройля испытывают дисперсию. Подставив в получим, что v_ф = f (λ). Из-за наличия дисперсии волны де Бройля нельзя представить в виде волнового пакета, т.к. он мгновенно “ расплывется “ (исчезнет) за время 10 -26 с.

§3 Соотношение неопределенностей Гейзенберга

Микрочастицы в одних случаях проявляют себя как волны, в других как корпускулы. К ним не применимы законы классической физики частиц и волн. В квантовой физике доказывается, что к микрочастице нельзя применять понятие траектории, но можно сказать, что частица находится в данном объеме пространства с некоторой вероятностью Р. Уменьшая объем, мы будем уменьшать вероятность обнаружить частицу в нем. Вероятностное описание траектории (или положения) частицы приводит к тому, что импульс и, следовательно, скорость частицы может быть определена с какой-то определенной точностью.

Далее, нельзя говорить о длине волны в данной точке пространства и отсюда следует, что если мы точно задаем координату Х, то мы ничего не сможем сказать о импульсе частицы, т.к. . Только рассматривая протяженный участок D C мы сможем определить импульс частицы. Чем больше D C , тем точнее D р и наоборот, чем меньше D C , тем больше неопределенность в нахождении D р .

Соотношение неопределенностей Гейзенберга устанавливает границу в одновременном определении точности канонически сопряженных величин, к которым относятся координата и импульс, энергия и время.

Соотношение неопределенностей Гейзенберга: произведение неопределенностей значений двух сопряженных величин не может быть по порядку величины меньше постоянной Планка h

( иногда записывают )

Таким образом. для микрочастицы не существует состояний, в которых её координата и импульс имели бы одновременно точные значения. Чем меньше неопределенность одной величины, тем больше неопределенность другой.

Соотношение неопределенностей является квантовым ограничением применимости классической механики к микрообъектам.

следовательно, чем больше m , тем меньше неопределенности в определении координаты и скорости. При m = 10 -12 кг , ? = 10 -6 и Δ x = 1% ?, Δv = 6,62·10 -14 м/с, т.е. не будет сказываться при всех скоростях, с которыми пылинки могут двигаться, т.е. для макротел их волновые свойства не играют никакой роли.

Пусть электрон движется в атоме водорода. Допустим Δ x » 1 0 -10 м (порядка размеров атома, т.е. электрон принадлежит данному атому). Тогда

Δv = 7,27· 1 0 6 м/с. По классической механике при движении по радиусу r » 0 , 5 · 1 0 — 1 0 м v = 2,3·10 -6 м/с. Т.е. неопределенность скорости на порядок больше величины скорости, следовательно, нельзя применять законы классической механики к микромиру.

Из соотношения следует, что система имеющая время жизни D t , не может быть охарактеризована определенным значением энергии. Разброс энергии возрастает с уменьшением среднего времени жизни. Следовательно, частота излученного фотона также должна иметь неопределенность D n = D E / h , т.е. спектральные линии будут иметь некоторую ширину n ± D E / h , будут размыты. Измерив ширину спектральной линии можно оценить порядок времени существования атома в возбужденном состоянии.

§4 Волновая функция и ее физический смысл

Дифракционная картина, наблюдающаяся для микрочастиц, характеризуется неодинаковым распределением потоков микрочастиц в различных направлениях — имеются минимумы и максимумы в других направлениях. Наличие максимумов в дифракционной картине означает, что в этих направлениях распределяются волны де Бройля с наибольшей интенсивностью. А интенсивность будет максимальной, если в этом направлении распространяется максимальное число частиц. Т.е. дифракционная картина для микрочастиц является проявлением статистической (вероятностной) закономерности в распределении частиц: где интенсивность волны де Бройля максимальная, там и частиц больше.

Волны де Бройля в квантовой механике рассматриваются как волны вероятности, т.е. вероятность обнаружить частицу в различных точках пространства меняется по волновому закону ( т.е.

е — iωt ). Но для некоторых точек пространства такая вероятность будет отрицательной (т.е. частица не попадает в эту область). М. Борн ( немецкий физик ) предположил, что по волновому закону меняется не сама вероятность, а амплитуда вероятности, которую также называют волновой функцией или y -функцией (пси — функцией).

Волновая функция — функция координат и времени.

Квадрат модуля пси-функции определяет вероятность того, что частица будет обнаружена в пределах объема dV — физический смысл имеет не сама пси-функция, а квадрат ее модуля.

Ψ * — функция комплексно сопряженная с Ψ

Если частица находится в конечном объеме V , то возможность обнаружить ее в этом объеме равна 1, (достоверное событие)

Р = 1 Þ

В квантовой механике принимается, что Ψ и АΨ, где А = const , описывают одно и то же состояние частицы. Следовательно,

интеграл по , означает, что он вычисляется по безграничному объему (пронстранству).

y — функция должна быть

1) конечной (так как Р не может быть больше1),

2) однозначной (нельзя обнаружить частицу при неизменных условиях с вероятностью допустим 0,01 и 0,9, так как вероятность должна быть однозначной).

непрерывной (следует из неприрывности пространства. Всегда имеется вероятность обнаружить частицу в разных точках пространства, но для разных точек она будет разная),
Волновая функция удовлетворяет принципусуперпозиции: если система может находится в различных состояниях, описываемых волновыми функциями y ₁ , y ₂ . y _n , то она может находится в состоянии y , описываемой линейной комбинаций этих функций:

С _n ( n =1,2. ) — любые числа.

С помощью волновой функции вычисляются средние значения любой физической величины частицы

§5 Уравнение Шредингера

Уравнение Шредингера, как и другие основные уравнения физики (уравнения Ньютона, Максвелла), не выводится, а постулируется. Его следует рассматривать как исходное основное предположение, справедливость которого доказывается тем, что все вытекающие из него следствия точно согласуются с экспериментальными данными.

(1)

— Временное уравнение Шредингера.

— набла — оператор Лапласа

— потенциальная функция частицы в силовом поле,

Ψ( y , z , t ) — искомая функция

Если силовое поле, в котором движется частица, стационарно (т.е. не изменяется с течением времени), то функция U не зависит от времени и имеет смысл потенциальной энергии. В этом случае решение уравнения Шредингера (т.е. Ψ — функция) может быть представлено в виде произведения двух сомножителей — один зависит только от координат, другой — только от времени:

(2)

Е — полная энергия частицы, постоянная в случае стационарного поля.

(3)

— Уравнение Шредингера для стационарных состояний.

Имеется бесконечно много решений. Посредством наложения граничных условий отбирают решения, имеющие физический смысл.

волновые функции должны быть регулярными, т.е.

Решения, удовлетворяющие уравнению Шредингера, называются собственными функциями, а соответствующие им значения энергии — собственными значениями энергии. Совокупность собственных значений называется спектром величины. Если Е _n принимает дискретные значения, то спектр — дискретный, если непрерывные — сплошной или непрерывный.

§6 Движение свободной частицы

Частица называется свободной, если на нее не действуют силовые поля, т.е. U = 0.

Уравнение Шредингера для стационарных состояний в этом случае:

И собственные значения энергии:

Т.к. k может принимать любые значения, то, следовательно, и Е принимает любые значения, т.е. энергетический спектр будет сплошным.

Временная волновая функция

(- уравнение волны)

т.е. представляет плоскую монохромную волну де Бройля.

§7 Частица в “потенциальной яме” прямоугольной формы.

Квантование энергии.

Найдем собственные значения энергии и соответствующие им собственные функции для частицы, находящейся в бесконечно глубокой одномерной потенциальной яме. Предположим что, частица может двигаться только вдоль оси x . Пусть движение ограничено непроницаемыми для частицы стенками x = 0, и x = ?. Потенциальная энергия U имеет вид:

Уравнение Шредингера для стационарных состояний для одномерной задачи

За пределы потенциальной ямы частица попасть не сможет, поэтому вероятность обнаружения частицы вне ямы равна 0.Следовательно, и Ψ за пределами ямы равна 0 .Из условий непрерывности следует, что Ψ = 0 и на границах ямы т.е.

В пределах ямы (0 £ x £ l ) U = 0 и уравнение Шредингера.

введя получим

;

из граничных условий следует

Из граничного условия

Энергия Е _n частицы в «потенциальной яме» с бесконечно высокими стенками принимает лишь определенные дискретные значения, т.е. квантуется. Квантованные значения энергии Е _n называются уровнями энергии, а число n , определяющее энергические уровни частицы, называется главным квантовым числом. Т.е. частицы в «потенциальной яме» могут находиться только на определенном энергетическом уровне Е _n (или находятся в квантовом состоянии n )

Собственные функции:

А найдем из усилия нормировки

— плотность вероятности. Из рис. видно, что плотность вероятности меняется в зависимости от n : при n = 1 частица, скорее всего, будет посередине ямы, но не на краях, при n = 2 — будет или в левой или в правой половине, но не посередине ямы и не на краях, и т.д. Т.е нельзя говорить о траектории движения частицы.

Энергетический интервал между соседними уровнями энергии:

При n = 1 имеет наименьшую энергию отличную от нуля

Наличие минимума энергии следует из соотношения неопределенностей, т.к.,

C ростом n расстояние между уровнями уменьшается и при n ® ¥ Е _n практически непрерывны, т.е. дискретность сглаживается, т.е. выполняется принцип соответствия Бора: при больших значениях квантовых чисел законы квантовой механики переходят в законы классической физики.

Общая трактовка принципа соответствия: всякая новая, более общая теория является развитием классической, не отвергает ее полностью, а включает в себя классическую, указывая границы её применимости.

§ 8 Туннельный эффект.

Прохождение частицы через потенциальный барьер

Для классической частицы : при Е > U она пройдет над барьером, при Е U — отразится от него; для квантовой : при Е > U есть вероятность того, что частица отразится, при Е U есть вероятность того, что пройдет сквозь барьер.

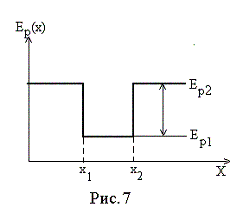
Потенциальная энергия:

Уравнение Шредингера: для области 1 и 3 :

для области 2:

Решение этих диф. уравнений;

Для 1;

Для 2;

Для 3:

Т.к. в области 3 возможно распределение только прошедшей волны, то, Þ , В₃=0.

В области 2 решение зависит от соотношений Е > U или Е U . Физический интерес представляет случай Е U .

q = i b , где

Тогда решение уравнения Шредингера запишутся в виде:

Для 1;

Для 2;

Для 3:

Качественный вид функций показан на рис. 2. Из рис. 2 видно, что функция не равна нулю внутри барьера, а в 3 имеет вид волны де Бройля, если барьер не очень широк.

Явление “проникновения” частицы сквозь потенциальный барьер, называется туннельным эффектом. Туннельный эффект является специфическим квантовым эффектом. Прохождение частицы можно объяснить используя соотношения неопределенностей: неопределенность импульса D р на отрезке D x = ? составляет . Связанная с этим разбросом в значениях импульса кинетическая энергия может оказаться достаточной для того, чтобы полная энергия частицы оказалась больше потенциальной энергии барьера.

§9 Линейный гармонический осциллятор

Линейный гармонический осциллятор — система, совершающая одномерное колебательное движение под действием квазиупругой силы — является моделью для изучения колебательного движения.

В классической физике — это пружинный, физический и математический маятники. В квантовой физике — квантовый осциллятор.

Записав потенциальную энергию в виде

Уравнение Шредингера запишется в виде:

Тогда собственные значения энергии:

т.е. энергия квантового осциллятора принимает дискретные значения, т.е. квантуется. Минимальное значение — энергия нулевых колебаний — является следствием состояния неопределенности так же, как и в случае частицы в “потенциальной яме”.

Наличие нулевых колебаний означает, что частицы не могут упасть на дно ямы, т.к. в этом случае был бы точно определен ее импульс p = 0, D p = 0, Þ , D x = ¥ — не соответствует соотношению неопределенностей. Наличие энергии нулевых колебаний противоречит классическим представлениям, по которым E _min = 0. — уровни энергии расположенные на равных расстояниях друг от друга. Из квантового рассмотрения следует, что частицу можно обнаружить вне области. По классическому рассмотрению только в пределах – x £ x £ x (Рис.2).

Уравнение Шрёдингера

Дуальная корпускулярно-волновая природа квантовых частиц описывается дифференциальным уравнением.

Согласно фольклору, столь распространенному среди физиков, случилось это так: в 1926 году физик-теоретик по имени Эрвин Шрёдингер выступал на научном семинаре в Цюрихском университете. Он рассказывал о странных новых идеях, витающих в воздухе, о том, что объекты микромира часто ведут себя скорее как волны, нежели как частицы. Тут слова попросил пожилой преподаватель и сказал: «Шрёдингер, вы что, не видите, что всё это чушь? Или мы тут все не знаем, что волны — они на то и волны, чтобы описываться волновыми уравнениями?» Шрёдингер воспринял это как личную обиду и задался целью разработать волновое уравнение для описания частиц в рамках квантовой механики — и с блеском справился с этой задачей.

Тут необходимо сделать пояснение. В нашем обыденном мире энергия переносится двумя способами: материей при движении с места на место (например, едущим локомотивом или ветром) — в такой передаче энергии участвуют частицы — или волнами (например, радиоволнами, которые передаются мощными передатчиками и ловятся антеннами наших телевизоров). То есть в макромире, где живём мы с вами, все носители энергии строго подразделяются на два типа — корпускулярные (состоящие из материальных частиц) или волновые. При этом любая волна описывается особым типом уравнений — волновыми уравнениями. Все без исключения волны — волны океана, сейсмические волны горных пород, радиоволны из далеких галактик — описываются однотипными волновыми уравнениями. Это пояснение нужно для того, чтобы было понятно, что если мы хотим представить явления субатомного мира в терминах волн распределения вероятности (см. Квантовая механика), эти волны также должны описываться соответствующим волновым уравнением.

Шрёдингер применил к понятию волн вероятности классическое дифференциальное уравнение волновой функции и получил знаменитое уравнение, носящее его имя. Подобно тому как обычное уравнение волновой функции описывает распространение, например, ряби по поверхности воды, уравнение Шрёдингера описывает распространение волны вероятности нахождения частицы в заданной точке пространства. Пики этой волны (точки максимальной вероятности) показывают, в каком месте пространства скорее всего окажется частица. Хотя уравнение Шрёдингера относится к области высшей математики, оно настолько важно для понимания современной физики, что я его все-таки здесь приведу — в самой простой форме (так называемое «одномерное стационарное уравнение Шрёдингера»). Вышеупомянутая волновая функция распределения вероятности, обозначаемая греческой буквой ψ («пси»), является решением следующего дифференциального уравнения (ничего страшного, если оно вам не понятно; главное — примите на веру, что это уравнение свидетельствует о том, что вероятность ведёт себя как волна):

где x — расстояние, h — постоянная Планка, а m, E и U — соответственно масса, полная энергия и потенциальная энергия частицы.

Картина квантовых событий, которую дает нам уравнение Шрёдингера, заключается в том, что электроны и другие элементарные частицы ведут себя подобно волнам на поверхности океана. С течением времени пик волны (соответствующий месту, в котором скорее всего будет находиться электрон) смещается в пространстве в соответствии с описывающим эту волну уравнением. То есть то, что мы традиционно считали частицей, в квантовом мире ведёт себя во многом подобно волне.

Когда Шрёдингер впервые опубликовал свои результаты, в мире теоретической физики разразилась буря в стакане воды. Дело в том, что практически в то же время появилась работа современника Шрёдингера — Вернера Гейзенберга (см. Принцип неопределенности Гейзенберга), в которой автор выдвинул концепцию «матричной механики», где те же задачи квантовой механики решались в другой, более сложной с математической точки зрения матричной форме. Переполох был вызван тем, что ученые попросту испугались, не противоречат ли друг другу два в равной мере убедительных подхода к описанию микромира. Волнения были напрасны. Сам Шрёдингер в том же году доказал полную эквивалентность двух теорий — то есть из волнового уравнения следует матричное, и наоборот; результаты же получаются идентичными. Сегодня используется в основном версия Шрёдингера (иногда его теорию называют «волновой механикой»), так как его уравнение менее громоздкое и его легче преподавать.

Однако представить себе и принять, что нечто вроде электрона ведёт себя как волна, не так-то просто. В повседневной жизни мы сталкиваемся либо с частицей, либо с волной. Мяч — это частица, звук — это волна, и всё тут. В мире квантовой механики всё не так однозначно. На самом деле — и эксперименты это вскоре показали — в квантовом мире сущности отличаются от привычных нам объектов и обладают другими свойствами. Свет, который мы привыкли считать волной, иногда ведёт себя как частица (которая называется фотон), а частицы вроде электрона и протона могут вести себя как волны (см. Принцип дополнительности).

Эту проблему обычно называют двойственной или дуальной корпускулярно-волновой природой квантовых частиц, причем свойственна она, судя по всему, всем объектам субатомного мира (см. Теорема Белла). Мы должны понять, что в микромире наши обыденные интуитивные представления о том, какие формы может принимать материя и как она себя может вести, просто неприменимы. Сам факт, что мы используем волновое уравнение для описания движения того, что привыкли считать частицами, — яркое тому доказательство. Как уже отмечалось во Введении, в этом нет особого противоречия. Ведь у нас нет никаких веских оснований полагать, будто то, что мы наблюдаем в макромире, должно с точностью воспроизводиться на уровне микромира. И тем не менее дуальная природа элементарных частиц остается одним из самых непонятных и тревожащих аспектов квантовой механики для многих людей, и не будет преувеличением сказать, что все беды начались с Эрвина Шрёдингера.

Волны де Бройля. Волновая функция и ее физический смысл. Уравнение Шредингера. Электрон в потенциальном ящике.

В 1923 году произошло примечательное событие, которое в значительной степени ускорило развитие квантовой физики. Французский физик Л. де Бройль выдвинул гипотезу об универсальности корпускулярно-волнового дуализма. Де Бройль утверждал, что не только фотоны, но и электроны и любые другие частицы материи наряду с корпускулярными обладают также и волновыми свойствами.

Согласно де Бройлю, с каждым микрообъектом связаны, с одной стороны, корпускулярные характеристики – энергия E и импульс p, а с другой стороны, волновые характеристики – частота ν и длина волны λ.

Корпускулярные и волновые характеристики микрообъектов связаны такими же количественными соотношениями, как и у фотона:

Гипотеза де Бройля постулировала эти соотношения для всех микрочастиц, в том числе и для таких, которые обладают массой m. Любой частице, обладающей импульсом, сопоставлялся волновой процесс с длиной волны λ = h / p. Для частиц, имеющих массу,

В нерелятивистском приближении (υ

В следующем 1928 году английский физик Г. Томсон (сын Дж. Томсона, открывшего за 30 лет до этого электрон) получил новое подтверждение гипотезы де Бройля. В своих экспериментах Г. Томсон наблюдал дифракционную картину, возникающую при прохождении пучка электронов через тонкую поликристаллическую фольгу из золота.

Впоследствии дифракционные явления были обнаружены также для нейтронов, протонов, атомных и молекулярных пучков. Экспериментальное доказательство наличия волновых свойств микрочастиц привело к выводу о том, что это универсальное явление природы, общее свойство материи. Следовательно, волновые свойства должны быть присущи и макроскопическим телам. Однако вследствие большой массы макроскопических тел их волновые свойства не могут быть обнаружены экспериментально. Например, пылинке массой 10 –9 г, движущийся со скоростью 0,5 м/с соответствует волна де Бройля с длиной волны порядка 10 –21 м, т. е. приблизительно на 11 порядков меньше размеров атомов. Такая длина волны лежит за пределами доступной наблюдению области. Этот пример показывает, что макроскопические тела могут проявлять только корпускулярные свойства.

Таким образом, подтвержденная экспериментально гипотеза де Бройля о корпускулярно-волновом дуализме коренным образом изменила представления о свойствах микрообъектов.

Всем микрообъектам присущи и волновые, и корпускулярные свойства, однако, они не являются ни волной, ни частицей в классическом понимании. Разные свойства микрообъектов не проявляются одновременно; они дополняют друг друга, и только их совокупность характеризует микрообъект полностью. В этом заключается сформулированный знаменитым датским физиком Н. Бором принцип дополнительности. Можно условно сказать, что микрообъекты распространяются как волны, а обмениваются энергией как частицы.

С точки зрения волновой теории, максимумы в картине дифракции электронов соответствуют наибольшей интенсивности волн де Бройля. В области максимумов, зарегистрированных на фотопластинке, попадает большее число электронов. Но процесс попадания электронов в различные места на фотопластинке не индивидуален. Принципиально невозможно предсказать, куда попадет очередной электрон после рассеяния, существует лишь определенная вероятность попадания электрона в то или иное место. Таким образом, описание состояния микрообъекта и его поведения может быть дано только на основе понятия вероятности.

Необходимость вероятностного подхода к описанию микрообъектов является важнейшей особенностью квантовой теории. В квантовой механике для характеристики состояний объектов в микромире вводится понятие волновой функции Ψ (пси-функции). Квадрат модуля волновой функции |Ψ| 2 пропорционален вероятности нахождения микрочастицы в единичном объеме пространства. Конкретный вид волновой функции определяется внешними условиями, в которых находится микрочастица. Математический аппарат квантовой механики позволяет находить волновую функцию частицы, находящейся в заданных силовых полях. Безграничная монохроматическая волна де Бройля есть волновая функция свободной частицы, на которую не действуют никакие силовые поля.

Наиболее отчетливо дифракционные явления проявляются в тех случаях, когда размеры препятствия, на котором происходит дифракция волн, соизмеримы с длиной волны. Это относится к волнам любой физической природы и, в частности, к электронным волнам. Для волн де Бройля естественной дифракционной решеткой является упорядоченная структура кристалла с пространственным периодом порядка размеров атома (приблизительно 0,1 нм). Препятствие таких размеров (например, отверстие в непрозрачном экране) невозможно создать искусственно, но для уяснения природы волн де Бройля можно ставить мысленные эксперименты.

Уравнение Шредингера. Электрон в потенциальном ящике.Потенциальным “ящиком” называют потенциальную яму с вертикальными стенками (рис. 7). Область пространства с координатами от x₁до x₂на рис. 7 и есть потенциальный “ящик”. В реальной действительности такая ситуация наблюдается, например, для электронов в металле: внутри металла они свободны, но чтобы покинуть металл, электроны должны совершить работу выхода А_вых, равную

Рассмотрим простейший пример решения уравнения Шрёдингера для частицы, находящейся в потенциальном ящике с бесконечно высокими стенками (т.е. на границах ящика E_p ® ¥ , рис.8). Это, безусловно, идеализация. В действительности стенки ящика будут всегда конечной высоты. Однако на данной модели наиболее просто показать, что дает решение уравнения Шрёдингера. Итак, рассмотрим одномерный потенциальный ящик с бесконечно высокими стенками (рис.8). Ширина ящика l. Внутри ящика Е_p = 0,т.е.частица свободна. Уравнение Шрёдингера для этого случая примет вид:

Граничные условия: 1) при x = 0 y (0) = 0, 2) при x = l y (l) = 0.

(25) (26)

Смысл этих условий прост: частица не может находиться на стенках ящика, так как значение Е_p = ¥ не имеет физического смысла.

(27)

Смысл его: частица достоверно находится внутри ящика, т.е. в области координат 0

источники:

http://elementy.ru/trefil/21/Uravnenie_Shryodingera

http://megalektsii.ru/s67505t3.html