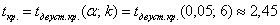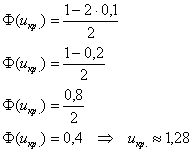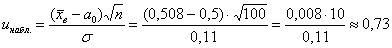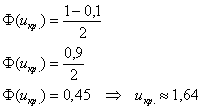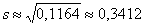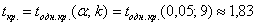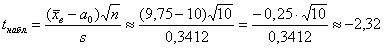Нормальное распределение (Гаусса) в Excel
В статье подробно показано, что такое нормальный закон распределения случайной величины и как им пользоваться при решении практически задач.
Нормальное распределение в статистике
История закона насчитывает 300 лет. Первым открывателем стал Абрахам де Муавр, который придумал аппроксимацию биномиального распределения еще 1733 году. Через много лет Карл Фридрих Гаусс (1809 г.) и Пьер-Симон Лаплас (1812 г.) вывели математические функции.
Лаплас также обнаружил замечательную закономерность и сформулировал центральную предельную теорему (ЦПТ), согласно которой сумма большого количества малых и независимых величин имеет нормальное распределение.
Нормальный закон не является фиксированным уравнением зависимости одной переменной от другой. Фиксируется только характер этой зависимости. Конкретная форма распределения задается специальными параметрами. Например, у = аx + b – это уравнение прямой. Однако где конкретно она проходит и под каким наклоном, определяется параметрами а и b. Также и с нормальным распределением. Ясно, что это функция, которая описывает тенденцию высокой концентрации значений около центра, но ее точная форма задается специальными параметрами.
Кривая нормального распределения Гаусса имеет следующий вид.
График нормального распределения напоминает колокол, поэтому можно встретить название колоколообразная кривая. У графика имеется «горб» в середине и резкое снижение плотности по краям. В этом заключается суть нормального распределения. Вероятность того, что случайная величина окажется около центра гораздо выше, чем то, что она сильно отклонится от середины.
На рисунке выше изображены два участка под кривой Гаусса: синий и зеленый. Основания, т.е. интервалы, у обоих участков равны. Но заметно отличаются высоты. Синий участок удален от центра, и имеет существенно меньшую высоту, чем зеленый, который находится в самом центре распределения. Следовательно, отличаются и площади, то бишь вероятности попадания в обозначенные интервалы.
Формула нормального распределения (плотности) следующая.
Формула состоит из двух математических констант:
π – число пи 3,142;
е – основание натурального логарифма 2,718;
двух изменяемых параметров, которые задают форму конкретной кривой:
m – математическое ожидание (в различных источниках могут использоваться другие обозначения, например, µ или a);
ну и сама переменная x, для которой высчитывается плотность вероятности.
Конкретная форма нормального распределения зависит от 2-х параметров: математического ожидания (m) и дисперсии ( σ 2 ). Кратко обозначается N(m, σ 2 ) или N(m, σ). Параметр m (матожидание) определяет центр распределения, которому соответствует максимальная высота графика. Дисперсия σ 2 характеризует размах вариации, то есть «размазанность» данных.
Параметр математического ожидания смещает центр распределения вправо или влево, не влияя на саму форму кривой плотности.
А вот дисперсия определяет остроконечность кривой. Когда данные имеют малый разброс, то вся их масса концентрируется у центра. Если же у данных большой разброс, то они «размазываются» по широкому диапазону.
Плотность распределения не имеет прямого практического применения. Для расчета вероятностей нужно проинтегрировать функцию плотности.
Вероятность того, что случайная величина окажется меньше некоторого значения x, определяется функцией нормального распределения:
Используя математические свойства любого непрерывного распределения, несложно рассчитать и любые другие вероятности, так как
P(a ≤ X 0 =1 и остается рассчитать только соотношение 1 на корень из 2 пи.
Таким образом, по графику хорошо видно, что значения, имеющие маленькие отклонения от средней, выпадают чаще других, а те, которые сильно отдалены от центра, встречаются значительно реже. Шкала оси абсцисс измеряется в стандартных отклонениях, что позволяет отвязаться от единиц измерения и получить универсальную структуру нормального распределения. Кривая Гаусса для нормированных данных отлично демонстрирует и другие свойства нормального распределения. Например, что оно является симметричным относительно оси ординат. В пределах ±1σ от средней арифметической сконцентрирована большая часть всех значений (прикидываем пока на глазок). В пределах ±2σ находятся большинство данных. В пределах ±3σ находятся почти все данные. Последнее свойство широко известно под названием правило трех сигм для нормального распределения.
Функция стандартного нормального распределения позволяет рассчитывать вероятности.
Понятное дело, вручную никто не считает. Все подсчитано и размещено в специальных таблицах, которые есть в конце любого учебника по статистике.
Таблица нормального распределения
Таблицы нормального распределения встречаются двух типов:
— таблица плотности;
— таблица функции (интеграла от плотности).
Таблица плотности используется редко. Тем не менее, посмотрим, как она выглядит. Допустим, нужно получить плотность для z = 1, т.е. плотность значения, отстоящего от матожидания на 1 сигму. Ниже показан кусок таблицы.
В зависимости от организации данных ищем нужное значение по названию столбца и строки. В нашем примере берем строку 1,0 и столбец 0, т.к. сотых долей нет. Искомое значение равно 0,2420 (0 перед 2420 опущен).
Функция Гаусса симметрична относительно оси ординат. Поэтому φ(z)= φ(-z), т.е. плотность для 1 тождественна плотности для -1, что отчетливо видно на рисунке.
Чтобы не тратить зря бумагу, таблицы печатают только для положительных значений.
На практике чаще используют значения функции стандартного нормального распределения, то есть вероятности для различных z.
В таких таблицах также содержатся только положительные значения. Поэтому для понимания и нахождения любых нужных вероятностей следует знать свойства стандартного нормального распределения.
Функция Ф(z) симметрична относительно своего значения 0,5 (а не оси ординат, как плотность). Отсюда справедливо равенство:
Это факт показан на картинке:
Значения функции Ф(-z) и Ф(z) делят график на 3 части. Причем верхняя и нижняя части равны (обозначены галочками). Для того, чтобы дополнить вероятность Ф(z) до 1, достаточно добавить недостающую величину Ф(-z). Получится равенство, указанное чуть выше.
Если нужно отыскать вероятность попадания в интервал (0; z), то есть вероятность отклонения от нуля в положительную сторону до некоторого количества стандартных отклонений, достаточно от значения функции стандартного нормального распределения отнять 0,5:
Для наглядности можно взглянуть на рисунок.
На кривой Гаусса, эта же ситуация выглядит как площадь от центра вправо до z.
Довольно часто аналитика интересует вероятность отклонения в обе стороны от нуля. А так как функция симметрична относительно центра, предыдущую формулу нужно умножить на 2:
Под кривой Гаусса это центральная часть, ограниченная выбранным значением –z слева и z справа.
Указанные свойства следует принять во внимание, т.к. табличные значения редко соответствуют интересующему интервалу.
Для облегчения задачи в учебниках обычно публикуют таблицы для функции вида:
Если нужна вероятность отклонения в обе стороны от нуля, то, как мы только что убедились, табличное значение для данной функции просто умножается на 2.
Теперь посмотрим на конкретные примеры. Ниже показана таблица стандартного нормального распределения. Найдем табличные значения для трех z: 1,64, 1,96 и 3.
Как понять смысл этих чисел? Начнем с z=1,64, для которого табличное значение составляет 0,4495. Проще всего пояснить смысл на рисунке.
То есть вероятность того, что стандартизованная нормально распределенная случайная величина попадет в интервал от 0 до 1,64, равна 0,4495. При решении задач обычно нужно рассчитать вероятность отклонения в обе стороны, поэтому умножим величину 0,4495 на 2 и получим примерно 0,9. Занимаемая площадь под кривой Гаусса показана ниже.
Таким образом, 90% всех нормально распределенных значений попадает в интервал ±1,64σ от средней арифметической. Я не случайно выбрал значение z=1,64, т.к. окрестность вокруг средней арифметической, занимающая 90% всей площади, иногда используется для проверки статистических гипотез и расчета доверительных интервалов. Если проверяемое значение не попадает в обозначенную область, то его наступление маловероятно (всего 10%).
Для проверки гипотез, однако, чаще используется интервал, накрывающий 95% всех значений. Половина вероятности от 0,95 – это 0,4750 (см. второе выделенное в таблице значение).
Для этой вероятности z=1,96. Т.е. в пределах почти ±2σ от средней находится 95% значений. Только 5% выпадают за эти пределы.
Еще одно интересное и часто используемое табличное значение соответствует z=3, оно равно по нашей таблице 0,4986. Умножим на 2 и получим 0,997. Значит, в рамках ±3σ от средней арифметической заключены почти все значения.
Так выглядит правило 3 сигм для нормального распределения на диаграмме.
С помощью статистических таблиц можно получить любую вероятность. Однако этот метод очень медленный, неудобный и сильно устарел. Сегодня все делается на компьютере. Далее переходим к практике расчетов в Excel.
Нормальное распределение в Excel
В Excel есть несколько функций для подсчета вероятностей или обратных значений нормального распределения.
Функция НОРМ.СТ.РАСП
Функция НОРМ.СТ.РАСП предназначена для расчета плотности ϕ( z ) или вероятности Φ(z) по нормированным данным (z).
z – значение стандартизованной переменной
интегральная – если 0, то рассчитывается плотность ϕ( z ) , если 1 – значение функции Ф(z), т.е. вероятность P(Z
Нормальный закон распределения и его параметры с примерами решения и образцами выполнения
Нормальный закон распределения и его параметры:
Нормальный закон распределения (часто называемый законом Гаусса) играет исключительно важную роль в теории вероятностей и занимает среди других законов распределения особое положение. Это — наиболее часто встречающийся на практике закон распределения. Главная особенность, выделяющая нормальный закон среди других законов, состоит в том, что он является предельным законом, к которому приближаются другие законы распределения при весьма часто встречающихся типичных условиях.
Можно доказать, что сумма достаточно большого числа независимых (или слабо зависимых) случайных величин, подчиненных каким угодно законам распределения (при соблюдении некоторых весьма нежестких ограничений), приближенно подчиняется нормальному закону, и это выполняется тем точнее, чем большее количество случайных величин суммируется. Большинство встречающихся на практике случайных величин, таких, например, как ошибки измерений, ошибки стрельбы и т. д., могут быть представлены как суммы весьма большого числа сравнительно малых слагаемых — элементарных ошибок, каждая из которых вызвана действием отдельной причины, не зависящей от остальных. Каким бы законам распределения ни были подчинены отдельные элементарные ошибки, особенности этих распределений в сумме большого числа слагаемых нивелируются, и сумма оказывается подчиненной закону, близкому к нормальному. Основное ограничение, налагаемое на суммируемые ошибки, состоит в том, чтобы они все равномерно играли в общей сумме относительно малую роль. Если это условие не выполняется и, например, одна из случайных ошибок окажется по своему влиянию на сумму резко превалирующей над всеми другими, то закон распределения этой превалирующей ошибки наложит свое влияние на сумму и определит в основных чертах ее закон распределения.
Теоремы, устанавливающие нормальный закон как предельный для суммы независимых равномерно малых случайных слагаемых, будут подробнее рассмотрены в главе 13.
Нормальный закон распределения характеризуется плотностью вероятности вида:
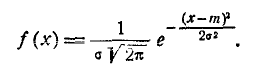
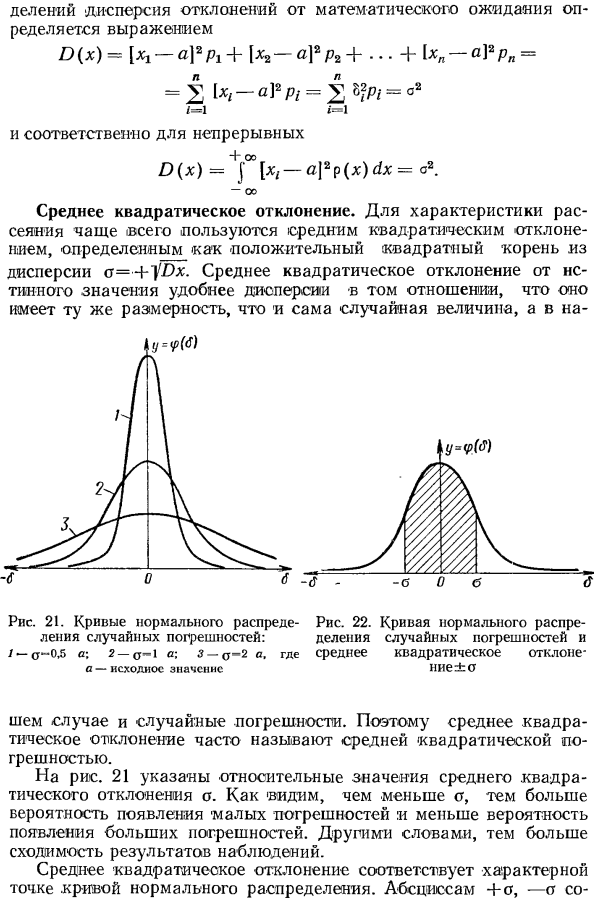
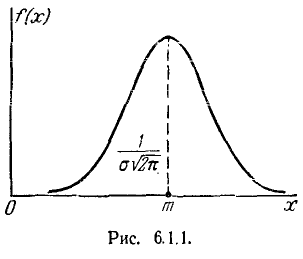
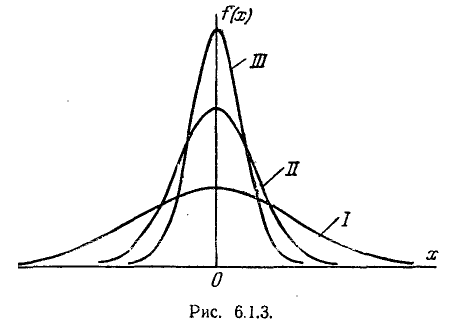
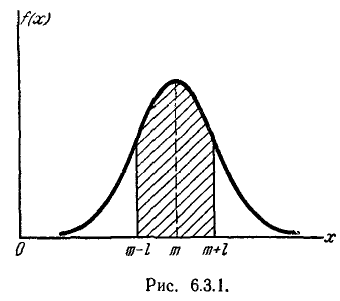
Кривая распределения по нормальному закону имеет симметричный холмообразный вид (рис. 6.1.1). Максимальная ордината кривой, равная 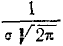
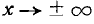
Выясним смысл численных параметров т и о, входящих в выражение нормального закона (5.1.1); докажем, что величина m есть не что иное, как математическое ожидание, а величина 
Применяя замену переменной
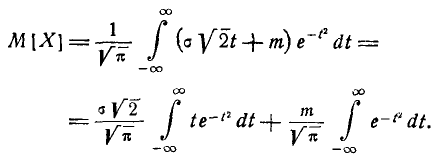
Нетрудно убедиться, что первый из двух интервалов в формуле (5.1.2) равен нулю; второй представляет собой известный интеграл Эйлера — Пуассона:
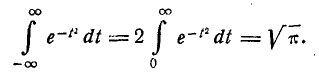
т. е. параметр m представляет собой математическое ожидание вели- величины X. Этот параметр, особенно в задачах стрельбы, часто называют центром рассеивания (сокращенно — ц. р.). Вычислим дисперсию величины X:
Применив снова замену переменной
Интегрируя по частям, получим:
Первое слагаемое в фигурных скобках равно нулю (так как 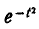
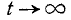
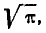
Следовательно, параметр о в формуле 5.1.1) есть не что иное, как среднее квадратическое отклонение величины X.
Выясним смысл параметров m и 
Размерность центра рассеивания—та же, что размерность случайной величины X.
Параметр о характеризует не положение, а самую форму кривой распределения. Это есть характеристика рассеивания. Наибольшая ордината кривой распределения обратно пропорциональна 

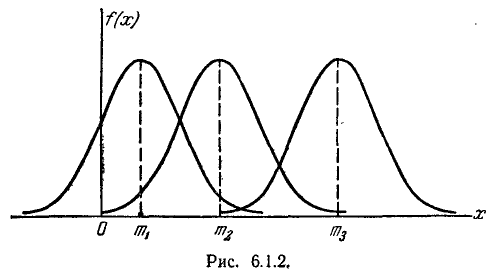
кривой распределения всегда должна оставаться равной единице, то при увеличении о кривая распределения становится более плоской, растягиваясь вдоль оси абсцисс; напротив, при уменьшении 
самому большому, а кривая /// — самому малому значению 

Размерность параметра 
В некоторых курсах теории вероятностей в качестве характеристики рассеивания для нормального закона вместо среднего квадратического отклонения применяется так называемая мера точности. Мерой точности называется величина, обратно пропорциональная среднему квадратическому отклонению 
Размерность меры точности обратна размерности случайной величины.
Термин «мера точности» заимствован из теории ошибок измерений: чем точнее измерение, тем больше мера точности. Пользуясь мерой точности h, можно записать нормальный закон в виде:
Моменты нормального распределения
Выше мы доказали, что математическое ожидание случайной вели- величины, подчиненной нормальному закону 6.1.1), равно m, а среднее квадратическое отклонение равно 
Выведем общие формулы для центральных моментов любого порядка.
Делая замену переменной
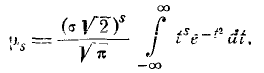
Применим к выражению (6.2.1) формулу интегрирования по частям:
Имея в виду, что первый член внутри скобок равен нулю, получим: 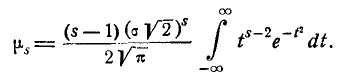
Из формулы (6.2.1) имеем следующее выражение для 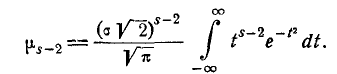
Сравнивая правые части формул (6.2.2) и (6.2.3), видим, что они отличаются между собой только множителем 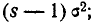
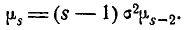
Формула (6.2.4) представляет собой простое рекуррентное соотношение, позволяющее выражать моменты высших порядков через моменты низших порядков. Пользуясь этой формулой и имея в виду, что 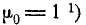


Для четных s из формулы (6.2.4) вытекают следующие выражения для последовательных моментов:
и т. д. Общая формула для момента s-гo порядка при любом четном s имеет вид:
где под символам (s—1)!! понимается произведение всех нечетных чисел от 1 до s— 1. Так как для нормального закона 
Из выражения четвертого момента
‘) Нулевой момент любой случайной величины равен единице как математическое ожидание нулевой степени этой величины.
т. е. эксцесс нормального распределения равен нулю. Это и естественно, так как назначение эксцесса — характеризовать сравнительную крутость данного закона по сравнению с нормальным.
Вероятность попадания случайной величины, подчиненной нормальному закону, на заданный участок. Нормальная функция распределения
Во многих задачах, связанных с нормально распределенными случайными величинами, приходится определять вероятность попадания случайной величины X, подчиненной нормальному закону с параметрами m, 
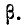
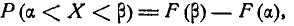
где F (х)— функция распределения величины X.
Найдем функцию распределения F(x) случайной величины X, распределенной по нормальному закону с параметрами m, 
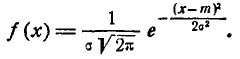
Отсюда находим функцию распределения
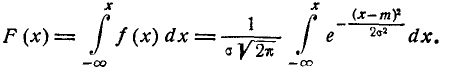
Сделаем в интеграле (6.3.3) замену переменной
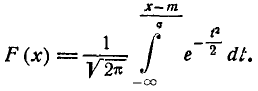
и приведем его к виду:
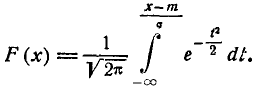
Интеграл (6.3.4) не выражается через элементарные функции, но его можно вычислить через специальную функцию, выражающую определенный интеграл от выражения 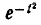
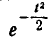
и т. д. Какой из этих функций пользоваться — вопрос вкуса. Мы выберем в качестве такой функции
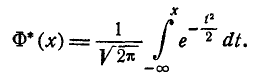
Нетрудно видеть, что эта функция представляет собой не что иное, как функцию распределения для нормально распределенной случайной величины с параметрами от m = 0, 
Условимся называть функцию Ф*(х) нормальной функцией распределения. В приложении (табл. 1) приведены таблицы значений функции Ф*(х)
Выразим функцию распределения (6.3.3) величины X с пара- параметрами m и 
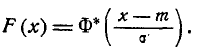
Теперь найдем вероятность попадания случайной величины X на участок от а до 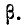
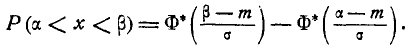
Таким образом, мы выразили вероятность попадания на участок случайной величины X, распределенной по нормальному закону с любыми параметрами, через стандартную функцию распределения Ф* (х), соответствующую простейшему нормальному . закону с параметрами 0,1. Заметим, что аргументы функции Ф* в фор- формуле (6.3.7) имеют очень простой смысл: 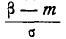
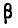
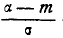
Как и всякая функция распределения,, функция Ф*(х) обладает свойствами:
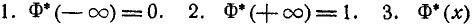
Кроме того, из симметричности нормального распределения с параметрами m = 0, 
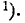
Пользуясь этим свойством, собственно говоря, можно было бы ограничить таблицы функции Ф(х) только положительными значениями аргумента, но, чтобы избежать лишней операции (вычитание из единицы), в таблице 1 приложения приводятся значения Ф(х) как для положительных, так и для отрицательных аргументов.
На практике часто встречается задача вычисления вероятности попадания нормально распределенной случайной величины на участок, симметричный относительно центра рассеивания m. Рассмотрим такой участок длины 2l (рис. 6.3.1). Вычислим вероятность попадания на этот участок по формуле (6.3.7):
Учитывая свойство (6.3.8) функции Ф*(х) и придавая левой части формулы (6.3.9) более компактный вид, получим формулу для вероятности попадания случайной величины, распределенной по нормальному закону, на участок, симметричный относительно центра рассеивания:
Решим следующую задачу. Отложим от центра рассеивания m последовательные отрезки длиной 
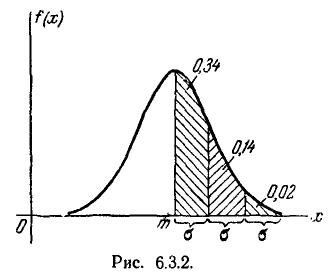
По формуле (6.3.7) находим:
Как видно из этих данных, вероятности попадания на каждый из следующих отрезков (пятый, шестой и т. д.) с точностью до 0,001 равны нулю.
Округляя вероятности попадания в отрезки до 0,01 (до 1%). получим три числа, которые легко запомнить: 0,34; 0,14; 0,02.
Сумма этих трех значений равна 0,5. Это значит, что для нормально распределенной случайной величины все рассеивание (с точностью до долей процента) укладывается на участке m± З
Это позволяет, зная среднее квадратическое отклонение и математическое ожидание случайной величины, ориентировочно указать интервал ее практически возможных значений. Такой способ оценки диапазона возможных значений случайной величины известен в математической статистике под названием «правило трех сигма«. Из правила трех сигма вытекает также ориентировочный способ определения среднего квадратического отклонения случайной величины: берут максимальное практически возможное отклонение от среднего и делят его на три. Разумеется, этот грубый прием может быть рекомендован, только если нет других, более точных способов определения 
Пример:
Случайная величина X, распределенная по нормальному закону, представляет собой ошибку измерения некоторого расстояния. При измерении допускается систематическая ошибка в сторону завышения на 1,2 (м)\ среднее квадратическое отклонение ошибки измерения равно 0,8 (м). Найти вероятность того, что отклонение измеренного значения от истинного не превзойдет по абсолютной величине 1,6 (м).
Решение:
Ошибка измерения есть случайная величина X, подчинен- подчиненная нормальному закону с параметрами m= 1,2 и 
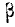
Пользуясь таблицами функции Ф* (х) (приложение, табл. 1), найдем:
откуда Р (—1,6 Закон нормального распределения случайных величин



Решение заданий и задач по предметам:
Дополнительные лекции по теории вероятностей:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
11. Статистические гипотезы
Надо сказать, капитально я «подзавяз» в интегралах, диффурах и тервере, и после основательной доработки этих разделов безмерно рад напечатать первый абзац 11-й статьи по матстату.
Есть ли жизнь после сессии смерти? Далеко не каждая гипотеза является статистической, и перед тем как перейти к теме, я на всякий случай поставлю ссылку на 1-й урок по математической статистике, если «чайникам» будет что-то не понятно в терминах.
Сначала кратко разберём теорию, затем наиболее распространённые задачи (сразу ссылка для «самоваров»). Зажигаем:
Пусть исследуется некоторый признак статистической совокупности. Успеваемость студентов, продолжительность жизни… каждый подумал о своём, точность измерений, да что угодно – хоть качество помидоров. Всё, что можно «оцифровать» и посчитать.
Как проводится исследование? Обычно так: из генеральной совокупности извлекается репрезентативная выборка (всё понятно?), и на основании изучения этой выборки делается вывод обо всей совокупности. Напоминаю, что это основной метод математической статистики и называется он выборочным методом. В зависимости от исследования, могут проводиться неоднократные выборки, выборки из нескольких ген. совокупностей, да и вообще анализироваться произвольные статистические данные.
И в результате анализа этих данных появляются мысли, которые оформляются в статистические гипотезы.
Статистической называют гипотезу о законе распределения статистической совокупности либо о числовых параметрах известных (!) распределений.
– рост танкистов распределен нормально;
– дисперсии стрельбы двух танковых дивизий равны между собой, при этом известно*, что точность стрельбы распределена нормально.
* из многочисленных ранее проведённых исследований.
В первом случае выдвигается гипотеза о законе распределения, во втором – о числовых характеристиках двух распределений, закон которых известен.
Откуда взялись эти гипотезы? В первом случае была проведена выборка танкистов (например, 100 человек) и в результате её исследования появилось обоснованное предположение, что рост ВСЕХ танкистов распределён нормально. Во втором случае исследовались выборочные данные по точности стрельбы двух дивизий, в результате чего возник интерес проверить – а одинакова ли генеральная результативность, или же какая-то дивизия стреляет точнее?
В обеих гипотезах речь идёт о генеральных совокупностях, и выдвигаются эти гипотезы на основании анализа выборочных данных. Это распространенная схема, но она не единственна, бывают и другие статистические гипотезы.
Выдвигаемую гипотезу называют нулевой и обозначают через 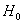
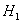
В рассмотренных выше примерах альтернативные гипотезы очевидны (отрицают нулевую), но существуют и другие варианты, так, например, к гипотезе 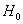
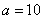
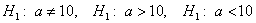
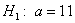
Поскольку нулевая гипотеза выдвигается на основе анализа ВЫБОРОЧНЫХ данных, то она может оказаться как правильной, так и неправильной. Более того, мы не сможем на 100% гарантировать её истинность либо ложность даже после статистической проверки! Ибо любая, самая «надёжная» выборка все равно остаётся выборкой и может нас дезинформировать (пусть с очень малой вероятностью).
Проверка осуществляется с помощью статистических критериев – это специальные случайные величины, которые принимают различные действительные значения. В разных задачах критерии разные, и мы рассмотрим их в конкретных примерах.
В результате проверки нулевая гипотеза либо принимается, либо отвергается в пользу альтернативной. При этом есть риск допустить ошибки двух типов:
Ошибка первого рода состоит в том, что гипотеза 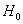
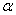
Ошибка второго рода состоит в том, что гипотеза 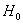
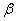
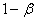
Уровень значимости задаётся исследователем самостоятельно, наиболее часто выбирают значения 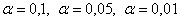
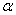
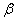
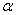
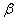
Понятие ошибок 1-го и 2-го рода используется не только в статистике, и для лучшего понимания я как раз приведу нестатистический пример…, опять напрашивается хардкор про диагностику болезни, но мы будем-таки настраиваться на позитив:
Танкист Вася поиграл с котами и зарегистрировался в почтовике. По умолчанию, 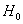
Какая ошибка более «тяжелая»? Васино письмо может быть ОЧЕНЬ важным для адресата, и поэтому при настройке фильтра целесообразно уменьшить уровень значимости 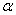
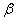
Существует примеры, где наоборот – более тяжкие последствия влечёт ошибка 2-го рода, и вероятность 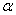
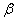
Ну а теперь возвращаемся к статистике.
Процесс проверки статистической гипотезы состоит из следующих этапов:
1) Обработка выборочных данных и выдвижение основной 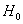
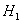
2) Выбор статистического критерия 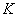
3) Выбор уровня значимости 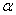
4) Нахождение критического значения 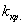
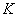
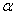
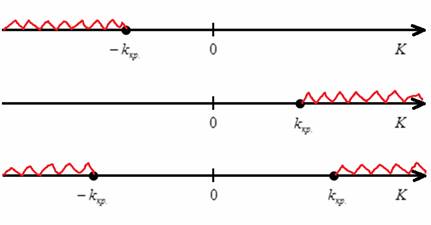
Критическая область – это область отвержения нулевой гипотезы. Незаштрихованную область называют областью принятия гипотезы.
Следует отметить, что это только одна из графических моделей. Существуют статистические критерии, которые принимают далеко не все действительные значения.
5) Далее на основании выборочных данных рассчитывается наблюдаемое значение критерия: 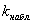
– Если 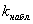
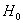
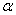
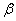
– Если 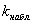
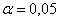
…Ну а что делать? – такая вот статистика неточная наука 🙂
И по горячей информации сразу разберём одну из наиболее распространённых гипотез:
Гипотеза о генеральной средней нормального распределения
Постановка задачи такова: предполагается, что генеральная средняя 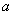
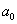
Для проверки гипотезы на уровне значимости 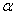
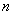
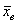
1) 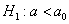
2) 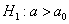
3) 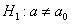
4) 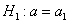
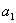
При этом возможны две принципиально разные ситуации:
а) если генеральная дисперсия  известна.
известна.
Тогда в качестве статистического критерия 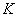
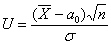
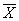
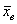
Далее находим критическую область. Для конкурирующих гипотез 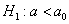
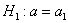
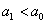
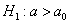
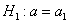
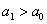
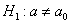
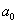
Чтобы найти критическую область нужно отыскать критическое значение 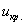
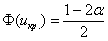
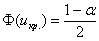
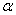
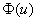
Теперь на основании выборочных данных рассчитываем наблюдаемое значение критерия: 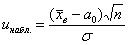
это можно было сделать и раньше, но такой порядок более последователен и логичен.
Результаты:
1) Для левосторонней критической области. Если 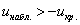
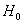
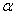
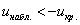
2) Правосторонняя критическая область. Если 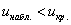
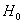
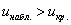
3) Двусторонняя критическая область. Если 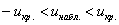
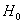

условие принятия гипотезы часто записывают компактно – с помощью модуля:
И немедленно приступаем к задачам, а то по студенческим меркам я тут уже на пол диссертации наговорил:)
Из нормальной генеральной совокупности с известной дисперсией 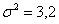
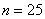
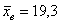
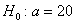
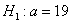
Прежде чем приступить к решению, пару слов о смысле такой задачи. Есть генеральная совокупность с известной дисперсией и есть веские основания полагать, что генеральная средняя равна 20 (нулевая гипотеза). В результате выборочной проверки получена выборочная средняя 19,3, и возникает вопрос: это результат случайный или же генеральная средняя и на самом деле меньше двадцати? – в частности, равна 19 (конкурирующая гипотеза).
Решение: по условию, известна генеральная дисперсия 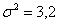
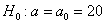
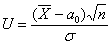
Найдём критическую область. Для этого нужно найти критическое значение. Так как конкурирующее значение 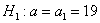
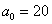
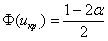
для уровня значимости 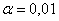
По таблице значений функции Лапласа или с помощью Калькулятора (Пункт 5*) определяем, что этому значению функции соответствует аргумент 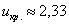
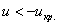
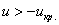
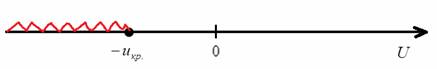
В данном случае 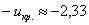
Вычислим наблюдаемое значение критерия:
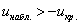
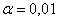
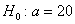
Такой, вроде бы неожиданный результат, объясняется тем, что генеральное стандартное отклонение достаточно великО: 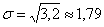
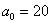
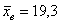
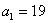
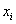
Ответ: на уровне значимости 0,01 нулевую гипотезу принимаем.
Что означает «на уровне значимости 0,01»? Это означает, что мы с 1%-ной вероятностью рисковали отвергнуть нулевую гипотезу, при условии, что она действительно справедлива. Однако не нужно забывать, что на самом деле она может быть и неверной и существует 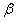
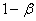
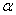
То была «обезличенная» задача, коих очень много, но мы будем менять мир к лучшему… физическими и химическими способами:) Заодно и понятнее будет, что здесь к чему:
По результатам 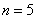
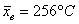
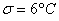

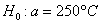
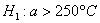
Сначала разберём, в чём жизненность этой ситуации. Есть печка. Для нормального технологического процесса нужна температура 250 градусов. Для проверки этой нормы 5 раз измерили температуру, получили 256 градусов. Из многократных предыдущих опытов известно, что среднеквадратическая погрешность измерений составляет 6 градусов (она обусловлена погрешностью самого термометра, случайными обстоятельствами проверки и т.д.)
И здесь не понятно, почему выборочный результат (256 градусов) получился больше нормы – то ли температура действительно выше и печь нуждается в регулировке, то ли это просто погрешность измерений, которую можно не принимать во внимание.
Решение: по условию, известно ген. среднее квадратическое отклонение 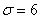
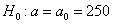
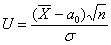
Найдём критическую область. Так как в конкурирующей гипотезе 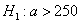
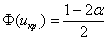
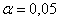
По таблице значений функции Лапласа или с помощью Калькулятора (Пункт 5*) определяем, что 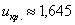
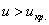
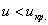
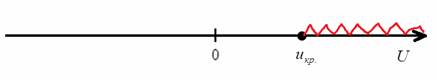
Вычислим наблюдаемое значение критерия:
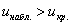
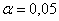
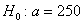
Как бы сказали статистики, выборочный результат 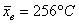
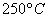
Ответ: на уровне значимости 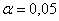
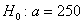
Ещё раз осмыслим – что означает «на уровне значимости 0,05»? Это означает, что с вероятностью 5% мы отвергли правильную гипотезу (совершили ошибку 1-го рода). И тут остаётся взвесить риск – насколько критично чуть-чуть уменьшить температуру (если мы всё-таки ошиблись и температура на самом деле в норме). Если даже небольшое уменьшение температуры недопустимо, то имеет смысл провести повторное, более качественное исследование: увеличить количество замеров 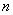
Следующая задача для самостоятельного решения, и на всякий случай я ещё раз продублирую ссылку на таблицу значений функции Лапласа и Калькулятор:
Средний вес таблетки сильнодействующего лекарства (номинал) должен быть равен 0,5 мг. Выборочная проверка 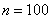
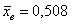
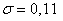
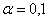
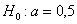
Рассмотрите как конкурирующую гипотезу 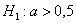
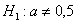
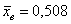
Краткое решение и ответы, как обычно, в конце урока.
Кстати, это тот самый пример, где ошибка 2-го рода (ошибочное принятие неверной нулевой гипотезы), может повлечь гораздо более тяжелые последствия (опасную передозировку). Поэтому в такой ситуации лучше включить паранойю и увеличить уровень значимости до 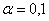
Можно ли одновременно уменьшить вероятности ошибок 1-го и 2-го рода ( 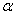
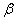
Теперь вторая ситуация. Та же самая задача, почти всё то же самое, но:
б) генеральная дисперсия  НЕ известна.
НЕ известна.
В этом случае остаётся ориентироваться на исправленную выборочную дисперсию 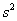
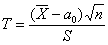
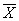
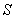
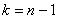
Алгоритм решения полностью сохраняется:
На основании 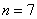
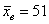
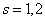
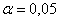
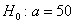
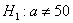
И начнём мы опять со смысла задачи, что здесь произошло? Здесь 7 раз измерили высоту этой камеры, получили среднее значение 51 мм и за неимением генеральной дисперсии вычислили исправленную выборочную дисперсию. Но, согласно норме, высота должна равняться 50 мм – эту гипотезу и проверяем.
Решение: так как генеральная дисперсия не известна, то для проверки гипотезы 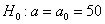
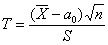
Конкурирующая гипотеза имеет вид 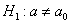
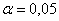
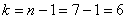
Таким образом, при 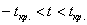
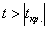
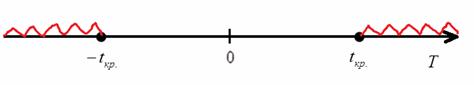
Вычислим наблюдаемое значение критерия:
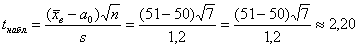
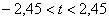
Ответ: на уровне значимости 0,05 гипотезу 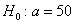
То есть, с точки зрения статистики, выборочный результат 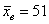
Творческая задача для самостоятельного решения:
Нормативный расход автомобильного двигателя составляет 10 л на 100 км. После конструктивных изменений, направленных на уменьшение этого показателя, были получены следующие результаты 10 тестовых заездов: 
На уровне значимости 0,05 выяснить, действительно ли расход топлива стал меньше.
Да, это не редкость – когда в предложенной задаче нужно не только проверить гипотезу, но и предварительно рассчитать выборочные значения. Кстати, даже при известной генеральной дисперсии, ориентироваться на неё тут нельзя, ибо конструктивные изменения могут изменить не только генеральную среднюю, но и генеральную дисперсию.
В лучших традициях курса все числа уже забиты в Эксель – там же инструкция по расчётам выборочных показателей. Если кто-то не знает или запамятовал, то вот ролик о том, как провести эти вычисления быстро (Ютуб).
В данной задаче критическая область левосторонняя, и критическое значение 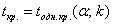
Постарайтесь грамотно оформить решение, свериться с образцом можно чуть ниже.
И я жду вас на следующем уроке, где мы продолжим проверять статистические гипотезы.
Решения и ответы:
Пример 37. Решение: поскольку известно ген. стандартное отклонение, то для проверки гипотезы 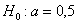
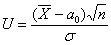
а) Рассмотрим конкурирующую гипотезу 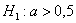
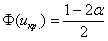
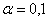
При 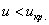
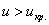
Вычислим наблюдаемое значение критерия:
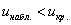
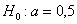
б) Рассмотрим конкурирующую гипотезу 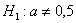
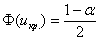
Для 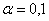
При 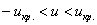
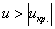

Наблюдаемое значение критерия 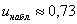
Ответ: в обоих случаях нулевую гипотезу на уровне значимости 0,1 принимаем.
Пример 39. Решение: вычислим сумму вариант 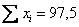
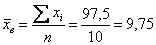
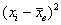
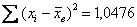
Вычисления удобно свести в таблицу: 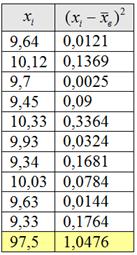
Выборочная дисперсия: 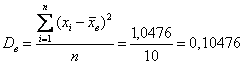
Исправленная выборочная дисперсия:
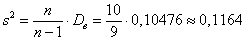
Исправленное стандартное отклонение.
На уровне значимости 0,05 проверим нулевую гипотезу 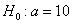
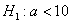
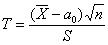
Найдём критическую область. Поскольку в конкурирующей гипотезе речь идёт о меньших значениях, то она будет левосторонней. Для уровня значимости 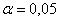
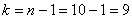
Таким образом, при 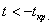
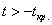
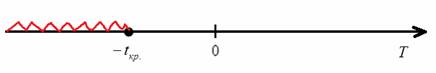
Вычислим наблюдаемое значение критерия:
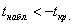
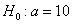
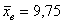
Ответ: на уровне значимости 0,05 можно утверждать, что расход топлива стал ниже.
Автор: Емелин Александр
(Переход на главную страницу)

http://lfirmal.com/zakon-normalnogo-raspredeleniya-sluchajnyh-velichin/
http://mathprofi.net/statisticheskie_gipotezy.html
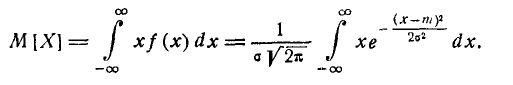
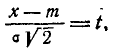
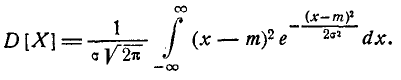
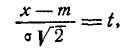
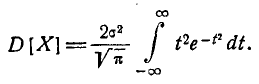
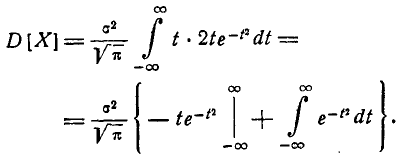
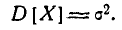
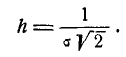
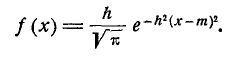

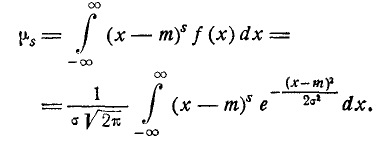
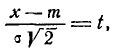
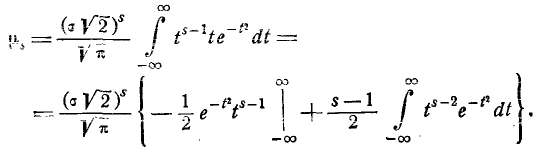
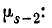
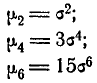
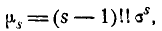
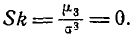
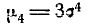
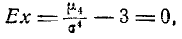
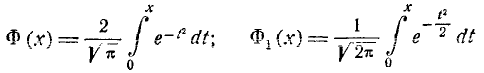
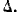
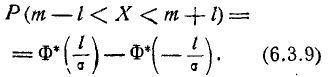
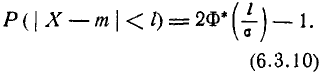
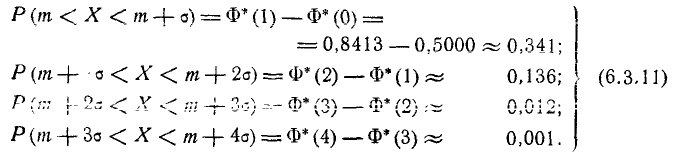
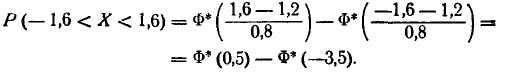

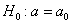
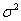 известна.
известна.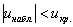
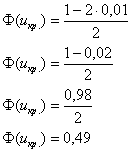
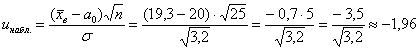
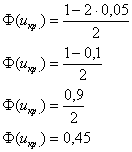
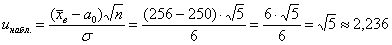
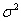 НЕ известна.
НЕ известна.