Уравнения длинной линии как четырехполюсника

5.2. Уравнения передачи четырехполюсника

5.2. Уравнения передачи четырехполюсника

Будем считать, что четырехполюсник (рис. 5.1) является линейным, а действующие в нем сигналы – гармоническими. Любой четырехполюсник характеризуется четырьмя величинами: входным напряжениемU1 и входным током I1, выходным напряжением U2 и выходным током I2. Уравнения, определяющие зависимость между U1, U2, I1 и I2 называются уравнениями передачи четырехполюсников.

Только две из этих величин являются независимыми. Например, если подать на вход и выход четырехполюсника напряжения U1 и U2, то они создадут вполне определенные входной I1 и выходной I2 токи. Поэтому для линейного четырехполюсника можно записать следующие два уравнения, связывающие его входные и выходные токи и напряжения:

Уравнения (5.1) можно записать в матричной форме:

(5.2)

Коэффициенты Y11, Y12, Y21, Y22 в уравнениях (5.1) называются Y-параметрами, а уравнения (5.1) называются уравнениями передачи четырехполюсника в Y-параметрах.

В рассмотренном случае в качестве воздействия на четырехполюсник были приняты входное и выходное напряжения (U1, U2), а в качестве откликов четырехполюсника на эти воздействия получили входной и выходной токи (I1, I2). Всего подобных комбинаций можно составить шесть и поэтому имеется шесть систем уравнений передачи четырехполюсника: в Y-параметрах; в Z-параметрах; в H-параметрах; в A-параметрах; в B-параметрах; в F-параметрах. Комбинации воздействий, откликов и названия параметров, которые связывают между собой воздействия и отклики приведены в таблице 5.1.

На основании таблицы 1 запишем другие уравнения передачи четырехполюсника.

Уравнения передачи четырехполюсника в Z-параметрах:

или в матричной форме:

. (5.4)

Уравнения передачи четырехполюсника в Н-параметрах:

или в матричной форме:

. (5.6)

Уравнения передачи четырехполюсника в A-параметрах:

или в матричной форме:

. (5.8)

Уравнения передачи четырехполюсников в B- и F-параметрах при дальнейшем изложении материала не будут использоваться и поэтому их формулы не пригодятся.

Все формы передачи уравнений равноправны. Выбор той или иной формы зависит от задачи, которая в данном случае решается. Уравнения передачи вH-параметрах и Y -параметрах широко используются, например, при расчетах транзисторных схем. Эти параметры приводятся в справочной литературе по транзисторам, или могут быть определены по их входным и выходным характеристикам.

Все системы параметров-коэффициентов описывают один и тот же четырехполюсник, поэтому между ними существует однозначная взаимосвязь.

Физический смысл параметров-коэффициентов. Для выяснения физического смысла необходимо четырехполюсник поставить в такой режим работы, при котором в уравнениях передачи будет содержаться только один параметр, который нас интересует, например,Z11 . Эти условия будут созданы, если четырехполюсник перевести в режим холостого хода (зажимы разомкнуты) или короткого замыкания (зажимы замкнуты).

Переведем четырехполюсник в режим короткого замыкания (КЗ) по выходу, т.е. замкнем зажимы (2-2). В этом случае U2 = 0 и уравнения (5.1) примут вид:

,

,

где Y11 и Y21 – входная и взаимная (передаточная) проводимости четырехполюсника при КЗ выхода.

Переведем четырехполюсник в режим КЗ по входу, т.е. замкнем зажимы (1-1). В этом случае U1 = 0 и уравнения (5.1) примут вид:

,

,

где Y12 и Y22 – взаимная (передаточная) и выходная проводимости четырехполюсника при КЗ входных зажимов.

Переводя четырехполюсник поочередно в режим холостого хода (ХХ) на зажимах (2-2) и (1-1) будем иметь то I2 = 0, то I1 = 0 и на основании уравнений (5.3) получим:

где Z11, Z21 – входное и взаимное (передаточное) сопротивления четырехполюсника при холостом ходе на входных зажимах (2-2);

Z22, Z12 – выходное и взаимное (передаточное) сопротивления четырехполюсника при холостом ходе на зажимах (1-1).

Рассуждая аналогичным образом можно установить, что:

параметры A11 и A22 являются безразмерными;

параметр А12 имеет размерность сопротивления;

параметр А21 имеет размерность проводимости;

параметры Н12 и Н21 являются безразмерными;

параметры Н11 и Н22 имеют размерность сопротивления и проводимости соответственно.

Четырехполюсники

Основные определения и классификация

Часть электрической цепи, рассматриваемая по отношению к двум парам её зажимов, называется четырехполюсником. Чаще всего четырехполюсник является промежуточным звеном между источником питания и нагрузкой. Зажимы, к которым подключен источник, называются входными (сокращенно — вход), а зажимы, к которым подключена нагрузка – выходными (выход). Поэтому говорят, что четырехполюсник — это цепь, имеющая два входных и два выходных зажима. Примеры четырехполюсников: линия электропередачи, трансформатор, фильтр, усилитель и всякое другое устройство, имеющее два входных и два выходных зажима. Классифицируются четырехполюсники по ряду признаков. Они делятся на активные, т. е. содержащие источники питания, и пассивные – не содержащие источников энергии. На схемах четырехполюсник изображают прямоугольником, слева и справа которого показывают его зажимы. Если четырехполюсник активный, то внутри прямоугольника ставится буква А (рис.5.1,а), а если пассивный – то либо буква П, либо никакой буквы (рис.5.1,б). Если четырехполюсник состоит только из линейных элементов, то он называется линейным, в противном случае – нелинейным. Различают симметричные и несимметричные четырехполюсники. Если при замене входных зажимов выходными и наоборот не изменяются напряжения и токи в цепи, к которой он подключается, то четырехполюсник симметричный, а в противном случае – несимметричный. Мы будем изучать только линейные, пассивные четырехполюсники, правда как симметричные, так и несимметричные, работающие в цепях синусоидального тока.

Теория четырехполюсников используется в случае, когда интересуются взаимосвязью его входных и выходных величин и не рассматривают напряжения и токи внутри самого четырехполюсника. В развитии теории четырехполюсников принимали участие как зарубежные, так и отечественные ученые.

Часто заменяют один четырехполюсник другим, но эквивалентным. Под эквивалентностью двух четырехполюсников понимают возможность замены одного из них другим без изменения напряжений и токов в той цепи, к которой они подключаются.

Системы основных уравнений четырехполюсника

Предположим, что имеется пассивный четырехполюсник (рис.5.2). Обозначим левую пару зажимов цифрами 1 и 1` и будем называть их первичными, а правую — цифрами 2 и 2` и будем называть их вторичными. Этих обозначений будем придерживаться все время, причем напряжению и току, относящимся к зажимам 1-1`, будем приписывать индекс 1 и называть их первичными, а напряжению и току, относящимся к зажимам 2-2`, будем приписывать индекс 2 и называть их вторичными. На практике возможны следующие варианты: а) питание четырехполюсника происходит только со стороны первичных зажимов; б) питание – только со стороны вторичных зажимов; в) питание – как со стороны первичных, так и со стороны вторичных зажимов. На рис.5.2 указаны положительные направления напряжений и токов, причем сплошные линии соответствуют варианту а) (в дальнейшем будем отражать так ), пунктирные – варианту б) (в дальнейшем будем отражать следующим образом ). Вариант в) в дальнейшем будем указывать так.

В первую очередь рассмотрим вариант в). Учитывая, что напряжения U1 и U2 могут быть заменены на ЭДС, на основании метода контурных токов могут быть записаны следующие уравнения

U1=I1Z11+Z12;

U2=I1Z21+Z22.

Уравнения (1) являются основными уравнениями четырехполюсника в форме |Z|. Здесь

— входное сопротивление со стороны первичных зажимов при разомкнутых вторичных;

— входное сопротивление со стороны вторичных зажимов при разомкнутых первичных;

.

Если уравнения (1) решить относительно токов I1 и , то получим основные уравнения четырехполюсника в форме |Y|

I1=U1Y11+U2Y12;

=U1Y21+U2Y22,

Достаточно широкое распространение, особенно в промэлектронике, получили уравнения в форме |Н| (гибридная форма), которая получается из системы (1), если её решить относительно U1 и

U1=I1H11+U2H12;

=I1H21+U2H22.

Чаще всего на практике используются основные уравнения в форме А. При питании четырехполюсника только со стороны первичных зажимов они имеют вид

U1=АU2+ВI2;

Входящие в уравнения (4) коэффициенты A, B, C, D характеризуют сам четырехполюсник и называются его коэффициентами. Они зависят от схемы четырехполюсника, от значений параметров его элементов и от частоты. Коэффициенты взаимосвязаны таким соотношением: AD—BC=1.

При питании четырехполюсника только со стороны вторичных зажимов основные уравнения принимают вид

U2=DU1+В;

=CU1+А.

Если четырехполюсник симметричный, то при перемене местами первичных и вторичных зажимов не изменяются напряжения и токи, поэтому для них, как следует из уравнений (4) и (5), А=D.

Опытное определение коэффициентов четырехполюсника

Коэффициенты A, B, C, D могут быть определены расчетным или опытным путем. Так как они взаимосвязаны, то для их определения необходимо еще 3 уравнения, для составления которых достаточно выполнить три опыта. Набор опытов может быть различным, но чаще всего используют следующий: холостой ход (ХХ) и короткое замыкание (КЗ) при питании со стороны первичных зажимов, а также опыт обратного КЗ, когда питание происходит со стороны вторичных зажимов. Первые два опыта выполняются по схеме рис.5.3,а, последний же по схеме рис.5.3,б. В каждом опыте по показаниям приборов определяются комплексы входных сопротивлений Z1х=Z1хejφ1х, Z1к=Z1кejφ1к и Z2к=Z2кejφ2к на основании следующих формул:

Z=U/I; r=P/I2; .

Для определения знака tgφ и φ необходимо либо включить фазометр, который показывает величину и знак угла φ, либо произвести дополнительный опыт. Для выполнения дополнительного опыта используют реактивный элемент (индуктивность или ёмкость), сопротивление которого примерно равна и который включают либо параллельно, либо последовательно с четырехполюсником, а по характеру изменения тока определяют знак φ.

Рассмотрим, как по известным Z1х=Z1хejφ1х, Z1к=Z1кejφ1к и Z2к=Z2кejφ2к, определить коэффициенты четырехполюсника. Свяжем входные сопротивления с коэффициентами. Для опыта ХХ (I2=0) уравнения (4) принимают вид: U1х=AU2х; I1х=CU2х. Поделив одно на другое, получаем

. (6)

Для опыта прямого КЗ (U2=0) уравнения (4) принимают вид: U1к=BI2к; I1к=DI2к. Поделив одно на другое, получаем

. (7)

Для опыта обратного КЗ (U1=0) уравнения (5) принимают вид: U2к=B; =А. Поделив одно на другое, получаем

. (8)

Схемы замещения четырехполюсника

С помощью основных уравнений могут быть построены различные схемы замещения любого четырехполюсника, которые облегчают исследование свойств рассматриваемой цепи. На практике наибольшее распространение получили Т — (рис.5.4,а) и П-образные (рис.5.4,б) схемы замещения. Задача замены любого четырехполюсника звездой (Т-образная схема) или треугольником (П-образная схема) является однозначной, поскольку четырехполюсник характеризуется коэффициентами, из которых независимыми являются только три, и каждая из схем замещения содержит три независимых параметра. Входящие в схемы рис.5.4 сопротивления должны быть рассчитаны исходя из того, чтобы схема замещения обладала такими же коэффициентами A, B, C, D, как и заменяемый четырехполюсник. Осуществим вывод формул определения коэффициентов Т-образной схемы по параметрам её сопротивлений, используя законы Ома и Кирхгофа.

.

Сравнивая полученное выражение со вторым уравнением системы (4), получаем

.

Сравнивая это выражение с первым уравнением системы (4), получаем

.

Из этих формул получаются следующие выражения для расчета сопротивлений Т-образной схемы замещения любого четырехполюсника

.

Аналогично для П-образной схемы

Из этих формул получаются следующие выражения для расчета сопротивлений П-образной схемы замещения любого четырехполюсника

Следует заметить, что бывают случаи, когда одна из рассмотренных схем замещения может оказаться физически нереализуемой.

Типы задач по четырехполюсникам

Различают два типа задач по четырехполюсникам. Первый тип: задан четырехполюсник, а также напряжение и ток на его входе или выходе; требуется же определить напряжение и ток на его выходе или входе. Четырехполюсник может быть задан следующим образом: а) своей схемой, что чаще всего и бывает; б) коэффициентами; в) Т — или П-схемой замещения; г) сопротивлениями Z1х, Z1к и Z1к. Для решения задач первого типа с помощью уравнений (4) или (5) необходимо знать коэффициенты четырехполюсника. Их определение по схеме четырехполюсника производится следующими способами: 1) с помощью законов Ома и Кирхгофа выражают U1, I1 через U2, I2 и сравнивают полученные выражения с уравнениями (4) (так мы поступали при выводе формул для коэффициентов Т — и П-схем); 2) через Т — или П-схему, для чего реальная схема четырехполюсника должна быть преобразована в эквивалентную Т — или П-схему, по параметрам которой и определяются коэффициенты по приведенным выше формулам; 3) через параметры Z1х, Z1к и Z1к, которые определяются аналитически по схеме четырехполюсника, а затем и коэффициенты по (9) и (10).

Второй тип задач: задан четырехполюсник, а также напряжение на его входе и сопротивление Z2 нагрузки на выходе; определять требуется I1, , I2. Задачи второго типа решаются через входное сопротивление

.

Затем определяем I1=U1/Z1 и задача сведена к первому типу.

Цепи с распределенными параметрами

До сих пор мы изучали цепи с сосредоточенными параметрами, т. е. такие, которые состоят из самостоятельно существующих R, L и С, расположенных в определенных точках цепи. Причем напряжения и токи в этих элементах мы связывали формулами ur=ir; uL=Ldi/dt; iC= CduC/dt, которые справедливы при том предположении, что ток, входящий в элемент равен току, выходящему из него. Однако представление электротехнических устройств в виде цепей с сосредоточенными параметрами не всегда возможно. Например, высоковольтная линия электропередачи (ЛЭП). Напомним, что в простейшем случае ЛЭП состоит из двух проводов, которые изолированы друг о друга и по которым собственно и передается электрическая энергия. В природе однако не существует идеальной изоляции, т. е. изоляции, обладающей бесконечно большим сопротивлением. Реальная изоляция имеет хотя и большое, но все же конечное значение сопротивления. В результате по такой изоляции начинает замыкаться ток, получивший название тока утечки. Если рабочее напряжение в линии высокое, то ток утечки достигает ощутимых значений. К чему приводит наличие тока утечки? Прежде всего к тому, что ток в различных местах линии становится неодинаковым, он непрерывно изменяется при переходе от одной точки линии к другой. И уж конечно нельзя утверждать, что ток в конце линии равен току на ее входе, как необходимо для цепи с сосредоточенными параметрами. Изменяется в линии и напряжение при переходе от одной точки к другой. Это происходит потому, что провода линии обладают активным и индуктивным сопротивлением. Рассмотрев данный пример, можно записать следующее определение: цепью с распределенными параметрами называется такая, у которой напряжение и ток непрерывно изменяются при переходе от одной точки к другой.

Кроме высоковольтных ЛЭП цепями с распределенными параметрами являются телефонные и телеграфные воздушные и кабельные линии связи. Цепями с распредпараметрами являются абсолютно все устройства, работающие на высоких частотах (антенные и фидерные устройства и т. д.). Строго говоря цепью с распредпараметрами следовало бы считать обычную катушку индуктивности. Действительно, индуктивность представляет собой катушку как правило цилиндрической формы, содержащую большое число витков медного или алюминиевого провода. Но между каждыми, рядом расположенными витками, имеется так называемая межвитковая емкость. Имеется емкость между каждым витком и землей (или корпусом катушки). Конечно эти емкости невелики, но они существуют. В связи с этим весь ток, замыкающийся по катушке условно может быть разбит на две части, одна из которых iL замыкается непосредственно по виткам катушки, а другая iC – по емкостям. Соотношение между этими частями может быть различным и в первую очередь оно зависит от частоты. При низких частотах, а низкими принято называть частоты до 1кГц, ток iC настолько мал, что им обычно пренебрегают. При повышении частоты картина изменяется поскольку индуктивное сопротивление прямо пропорционально частоте, а емкостное обратно пропорционально ей. Это приводит к тому, что при очень высоких частотах (109 ¸1011 Гц) ток iC становится большим тока iL и устройство следует считать уже обладающим емкостным сопротивлением. При промежуточных частотах (106 ¸ 108 Гц) токи iL и iC сравнимы друг с другом, пренебрегать нельзя ни тем ни другим, а, следовательно, катушка является цепью с распределенными параметрами. В связи с этим цепями с распредпараметрами считают обмотки высоковольтных электрических машин и трансформаторов.

Цепи с распредпараметрами делятся на линейные и нелинейные. Мы бодем изучать только линейные цепи, причем на конкретном примере высоковольтных ЛЭП, о которых поговорим чуть подробнее. В таких ЛЭП эффект непрерывного изменения напряжений и токов имеет место потому, что они обладают продольным и поперечным сопротивлениями. Продольное сопротивление образовано активным и индуктивным сопротивлениями самих проводов линии. Поперечное сопротивление представлено сопротивлением несовершенной изоляции и сопротивалением емкости между проводами. Ознакомившись с этими понятиями, можно записать еще одно определение: линия с распредпараметрами называется однородной, если продольное и поперечное сопротивления равномерно распределены по ее длине. В реальных линиях это не совсем так (из-за утечки тока в основном через гирлянды изоляторов, провеса проводов и т. д.), но с достаточно высокой степенью точности их можно считать однородными. Мы будем изучать именно однородные линии с распредпараметрами.

Основные дифуравнения однородной длинной линии

Линии с распредпараметрами часто называют длинными линиями. Произведем вывод уравнений, описывающих процессы, происходящие в них. При этом будем полагать, что известны первичные параметры линии, к числу которых относятся :

· r0 – активное сопротивление прямого и обратного проводов линии длиной 1 км;

· L0 – индуктивность петли, образованной прямым и обратным проводом линии длиной 1 км;

· g0 – проводимость изоляции между прямым и обратным проводами линии длиной 1 км;

· С0 – емкость между прямым и обратным поводом линии длиной 1 км.

Эти параметры могут быть либо раcсчитаны либо определены экспериментальным путем как будет показано ниже. 3

Для вывода основных уравнений представим, что линия состоит из бесконечно большого числа участков бесконечно малой длины, параметры которых можно считать сосредоточенным (рис.5.5). Это позволит применить законы Кирхгофа, которые справедливы только для цепей с сосредоточенными параметрами. Рассмотрим один из таких участков, расположенный на расстоянии x от начала линии и имеющий длину dx. Пусть напряжение и ток на входе этого участка u и i, а его параметры — r0dx, L0dx, g0dx и C0dx. Тогда напряжение и ток на входе следующего участка будут u+dx*¶u/¶x и i+dx*¶i/¶x, где ¶u/¶x и ¶i/¶x – скорости изменения напряжения и тока из-за изменения только x.

На основании второго закона Кирхгофа для контура, образованного рассматриваемым участком, имеем

По первому закону Кирхгофа

Если пренебречь величинами второго порядка малости, то получим

(2)

Уравнения (1) и (2) являются основными дифуравнениями однородной длинной линии. Они описывают как установившиеся режимы, так и переходные процессы. В математическом отношении решение этих уравнений в общем случае является весьма не простой задачей, но оно позволяет определить напряжение и ток в любой точке линии и в любой момент времени.

Установившийся режим в длинной линии при синусоидальном напряжении

Если в установившемся режиме на вход однородной ЛЭП подать синусоидальное напряжение, то во всех ее точках напряжения и токи также будут синусоидальными и иметь частоту источника питания из-за того, что цепь линейна. Это позволяет использовать комплексный метод. Пусть в некоторой точке линии, отстоящей от ее начала на расстояние x, напряжение и ток будут соответственно u=Umsin(wt+yu) i=Imsin(wt+yi). Им будут соответствовать комплексы uºUejwt и iºIejwt , где U=Umejwt/; I=Imejwt/.

Тогда величины, входящие в уравнения (1) и (2), принимают вид:

поскольку U зависит только от x и частная производная по x совпадает с полной производной.

, поскольку I от t не зависит.

, поскольку I также зависит только от x.

, поскольку U от t также не зависит.

Подставляя эти значения в уравнения (1) и (2), имеем:

или

где

Y0=g0+jwC0 — поперечная комплексная проводимость. (4)

Разделив переменные в двух последних дифуравнениях, получим:

Это линейное дифуравнение второго порядка, решение которого имеет вид:

где А1 и А2 — постоянные интегрирования, р1 и р2 — корни характеристического уравнения

В ТОЭ условились считать р1=-g, а р2=g, где

— (5)

это весьма важный параметр линии, который называется коэффициентом распространения. Он является комплексным числом g=a+b, причем a называется коэффициентом затухания и измеряется в Неперах (Нп) на километр, а b называется коэффициентом фазы и измеряется в рад/км.

(6)

Ток в рассматриваемой точке линии определится из выражения

, (7)

.

ZC называется характеристическим (волновым) сопротивлением и в общем случае оно является комплексным числом. Действительно

(8)

g, a, b и ZC характеризуют саму линию и называются ее вторичными параметрами.

Входящие в уравнения (6) и (7) постоянные интегрирования определяются по граничным условиям (значениям U и I в какой-либо точке линии). Если известны напряжение U1 и ток I1 в начале линии, т. е. при x=0. В этом случае уравнения (6) и (7) принимают вид

совместное решение которых дает:

и

Подставив их значения в формулы (6) и (7) и проделав несложные преобразования, получим

(9)

(10)

Формулы (9) и (10) являются основными уравнениями длинной линии в гиперболических функциях по U1, I1.

На практике однако чаще всего известны напряжение U2 и ток I2 в конце линии, т. е. при x=l, где l – длина линии. Подставив эти значения в формулы (6) и (7), получим:

, совместное решение которых дает

и

Если эти значения А1 и А2 подставить в (6) и (7) и собрать слагаемые, содержащие U2, а так же I2, то получим

(11)

(12)

где y=l-x — это расстояние от конца линии до рассматриваемой точки.

Формулы (11) и (12) являются основными уравнениями длинной линии в гиперболических функциях по U2, I2.

Бегущие волны в линиях

Проясним физическую сущность процессов, происходящих в длинных линиях при передаче энергии при синусоидальных напряжениях и токах. Исходить при этом будем из уравнений (6) и (7), но учтем, что все величины, входящие в эти формулы, являются комплексами.

.

Перейдем от комплексов к мгновенным значениям

Как следует из этих выражений напряжение представляет собой сумму, а ток – разность двух синусоид, являющихся функцией двух переменных – времени t и координаты x. Первые составляющие представляют собой напряжение и ток падающей волны. Чтобы в этом убедиться изобразим график распределения вдоль линии (от x) первой составляющей, например, напряжения, предположительно являющейся падающей волной, в некоторый фиксированный момент времени t1 (рис.5.6)

и в момент времени t1+dt

где dx=vdt, а – это скорость движения волны вдоль линии.

Из этих выражений следует, что с ростом t uпад перемещается в сторону больших х, т. е. от начала линии к ее концу.

Падающей электромагнитной волной называется процесс перемещения волны от начала линии к её концу. Она состоит из волны напряжения, волны тока и несет энергию от приемника к источнику.

Аналогично можно показать, что вторые составляющие напряжения и тока представляют собой напряжение и ток отраженной волны. Убедимся в этом, построив график распределения второй составляющей напряжения вдоль линии (только от x) в моменты времени t=t1 и t=t1+dt (рис.5.7)

Отраженной электромагнитной волной называется процесс перемещения волны от конца линии к началу. Она состоит из волны напряжения и волны и несет энергию от приемника к источнику.

Падающие и отраженные волны, взятые вместе, называются бегущими волнами. Основными характеристиками бегущих волн являются фазовая скорость и длина волны. Фазовой скоростью v принято называть скорость перемещения неизменного фазового состояния. Для вывода формулы расчета v возьмем фазу допустим падающей волны, которая с ростом t должна оставаться неизменной w t + y1 — bx = const. Взяв производную по t, получим

. (13)

Длиной волны l называется наименьшее расстояние, взятое в направлении распространения волны, фаза колебания которых отличается на 2p, т. е.

откуда . (14)

Представляет интерес взаимосвязь между v и l

.

Бегущие волны по мере их продвижения по линии затухают и степень их затухания определяется величиной коэффициента a. С физической точки зрения затухание объясняется потерями энергии в активных элементах (r0, g0) линии.

Подводя итог, можно отметить, что

Из последних выражений следует закон Ома для падающих и отраженных волн

В заключение следует заметить, что реально существуют полные напряжение и ток, а их разложение на падающие и отраженные волны — это математический прием, облегчающий представление физических явлений в линии.

Входное сопротивление длинной линии

При расчете и анализе линий с распределенными параметрами широко используется её входное сопротивление, под которым понимают такое сосредоточенное сопротивление, которым в установившемся режиме можно заменить всю линию вместе с её нагрузкой и которое равно . Свяжем Z1 с параметрами линии. С этой целью запишем формулы (11) и (12) для начала линии (y=l) Тогда

, (15)

поскольку — это сопротивление нагрузки линии.

Особый интерес представляет входное сопротивление линии в режимах холостого хода (ХХ) и короткого замыкания (КЗ).

При ХХ (Z2 = ¥) I2 = 0 и уравнения (11) и (12), записанные для начала линии, принимают вид

(16)

При КЗ (Z2 = 0) U2 = 0 и уравнения (11) и (12), записанные для начала линии, принимают вид

. (17)

Зная Z1х и Z1к, которые могут быть определены экспериментальным путем, можно определить Z1 при любом сопротивлении Z2. Действительно

(18)

Осуществив опыты ХХ и КЗ, можно определить все параметры линии: как вторичные, так и первичные, а именно

или (19)

(20)

с другой стороны

тогда

где n – число длин волн, укладывающихся на длине линии.

Первичные параметры определяются по вторичным параметрам:

откуда

откуда .

Линия, согласованная с нагрузкой

ЛЭП является связующим звеном между источником питания и нагрузкой и её параметры могут находиться в различном соотношении с сопротивлением нагрузки Z2. Если ZC = Z2 , то такая линия называется согласованной с нагрузкой. Выясним её особенности, определив в первую очередь постоянные интегрирования:

Это означает, что в такой линии не возникает отраженная волна. По этой причине на практике стараются линию с нагрузкой согласовать.

Подставив эти значения в формулы (6) и (7), получим

. (21)

Формулы (21) являются основными уравнениями линии, согласованной с нагрузкой, они значительно более простые, чем формулы (11) и (12).

Формулы (21), записанные для начала линии, дают:

Тогда входное сопротивление линии

(22)

Из соотношения (22) следует, что, во-первых, Z1 не зависит от длины линии и, во вторых, что характеристическое сопротивление линии – это входное сопротивление линии, согласованной с нагрузкой, или входное сопротивление бесконечно длинной линии, в которой также не может возникнуть отраженная волна.

Определим КПД линии, согласованной с нагрузкой где Тогда

(23)

Как следует из (23) отличие между Р1 и Р2 определяется величиной al, которая называется затуханием линии и измеряется в Нп. Это условная единица измерения затухания. Последнее будет равняться 1Нп, если В связи широко используется другая единица измерения затухания – децибелл (1дБ=0.115Нп).

Линия без искажений

В ряде случаев к линии предъявляется требование, чтобы передаваемые по ней сигналы не искажались. Это особенно важно для линий связи (телефонных, телеграфных, радиорелейных и т. д.). Особенно ощутимы искажения при передаче музыки. Линия, которая не искажает сигналы и называется линией без искажений. Для того, чтобы передаваемые сигналы не искажались, необходимо выполнить два условия: а) все частоты, образующие сигнал, должны затухать в одинаковой степени, т. е. коэффициент затухания не должен зависеть от частоты; б) все частоты, образующие сигнал, должны распространяться с одинаковой скоростью, т. е. фазовая скорость не должна зависеть от частоты. Если не будет выполняться первое условие, то в линии имеют место амплитудные искажения, при невыполнении второго условия – фазовые искажения.

Известный ученый Хевисайд показал, что для того, чтобы линия не искажала передаваемые сигналы, её первичные параметры должны находиться во вполне определенном соотношении, а именно:

(24)

Убедимся в том, что при выполнении условия (24), искажений в линии не будет. С этой целью определим вторичные параметры линии

Отсюда (25)

(26)

(27)

(28)

Из (25) и (27) следует, что условия неискажающей передачи сигналов выполняются (a и v не зависят от частоты), а из (28) следует, что у такой линии ZC является чисто активным ( в ряде случаев это очень ценно). Кроме того линия без искажений обладает минимальным значением a при заданных r0 и g0, а, следовательно, максимальным значением КПД, определяемым при согласованной нагрузке по (23).

У реальных линий без специальных приспособлений , т. е. условие (24) не выполняется и они искажают передаваемые сигналы. Есть несколько способов сделать линию неискажающей. Наиболее распространенный из них заключается в искуственном увеличении L0. С этой целью, например, в телеграфных линиях равномерно (через 1.7 км) по всей её длине включают сосредоточенные катушки индуктивности. Следует заметить, что при увеличении L0 , как следует из (27), автоматически падает фазовая скорость и она оказывается существенно ниже скорости света.

Линия без потерь

Часто при высоких частотах имеет место соотношение r0

Уравнения длинной линии как четырехполюсника

Уравнения длинной линии как четырехполюсника — раздел Электротехника, Вращающееся магнитное поле В Соответствии С (11) И (12) Напряжения И Токи В Начале И В Конце Линии Связа.

В соответствии с (11) и (12) напряжения и токи в начале и в конце линии связаны между собой соотношениями

;

.

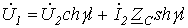
Эти уравнения соответствуют уравнениям симметричного четырехполюсника, коэффициенты которого ; и ; при этом условие выполняется.

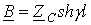
Указанное означает, что к длинным линиям могут быть применены элементы теории четырехполюсников, и, следовательно, как всякий симметричный четырехполюсник, длинная линия может быть представлена симметричной Т- или П- образной схемами замещения.

Эта тема принадлежит разделу:

Вращающееся магнитное поле

На сайте allrefs.net читайте: «вращающееся магнитное поле»

Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Уравнения длинной линии как четырехполюсника

Что будем делать с полученным материалом:

Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:

Все темы данного раздела:

Магнитное поле катушки с синусоидальным током
При пропускании по обмотке катушки синусоидального тока она создает магнитное поле, вектор индукции которого изменяется

Круговое вращающееся магнитное поле двух- и трехфазной обмоток
Круговым вращающимся магнитным полем называется поле, вектор магнитной индукции которого, не изменяясь по модулю, вращается в пространстве с постоянной угловой частотой. Для создания круго

Магнитное поле в электрической машине
С целью усиления и концентрации магнитного поля в электрической машине для него создается магнитная цепь. Электрическая машина состоит из двух основных частей (см. рис. 4): неподвижного статора и в

Принцип действия асинхронного и синхронного двигателей
Устройство асинхронного двигателя соответствует изображению на рис. 4. Вращающееся магнитное поле, создаваемое расположенными на статоре обмотками с током, взаимодействует с токами ротора, приводя

Линейные электрические цепи при несинусоидальных периодических токах
Предыдущие лекции были посвящены анализу электрических цепей при синусоидальных токах и напряжениях. На практике ЭДС и токи в большей или меньшей степени являются несинусоидальными. Это связано с т

Характеристики несинусоидальных величин
Для характеристики несинусоидальных периодических переменных служат следующие величины и коэффициенты (приведены на примере периодического тока): Максимальное значение —

Разложение периодических несинусоидальных кривых в ряд Фурье
Из математики известно, что всякая периодическая функция , где Т – период, удовлетворяющая условиям Дирихле, может быть

Свойства периодических кривых, обладающих симметрией
Коэффициенты ряда Фурье для стандартных функций могут быть взяты из справочной литературы или в общем случае рассчитаны по приведенным выше формулам. Однако в случае кривых, обладающих симметрией,

Действующее значение периодической несинусоидальной переменной
Как было показано выше, действующим называется среднеквадратичное за период значение величины: . При н

Методика расчета линейных цепей при периодических
несинусоидальных токах Возможность разложения периодических несинусоидальных функций в ряд Фурье позволяет свес

Резонансные явления в цепях несинусоидального тока
В цепях несинусоидального тока резонансные режимы возможны для различных гармонических составляющих. Как и при

Высшие гармоники в трехфазных цепях
Напряжения трехфазных источников энергии часто бывают существенно несинусоидальными (строго говоря, они несинусоидальны всегда). При этом напряжения на фазах В и С повторяют несинусоидальную кривую

Переходные процессы в линейных электрических цепях с сосредоточенными параметрами
При всех изменениях в электрической цепи: включении, выключении, коротком замыкании, колебаниях величины каког

Электрической цепи
Резистор (идеальное активное сопротивление) Катушка индуктивности (идеальная индуктивность) Конденсатор (идеальная емкость)

Корни характеристического уравнения. Постоянная времени
Выражение свободной составляющей общего решения х дифференциального уравнения (2) определяется видом корней характерист

Способы составления характеристического уравнения
Характеристическое уравнение составляется для цепи после коммутации. Оно может быть получено следующими способ

Переходные процессы в цепи с одним накопителем энергии и произвольным числом резисторов
Как отмечалось в предыдущей лекции, линейная цепь охвачена единым переходным процессом. Поэтому в рассматривае

Некоторые свойства изображений
Изображение суммы функций равно сумме изображений слагаемых: . При умножении оригина

Изображения производной и интеграла
В курсе математики доказывается, что если , то

Переход от изображений к оригиналам
Переход от изображения искомой величины к оригиналу может быть осуществлен следующими способами: 1. Посредством обратного преобразования Лапласа

Формулы включения
Формулу разложения можно использовать для расчета переходных процессов при нулевых и ненулевых начальных условиях. Если начальные условия нулевые, то при подключении цепи к источнику постоянного, э

Сведение расчета переходного процесса к расчету с нулевыми начальными условиями
Используя принцип наложения, расчет цепи с ненулевыми начальными условиями можно свести к расчету схемы с нулевыми начальными условиями. Последнюю цепь, содержащую пассивные элементы, можно затем с

Переходная проводимость
При рассмотрении метода наложения было показано, что ток в любой ветви схемы может быть представлен в виде ,

Переходная функция по напряжению
Переходная функция по напряжению наиболее часто используется при анализе четырехполюсников. Если линейную электрическую цепь с нулевыми начальными условиями подключить к источнику постоянн

Расчет переходных процессов с использованием интеграла Дюамеля
Зная реакцию цепи на единичное возмущающее воздействие, т.е. функцию переходной проводимости

Метод переменных состояния
Уравнения элекромагнитного состояния – это система уравнений, определяющих режим работы (состояние) электрической цепи. Метод переменных состояния основывается на упорядоченном составлении

Методика составления уравнений состояния
Эта методика включает в себя следующие основные этапы: 1. Составляется ориентированный граф схемы (см. рис. 4,б), на котором выделяется дерево, охватывающее все конденсаторы и источники на

Нелинейные цепи
Нелинейными называются цепи, в состав которых входит хотя бы один нелинейный элемент. Нелинейными наз

Параметры нелинейных резисторов
В зависимости от условий работы нелинейного резистора и характера задачи различают статическое, дифференциальное и динамическое сопротивления. Если нелинейный элемент является безынерционн

Методы расчета нелинейных электрических цепей постоянного тока
Электрическое состояние нелинейных цепей описывается на основании законов Кирхгофа, которые имеют общий характер. При этом следует помнить, что для нелинейных цепей принцип наложения неприм

Графические методы расчета
При использовании этих методов задача решается путем графических построений на плоскости. При этом характеристики всех ветвей цепи следует записать в функции одного общего аргумента. Благодаря этом

Метод двух узлов
Для цепей, содержащих два узла или сводящихся к таковым, можно применять метод двух узлов. При полностью графическом способе реализации метода он заключается в следующем: Строятся графики

Расчет нелинейных цепей методом эквивалентного генератора
Если в сложной электрической цепи имеется одна ветвь с нелинейным резистором, то определение тока в ней можно

Аналитические методы расчета
Исследования общих свойств нелинейных цепей удобно осуществлять на основе математического анализа, базирующегося на аналитическом выражении характеристик нелинейных элементов, т.е. их аппроксимации

Итерационные методы расчета
Решение нелинейного уравнения (системы нелинейных уравнений), описывающего (описывающих) состояние электрической цепи, может быть реализовано приближенными численными методами. Решение находится сл

Характеристики ферромагнитных материалов
Свойства ферромагнитных материалов характеризуются зависимостью магнитной индукции от напряженности магнитного поля. При

Магнитомягкие и магнитотвердые материалы
Перемагничивание ферромагнитного материала связано с расходом энергии на этот процесс. Как уже указывалось, площадь петли гистерезиса характеризует энергию, выделяемую в единице объема ферромагнети

Статическая и дифференциальная магнитные проницаемости
Статическая магнитная проницаемость(в справочниках начальная и максимальная)

Основные законы магнитных цепей
В основе расчета магнитных цепей лежат два закона (см. табл. 4). Таблица 4.. Основные законы магнитной цепи Наименование закона

Общая характеристика задач и методов расчета магнитных цепей
Указанная в предыдущей лекции формальная аналогия между электрическими и магнитными цепями позволяет распростр

Прямая” задача для неразветвленной магнитной цепи
Решение задач подобного типа осуществляется в следующей последовательности: 1. Намечается средняя линия (см. пунктирную линию на рис.1), которая затем делится на участки с одинаковым сечен

Прямая” задача для разветвленной магнитной цепи
Расчет разветвленных магнитных цепей основан на совместном применении первого и второго законов Кирхгофа для магнитных цепей. Последовательность решения задач данного типа в целом соответствует рас

Графические методы расчета
Графическими методами решаются задачи второго типа — “обратные” задачи. При этом в качестве исходных данных для расчета заданы конфигурация и геометрические размеры магнитной цепи, кривая (кривые)

Обратная” задача для неразветвленной магнитной цепи
Решение задач подобного типа осуществляется в следующей последовательности: 1. Задаются значениями потока и определяют для них НС

Обратная” задача для разветвленной магнитной цепи
Замена магнитной цепи эквивалентной электрической схемой замещения (см. рис. 3, на котором приведена схема замещения маг

Итерационные методы расчета
Данные методы, сущность которых была рассмотрена при анализе нелинейных резистивных цепей постоянного тока, являются приближенными численными способами решения нелинейных алгебраических уравнений,

Статическая и дифференциальная индуктивности катушки с ферромагнитным сердечником
Пусть имеем катушку с ферромагнитным сердечником, представленную на рис. 4. В соответствии с определением поток

Особенности нелинейных цепей при переменных токах
Наиболее существенная особенность расчета нелинейных цепей при переменных токах заключается в необходимости учета в общем случае динамических свойств нелинейных элементов, т.е. их анализ следует ос

Основные типы характеристик нелинейных элементов в цепях переменного тока
Использование динамических характеристик нелинейных элементов позволяет осуществлять расчет нелинейных цепей для мгновенных значений переменных, т.е. проводить принципиально ее наиболее точный и по

Графический метод с использованием характеристик для мгновенных значений
В общем случае методика анализа нелинейной цепи данным методом включает в себя следующие этапы: -исходя из физических соображений находят (если он не задан) закон изменения одной из величи

Решение
1. Строим результирующую ВАХ цепи (см. рис. 4) согласно соотношению

Графический метод с использованием характеристик по первым гармоникам
При анализе нелинейной цепи данным методом изменяющиеся по сложному закону переменные величины заменяются их п

Феррорезонансные явления
Различают феррорезонанс в последовательной цепи (феррорезонанс напряжений) и феррорезонанс в параллельной цепи (феррорезонанс токов). Рассмотрим первый из

Аналитические методы расчета
Аналитические методы, в отличие от рассмотренных выше графических, позволяют проводить анализ нелинейной цепи в общем виде, а не для частных значений параметров элементов схемы. В этом заключается

Метод аналитической аппроксимации
Данный метод основан на аппроксимации характеристик нелинейных элементов аналитическими выражениями с последующим аналитическим решением системы нелинейных уравнений состояния цепи. Точность, а с д

Метод кусочно-линейной аппроксимации
В соответствии с определением данного метода, расчет нелинейной цепи с его использованием включает в себя в об

Метод гармонического баланса
Применение аналитического выражения для аппроксимации характеристики нелинейного элемента позволяет наименее трудоемко провести расчет, когда закон изменения во времени одной из переменных, определ

Лекция N 37
Метод эквивалентных синусоид (метод расчета по действующим значениям) Сущность метода эквивалентных синусоид была изложена в лекции №35 при рассмотрении его графической ре

Катушка с ферромагнитным сердечником
Нелинейная катушка индуктивности изображена на рис. 3. Здесь R-активное сопротивление обмотки с числом витков w; Ф-осно

Трансформатор с ферромагнитным сердечником
Трансформатор с ферромагнитным сердечником изображен на рис. 4. Здесь

Особенности расчета переходных процессов в нелинейных цепях
Переходные процессы в нелинейных электрических цепях описываются нелинейными дифференциальными уравнениями, общих методов интегрирования которых не существует. На нелинейные цепи не распространяетс

Аналитические методы расчета
Аналитическими называются методы решения, базирующиеся на аналитическом интегрировании дифференциальных уравнений, описывающих состояние нелинейной цепи с использованием аналитических выражений хар

Метод условной линеаризации
Метод условной линеаризации применяется в случаях, когда в нелинейном уравнении одно из слагаемых в левой части мало по сравнению с другими, вследствие чего, без внесения существенной погрешности,

Метод аналитической аппроксимации
Метод основан на аппроксимации характеристики нелинейного элемента аналитической функцией, которая должна, с одной стороны, достаточно точно отображать исходную нелинейную характеристику на участке

Метод кусочно–линейной аппроксимации
Данный метод основан на замене характеристики нелинейного элемента отрезками прямых, на основании чего осуществляется переход от нелинейного дифференциального уравнения к нескольким (по числу прямо

Графические методы анализа переходных процессов в нелинейных цепях
Графическими называются методы, в основе которых лежат графические построения на плоскости. По сравнению с рас

Метод изоклин
Данный метод является одним из наиболее широко используемых графических методов приближенного интегрирования. Он непосредственно используется для решения уравнений первого порядка вида

Метод фазовой плоскости
Метод позволяет осуществлять качественное исследование динамических процессов в нелинейных цепях, описываемых дифференциальными уравнениями первого и второго порядков. При этом без непосредственног

Численные методы расчета переходных процессов
Численные методы анализа динамических процессов в нелинейных электрических цепях базируются на различных численных способах приближенного интегрирования нелинейных дифференциальных уравнений. В их

Метод переменных состояния
Метод переменных состояния, как было показано при анализе переходных процессов в линейных цепях, основывается на составлении и интегрировании дифференциальных уравнений, записанных в нормальной фор

Методика составления уравнений состояния на основе принципа наложения
Данная методика составления уравнений состояния вытекает из разделения исходной цепи на две подсхемы: — первая включает в себя элементы, запасающие энергию, а также нелинейные резистивные

Метод дискретных моделей
Метод основан на использовании дискретных моделей индуктивного и емкостного элементов и позволяет свести численный анализ динамических процессов в нелинейных цепях к последовательному расчету на ка

Цепи с распределенными параметрами
В предыдущих лекциях рассматривались электрические цепи, геометрические размеры которых, а также входящих в ни

Уравнения однородной линии в стационарном режиме
Под первичными параметрами линии будем понимать сопротивление , индуктивность

Линия без искажений
Пусть сигнал, который требуется передать без искажений по линии, является периодическим, т.е. его можно разложить в ряд Фурье. Сигнал будет искажаться, если для составляющих его гармонических затух

Уравнения линии конечной длины
Постоянные и в полученных в предыдущей

Определение параметров длинной линии из опытов холостого хода и короткого замыкания
Как и у четырехполюсников, параметры длинной линии могут быть определены из опытов холостого хода (ХХ) и короткого замыкания (КЗ). При ХХ

Линия без потерь
Линией без потерь называется линия, у которой первичные параметры и

Стоячие волны в длинных линиях
Как было показано выше, решение уравнений длинной линии можно представить в виде суммы прямой и обратной волн. В результате их наложения в цепях с распределенными параметрами возникают стоячие волн

Входное сопротивление длинной линии
Входным сопротивлением длинной линии (цепи с распределенными параметрами) называется такое сосредоточенное сопротивление, подключение которого вместо линии к зажимам источника не изменит режим рабо

Переходные процессы в цепях с распределенными параметрами
Переходные процессы в цепях с распределенными параметрами имеют характер блуждающих волн, распространяющихся по цепи в различных направлениях. Эти волны могут претерпевать многократные отражения от

Уравнения переходных процессов в цепях с распределенными параметрами
При рассмотрении схемы замещения цепи с распределенными параметрами были получены дифференциальные уравнения в частных производных

Переходные процессы при включении на постоянное напряжение разомкнутой и замкнутой на конце линии
При замыкании рубильника (см. рис. 2) напряжение в начале линии сразу же достигает величины , и

Сведение расчета переходных процессов в цепях с распределенными параметрами к нулевым начальным условиям
С учетом граничных условий расчет переходных процессов в цепях с распределенными параметрами можно проводить к

Правило удвоения волны
Пусть волна произвольной формы движется по линии с волновым сопротивлением и падает на некоторую нагрузку