Уравнения длинной линии с гиперболическими функциями

Гиперболическая форма уравнений длинной линии

Гиперболическая форма уравнений длинной линии (ДЛ) имеет следующий вид (после применения формул Эйлера для решения уравнений длинной линии с использованием падающей и отраженной волн)

U ( x ) = U 2 c h γ x + I 2 Z В s h γ x ; I ( x ) = U 2 Z В s h γ x + I 2 c h γ x ,

что соответствует гиперболической форме уравнений симметричного четырехполюсника

U 1 = U 2 c h γ + I ′ 2 Z C s h γ ; I 1 = U 2 Z C s h γ + I ′ 2 c h γ .

Поскольку I’₂ соответствует току I₂ ДЛ, волновое сопротивление Z_B = Z_C соответствует характеристическому сопротивлению четырехполюсника, а характеристическая мера передачи четырехполюсника γ соответствует γ·l.

Здесь l – длина длинной линии; x – координата длинной линии, отсчитанная от ее конца (нагрузки); U₁, I₁ и U₂, I₂ – переменные входа и выхода длинной линии.

Таким образом, длинной линии – симметричный четырехполюсник.

Гиперболическая форма уравнений, длинная линия

Цепи с распределенными параметрами

5. Решение уравнений состояния. Выполняется численным методом (например, Рунге-Кутта [9]). Если характеристики рис. 11.53 линеаризовать (подобно тому, как это было сделано в примере 11.13) и оценить реальную длительность переходного процесса, то можно выбрать шаг по времени Dt. При наличии колебательного процесса в линеаризованной цепи должно быть и , где и – постоянная времени и период свободных колебаний. Если же в этой цепи протекает апериодический процесс, то следует принять . При этом будет обеспечена приемлемая для учебных целей точность расчета. Вычисления начинаются с найденных в п.1 значений q(0), и продолжаются до тех пор, пока не будут достигнуты (с заданной точностью) значения q(¥), из п.2.

12. ЦЕПИ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ

12.1. Общие положения

12.1.1. основные понятия и определения

Параметры реальной электрической цепи практически всегда распределены по длине ее участков. Но при решении большинства практических задач это обстоятельство не оказывает существенного влияния на результаты анализа. В этих случаях можно считать, что сопротивления, индуктивности, емкости сосредоточены на определенных участках цепи и соответствующим образом отражаются в схеме замещения. Такое допущение с успехом использовалось во всех предыдущих разделах курса, где рассматривались цепи с сосредоточенными параметрами.

Однако существуют и задачи, условия которых просто не позволяют пренебречь распределением параметров. Устройство можно рассматривать как электрическую цепь, если оно имеет достаточно большую протяженность только в определенном направлении. В этом случае можно говорить о распределении параметров именно в этом направлении. Необходимость учета распределения параметров цепи вдоль некоторого направления возникает в тех случаях, когда промежуток времени, за который электромагнитная волна распространяется вдоль цепи в этом направлении, соизмерим с интервалом времени, за который токи и напряжения в цепи могут измениться на заметную величину. Разумеется, токи и напряжения при этом оказываются функциями двух независимых переменных: времени t и расстояния x. Поэтому уравнения, описывающие состояние цепи с распределенными параметрами, – это уравнения в частных производных.

Примерами таких цепей служат, в первую очередь, протяженные линии электропередачи, линии связи, высокочастотные линии радиотехнических и телевизионных устройств. Впрочем, и обмотки трансформаторов, и обмотки электрических машин, работающих в импульсном режиме, также должны рассматриваться как цепи с распределенными параметрами.

Выберем в качестве объекта исследования двухпроводную линию. Нам придется считать, что каждый сколь угодно малый элемент длины линии обладает параметрами, отражающими в схеме замещения известные явления. Как обычно, сопротивление будет учитывать тепловые потери в проводах, индуктивность – явление самоиндукции при изменении магнитного потока, емкость – токи смещения между проводами, а проводимость – токи утечки по изоляции. Если эти параметры равномерно распределены по длине, то такую линию называют однородной. Выведем уравнения, описывающие состояние однородной двухпроводной линии, считая ее параметры на единицу длины , , , известными и независящими от частоты. Эти параметры называют первичными. Заметим, что при необходимости подобные уравнения нетрудно применить и к исследованию трехфазной линии, работающей в симметричном режиме, используя ее схему замещения на одну фазу.

12.1.2. Уравнения однородной двухпроводной линии

в частных производных

Выделим на расстоянии х от начала линии элемент линии длиной dx, на входе которого существуют напряжение u и ток i (рис. 12.1,а). На выходе эти величины получают приращения и . Первое связано с падениями напряжения на сопротивлении и индуктивности , по которым в схеме замещения (рис. 12.1,б) протекает ток i. Второе – с утечками по проводимости и током смещения через емкость , которые находятся под напряжением . По законам Кирхгофа имеем:

Приводя подобные, пренебрегая величинами второго порядка малости, после деления на dx, получим уравнения однородной двухпроводной линии в частных производных:

(12.1)

Решение этой системы уравнений при заданных начальных и граничных условиях позволяет определить искомые зависимости i(x,t) и u(x,t). Уравнения справедливы для описания как установившихся, так и переходных режимов.

12.2. установившийся синусоидальный режим

работы однородной двухпроводной линии

12.2.1. Уравнения линии в установившемся

Для решения уравнений линии в частных производных в установившемся синусоидальном режиме используем комплексный метод. При переходе от синусоидальных функций времени к их комплексным изображениям окажется, что

Поэтому уравнения (12.1) в комплексной форме записи примут вид:

Обозначив здесь – комплексное продольное сопротивление, а – комплексную поперечную проводимость единицы длины линии, получим

(12.2)

Подстановка I из первого уравнения системы (12.2) во второе, приводит к линейному дифференциальному уравнению второго порядка

с комплексно сопряженными корнями характеристического уравнения ±g. Решение такого уравнения можно записать в виде суммы экспонент:

. (12.3)

Здесь – (12.4)

коэффициент распространения линии, , , и – постоянные интегрирования.

Подстановка выражения (12.3) в первое уравнение системы (12.2) позволяет найти комплекс тока

, (12.5)

где величина (12.6)

имеет размерность сопротивления.

Для того, чтобы выяснить физический смысл слагаемых, входящих в формулы (12.3), (12.5), и их отношения (12.6), перейдем от комплексных величин к функциям времени.

12.2.2. Бегущие волны

Запишем в показательной форме комплексы

и

Тогда мгновенные значения величин, соответствующих комплекс­ным слагаемым в выражении (12.3), примут вид:

При фиксированном значении координаты каждая из этих величин изменяется во времени по синусоидальному закону с периодом . А в любой фиксированный момент времени распределение напряжения вдоль линии происходит по закону затухающей синусоиды с (длина волны – расстояние между двумя ближайшими точками линии, в которых фазы синусоид тока или напряжения волны отличаются на ). При этом затухание происходит от начала линии к концу, то есть в сторону увеличения координаты х, а затухает от конца к началу (в сторону уменьшения х). На рис. 12.2 показано распределение составляющей вдоль х в моменты времени и . Подобным же образом ведет себя и зависимость

Если же зафиксировать фазу синусоиды и продифференцировать это выражение по времени, то получится

, отсюда

. (12.7)

Это означает, что мы имеем дело с электромагнитной волной, которая движется в сторону увеличения х с фазовой скоростью . По мере перемещения амплитуды напряжения и тока затухают. Назовем эту волну прямой. На рис. 12.2 видно, что за время нули на графике функции перемещаются на расстояние .

Очевидно, с помощью аналогичных рассуждений можно показать, что вторая пара составляющих напряжения и тока

характеризует обратную волну, которая движется в сторону уменьшения х с той же самой скоростью. Причем амплитуды напряжения и тока также затухают по мере продвижения волны.

Поэтому комплекс можно назвать волновым сопротивлением линии. Оно равно отношению комплексов напряжения и тока в любой точке линии, когда в ней существует только одна волна – неважно какая, прямая или обратная.

В свою очередь коэффициент распространения характеризует изменение тока и напряжения волны по мере ее продвижения. Действительно, из формул (12.3–12.6) следует:

.

Выбор отрезка Dх, равного единице длины, позволяет дать следующие определения.

Коэффициент затухания показывает, насколько отличаются логарифмы действующих значений напряжений или токов одной волны в точках, отстоящих друг от друга на единицу длины. Единица измерения – непер на метр [Нп/м] или на километр.

Коэффициент фазы показывает, насколько отличаются фазы напряжений или токов одной волны в тех же самых точках. Единица измерения – радиан на метр [рад/м] или на километр.

и называют вторичными параметрами линии, они, также как и первичные, полностью характеризуют линию.

Таким образом, установившийся синусоидальный режим работы линии можно рассматривать как результат наложения двух затухающих бегущих в противоположных направлениях с одинаковой скоростью волн. Если х отсчитывается от начала линии (рис. 12.1,а), то возникновение обратной волны можно рассматривать как результат отражения прямой волны от нагрузки и называть волны падающей и отраженной.

Пометим индексом 2 значения величин в конце линии (x = l), где включена нагрузка с комплексным сопротивлением . Тогда

Отсюда нетрудно найти коэффициент отражения:

. (12.8)

В частности в режимах холостого хода и короткого замыкания происходит полное отражение волны (N = ±1 соответственно). При отражения не происходит (N = 0), в линии существует только одна волна и вся принесенная ею энергия поглощается нагрузкой. Такой режим называется режимом согласованной нагрузки.

При согласованной нагрузке мощность в начале линии равна

и коэффициент полезного действия

.

Известны волновое сопротивление и коэффициент распространения линии электропередачи, работающей на промышленной частоте f = 50 Гц: , 1/км.

Определить первичные параметры линии: , , , .

Воспользовавшись формулами (12.4) и (12.6), найдем:

Отсюда и

Затем вычисляем угловую частоту и, наконец,

12.2.3. Уравнения линии в гиперболических функциях

Определим постоянные интегрирования в уравнениях (12.3) и (12.5) из граничных условий, считая, что в начале линии (х = 0 на рис. 12.3,а) и напряжение , и ток известны. Тогда эти уравнения переписываются в виде: откуда легко найти

После подстановки постоянных в уравнения (12.3), (12.5) и приведения подобных заметим, что

В результате получим уравнения линии в гиперболических функциях:

(12.9)

Подстановка x = l дает:

Если разрешить эти уравнения относительно , , то они примут вид:

Последние две системы уравнений совпадают по форме с уравнениями четырехполюсника в гиперболических функциях, характеристическое сопротивление и постоянная передачи которого очень просто выражаются через вторичные параметры линии:

Соответственно коэффициенты затухания и фазы такого эквивалентного линии четырехполюсника равны:

Все эти параметры определяются в режиме согласованной нагрузки (см. раздел 9.7 [6]).

Очевидно, при отсчете расстояния y от конца линии (рис.12.3,б) уравнения линии в гиперболических функциях примут следующий вид:

(12.10)

Для вывода этих формул достаточно в предыдущей системе уравнений произвести обратную замену l на y. Эту запись удобно использовать для исследования режимов работы линии при изменении сопротивления нагрузки

12.2.4. Линия без искажений

Если линия используется для передачи информации (линия связи, радио и т. п.), то для достоверности передачи необходимо, чтобы коэффициент затухания и волновое сопротивление линии не зависели от частоты. В этом случае, несмотря на затухание, форма передаваемого сигнала не будет изменяться и при согласованной нагрузке не возникнут отраженные волны. Если к тому же коэффициент фазы будет пропорционален частоте β = const·ω, то и фазовая скорость не будет зависеть от частоты. Такая линия называется линией без искажений и для выполнения выше перечисленных условий необходимо:

. (12.11)

Действительно, из (12.4) и (12.6) легко получить

(12.12)

(12.13)

Так что ни в волновое сопротивление , ни в коэффициент затухания частота не входит (это вещественные числа), а коэффициент фазы частоте пропорционален. Характерно, что оба коэффициента принимают в этом случае минимальные значения:

(12.14)

Фазовая скорость волн в линии достигает в этом случае наибольшего значения:

. (12.15)

Если линия работает в режиме согласованной нагрузки, то в линии существует только одна волна, поэтому в любой точке линии в любой момент времени причем ток и напряжение совпадают по фазе.

Следует иметь в виду, что как у воздушных, так и у кабельных линий поэтому для выполнения условия (12.11) приходится включать через равные расстояния дополнительную сосредоточенную индуктивность. Правда, при этом уменьшается скорость распространения волн в линии.

Известны первичные параметры линии связи:

Определить, какую дополнительную индуктивность нужно включать через каждый километр линии, чтобы сигналы по ней передавались без искажения.

Из условия (12.11) найдем, какой должна быть индуктивность единицы длины линии без искажения:

Поэтому мГн, где l = 1 км.

12.2.5. Линия без потерь

В некоторых практически важных случаях (особенно при высоких частотах в линиях связи, телевидения, радио) оказывается и можно для упрощения анализа пренебречь потерями в линии, приняв

Тогда коэффициент затухания a = 0, коэффициент распространения – мнимое число, поэтому от гиперболических функций мнимого аргумента можно перейти к тригонометрическим функциям вещественного аргумента:

, .

Тогда и уравнения линии в гиперболических функциях (12.10) переходят в уравнения линии без потерь в тригонометрических функциях:

(12.16)

Здесь координата y отсчитывается от конца линии (рис. 12.3,б), причем, как в линии без искажений, волновое сопротивление линии без потерь – вещественное число, а фазовая скорость имеет наибольшее значение , которое в воздушных линиях достигает скорости света с = 300000 км/с. Длина волны .

Рассмотрим характерные режимы работы линии.

Холостой ход.

При этих условиях уравнения (36.5) превращаются в

(12.17)

В результате наложения двух незатухающих волн одинаковой амплитуды, движущихся в противоположных направлениях, в линии существуют стоячие волны. Узлы напряжения соответствуют пучностям тока и оказываются в точках с координатами , , . а узлы тока и пучности напряжения – соответственно в точках , , l, .

Входное сопротивление линии длиной l

(12.18)

имеет чисто реактивный характер. При , и т. д. оно емкостное, а при , и т. д. – индуктивное. При , и т. д. это сопротивление равно нулю (резонанс напряжений), а при , l и т. д. стремится к бесконечности (резонанс токов). Соответствующие кривые построены на рис. 12.4,а.

Короткое замыкание. N = –1.

. (12.19)

В этом режиме тоже существуют стоячие волны, но по сравнению с предыдущим случаем узлы и пучности токов и напряжений сдвинуты на четверть длины волны. Входное сопротивление

тоже чисто реактивное. Но его характер противоположен характеру в режиме холостого хода на тех же участках. Зависимости |U(y)|, |I(y)|, показаны на рис. 12.4,б.

где причем так что Поэтому

(12.21)

И здесь обнаружились стоячие волны, но узлы и пучности напряжения (тока) смещены в сторону увеличения y по отношению к их расположению в режиме короткого замыкания на расстояние при емкостной нагрузке и на расстояние, большее четверти длины волны, при индуктивной нагрузке. Соответствующий сдвиг имеет и график .

Три режима, рассмотренные выше, объединяет общее обстоятельство: отсутствует потребление энергии и в нагрузке, и в линии. Только в этом случае могут существовать точки, через которые не передается энергия – узлы тока и напряжения. На участках между этими точками осуществляется обмен энергией между электрическим и магнитным полями.

Известно, что высокочастотная линия с волновым сопротивлением Ом нагружена на чисто реактивный двухполюсник.

Определить величину и характер сопротивления нагрузки, если ближайший к концу линии узел тока находится на расстоянии м, а следующий за ним узел напряжения – на расстоянии м.

Расстояние между узлами тока и напряжения – это четверть длины волны. Поэтому м. В режиме реактивной нагрузки рад/с, и . Значит, линия нагружена на индуктивность. Тогда Ом.

где

(12.22)

Проанализировав эти выражения, можно заметить, что ни кривая U(y), ни кривая I(y) не имеют ни узлов, ни пучностей при любых хотя и сохраняют волнообразный характер (рис. 12.5). При максимумы напряжения и минимумы тока лежат в тех же точках, что и пучности напряжения и узлы тока в режиме холостого хода. В данном случае максимум действующего значения напряжения А минимум напряжения отстоит от конца линии на расстоянии и, как следует из (12.22), В радиотехнике вводится понятие коэффициента бегущей волны как отношения этих величин Так что при оказывается

Если же то минимумы напряжения и максимумы тока расположены там же, где пучности тока и узлы напряжения в режиме короткого замыкания. Поэтому в конце линии а на расстоянии от конца линии лежит точка, в которой Значит, при получится Так что по распределению напряжения в линии с известным волновым сопротивлением нетрудно вычислить и сопротивление нагрузки.

Естественно, наибольшее значение достигается в режиме согласованной нагрузки, когда в линии существует только одна бегущая волна, которая не отражается от нагрузки.

Согласованная нагрузка.

(12.11)

Действующие значения тока и напряжения во всех точках линии одинаковы (рис. 12.5), причем мгновенные значения этих величин совпадают по фазе.

Линия без потерь длиной обладает весьма полезными для практического использования свойствами. Для нее , тогда

В режиме короткого замыкания входное сопротивление линии стремится к бесконечности, то есть четвертьволновая линия представляет собой идеальный изолятор.

В режиме активной нагрузки четвертьволновую линию можно рассматривать как «трансформатор сопротивлений» и применять для согласования генератора с внутренним сопротивлением и приемника с сопротивлением . Параметры линии следует подобрать таким образом, чтобы Тогда входное сопротивление пассивного двухполюсника, подключенного к генератору (система линия–нагрузка), а эквивалентное внутреннее сопротивление активного двухполюсника (система генератор–линия), к которому подключена нагрузка, равно При таком подборе параметров генератор будет выдавать за период максимально возможную энергию, причем вся эта энергия перейдет в нагрузку, поскольку потери в линии отсутствуют. Аналогичное условие используется для согласования двух линий с разными волновыми сопротивлениями и при помощи третьей (четвертьволновой) линии, включенной между ними. Ее волновое сопротивление должно быть .

12.3. ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЦЕПЯХ

С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ

12.3.1. Прямая и обратная волны

В линиях электропередачи, связи, обмотках трансформаторов и других цепях с распределенными параметрами переходные процессы возникают чаще всего по тем же причинам, что и в цепях с сосредоточенными параметрами. Это может быть подключение цепи к источнику и отключение от него, подключение нагрузки и ее отключение, скачкообразное изменение параметров какого-либо участка цепи (например, в случае аварии). Кроме того, при достаточной протяженности цепи переходные процессы могут возникнуть и в случае изменения электромагнитных полей в окружающем пространстве (например, во время грозы). Токи и напряжения во время переходных процессов зависят от двух переменных – времени t и расстояния x. Переходные процессы имеют волновой характер.

Ниже рассматриваются примеры переходных процессов в однородной двухпроводной линии без потерь Из (12.1) следуют уравнения линии без потерь в частных производных:

(12.24)

Решим их операторным методом, подобно тому, как в разделе 12.2.1 решали уравнения (12.1) комплексным методом.

Пусть , – операторные изображения соответствующих функций времени , . Тогда в соответствии с теоремой дифференцирования можно найти изображения частных производных тех же величин при нулевых начальных условиях

Уравнения длинной линии с гиперболическими функциями

Кривая, форма которой соответствует однородной гибкой нерастяжимой тяжелой нити, закрепленной с обоих концов и находящейся под действием силы тяжести, называется цепной линией. Очевидно, цепная линия является плоской кривой, то есть такой кривой, все точки которой лежат в одной плоскости.

Долгое время считалось, что цепная линия представляет собой параболу, подобно тому, как траектория движения камня в поле земного тяготения есть парабола. Однако уже в начале 17 века великий итальянский мыслитель Галилео Галилей высказал предположения, что цепная линия не является параболой. Строгое решение задачи с выводом уравнения цепной линии впервые было найдено в трудах великих немецких мыслителей Готфрида Лейбница и Иоганна Бернулли, а также великого нидерландского естествоиспытателя Христиана Гюйгенса в 1691 году.

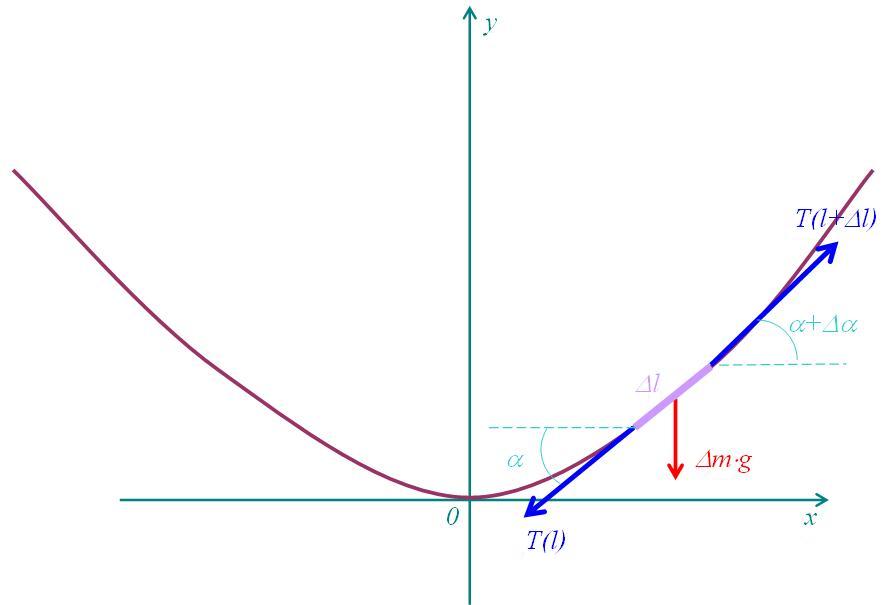
Рассмотрим элементарный участок нити длиной \(\Delta l\) (Рисунок 3). Масса этого участка равна \(\Delta m = \rho S \Delta l\) и на него действуют распределенная по длине сила тяжести интенсивности \(\rho gS\), направленная вниз и равная \(\Delta m g = \rho g S \Delta l\). Здесь \(\rho\) — объемная плотность материала нити, \(g\) — ускорение свободного падения, \(S\) — площадь поперечного сечения нити.

Также на концах данного участка действуют силы натяжения \(T(l)\) и \(T(l+\Delta l)\).

Рисунок 1. Цепи, используемые при штабелирование парахода “Бремен”. Фото из Федерального архива Германии.
Bundesarchiv Bild 102-06406, Bremen, Stapellauf des Dampfers «Bremen».

Рисунок 2. Цепи ограждения Царь-пушки в московском кремле. http://www.fotokonkurs.ru/photo/58515

Условие равновесия рассматриваемого участка запишется в виде: $$ \vec T(l) + \vec T(l+\Delta l) + \Delta m\vec g = 0. $$ В проекции на оси координат получим $$ — T(l)\cos(\alpha) + T(l+\Delta l)\cos(\alpha + \Delta \alpha) = 0. $$ $$ — T(l)\sin(\alpha) + T(l+\Delta l)\sin(\alpha + \Delta \alpha) — \rho gS\Delta l = 0.$$ Из первого уравнения получаем, что горизонтальная компонента силы натяжения \(T(l)\) всегда постоянна: \( T(l)\cos\alpha(l) = T_0 = const.\) Второе уравнение перепишем в виде: $$ d(T(l)\sin(\alpha(l)) = d(\rho gSl).$$ С учётом сказанного, можем записать $$ T_0 d(tg(\alpha(l)) = \rho gSdl).$$ Памятуя о геометрическом смысле производной, запишем \(tg\alpha = y’\) и тогда получим $$\frac

= \frac<\rho gS>.$$ Переходя к переменной x, используя правило дифференцирования сложной функции и выражение для дифференциала дуги кривой, получим $$\frac

= \frac \cdot \frac

= \frac \cdot \frac> = $$ $$ = \frac \cdot \frac <1><\sqrt<1+(y')^2>> = \frac <\rho gS>.$$ Отсюда, учитывая, что производная от первой производной есть вторая производная, получаем $$y» = \frac <\rho gS> \cdot \sqrt<1+(y')^2>.$$
Последнее уравнение называется дифференциальным уравнением цепной линии. Это уравнение второго порядка, допускающее понижение порядка. Чтобы понизить порядок уравнения сделаем замену \(z(x)=y’\). Тогда \(y»=z’\). Подставляя в последнее дифференциальное уравнение, получим $$\frac = z’ \frac <\rho gS> \cdot \sqrt<1+z^2>.$$

Рисунок 3. Ценная линия и расчётная схема.

Получили уравнение с разделяющимися переменными, которое после элементарных преобразований принимает вид $$\frac<\sqrt<1+z^2>> = \frac<\rho gS> \cdot dx.$$ Интегрируем последнее уравнение $$\int\frac<\sqrt<1+z^2>> = \frac<\rho gS> \int dx,$$ $$\ln|z + \sqrt<1+z^2>| = \frac<\rho gS> \cdot x + C_1.$$ Принимая за начало координат нижнюю точку цепной линии, заметим, что касательная в нижней точке горизонтальная, другими словами, нижняя точка является точкой экстремума для функции \(y(x)\). Следовательно, \(y’(0)=z(0)=0\). Подставим в последнее выражение \(x=0, y=0, z=0\). В результате получим \(С_1 = 0\). Тогда уравнение цепной линии перепишется в виде $$\ln|z + \sqrt<1+z^2>| = \frac<\rho gS> \cdot x.$$ Потенцируя полученное уравнение, перепишем его в показательной форме

Здесь для сокращения записи мы ввели обозначение \(\frac<\rho gS> = \kappa.\)
Умножим обе части уравнение (1) на выражение сопряжённое к левой части \(z-\sqrt<1+z^2>\). Получим $$(z + \sqrt<1+z^2>)\cdot(z — \sqrt<1+z^2>) = e^<\kappa x>\cdot(z — \sqrt<1+z^2>).$$ Нетрудно заметить, что $$(z + \sqrt<1+z^2>)\cdot(z — \sqrt<1+z^2>) = z^2 — (\sqrt<1+z^2>)^2 = z^2 -1 + z^2 = -1.$$ Вследствие последнего замечания, уравнение можно переписать в виде $$e^<\kappa x>\cdot(z — \sqrt<1+z^2>) = -1.$$ или в виде $$z — \sqrt <1+z^2>= -e^<\kappa x>. $$ Прибавим последнее выражением к выражению (1), и поделим полученное равенство на 2. В результате получим $$z = \frac — e^<-\kappa x>><2>. $$ Определение 1. Гиперболическим синусом от \(x\) называется функция, определённая следующим выражением $$sh(x) = \frac — e^<-x>><2>. $$ Определение 2. Гиперболическим косинусом от \(x\) называется функция, определённая следующим выражением $$sh(x) = \frac + e^<-x>><2>. $$ Предложение 1. Производная от гиперболического косинуса есть гиперболический синус, производная от гиперболического синуса есть гиперболический косинус, то есть$$sh'(x) = ch(x),$$ $$ch'(x) = sh(x).$$ Доказательство. $$sh'(x) = \left(\frac — e^<-x>><2>\right)’ = \frac <(e^— e^<-x>)’> <2>= \frac <(e^)’ — (e^<-x>)’> <2>= \frac <(e^)’ + (e^<-x>)’> <2>= ch(x);$$ $$ch'(x) = \left(\frac + e^<-x>><2>\right)’ = \frac <(e^+ e^<-x>)’> <2>= \frac <(e^)’ + (e^<-x>)’> <2>= \frac <(e^)’ — (e^<-x>)’> <2>= sh(x).$$ Доказательство завершено. ❑

Следствие 1. Первообразная от гиперболического косинуса есть гиперболический синус, а первообразная от гиперболического синуса есть гиперболический косинус.

Следствие 2. $$\int sh(x)dx = ch(x) + C, $$ $$ \int ch(x)dx = sh(x) + C.$$
С учётом сформулированных определений, а также памятуя о сделанной ранее замене \(z(x)\), перепишем выражение для прогиба в следующем виде $$ y’ = z = \frac — e^<-\kappa x>> <2>= sh(\kappa x).$$
На основании предложения 1 и следствий к нему, после интегрирования получим $$ y(x) = \int sh(\kappa x)dx = \frac <1> <\kappa>\cdot ch(\kappa x) + C.$$
В принятой системе координат, когда нижняя точка цепной линии является началом системы координат, справедливо следующее начальное условие \(y(0)=0\). Подставим это условие в найденное уравнение цепной линии и получим $$ y(0) = \frac <\kappa>+ C = 0,$$ $$ \frac <1> <\kappa>\cdot \frac <2>+C = \frac <1> <\kappa>\cdot \frac <1+1> <2>+C = \frac <1> <\kappa>+ C = 0. $$ Отсюда \(С=-\frac <1><\kappa>\) и уравнение цепной линии запишется в виде $$ y(x) = \frac <1> <\kappa>\left(ch(\kappa x) — 1\right).$$
Таким образом, форма цепной линии определяется как гиперболический косинус с параметром \(\kappa\). Кроме гиперболического синуса и гиперболического косинуса существуют также гиперболический тангенс и котангенс, которые определяются по тому же принципу, что и тригонометрический тангенс и котангенс, а именно:

Определение 3. Гиперболическим тангенсом от \(x\) называется функция, определённая следующим выражением $$th(x) = \frac .$$
Определение 4. Гиперболическим котангенсом от \(x\) называется функция, определённая как частное гиперболического скосинуса и гиперболического синуса. То есть гиперболический котангенс это функция, определённая следующим выражением $$cth(x) = \frac .$$
Из сделанных определений следуют равенства $$th(x) \cdot cth(x) = 1;$$ $$th(x) =\frac >>;$$ $$cth(x) =\frac >>.$$
Исследуем ряд других замечательных свойств гиперболических функций.

Предложение 2. Справедливы следующие тождества $$сh^2(x) — sh^2(x) = 1;$$ $$1-th^2(x) = \frac <1>,$$ $$cth^2(x) — 1 = \frac <1>.$$ Доказательство.

Из определений гиперболического косинуса и гиперболического синуса следует: $$ch^2(x) — sh^2(x) = \left(\frac + e^<-x>><2>\right)^2 — \left(\frac <(e^— e^<-x>)><2>\right)^2 = $$ $$ = \frac <(e^)^2 + 2e^xe^ <-x>+ (e^<-x>)^2> <4>— \frac <(e^)^2 — 2e^xe^ <-x>+ (e^<-x>)^2> <4>= e^xe^ <-x>= e^ = e^0 = 1.$$ Первое тождество доказано. Из него следует $$ch^2(x) = 1 + sh^2(x);$$ $$sh^2(x) = ch^2(x) — 1.$$ Тогда $$1 — th^2(x) = 1 — \frac = \frac = \frac <1>.$$ $$cth^2(x) — 1 = \frac — 1 = \frac = \frac <1>.$$ Все три тождества доказаны. ❑

Задание.
Найти производные гиперболического тангенса и гиперболического котангенса.

Решение.
По правилу дифференцирования частного, получим для производной гиперболического тангенса $$th'(x) = \left(\frac\right)’ = \frac = $$ $$ = \frac = \frac = \frac <1>.$$
Аналогично получим производную для функции гиперболический котангенс $$cth'(x) = \left(\frac\right)’ = \frac = $$ $$ = \frac = \frac = — \frac <1>.$$
Таким образом, мы доказали следующие соотношения $$ th'(x) = \frac <1>;$$ $$ cth'(x) = — \frac <1>.$$
Обратим внимание на некоторое сходство полученных тождеств с соответствующими тригонометрическими тождествами.