Метод интервалов, решение неравенств
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Определение квадратного неравенства
Неравенство — алгебраическое выражение, в котором используются знаки ≠, , ≤, ≥.
Числовое неравенство — это такое неравенство, в записи которого по обе стороны от знака находятся числа или числовые выражения.
Решение — значение переменной, при котором неравенство становится верным.
Решить неравенство значит найти множество, для которых оно выполняется.
Квадратное неравенство выглядит так:
 |
где x — переменная,
Квадратное неравенство можно решить двумя способами:
- графический метод;
- метод интервалов.
Решение неравенства графическим методом
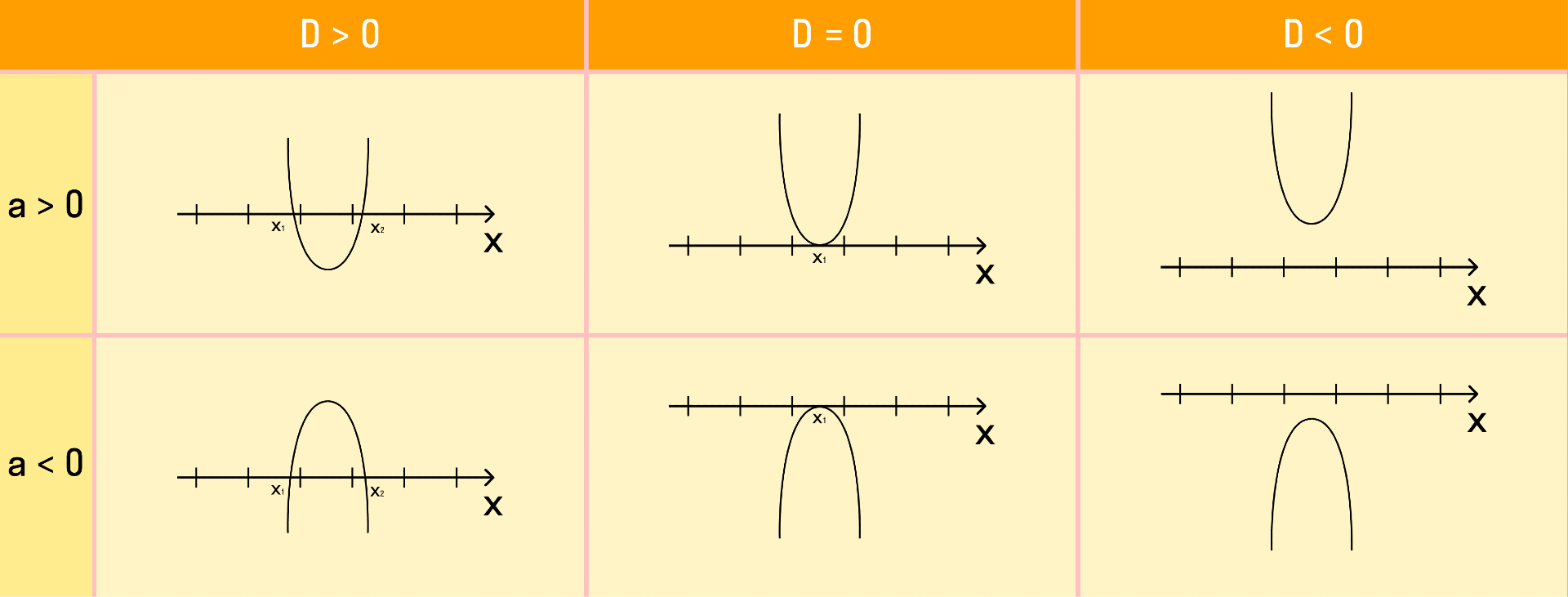
При решении квадратного неравенства необходимо найти корни соответствующего квадратного уравнения ax 2 + bx + c = 0. Чтобы найти корни, нужно найти дискриминант данного уравнения.
Как дискриминант влияет на корни уравнения:
- D = 0. Если дискриминант равен нулю, тогда у квадратного уравнения есть один корень;
- D > 0. Если дискриминант больше нуля, тогда у квадратного уравнения есть два различных корня;
- D 2 + bx + c.
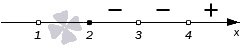
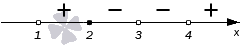
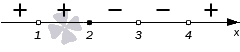
Если требуется найти числовой промежуток, на котором квадратный трехчлен ax 2 + bx + c больше нуля, то этот числовой промежуток находится там, где парабола лежит выше оси ОХ.
Если нужно найти числовой промежуток, на котором квадратный трехчлен ax 2 + bx + c меньше нуля — это числовой промежуток, где парабола лежит ниже оси ОХ.
Если квадратное неравенство нестрогое, то корни входят в числовой промежуток. А если строгое — не входят.
Обучение на курсах по математике в онлайн-школе Skysmart сделает сложные темы понятными, а высокий балл на экзаменах — достижимым!
Решение неравенства методом интервалов
Метод интервалов — это специальный алгоритм, который предназначен для решения рациональных неравенств.
Рациональное неравенство имеет вид f(x) ≤ 0, где f(x) — рациональная функция. При этом знак может быть любым: >, 2 + bx + c из левой части квадратного неравенства.
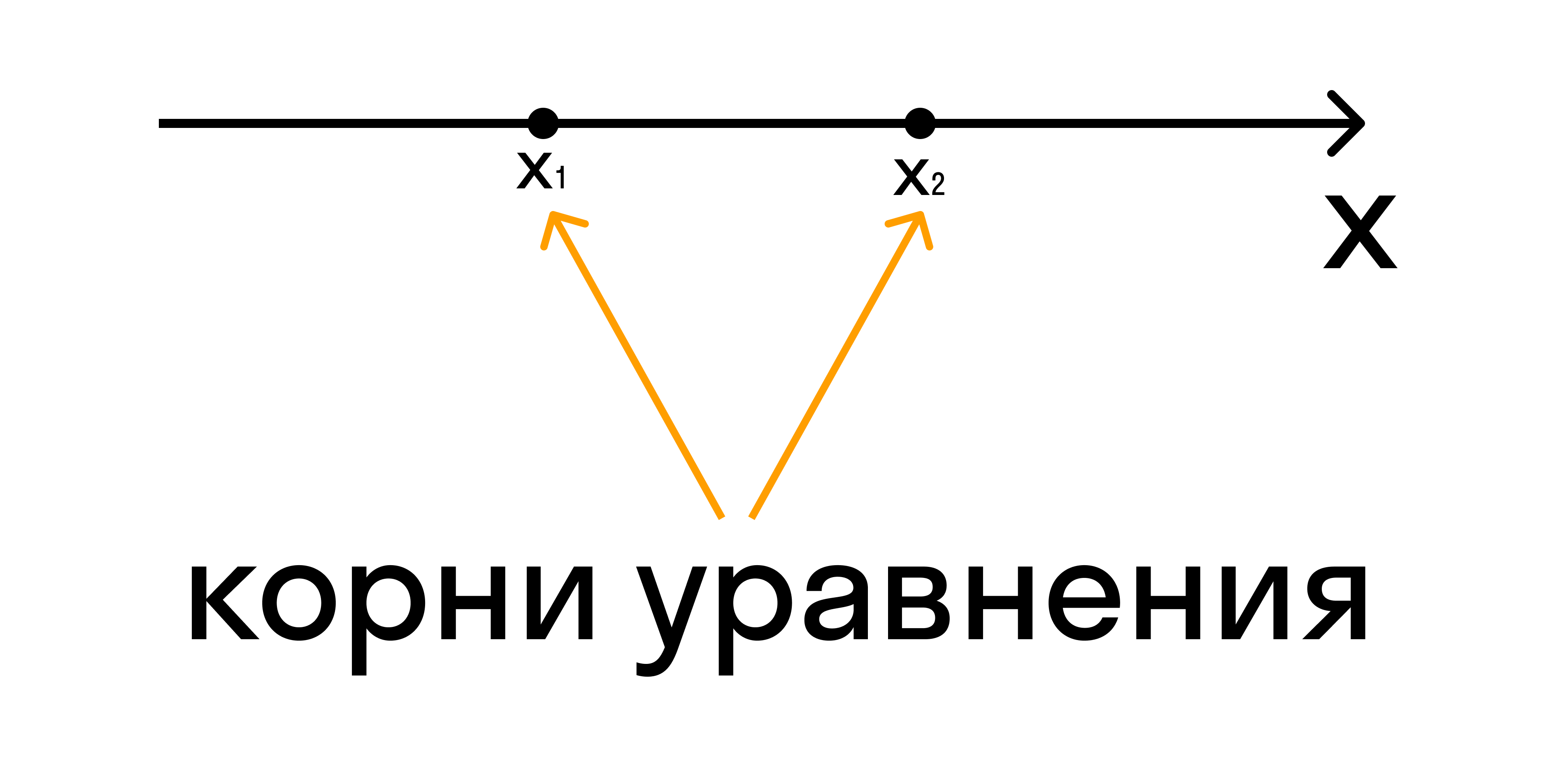
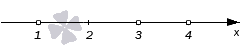
Изобразить координатную прямую и при наличии корней отметить их на ней.
Если неравенство строгое, нужно отметить корни пустыми (выколотыми) точками. Если нестрогое — обычными точками. Именно эти точки разбивают координатную ось на промежутки.
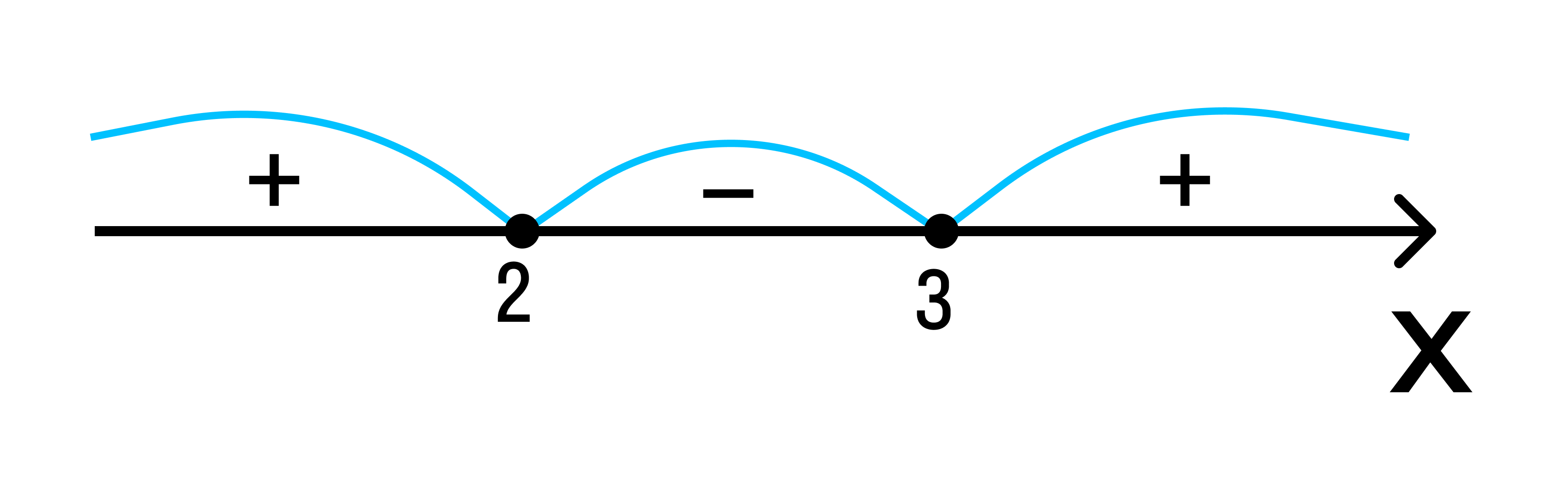
Если неравенство со знаком 2 + 4x — 5, его корнями являются числа -5 и 1, они разбивают числовую ось на три промежутка: (-∞, -5), (-5, 1) и (1, +∞).
Определим знак трехчлена x 2 + 4x — 5 на промежутке (1, +∞). Для этого вычислим значение данного трехчлена при некотором значении x из этого промежутка. Можно брать любое значение переменной, главное — чтобы вычисления были простыми. В нашем случае, возьмем x = 2. Подставим его в трехчлен вместо переменной x:
- 2 2 + 4 * 2 — 5 = 4 + 8 — 5 = 7.
7 — положительное число. Это значит, что любое значение квадратного трехчлена на интервале (1, +∞) будет положительным. Так мы определили знак плюс.
Определим знаки на оставшихся двух промежутках. Начнем с интервала (-5, 1). Из этого интервала можем взять x = 0 и вычислить значение квадратного трехчлена при этом значении переменной:
- 0 2 + 4 * 0 — 5 = 0 + 0 — 5 = -5.
Так как -5 — отрицательное число, то на этом интервале все значения трехчлена будут отрицательными. Так мы определили знак минус.
Осталось определиться со знаком на промежутке (-∞, -5). Возьмем x = -6, подставляем:
- (-6) 2 + 4 * (-6) — 5 = 36 — 24 — 5 = 7.
Следовательно, искомый знак — плюс.
Можно расставить знаки быстрее, если запомнить эти факты:
Плюс или минус: как определить знаки
Можно сделать вывод о знаках по значению старшего коэффициента a:
если a > 0, последовательность знаков: +, −, +,
если a 0, последовательность знаков: +, +,
если a 2 — 7 не имеет корней и на промежутке (−∞, +∞) его значения отрицательны, так как коэффициент при x 2 есть отрицательное число -4, и свободный член -7 тоже отрицателен.
- Когда квадратный трехчлен при D > 0 имеет два корня, то знаки его значений на промежутках чередуются. Это значит, что достаточно определить знак на одном из трех промежутков и расставить знаки над оставшимися промежутками, чередуя их. В результате возможна одна из двух последовательностей: +, −, + или −, +, −.
- Если квадратный трехчлен при D = 0 имеет один корень, то этот корень разбивает числовую ось на два промежутка, а знаки над ними будут одинаковыми. Это значит, что достаточно определить знак над одним из них и над другим поставить такой же. При этом получится, либо +, +, либо −, −.
- Когда квадратный трехчлен корней не имеет (D
Теперь мы знаем пошаговый алгоритм. Чтобы закрепить материал потренируемся на примерах и научимся использовать метод интервалов для квадратных неравенств.
Пример 1. Решить неравенство методом интервалов: x^2 — 5x + 6 ≥ 0.
Разложим квадратный трехчлен на множители.
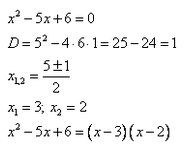
Неравенство примет вид:
Проанализируем два сомножителя:
Первый: х — 3. Этот сомножитель может поменять знак при х = 3, значит при х 0 принимает положительные значения: х — 3 > 0.
Второй: х — 2. Для этого сомножителя такая «знаковая» точка: х = 2.
Вывод: знак произведения (х — 3) * (х — 2) меняется только при переходе переменной через значения х = 3 и х = 2.
В этом весь смысл метода интервалов: определить интервалы значений переменной, на которых ситуация не меняется и рассматривать их как единое целое.
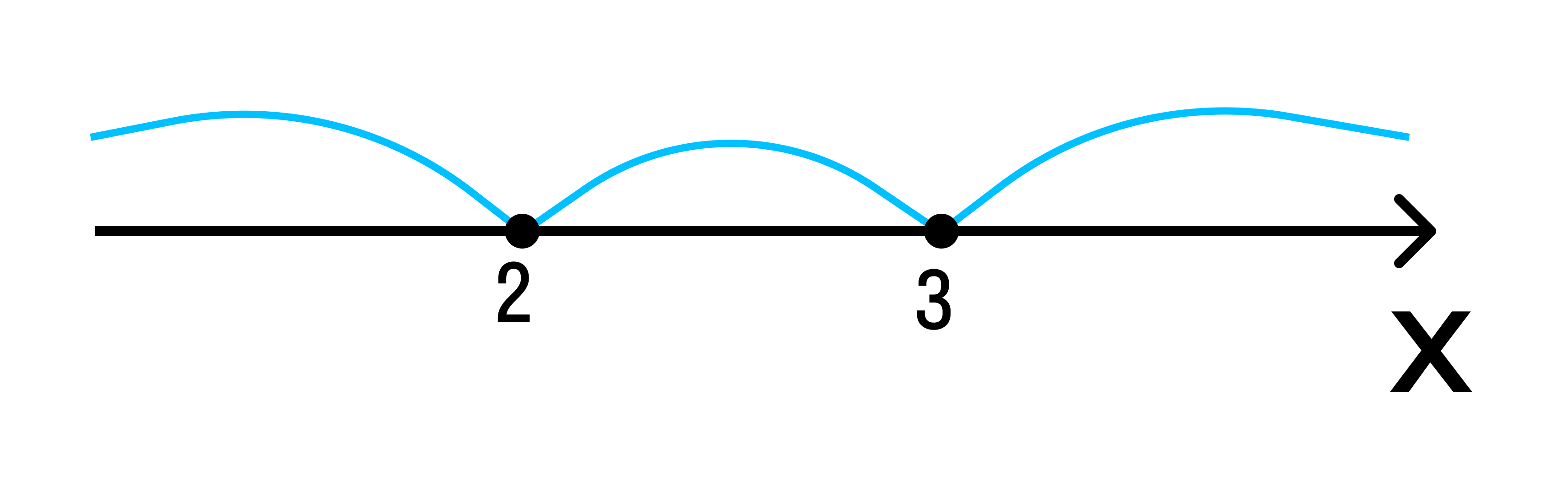
Отобразим эти данные на чертеже:
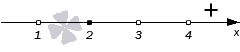
2 3 — на этом интервале ситуация не изменяется. Значит нужно взять любое значение из этого интервала и подставить его в произведение. Например: х = 25.
- (25 — 3) (25 — 2) = 22*23 = 506 > 0
Вывод: при х > 3 верно неравенство (х — 3) * (х — 2) > 0. Внесем эти данные в чертеж.
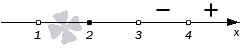
Исходное неравенство: (х — 3) * (х — 2) ≥ 0.
Если (х — 3) * (х — 2) > 0:
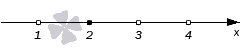
Если (х — 3) (х — 2) = 0 — при х1 = 3, х2 = 2.
Удовлетворяющие неравенству точки закрасим, а не удовлетворяющие — оставим пустыми.
Ответ: х ≤ 0, х ≥ 3.
Пример 2. Применить метод интервалов для решения неравенства х2+4х+3
Метод интервалов, примеры, решения
Метод интервалов принято считать универсальным для решения неравенств. Иногда этот метод также называют методом промежутков. Применим он как для решения рациональных неравенств с одной переменной, так и для неравенств других видов. В нашем материале мы постарались уделить внимание всем аспектам вопроса.
Что ждет вас в данном разделе? Мы разберем метод промежутков и рассмотрим алгоритмы решения неравенств с его помощью. Затронем теоретические аспекты, на которых основано применение метода.
Особое внимание мы уделяем нюансам темы, которые обычно не затрагиваются в рамках школьной программы. Например, рассмотрим правила расстановки знаков на интервалах и сам метод интервалов в общем виде без его привязки к рациональным неравенствам.
Алгоритм
Кто помнит, как происходит знакомство с методом промежутков в школьном курсе алгебры? Обычно все начинается с решения неравенств вида f ( x ) 0 (знак неравенства может быть использован любой другой, например, ≤ , > или ≥ ). Здесь f ( x ) может быть многочленом или отношением многочленов. Многочлен, в свою очередь, может быть представлен как:
- произведение линейных двучленов с коэффициентом 1 при переменной х ;
- произведение квадратных трехчленов со старшим коэффициентом 1 и с отрицательным дискриминантом их корней.
Приведем несколько примеров таких неравенств:
( x + 3 ) · ( x 2 − x + 1 ) · ( x + 2 ) 3 ≥ 0 ,
( x — 2 ) · ( x + 5 ) x + 3 > 0 ,
( x − 5 ) · ( x + 5 ) ≤ 0 ,
( x 2 + 2 · x + 7 ) · ( x — 1 ) 2 ( x 2 — 7 ) 5 · ( x — 1 ) · ( x — 3 ) 7 ≤ 0 .
Запишем алгоритм решения неравенств такого вида, как мы привели в примерах, методом промежутков:
- находим нули числителя и знаменателя, для этого числитель и знаменатель выражения в левой части неравенства приравниваем к нулю и решаем полученные уравнения;
- определяем точки, которые соответствуют найденным нулям и отмечаем их черточками на оси координат;
- определяем знаки выражения f ( x ) из левой части решаемого неравенства на каждом промежутке и проставляем их на графике;
- наносим штриховку над нужными участками графика, руководствуясь следующим правилом: в случае, если неравенство имеет знаки или ≤ изображается, штрихуются «минусовые» промежутки, если же мы работаем с неравенством, имеющим знаки > или ≥ , то выделяем штриховкой участки, отмеченные знаком « + ».
Четреж, с которым мы будем работать, может иметь схематический вид. Излишние подробности могут перегружать рисунок и затруднять решение. Нас будет мало интересовать маштаб. Достаточно будет придерживаться правильного расположения точек по мере роста значений их координат.
При работе со строгими неравенствами мы будем использовать обозначение точки в виде круга с незакрашенным (пустым) центром. В случае нестрогих неравенств точки, которые соответствуют нулям знаменателя, мы будем изображать пустыми, а все остальные обычными черными.
Отмеченные точки разбивают координатную прямую на несколько числовых промежутков. Это позволяет нам получить геометрическое представление числового множества, которое фактически является решением данного неравенства.
Научные основы метода промежутков
Основан подход, положенный в основу метода промежутков, основан на следующем свойстве непрерывной функции: функция сохраняет постоянный знак на интервале ( a , b ) , на котором эта функция непрерывна и не обращается в нуль. Это же свойство характерно для числовых лучей ( − ∞ , a ) и ( a , + ∞ ) .
Приведенное свойство функции подтверждается теоремой Больцано-Коши, которая приведена во многих пособиях для подготовки к вступительным испытаниям.
Обосновать постоянство знака на промежутках также можно на основе свойств числовых неравенств. Например, возьмем неравенство x — 5 x + 1 > 0 . Если мы найдем нули числителя и знаменателя и нанесем их на числовую прямую, то получим ряд промежутков: ( − ∞ , − 1 ) , ( − 1 , 5 ) и ( 5 , + ∞ ) .
Возьмем любой из промежутков и покажем на нем, что на всем промежутке выражение из левой части неравенства будет иметь постоянный знак. Пусть это будет промежуток ( − ∞ , − 1 ) . Возьмем любое число t из этого промежутка. Оно будет удовлетворять условиям t − 1 , и так как − 1 5 , то по свойству транзитивности, оно же будет удовлетворять и неравенству t 5 .
Используя оба полученных неравенства и свойство числовых неравенств, мы можем предположить, что t + 1 0 и t − 5 0 . Это значит, что t + 1 и t − 5 – это отрицательные числа независимо от значения t на промежутке ( − ∞ , − 1 ) .
Используя правило деления отрицательных чисел, мы можем утверждать, что значение выражения t — 5 t + 1 будет положительным. Это значит, что значение выражения x — 5 x + 1 будет положительным при любом значении x из промежутка ( − ∞ , − 1 ) . Все это позволяет нам утверждать, что на промежутке, взятом для примера, выражение имеет постоянный знак. В нашем случае это знак « + ».
Нахождение нулей числителя и знаменателя
Алгоритм нахождения нулей прост: приравниваем выражения из числителя и знаменателя к нулю и решаем полученные уравнения. При возникновении затруднений можно обратиться к теме «Решение уравнений методом разложения на множители». В этом разделе мы ограничимся лишь рассмотрением примера.
Рассмотрим дробь x · ( x — 0 , 6 ) x 7 · ( x 2 + 2 · x + 7 ) 2 · ( x + 5 ) 3 . Для того, чтобы найти нули числителя и знаменателя, приравняем их к нулю для того, чтобы получить и решить уравнения: x · ( x − 0 , 6 ) = 0 и x 7 · ( x 2 + 2 · x + 7 ) 2 · ( x + 5 ) 3 = 0 .
В первом случае мы можем перейти к совокупности двух уравнений x = 0 и x − 0 , 6 = 0 , что дает нам два корня 0 и 0 , 6 . Это нули числителя.
Второе уравнение равносильно совокупности трех уравнений x 7 = 0 , ( x 2 + 2 · x + 7 ) 2 = 0 , ( x + 5 ) 3 = 0 . Проводим ряд преобразований и получаем x = 0 , x 2 + 2 · x + 7 = 0 , x + 5 = 0 . Корень первого уравнения 0 , у второго уравнения корней нет, так как оно имеет отрицательный дискриминант, корень третьего уравнения — 5 . Это нули знаменателя.
0 в данном случае является одновременно и нулем числителя, и нулем знаменателя.
В общем случае, когда в левой части неравенства дробь, которая не обязательно является рациональной, числитель и знаменатель точно также приравниваются к нулю для получения уравнений. Решение уравнений позволяет найти нули числителя и знаменателя.
Определение знаков на интервалах
Определить знак интервала просто. Для этого можно найти значение выражения из левой части неравенства для любой произвольно выбранной точки из данного интервала. Полученный знак значения выражения в произвольно выбранной точке промежутка будет совпадать со знаком всего промежутка.
Рассмотрим это утверждение на примере.
Возьмем неравенство x 2 — x + 4 x + 3 ≥ 0 . Нулей числителя выражение, расположенное в левой части неравенства, нулей не имеет. Нулем знаменателя будет число — 3 . Получаем два промежутка на числовой прямой ( − ∞ , − 3 ) и ( − 3 , + ∞ ) .
Для того, чтобы определить знаки промежутков, вычислим значение выражения x 2 — x + 4 x + 3 для точек, взятых произвольно на каждом из промежутков.
Из первого промежутка ( − ∞ , − 3 ) возьмем − 4 . При x = − 4 имеем ( — 4 ) 2 — ( — 4 ) + 4 ( — 4 ) + 3 = — 24 . Мы получили отрицательное значение, значит весь интервал будет со знаком « — ».
Для промежутка ( − 3 , + ∞ ) проведем вычисления с точкой, имеющей нулевую координату. При x = 0 имеем 0 2 — 0 + 4 0 + 3 = 4 3 . Получили положительное значение, что значит, что весь промежуток будет иметь знак « + ».
Можно использовать еще один способ определения знаков. Для этого мы можем найти знак на одном из интервалов и сохранить его или изменить при переходе через нуль. Для того, чтобы все сделать правильно, необходимо следовать правилу: при переходе через нуль знаменателя, но не числителя, или числителя, но не знаменателя мы можем поменять знак на противоположный, если степень выражения, дающего этот нуль, нечетная, и не можем поменять знак, если степень четная. Если мы получили точку, которая является одновременно нулем числителя и знаменателя, то поменять знак на противоположный можно только в том случае, если сумма степеней выражений, дающих этот нуль, нечетная.
Если вспомнить неравенство, которое мы рассмотрели в начале первого пункта этого материала, то на крайнем правом промежутке мы можем поставить знак « + ».
Теперь обратимся к примерам.
Возьмем неравенство ( x — 2 ) · ( x — 3 ) 3 · ( x — 4 ) 2 ( x — 1 ) 4 · ( x — 3 ) 5 · ( x — 4 ) ≥ 0 и решим его методом интервалов. Для этого нам необходимо найти нули числителя и знаменателя и отметить их на координатной прямой. Нулями числителя будут точки 2 , 3 , 4 , знаменателя точки 1 , 3 , 4 . Отметим их на оси координат черточками.
Нули знаменателя отметим пустыми точками.
Так как мы имеем дело с нестрогим неравенством, то оставшиеся черточки заменяем обычными точками.
Теперь расставим точки на промежутках. Крайний правый промежуток ( 4 , + ∞ ) будет знак + .
Продвигаясь справа налево будем проставлять знаки остальных промежутков. Переходим через точку с координатой 4 . Это одновременно нуль числителя и знаменателя. В сумме, эти нули дают выражения ( x − 4 ) 2 и x − 4 . Сложим их степени 2 + 1 = 3 и получим нечетное число. Это значит, что знак при переходе в данном случае меняется на противоположный. На интервале ( 3 , 4 ) будет знак минус.
Переходим к интервалу ( 2 , 3 ) через точку с координатой 3 . Это тоже нуль и числителя, и знаменателя. Мы его получили благодаря двум выражениям ( x − 3 ) 3 и ( x − 3 ) 5 , сумма степеней которых равна 3 + 5 = 8 . Получение четного числа позволяет нам оставить знак интервала неизменным.
Точка с координатой 2 – это нуль числителя. Степень выражения х — 2 равна 1 (нечетная). Это значит, что при переходе через эту точку знак необходимо изменить на противоположный.
У нас остался последний интервал ( − ∞ , 1 ) . Точка с координатой 1 – это нуль знаменателя. Он был получен из выражения ( x − 1 ) 4 , с четной степенью 4 . Следовательно, знак остается прежним. Итоговый рисунок будет иметь вот такой вид:
Применение метода интервалов особенно эффективно в случаях, когда вычисление значения выражения связано с большим объемом работы. Примером может стать необходимость вычисления значения выражения
x + 3 — 3 4 3 · x 2 + 6 · x + 11 2 · x + 2 — 3 4 ( x — 1 ) 2 · x — 2 3 5 · ( x — 12 )
в любой точке интервала 3 — 3 4 , 3 — 2 4 .
Будем считать, что с правилами определения знаков для промежутков мы разобрались. Идем дальше.
Метод интервалов
Содержание:
Пусть 


Для этого прежде всего выясним, когда
Обозначим на числовой оси корни этой функции. Эти числа разбили числовую ось на несколько интервалов. Рассмотрим знаки функции на каждом из этих интервалов.
Отсюда 
б)
тогда
в)
тогда
По этой ссылке вы найдёте полный курс лекций по высшей математике:
Любопытно отметить, что при прохождении корней функции, функция поменяла знак на противоположный и в пункте б), и в пункте в).
г)
и знак функции снова изменился на противоположный.
Итак, простейшие наблюдения позволяют сделать вывод:
При прохождении корня функция меняет свой знак на противоположный.
Возможно вам будут полезны данные страницы:
Покажем, как, используя этот факт, можно довольно быстро и экономно решать довольно сложные неравенства. Рассмотрим 

Но можно иначе. Заметим, что все коэффициенты в этом разложении при 
Для решения неравенства необходимо:
а) разложить функцию на множители в каноническом виде (т.е. все коэффициенты при 
б) найти все корни функции и отметить их на числовой оси в порядке возрастания;
в) распределение знаков функции начинается всегда справа сверху (в виде змейки) и чередуется при прохождении корней функции;
г) если требуется знать, когда значения функции положительны, т.е. 

Найдем интервалы, для которых
Очевидно, что вид канонический (т.е. все коэффициенты положительны). Найдем корни, т.е.
Отметим их на числовой оси,
а затем проведем змейку, начиная ее справа, сверху.


Примечание. Неравенство строгое, поэтому корни на оси отмечаются кружочками, не заштрихованными внутри. Ответ можно записать в виде интервалов:
Выясним, на каких промежутках
Рассуждая аналогично, получим



Примеры с решением использования метода интервалов
Рассмотрим на различных примерах реализацию этой идеи и необходимое уточнение в ряде случаев.
Пример 1:
Корни функции легко найти устно. Знак функции 

Ответ:
Пример 2:
Знак функции 
Ответ:
Пример 3:
Ответ:
Пример 4:
Для применения метода интервалов необходимо выражение в левой части разложить на множители. Известно, что 


Решим
Ответ:
Пример 5:

Пример 6:
Ответ:
Пример 7:
Интересно, что метод годится и для дробно-рациональных неравенств. Действительно, ведь чередование знаков не зависит от того, произведение сомножителей дано или их частное.

Некоторые итоги
Для того, чтобы использовать метод интервалов для решения неравенств, необходимо:
1. Разложить 
2. Определить вид разложения функции:
а) если вид канонический, то распределение знаков функции начинается всегда справа сверху, и знаки чередуются;
б) если вид неканонический, то распределение знаков функции начинается всегда справа снизу, и знаки чередуются, проходя корни функции;
3. Уточнить кратность корней: если есть корни четной кратности, то, проходя через них, функция дважды меняет свой знак на противоположный; если есть корни нечетной кратности, то, проходя через них, функция меняет свой знак на противоположный;
4. Обратить внимание на то, какое дано неравенство, строгое или нет, так как в зависимости от этого на оси абсцисс нужно отметить или незаштрихованные (полые) точки, или заштрихованные точки;
5. Для дробных неравенств не забыть отметить на оси абсцисс корни знаменателя как полые точки;
6. Для нестрогого дробного неравенства при наличии корней в разложении и в числителе, и в знаменателе на оси абсцисс отметить полые точки.
Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
http://zaochnik.com/spravochnik/matematika/systems/metod-intervalov/
http://natalibrilenova.ru/metod-intervalov/