Уравнения для олимпиады 8 класс

Олимпиада по математике для учащихся 8 класса

Олимпиада по математике для 8 класса состоит из 5 заданий. Общее время выполнения работы – 4 урока, 180 минут.

Общее максимальное количество баллов — 35 (по 7 баллов за каждое правильно выолненное задание).

Задание № 1
45 конфет стоят столько же рублей, сколько их можно купить на 20 рублей. Сколько конфет можно купить на 50 рублей?

Задание № 2
При каких значениях параметра р отношение корней уравнения x 2 + 2px +1 = 0 равно 9?

Задание № 3
Мальчик стоит на автобусной остановке, а автобуса нет. Ему хочется пройтись до следующей остановки. Мальчик бегает вчетверо медленнее автобуса и может увидеть автобус на расстоянии 2 км. До следующей остановки ровно километр. Имеет ли смысл идти, или есть риск упустить автобус?

Задание № 4
В трапеции длина одной из диагоналей равна сумме длин оснований, а угол между диагоналями равен 60°. Докажите, что трапеция – равнобедренная.

Задание № 5
Докажите, что в любой компании найдутся два человека, имеющие равное число знакомых в этой компании (если A знаком с B, то и B знаком с A).

Ответы и критерии оценивания олимпиады по математике

Решение задания № 1

Пусть x — стоимость одной конфеты в рублях. Тогда 45x = 20/x , откуда x = 2/3 . Тогда на 50 рублей можно купить 50/x = 75 конфет.
Ответ: 75 конфет.

Баллы

Критерии оценивания задания №1

Приведено полное обоснованное решение и получен верный ответ.

Верно и обосновано получено необходимое равенство, но допущена вычислительная ошибка, не повлиявшая на ответ.

Необходимое равенство получено, но дальнейших продвижений нет.

Приведено частное решение задачи с конкретными числами и сделан правильный вывод.

Приведен только ответ.

Приведено неверное решение или оно отсутствует.

Решение задания № 2

Пусть x₁ = 9x₂, тогда по теореме Виета:

Ответ к заданию № 2 олимпиады по математике

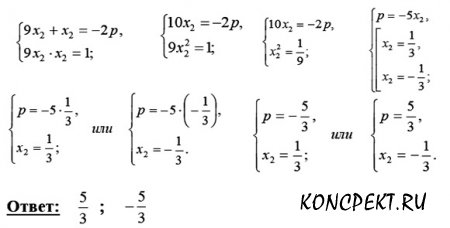
Баллы

Критерии оценивания задания № 2

Полное верное обоснованное решение.

Верное решение. Имеются небольшие недочеты, в целом не влияющие на решение. Или полное верное решение, но не записан ответ.

Верное рассуждение, но решение не доведено до конца и найден только один корень.

Правильно найден дискриминант. Дальнейшие продвижения в решении задачи отсутствуют.

Решение неверное, продвижения отсутствуют или решение отсутствует, записан только номер задания.

Решение задания № 3

Пусть мальчик пробежит х км, тогда автобус проедет 4х км. Если они двигаются навстречу друг другу, до встречи с автобусом мальчик пробежит 2/5 км (из уравнения 4х+х=2). Это значит, что, отойдя от остановки не более, чем на 2/5 км, мальчик сможет успеть на автобус, побежав назад.

Если автобус догоняет мальчика, мальчик успеет пробежать 2/3 км до момента, когда автобус его догонит (из уравнения 4х-х=2). Это означает, что он сможет успеть на автобус, если до следующей остановки осталось не более 2/3 км, то есть, если он успел пройти не менее 1/3 км до момента, когда заметил автобус. Так как, 1/3 Губина Ольга Алексеевна, учитель математики МОУ СОШ № 7, г. Алексеевка Белгородская область

олимпиадные задания 8 класс
олимпиадные задания по алгебре (8 класс) на тему

задачи для подготовки к олимпиаде

Скачать:

Предварительный просмотр:

Олимпиадные задания по математике 8 класс

Какой цифрой оканчивается сумма 9 2007 + 9 2006 ?

9 2007 + 9 2006 = 9 2006 ( 9 + 1) = 9 2006 * 10.
Нулем.

В оранжерее было срезано 360 гвоздик. Причем красных на 80 больше, чем белых, а розовых на 160 штук меньше, чем красных.
Какое наибольшее число одинаковых букетов можно составить из этого количества цветов ?
Сколько и каких цветов было в каждом букете?

Решая уравнение, получаем 40 розовых гвоздик,120 белых гвоздик, 200 красных гвоздик. НОД (40, 120,200) равен 40, следовательно из 360 гвоздик можно составить 40 букетов, причем каждый букет будет состоять из 1 розовой, 3 белых и 5 красных гвоздик.

Существует ли такой круг, чтобы его площадь и длина окружности выражались одним и тем же числом ?

Да, при радиусе равном 2.

После семи стирок измерения куска хозяйственного мыла, имеющего форму прямоугольного параллелепипеда, уменьшились в двое.
На сколько еще стирок хватит оставшегося куска мыла ?

Мыла хватит еще на одну стирку, т.к. объем оставшегося мыла составил 1/8 часть первоначального, израсходовано мыла: 1 — 1/8 = 7/8 куска,
значит на каждую стирку расходовалось 1/8 часть куска, именно столько осталось.

Какими двумя цифрами заканчивается число 13! ?

В произведении 1*2*3…*13 есть множители 2, 5 и 10, значит число 13!
Заканчивается двумя нулями.

Из 38 учащихся 28 посещают хор и 17 лыжную секцию.
Сколько лыжников посещает хор, если в классе нет учащихся, которые не посещают хор или лыжную секцию ?

7 человек. Хор не посещают 10 человек, все они лыжники.
Лыжников всего 17человек, значит 7 человек надо «взять» из хора.

Окружность касается квадрата извне и «катится» по нему без скольжения.
Сколько полных оборотов сделает эта окружность около своего центра и какой путь пройдет центр окружности к моменту возвращения в исходную точку, если длина стороны квадрата равна длине окружности и радиус окружности равен а см ?
Те же вопросы, если окружность «катится» по сторонам равностороннего треугольника.

В случае квадрата каждая точка окружности сделает 4 оборота около своего центра.
Центр окружности сделает четверть оборота около каждой вершины квадрата.
За один обход центр окружности совершает путь, равный 5*2Па см.
В случае треугольника — соответственно 3 оборота и 8П а см

Во время похода палатки расположились в т. А,В, и С.
В каком месте удобно выбрать площадку для проведения общего костра,
чтобы расстояние от него до палаток было одинаковым ?

Точка осей симметрии точек А и В и точек В и С будет искомой.

Найдите произведение всех целых чисел от (-99) до 99.

Две семьи выехали каждая на машине «Жигули» на прогулку одновременно из одного места.
Обе семьи проехали на машинах одинаковые расстояния и вернулись домой в одно и то же время.
В пути они отдыхали.
Первая семья была в пути в двое больше времени, чем вторая.
Вторая была в пути втрое больше времени. Чем отдыхала первая.
Какая из этих семей двигалась на машине быстрее ?

1-я семья: 2х часов — время на езду, у часов — время на отдых.
2-я семья: 3у часов — время на езду, х часов — время на отдых 2х + у = 3у + х; х = 2у.
Вторая семья отдыхала в два раза больше, чем первая следовательно, она ехала быстрее первой.

Сосуд имеет форму прямоугольного параллелепипеда.
Как, не делая никаких измерений и не имея других емкостей, наполнить водой ровно половину объема этого сосуда ?

Наклонить параллелепипед так, чтобы уровень воды находился по диагональному сечению параллелепипеда.

В трех кучках лежат соответственно 12, 24 и 19 спичек. За ход можно переложить спичку из одной кучки в другую. За какое наименьшее число ходов можно получить три кучки с 8, 21 и 26 спичками?

Менее чем 4 ходами не обойтись: чтобы получить кучку из 8 спичек, придется из любой первоначальной кучки убрать как минимум 4 спички. Четырех ходов достаточно: перекладываем из кучки с 12 спичками по 2 спички в кучки с 19 и 24 спичками.

Сколько всего есть четырехзначных чисел, которые делятся на 19 и оканчиваются на 19?

Решение :
Пусть — такое число. Тогда N – 19 тоже кратно 19. Но Поскольку 100 и 19 взаимно просты, то двузначное число делится на 19. А таких всего пять: 19, 38, 57, 76 и 95. Легко убедиться, что все числа 1919, 3819, 5719, 7619 и 9519 нам подходят.

У даты 12.04.1961 (то есть 12 апреля 1961 года) сумма цифр равна 24. Найдите ближайшую дату после 01.01.2008, у которой сумма цифр равна: а) 35; б) 7.

Ответ : а) 29.09.2049; б) 03.01.2010.

Решение :
а) Наибольшая сумма цифр числа равна 11 для 29-го числа. Наибольшая сумма цифр месяца равна 9 для сентября, то есть для 09. Значит, наибольшая сумма цифр в текущем году будет у даты 29.09.2008. Она равна 30, что меньше 35. Следовательно, надо менять и год. Последняя цифра года не более 9, и если мы сохраняем первые две цифры, то придется цифру десятилетий увеличить до 4.

б) Для 2008 года сумма цифр года уже больше 27, поэтому год придется изменить. Ближайший год в будущем с меньшей суммой цифр — 2010-й. Соответственно, ближайшая подходящая дата 03.01.2010.

Среди целых чисел от 8 до 17 включительно зачеркните как можно меньше чисел так, чтобы произведение оставшихся было точным квадратом. В ответе укажите сумму всех вычеркнутых чисел.

Решение :
Чтобы произведение было точным квадратом, нужно, чтобы каждый простой множитель входил в него в четной степени. В произведение 8 · 9·. · 17 в нечетной степени входят 2, 7, 11, 13 и 17. Значит, мы обязаны вычеркнуть сомножители 11, 13 и 17. А вот чтобы «убить» лишние простые множители 2 и 7, хватит одного вычеркнутого сомножителя 14. Итого сумма вычеркнутых чисел равна 11 + 13 + 14 + 17 = 55.

На гранях кубика расставлены 6 различных чисел от 6 до 11. Кубик бросили два раза. В первый раз сумма чисел на четырех боковых гранях оказалась равна 36, во второй — 33. Какое число написано на грани, противоположной той, где написана цифра 10?

Cумма чисел на всех гранях равна 6 + 7 + 8 + 9 + 10 + 11 = 51. При первом броске сумма на верхней и нижней гранях равна 51 – 36 = 15, при втором — 51 – 33 = 18. Значит, на третьей паре противоположных граней сумма равна 51 – 15 – 18 = 18. Сумму 18 можно получить двумя способами: 11 + 7 или 10 + 8. Значит, на парах граней с суммой 18 напротив 11 находится 7, а напротив 10 — 8.

В конкурсе участвовали 5 человек. На каждый вопрос один из них дал неправильный ответ, остальные — правильный. Число правильных ответов у Пети равно 10 — меньше, чем у любого другого. Число правильных ответов у Васи равно 13 — больше, чем у любого другого. Сколько всего вопросов было в конкурсе?

Решение :
Так как на каждый вопрос были даны 4 правильных ответа, общее число правильных ответов делится на 4. Поскольку Петя дал 10 верных ответов, Вася — 13, а остальные трое — от 11 до 12, то общее число правильных ответов не меньше, чем 10 + 13 + 3·11 = 56, и не больше, чем 10 + 13 + 3·12 = 59. Из чисел в этих пределах только 56 кратно 4, поэтому число вопросов равно

Команда из Пети, Васи и одноместного самоката участвует в гонке. Дистанция разделена на участки одинаковой длины, их количество равно 42, в начале каждого — контрольный пункт. Петя пробегает участок за 9 мин, Вася — за 11 мин, а на самокате любой из них проезжает участок за 3 мин. Стартуют они одновременно, а на финише учитывается время того, кто пришел последним. Ребята договорились, что один проезжает первую часть пути на самокате, остаток бегом, а другой — наоборот (самокат можно оставить на любом контрольном пункте). Сколько участков Петя должен проехать на самокате, чтобы команда показала наилучшее время?

Решение :
Если Петя проедет 18 участков и пробежит оставшиеся 42 – 18 = 24, он затратит 18·3 + 24·9 = 270 мин. При этом Васе, наоборот, достанется проехать 24 участка, а пробежать 18, на что уйдет 24·3 + 18·11 = 270 мин — то же самое время. Если же Петя проедет меньшее число участков, то его время (и, соответственно, время команды) увеличится. Если Петя проедет большее количество участков, то увеличится время Васи (и время команды).

Достаточно обозначить число проезжаемых Петей участков через x и решить уравнение

x ·3 + (42 – x )·9 = (42 – x )·3 + 11 x .

Нарисуйте на плоскости пять различных прямых так, чтобы они пересекались ровно в семи различных точках.

Решение :
Три возможных ответа изображены на рисунке 1. Можно показать, что других конфигураций из пяти прямых, пересекающихся ровно в семи различных точках, нет.

Мальчик пошел с отцом в тир. Отец купил ему 10 пулек. В дальнейшем отец за каждый промах отбирал у сына одну пульку, а за каждое попадание давал одну дополнительную пульку. Сын выстрелил 55 раз, после чего пульки у него кончились. Сколько раз он попал?

Решение :
Каждый раз, когда мальчик попадал в цель, число имеющихся у него пулек оставалось прежним (одну использовал и одну получил от отца). Каждый раз, когда мальчик промахивался, число имеющихся у него пулек уменьшалось на 2 (одну использовал и одну отобрал отец). Это значит, что сын за 55 выстрелов промахнулся 10 : 2 = 5 раз, стало быть, попал 55 – 5 = 50 раз.

Две биссектрисы треугольника пересекаются под углом 60°. Докажите, что один из углов этого треугольника равен 60°.

Решение :
Пусть биссектрисы AA 1 и CC 1 треугольника ABC пересекаются в точке I (рис.2). Допустим, что AIC 1 = 60°. По теореме о внешнем угле треугольника

ABC = 180°– BAC – BCA = 60°.

Но это еще не все решение: ведь может случиться, что AIC = 60°. Однако тогда

Когда Винни-Пух пришел в гости к Кролику, он съел 3 тарелки меда, 4 тарелки сгущенки и 2 тарелки варенья, а после этого не смог выйти наружу из-за того, что сильно растолстел от такой еды. Но известно, что если бы он съел 2 тарелки меда, 3 тарелки сгущенки и 4 тарелки варенья или 4 тарелки меда, 2 тарелки сгущенки и 3 тарелки варенья, то спокойно смог бы покинуть нору гостеприимного Кролика. От чего больше толстеют: от варенья или от сгущенки?

Ответ : от сгущенки.

Решение :
По условию

3м + 4с + 2в > 2м + 3с + 4в,

3м + 4с + 2в > 4м + 2с + 3в,

Складывая последнее неравенство с неравенством (*), получаем м + 3с > м + 3в, откуда с > в.

В каждой клетке клетчатой доски размером 50 ? 50 записано по числу. Известно, что каждое число в 3 раза меньше суммы всех чисел, записанных в клетках, соседних с ним по стороне, и в 2 раза меньше суммы всех чисел, записанных в клетках, соседних с ним по диагонали. Докажите, что каждую клетку доски можно покрасить в красный или синий цвет так, что сумма всех чисел, записанных в красных клетках, равна сумме всех чисел, записанных в синих клетках.

Решение :
Покажем, что подойдет раскраска клеток доски в шахматном порядке. Заметим, что сумма данного числа и его соседей по диагоналям равна сумме соседей этого числа по сторонам: обе суммы втрое больше данного числа. Поэтому в квадрате 2 ? 2, находящемся в углу доски, суммы чисел в красных и синих клетках совпадают: обе они втрое больше числа, стоящего в угловой клетке доски. Также совпадают суммы чисел в красных и синих клетках любого прямоугольника 3 ? 2, примыкающего длинной стороной к краю доски: обе они втрое больше числа, стоящего в средней клетке стороны, примыкающей к краю доски. Наконец, совпадают суммы чисел в красных и синих клетках любого квадрата 3 ? 3: обе они втрое больше числа, стоящего в центре квадрата.

Разобьем доску 50 ? 50 на квадрат 48 ? 48, квадрат 2 ? 2 и два прямоугольника 2 ? 48, как показано на рисунке 3. Квадрат 48 ? 48 разобьем на квадраты 3 ? 3, а прямоугольники 2 ? 48 — на прямоугольники 3 ? 2, примыкающие длинной стороной к краю доски. В каждом из этих квадратов и прямоугольников суммы чисел, стоящих в красных и синих клетках, равны. Значит, они равны и на всей доске.

Олимпиада по математике. 6-8 классы. Ответы.

Олимпиады по математике 8 класс

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Олимпиады по математике с решением. 8 класс. Вариант 1.

Сумма квадратов n простых чисел, каждое из которых больше 5, делится на 6. Докажите что и n делится на 6.

Решение.
Если сумма нескольких чисел делится на шесть,
то и сумма их остатков при делении на шесть тоже будет делится на 6.
Простое число, большее пяти, может иметь при делении на 6 только остатки 1 или 5
(иначе это число будет делиться на 2 или 3).
Следовательно, квадрат любого простого числа, большего чем 5, имеет при делении на 6 остаток 1.
Так как сумма этих остатков равна количеству чисел n, значит n делится на 6.

Петя и Вася сделали в тире по 5 выстрелов.
Первыми тремя выстрелами они выбили поровну, а последними тремя Петя выбил в три раза больше очков, чем Вася. На мишени остались пробоины в 10, 9, 9, 8, 8, 5, 4, 4, 3, 2 очков. Куда попал каждый из них третьим выстрелом?
Приведите все возможные варианты ответа и докажите, что других нет.

Ответ. Третьим выстрелом Петя выбил 10, а Вася — 2 очка.

Решение.
Последними тремя выстрелами Вася не мог выбить больше, чем 9 очков
(иначе Петя бы выбил последними тремя выстрелами не меньше 30).
Меньше 9 очков Вася тоже выбить не мог, так как наименьшая сумма за три выстрела 2 + 3 + 4 = 9.
Следовательно, Вася выбил 2, 3 и 4 очка а Петя 10, 9 и 8 очков
(других вариантов набрать 27 очков тремя выстрелами нет).
Значит первыми двумя выстрелами мальчики выбили 9, 8, 5 и 4 очка.
При этом Петя третьим выстрелом выбил не меньше, чем 8, а Вася — не больше, чем 4 очка.
Так как сумма очков после первых трех выстрелов была равной,
значит, первыми двумя выстрелами Петя выбил по крайней мере на четыре очка меньше, чем Вася.
Единственная возможность — Вася выбил 9 и 8, а Петя 5 и 4 очка,
следовательно, третьим выстрелом Вася выбил 2, а Петя 10 очков.

Если дату 10 февраля 2001 года записать в виде 10.02.2001, а затем убрать точки,
то получится палиндром (т.е. число, читающееся слева направо и справа налево одинаково).
Найдите ближайшую к 10.02.2001 дату, обладающую тем же свойством. Рассмотрите два случая:
1) требуемая дата еще не наступила,
2) требуемая дата уже прошла.
Ответ обосновать.

Ответ.
1) 20 февраля 2002
2) 29 ноября 1192 года.

Решение.
Заметим, что при условии, что дата записывается как палиндром,
день и месяц однозначно находятся по заданному году.

(1): в 2001 году других палиндромов быть не может,
а в следующем (2002) году это должен быть 20 день второго месяца.

(2): Чтобы дата была как можно ближе к 2001 году, необходимо брать самый большой возможный год, меньший 2001. Вторая цифра года должна быть первой цифрой месяца, то есть 0 или 1, т.к. месяцев не больше 12.
В 2000 году палиндрома быть не может (нулевого дня не бывает),
следовательно, первые две цифры года — 11 (соответственно, месяц — ноябрь).
Третью цифру года нужно взять максимально возможную, т.е. девять, тогда четвертой
(так как в ноябре не больше 31 дня) может быть два.
Получится дата-палиндром 29.11.1192.

В выпуклом четырехугольнике ABCD стороны AB и CD параллельны, а диагонали AC и BD перпендикулярны. Докажите, что AD + BC = AB + CD.

Решение.
Впишем четырехугольник ABCD в прямоугольник EFGH со сторонами,
параллельными диагоналям (EF  AC и EH  BD) — смотри рисунок.
Пусть L — точка пересечения прямых DC и EF, а M — точка на прямой HG такая, что LM  FG.
Тогда ABLC — параллелограмм, следовательно, AB = CL.
Так как GM = FL = EB = HD и AH = CG, то треуг-к AHD = треуг-ку CGM ,
следовательно, AD = CM. BC + CM = BC + AD .
Но BM = DL как диагонали прямоугольника BLDM, и DL = DC + CL = DC + AB.
Следовательно, AD + BC = DL = DC + CL = DC + AB, что и требовалось доказать.