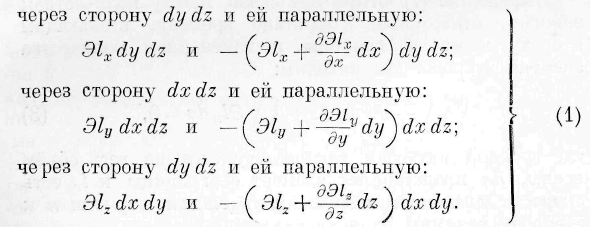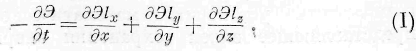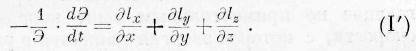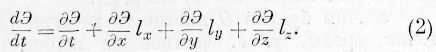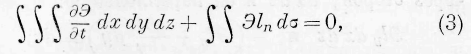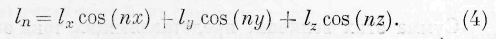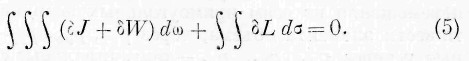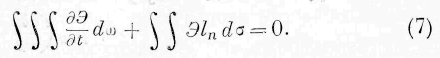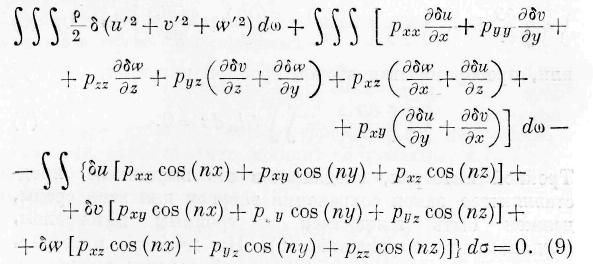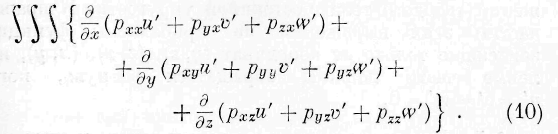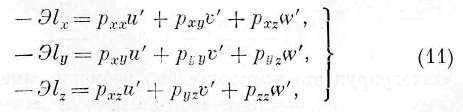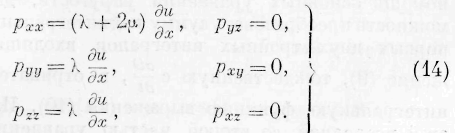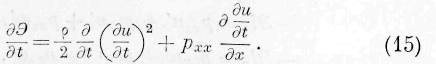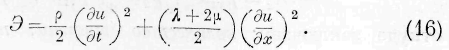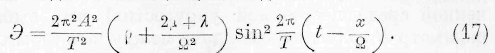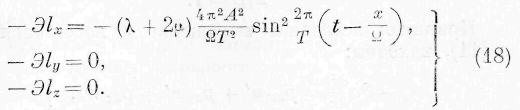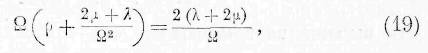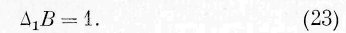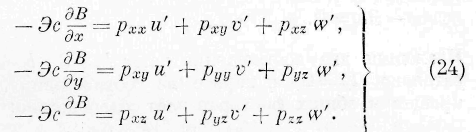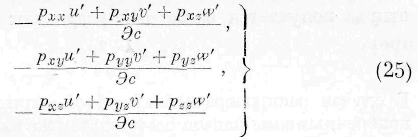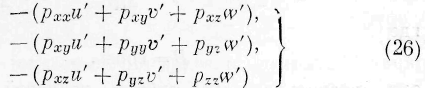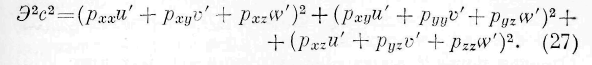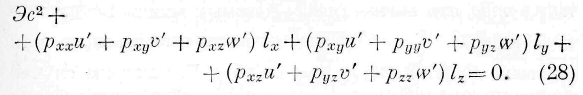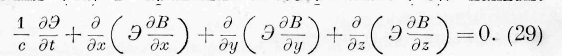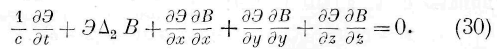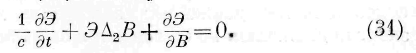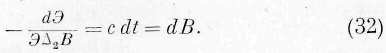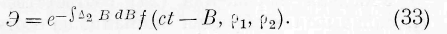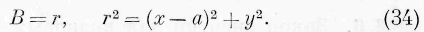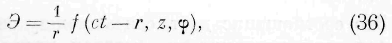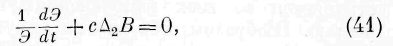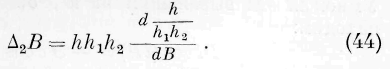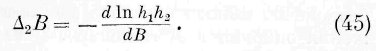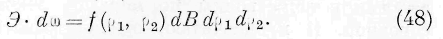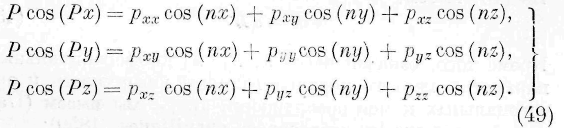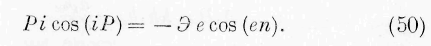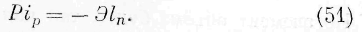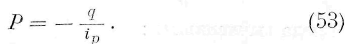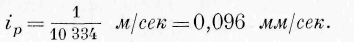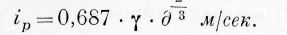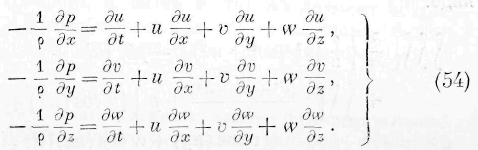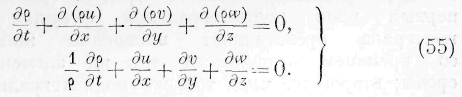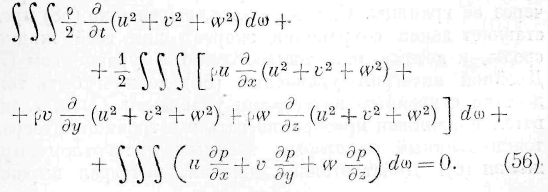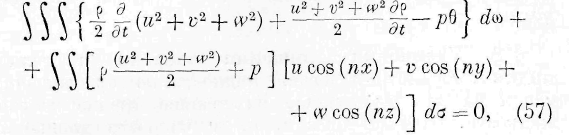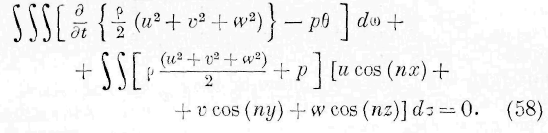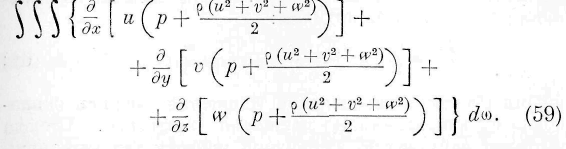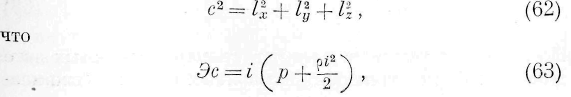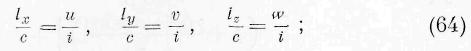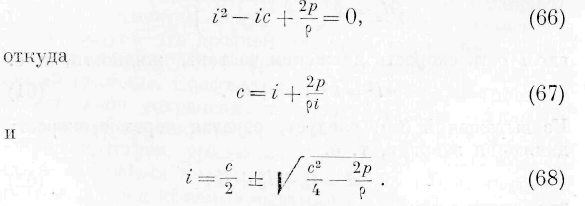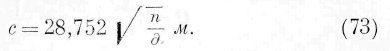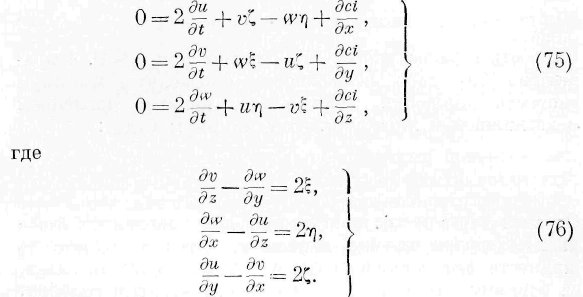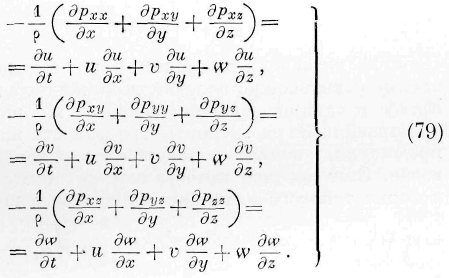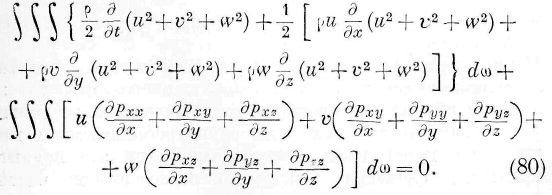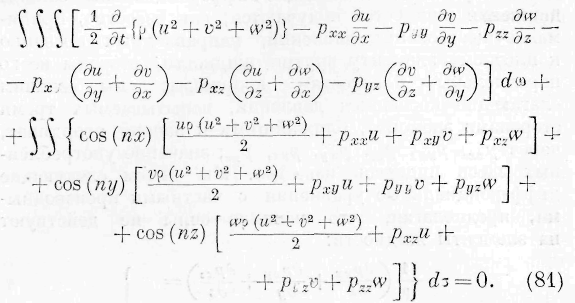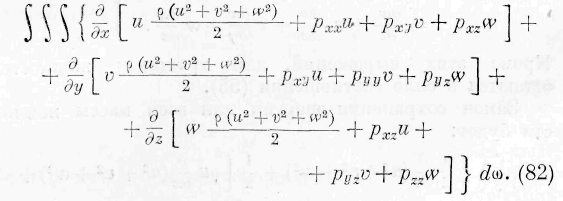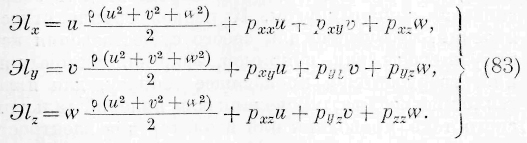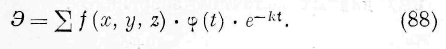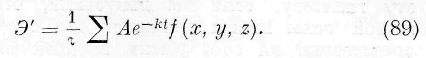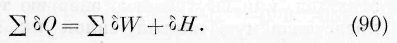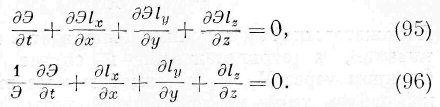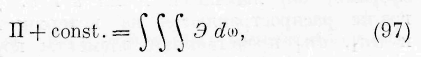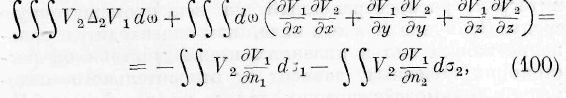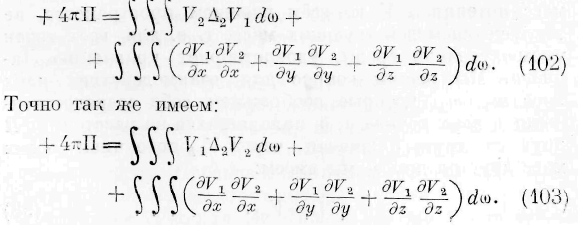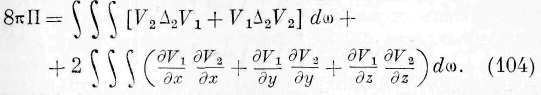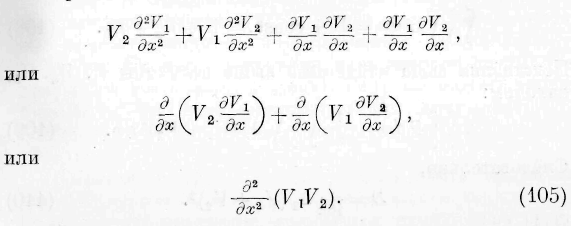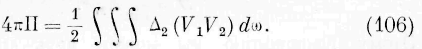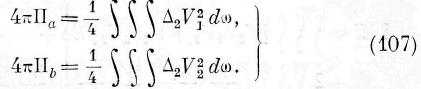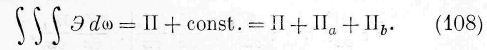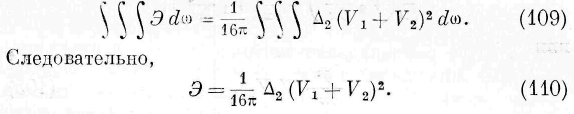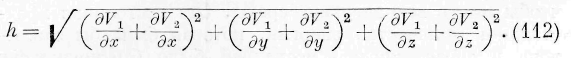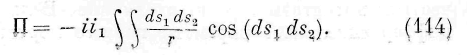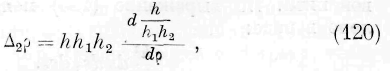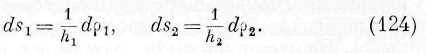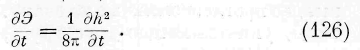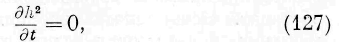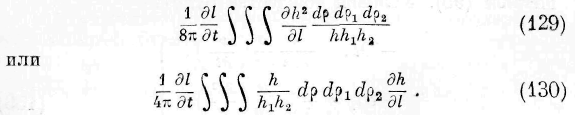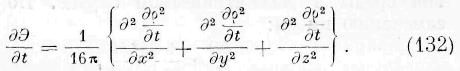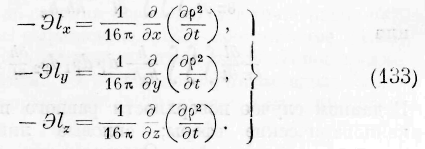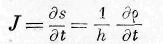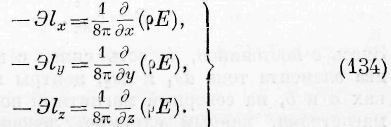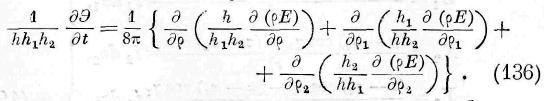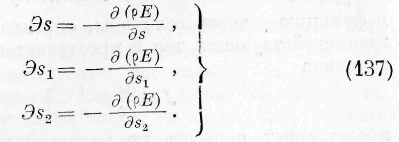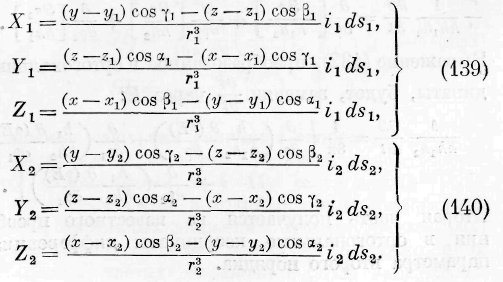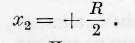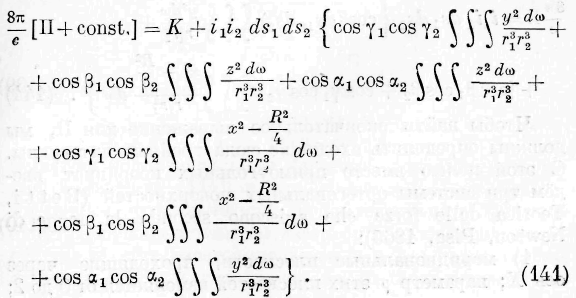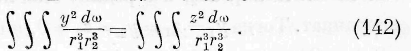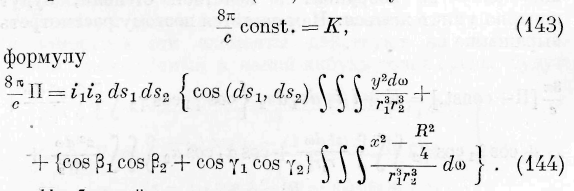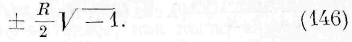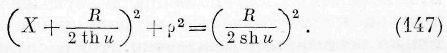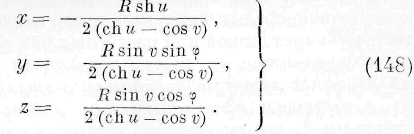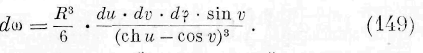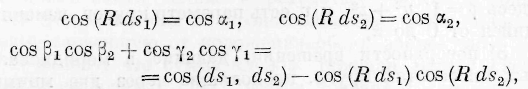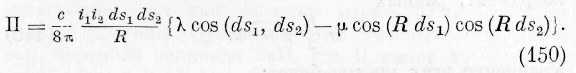4. 3. 018 Поток энергии Умова
4.3.018 Поток энергии Умова
(к сожалению, формулы воспроизводятся не точно)
Физик, философ, педагог, лектор, пропагандист, популяризатор науки, общественный деятель; профессор Новороссийского и Московского университетов, Московского технического училища; почетный доктор Глазговского университета; основатель (совместно с П.Н. Лебедевым) Физического института при Московском университете; президент Московского общества испытателей природы, председатель Московского педагогического общества, товарищ председателя «Общества содействия успехам опытных наук и практических применений им. Х.С. Леденцова»; издатель и главный редактор журнала «Научное слово» — Николай Алексеевич Умов (1846—1915) является автором учения о движении энергии в телах, базового понятия в новейшей физике — потока энергии, т.н. вектора Умова.
Умов — первооткрыватель классической формулы общего уравнения движения энергии.
Человечество с каждым годом все больше нуждается в энергии — механической, тепловой, химической, электрической, ядерной. Все эти формы энергии, трансформируясь друг в друга, дают совокупность энергетических процессов, без которых не обойтись ни обывателям, ни ученым. Последних всегда интересовал вопрос — каким образом происходит эта трансформация и как повысить ее к.п.д.
Схематично это выглядит так. В замкнутый объем через поверхность поступает первичная энергия, а затем выходит преобразованная (разумеется, в рамках закона сохранения энергии). Плотность потока энергии (Su) при этом ограничена физическими свойствами среды, через которую она течет.
Этот термин — плотность потока энергии ввел в начале 1870-х гг. русский физик Н.А. Умов, опубликовавший несколько работ о движении энергии, в которых развил представления о плотности энергии в данной точке среды, скорости и направлении движения энергии, о локализации потока энергии в пространстве.
Ученый составил дифференциальные уравнения движения энергии в твердых телах постоянной упругости и в жидких телах, интегрируя которые и применяя к распространению волн в упругой среде, пришел к заключению, что энергия целиком переносится волной от одной точки к другой.
«Количество энергии, проходящей через элемент поверхности тела в единицу времени, равно силе давления или натяжения, действующей на этот элемент, умноженной на скорость движения элемента» — этот вывод называется теоремой Умова.
Уравнение непрерывности в свободном пространстве для движущихся упругих сред и вязких жидкостей имеет вид:
dw/dt + div Su = 0,
где Su = wv; w — плотность энергии; v — скорость движения среды.
После защиты ученым в 1874 г. докторской диссертации «Уравнения движения энергии в телах» Su принято называть в нашей стране вектором Умова.
В 1884 г. английский физик Д. Пойнтинг, независимо от Умова и ничего не зная о трудах русского ученого, получил подобное выражение для частного случая — электромагнитного поля (поперечных электромагнитных волн). На Западе без особых рефлексий вектор Умова переименовали в вектор Пойнтинга (Sp).
Sp = [E ; H]; E и H — напряженности электрического и магнитного полей.
Сам Умов, кстати, отмечал, что его выводы применимы и в электромагнитных полях.
Необходимо различать принципиальную разницу между этими понятиями — Su и Sp. Вектор Пойнтинга можно рассматривать только применительно к электромагнитным полям, тогда как вектор Умова применим ко всем силовым полям без исключения, поскольку сами уравнения движения энергии получены Умовым для движения любого вида энергии, происходящего в любой среде, т.е. носят самый общий характер.
Не прибегая к выкладкам, заметим еще, что вектор Умова Su описывает конвективный перенос энергии из одной точки пространства в другую, в частности, полем движущегося заряда; а вектор Пойнтинга связан лишь с переносом энергии электромагнитными волнами.
Труды Умова своей математической сложностью представляли «крепкий орешек» для российских и зарубежных коллег Николая Алексеевича. Утверждали даже, что они «лишены какого бы то ни было научного смысла и представляют собой… простой набор математических формул». Раскусили их не сразу, но, раскусив, буквально растащили на цитаты, при этом не всегда озвучивая автора.
Так было и в других случаях. Когда Умов показал свою блестящую работу «О стационарном движении электричества на проводящих поверхностях произвольного вида» немецкому физику Г. Кирхгофу, тот тут же умыкнул главные положения этого исследования и опубликовал их под своим именем (не забыв, правда, упомянуть и русского ученого).
Фактически то же самое произошло и со знаменитой формулой E = mc2, которую русский физик получил лет за тридцать до А. Эйнштейна — опять же как общий случай для волновых процессов в упругих средах. (Умов вывел соотношение между энергией волновых полей и их инерцией: dE = c2dm).
Но вернемся к вектору и к области его применения. Надо сказать, что область эта — широчайшая, как в науке, так и в технике. Без вектора Умова не обойтись при освоении нового вида энергии (скажем, термоядерной), при разработке сложного и дорогостоящего технического устройства (ТОКОМАК).
35 лет назад, в преддверии глобального мирового энергетического кризиса из-за исчерпания природных энергетических ресурсов, П.Л. Капица в одном из своих докладов, посвященных энергетической проблеме, обосновывая свои положения в выборе того или иного вида энергии, оперировал только вектором Умова.
Рассматривая альтернативные способы получения энергии, академик подчеркивал удобство вектора Умова для изучения процессов преобразования энергии. При этом Капица привел примеры, как с помощью этого вектора определяют предельную мощность мотора или турбины; мощность трансмиссии ременной передачи; предельную мощность, передаваемую лентой в генераторе типа Ван-де-Граафа; предельную мощность в газовых, химических элементах, в солнечных батареях, геотермальных источниках; как находят предельную высоту, на которой может летать турбореактивный самолет и т.д.
К сказанному Капицей можно добавить, что вектор Умова применяют для проектирования электромагнитных излучателей и направляющих систем в радиоэлектронной аппаратуре, для расчета энергетических характеристик антенн, в частности, сопротивления излучения выпускных самолетных антенн.
Вектор необходим при определении оптимальной аэродинамической конструкции летательного аппарата в поле скоростей. В процессах и аппаратах химических технологий его используют для составления детерминированных и идеальных математических моделей. В электротехнике с его помощью определяют внутреннее активное и реактивное сопротивление проводника. И т.д. и т.п.
«Представления Умова о движении и распределении энергии в средах, о ее потоке, скорости и направлении являются общепризнанными в современной физике. Они прочно завоевали себе место в таких ее разделах, как теория поля, электродинамика, оптика, акустика, гидродинамика… Именно Умов изложил очень ценную идею об универсальности всех силовых взаимодействий в природе» (профессор А.Л. Шаляпин).
Уравнения движения энергии в телах
УЧЕНИЕ Н.А. УМОВА О ДВИЖЕНИИ ЭНЕРГИИ В РАЗЛИЧНЫХ СРЕДАХ
“Крупнейшей научной заслугой Н.А. Умова является то, что он на протяжении ряда лет с материалистических позиций разрабатывал важнейшую проблему физики — проблему сохранения и превращения энергии. Он явился одним из выдающихся продолжателей материалистических идей М.В. Ломоносова о неуничтожимости и несотворимости движения и материи” [1].
«. Все встречающиеся в природе изменения, — писал Ломоносов [2], — происходят так, что если к чему-либо нечто прибавилось, то это отнимается у чего-то другого. Так, сколько материи прибавляется какому-либо телу, столько же теряется у другого. Так как это всеобщий закон природы, то он распространяется и на правила движения: тело, которое своим толчком возбуждает другое к движению, столько же теряет от своего движения, сколько сообщает другому, им двинутому».
Закон сохранения и превращения энергии Энгельс называл великим, основным законом движения, абсолютным законом природы. Открытие этого закона составило целую эпоху в науке. Оно показало, что различные виды энергии (тепловая, электрическая, химическая и др.) представляют собой различные формы проявления универсального движения материи; которые переходят одна в другую, что в природе мы имеем непрерывный процесс превращения одной формы движения материи в другую [1].
Доказательство взаимной превращаемости различных форм движения материи друг в друга в корне подрывало метафизическое понимание явлений природы. До установления этого факта при истолковании теплоты, электричества, магнетизма и т. д. прибегали к особым таинственным материям — теплороду, электрическим, магнитным и другим невесомым жидкостям. Когда же была открыта взаимная превращаемость различных форм движения, тогда сама собой отпала потребность в том, чтобы выдумывать различного рода лжематерии. Стало ясно, что теплота, электричество, свет и т. п. есть результат превращения различных форм движения материи друг в друга [1].
Учение о превращении энергии привело к тому, отмечал Энгельс, что исчезло последнее воспоминание о внемировом творце [3].
Заслуга Умова состоит в том, что он в этот период решительно отстаивал материалистический взгляд на энергию. Еще в 1870 г. на заседании Московского математического общества он сделал сообщение о своей первой научной работе «Законы колебаний в неограниченной среде постоянной упругости», где развил начала своего учения о движении энергии. Она напечатана в «Математическом сборнике» в марте 1870 г. Проблема колебаний в неогра ниченной среде поставлена Умовым во всей своей ши роте и разобрана с большим изяществом и глубиной. Результаты работы не устарели и по сие время. Своим идейным содержанием и приёмами исследования она мо жет ещё и должна оказать влияние на развитие науки. Это сообщение с большим одобрением встретили Столетов, Бредихин, Жуковский.
Умов исследовал в наиболее общем виде вопрос о поперечных и продольных колебаниях в средах постоянной упругости — вопрос, играющий большую роль в трактовке проблемы движения энергии и природы теплоты
Такой подход к проблеме колебаний в неограниченной среде дал возможность Умову разделить задачу о поперечных и продольных колебаниях, получить ряд интересных заключений о характере этих колебаний. Опираясь на вышеуказанное положение, Умов в своем монументальном труде «Уравнения движения энергии в телах» (1874) [4,7] нашел общие соотношения между формой волн, несущих продольные или поперечные колебания, и движениями частиц упругого тела.
Предположив, что поверхность волны есть поверхность изотермическая, Умов доказал, что из всех изотермических поверхностей только плоскость, сфера и круглый цилиндр могут быть поверхностями волны.
Мастерски использовав метод криволинейных координат, который является основой многих его физико-математических работ, Умов определил по данному виду волны поперечные колебания, распространяемые ею. Молодой ученый пришел к выводу, что все волновые поверхности могут быть разделены на три группы: 1) поверхности, допускающие прямолинейную поляризацию по той или другой линии кривизны (поверхности сферы и круглого цилиндра), 2) поверхности, допускающие прямолинейную поляризацию по одной из линий кривизны (поверхности вращения, допускающие поляризацию по одной из двух линий кривизны), 3) все остальные поверхности, не допускающие прямолинейной поляризации ни по одной из линий кривизны. Развитая Умовым теория поперечных колебаний позволяет по данному виду волны определить законы колебаний, происходящих на ее поверхности.
Умов сформулировал и развил чрезвычайно важные научные положения и относительно продольных колебаний. Он писал, что «одни изотермические волновые поверхности могут распространять колебания продольные. Итак, если поверхность сотрясения или начальная волна не принадлежат к поверхностям изотермических волн, то вблизи их колебания происходят смешанные; но на значительных расстояниях волна приближается к виду одной из изотермических волн, и в явлении обнаруживаются колебания продольные. Это заключение было выведено иным путем Пуассоном».
Характеризуя значение работы Умова «Законы колебаний в неограниченной среде постоянной упругости» для современной физики, советский ученый А.С. Предводителев справедливо отмечает, что положения ее сохраняют научную ценность и в настоящее время [1].
Исследование Н.А. Умова «Уравнения движения энергии в телах» [4,7] явилось результатом двух других его исследований [5,6], напечатанных в «Математическом сборнике» за 1872-73 гг.
Указанная работа была представлена Н.А. Умо вым в Московский университет в качестве докторской диссертации. Она вызвала большие споры и резкую кри тику со стороны официальных оппонентов, профессо ров А.Г. Столетова и Ф.А. Слудского. Неофициальный оппонент проф. В.Я. Цингер тоже выступал в реши тельных тонах против идеи диссертации. Диспут про должался шесть часов и на всю жизнь оставил у Умова неприятное воспоминание. История повторилась: све жие, необычные взгляды не могли проложить себе путь в жизнь без боя.
7 сентября 1874 г. на заседании ученого совета физико-математического факультета Московского университета состоялась защита докторской диссертации Умова «Уравнения движения энергии в телах». Противники Умова выступили с резкой критикой коренных положений его докторской диссертации — о движении энергии, о ее плотности и т. д. Однако Умов решительно опроверг все возражения своих оппонентов. Ученый совет присудил Умову степень доктора физико-математических наук.
В том же году результаты работы «Уравнение движения энергии в телах» были изложены Умовым в статье «A b leitung der Bewegungleichungen der Energie in continuirlichen Körpern», которая была напечатана в журнале «Zeitschrift für Mathematik und Physik» [8].
В докторской диссертации «Уравнения движения энергии в телах» (1874) [4,7] Умов впервые в истории науки всесторонне развивает вопрос о движении и распределении энергии в средах, т. е. вопрос о переносе, передаче, переходе энергии с частиц одной среды на частицы другой, об обмене энергии между частицами среды, между телами и промежуточной средой, об изменении количества энергии со временем, о превращении одной формы энергии в другую. Он вводит в теоретическую физику понятия о скорости и направлении движения энергии, о ее плотности в данной точке среды, о потоке энергии и векторе плотности этого потока, а также представление о пространственно-временной непрерывности энергии. Эти идеи Умова подняли учение о сохранении и превращении энергии на новую, более высокую ступень. Они составляют твердую основу важнейших представлений современной физики [1].
Весьма примечательно, что положения Умова о движении энергии перекликаются с мыслями Энгельса о переносе, передаче, движении энергии, о превращении одной формы энергии в другую [3] . Энгельс подчеркивал, что движение не может быть создано, а только передано. Критикуя Дюринга, Энгельс писал, что никому не приходит в голову объяснять происшедшее движение из «ничего» а всегда, напротив, предполагается, что это движение является результатом перенесения, «Преобразования или продолжения какого-нибудь предшествующего движения». «Теперь уже не нужно проповедывать как нечто новое, — писал Энгельс, — что количество движения (так называемой энергии) не изменяется, когда оно из кинетической энергии (так называемой механической силы) превращается в электричество, теплоту, потенциальную энергию положения и т. д., и обратно; мысль эта служит добытой раз навсегда основой гораздо более содержательного отныне исследования самого процесса превращения, того великого основного процесса, в понимании которого находит свое обобщение все познание природы».
Энгельс тогда не мог себе и представить, что идеологи ХХ века будут даже взрывать всю Вселенную из «ничего», чтобы удовлетворить своим абстрактным теориям (авт.).
Умов рассматривал движение энергии, превращение отдельной ее формы в другую материалистически, т. е. как материальный процесс, обусловленный движением материи и совершающийся независимо от сознания человека. Различные виды энергии он связывал с различными формами движения материальных частиц. Свою диссертацию Умов начинает словами: «Элемент объема, произвольно взятый внутри какой-нибудь среды, частицы коей находятся в движении, заключает в данный момент времени определенное количество энергии» [4,7]. Умов доказывал, что, зная законы движения энергии, которые часто могут быть определены опытным путем, можно найти соответствующие законы движения материи, иначе говоря, дифференциальные уравнения движения частиц среды.
Именно, так и были впервые выведены все основные уравнения классической электродинамики из самых простых волновых процессов в физическом вакууме-эфире [9] (авт.).
Умов проводит мысль, что движение немыслимо без материи. Он отстаивал положение материализма о том, что в мире нет ничего кроме вечно движущейся и развивающейся материи, что движение невозможно без материи. «Все физические явления, — подчеркивал Умов,- вызываются движениями» [10]. Эти положения Умова были направлены против энергетики Оствальда.
Умов следующим образом формулировал задачу своего исследования: «Законы перехода энергии с одного элемента среды на другой определялись до сих пор только для частных форм движений. Задача настоящего труда заключается в установлении на общих началах учения о движении энергии в средах. Раскрытие общей связи между распределением и движением энергии в средах и перемещениями их частиц, независимо от частных форм движений, должно дать возможность из известных законов движения и распределения энергии в теле выводить заключения о роде движений его частиц. Задачи подобного рода имеют особую важность ввиду стремления современной физики сводить все явления природы на явления движения. Простейшие опытные данные, на которые могли бы опереться теоретические изыскания современной физики, идущие в указанном направлении, представляют распределения и движения энергии в различных явлениях природы.
Орудия опытного исследования не настолько, однако, усовершенствованы, чтобы давать возможность определять законы каждой из составных частей энергии в отдельности. Поэтому важно отыскать метод, который давал бы возможность перейти от определенных путем опыта законов движения энергии к дифференциальным уравнениям движения частиц тела, которое, по предположению, дает место наблюдаемому явлению».
В приведенном рассуждении в сжатой форме изложена суть учения Умова о движении и локализации энергии. Уже «Введение» ярко раскрывает материалистическую направленность воззрений великого русского физика на проблему энергии.
Одна из характерных особенностей работ Умова состоит в том, что в них учение о движении и распределении энергии в средах изложено при помощи сложного математического аппарата, облечено в строгую математическую форму. Этим, очевидно, отчасти объясняется то, что оригинальные идеи Умова долго не были поняты многими даже крупными физиками.
Вполне возможно, что с этим как раз и связаны те самые кризисные моменты, возникшие при использовании вектора Умова и вектора Умова-Пойнтинга в современных учебниках, о чем более подробно пойдет речь в параграфе 6 (авт.).
Работа Умова «Уравнения энергии в телах» состоит из трех разделов: 1. Общее выражение закона сохранения энергии в элементе объема среды; 2. Уравнения движения энергии в различных телах; 3. Переход от законов движения энергии к частичным движениям, обусловливающим явления.
Центральное место в работе занимает первый раздел. Именно здесь в самом общем виде выведено знаменитое уравнение движения энергии в средах и введен в учение о сохранении и превращении энергии ряд новых понятий — поток энергии, ее скорость, направление, плотность и т. п.
Объектом исследования явилась однородная среда с определенными конечными или бесконечно большими границами. Предполагалось, что на частицы этой среды не действуют внешние силы, а прилив энергии к ним или отдача ее от них происходит через границы среды. «Если мы, — пишет Умов, — выделим мысленно элемент объема, изменение его энергии (т. е. суммы его живой силы (кинетической энергии) и потенциальной энергии) по закону сохранения энергии может совершиться только на счет прибыли или убыли последней в смежных элементах. Математическое выражение связи приращения количества энергии в элементе объема с ее потерями в смежных элементах и будет математическим выражением элементарного закона сохранения энергии в средах» [4,7].
Из своих дифференциальных уравнений Умов получает основное уравнение движения энергии
характеризующее изменение плотности энергии w в элементе объема
со временем. Здесь vx , vy , vz — слагающие по осям прямоугольных координат скорости, с которой энергия движется в рассматриваемой точке среды.
Основное уравнение движения энергии, полученное Умовым, в математической (дифференциальной) форме фиксирует закон сохранения энергии. Именно в нем выражена основная мысль Умова о непрерывности энергии, о том, что энергия может распространяться, передаваться от одной точки среды к другой только непрерывно. Положение Умова о непрерывности энергии, о том, что энергия распространяется не только в определенном пространстве, но и в определенный промежуток времени, исключает всякую мысль о ньютоновском мгновенном дальнодействии.
Умовское уравнение движения (непрерывности) энергии на современном математическом языке может быть записано в следующей форме (для непоглощающего и не содержащего источников энергии пространства):
где S = w v — знаменитый «вектор Умова», прочно вошедший в науку.
Примерно так же обозначается и вектор Умова-Пойнтинга в аналогичном выражении для поперечных электромагнитных волн, что является просто частным случаем более общего уравнения движения энергии.
Умов показывает, каким образом можно получить математические выражения, связывающие законы движения и распределения энергии с движениями частиц среды.
В своей работе «Ableitung der Bewegungsgleichungen der Energie in continuirlichen Körpern» [8] Умов писал :
«Если движение частицы тела М испытывает изменение благодаря каким-либо причинам, то пертурбация (возмущение) движения частицы тела постепенно будет распространяться по всему телу. Поскольку никакое изменение движения не может происходить без увеличения или уменьшения энергии, т. е. без ее притока или отдачи, то наряду с распространением пертурбации (возмущения) движений будет происходить само собой движение энергии в том или ином смысле. И, наоборот, любой приток или отдача энергии влечет за собой пертурбацию (возмущение) движения. Так как эта пертурбация (возмущение) выражается в изменении прежнего состояния движения или в поддержании движения, когда оно затухает, то направление и скорость движения энергии будут идентичны с направлением и скоростью распространения пертурбации (возмущения) «.
Из этих рассуждений видно, что Умов говорил о движении энергии в самом широком смысле, т.е. для любых объектов природы.
Направление и скорость движения энергии есть, по Умову, направление и скорость распространения пертурбаций (возмущений).
Исходя из основного уравнения, он выводит уравнения движения энергии для различных сред (твердых тел постоянной упругости, волновых поверхностей произвольного вида, жидких тел), которые связывают законы движения и распределения энергии в среде с законами ее частичных движений.
Подавляющее большинство историков и библиографов, по какой-то причине, отметили, в основном, только эти прикладные стороны научных разработок Умова (авт.).
Для твердых тел постоянной упругости Умов получил следующие равенства, показывающие, что движение энергии связано с движением материальных частиц:
где через U , V, W обозначаются скорости перемещения по осям прямоугольных координат центра тяжести элемента объема, через Р xx , Руу, Pzz — нормальные и через Рху, Р xz , Р yz . — тангенциальные силы упругости, действующие на стороны бесконечно малого параллелепипеда. Это и есть уравнение движения энергии в твердых упругих телах, связывающее поток энергии в каждой точке тела с характером движения материальных частиц.
Вот на эти-то уравнения почти все и обращают свое главное внимание.
Но мы хорошо видим, что этими уравнениями далеко не исчерпываются результаты научных исследований Умова (авт.).
Исходя из этих равенств, Умов пришел к следующему выводу: «. количество энергии, протекающее через бесконечно малый плоский элемент в бесконечно малое время, равно отрицательной работе сил упругости, действующих на этот элемент» [4,7]. Эти выражения, по его мнению, дают возможность найти общие соотношения между формой волн, несущих продольные и поперечные колебания, и движениями частиц упругого тела.
Особое внимание Умова привлекает исследование волновых процессов, доказательство того, что распространение волн связано с движением энергии, что с одной и той же волновой поверхностью всегда связано и движется вместе с нею вполне определенное количество энергии.
«Явления волнообразных движений, — писал он, — суть простейшие и легко поддаются теоретическим изысканиям. Причина заключается в том, что геометрическая система — волна и луч, характеризующая рассматриваемое движение, принадлежит к простейшим геометрическим комбинациям поверхностей и линий».
Развивая положения, изложенные в работе «Законы колебаний в неограниченной среде постоянной упругости», Умов прилагает уравнения движения энергии к определению скорости распространения продольных и поперечных волн в упругой среде.
Найдя уравнение, характеризующее связь между энергией и формой волновой поверхности, Умов показал, что в случае плоской волны «энергия целиком переносится волной от одной точки луча к другой» [4,7].
Умов рассмотрел вопрос о движении энергии в упругой среде и для более общего случая, когда во всех направлениях энергия распространяется с постоянной скоростью. Для бесконечно малого плоского элемента среды получается следующее выражение:
где Р — сила упругости, действующая на элемент, ip — слагающая скорость элемента по направлению силы упругости, vn — слагающая скорости энергии по нормали к элементу. Из этого выражения, как указывал Умов, непосредственно следует, что сила упругости, взятая с отрицательным знаком, пропорциональна количеству протекающей через элемент в единицу времени энергии и обратно пропорциональна слагающей скорости частиц самого элемента по направлению силы упругости.
Таким образом, Умов выдвинул и обосновал теорему, связывающую величину энергии, скорость ее движения и работу сил, действующих на площадку, через которую она протекает. Частным случаем этой теоремы, по сути дела, является гипотеза Максвелла о световом давлении, существование которого экспериментально и теоретически впервые в науке было доказано русским физиком П.Н. Лебедевым в 1899 г.
Как хорошо известно, именно силовые волны и ответственны за передачу импульса частицам. Из акустики также хорошо известно, что упругие волны переносят не только энергию, но и массу вместе с энергией в соотношении dE = c 2 dm [9] . К такому основополагающему выводу и пришел Умов в своих исследованиях (авт.).
Умов показал, что сумма из количества энергии, протекающей через произвольный плоский элемент, и работы сил упругости на элемент равна нулю. Полученное им уравнение дает возможность определить по давлению, испытываемому границами среды, количество входящей в нее энергии, зная при этом скорость движения частиц на границах. Точно так же, зная количество энергии, входящей в среду в единицу времени, и зная скорость частиц на границах, можно определить давление или натяжение, соответствующее этому переходу.
Здесь же Умов получает еще один интересный вывод: скорость движения частиц тела на границе по направлению силы равна частному из количества энергии, прошедшей через весьма малый плоский элемент, центр которого совпадает с частицей и отнесенного к единице площади и времени, на давление или натяжение.
В третьей главе — «Переход от законов движения энергии к частичным движениям, обусловливающим явления» — Умов рассматривает вопрос о движении энергии в полях.
Все явления природы он разделил на две группы. К первой группе отнесены явления, наблюдаемые в непрерывных средах; ко второй — явления, наблюдаемые в телах, не находящихся в непосредственном соприкосновении друг с другом. При этом Умов указал весьма простой способ сведения явлений, требующих для своего существования какой-либо среды, на движения частиц этой среды.
В данной главе Умов исследует преимущественно явления второй группы.
Когда взаимодействующие тела удерживаются внешними силами в покое или удалены друг от друга на громадные расстояния, тогда количество энергии, сообщаемое в бесконечно малый промежуток времени всем взаимодействующим телам, равняется, по Умову, изменению внутренней энергии этих тел плюс изменение энергии промежуточной среды за тот же период времени. В случае стационарных явлений энергия промежуточной среды не изменяется.
Умов рассматривает и такие тела, для взаимодействий которых существует потенциал П. Изменение энергии промежуточной среды, по его мнению, равно отрицательной величине этого потенциала. «Опыт показывает, с другой стороны, — говорит он, — что существует целый класс явлений, в которых приращение живой силы (кинетической энергии) явных движений взаимодействующих тел связано с уменьшением внутренней энергии самих тел. энергия среды, способная в каждый отдельный момент времени превращаться в живую силу (кинетическую энергию) явных движений тел, а также энергия среды, в которую способна превращаться в каждый момент времени живая сила (кинетическая энергия) движений тел, представляется величиной П + const. «.
Умов поставил перед собой задачу отыскать закон распределения энергии внутри промежуточной среды, при котором сумма энергий всех элементов пространства, занятого средой, представляется величиной потенциала плюс некоторая постоянная. При этом он заметил, что величина потенциала, в том виде, как она входит в уравнение живых сил (кинетических энергий) в явлениях взаимодействия на расстояниях конечных, зависит от относительного положения взаимодействующих тел и от их формы.
В третьей главе диссертации подробно исследуется вопрос об энергии электрического и магнитного поля, о ее движении, переносе от одной точки среды к другой.
Умов доказал, что плотность энергии w в какой угодно точке поля пропорциональна квадрату силы, действующей на частицы, т.е. напряженности полей Е или Н в той же точке. Для случая электрических и магнитных полей плотность энергии по Умову примет знакомую форму:
Весьма характерно, что к этому результату Умов пришел самостоятельно еще в начале 70-х годов прошлого столетия, независимо от Максвелла.
Умов отыскивает скорость движения энергии в промежуточной среде. Он доказывает, что если в промежуточной среде движется только одна масса, сосредоточенная в одной точке (по современному — материальная точка), то энергия этой среды остается неизменной, т. е. между массой (материальной точкой) и средой нет обмена энергиями. При этом он добавляет, что неизменность энергии среды при движении массы m в указанных условиях есть только иное выражение закона инерции. Умов полагал, что тот же результат будет и для произвольного числа масс, находящихся в таком движении, что их относительные положения остаются неизменными.
Представления Умова о взаимодействии между двумя «деятелями» (объектами) природы а1 и а2 посредством третьего деятеля а3 , играющего роль передатчика, промежуточной среды, перекликаются с современными физическими представлениями, согласно которым взаимодействие между элементарными частицами осуществляется (передается) через поле или посредством третьих частиц.
В работе «Прибавление» к докторской диссертации «Уравнения движения энергии в телах», опубликованной в 1874 г. [11], Умов определяет направление движения энергии, вводя представление о направлении движения энергии в точке.
Умов подчеркивает, что направление движения энергии вообще не совпадает с направлением линий, нормальных к поверхностям равной энергии или к поверхностям изодинамическим.
Далее Умов наглядно показал, что если в упругом теле движения распространяются волнами, то условием движения энергии по нормалям к волновым поверхностям будет совпадение волновых и изодинамических поверхностей.
Умов вводит в науку новое определение луча. «Луч, — говорит он, — есть частный вид линий, по которым движется в теле энергия. «. Эти линии, по которым движется энергия, Умов называет динамическими линиями. Поверхности, к ним нормальные, он называет статическими поверхностями, так как по ним нет движения энергии. Для случая распространения волн луч, следовательно, есть частный вид динамических линий.
Следует заметить, что умовское определение луча позже было заимствовано Кирхгофом и применено при определении светового луча. Умов писал по этому поводу, что он «сообщил Кирхгофу свои идеи о движении энергии в телах, и не исключается возможность, что данное Кирхгофом определение луча (в его работе — А. Компанеец) было сделано им под влиянием сообщенных ему идей» [4,7].
Идеи Умова не сразу были поняты и оценены. Только спустя семь лет после защиты и опубликования докторской диссертации Умова «Уравнения движения энергии в телах» ее идеи применил голландский физик Гринвис к исследованию вопроса о переносе энергии от одного тела к другому для случая удара упругих и неупругих шаров. Гринвис нашел, что этот перенос энергии N (мощность) равен произведению силы отдачи (обусловленной давлением) F на скорость центра массы v , т. е.
«Этот простой закон, — писал Гринвис, — согласуется с результатами Умова, найденными другим путем для движения энергии в твердых телах. Этот русский ученый, который специально не занимался соударениями и даже не упоминает о них, изучал движение энергии в предположении, что оно происходит в упругой и сжимаемой среде. Он нашел, что энергия, которая за определенное время проходит через единицу поверхности тела в направлении силы давления, равна произведению этой силы на составляющую по направлению силы скорости центра масс. В случае прямого удара уравнение (1.6) показывает, что это есть частный случай закона Умова (loi de Umov), и что эта часть энергии ведет себя как сжимаемая и упругая жидкость или, по крайней мере, подчиняется законам, соответствующим такому предположению. Правило Умова подтверждается также при косвенных столкновениях»‘.
1. Компанеец А.И. Борьба Н.А. Умова за материализм в физике. – Изд-во АН СССР, Москва, 1954.
2. Ломоносов М.В. Полное собрание сочинений. Изд-во АН СССР, Л., 1951,
3. Энгельс Ф. Диалектика природы, М. 1952.
4. Умов Н.А. Уравнения движения энергии в телах (докт. диссерт.). Одесса, 1874.
5. Умов Н.А. Теория взаимодействий на расстояниях конечных и ее приложение к выводу электростатических и электродинамических законов. М., 1873. См. также «Математический сборник», 1872, т. 6.
6. Умов Н.А. Теория простых сред и ее приложение к выводу основных законов электростатических и электродинамических взаимодействий. Одесса, т. 9, 1873.
7. Умов Н.А. Избранные сочинения. Классики естествознания. Математика. Механика. Физика. Астрономия. (Под ред. чл.-корр. АН СССР проф. А.С. Предводителева), Гостехиздат, М.-Л. 1950, стр. 66.
8. Umov N.A. Ableitung der Bewegungsgleichungen der Energie in continuirlichen Körpern. Zeitschrift für Mathematik und Physik», 1874, В d. XIX, Н. 5, 5. 429.
9. Шаляпин А.Л., Стукалов В.И. Введение в классическую электродинамику и атомную физику. Второе издание, переработанное и дополненное. Екатеринбург, Изд-во Учебно-метод. Центр УПИ, 2006, 490 с.
10. Умов Н.А. Собрание сочинений, М., 1916, т. 3, стр. 107.
11. Умов Н.А. «Прибавление» к докторской диссертации «Уравнения движения энергии в телах», 1874 г.
12. Умов Н.А. Законы колебания в изотропной среде постоянной упругости. «Математический сборник», т. 5, 1870 – 72.
13. Umov N.A. Ein Theorem über die Wechselwirkungen in Endlichen Entfernunden. (Теорема относительно взаимодействий на расстояниях конечных). Zeitschrift für Mathematik und Physik. Bd. 19, 1874, H. 2. § 12 .
14. Умов Н.А. О стационарном движении электричества на проводящих поверхностях произвольного вида. «Математический сборник», 1878, т. 9.
15. Умов Н.А. Вывод законов электродинамической индукции. «Журн. Рус. физ.-хим. общества, физ. отд., 1881, т. 13, вып. 3.
16. Умов Н.А. Курс физики. Лекции, т. 2. Звук. Свет. Электричество. Магнетизм. М., 1902. См. также Архив АН СССР, ф. 320, оп. 1, № 83-84.
17. Умов Н.А. Теория электромагнитного поля. Архив АН СССР, ф. 320, оп. 1, № 21/3, лл. 1-90.
18. Умов Н.А. Лекции об электромагнитном поле (1895). Архив АН СССР, ф. 320, оп. 1, № 100, лл. 1-520.
19. Kirchhoff. Gesämmelte Abbandungen, p. 156 (1872). “Uber die stationaren elektrischen Stromungen in einer gekrummten leitenden Flache”. «Monatsberichte der К onigl. Akademie der Wissenschaften zu Berlin» (1875).
20. Калашников С.Г. Электричество. Издание пятое, исправленное и дополненное. М.: Наука, 1985, с. 524-525.
21. Савельев И.В. Курс общей физики. Т. 2. Электричество и магнетизм. Волны. Оптика. – М.: Наука, 1988. C. 309.
22. Фейнман Р., Лэйтон Р., Сэндс М. Фейнмановские лекции по физике. Электродинамика. – М.: Мир, 1977. Вып. 6. С. 296-299.
23. Умов Н.А. Возможный смысл теории квант. «Вестник опытной физики и математики», 1914, с. 50. См. также Избранные сочинения, 1913.
24. Умов Н.А. Метод истолкования теории Планка. Архив АН СССР, ф. 320, оп. 1, № 49, лл. 1-33.
25. Умов Н.А. Вступительная речь в Московском университете (О законе сохранения и превращения энергии, 1893). Архив АН СССР, ф. 320, оп. 1, № 112, лл. 1-24.
Уравнения движения энергии в телах
УРАВНЕНИЯ ДВИЖЕНИЯ ЭНЕРГИИ В ТЕЛАХ
I. ОБЩЕЕ ВЫРАЖЕНИЕ ЗАКОНА СОХРАНЕНИЯ ЭНЕРГИИ В ЭЛЕМЕНТЕ ОБЪЕМА СРЕДЫ
§ 1. Определения и задача исследования. Элемент объёма, произвольно взятый внутри какой-нибудь среды, частицы коей находятся в движении, заключает в данный момент времени определённое количество энергии. Эта энергия слагается из двух частей: из живой силы движения частиц элемента объёма и потенциальной энергии, т. е. работы, которая может быть отдана этими частицами при возвращении их из данного положения в некоторое начальное, соответствую-, щее устойчивому равновесию. Под энергией элемента я буду разуметь сумму живых сил частиц элемента» и его потенциальной энергии, определённой, как было сказано выше.
Законы перехода энергии с одного элемента среды'» на другой определялись до сих пор только для частных форм движений. Задача настоящего труда заключается в установлении на общих началах учения о движении энергии в средах.
Раскрытие общей связи между распределением и движением энергии в средах и перемещениями их частиц, независимо от частных форм движений, должно дать возможность из известных законов движения и распределения энергии в теле выводить заключения о роде движений его частиц. Задачи подобного рода
имеют важность ввиду стремления современной физики сводить все явления природы на явления движения. Простейшие опытные данные, на которые могли бы опереться теоретические изыскания современной физики, идущие в указанном направлении, представляют распределения и движения энергии в различных явлениях природы. Орудия опытного исследования не настолько, однако, усовершенствованы, чтобы давать возможность определять законы каждой из составных частей энергии в.отдельности. Поэтому важно отыскать метод, который давал бы возможность перейти от определённых путём опыта законов движения энергии к дифференциальным уравнениям движения частиц тела, которое, по предположению, даёт место наблюдаемому явлению.
§ 2. Уравнение сохранения энергии в элементе тела. Представим себе однородную среду с определёнными границами, конечными или бесконечно большими. Пусть па частицы этой среды не действуют внешние силы и прилив энергии к частицам обусловливается принятием или отдачей энергии средой через её границы.
Если мы выделим мысленно элемент объёма, изменение его энергии (т. е. суммы его живой силы и потенциальной энергии) по закону сохранения энергии может совершиться только на счёт прибыли или убыли последней в смежных элементах. Математическое выражение связи приращения количества энергии в элементе объёма с её потерями в смежных элементах и будет математическим выражением элементарного закона сохранения энергии в средах.
Математическое выражение, указанной связи может быть нами почерпнуто из явления иного рода, опирающегося на закон, аналогичный закону сохранения энергии. Распределение вещества при движениях непрерывной сжимаемой среды подчиняется закону сохранения вещества. Насколько движение энергии и движение сжимаемого вещества обусловливаются за-
коном их сохранения, настолько мы имеем право уподоблять движение энергии движению подвижного и сжимаемого вещества.
Количество энергии в элементе объёма среды, отнесённое к единицо объёма, может быть названо плотностью энергии в данной точке среды.
Мы можем следить за изменениями, происходящими в количестве энергии и её скоростях в одной и той же точке пространства или же в одном и том же движущемся количестве (массе) энергии.
Означим буквой Э плотность энергии в произвольной точке среды, т. е. частное из количества энергии, заключённого внутри бесконечно малого элемента объёма, на этот элемент. Назовем через l x , l. L слагающие по прямоугольным осям координат х, у та z скорости, с которой энергия движется в рассматриваемой точке среды.
Вообразим себе элемент объема dxdydz. При введённых нами обозначениях количества энергии, входящие и выходящие через различные стороны элемента, будут:
Сумма этих величин, представляющих токи энергии,, даёт нам отнесённое к единице времени изменение количества энергии Э dx dy dz в элементе объёма со временем t, Следовательно, делая сокращения.
“здесь st- есть частная производная от У по времени.
Выражение (I), аналогичное с выражением закона сохранения вещества в гидродинамике, есть выражение элементарного закона сохранения энергии в телах.
Означая через — г полную производную от Э по времени, мы находим следующее выражение для изменения плотности энергии со временем в одной и той же движущейся массе энергии:
Аналогия между дифференциальными законами движения энергии и движения вещества, вообще, не простирается далее сходства уравнении (I) и (Г) с соответственными уравнениями гидродинамики.
Выражение (I) открывает связь между количеством энергии, отнесённым к единице времени, втекающим в среду через сё границы, и изменением количества энергии в среде. Мы находим:
где тройной интеграл распространяется на весь объём среды, d представляет элемент её границы и /„ есть скорость движения энергии по внешней нормали n к элементу границы, т. о.
§ 3. Связь законов движения энергии с законами частичных движений сред. Дифференциальные законы движений частиц различных сред дают, как известно, возможность установить математическое выражение, представляющее закон сохранения энергии для всей
среды. Если через с/ означим приращение живой силы в элементе объёма среды, через &VV — приращение работы частичных сил элемента u через S L— приращение работы давлений на элементе da поверхности тела, причём все эти приращения отнесены к единице времени, мы всегда имеем возможность но основным дифференциальным законам движений частиц среды составить следующее выражение, причём предполагается, что внешние силы не действуют на частицы среды:
В этом выражении dw представляет элемент объёма среды, тройной интеграл распространяется на всю среду, а двойной —на её поверхность. Выражение (5) представляет не что иное, кат-: закон сохранения энергии для всей среды.
Для данной среды подобное выражение может быть составлено ещё другим образом, исходя из уравнения (1). Умножая обе части этого уравнения на элемент объёма d(.o и интегрируя на всю среду, мы находим:
или, преобразовывая второй тройной интеграл,
Тройной интеграл, входящий в это выражение, представляющее закон сохранения энергии для всей среды, должен быть тождествен с тройным интегралом, входящим в выражение (5). Но двойной интеграл, входящий в выражение (7), преобразуется во второй тройной интеграл выражения (6); следовательно, и двойной интеграл, входящий в выражение (5), должен преобразоваться в тройной интеграл, тождественный со вторым тройным интегралом, входящим в выраже-
ние (6). Математическое выражение этого тождества и приведёт к выражениям, связывающим законы движения и распределения энергии с частичными движениями сред.
II. УРАВНЕНИЯ ДВИЖЕНИЯ ЭНЕРГИИ В РАЗЛИЧНЫХ ТЕЛАХ
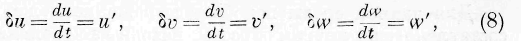
§ 4. Уравнения движения энергии в твёрдых телах постоянной упругости. Означим через и, v, w перемещения по осям прямоугольных координат центра тяжести элемента объёма, через p xl , p a!/ , p,, — нормальные и через р ху , p yz , p x z — тангенциальные силы упругости, действующие на стороны бесконечно малого параллелепипеда (причём натяжения принимаются положительными, а давления отрицательными), и через p — плотность в какой-нибудь точке среды. Полагая, далее,
Первые два тройных интеграла представляют приращение энергии, отнесённое к единице времени, во всей упругой среде. Двойной интеграл распространяется на всю поверхность среды и представляет работу внешних
давлений. Мы опускаем действие внешних сил на элементы упругой среды. Обращая внимание на значение величин 8м, Ви и Stv по формуле (8), мы замечаем, что двойной интеграл выражения (9) преобразуется в следующий тройной интеграл:
Так как первые два тройных интеграла выражения (9) тождественны с первым тройным интегралом выражения (6), то двойной интеграл, входящий в выражение (9), взятый с тем знаком, с которым он входит в это выражение, или тождественный с ним тройной интеграл (10), взятый с отрицательным знаком, должен быть тождествен со вторым тройным интегралом, входящим в выражение (6); следовательно, подинте-гральная * функция тройного интеграла (10), взятая с отрицательным знаком, должна быть тождественна подинтегральной функции второго тройного интеграла выражения (6), или, что всё равно, второй части уравнения (I). Это заключение легко поверяется при помощи основных уравнений упругости, дающих возможность преобразовать сумму подинтегральных функций первых двух тронных интегралов, входящих в выра-
жение (У), тождественную с -г— , в отрицательную под-
интегральную функцию выражения (10). Из тождества этой последней со второй частью уравнения (I) вытекают следующие равенства:
откуда заключаем: количество энергии, протекающее
через бесконечно малый плоский элемент в бесконечно малое время, равно отрицательной работе сил упругости, действующих на этот элемент.
Найденные выражения (11) представляют связь законов движения энергии с законами частичных движений твёрдого тела достоянной упругости. К правым частям этих выражений не прибавлены функции, зависящие только от координат (у, z), (z,x), (x, у), ибо левые части должны обращаться в нуль, когда
§ 5. Для выяснения найденных нами заключений приложим формулы (10) к определению скорости распространения в упругой среде плоских волн с продольными и поперечными колебаниями.
Рассмотрим колебания продольные. Пусть несущие их плоские волны перпендикулярны к оси х. Следовательно,
Положим, кроме того,
где Ь есть искомая скорость распространения продольных колебаний. Пользуясь выражениями сил упругости, данными Ламе, мы имеем в нашем случае:
Кроме того, мы имеем:
Интегрируя это выражение по времени, имееь-
Вставляя сюда величину и, находим:
С другой стороны, подставляя (13) и (14) в (11), находим:
Последние два соотношения дают / 3 =0, 1
— 0. Следовательно, 1 Х — Q, и первое- из соотношений (18) но сокращении общих факторов даёт соотношение:
откуда получается известный результат:
В случае распространения плоской волны с колебаниями поперечными мы нашли бы точно так же известное выражение для скорости распространения поперечных колебаний. Выражения (11) дают возможность найти общие соотношения между формой волн, несущих продольные или поперечные колебания, и движениями частиц упругого тела. Известно, что скорость распространения тех или других волн постоянна и что волны, исходящие из одной ‘ и той же поверхности сотрясения, имеют общиз нормали. Означая через с скорость распространения волны, мы имеем, следовательно,
I _. дх i _ <>У i __ д — /2Ц
есть уравнение какой-нибудь волновой поверхности, а а г В — её дифференциальный параметр первого порядка.
Мною было показано (“Законы колебаний в неограниченной среде постоянной упругости”), что, выбирая за параметр В волны отрезок луча между некоторым начальным положением волны и последующим, мы имеем:
Принимая последнее выражение и подставляя (21) в (И), находим:
‘dz Эти выражения показывают, что
суть выражения косинусов углов нормали в какой-нибудь точке волны с осями координат. Так как .по закону общих нормалей все элементы нормалей, проведённые в соответствующих точках одной и той же волны в различных её положениях, лежат на одной прямой, носящей название луча, то выражения (25) остаются неизменными на протяжении одного и того же луча.
Выражения (25) показывают также, что, воображая себе в какой-нибудь точке луча линию, равную по величине произведению из энергии на скорость её распространения, величины
Возвышая выражения (24) в квадрат п складывая, находим:
Умножая выражения (24) соответственно на l x , l v , / г , складывая и обращая: внимание на соотношения (21), находим следующее выражение:
Величина -9с 2 может быть названа двойной живой силой движения энергии.
§ 6. Закон энергии для волновых поверхностей произвольного вида. Вставляя в уравнение (I) выражения (21) и принимая в соображение (23), найдём:
Это соотношение даёт связь между энергией и формой волновой поверхности, которая приводится по отношению к энергии к дифференциальному уравнению с частными производными первого порядка. Мы находим, раскрывая выражение (29):
Здесь А 2 означает дифференциальный параметр второго порядка.
Введём ортогональные координаты, причём параметры двух систем поверхностей, ортогональных между собой и к волновой поверхности В, означим через р х , р 2 . Принимая во внимание условия ортогональности, мы представим выражение (30) в следующем виде:
Это выражение интегрируется при помощи совместных дифференциальных уравнений:
Означая через / произвольную функцию, находим:
Таково общее выражение энергии для колебаний в одной и той же точке среды, несомых волной произвольного вида В. \ \*BdB можно взять в общем виде, как
показано будет ниже [формула (46)]. Рассмотрим случай волны цилиндрической. Пусть ось цилиндра параллельна оси z и координаты точки её пересечения с плоскостью ху суть о, 0, 0. Мы имеем в данном случае:
и выражение (33) даёт нам:
где tp есть параметр плоскостей, проходящих через ось цилиндра.
Для волны сферической, центр которой имеет координаты а, Ь, с, мы имеем:
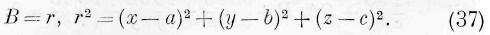
и выражение (33) даёт:
Подобные результаты были известны для живой силы колебательных движений; здесь они даны для всей энергии движения-, не определяя в подробности его формы.
Из выражения (33) мы можем заключить о законе энергии в точке волны по мере её движения вместе с волной. Я предпочитаю, однако, вывести этот закон непосредственно из основного уравнения (Г). Обращая внимание на указанный выше выбор параметра В волны, мы имеем:
где с и с г суть постоянные.
Подставляя в уравнение (Г) величины (21) и принимая в соображение (23), находим:
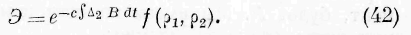
Кроме того, означая через h, 1г ъ Л 2 дифференциальные параметры первого порядка волновой поверхности и ортогональных к ной поверхностей [> г , р 2 , мы имеем (Lame, Lecons sur les coordonnees curvilignes, 1859):
Замечая, что в нашем случае h = i, имеем:
Подставляя (43) и (45) в (42) и производя интеграцию, находим:
Но элемент объёма будет, так как /2=1,
Умножая выражение (46) на (47), находим:
Так как во всё время движения энергии вдоль одного и того же луча величины ^ и [> 2 остаются неизменными, то из выражения (48) заключаем, что энергия целиком переносится волной от одной точки луча к другой .
§ 7. Я закончу настоящий отдел несколькими общими соображениями относительно законов движения энергии, не ограничиваясь случаем, когда она распространяется во всех направлениях с постоянной скоростью. Вообразим себе внутри упругого тела бесконечно малый плоский элемент, нормаль коего обозначим через п. Пусть сила упругости, действующая на элемент, будет Р. Мы имеем по известным формулам теории упругости соотношения:
Умножая эти выражения ла и’, v,’ w’ и складывая, находим:
Здесь i есть скорость центра рассматриваемого нами бесконечно малого плоского элемента, е— скорость движения энергии в этом центре. Означая через i p слагающую скорости элемента по направлению силы упругости и через /„ — слагающую скорости энергии по нормали к элементу, выражение (50) может быть написано в следующем виде:
Мы видим из этого выражения, что сила упругости, взятая с отрицательным знаком, пропорциональна коли-
честву протекающей через элемент в единицу времени энергии и обратно пропорциональна слагающей скорости частиц самого элемента по направлению силы упругости.
В каждой точке M упругого тела всегда существуют три взаимно перпендикулярных плоских элемента, испытывающих одни только нормальные силы упругости. Воображая себе в точке M оси прямоугольных координат проведёнными таким образом, что плоскости координат параллельны указанным трём плоским элементам, мы имеем по формуле ( 51):
Выражения (11), (51) и (52) показывают, что сумма из количества энергии, протекающей через произвольный плоский элемент, и, работы сил упругости на элемент равна нулю. Уравнение (51), будучи справедливым для каждого плоского элемента внутри среды, имеет место на границах среды. Оно даёт, следовательно, возможность по давлению, испытываемому границами среды, определить количество входящей в нес энергии, зная при этом скорость движения частиц на границах. Точно так же, зная количество энергии д, входящей в среду в единицу времени, и зная скорость частиц на границах, мы можем определить давление или натяжение, соответствующее этому переходу. Заметим, что q имеет знак положительный, когда энергия выходит из тела, и отрицательный, когда энергия входит в тело. Следовательно, из (511 мы находим:
Если дано q n P, то найдём отсюда i p ; соотношение (53) показывает именно, что скорость движения частиц тела на границе по направлению силы P равна частному из количества энергии, прошедшей через весьма малый плоский элемент, центр коего совпадает с частицей,
и отнесённого к единице площади и времени, на давление или натяжение Р.
Возьмём числовой пример. Пусть давление Р, испытываемое элементом границы тела, нормально к его поверхности и в данный момент времени равно давлению атмосферы. Давление Р, отнесённое на квадратный метр поверхности, есть 10 334 кг. Пусть количество энергии, протекающее в данный момент времени через бесконечно малый элемент поверхности, отнесённое к 1 сек. и к квадратному метру, есть 1 килограммометр в 1 сек. Тогда для данного момента скорость i p движения частиц взятого элемента поверхности будет по формуле (53):
Возьмём ещё другой пример. Положим, что теплота, сообщаемая упругому телу, заключается в энергии его частичных движений, удовлетворяющих уравнениям упругости. Положим, что температура 1 кг тела повышена на 1°С в 1 сек. Означим плотность тела через д, его теплоёмкость под давлением атмосферы — через у и положим, что тело имеет кубическую форму. Объём тела
б >’ дет -ШГд м «‘ пов0 Р хн ость s = 6 ( 1 щ Т )4 i количество энергии, прошедшее в 1 сек. через 1 м поверхности, есть -^—;,’ — кгм. По формуле (53) вычисляется средняя
скорость i p частиц его поверхности при давлении одной атмосферы, т. е. 10344 кг/м 2 :
платина 1,8 м/сек.
Формула (53) приводит пас еще к следующему заключению: скорости i p граничных частиц всех упругих
тел при одном и том мсе давлении ила натяжении, и при одном и том мсе количестве энергии, проходящем через них в бесконечно малый элемент времени, равны.
§ 8. Уравнения движения энергии в телах
жидких. Рассмотрим сначала жидкости, не обращая внимания на так называемое внутреннее трение частиц жидкости. Означая через и, v, w скорости движения частиц жидкости в одной и toi’l же точке пространства, через p -давление и \> — плотность, мы имеем следующие уравнения гидродинамики:
Мы снова опускаем случай действия внешних сил л а частицы жидкости. Кроме приведённых соотношений, мы имеем ещё следующие:
Умножая выражения (54) соответственно на н dt, v dt, w dt, складывая, деля на dt и пнтогрируя для всею объёма среды, находим:
где da есть элемент границ и б — кубическое расширение. Это выражение может быть написано ещё в таком виде:
Тройной интеграл, входящий в это выражение, представляет сумму изменений энергии во всех элементах пространства, занятого средой. Действительно, первый член подинтегральной функции тройного интеграла представляет изменение живой силы со временем в одном и том же элементе объёма среды; второй же член той же подинтегральной функции представляет изменение работы давлений в одном и том же элементе, взятое с надлежащим знаком. Отсюда следует, что двойной интеграл выражения (58) представляет количество энергии, входящее в среду через её границы. Следовательно, выражение (58) представляет закон сохранения энергии для всей жидкой среды, и потому оно тождественно с уравнением (7). Двойной интеграл уравнения (58) должен быть тождествен с двойным интегралом уравнения (7) и, следовательно, должен преобразовываться в тройной интеграл, тождественный со вторым тройным интегралом выражения (6). Действительно, двойной интеграл выраже-
ния (58) может быть преобразован в тройной интеграл следующего вида:
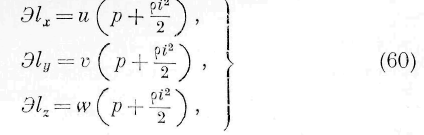
Подинтегральная функция, входящая в это выражение, представляет уже количество энергии, проникающей в единицу времени в один и тот же элемент объёма жидкости. Справедливость этого заключения может быть поверена непосредственно, преобразовывая под-интегральную функцию тройного интеграла выражения (58) при помощи приведённых выше уравнений гидродинамики. Итак, подинтегральная функция выражения (59) тождественна с подинтегралъной функцией второго тройного интеграла выражения (7) или со второй частью основного уравнения (I). Из этого тождества вытекают следующие соотношения между законами энергии и законами частичных движений жидких сред:
Из выражений (60) следует, означая через с скорость движения энергии, т. е.
т. е. количество движения энергии равно произведению скорости движения жидкости на сумму гидростатического давления и живой силы. Деля каждое из уравнении (60) на (63), находим:
иными словами, направление движения энергии одинаково с направлением движения жидкости. Отсюда вытекает заключение, что внутри жидких тел невозможны такие формы движений, при которых направление движения частиц не совпадает с направлением движения энергии. Так, например, в жидких телах невозможно распространение воли с колебаниями поперечными. Выражение (63) существует и на поверхности жидкости; подобно выражению (53) оно даёт возможность вычислять скорости частиц у поверхности жидкости по давлению на этой поверхности и количеству энергии, входящей в тело.
§ 9. Случай несжимаемой жидкости. Для жидкости несжимаемой величина энергии равна живой силе движения частиц жидкости. Следовательно,
Последнее выражение показывает нам, во-первых, что для всех форм движения, возможных внутри нссжимае-

Скорость i равна скорости с только при p = 0. Выражение (69) даёт возможность определить минимум скорости движения энергии под данным давлением в несжимаемой жидкости. Этот минимум будет:
Означая через n число атмосфер, иод давлением которых находится частица жидкости, через д— плотность жидкости относительно воды при 4° С, принимая, далее, за единицу длины метр п за единицу времени секунду, мы находим:
где P есть вес кубического метра воды при 4°С, т. е. 1000 кг, и g — ускорение тяжести, равное приблизительно 10 м. Вставляя величины (72) в (71), находим:
Следовательно, для воды наименьшая возможная скорость движения энергии в частях жидкости, находящихся под давлением одной атмосферы, есть 28,752 м. Формула (73) показывает, что для жидкостей различной плотности минимум скорости энергии понижается с jbc-личением плотности; для одной п тон же жидкости минимум скорости движения энергии повышается с увеличением давления.
подставляя эту величину в уравнения гидродинамики (54), мы приведём их к следующему виду:
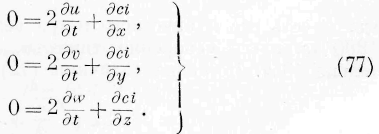
Величины I, т) и С представляют вращения элемента объёма около осей х, у, z. Если в жидкости вращательные движения не существуют, то выражения (75) принимают вид:
т. е. отрицательная частная производная от потенциала скоростей по времени равна половине произведения скорости движения энергии па скорость движения частиц. Функция времени, которая должна быть прибавлена к выражению (78), подразумевается под знаком “р.
§ 10. Уравнения движения энергии в жидкостях с трением. Более общие дифференциальные законы движения жидкостей получаются, как известно, принимая существование давлений, направленных косвенно к плоскому элементу внутри жидкости, стороны коего параллельны плоскостям координат; мы означим слагающие косвенных давлений, испытываемых тремя сторонами элемента, ближайшими к началу координат, через р хх , p vll , p. pxij, Риг, р, х ‘, значение употреблённых здесь индексов известно. Мы имеем следующие дифференциальные уравнения с частными производными, предполагая, что внешние силы не действуют на элементы жидкости:
Кроме этих выражений, для трущихся жидкостей остаются в силе соотношения (55).
Закон сохранения энергии для всей массы жидкости будет:
Простой интеграл, входящий в это выражение, представляет изменение энергии всей жидкой массы, отнесённое к единице времени; двойной же интеграл, распространённый на элементы поверхности жидкой массы, представляет количество энергии, входящей в жидкость извне. Этот двойной интеграл может быть представлен в форме тронного интеграла следующего вида:
Подиитегральпая функция этого выражения представляет количество энергии, проникающее в один и тот же элемент объёма жидкости от смежных частей жидкости. Путём заключений, сходных с употреблёнными в предыдущих параграфах, мы убедимся, что эта подинте-гральная функция тождественна со второй частью
основного уравнения (I). Математическое выражение этого тождества представится следующими соотношениями :
Законы движения энергии представляют в данном случае средину между законами, имеющими место для тела упругого и для тела жидкого.
III. ПЕРЕХОД ОТ ЗАКОНОВ ДВИЖЕНИЯ ЭНЕРГИИ
К ЧАСТИЧНЫМ ДВИЖЕНИЯМ, ОБУСЛОВЛИВАЮЩИМ
В предыдущем отделе было найдено выражение закона сохранения энергии для бесконечно малого элемента непрерывной среды, частицы которой находятся в движении. Затем для ряда различных сред были найдены соотношения, связывающие законы движения и распределения энергии в среде с законами сё частичных движений. Результаты, нами найденные, с одной стороны, служили оправданием той формы элементарного закона сохранения энергии, которая была положена в основание исследования, с другой — дали метод отыскания связи между законами движения и распределения энергии в какой-нибудь среде и её частичными движениями. В настоящем отделе я постараюсь, основываясь на добытых результатах, наметить путь, которому должно следовать теоретическое изыскание, ставящее себе задачей объяснение явлений природы частичными движениями.
При поверхностном взгляде все явления природы могут быть разделены на две группы, как будто
стоящие особняком друг от друга: группа первая — явления, наблюдаемые в средах непрерывных; группа вторая — явления, наблюдаемые над телами разрозненными, не находящимися в непосредственном соприкосновении друг с другом. К первой группе относятся явления, требующие для своего существования какой-нибудь среды, как, например, эфир для световых явлений, твёрдое тело, проводящее теплоту, для явлений теплопроводности, проводник для явлений гальванического тока, проводник или изолятор для электростатических явлений и пр. Ко второй группе относятся явления, обусловливаемые так называемым взаимодействием различных деятелей природы на конечных расстояниях. Из этих двух групп вторая будет нами рассмотрена подробнее, чем первая.
§11. Способ сведения явлений первой группы на частичные движения сред. Из предыдущего отдела вытекает следующий весьма простой метод объяснения явления природы, происходящего в какой-нибудь среде, частичными движениями этой среды. Представим дифференциальные уравнения с частными производными, управляющие движениями частиц внутри среды, в следующем виде:
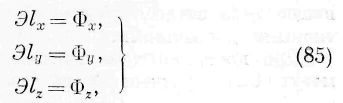
Здесь функция b зависит только от ускорении частиц, скоростей, перемещений и их производных по координатам. При помощи этих уравнений мы найдём связь между законами движения и распределения энергии в среде и законами частичных движений—связь, которая представится соотношениями следующего вида:
где функции Ф зависят от скоростей, перемещений и их производных по координатам. Если нам известны путём опыта величины Э, 1 Х , 1 а , 1„ для каждой точки среды, то весь вопрос приводится к чисто математической задаче: требуется обинтегрировать уравнения (84), причём найденные интегралы должны удовлетворять условиям (85), в которых левые части даны на—перёд. Таким образом, в этой форме успех решения задачи обусловливается силами одного математического анализа.
Приведение задачи к указанной простой форме представляет, однако, немаловажные затруднения, которые могут быть устранены отчасти путём опыта и анализа его результатов. Возможность приведения задачи к указанной простой форме предполагает знание среды, в которой происходит явление, и знание законов распределения и движения энергии в данном явлении.
Определение среды, служащей местом явлению, представляет большие трудности. Все тела природы предполагаются проникнутыми световым эфиром, и u большинстве случаев нельзя сказать утвердительно — весомые частицы тела служат местом явлению, или окружающий их эфир, или, наконец, то и другое вместе. Орудия опытного исследования дают возможность определять характер явления только за известные, весьма малые, но не бесконечно малые промежутки времени. Поэтому закон энергии, находимый нами путём опыта, представляет некоторый интегральный закон. Означая через т наименьший промежуток времени, за который орудия опытного исследования могут дать отчёт о происходящем явлении, означая через д величину энергии, существующую в каждой точке среды в каждый момент времени, мы находим из опытных данных величину энергии Э’:
В формулы (85) должна быть подставлена величина Э, по не величина Э’, даваемая опытом. Поэтому является задача определения величины Э по Э’ из соотношения (86).
Эта задача может быть, однако, обойдена или облегчена в некоторых специальных случаях:
а) явление может быть приведено в такую форму, для которой энергия изменяется только в пространстве, но не во времени; в этом случае
Это соотношение имеет место в явлениях интерференции. Так как в этом случае величина Э известна с достоверностью, то первый успех объяснения явления путём частичных движений предстоит явлениям, для которых возможна интерференция производящих их движений. В этом заключается одна из причин успешной разработки теории световых явлений;
б) если закон энергии, найденный из опыта, носит характер настолько общий, что может быть принят справедливым для моментов времени, бесконечно близких друг к другу; примером такого закона может служить закон обмена тепла между двумя бесконечно близкими частицами тел, служащий основанием теории теплопроводности. Здесь величина Э’ не может быть, однако, приравнена величине Э.
В последнем случае, так же как и в остальных, мы должны решить соотношения (86) по отношению к Э. Эта задача облегчается тем условием, что мы наблюдаем явления, энергия коих вместе со временем приближается в каждой точке среды к некоторому пределу. В данном случае мы можем представить величину Э следующим рядом:
§ 12. Определение законов движения и распределения энергии в явлениях взаимодействия на расстояниях конечных. Я постараюсь теперь решить часть вопросов, связанных с объяснением явлений второй группы, т. е. взаимодействий на расстояниях конечных, из частичных движений. Эти движения должны происходить, в общем случае, как во взаимодействующих телах, так и в среде, в которую последние погружены. Эту среду я буду называть промежуточной средой. Определению формы частичных движений должно предшествовать, по указанному выше методу, определение законов энергии в промежуточной среде, определение закона обмена энергии между телами и промежуточной средой и, наконец, определение законов энергии в самих телах. Я буду разделять энергию тел на две части: на энергию бесконечно малых частичных движений этих тел, или внутреннюю энергию тел, и на энергию, представляемую живой силой их явных движений, приписываемых обыкновенно взаимодействию ^ на расстояниях конечных. ‘ Энергия промежуточной среды состоит, вообще, из двух частей, значение которых определяется следующими соображениями.
Представим себе, что взаимодействующие тела удерживались в покое какими-нибудь внешними силами. По истечении бесконечно малого времени после устранения этих сил тела приобретут скорости, и каждое из них будет обладать некоторым количеством живой силы. Приобретение последней может совершиться только на счёт энергии, заключавшейся, до момента устранения внешних сил, в движениях промежуточной среды. Это заключение справедливо и в тех случаях, когда приращение живой силы явного движения тел сопровождается уменьшением их внутренней энергии. В самом деле, признавши раз необходимость участия
промежуточной среды в явлениях взаимодействия на расстояниях конечных, мы отвергали бы, в сущности, ату гипотезу, если бы допустили, что приращение живой силы явных движений тел совершается непосредственно на счёт убыли внутренней энергии тел, “без участия среды. Допуская же это участие, мы на-„ходим для него одно только возможное толкование: после устранения внешних сил первый акт явления заключается в приращении живой силы явных движений тел на счёт убыли энергии частичных движений промежуточной среды, и второй акт явления, непосредственно следующим за первым, —пополнение убыли энергии промежуточной среды из внутренней энергии тел. Означим через j] IQ количество энергии, сообщаемое всем взаимодействующим телам в бесконечно малый элемент времени. Через 2 »W обозначим сумму изменений внутренних энергий тел за тот же промежуток времени. Через означим изменение энергии -.промежуточной среды. Если взаимодействующие тела удерживаются в покое внешними силами или удалены друг от друга на громадные расстояния, то мы имеем соотношение:
Нам известно, что в том случае, когда частичные движения тел достигли некоторого стационарного состояния, т. е. когда наблюдаемые нами явления в телах .стационарны, величина 5# = 0 (например, в случае стационарного гальванического тока работа химических сил в элементах» пени идёт исключительно на развитие тепла в цепи). Следовательно,
Этот закон, как показывает опыт, имеет место во всё время, в течение коего явления остаются стационарны; сравнивая его с законом (90), мы видим, что некоторое количество энергии должно было быть отдано про-, межуточной среде, прежде чем явление достигло .стационарного состояния.
Означим через 2 z приращение живой силы явных движений взаимодействующих тел. Рассматривая такие тела, для взаимодействия коих существует потенциал, который я обозначу через II, мы имеем в первый момент взаимодействия:
Для последующего момента величина II может видоизмениться не только вследствие изменения относительного расположения тел, но и вследствие изменения частичных движений самих тел. Соображения, приведённые нами выше, показывают, что изменение энергии промежуточной среды равняется величине—811. Опыт показывает, с другой стороны, что существует целый класс явлений, в которых приращение живой силы явных движений взаимодействующих тел связано с уменьшением внутренней энергии самих тел. Для этих явлений за первым актом, характеризующимся соотношением (92), следует второй, характеризующийся соотношением
Пополнение убыли энергии в промежуточной среде из внутренней энергии тел, связанное, как показывает опыт, с временным нарушением стационарности явления в телах, может иметь основание в том, что стационарность этих явлений обусловливается существованием определённого количества энергии в среде. Мы не имеем, однако, никаких данных для того, чтобы утверждать, тождественна ли форма движений, приобретаемых средой при пополнении убылей её энергии вследствие постепенного изменения живой силы явных движений взаимодействующих тел, с той формой движения, которая вызывается в среде при сообщении ей энергии телами до того момента, когда происходящие в лих явления достигнут состояния стационарного и когда они удалены друг от друга на бесконечно большие расстояния,
у Я займусь подробным рассмотрением только некоторых вопросов из указанных мною выше и именно тех, о которых можно рассуждать с наибольшей достоверностью. С наибольшей ясностью выступает для нас значение величин П и 2 z ‘ 2 и их взаимные превращения. Если мы вычисляем для каждого относительного положения тел величину П, оставляя без внимания временную нестационарность явления, могущую происходить в телах во время их перемещения, то. соотношение (92) остаётся справедливым при перемещении тел из всякого относительного их положения, если вначале тела удерживались в нём в покое. Отсюда мы заключаем, что энергия среды, способная в каждый отдельный момент времени превращаться в живую силу явных движений тел, а также энергия среды, в которую способна превращаться в каждый момент времени живая сила движений тел, представляется величиною
(см. также мою статью: “Ein Theorem ьber die Wechselwirkungen” и пр., § 12, Zeitschrift f. Mathematik und Physik, XIX, 2, 1874). Наша задача будет заключаться в отыскании закона распределения энергии внутри промежуточной среды, при котором сумма энергий всех элементов пространства, занятого средою , представляется величиною (94). Затем мы должны будем определять закон движения энергии в среде.
Законы, которые могут быть нами при этом найдены, по причинам, изложенным в § 11, будут некоторые интегральные законы; тем не менее, основной закон энергии (I) остаётся справедливым, потому что при его выводе не было сделано никаких условий для того промежутка времени, за который определяются величины энергии ц её скорости. Означая, следовательно, через Э среднюю величитту энергии за некоторый весьма малый промежуток времени, через l x , l , | ? —средние скорости энергии за тот же самый весьма
§ 13. Превращение величины Il+const. в тройной интеграл, распространённый на всю промежуточную среду. Величина П в том виде, как она входит в уравнение живых сил в явлениях взаимодействия на расстояниях конечных, зависит от относительного положения взаимодействующих тел и от их формы. По отношению к промежуточной среде эти тела определяют положение и форму границ промежуточной среды. Если я означу через Э количество энергии в элементе промежуточной среды, то эта последняя должна быть найдена из условия:
где тройной интеграл распространяется на всю промежуточную среду.
Мы решим соотношение (97) для специальных случаев, которыми исчерпываются все известные нам роды взаимодействий на конечных расстояниях.
Случай первый. Взаимодействие весомых, электрических и магнитных масс. Для взаимодействия этих масс потенциал V во всём внешнем пространстве, не заключающем действующих масс, т. е. для всех точек промежуточной среды, удовлетворяет уравнению Лапласа. Мы решим вопрос для взаимодействия двух масс m lt m. 2 , которые воображаем себе сосредоточенными в двух точках а, Ь, находящихся на расстоянии R друг от друга. Означая через V\ ъ потенциал обеих масс друг на друга, мы имеем:
Положительный знак должен оыть взят в случае отталкивания, а отрицательный — в случае притяжения. Означим через V lt V% потенциалы масс т, и т 2 в какой-нибудь точке промежуточной среды. Мы имеем по теореме Грина:
где знак Д 2 представляет дифференциальный параметр второго порядка, тройной интеграл распространяется на всю промежуточную среду, т. е. на пространство, ограниченное с одной стороны поверхностью бесконечно большой сферы, с другой — двумя бесконечно малыми сферами, окружающими точки а и Ь. Двойные интегралы распространяются на поверхности этих сфер, и dn lt drin представляют элементы нормалей к этим сферам, направленные внутрь промежуточной среды. Первый двойной интеграл, входящий во вторую часть предыдущего выражения, будет
Второй же двойной интеграл будет величиной бесконечно малой. Следовательно, по (98)
Подинтегральная функция этого выражения может быть весьма просто преобразована. Собирая члены, содержащие производные по х, имеем:
Подобное преобразование может быть произведено и над другими членами. Мы получаем таким образом:
Ближайшей нашей задачей будет определение постоянной, которая должна быть прибавлена к величине 11, чтобы иметь всю энергию среды. Эта постоянная представляет количество энергии, которая была бы заключена в среде, когда в последней было бы погружено только одно из взаимодействующих тел. Величину этой энергии легко найти из выражения (106), замечая, что она должна быть вдвое меньше той энергии, которая вычислится по формуле (106) для того случая, когда массы m l и т 2 , равные друг другу и тождественные, совпадут. В этом случае мы должны положить F 1 = F 2 , и из (106) находим, означая через 11„ и П 5 части энергии среды, обусловливаемые в ней каждой массой т^
и пг 2 в отдельности:
Величины П а и >\ ь представляют количества энергии, которыми обладала бы среда, если бы в ней находилась или только масса т ъ или только масса т 2 .
Полная энергия среды есть, следовательно, по (97):
Подставляя сюда найденные выше величины II, \\ а , П ь , находим:
Означая через p параметр поверхностей равного потенциала в среде, имеем: V 2 + Vi = [j’, следовательно,
Этому выражению мы можем дать ещё иной вид. Означим через h дифференциальный параметр первого порядка от параметра р, т. е.
Величина h представляет силу, с которой действовали бы массы nii и те, на массу, равную единице и помещённую в какой-нибудь точке промежуточной среды. Замечая, что по условию во всех точках промежуточной среды функции V i, V% удовлетворяют уравнению Лапласа, мы можем дать выражению (111) следующую форму:
т. е. количество энергии в каждой точке промежуточной среды пропорционально квадрату силы, с которой массы т 1 и т 2 действовали бы на массу, равную единице, помещённую в этой точке промежуточной среды.
В том случае, когда массы притягиваются, мы должны брать потенциалы V 1 и 7 2 с противными знаками; в случае же, когда они отталкиваются, — со знаками одинаковыми. Это знакоположение вытекает из соотношения (99). Отсюда следует, что энергия среды в случае притягивающихся масс будет наибольшей, когда эти массы находятся в бесконечном удалении друг от друга. По мере сближения масс энергия среды превращается постепенно в живую силу их явного движения. В случае масс, отталкивающих друг друга, их бесконечному удалению соответствует наименьшая величина энергии среды.
Выражения (111) и (113) имеют место не только для действующих масс, сосредоточенных в двух точках, но и для произвольного количества произвольно расположенных масс. Эти же выражения имеют место и для взаимодействия замкнутого тока на магнитный полюс, ибо, заменяя первый магнитными поверхностями, мы приходим к случаю только что разобранному.
§ 14. Закон энергии в случае взаимодействия двух замкнутых токов друг на друга. Этот случай приводится к предыдущему, заменяя взаимодействующие замкнутые токи магнитными поверхностями и разумея под величиной V потенциал магнитных масс, лежащих па одной из этих поверхностей, на северный полюс с количеством магнетизма, равным единице, лежащий в какой-нибудь точке среды. Вопрос этот может быть решён ещё иначе. Потенциал двух замкнутых токов друг на друга в том случае, когда напряжения токов измеряются электромагнитными единицами, есть
Здесь ds l и ds 2 представляют элементы токов а и Ь, а г — расстояние между ними. Этот двойной интеграл может быть преобразован в тройной, распространённый на всю промежуточную среду, при помощи следующих соображений, аналогичных употреблённым выше. Каждый из замкнутых токов заменяем двумя бесконечно близкими поверхностями, обложенными противоположными магнитными жидкостями. Означим через fj и F 2 потенциалы замкнутых токов на магнитный полюс с северным магнетизмом, количество коего равно единице и который лежит в какой-нибудь точке промежуточной среды. Во всей части среды, ограниченной с одной стороны поверхностью бесконечно большой сферы, с другой — магнитными поверхностями, заменяющими токи, потенциалы F, и F 2 удовлетворяют уравнению Лапласа. Для указанной части среды имеет место соотношение (100). Двойные интегралы, в него входящие, распространяются на элементы магнитных поверхностей. Эти двойные интегралы равны 4-П (см. статью Кирхгофа “Ьber die Krдfte, welche zwei unendlich dьnne, starre Ringe in einer Flьssigkeit scheinbar auf einander ausьben kцnnen”, Grelle, 1870). Отыскивая методом предыдущего параграфа постоянное, которое должно быть прибавлено к величине П, чтобы получить выражение полной энергии среды, мы найдём, как легко видеть, снова:
где ;, есть параметр поверхностей равного потенциала в точках промежуточной среды с указанными выше границами, причём под потенциалом разумеется потенциал обоих токов на северный магнитный полюс с количеством магнетизма, равным единице. Величина k есть дифференциальный параметр первого порядка от пара-
метра \j. Относительно величины Э мы вправе сделать те же заключения, как и в предыдущем параграфе.
§ 15. Исследование законов энергии в случае, когда для взаимодействия тел существует потенциал. Для этого случая выражение величины энергии найдено в предыдущих параграфах. Оно есть:
где [> есть параметр поверхностей равного потенциала, проведённых мысленно в промежуточной среде. Здесь потенциалом может быть функция, совершенно отличная от потенциала самих взаимодействующих тел друг на друга. Например, в случае замкнутых токов величина p представляет потенциал этих токов на магнитные полюсы, которыми мы должны мысленно наполнить среду.
Для рассмотренных нами явлений имеет место соотношение
Вообразим себе в промежуточной среде тройную систему ортогональных поверхностей, коих параметры означим через р,:’!> i’2- Мы имеем (Lame, Lecon sur los coordon-nees curviiignes):
где h, h lt h 2 суть дифференциальные параметры первого порядка от параметров p, pj, р 2 . Вследствие соотношения (119) имеем:
Умножая элемент объёма на величину энергии Э, мы найдём количество энергии, заключённое в элементе объёма. По (118) и (122) оно будет:
Сечение поверхностей pj и р 2 представляет кривую линию, носящую название силовой линии. Вообразим себе па одной из поверхностей p бесконечно малый прямоугольник, две стороны коего составлены из элементов ds 1 и ds 2 нормалей к поверхностям р г , р 2 . Здесь
Проведём через периферию этого четырёхугольника все возможные силовые линии. Они выделят из среды бесконечно тонкий объём криволинейного вида, который я назову (по аналогии с одним термином, введённым Гельмгольцем) силовою нитью. Изменяя один параметр р, оставляя постоянными р ъ р 2 , мы двигаемся вдоль силовой нити, площадь сечения коей в каждой точке равна dsi, ds z . Прилагая к выражению (123) соотношение (121), мы видим, что количество энергии, заключённое в каждом элементе объёма, остаётся неизменным вдоль силовой нити. Но выражение (123) может быть представлено в виде:
Отсюда заключаем, что вдоль силовой нити плотность энергии изменяется обратно пропорционально сечению нити.
Обратимся теперь к отысканию скоростей движения энергии в промежуточной среде.
Изменение энергии со временем в одном и том же элементе объёма будет по (118):
Время может входить в величину /г 2 только через величины, определяющие положения взаимодействующих тел. Если взаимодействующие тела удерживаются в покое, мы имеем:
а следовательно, количество энергии во всей среде остаётся неизменным.

Вообразим себе в промежуточной среде одну только массу /hi, сосредоточенную в одной точке а. Пусть эта точка двинулась в направлении l вследствие сообщённого ей внешнего толчка. Найдём изменение энергии среды в рассматриваемом случае. По сделанному замечанию имеем:
В данном случае поверхности равного потенциала суть концентрические сферы; силовые линии совпадают с радиусами этих сфер. Означая через г — радиус одной из сфер, имеем:
Но на одной и той же сфере для одного и того же
( изменяется от U до -^ ) существуют, очевидно, две
точки, для которых —у — g— -щ- имеет величины рав
ные, но противоположные по знаку. На такие парные вели
чины, уничтожающие друг друга, разложится всё выра
жение (130). Следовательно, оно равно нулю.
Отсюда заключаем, что при движении массы т г , сосредоточенной в одной точке, когда пет других масс, энергия среды остаётся неизменной, т. е. масса т г не отдает живой силы своего движения среде и не приобретает. Неизменность энергии среды при движении массы 7П] в указанных условиях есть только иное выражение закона инерции. Мы получим, очевидно, тот же результат и в случае произвольного числа масс, обладающих движением, при котором их относительные положения не изменяются. Рассмотрим теперь случай, когда взаимодействующие тела описывают произвольные пути. Мы находим по выражению (117’l:
Это выражение представляет элементарный закон сохранения энергии и должно быть тождественно с соотношением (95). Условия тождества будут:
с , l u , L, так как величина Э известна. Руководствуясь соображениями, изложенными в § 11, соотношения (133) должны быть поставлены исходными пунктами при изыскании форм частичных движений промежуточных сред. Я представлю выражения (133) в несколько ином виде. В правых частях выражений (133) производная
ay -. от -дy- берется постольку, поскольку время t входит
в функцию p через величины, определяющие положение взаимодействующих тел в пространстве. В этом смысле величина
представляет скорость по направлению ds, с которой перемещается точка пересечения поверхностей p, pj, p 2 в пространстве при изменении относительного положения взаимодействующих тел. Эту скорость не должно смешивать со скоростью энергий в направлении нормали ds к поверхности p в той же точке. Означим через E
величину hs или
; выражения (133) примут вид:
Означим через s, s 1 , s 2 скорости движения энергии по направлениям элементов нормалей ds, ds lt ds z к поверхностям p, р 3 , р 2 .
Соотношение (95), представленное в ортогональных координатах, будет:
Выражение (132), преобразованное в ортогональные коор-
динаты, будет, заменяя -г— через А:
Вторая часть получается из известного преобразования в ортогональные координаты дифференциального параметра второго порядка.
§ 16. Закон энергии для взаимодействия двух элементов тока. При выводе закона энергии в данном случае я употреблю метод, обратный употреблённому в предыдущих параграфах. Полученный результат будет служить оправданием нашего способа. Я предположу, что и в данном случае мы имеем соотношение (118), т. о.
Здесь с постоянное, h есть сила, с которой действуют два элемента тока ds 1 и ds 2 , центры коих лежат в точках а и 5, на северный магнитный полюс с количеством магнетизма, равным единице, лежащий в точке промежуточной среды, для которой берётся величина Э. Означая через a lt Яj, yi, а а> р2 и ?2 углы элементов ds l и ds z с осями координат, величины слагающих сил, с которыми эти элементы действуют на магнитный полюс, помещённый в какой-нибудь точке среды, будут:
Величины z’j, г.” суть напряжения токов, протекающих через элементы, в электромагнитных единицах; х 1 ,у г , z b х-и У ч’ z z — координаты точек а и 6, с которыми совпадают центры элементов ds lt й.? 2 ; х, у, z — координаты какой-нибудь точки среды, г 1 и г 2 — её расстояния от точек а и Ъ.
Составляя по выражениям (139) и (140) величину /г 2 , умножая её па элемент объёма и интегрируя на всю промежуточную среду, т. е. на всё пространство, лежащее между бесконечно отдалённой сферой и бесконечно малыми сферами, окружающими элементы ds^ и c ?s 2 , мы должны получить, если наше предположение справедливо, величину энергии среды, т. е. 11 + const., где Л есть потенциал элементов ds-^ и ds 2 друг на друга.
Для простоты примем за ось х линию, соединяющую оба элемента ds lr ds 2 , и середину этой линии — за начало
координат. Тогда у г = Zi = г/ 2 «— z z = 0, и пусть х^= — ^ ,
Легко видеть, что члены, входящие в тройной интеграл, представляющий величину ll-f-const., и содержащие одну из координат в нечётной степени, будут попарно уничтожаться. Нам остаётся поэтому рассмотреть выражение
Величина К поставлена на место тех членов, которые содержат координаты одного только из элементов ds lt ds z и, следовательно, по интеграции дадут величину постоянную. Форма этих членов для нас тте существенна, так как оправдание нашего способа мы можем найти только в результате, который получится для величины 1J, представляющей часть энергии среды, зависящую от положения обоих элементов.
Я замечу, что сумма членов, стоящая между скобками в выражении (141), всегда конечна. В самом деле, она всегда меньше суммы входящих в неё тройных интегралов, так как стоящие перед ними факторы меньше единицы. Сумма же этих тройных интегралов есть конечная величина 8
Л, где II имеет то же значение, как в § 13 формулы (98), (102).
Вследствие полной симметрии около оси X мы имеем:
Означая через (а$ц ds 2 ) угол между обоими элементами dsi, ds 2 , мы находим, рассматривая только члены, зависящие от относительного положения элементов ds t и ds 9 , т. с. вычитая из (141) величину
Чтобы найти окончательное выражение для II, мы должны определить входящие сюда тройные интегралы. С этой целью вместо прямоугольных координат введём три системы ортогональных поверхностей (В е 11 i, Teorica delle forze ehe agiscono secondo la legge di Newton, Pisa, 1865):
1) меридиональные плоскости, проходящие через ‘ось X; параметр p этих плоскостей изменяется от 0 до 2;
2) поверхности вращения, дающие в пересечении с меридиональными плоскостями круги, проходящие через точки а и 6. Уравнение этих кругов будет:
Здесь p = I/ г/ 2 + z 2 , и v есть параметр кругов, изменяющийся от 0 до тс;
3) поверхности вращения, дающие в меридиональных плоскостях круги, проходящие через две мнимые точки, лежащие на оси X, на расстояниях от начала координат, равных
Уравнение этих кругов будет:
Здесь и есть параметр этих кругов, изменяющийся от—со до+оо; th, sh, ch суть гиперболические тангенсы, синусы ц косинусы.
Уравнения для перехода от прямоугольных координат х, у, z к введённым суть следующие:
Кроме того, элемент объёма будет:
Выражая подпнтегральные функции тройных интегралов выражения (144) в криволинейных координата?;, мы видим, что числители подинтегральных функций будут содержать постоянный фактор R 5 , а знаменатели — R s , где R есть расстояние точек а и Ъ. Следовательно, за знаки тройных интегралов может быть вынесен по-
стоянный фактор -jt . Под знаками же интегралов будут стоять выражения, зависящие исключительно от и, v, Ф. Тройные интегралы не будут, следовательно, зависеть от положения элементов, а только от пределов. Означая через X и v- две постоянные и замечая, что
Это выражение для потенциала двух элементов тока друг на друга отличается от потенциала Гельмгольца только постоянными факторами, что и служит оправданием справедливости предположения ( 138).
§ 17. Общий метод определения законов взаимодействий на расстояниях конечных. Приведённые выше исследования потенциальной энергии двух взаимодействующих тел, в предположении существования промежуточной среды, дают нам право считать следующую теорему оправданной для известных нам взаимодействий:
если известен закон взаимодействия на расстояниях конечных между однородными деятелями природы к, а г с третьим, однородным или разнородным с ними деятелем Я, то выражение потенциальной, энергии для взаимодействия деятелей а и a t друг на друга будет:
где а есть постоянный фактор и X a $X ai $ и пр. представляют слагающие сил, с которыми деятели а и а, 1 действуют па деятелей Я : , которыми мысленно непрерывно наполняется пространство, окружающее деятелей о: и а х . Тройной интеграл распространяется па всё пространство, лежащее между поверхностью
бесконечно большой сферы и двумя другими поверхностями, бесконечно близко облегающими деятелей и и а, 1 .
Если деятели я и я х суть весомые, магнитные или электрические массы, то деятель Я есть соответственно весомая масса, магнитная масса или элемент тока и, наконец, электрическая масса.
Если деятели а и а п суть замкнутые гальванические токи или элементы токов, то 8 суть магнитные полюсы или элементы токов, таким образом расположенных в пространстве, что сами по себе они не вызывают движения ни одного из деятелей а, а г (последнее оправдано для частных случаев в упомянутой мною выше статье “Ein Theorem и пр.”). Справедливость этих заключений вытекает, как легко видеть, из предыдущих параграфов.
Хотя теорема, здесь приведённая, доказана только для известных нам взаимодействий на расстояниях конечных, тем не менее я считаю возможным видеть в ней вырая^ение неизвестного нам физического соотношения или сродства между деятелями природы, действующими друг на друга на расстояниях конечных.
Из приведённой теоремы вытекает следующее заключение: однородные функции координат, представляющие силы, с которыми деятели природы действуют друг на друга на расстояниях конечных, должны быть второй степени.
Пусть силы, с которыми однородные деятели a, Xj Действуют на Я, представляются однородными функциями ти-й степени от координат, причём коэффициенты, входящие в функцию, .могут зависеть от различных условий, определяемых самим характером деятелей. В данном случае произведения Х^Ха.^ и пр. будут однородными функциями 2т-й степени. Выражая прямоугольные координаты в криволинейных, употреблённых уже нами в § 16, мы вынесем за знак тройного интеграла выражения (155) величину R 2m + 3 , где R есть расстояние между деятелями а и а ь которые предполагаются занимающими бесконечно малые объёмы. Означая через M некоторое постоянное, мы получим,
Мы находим отсюда выражение силы:
Если деятель Я однороден с а и а-,, то степень т однородных функций, представляющих силы, с которыми а и а 1 действует на Я, должна быть одинакова со степенью расстояния R в предыдущем выражении, представляющем силу, с которой а и а г действуют друг на друга, т. е.
чем и оправдывается наша теорема для взаимодействия деятелей однородных.
Если а и ”л попрежнему суть деятели однородные, a Я — с ними разнородный деятель, то, по только что доказанному, степень величины R в выражении (153) должна равняться —2, т. е.
откуда степень т однородных функций, представляющих силы, с которыми взаимодействуют разнородные деятели, есть
чем и доказывается наше положение для случая взаимодействия разнородных деятелей. Заметим, что для данного случая положение доказано независимо от направления силы взаимодействия разнородных деятелей.
http://osh9.narod.ru/gl/um/dv.htm
http://www.bourabai.ru/umov/motion.htm