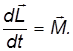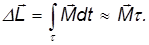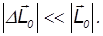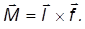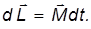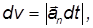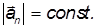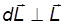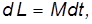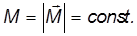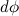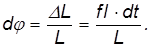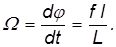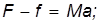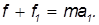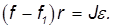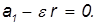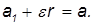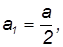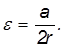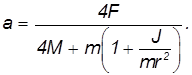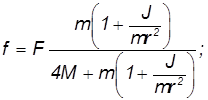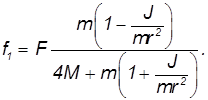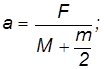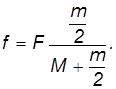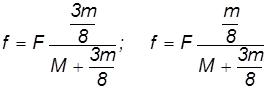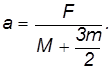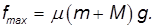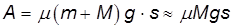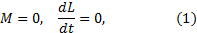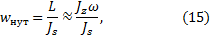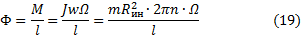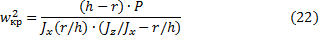Уравнения движения эйлера для свободного гироскопа

О допущениях в приближенной теории гироскопов

Приближенная теория гироскопа

• В этой технике используется гироскоп с соответствующей угловой скоростью 2000 5000 с 1 (20 000 50 000 об мин). В современных технологиях гироскопы очень широко используются. Явление гироскопа проявляется во всех видах движений тела, когда тело совершает сложные движения, включая вращательные движения в своей части. Предполагая, что гироскоп имеет свою собственную угловую скорость o вокруг оси симметрии или оси Oz гироскопа , давайте приблизительно рассмотрим базовое явление гироскопа быстро вращающегося гироскопа.

Основные положения приближенной теории При использовании гироскопа на различных устройствах важно знать движение его оси. Обычно соответствующее вращение вокруг оси задается, а угловая скорость соответствующего вращения поддерживается постоянной. Движение оси высокоскоростного вращающегося гироскопа можно определить по гироскопическому моменту движения, рассчитанному по неподвижной точке. Это связано с тем, что считается, что момент движения находится приблизительно вдоль оси гироскопа. В случае быстро вращающегося гироскопа угловая скорость прецессии мала по сравнению с угловой скоростью его собственного вращения, и изменение угла нутации, то есть угла между соответствующей осью вращения и осью прецессии, также маленький.

Эта энергия может быть использована для получения внешней работы путем приведения маятника обратно в его положение равновесия, в котором его скорость в самом начале была равна нулю. Людмила Фирмаль

Гироскопическая мгновенная угловая скорость = = 11 + 22 + 33 может быть получена из вращения вокруг неподвижной точки в первом приближении (рис. 143). WS , Где это Угловая скорость собственного вращения; S2 и z угловые скорости прецессии и нутации соответственно. Учитывая, что оси Ox, Oy и Oz являются главными осями инерции и Jx = Jy, проекция момента движения на эти оси KX = JX X, Ky = Jyay; Kz = Jz oz. Поскольку th почти вдоль соответствующей оси вращения Oz, cox 0 ko = y ki + k + k1 .

Следовательно, в случае высокоскоростного вращающегося гироскопа с большим собственным моментом движения момент движения К имеет абсолютную величину, равную моменту собственного движения гироскопа, Ось гироскопа, (49) Это приближение гироскопического момента движения является точным, когда ось гироскопа является его фиксированной осью вращения. Для решения этих задач о движении гироскопической оси мы можем использовать теорему Резала, которая может характеризовать движение конца вектора момента движения по известному главному моменту внешней силы. Чтобы сохранить основные характеристики гироскопа, необходимо учитывать угловую скорость прецессии w 2, игнорируя только угловую скорость нутации, но при расчете момента движения гироскопа, вы используете.

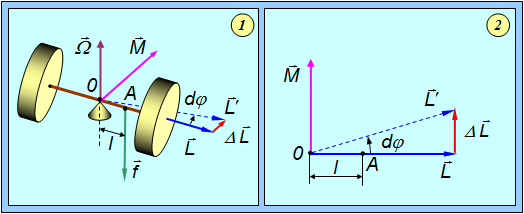
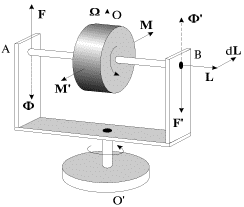
Характеристики движения оси гироскопа Рассмотрим характеристики движения гироскопической оси по сравнению с движением оси одного и того же объекта без его собственного вращения вокруг оси симметрии Oz. Поместите центр тяжести в обоих случаях в фиксированной точке O и игнорируйте трение в этой точке. Когда сила F прикладывается к телу, которое неподвижно перпендикулярно оси Oz в точке A с осью симметрии (рис. 144), тело начинает вращаться вокруг оси Ox, которая перпендикулярна оси силы и симметрии.

А начинает двигаться в направлении силового действия. Когда действие силы прекращается, если тело может быть зафиксировано в точке O, тело вращается дальше вокруг оси Ox с постоянной угловой скоростью из за инерции. Быстро вращающийся гироскоп ведет себя совершенно по разному при той же силе F, приложенной к точке A (рис. 145). Точка A не следует направлению силы F в соответствии с теорией приближения, но начинает двигаться в направлении, следующем из теоремы Лезала, векторный момент этой силы относительно неподвижной точки O параллелен оси Ox. Ось гироскопа вращается вокруг оси Oy.

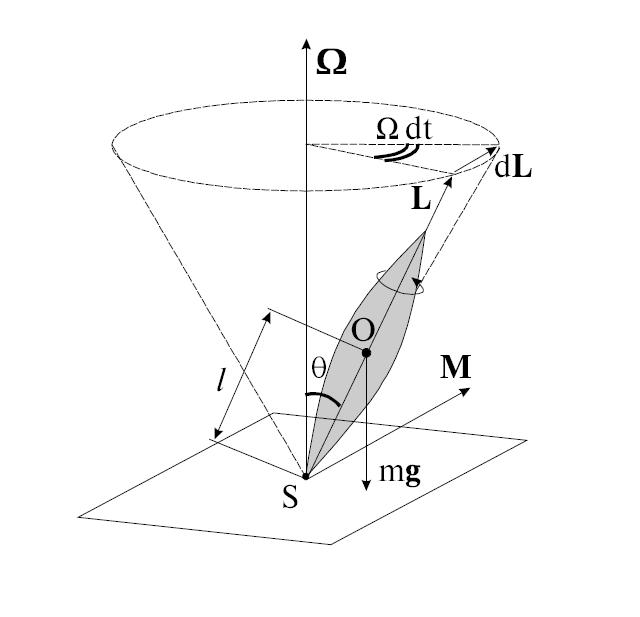
Фактически, гироскоп вращается только вокруг своей собственной оси Oz с угловой скоростью d1, поэтому даже до того, как сила приложена, момент движения A0 = r 1, направленный вдоль оси гироскопа, равен Был. Согласно теореме Резала, скорость в конце вектора Ko равна L (o vector sum Рис. 144 Рис. 145 Моменты для всех внешних силовых точек О, т.е. В этом случае L = MO (F) и момент MO (F) направлены вдоль оси Ox. Следовательно, в конце вектора Ko скорость точки при принятых допущениях теории приближений всех других точек оси гироскопа представляет собой вращение оси гироскопа Oz или прецессию гироскопа вокруг оси Oy. Параллельно Мо (F), соответствующему движению.

Ось гироскопа прецессирует под действием силы в направлении этого момента силы. Если момент силы в любой точке равен нулю, прецессия оси гироскопа также прекратится. Ось гироскопа не имеет инерции. В случае гироскопа сила F не важна, потому что прецессия определяется только моментом этой силы относительно фиксированной точки гироскопа. Если центр тяжести гироскопа не находится в фиксированной точке, момент силы тяжести должен учитываться в общем моменте силы. Сформулируем следующие правила прецессии: когда к гироскопу, который вращается вокруг оси, прикладывается внешняя сила, а момент силы генерируется относительно его неподвижной точки.

Часть начинает прецессию в направлении вектора момента этих сил. Получите приблизительное выражение для оценки угла прецессии , когда рассматривается действие силы F. За достаточно короткое время m конечная точка вектора Ko смещается вдоль дуги годографа pa. sB MBT = Af0 (F) t = Fit = Ftl. Угол поворота вокруг оси Oy zy mo (G) g M vOO Ko Ko J, Wi 0B = Ko = J ^ i. с того времени Из (50) угол мал, а момент движения гироскопа большой, а угол прямо пропорционален угловому моменту силы относительно неподвижной точки гироскопа. Уравнение (50) используется для оценки влияния кратковременных возмущающих сил на гироскоп, когда величина m очень мала.

Если собственный момент движения Jjio достаточно велик по сравнению с угловым моментом силы, ось гироскопа вряд ли будет отклоняться. Другими словами, это не зависит от краткосрочного воздействия силы или удара. Вал гироскопа устойчив к таким воздействиям. Удары вдоль оси гироскопа не приводят к значительному отклонению от первоначального направления. Гироскопический момент Как уже известно, когда внешняя сила действует на гироскоп и создает момент против этой фиксированной точки, гироскоп прецессирует с определенной угловой скоростью.

• Когда момент внешней силы становится равным нулю, прецессия гироскопа заканчивается. Следовательно, для создания гироскопической прецессии в соответствии с теорией приближения требуется момент внешней силы и наоборот. Сделайте прецессию гироскопа с угловой скоростью B2. Рассчитайте момент внешней силы, которая вызывает эту прецессию. Согласно теореме Резала, момент внешней силы к неподвижной точке гироскопа Lg = dKo d = SB. Вектор Ko, направленный вдоль оси гироскопа, вращается вокруг фиксированной точки с угловой скоростью прецессии ω2, поэтому скорость точки B, совпадающая с конечной точкой вектора Ko, является точкой на объекте при сферическом движении.

Рассчитывается по формуле, аналогичной векторной формуле Эйлера для скорости , yb = y2 x OV = a2 x Ko, Из OB = K () J2ii x. На момент внешней силы Lff, = = 22xо0 = (22×1). (51) Применение одного из результатов принципа Даламбера к гироскопу означает, что сумма векторного момента внешней силы и момента инерции точки гироскопа равна нулю. Рисунок 146 или, наконец, Где L момент всей силы инерции гироскопа относительно неподвижной точки. Этот момент L называется моментом гироскопа. С учетом счета (51) = = = , ( X cb2), = , (a X B2); Z. = JIcoIco2sin0, (52) Где 0 угол нутации, то есть угол между соответствующей осью вращения и осью прецессии.

Доказать, что в этом движении давление точки на эллипсоид изменяется пропорционально кубу расстояния от центра до касательной плоскости, проведенной к эллипсоиду в движущейся точке. Людмила Фирмаль

Момент гироскопа может быть выражен как момент пары гироскопов силы, которую гироскоп воздействует на тело, заставляя его прецессировать под действием момента внешней силы. В виде пары силовых гироскопов они передаются на эти тела через подшипники, где расположена ось гироскопа. Если эти тела или одно из них могут двигаться, пара сил гироскопа может вызвать это движение. Из (52) видно, что момент гироскопа равен нулю, если угловая скорость прецессии o2 равна нулю или если ось гироскопа параллельна оси прецессии. Поведение пары силовых гироскопов полностью определяется гироскопическим моментом этой пары, рассчитанным по уравнению (52).

Однако во многих случаях более желательно определять это действие по правилам Жуковского, основанным на той же формуле. Правило Жуковского. Когда к принудительному вращению гироскопа применяется принудительная прецессия, сила гироскопической пары проявляется так, что ось гироскопа параллельна оси прецессии, а направления этих осей совпадают. Позже оба поворота вокруг них будут в одном направлении Если есть объект, который препятствует движению гироскопа, так что гироскоп параллелен оси прецессии, гироскоп выдвигает фиксированную точку между этим телом и гироскопом. Когда гироскоп представляет собой ротор турбины, установленный на корабле и вращающийся вокруг вертикальной оси (рис. 146), давление в гироскопе измеряется подшипником турбины.

Сила этого давления N дается формулой M = = JIco1 (o2sin0 Где расстояние между подшипниками турбины. W2 угловая скорость корабля (угловая скорость прецессии); 0 кинематический угол (9 = 90 °, если рассматривается). Техническое использование гироскопа Например, рассмотрим измерение угловой скорости из множества прецессионных гироскопов, движение которых легко оценить по правилам Жуковского. Гироскоп, ось которого расположена в подшипнике на любом самолете, будет быстро вращаться вокруг этой оси. Если летательный аппарат вращается вокруг мгновенной оси с угловой скоростью 22, эта гироскопическая угловая скорость является угловой скоростью прецессии и может быть оценена по давлению гироскопа N.

Эта сила может быть измерена, например, по деформации пружины и снабжена одним из подшипников гироскопа (Рисунок 147). Если o2, уравнение (53) o2 = N (Jzco1 sinO). (54) На практике для измерения угловой скорости обычно используется 0 = 90 °. Если, например, на летательном аппарате реализовано устройство управления, которое создает угол поворота руля, угловая скорость o 2 равна нулю и летательный аппарат устойчив по угловой скорости относительно соответствующей оси. С помощью привода этот контроллер с рулем направления может управлять самолетом, создавая давление N, соответствующее опоре пружины, соответствующей угловой скорости прецессии.

Очевидно, что для полной стабилизации и управления самолетом существуют три гироскопа с взаимно перпендикулярными осями. Помимо стабилизации, рассматриваемой с помощью регулировочного устройства, при использовании гироскопа в качестве чувствительного элемента его также можно использовать для непосредственной стабилизации обстрела судна и других установок. Другой важной характеристикой гироскопа является его способность сохранять ориентацию оси, когда он не применяется широко, хотя он широко применяется. Оборудования достаточно г 1 Рис. 147 Гироскоп в момент внешней силы.

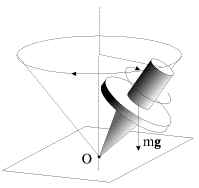
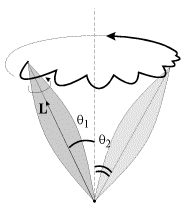
В этом случае ось гироскопа не прецессирует и не меняет направление в пространстве. Эта характеристика сбалансированного гироскопа это гирокомпас Используются поворотники, стабилизаторы и т. Д. Для этой цели используется гироскоп 3 DOF или свободный гироскоп. Прецессия тяжелого гироскопа по теории приближений Рассмотрим прецессию тяжелого гироскопа (рис. 148) под действием силы тяжести. Согласно закону прецессии гироскоп прецессирует вокруг вертикальной оси Oz под воздействием гравитационного момента P относительно точки O. Направление указано стрелкой дуги на рисунке. в любое время = ; L = L.

Поэтому, следовательно, Jz co, co 1 sin 9 = Pl sin 0, где l = OC расстояние от фиксированной точки до центра тяжести гироскопа. Угловая скорость прецессии 2 = W i) (55) (55) показывает, что угловая скорость прецессии тяжелого гироскопа не зависит от угла наклона оси гироскопа: Liu1 обратно пропорционален собственному моменту движения гироскопа. Прямо пропорционально расстоянию от до фиксированной точки. Пример. Бегун вращается вокруг вертикальной оси Oz с помощью машины скорой помощи под определенным углом (рис. 149). Гравитация каждого бегуна P. Радиус I; радиус инерции Oz p вокруг своей оси вращения.

Используя приблизительную теорию гироскопа, определите давление бегуна на дне чаши, давление бегуна на шарнире О. Решения. Рассмотрим бегунка как гироскоп прецессии с соответствующей осью вращения Oz и осью прецессии Ozt. Давление бегуна Q относительно нижней части гироскопического давления N, то есть Q = P + N Предполагая, что средняя точка бегуна A является стационарной, то есть на мгновенной оси бегуна, ОА это мгновенная ось бегуна, ориентированная вдоль его угловой скорости, состояния прецессии и собственной угловой скорости бегуна.

Это было 0 От подобия треугольника к угловой скорости делящегося количества, Рис. 149 Отсюда o = a , L. Рассматривая бегуна как прецессию Se ssssiaω0 и угловую скорость Уковского, бегун g: шарнир O та же формула (53) Гироскоп с угловой скоростью Up. с того времени с того времени значение Серая сфера Бегун применяет, я пропорциональна Если радиус большой, радиус бегуна.

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

7.5. Гироскопы

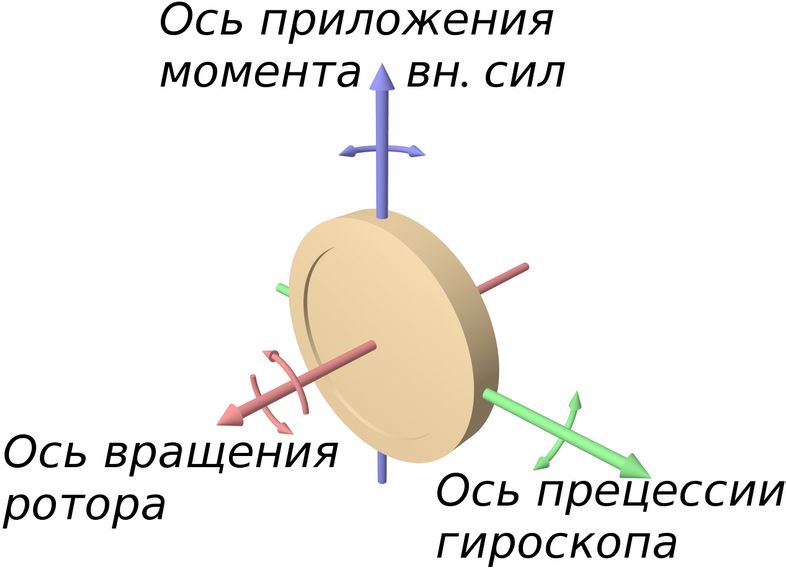
Гироскопом называется массивное осесимметричное тело (симметричный волчок), быстро вращающееся вокруг оси симметрии, причем ось вращения может изменять положение в пространстве. Ось симметрии называется осью фигуры гироскопа.

Видео 7.6. Что же такое гироскоп?

Рис. 7.17. Движение системы гироскопов

Ось симметрии является одной из главных осей гироскопа. Поэтому его момент импульса совпадает по направлению с осью вращения.

Для того, чтобы изменить положение в пространстве положение оси фигуры гироскопа, необходимо подействовать на него моментом внешних сил.

Видео 7.7. Гироскопические силы:большой гироскоп рвет веревку

Рис. 7.18. Направление векторов при вращении гироскопа

При этом наблюдается явление, получившее название гироскопического: под действием сил, которые, казалось бы, должны были вызвать поворот оси 1 вокруг оси 2 (рис. 7.19), наблюдается поворот оси фигуры вокруг оси 3.

Рис. 7.19. Движение оси фигуры гироскопа под действием момента внешних сил

Видео 7.8. Гироскоп с перегрузами: направление и скорость прецессии, нутации

Гироскопические явления проявляются всюду, где имеются быстро вращающиеся тела, ось которых может поворачиваться в пространстве.

Рис. 7.20. Реакция гироскопа на внешнее воздействие

Странное на первый взгляд поведение гироскопа, рис. 7.19 и 7.20, полностью объясняется уравнением динамики вращательного движения твердого тела

Видео 7.9. «Любвеобильный» гироскоп: ось гироскопа бежит вдоль направляющей, не покидая её

Видео 7.10. Действие момента силы трения: «Колумбово» яйцо

Если гироскоп привести в быстрое вращение, он будет обладать значительным моментом импульса. Если на гироскоп будет действовать внешняя сила в течение времени 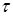, то приращение момента импульса будет

Если сила действует в течение короткого времени 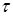, то

Другими словами, при коротких воздействиях (толчках) момент импульса гироскопа практически не меняется. С этим связана замечательная устойчивость гироскопа по отношению к внешним воздействиям, которая используется в различных приборах, таких как гирокомпасы, гиростабилизированные платформы и т. д.

Видео 7.11. Модель гирокомпаса, гиростабилизация

Видео 7.12. Большой гирокомпас

7.21. Гиростабилизатор орбитальной станции

В гироскопах, применяющихся в авиации и космонавтике, используется карданов подвес, который позволяет сохранять направление оси вращения гироскопа независимо от ориентации самого подвеса:

Видео 7.13. Гироскопы в цирке: езда на одном колесе по проволоке

http://www.plib.ru/library/book/14978.html Сивухин Д.В. Общий курс физики, том 1, Механика Изд. Наука 1979 г. — стр. 245–249 (§ 47): кинематическая теорема Эйлера о вращениях твердого тела вокруг неподвижной точки.

Рассмотрим движение гироскопа с неподвижной точкой опоры, как показано на на рис. 7.22.

Движение гироскопа под действием внешней силы называется вынужденной прецессией.

Рис. 7.22. Вынужденная прецессия гироскопа: 1 — общий вид; 2 — вид сверху

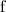
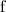
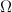
Приложим в точке А силу . Если гироскоп не вращается, то, естественно, правый маховик будет опускаться, а левый — подниматься. Другая ситуация будет, если предварительно гироскоп привести в быстрое вращение. В этом случае под действием силы ось гироскопа будет вращаться с угловой скоростью вокруг вертикальной оси. То есть ось гироскопа приобретает скорость в направлении, перпендикулярном направлению действующей силы.

Таким образом, прецессия гироскопа представляет собой движение под действием внешних сил, происходящее таким образом, что ось фигуры описывает коническую поверхность.

Рис. 7.23. К выводу формулы прецессии гироскопа.

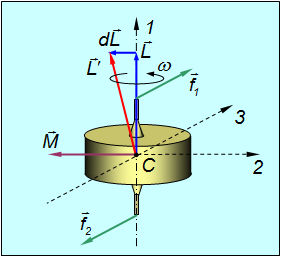
Объяснение этого явления заключается в следующем. Момент силы 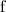относительно точки 0 будет

Приращение момента импульса гироскопа за время 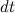равно

Это приращение перпендикулярно моменту импульса и, следовательно, меняет его направление, но не величину.

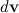
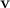
Вектор момента импульса ведет себя подобно вектору скорости при движении частицы по окружности. В последнем случае приращения скорости перпендикулярно скорости частицы и равно по модулю

В случае гироскопа элементарное приращение момента импульса

и равно по модулю

За время 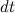вектор момента импульса повернется на угол

Угловая скорость вращения плоскости, проходящей через ось конуса, описываемого осью фигуры, и ось фигуры, называется угловой скоростью прецессии гироскопа.

Возникающие при определенных условиях колебания оси фигуры гироскопа в плоскости, проходящей через ось указанного выше конуса и саму ось фигуры, называются нутациями. Нутации могут быть вызваны, например, коротким толчком оси фигуры гироскопа вверх или вниз (см. рис. 7.24):

Рис. 7.24. Нутации гироскопа

Угловая скорость прецессии в рассматриваемом случае равна

Отметим важное свойство гироскопа — его безынерционность, заключающееся в том, что после прекращения действия внешней силы вращение оси фигуры прекращается.

http://www.plib.ru/library/book/14978.html Сивухин Д.В. Общий курс физики, том 1, Механика Изд. Наука 1979 г. — стр. 288–293 (§ 52): изложены основы точной теории гироскопа.

http://femto.com.ua/articles/part_1/0796.html — физическая энциклопедия. Описаны разнообразные механические гироскопы, которые используются для навигации — гирокомпасы.

http://femto.com.ua/articles/part_1/1901.html — физическая энциклопедия. Описан лазерный гироскоп для целей космической навигации.

Влияние гироскопических сил в технике иллюстрируется следующими рисунками.

Рис. 7.25. Гироскопические силы,действующие на самолет при вращении винта

Рис. 7.26. Перевертывание волчка под действием гироскопических сил

Рис. 7.27. Как поставить яйцо «на попа»

http://www.pereplet.ru/nauka/Soros/pdf/9809_096.pdf — Соросовский образовательный журнал, 1998 г., № 9, — в статье обсуждаются проблемы динамики вращающихся тел (кельтских камней), соприкасающихся с твердой поверхностью (А.П. Маркеев).

http://ilib.mirror1.mccme.ru/djvu/bib-kvant/kvant_35.djvu — Михайлов А.А. Земля и ее вращение, Библиотечка Квант, выпуск 35 стр. 50–56 — планета Земля — большой волчок, ее ось прецессирует в пространстве.

О принципе работы колеса

Раз уж мы много говорили в этой главе о вращении тел, остановимся на самом великом и важном открытии человечества — изобретении колеса. Всем известно, что волочить груз гораздо труднее, чем перевозить его на колесах. Встает вопрос, почему? Колесо, играющее огромную роль в современной технике, по праву считается одним из гениальнейших изобретений человечества.

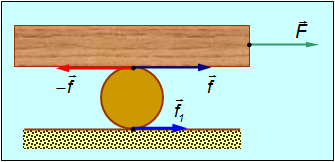
Передвижение груза с помощью катка. Прототипом колеса был каток, подкладываемый под груз. Его первые применения теряются во мгле веков. Прежде чем разбираться с колесом, поймем принцип действия катка. Для этого рассмотрим пример.

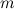
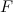
Пример. Груз массой M положен на цилиндрический каток массой и радиусом , который может двигаться по плоскому горизонтальному настилу. К грузу приложена горизонтальная сила (рис. 7.28). Найдем ускорения груза и катка. Силой трения качения пренебречь. Считать, что движение системы происходит без проскальзывания.

Рис. 7.28. Передвижение груза с помощью катка

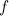
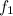
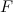
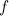
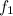
Обозначим силу трения между катком и грузом и — между катком и настилом. За положительное направление примем направление внешней силы . Тогда положительным значениям и соответствуют направления сил трения, показанные на рис. 7.28.

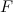
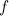
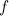
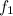
Таким образом, на груз действуют силы и , а на каток — силы и . Обозначим a ускорение груза и a₁ — ускорение катка. Кроме того, каток вращается по часовой стрелке с угловым ускорением .

Уравнения поступательного движения принимают вид:

для катка

Уравнение вращательного движения катка записывается так:

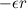
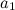
Обратимся теперь к условиям отсутствия проскальзывания. Из-за вращения катка его нижняя точка имеет линейное ускорение и, кроме того, участвует в поступательном движении с ускорением . В отсутствие проскальзывания между катком и настилом полное ускорение нижней точки катка должно быть равно нулю, так что

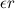
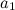
Верхняя точка катка приобретает из-за вращения противоположно направленное линейное ускорение и то же ускорение поступательного движения. Чтобы не было проскальзывания между катком и грузом, полное ускорение верхней точки должно быть равно ускорению груза:

Из полученных уравнений для ускорений следует, что ускорение катка в два раза меньше ускорения груза:

Из непосредственного опыта каждый знает, что каток действительно отстает от груза.

Подставляя соотношения для ускорений в уравнения движения и решая их относительно неизвестных , , , получаем следующие выражение для ускорения груза

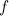
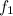
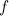
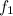
Обе силы трения и оказываются при этом положительными, так что на рис. 12 их направления выбраны правильно:

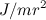
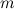
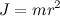
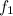
Как видно, радиус катка особой роли не играет: отношение зависит только от его формы. При данных массе и радиусе момент инерции катка максимален, когда каток представляет собой трубу: . В этом случае сила трения между катком и настилом отсутствует ( = 0) а уравнения для ускорения груза и силы трения между грузом и катком принимают вид:

При уменьшении массы катка сила трения уменьшается, ускорение груза увеличивается — груз легче перемещать.

В случае катка-цилиндра (бревна) 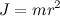/2 и мы находим силы трения

и ускорение груза.

Сравнивая с результатами для катка-трубы, видим, что эффективно масса катка как бы уменьшилась: ускорение груза возрастает при прочих равных условиях.

Главный итог рассмотренного примера: ускорение отлично от нуля (то есть груз начинает двигаться) при сколь угодно малой внешней силе. При волочении же груза по настилу для его смещения необходимо приложить как минимум силу .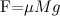

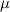
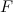
Второй вывод: ускорение вовсе не зависит от величины трения между частями данной системы. Коэффициент трения не вошел в найденные решения, он появится только в условиях отсутствия проскальзывания, которые сводятся к тому, что приложенная сила не должна быть слишком велика.

Полученный результат, что каток как бы полностью «уничтожает» силу трения, не удивителен. Действительно, в отсутствие относительного перемещения соприкасающихся поверхностей силы трения не совершают работы. На самом деле каток «заменяет» трение скольжения на трение качения, которым мы пренебрегли. В реальном случае минимальная сила, необходимая для движения системы, отлична от нуля, хотя и гораздо меньше, чем при волочении груза по настилу. В современной технике принцип действия катка реализуется в шарикоподшипниках.

Качественное рассмотрение работы колеса. Разобравшись с катком, перейдем к колесу. Первое колесо в виде деревянного диска, насаженного на ось, появилось, по-видимому, в IV тысячелетии до н.э. в цивилизациях Древнего Востока. Во II тыс. до н.э. конструкция колеса совершенствуется: появляются спицы, ступица и гнутый обод. Изобретение колеса дало гигантский толчок развитию ремесел и транспорта. Однако многие не понимают самого принципа действия колеса. В ряде учебников и энциклопедий можно найти неверное утверждение, что колесо, подобно катку, также дает выигрыш, заменяя силу трения скольжения на силу трения качения. Иногда приходится слышать ссылки на использование смазки или подшипников, но дело не в этом, поскольку колесо с очевидностью появилось раньше, чем додумались до смазки (и, тем более, подшипников).

Действие колеса проще всего понять, исходя из энергетических соображений. Древние повозки устроены просто: кузов прикрепляется к деревянной оси радиусом (общая масса кузова с осью равна M). На ось насаживаются колеса массой и радиусом R (рис. 7.29).

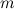
Рис. 7.29. Передвижение движение груза с помощью колеса

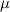
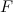
Предположим, что такую повозку везут по деревянному же настилу (тогда во всех соприкасающихся местах имеем тот же коэффициент трения ). Сначала заклиним колеса и, действуя силой , протащим повозку на расстояние s . Поскольку повозка скользит по настилу, сила трения достигает своего максимально возможного значения

Работа против этой силы равна

(так как обычно масса колес много меньше массы повозки

Лекция 11. Гироскопы.

В данной лекции рассматриваются следующие вопросы:

1. Гироскопы. Свободный гироскоп.

2. Прецессия гироскопа под действием внешних сил. Угловая скорость прецессии. Нутации.

3. Гироскопические силы, их природа и проявление.

4. Волчки. Устойчивость вращения симметричного волчка.

Изучение данных вопросов необходимо в дисциплине «Детали машин».

Гироскопы. Свободный гироскоп.

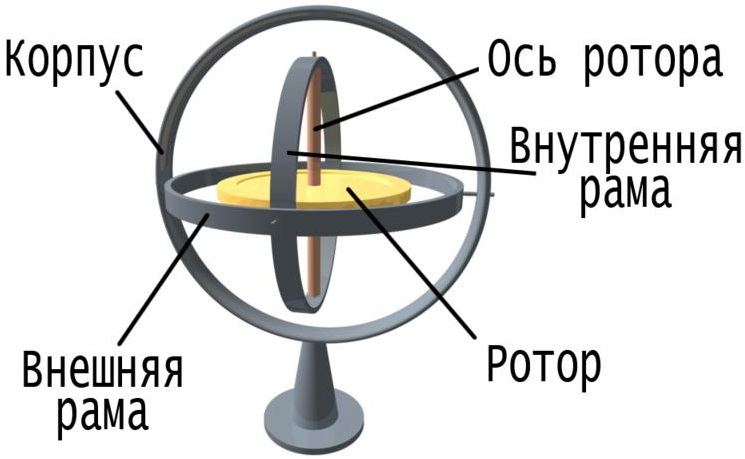
Гироскоп — это массивное аксиально-симметричное тело, вращающееся с большой угловой скоростью вокруг своей оси симметрии.

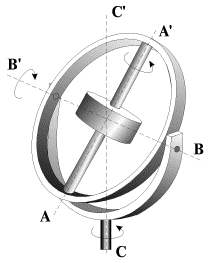
В этом случае моменты всех внешних сил, включая и силу тяжести, относительно центра масс гироскопа равны нулю. Это можно реализовать, например, поместив гироскоп в карданов подвес, изображенный на рис.1.

M =0, dL dt =0, (1)

и момент импульса сохраняется:

Гироскоп ведет себя так же, как и свободнее тело вращения. В зависимости от начальных условий возможны два варианта поведения гироскопа:

1. Если гироскоп раскручен вокруг оси симметрии, то направления момента импульса и угловой скорости совпадают:

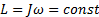
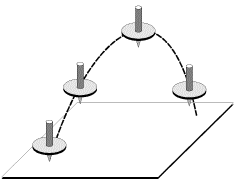
L = Jω = const , (3)

и направление оси симметрии гироскопа остается неизменным. В этом можно убедиться, поворачивая подставку, на которой расположен карданов подвес — при произвольных поворотах подставки ось гироскопа сохраняет неизменное направление в пространстве. По этой же причине волчок, «запущенный» на листе картона и подброшенный вверх (рис.2), сохраняет направление своей оси во время полета, и, падая острием на картон, продолжает устойчиво вращаться, пока не израсходуется запас его кинетической энергии.

Свободный гироскоп, раскрученный вокруг оси симметрии, обладает весьма значительной устойчивостью. Из основного уравнения моментов следует, что изменение момента импульса

∆ L = 0 ∆ t Mdt (4)

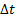
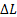
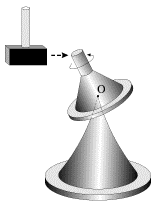
Если интервал времени ∆ t мал, то и ∆ L мало, то есть при кратковременных воздействиях даже очень больших сил движение гироскопа изменяется незначительно. Гироскоп как бы сопротивляется попыткам изменить его момент импульса и кажется «затвердевшим».

Возьмем гироскоп конусообразной формы, опирающийся на стержень подставки в своем центре масс О (рис. 3). Если тело гироскопа не вращается, то оно находится в состоянии безразличного равновесия, и малейший толчок сдвигает его с места. Если же это тело привести в быстрое вращение вокруг своей оси, то даже сильные удары деревянным молотком не смогут сколько-нибудь значительно изменить направление оси гироскопа в пространстве. Устойчивость свободного гироскопа используется в различных технических устройствах, например, в автопилоте.

2. Если свободный гироскоп раскручен так, что вектор мгновенной угловой скорости и ось симметрии гироскопа не совпадают (как правило, это несовпадение при быстром вращении бывает незначительным), то наблюдается движение, описанное как «свободная регулярная прецессия». Применительно же к гироскопу его называют нутацией. При этом ось симметрии гироскопа, векторы L и ω 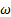лежат в одной плоскости, которая вращается вокруг направления L = const с угловой скоростью, равной L / J x где J x — момент инерции гироскопа относительно главной центральной оси, перпендикулярной оси симметрии. Эта угловая скорость (назовем ее скоростью нутации) при быстром собственном вращении гироскопа оказывается достаточно большой, и нутация воспринимается глазом как мелкое дрожание оси симметрии гироскопа.

Нутационное движение легко продемонстрировать с помощью гироскопа, показанного на рис. 3 — оно возникает при ударах молотком по стержню вращающегося вокруг своей оси гироскопа. При этом чем сильнее раскручен гироскоп, тем больше его момент импульса L — тем больше скорость нутации и тем «мельче» дрожания оси фигуры. Этот опыт демонстрирует еще одну характерную особенность нутации — с течением времени она постепенно уменьшается и исчезает. Это — следствие неизбежного трения в опоре гироскопа.

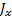
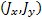
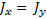
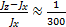
Наша Земля — своего рода гироскоп, и ей тоже свойственно нутационное движение. Это связано с тем, что Земля несколько приплюснута с полюсов, в силу чего моменты инерции относительно оси симметрии J x и относительно оси, лежащей в экваториальной плоскости ( J x , J y ) различаются. При этом J x = J y , а J z — J x J x ≈ 1 300 . В системе отсчета, связанной с Землей, ось вращения движется по поверхности конуса вокруг оси симметрии Земли с угловой скоростью w₀, то есть она совершает один оборот примерно за 300 дней. На самом деле в силу, как предполагается, неабсолютной жесткости Земли, это время оказывается больше — оно составляет около 440 суток. При этом расстояние точки земной поверхности, через которую проходит ось вращении, от точки, через которую проходит ось симметрии (Северный полюс), равно всего нескольким метрам. Нутационное движение Земли не затухает — по-видимому, его поддерживают сезонные изменения, происходящие на поверхности

Прецессия гироскопа под действием внешних сил. Элементарная теория.

Рассмотрим теперь ситуацию, когда к оси гироскопа приложена сила, линия действия которой не проходит через точку закрепления. Опыты показывают, что в этом случае гироскоп ведет себя весьма необычным образом.

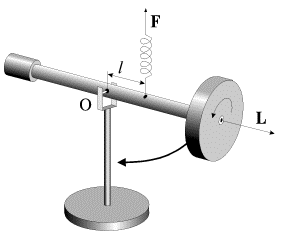
Если к оси шарнирно закрепленного в точке О гироскопа (рис. 4) прикрепить пружину и тянуть за нее вверх с силой F , то ось гироскопа будет перемещаться не в направлении силы, а перпендикулярно к ней, вбок. Это движение называется прецессией гироскопа под действием внешней силы.

Опытным путем можно установить, что угловая скорость прецессии зависит не только от величины силы F (рис.4), но и от того, к какой точке оси гироскопа эта сила приложена: с увеличением F и ее плеча l относительно точки закрепления О скорость прецессии увеличивается. При этом оказывается, что чем сильнее раскручен гироскоп, тем меньше угловая скорость прецессии при данных F и l .

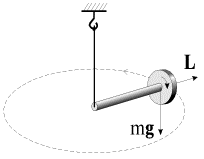
В качестве силы F , вызывающей прецессию, может выступать сила тяжести, если точка закрепления гироскопа не совпадает с центром масс. Так, если стержень с быстро вращающимся диском подвесить на нитке (рис. 5), то он не опускается вниз, как это можно было бы предположить, а совершает прецессионное движение вокруг нитки. Наблюдение прецессии гироскопа под действием силы тяжести в некотором смысле даже удобнее — линия действия силы «автоматически» смещается вместе с осью гироскопа, сохраняя свою ориентацию в пространстве.

Можно привести и другие примеры прецессии — например, движение оси хорошо известной детской игрушки — юлы с заостренным концом (рис.6). Юла, раскрученная вокруг своей оси и поставленная на горизонтальную плоскость слегка наклонно, начинает прецессировать вокруг вертикальной оси под действием силы тяжести (рис.6).

Точное решение задачи о движении гироскопа в поле внешних сил довольно выражение для угловой скорости прецессии можно легко получить в рамках так называемой элементарной теории гироскопа. В этой теории делается допущение, что мгновенная угловая скорость вращения гироскопа и его момент импульса направлены вдоль оси симметрии гироскопа. Другими словами, предполагается, что угловая скорость вращения гироскопа вокруг своей оси значительно больше угловой скорости прецессии:

ω ≫ Ω 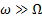(5)

так что вкладом в L , обусловленным прецессионным движением гироскопа, можно пренебречь. В этом приближении момент импульса гироскопа, очевидно, равен

L = J z ω 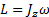(6)

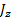
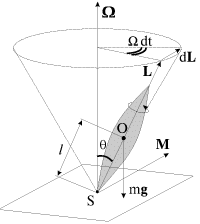
где J z — момент инерции относительно оси симметрии.

Итак, рассмотрим тяжелый симметричный гироскоп, у которого неподвижная точка S (точка опоры о подставку) не совпадает с центром масс О (рис. 7).

Момент силы тяжести относительно точки S

M = mglsunθ 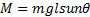(7)

где θ — угол между вертикалью и осью симметрии гироскопа. Вектор M направлен по нормали к плоскости, в которой лежат ось симметрии гироскопа и вертикаль, проведенная через точку S (рис. 7). Сила реакции опоры проходит через S, и ее момент относительно этой точки равен нулю.

Изменение момента импульса L определяется выражением

При этом и L , и ось волчка прецессируют вокруг вертикального направления с угловой скоростью Ω . Еще раз подчеркнем: делается допущение, что выполнено условие (5) и что L постоянно направлен вдоль оси симметрии гироскопа. Из рис.95 следует, что

dL = Lsinθ Ω dt 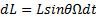(9)

В векторном виде

dL = Ω × Ldt 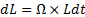(10)

Сравнивая (8) и (10), получаем следующую связь между моментом силы M , моментом импульса L и угловой скоростью прецессии Ω :

M = Ω × L 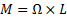(11)

Это соотношение позволяет определить направление прецессии при заданном направлении вращения волчка вокруг своей оси.

Обратим внимание, что M определяет угловую скорость прецессии, а не угловое ускорение, поэтому мгновенное «выключение» M приводит к мгновенному же исчезновению прецессии, то есть прецессионное движение является безынерционным.

Сила, вызывающая прецессионное движение, может иметь любую природу. Для поддержания этого движения важно, чтобы вектор момента силы M поворачивался вместе с осью гироскопа. Как уже было отмечено, в случае силы тяжести это достигается автоматически. При этом из (11) (см. также рис. 7) можно получить:

mglsinθ = Ω J z ωsinθ 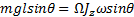(12)

Если учесть, что в нашем приближении справедливо соотношение (6), то для угловой скорости прецессии получим

Ω = mgl J z ω (13)

Следует отметить, что Ω не зависит от угла θ наклона оси гироскопа и обратно пропорциональна w, что хорошо согласуется с опытными данными.

Прецессия гироскопа пол действием внешних сил. Отход от элементарной теории. Нутации.

Опыт показывает, что прецессионное движение гироскопа под действием внешних сил в общем случае сложнее, чем то, которое было описано выше в рамках элементарной теории. Если сообщить гироскопу толчок, изменяющий угол θ 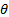(см. рис.7), то прецессия перестанет быть равномерной (часто говорят: регулярной), а будет сопровождаться мелкими вращениями и дрожаниями вершины гироскопа — нутациями. Для их описания необходимо учесть несовпадение вектора полного момента импульса L , мгновенной угловой скорости вращения w и оси симметрии гироскопа.

Точная теория гироскопа выходит за рамки курса общей физики. Из соотношения dL = Mdt следует, что конец вектора L движется в направлении M , то есть перпендикулярно к вертикали и к оси гироскопа. Это значит, что проекции вектора L на вертикаль L_B и на ось гироскопа L ₀ остаются постоянными. Еще одной постоянной является энергия

E = T + mg l cosθ 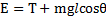(14)

где T — кинетическая энергия гироскопа. Выражая L_B , L ₀ и T через углы Эйлера и их производные, можно, с помощью уравнений Эйлера, описать движение тела аналитически.

Результат такого описания оказывается следующим: вектор момента импульса L описывает неподвижный в пространстве конус прецессии, и при этом ось симметрии гироскопа движется вокруг вектора L по поверхности конуса нутаций. Вершина конуса нутаций, как и вершина конуса прецессии, находится в точке закрепления гироскопа, а ось конуса нутаций совпадает по направлению с L и движется вместе с ним. Угловая скорость нутаций определяется выражением

w нут = L J s ≈ J z ω J s , (15)

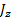
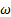
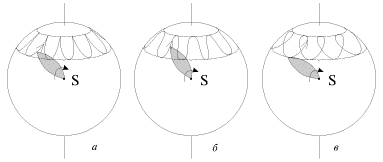
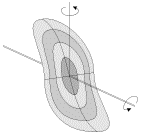
где J z и J s — моменты инерции тела гироскопа относительно оси симметрии и относительно оси, проходящей через точку опоры и перпендикулярной оси симметрии, ω — угловая скорость вращения вокруг оси симметрии.

Таким образом, ось гироскопа участвует в двух движениях: нутационном и прецессионном. Траектории абсолютного движения вершины гироскопа представляют собой замысловатые линии, примеры которых представлены на рис. 8.

Характер траектории, по которой движется вершина гироскопа, зависит от начальных условий. В случае рис. 8, а гироскоп был раскручен вокруг оси симметрии, установлен на подставке под некоторым углом к вертикали и осторожно отпущен. В случае рис. 8, б ему, кроме того, был сообщен некоторый толчок вперед, а в случае рис. 8, в — толчок назад по ходу прецессии. Кривые на рис. 8 вполне аналогичны циклоидам, описываемым точкой на ободе колеса, катящегося по плоскости без проскальзывания или с проскальзыванием в ту или иную сторону. И лишь сообщив гироскопу начальный толчок вполне определенной величины и направления, можно добиться того, что ось гироскопа будет прецессировать без нутаций. Чем быстрее вращается гироскоп, тем больше угловая скорость нутаций и тем меньше их амплитуда. При очень быстром вращении нутации делаются практически незаметными для глаза.

Может показаться странным: почему гироскоп, будучи раскручен, установлен под углом к вертикали и отпущен, не падает под действием силы тяжести, а движется вбок? Откуда берется кинетическая энергия прецессионного движения?

Ответы на эти вопросы можно получить только в рамках точной теории гироскопам. На самом деле гироскоп действительно начинает падать, а прецессионное движение появляется как следствие закона сохранения момента импульса. В самом деле, отклонение оси гироскопа вниз приводит к уменьшению проекции момента импульса на вертикальное направление. Это уменьшение должно быть скомпенсировано моментом импульса, связанным с прецессионным движением оси гироскопа. С энергетической точки зрения кинетическая энергия прецессии появляется за счет изменения потенциальной энергии гироскопам.

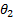
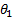
Если за счет трения в опоре нутации гасятся быстрее, чем вращение гироскопа вокруг оси симметрии (как правило, так и бывает), то вскоре после «запуска» гироскопа нутации исчезают и остается чистая прецессия (рис. 9). При этом угол наклона оси гироскопа к вертикали θ 2 оказывается больше, чем он был вначале θ 1 , то есть потенциальная энергия гироскопа уменьшается. Таким образом, ось гироскопа должна немного опуститься, чтобы иметь возможность прецессировать вокруг вертикальной оси.

Гироскопические силы.

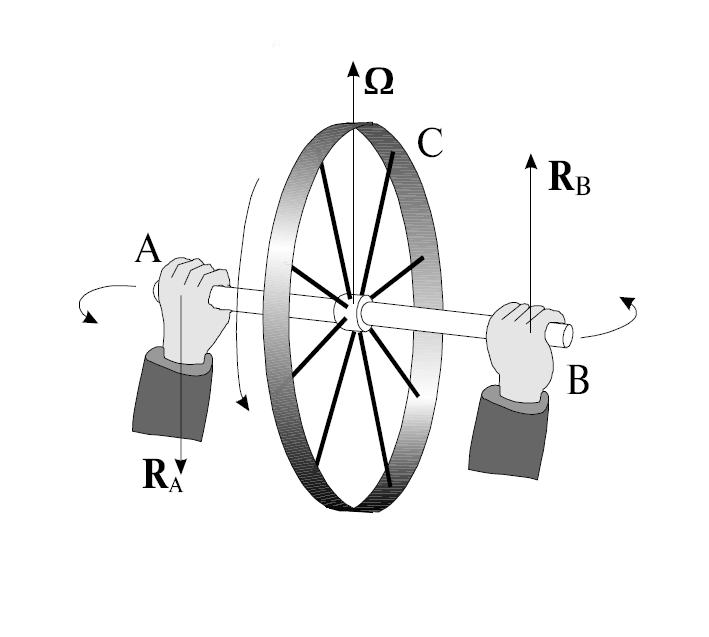
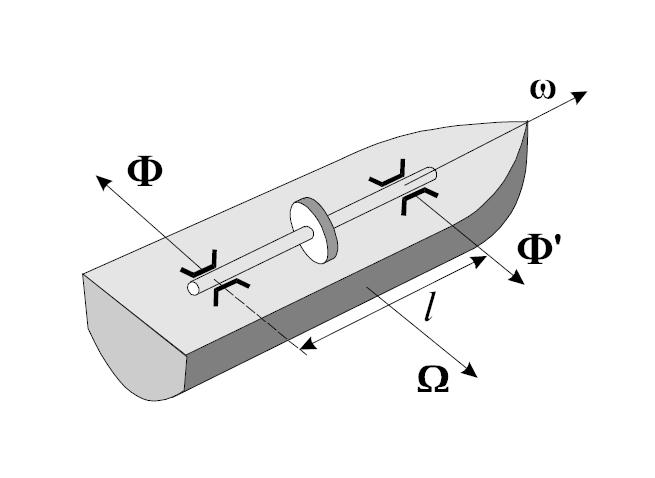
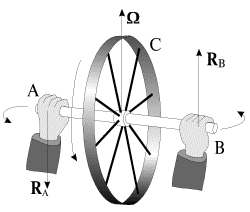
Обратимся к простому опыту: возьмем в руки вал АВ с насаженным на него колесом С (рис. 10). Пока колесо не раскручено, не представляет никакого труда поворачивать вал в пространстве произвольным образом. Но если колесо раскручено, то попытки повернуть вал, например, в горизонтальной плоскости с небольшой угловой скоростью Ω приводят к интересному эффекту: вал стремится вырваться из рук и повернуться в вертикальной плоскости; он действует на кисти рук с определенными силами R_A и R_B (рис. 10). Требуется приложить ощутимое физическое усилие, чтобы удержать вал с вращающимся колесом в горизонтальной плоскости.

Рассмотрим эффекты, возникающие при вынужденном вращении оси гироскопа, более подробно. Пусть ось гироскопа будет укреплена в U-образной раме, которая может поворачиваться вокруг вертикальной оси OO’ (рис. 11). Такой гироскоп обычно называют несвободным — его ось лежит в горизонтальной плоскости и выйти из нее не может.

Раскрутим гироскоп вокруг его вокруг его оси симметрии до большой угловой скорости (момент импульса L ) и станем поворачивать раму с укрепленным в ней гироскопом вокруг вертикальной оси OO’ с некоторой угловой скоростью Ω как показано на рис. 11. Момент импульса L , получит при этом приращение dL которое должно быть обеспечено моментом сил M , приложенным к оси гироскопа. Момент M , в свою очередь, создан парой сил F ÷ F ‘ возникающих при вынужденном повороте оси гироскопа и действующих на ось со стороны рамы. По третьему закону Ньютона ось действует на раму с силами Ф÷ Ф ‘ (рис. 11). Эти силы называются гироскопическими; они создают гироскопический момент M ‘ . Появление гироскопических сил называют гироскопическим эффектом. Именно эти гироскопические силы мы и чувствуем, пытаясь повернуть ось вращающегося колеса (рис.10).

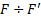
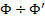
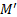
Гироскопический момент нетрудно рассчитать. Положим, согласно элементарной теории, что

L = Jω 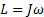(16)

где J — момент инерции гироскопа относительно его оси симметрии, а ω — угловая скорость собственного вращения. Тогда момент внешних сил, действующих на ось, будет равен

M = Ω×L=Ω×(Jω) 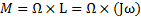(17)

где ω — угловая скорость вынужденного поворота (иногда говорят: вынужденной прецессии). Со стороны оси на подшипники действует противоположный момент

M ‘ =- M = Jω × Ω 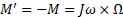(18)

Таким образом, вал гироскопа, изображенного на рис. 11, будет прижиматься кверху в подшипнике В и оказывать давление на нижнюю часть подшипника А.

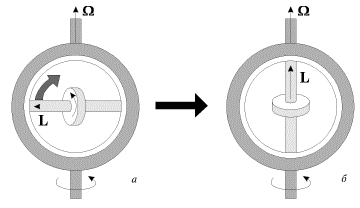
Направление гироскопических сил можно легко найти с помощью правила, сформулированного Н.Е. Жуковским: гироскопические силы стремятся совместить момент импульса L гироскопа с направлением угловой скорости вынужденного поворота. Это правило можно наглядно продемонстрировать с помощью устройства, представленного на рис. 12.

Ось гироскопа закреплена в кольце, которое может свободно поворачиваться в обойме. Приведем обойму во вращение вокруг вертикальной оси с угловой скоростью Ω (вынужденный поворот), и кольцо с гироскопом будет поворачиваться в обойме до тех пор, пока направления L и Ω не совпадут. Такой эффект лежит в основе известного магнитомеханического явления — намагничивания железного стержня при его вращении вокруг собственной оси — при этом спины электронов выстраиваются вдоль оси стержня (опыт Барнетта ).

Гироскопические усилия испытывают подшипники осей быстро вращающихся частей машины при повороте самой машины (турбины на корабле, винта на самолете и т.д.). При значительных величинах угловой скорости вынужденной прецессии Ω и собственного вращения ω а также больших размерах маховика эти силы могут даже разрушить подшипники. Рассмотрим некоторые примеры проявления гироскопических сил.

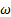
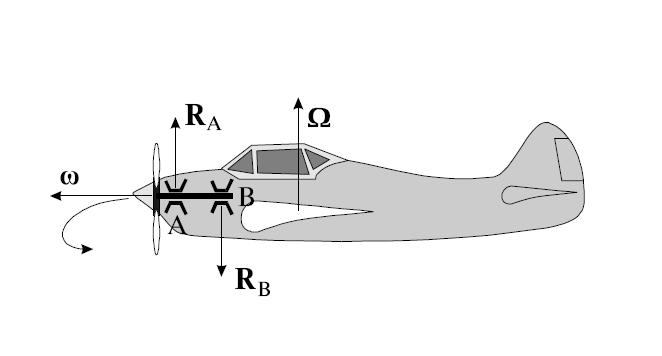
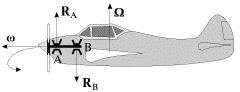
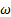
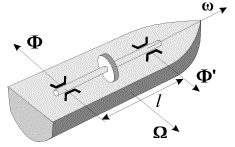
Пример 1. Легкий одномоторный самолет с правым винтом совершает левый вираж (рис. 13). Гироскопический момент передается через подшипники А и В на корпус самолета и действует на него, стремясь совместить ось собственного вращения винта (вектор ω ) с осью вынужденной прецессии (вектор Ω ). Самолет начинает задирать нос кверху, и летчик должен «дать ручку от себя», то есть опустить вниз руль высоты. Таким образом, момент гироскопических сил будет компенсирован моментом аэродинамических сил.

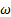
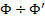
Пример 2. При килевой качке корабля (с носа на корму и обратно) ротор быстроходной турбины участвует в двух движениях: во вращении вокруг своей оси с угловой скоростью ω и в повороте вокруг горизонтальной оси, перпендикулярной валу турбины, с угловой скоростью Ω (рис. 14). При этом вал турбины будет давить на подшипники с силами Ф÷ Ф ‘ лежащими в горизонтальной плоскости. При качке эти силы, как и гироскопический момент, периодически меняют свое направление на противоположное и могут вызвать «рыскание» корабля, если он не слишком велик (например, буксира).

Допустим, что масса турбины m =3000 кг ее радиус инерции R _ин = 0,5 м, скорость вращения турбины n =3000 об/мин, максимальная угловая скорость корпуса судна при килевой качке Ω =5 град/с, расстояние между подшипниками l =2 м. Максимальное значение гироскопической силы, действующей на каждый из подшипников, составляет

Ф= M l = JwΩ l = m R ин 2 ∙2 πn ∙ Ω l (19)

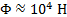
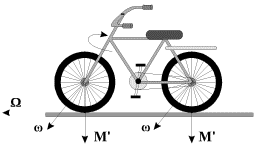
После подстановки числовых данных получим Ф≈ 10 4 Н то есть около 1 тонны.

Пример 3. Гироскопические силы могут вызвать так называемые колебания «шимми» колес автомобиля (рис. 15) [В.А. Павлов, 1985]. Колесу, вращающемуся вокруг оси AA’ с угловой скоростью w в момент наезда на препятствие сообщается дополнительная скорость вынужденного поворота вокруг оси, перпендикулярной плоскости рисунка. При этом возникает момент гироскопических сил, и колесо начнет поворачиваться вокруг оси BB’. Приобретая угловую скорость поворота вокруг оси BB’, колесо снова начнет поворачиваться вокруг оси, перпендикулярной плоскости рисунка, деформируя упругие элементы подвески и вызывая силы, стремящиеся вернуть колесо в прежнее вертикальное положение. Далее ситуация повторяется. Если в конструкции автомобиля не принять специальных мер, возникшие колебания «шимми» могут привести к срыву покрышки с обода колеса и к поломке деталей его крепления.

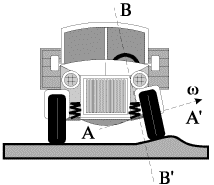
Пример 4. С гироскопическим эффектом мы сталкиваемся и при езде на велосипеде (рис. 16). Совершая, например, поворот направо, велосипедист инстинктивно смещает центр тяжести своего тела вправо, как бы заваливая велосипед. Возникшее принудительное вращение велосипеда с угловой скоростью Ω приводит к появлению гироскопических сил с моментом M ‘ . На заднем колесе этот момент будет погашен в подшипниках, жестко связанных с рамой. Переднее же колесо, имеющее по отношению к раме свободу вращения в рулевой колонке, под действием гироскопического момента начнет поворачиваться как раз в том направлении, которое было необходимо для правого поворота велосипеда. Опытные велосипедисты совершают подобные повороты, что называется, «без рук».

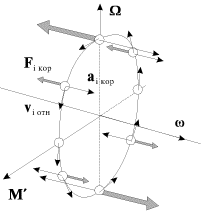
Вопрос о возникновении гироскопических сил можно рассматривать и с другой точки зрения. Можно считать, что гироскоп, изображенный на рис. 11, участвует в двух одновременных движениях: относительном вращении вокруг собственной оси с угловой скоростью w и переносном, вынужденном повороте вокруг вертикальной оси с угловой скоростью Ω . Таким образом, элементарные массы Δ m i , на которые можно разбить диск гироскопа (маленькие кружки на рис. 17), должны испытывать кориолисовы ускорения

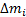
a i кко =2 Ω × v i оот 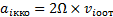(20)

Эти ускорения будут максимальны для масс, находящихся в данный момент времени на вертикальном диаметре диска, и равны нулю для масс, которые находятся на горизонтальном диаметре (рис. 17).

В системе отсчета, вращающейся с угловой скоростью Ω (в этой системе отсчета ось гироскопа неподвижна), на массы Δ m i будут действовать кориолисовы силы инерции

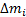
F i кко =2 Δ m i v отн × Ω 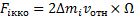(21)

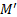
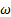
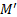
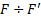
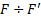
Эти силы создают момент M ‘ который стремится повернуть ось гироскопа таким образом, чтобы вектор Ω совместился с ω . Момент M ‘ должен быть уравновешен моментом сил реакции F ÷ F ‘ действующих на ось гироскопа со стороны подшипников. По третьему закону Ньютона, ось будет действовать на подшипники, а через них и на раму, в которой эта ось закреплена, с гироскопическими силами F ÷ F ‘ . Поэтому и говорят, что гироскопические силы обусловлены силами Кориолиса.

Возникновение кориолисовых сил можно легко продемонстрировать, если вместо жесткого диска (рис. 17) взять гибкий резиновый лепесток (рис. 18). При повороте вала с раскрученным лепестком вокруг вертикальной оси лепесток изгибается при прохождении через вертикальное положение так, как изображено на рис. 18.

Волчки.

Волчки кардинально отличаются от гироскопов тем, что в общем случае они не имеют ни одной неподвижной точки. Произвольное движение волчков имеет весьма сложный характер: будучи раскручены вокруг оси симметрии и поставлены на плоскость, они прецессируют , «бегают» по плоскости, выписывая замысловатые фигуры, а иногда даже переворачиваются с одного конца на другой. Не вдаваясь в детали такого необычного поведения волчков, отметим лишь, что немаловажную роль здесь играет сила трения, возникающая в точке соприкосновения волчка и плоскости.

Кратко остановимся на вопросе об устойчивости вращения симметричного волчка произвольной формы. Опыт показывает, что если симметричный волчок привести во вращение вокруг оси симметрии и установить на плоскость в вертикальном положении, то это вращение в зависимости от формы волчка и угловой скорости вращения будет либо устойчивым, либо неустойчивым.

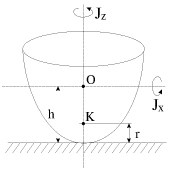
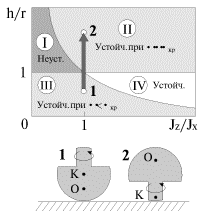
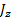
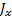
Пусть имеется симметричный волчок, изображенный на рис. 19. Введем следующие обозначения: О — центр масс волчка, h — расстояние от центра масс до точки опоры; K — центр кривизны волчка в точке опоры, r — радиус кривизны; J z — момент инерции относительно оси симметрии, J x — момент инерции относительно главной центральной оси, перпендикулярной оси симметрии.

Анализ устойчивости вращения волчка приводит к диаграмме, изображенной на рис. 20. Здесь по оси абсцисс отложено отношение J z / J x 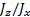, а по оси ординат – отношение h / r .

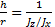
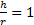
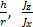
Проведем гиперболу h r = 1 J z / J x и прямую h r =1 . Эти линии делят область положительных значений h r , J z J x на 4 части.

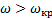
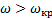
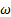
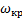
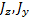
Область I соответствует неустойчивому вращению волчка при всех угловых скоростях, область II — устойчивому вращению при достаточно больших угловых скоростях ω > ω кр . Область III соответствует устойчивому вращению при малых угловых скоростях ω > ω кр , область IV — устойчивому вращению при произвольных ω . Критическая угловая скорость ω кр зависит от моментов инерции J z , J y , расстояний r , h и веса тела P = mg [К. Магнус , 1974]:

w кр 2 = (h- r )∙ P J x ( r /h)∙( J z / J x — r /h) (22)

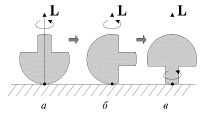
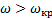
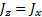
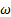
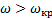
Рассмотрим, например, китайский волчок, раскрученный до ω > ω кр и поставленный на плоскость вертикально, как показано на рис. 20, а. Пусть J z = J x . Поскольку h r то этой ситуации соответствует точка 1 в области III на рис. 19, то есть область устойчивого вращения лишь при малых ω . Таким образом, в нашем случае ω > ω кр вращение будет неустойчивым, и волчок перевернется на ножку (точка 2 в области II на рис. 20).

Следует обратить внимание, что в процессе переворачивания волчка результирующий момент импульса сохраняет свое первоначальное направление, то есть вектор L , все время направлен вертикально вверх. Это означает, что в ситуации, изображенной на рис. 21, б, когда ось волчка горизонтальна, вращение вокруг оси симметрии волчка отсутствует! Далее, при опрокидывании на ножку, вращение вокруг оси симметрии будет противоположно исходному (если смотреть все время со стороны ножки, рис. 21, в).

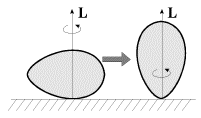
В случае яйцеобразного волчка поверхность тела в окрестности точки опоры не является сферой, но существуют два взаимно перпендикулярных направления, для которых радиус кривизны в точке опоры принимает экстремальные (минимальное и максимальное) значения. Опыты показывают, что в случае, изображенном на рис. 21, а, вращение будет неустойчивым, и волчок принимает вертикальное положение, раскручиваясь вокруг оси симметрии и продолжая устойчивое вращение на более остром конце. Это вращение будет продолжаться до тех пор, пока силы трения не погасят в достаточной мере кинетическую энергию волчка, угловая скорость уменьшится (станет меньше ω ₀ ), и волчок упадет.

Вопросы для самопроверки

— Какое твердое тело называют гироскопом?

— Чему равен и как направлен кинетический момент быстровращающегося гироскопа относительно его неподвижной точки?

— Какими физическими свойствами обладает быстровращающийся гироскоп с тремя степенями свободы?

— Какой эффект производит действие одной и той же силы, приложенной к оси неподвижного и быстровращающегося гироскопа с тремя степенями свободы?

— Выведите формулу для вычисления угловой скорости прецессии оси гироскопа.

— В чем состоит разница в свойствах гироскопов с двумя и тремя степенями свободы?

— Какова физическая сущность гироскопического эффекта и при каких условиях он наблюдается?

— По каким формулам определяются динамические реакции подшипников, в которых вращается рама вращающегося гироскопа с двумя степенями свободы?

1. А.Н. Матвеев. Механика и теория относительности. М.: Высшая школа, 1986.

2. С.П. Стрелков. Механика. М.: Наука, 1975.

3. С.Э. Хайкин. Физические основы механики. М.: Наука, 1971.

4. Д.В. Сивухин . Общий курс физики. Т.1. Механика. М.: Наука, 1989.

5. Р.В. Поль. Механика, акустика и учение о теплоте. М.: Наука, 1971.

6. Р. Фейнман и др. Фейнмановские лекции по физике. М.: Мир, 1977.

7. Ч. Киттель , У. Найт , М. Рудерман . Механика. М.: Наука, 1983.

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21