Тейлоровская диффузия
Кроме молекулярной диффузии (теплопроводности), в природе и технике приходится сталкиваться с явлениями типа диффузионных, когда переносу подвергаются более крупные, чем молекулы, объекты. Например, при турбулентном движении жидкости перемешиваются макроскопические объемы вещества (моли), содержащие количества молекул порядка числа Авогадро. Другим примером является перенос частиц в потоке жидкости, в частности броуновская диффузия. При создании композиционных материалов часто интерес представляет коэффициент диффузии (теплопроводности) смеси, что также является некоторой крупномасштабной (осредненной) характеристикой среды. Встречаются также случаи, когда диффузионный перенос формируют физические процессы разной природы. При этом можно говорить об эффективной диффузии.
Примером такого рода является диффузия Тейлора. В данном случае в качестве объектов переноса могут выступать как молекулы, так и более крупные образования. Понятие тейлоровской диффузии связано с процессом продольного рассеяния (дисперсии) растворенного вещества (примеси) в прямых трубах или каналах. Главным механизмом такого процесса выступает обычный конвективный перенос при наличии радиального сдвигового течения, которое взаимодействует с радиальной молекулярной или турбулентной диффузией.
Уравнение Эйлера — одно из основных уравнений гидродинамики идеальной жидкости. Названо в честь Л. Эйлера, получившего это уравнение в 1752 году (опубликовано в 1757 году). По своей сути является уравнением движения жидкости.
получаем уравнение Эйлера для движения идеальной жидкости в поле тяжести:
 |
где 
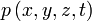

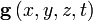

Идеа́льная жи́дкость — в гидродинамике — воображаемая несжимаемая жидкость, в которой отсутствуют вязкость и теплопроводность. Так как в ней отсутствует внутреннее трение, то нет касательных напряжений между двумя соседними слоями жидкости.
Моделью идеальной жидкости пользуются при теоретическом рассмотрении задач, в которых вязкость не является определяющим фактором и ею можно пренебречь. В частности, такая идеализация допустима во многих случаях течения, рассматриваемыхгидроаэромеханикой, и даёт хорошее описание реальных течений жидкостей и газов на достаточном удалении от омываемых твёрдых поверхностей и поверхностей раздела с неподвижной средой. Математическое описание течений идеальных жидкостей позволяет найти теоретическое решение ряда задач о движении жидкостей и газов в каналах различной формы, при истечении струй и при обтекании тел.
Уравнение Громеки — Лэмба [1] [2] (уравнение Лэмба [3] ) — принятое в русскоязычной литературе название специальной формы записи уравнений движенияидеальной жидкости (уравнений Эйлера) с использованием ротора скорости.
Уравнение Громеки — Лэмба имеет вид
Диссипация энергии (лат. dissipatio — рассеяние) — переход части энергии упорядоченных процессов (кинетической энергии движущегося тела, энергииэлектрического тока и т. п.) в энергию неупорядоченных процессов, в конечном счёте — в теплоту. Системы, в которых энергия упорядоченного движения с течением времени убывает за счёт диссипации, переходя в другие виды энергии, например в теплоту или излучение, называются диссипативными. Для учёта процессов диссипации энергии в таких системах при определённых условиях может быть введена диссипативная функция. Если диссипация энергии происходит в замкнутой системе, то энтропия системы возрастает. Диссипация энергии в открытых системах, обусловленная процессами уноса энергии из системы, например в виде излучения, может приводить к уменьшению энтропии рассматриваемой системы при увеличении полной энтропии системы и окружающей среды. Это, в частности, обеспечивает важную роль процессов диссипации энергии в уменьшении удельной энтропии вещества на стадиях образования галактик и звёзд в модели горячей Вселенной.
Уравне́ния Навье́ — Сто́кса — система дифференциальных уравнений в частных производных, описывающая движение вязкойньютоновской жидкости. Уравнения Навье — Стокса являются одними из важнейших в гидродинамике и применяются вматематическом моделировании многих природных явлений и технических задач. Названы по имени французского физика Анри Навьеи британского математика Джорджа Стокса.
Система состоит из двух уравнений:
Часто уравнениями Навье — Стокса называют только одно векторное уравнение движения [1] .
В векторном виде для несжимаемой жидкости они записываются следующим образом:
где 





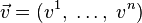







Иногда в систему уравнений Навье — Стокса дополнительно включают уравнение теплопроводности и уравнение состояния.
При учёте сжимаемости уравнения Навье — Стокса принимают следующий вид:
где 


Преобразование Громеки-Лэмба.
Читайте также:
|
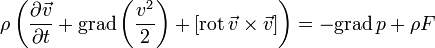






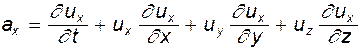 (7.3)
(7.3)



 и
и  , т.е. можем записать
, т.е. можем записать
 (7.4)
(7.4) (7.5)
(7.5) (7.6)
(7.6) (7.7)
(7.7) (7.8)
(7.8)