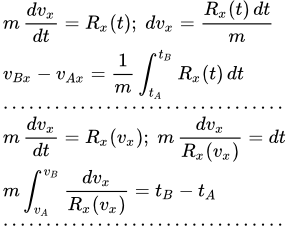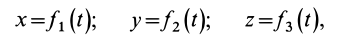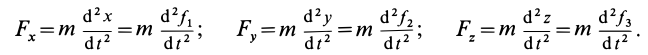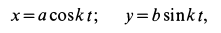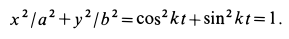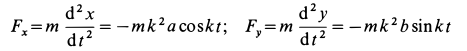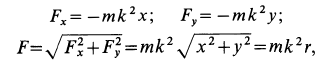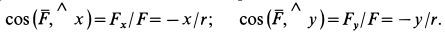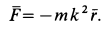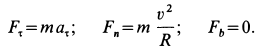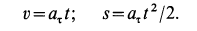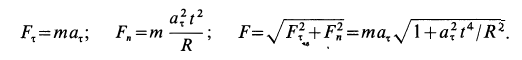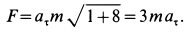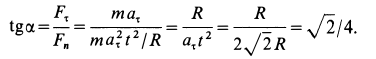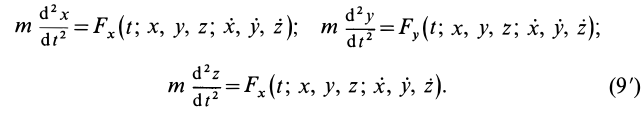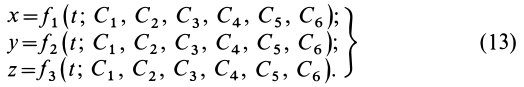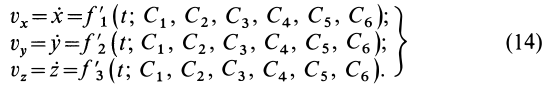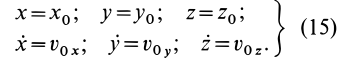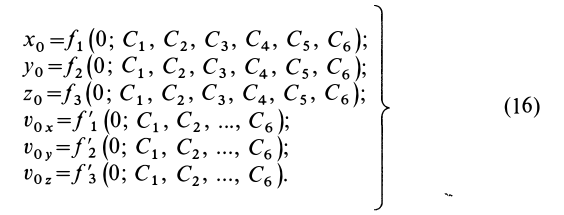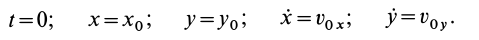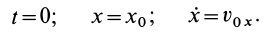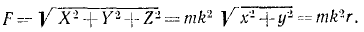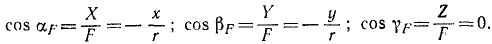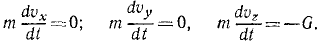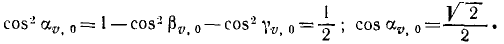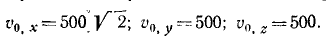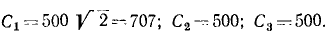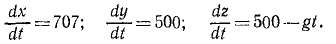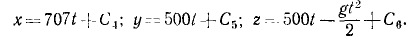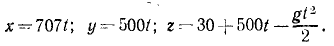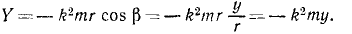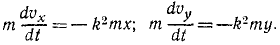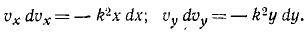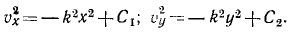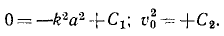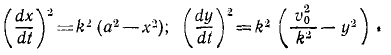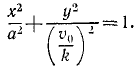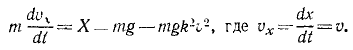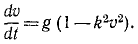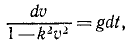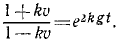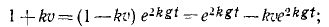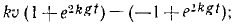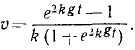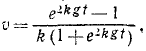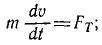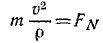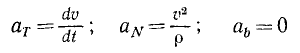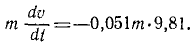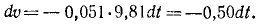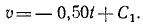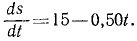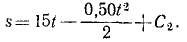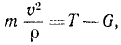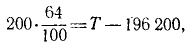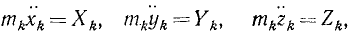Уравнения движения и их интегрирование

Интегрирование дифференциальных уравнений прямолинейного движения материальной точки

Краткое изложение результатов

Здесь мы кратко изложим основные результаты, полученные при интегрировании дифференциальных уравнений прямолинейного движения материальной точки. Далее следует их подробное изложение.

Сила, зависящая от времени

Если на материальную точку действует сила, зависящая от времени , то дифференциальное уравнение прямолинейного движения вдоль оси Ox имеет вид:
.
Вводим ускорение и интегрируем это уравнение.
.
Здесь и далее A и B – произвольные точки на оси Ox . Заменим . Получаем закон изменения скорости от времени:
.
Интегрируя уравнение , получаем закон движения точки :
;
.

Сила, зависящая от скорости

Пусть на точку действует сила, зависящая от скорости . Составляем дифференциальное уравнение движения и интегрируем его:
.
Последнее уравнение дает в неявном виде зависимость . Решаем его. После чего интегрируем уравнение , как описано выше.

Есть второй способ интегрирования уравнения движения в случае зависимости силы от скорости. Для этого переходим от переменных x и t к переменным и x . Считаем, что скорость является функцией от координаты x :
;
.
Последнее уравнение дает в неявном виде зависимость . Далее интегрируем уравнение :
.
Это уравнение дает в неявном виде закон движения точки .

Сила, зависящая от перемещения

Пусть на точку действует сила, зависящая от перемещения . Составляем уравнение движения, переходим от переменных x и t к переменным и x , и интегрируем полученное дифференциальное уравнение:
;
;
.
Это уравнение представляет собой закон сохранения механической энергии для прямолинейного движения. Из него находим зависимость скорости от перемещения . После чего интегрируем уравнение , как это описано выше.

Дифференциальное уравнение движения точки

Рассмотрим прямолинейное движение материальной точки, находящейся под действием постоянных и переменных сил. Направим ось Ox системы координат вдоль линии движения точки. Пусть на нее действуют n сил, проекции которых на ось Ox мы обозначим как . Положение точки, при прямолинейном движении, однозначно определяется ее координатой x . Нам нужно определить закон движения точки , то есть закон изменения ее координаты со временем.

Уравнение движения точки определяется вторым законом Ньютона, который в случае прямолинейного движения имеет вид:
(1) .

Вместо того, чтобы в каждом уравнении выписывать все n сил, введем их равнодействующую, проекция которой, на ось x равна сумме проекций всех сил на эту ось:
.
Тогда задача сведется к движению материальной точки под действием одной силы . При этом уравнение движения примет наиболее простой вид:
(2) .
В дальнейшем, проекцию равнодействующей мы будем называть просто силой, действующей на точку.

Сила может быть как постоянной, так и зависеть от времени t , координаты x и от скорости . К сожалению, если зависит от всех перечисленных факторов, то не всегда возможно решить уравнение (2) аналитически. Поэтому мы рассмотрим те случаи, когда возможно получить аналитическое решение этого уравнения. Заметим, что если сила является постоянной, то уравнение (2) можно решать любыми, приводимыми ниже, способами.

Почему мы обозначаем в виде проекции силы на ось x , хотя рассматриваем только движение вдоль одной оси? – Потому что под обозначением силы R в виде одной буквы, часто подразумевается ее абсолютная величина: . Она имеет неотрицательные значения: . А когда мы пишем силу как проекцию , то подразумеваем, что эта величина может быть как положительной (если сила направлена вдоль оси x ), так и отрицательной (когда она направлена противоположно оси x ). В теоретической механике, в подобных случаях, иногда также говорят, что есть алгебраическое значение силы. Это относится не только к силе, ни и ко всем другим, рассматриваемым далее, векторным величинам.

Интегрирование уравнения движения с силой, зависящей от времени

Вначале рассмотрим случай, когда задан закон изменения силы со временем: . Перепишем уравнение (2), явно указав эту зависимость:
(t1) .

В этом уравнении время t является независимой переменной; координата x – зависимой переменной; – это вторая производная координаты по времени: . Масса m – это постоянная, то есть заданное число. С математической точки зрения, уравнение (t1) есть дифференциальное уравнение второго порядка, не содержащую зависимую переменную x в явном виде.

Решение такого уравнения выполняется с помощью подстановки
.
Тогда
.
Подставляя в (t1), мы получаем дифференциальное уравнение первого порядка:
(t2) .
Выполняя подстановку, мы ввели новую переменную , равную производной координаты x по времени t . Эта производная является проекцией скорости точки на ось Ox . Таким образом, процесс решения разбивается на две части. Сначала мы, решаем уравнение (t2), и находим закон изменения скорости со временем: . Затем, используя уравнение , находим закон изменения координаты .

Упростим уравнение (t2), разделив его на массу m :
(t3) ,
где – ускорение точки. Поскольку зависимость силы от времени известна, то и зависимость ускорения от времени также известна.

Уравнение (t3) является дифференциальным уравнением первого порядка с разделяющимися переменными. Разделяем переменные и интегрируем.
;
(t4) ;
(t5) .
Здесь – постоянная интегрирования. Чтобы ее определить, нужно знать значение скорости в какой-либо момент времени . Если мы сможем выразить интеграл через известные функции, то подставив в (t5) значения времени и значение скорости в этот момент, мы сможем определить постоянную .

Для простых задач, формула (t5) вполне удобна. Но если интеграл не выражается через известные функции, то выполнить численное интегрирование по этой формуле нельзя. Поэтому найдем закон изменения скорости со временем в более удобном виде.

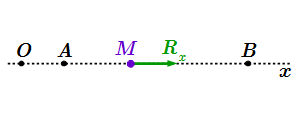
Прямолинейное движение точки M под действием силы R_x.

Пусть нам известно, что в момент времени , точка M находилась в положении A, имела координату и скорость . Рассмотрим произвольный момент времени . Пусть в этот момент времени точка M находится в положении B, с координатой и скоростью . Величины и нам пока не известны. Наша задача их найти.

Перепишем (t4) явно указав, что есть функция от t :
(t6) .
Интегрируем (t6) от момента времени до :
.
Слева – интеграл от полного дифференциала. Поэтому он интегрируется элементарно:
.
Здесь мы учли, что . В результате получаем:
;
.

Этот результат можно получить и несколько иначе, если в интеграле сразу перейти к переменной . Тогда пределы интегрирования станут и . В результате получим тоже самое:
.

Итак, мы нашли значение скорости в произвольный момент времени :
(t7) .
Заменим обозначение момента времени на t . В результате получим закон изменения скорости со временем t :
(t8) .

Интеграл справа записан не вполне корректно, хотя так часто пишут. Рассмотрим пример определенного интеграла . Он зависит от пределов интегрирования a и b , но не зависит от переменной интегрирования t . Можно сказать, что переменная t принимает заданные значения из отрезка , которые применяются только для вычисления интеграла. Поэтому для переменной интегрирования t можно использовать любое обозначение. Например, можно использовать переменную . Тогда .

В (t8) мы использовали одно и то же обозначение, как для верхнего предела интеграла, так и для переменной интегрирования. Это может привести к путанице. Поэтому используем для переменной интегрирования любое другое, не используемое обозначение, например . Тогда формула (t8) примет следующий вид:
(t9) .

Теперь найдем закон изменения координаты x от времени. Интегрируем уравнение
.
Разделяем переменные:
(t10) .
Здесь мы также можем выполнить интегрирование от A до B, но мы продемонстрируем другой способ, как получить результат в удобном виде, применяя неопределенный интеграл. Поскольку неопределенный интеграл определен с точностью до постоянной, то запишем его с нижним пределом интегрирования . Интегрируем (t10):
(t11) .
Найдем значение постоянной интегрирования . Для этого подставим сюда :
.
Далее учитываем, что значение координаты точки в момент времени нам известно: . Также учитываем, что интеграл в правой части имеет равные пределы интегрирования и поэтому равен нулю. В результате получаем:
.
Отсюда находим значение постоянной интегрирования: . В результате получаем закон движения точки:
(t12) .

Итак, мы нашли, что если на точку действует сила , то для определения ее закона движения, нужно сначала определить закон изменения скорости со временем:
(t7) .
А затем определить закон движения:
(t12) .
При этом мы полагаем, что нам известны скорость и координата в некоторый момент времени . Если бы мы проводили интегрирование через неопределенные интегралы в общем виде, то и были бы постоянными интегрирования и .

Постоянная сила

Разберем случай, когда действующая на точку сила имеет постоянное значение: . В этом случае ускорение также постоянно: . Интегрируем, используя таблицу неопределенных интегралов. Из (t7) находим закон изменения скорости со временем:
;
(t14) .
Мы видим, что скорость линейно изменяется со временем.

Подставляем в (t12) и находим закон движения точки:

;
(t15) .

Если в начальный момент времени , скорость точки была , а координата , то . Из (t14) и (t15) получаем:
;
.

Равномерное движение

Если проекция силы на ось Ox равна нулю: , то ускорение также равно нулю: . В этом случае из (t14) находим, что скорость точки постоянна:
.
Из (t15) находим, что координата линейно меняется со временем:
.

Если в начальный момент времени , скорость точки была , а координата , то ;
;
.

Интегрирование уравнения движения с силой, зависящей от скорости

Разберем случай прямолинейного движения материальной точки, когда действующая сила зависит от скорости . Такие задачи встречаются при движении в жидкой или газообразной среде, когда на точку помимо постоянных сил, действует сила трения, зависящая от скорости. В этом случае, уравнение движения имеет вид:
(v1) .
Разделим обе части уравнения на массу m :
(v2) ,
где – ускорение точки. Теперь нам известна зависимость ускорения точки от ее скорости. Уравнение (v2) не содержит в явном виде как зависимую переменную x , так и независимую переменную t . Поэтому его можно решать двумя способами.

Решение уравнения, определяя v_x(t)

Применим к уравнению (v2) метод решения дифференциального уравнения, не содержащего зависимую переменную в явном виде. Для этого, как и в предыдущем случае, делаем подстановку
.
Тогда
.
Подставляя в (v2), мы получаем дифференциальное уравнение первого порядка:
(v3) .

Пусть, как и в предыдущем случае, в момент времени , точка находилась в положении A, имела координату и скорость . И пусть в произвольный момент времени , точка находится в положении B с координатой и скоростью . Нам нужно найти величины и .

Разделяем переменные.
;
.
Перепишем это уравнение, указав, что скорость является функцией от времени:
.
Интегрируем по времени от до :
.
В левой части сделаем замену переменной. От переменной t перейдем к переменной . При этом изменим пределы интегрирования учитывая, что при ; и при :
(v4) .

Заменим обозначения переменных , и переменной интегрирования . Подставим в (v4):
(v5) .
Это уравнение, в неявном виде, дает закон изменения скорости от времени t . Вычислив интеграл, и выполнив преобразование, мы можем выразить через t : .

Далее, по формуле (t12) ⇑ определяем закон движения материальной точки:
(t12) .

Решение уравнения, определяя v_x(x)

Выпишем уравнение (v2) еще раз.
(v2) .
Для применения этого метода, в качестве независимой переменной возьмем координату x , а в качестве зависимой – скорость . То есть считаем, что скорость является функцией от координаты: .

Выразим через переменные x и вторую производную координаты по времени:
.
Подставим в (v2) и разделяем переменные:
;
.
В левой части в явном виде запишем как функцию от x , и интегрируем по x от положения A до B:
;
.
В интеграле слева переходим от переменной x к :
(v6) .

Переобозначим переменные:
(v7) .
Это уравнение дает в неявном виде зависимость скорости от координаты:
.
Подставив сюда , получим для x дифференциальное уравнение первого порядка. Решаем его методом разделения переменных:
;
.
Интегрируем от положения A до B:
;
.
Заменим переменные:
(v8) .

Уравнение (v8) дает в неявном виде закон движения материальной точки .

Интегрирование уравнения движения с силой, зависящей от перемещения

Наконец рассмотрим случай прямолинейного движения материальной точки, когда действующая сила зависит от перемещения x . Такие задачи встречаются при движении в потенциальных полях – в гравитационных или электрических. Сюда также относится движение груза, прикрепленного к упругой пружине.

Выписываем уравнение движения для этого случая:
(x1) .
Это дифференциальное уравнение второго порядка. Оно не содержит независимую переменную t в явном виде. Также как и в предыдущем случае, применяем метод решения дифференциального уравнения, не содержащего независимую переменную в явном виде.

Перейдем к новым переменным. В качестве независимой переменной возьмем координату x , а в качестве зависимой – скорость . Считаем, что скорость является функцией от координаты: .

Выразим вторую производную координаты по времени через переменные x и :
;
Подставим в (x1) и разделяем переменные:
(x2) ;
.
Интегрируем по x от A до B:
(x3) .
Вычисляем интеграл, используя таблицу неопределенных интегралов:
;
.
Подставляем в (x3):
(x4) . Нетрудно видеть, что слева стоит изменение кинетической энергии материальной точки. Справа – работа, которую совершает сила при перемещении материальной точки из A в B. Само уравнение (x4) представляет собой теорему об изменении кинетической энергии точки для прямолинейного движения.

Вернемся снова к уравнению (x2).
(x2) .
Его можно проинтегрировать и другим способом.

Для этого представим правую часть в виде производной по координате:
,
где – координата произвольной заранее выбранной точки C .
Левую часть также представим в виде производной по координате:
.
Тогда (x2) можно записать в виде:
.

Поскольку производная по x от выражения в скобках равна нулю, то само выражение является постоянной, не зависящей от x величиной:
.
Такая форма записи, когда некоторая функция от переменных приравнивается постоянной, называется интегралом дифференциального уравнения. Перепишем его в следующем виде:
(x5) .
Здесь – кинетическая энергия точки; – потенциальная энергия, отсчитываемая от, произвольным образом выбранной, точки C ; E – постоянная интегрирования, которая в данном случае имеет определенный физический смысл – это полная механическая энергия материальной точки. Поэтому мы ее обозначили привычной для этого случая буквой E . Само уравнение (x5) представляет собой закон сохранения механической энергии. С математической точки зрения, энергия E является интегралом дифференциального уравнения, или, как говорят в механике, интегралом движения точки. То есть величиной, сохраняющей при движении постоянное значение.

Выше мы пришли к выводу, что постоянная интегрирования E не зависит от координаты x , но ничего не сказали о ее зависимости от времени. Однако, для одномерного движения, со временем может изменяться только одна координата x . Поскольку постоянная E от нее не зависит, то она не зависит также и от времени t . Поэтому полная механическая энергия сохраняет постоянное значение и в различные моменты времени.

Нетрудно видеть, что формулировки (x4) ⇑ и (x5) ⇑ эквивалентны. Для доказательства, приравняем механическую энергию точки для двух положений A и B:
;

.
Здесь мы разбили интеграл от до на два интеграла – от до ; и от до . Интегралы от до сократились.

Найдем зависимость скорости точки от координаты. При этом мы считаем, что скорость точки в положении A нам известна. Рассмотрим два положения: A и B. Из (x4) ⇑ имеем:
,
где – работа, которая производит сила при перемещении точки из A в B. Наконец, заменим на x , и на . В результате получим искомую зависимость:
(x6) ,
где – работа, которая производит сила при перемещении материальной точки из A в точку с координатой x . Скорость определена с точностью до знака (плюс или минус). Знак нужно выбирать из начальных условий и исследования движения. Если в точке , то при достаточно малых значениях . Далее точка может остановиться и начать движение в обратную сторону. Тогда нужно выбрать знак минус, чтобы скорость стала отрицательной.

Теперь, зная зависимость , находим закон движения материальной точки. Для этого интегрируем уравнение:
;
;
;
.
Это уравнение дает в неявном виде зависимость координаты x от времени t .

Приложение к движению в пространстве

Приведенные выше результаты могут быть применимы и для некоторых случаев движения материальной точки в двухмерном или трехмерном пространстве.

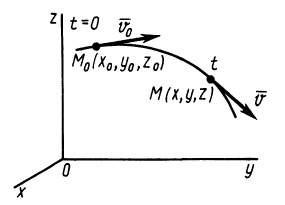
Пусть нам известно, что в момент времени , материальная точка находилась в точке A, и имела скорость . Выберем трехмерную систему координат Oxyz , и распишем эти начальные условия по компонентам:
При ;
При ;
При .

Сила в пространстве, зависящая от времени

Пусть на материальную точку действует сила, зависящая от времени: . Составим уравнения ее движения:
.

Выпишем уравнение для координаты x с начальными условиями:
; при .
Здесь все необходимые величины известны, и они не зависят от значений других координат. Мы можем найти закон изменения координаты x со временем, применяя интегрирование уравнения движения с силой, зависящей от времени ⇑ для прямолинейного движения.

Выпишем уравнение для координаты y с начальными условиями:
; при .
Здесь также известны все необходимые величины, и они не зависят от значений других координат. Мы также можем найти закон изменения координаты y со временем, применяя интегрирование, как для прямолинейного движения.

Точно также мы можем найти закон изменения координаты z со временем. В этом случае говорят, что переменные разделились. Уравнения движения, составленные для каждой из координат, вместе с начальными условиями, не зависят от значений других координат. Поэтому каждое такое уравнение можно проинтегрировать отдельно. В результате мы получим закон движения материальной точки в трехмерном случае: .

Силы, приводящие к разделению переменных

Пусть теперь на точку действуют три взаимно перпендикулярные силы. И пусть одна из них зависит только от времени; вторая – от проекции скорости на направление силы; третья – от проекции радиус-вектора на направление силы.

Выберем систему координат Oxyz , оси которой направим вдоль направлений действующих сил. Тогда в этой системе координат отличными от нуля будут только три проекции сил: . Составляем уравнения движения:
;
;
.
Мы видим, что и в этом случае переменные разделились. Каждое из этих уравнений зависит только от одной переменной. И мы можем решить его, применяя изложенные выше методы. Все это применимо и к случаю, когда любая из этих сил является постоянной.

И, разумеется, тут могут быть различные вариации, приводящие к разделению переменных. Например, если зависящая от времени сила лежит в плоскости xy , а перпендикулярная ей сила зависит только от координаты z . В этом случае переменные также разделяются.

Автор: Олег Одинцов . Опубликовано: 12-10-2020

Интегрирование уравнений движения

Симуляция физики делает небольшие предсказания на основании законов физики. Эти предсказания на самом деле достаточно просты, что-то вроде «если объект вот здесь и он движется с такой скоростью в этом направлении, то за краткий промежуток времени он окажется вот тут». Мы создаём такие предсказания с помощью математической техники под названием интегрирование.

Темой этой статьи как раз и будет реализация такого интегрирования.

Интегрирование уравнений движения

Вы можете помнить из курса старшей школы или вуза, что сила равна произведению массы на ускорение.

Преобразуем это уравнение и увидим, что ускорение равно силе, делённой на массу. Это соответствует нашим интуитивным ожиданиям, потому что тяжёлые объекты труднее бросать.

Ускорение — это темп изменения скорости от времени:

Аналогично, скорость — это темп изменения позиции от времени:

Это значит, что если мы знаем текущие позицию и скорость объекта, а также приложенные к нему силы, то сможем проинтегрировать, чтобы найти его позицию и скорость в определённый момент времени.

Численное интегрирование

Если вы не изучали дифференциальные уравнения в вузе, то можете вздохнуть спокойно — вы почти в такой же ситуации, что и те, кто их изучал, потому что мы не будем решать дифференциальные уравнения аналитически. Вместо этого мы будем искать решение численным интегрированием.

Вот как работает численное интегрирование: во-первых, начнём с исходной позиции и скорости, затем сделаем небольшой шаг вперёд, чтобы найти скорость и позицию в будущем. Затем повторим это, двигаясь вперёд небольшими шагами, используя результат предыдущих вычислений как исходную точку следующих.

Но как нам найти изменение скорости и позиции на каждом шаге?

Ответ лежит в уравнениях движения.

Давайте назовём наше текущее время t, а шаг времени dt или «delta time».

Теперь мы можем представить уравнения движения в понятном всем виде:

Интуитивно это понятно: если вы находитесь в автомобиле, движущемся со скоростью 60 км/ч, то за один час вы проедете 60 км. Аналогично, автомобиль, ускоряющийся на 10 км/ч в секунду, через 10 секунд будет двигаться на 100 км/ч быстрее.

Разумеется, эта логика сохраняется, только когда ускорение и скорость постоянны. Но даже если они меняются, то это для начала вполне неплохая аппроксимация.

Давайте представим это в коде. Начнём с стационарного объекта массой один килограмм и приложим к нему постоянную силу в 10 кН (килоньютонов) и сделаем шаг вперёд, принимая, что один временной шаг равен одной секунде:

Вот каким будет результат:

Как вы видите, на каждом шаге мы знаем и позицию, и скорость объекта. Это и есть численное интегрирование.

Явный метод Эйлера

Вид интегрирования, который мы только что использовали, называется явным методом Эйлера.

Он назван в честь швейцарского математика Леонарда Эйлера, впервые открывшего эту технику.

Интегрирование Эйлера — это простейшая техника численного интегрирования. Она точна на 100% только когда темп изменений в течение шага времени постоянен.

Поскольку в примере выше ускорение постоянно, интегрирование скорости выполняется без ошибок. Однако мы ещё интегрируем и скорость для получения позиции, а скорость увеличивается из-за ускорения. Это значит, что в проинтегрированной позиции возникает ошибка.

Но насколько велика эта ошибка? Давайте выясним!

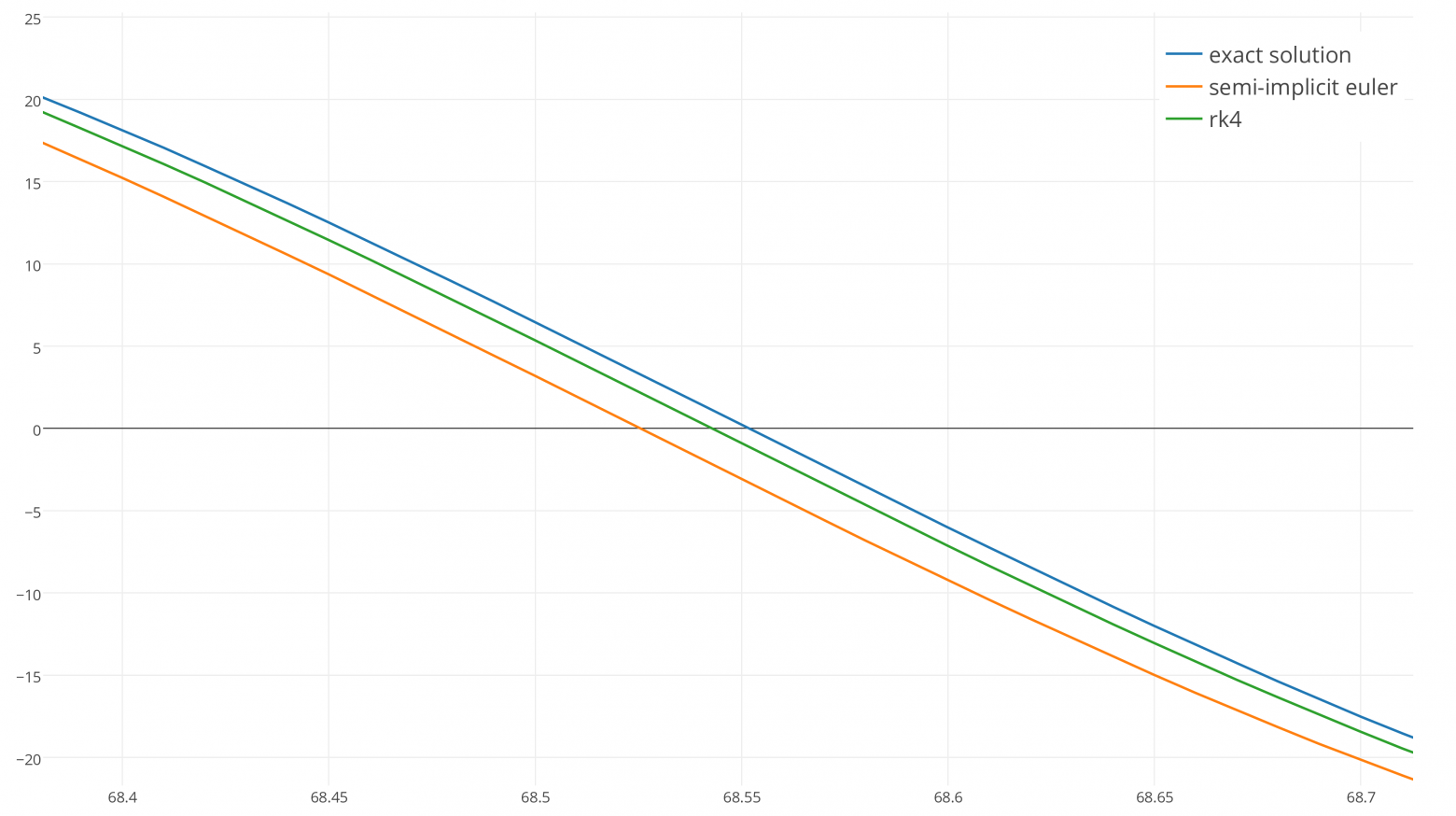
Существует аналитическое решение движения объекта при постоянном ускорении. Мы можем использовать его, чтобы сравнить численно интегрированную позицию с точным результатом:

Через 10 секунд объект должен был переместиться на 500 метров, но явным метод Эйлера даёт нам результат 450. То есть погрешность в целых 50 метров всего за 10 секунд!

Кажется, что это невероятно плохо, но в играх обычно для шага физики берётся не такой большой временной интервал. На самом деле, физика обычно вычисляется с частотой, примерно равной частоте кадров дисплея.

Если задать шаг dt = 1 ⁄₁₀₀, то мы получим гораздо лучший результат:

Как вы видите, это достаточно хороший результат, определённо вполне достаточный для игры.

Почему явный метод Эйлера не (всегда) так уж хорош

С достаточно малым шагом времени явный метод Эйлера при постоянном ускорении даёт вполне достойные результаты, но что будет, если ускорение не постоянно?

Хорошим примером переменного ускорения является система пружинного амортизатора.

В этой системе масса присоединена к пружине, и её движение гасится чем-то вроде трения. Существует сила, пропорциональная расстоянию до объекта, которая притягивает его к исходной точке, и сила, пропорциональная скорости объекта, но направленная в противоположном направлении, которая замедляет его.

Здесь ускорение в течение шага времени совершенно точно изменяется, но эта постоянно меняющаяся функция является сочетанием позиции и скорости, которые сами постоянно изменяются за шаг времени.

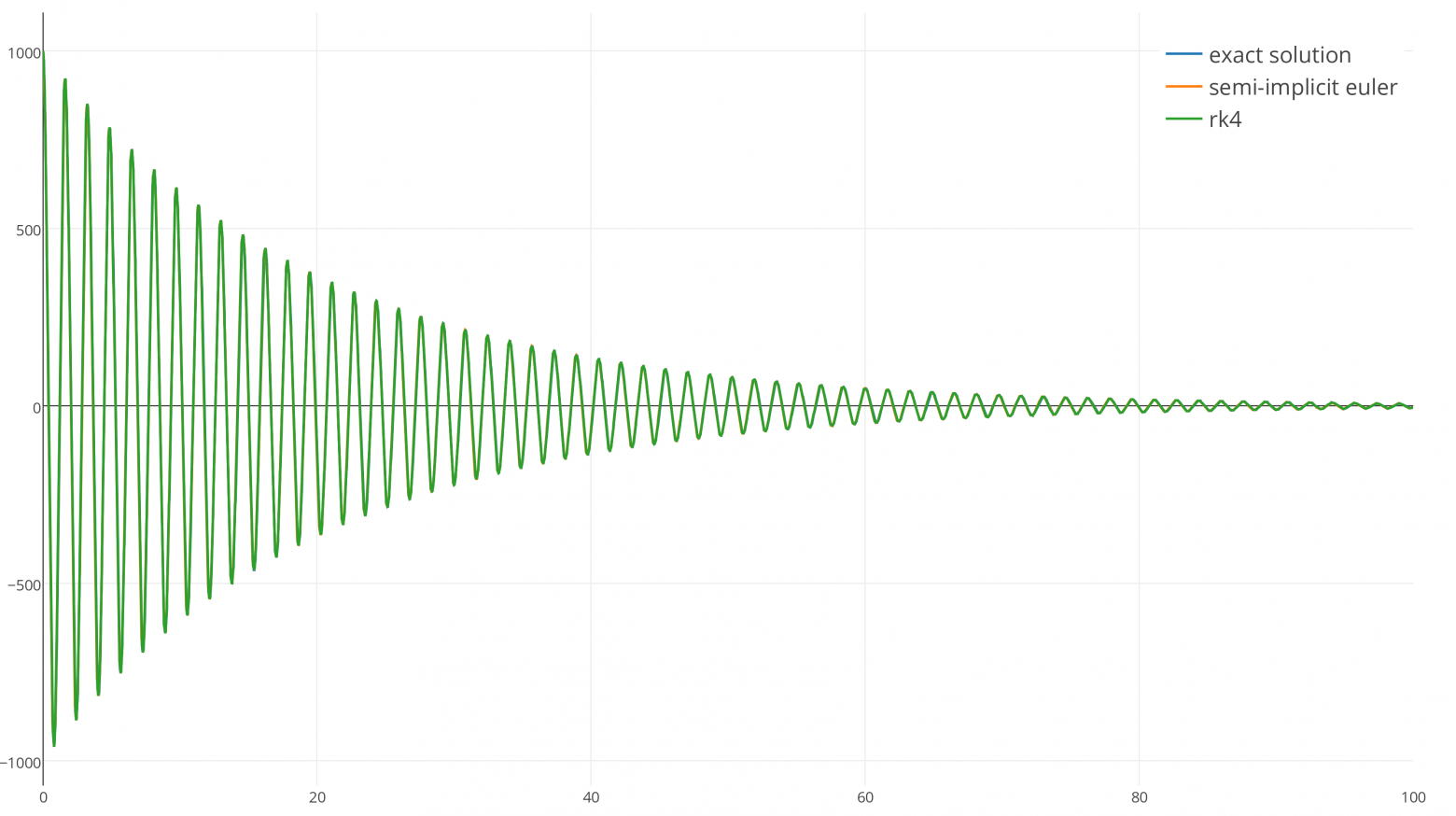
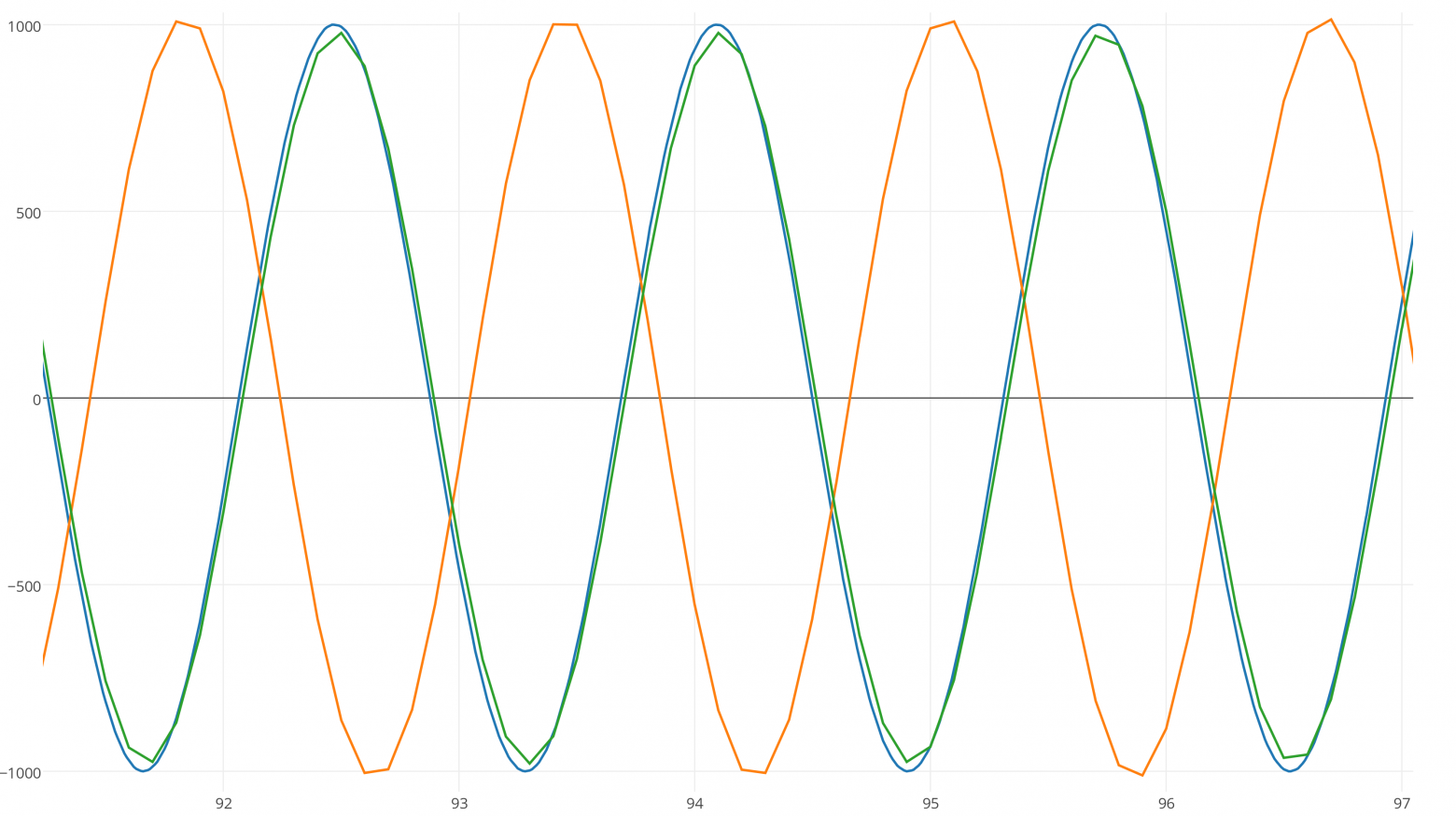
Вот пример гармонического осциллятора с затуханием. Это хорошо изученная задача, и для него существует аналитическое решение, которое можно использовать для проверки результата численного интегрирования.

Давайте начнём со слабозатухающей системы, в которой масса колеблется рядом с исходной точкой, постепенно замедляясь.

Вот входные параметры системы масса-пружина:

• Масса: 1 килограмм
• Исходная позиция: 1000 метров от исходной точки
• Коэффициент упругости по закону Гука: k = 15
• Коэффициент затухания по закону Гука: b = 0.1

И вот график точного решения:

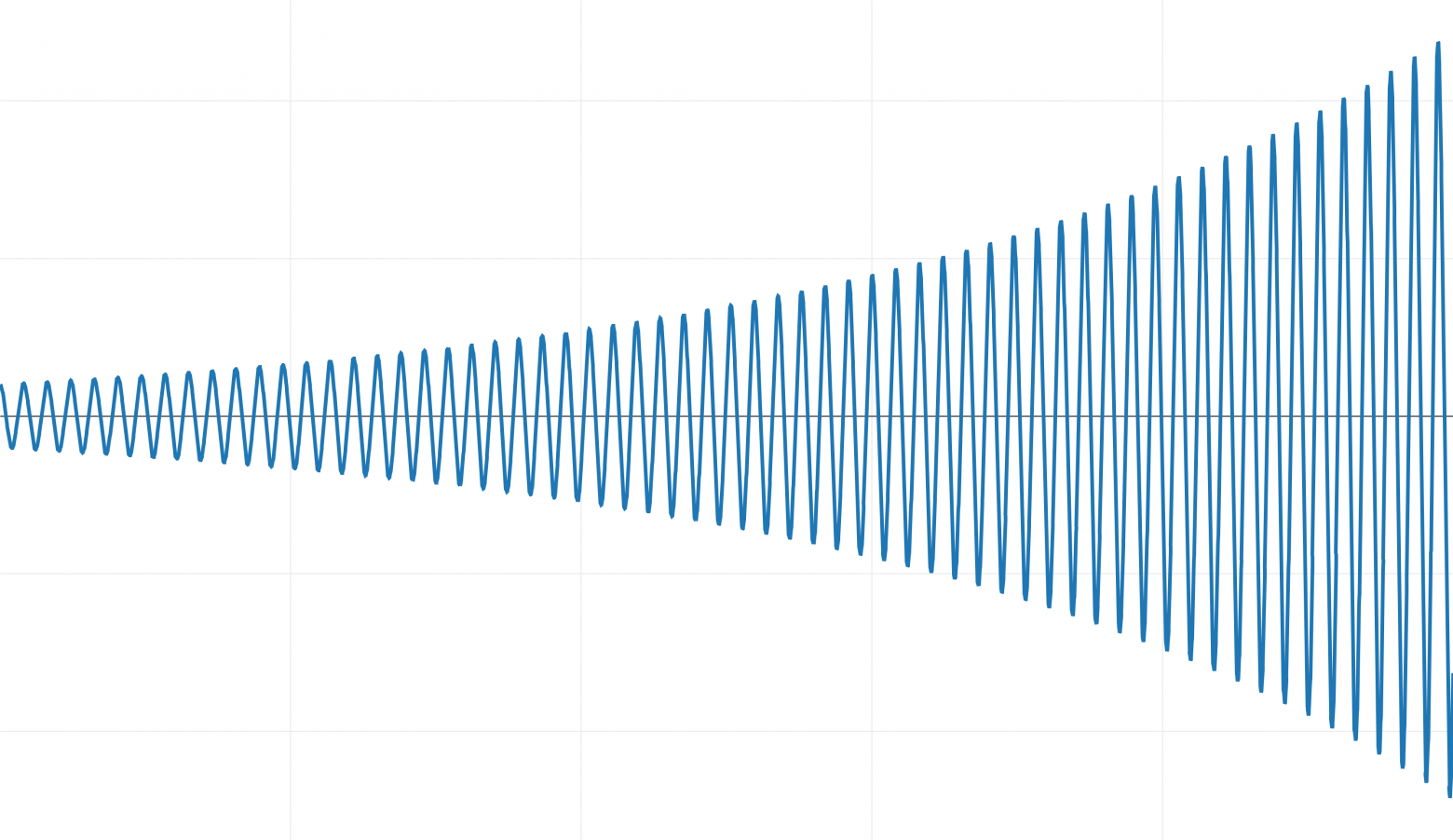
Если для интегрирования этой системы мы применим явный метод Эйлера, то получим следующий результа, который я отмасштабировал по вертикали:

Вместо затухания и сближения с исходной точкой, система со временем набирает энергию!

При интегрировании явным методом Эйлера и с dt= 1 ⁄₁₀₀ такая система нестабильна.

К сожалению, поскольку мы уже интегрируем с малым шагом времени, то не имеем практичных способов повышения точности. Даже если мы уменьшим шаг времени, то всегда будет коэффициент упругости k, при котором мы получим такое поведение.

Симплектический метод Эйлера

Мы можем рассмотреть ещё один интегратор — симплектический метод Эйлера.

В большинстве коммерческих игровых физических движков используется этот интегратор.

Переход от явного к симплектическому методу Эйлера заключается только в замене:

Использование симплектического интегратора Эйлера при dt = 1 ⁄₁₀₀ для системы пружинного амортизатора даёт стабильный результат, очень близкий к точному решению:

Даже несмотря на то, что симплектический метод Эйлера имеет ту же степень точности, что и явный метод (степень 1), при интегрировании уравнений движения мы получаем намного лучший результат, потому что оно является симплектическим.

Существует множество других методов интегрирования

И теперь нечто совершенно другое.

Неявный метод Эйлера — это способ интегрирования, хорошо подходящий для интегрирования жёстких уравнений, которые при других методах становятся нестабильными. Его недостаток заключается в том, что он требует решения системы уравнений на каждом шаге времени.

Интегрирование Верле обеспечивает бо́льшую точность, чем неявный метод Эйлера, и требует меньше памяти при симуляции большого числа частиц. Это интегратор второй степени, который тоже является симплектическим.

Существует целое семейство интеграторов, называемое методами Рунге-Кутты. На самом деле, явный метод Эйлера считается частью этого семейства, но в него входят интеграторы и более высокого порядка, самым классическим из которых является метод Рунге-Кутты порядка 4 (Runge Kutta order 4) или просто RK4.

Это семейство интеграторов названо в честь открывших их немецких физиков: Карла Рунге и Мартина Кутты.

RK4 — это интегратор четвёртого порядка, то есть накапливаемая ошибка имеет порядок четвёртой производной. Это делает метод очень точным, гораздо более точным, чем явный и неявный методы Эйлера, имеющие только первый порядок.

Но хотя он более точен, нельзя сказать, что RK4 автоматически становится «лучшим» интегратором, или даже что он лучше симплектического метода Эйлера. Всё гораздо сложнее. Тем не менее, это довольно интересный интегратор и его стоит изучить.

Реализация RK4

Существует уже много объяснений математики, используемой в RK4. Например: здесь, здесь и здесь. Я настоятельно рекомендую изучить его выведение и понять, как и почему он работает на математическом уровне. Но я понимаю, что целевая аудитория этой статьи — программисты, а не математики, поэтому мы здесь будем рассматривать только реализацию. Так что давайте приступим.

Прежде чем приступить, давайте зададим состояние объекта как struct в C++, чтобы можно было удобно хранить позицию и скорость в одном месте:

Также нам нужна структура для хранения производных значений состояний:

Теперь нам нужна функция для вычисления состояния физики из t в t+dt с помощью одного набора производных, а после этого для вычисления производных в новом состоянии:

Функция ускорения управляет всей симуляцией. Давайте используем её в системе пружинного амортизатора и вернём ускорение для единичной массы:

То, что нужно здесь записать, разумеется, зависит от симуляции, но необходимо структурировать симуляцию таким образом, чтобы можно было вычислять ускорение внутри этого метода для заданных состояния и времени, в противном случае он не подойдёт для интегратора RK4.

Наконец, мы получаем саму процедуру интегрирования:

Интегратор RK4 делает выборку производной в четырёх точках, чтобы определить кривизну. Заметьте, как производная a используется при вычислении b, b используется при вычислении c, и c для d. Эта передача текущей производной в вычисление следующей и даёт интегратору RK4 его точность.

Важно то, что каждая из этих производных a, b, c и d будет разной, когда темп изменения в этих величинах является функцией времени или функцией самого состояния. Например, в нашей системе пружинного амортизатора ускорение является функцией текущей позиции и скорости, которые меняются в шаге времени.

После вычисления четырёх производных наилучшая общая производная вычисляется как взвешенная сумма, полученная из разложения в ряд Тейлора. Эта комбинированная производная используется для перемещения позиции и скорости вперёд во времени, точно так же, как мы делали это в явном интеграторе Эйлера.

Сравнение симплектического метода Эйлера и RK4

Давайте подвергнем проверке интегратор RK4.

Очевидно, что поскольку он является интегратором более высокого порядка (четвёртый против первого) он наглядно будет более точен, чем симплектический метод Эйлера, правда?

Неправда. Оба интегратора так близки к точному результату, что при таком масштабе почти невозможно найти между ними разницу. Оба интегратора стабильны и очень хорошо повторяют точное решение при dt= 1 ⁄₁₀₀.

При увеличении видно, что RK4 действительно более точен, чем симплектический метод Эйлера, но стоит ли эта точность сложности и лишнего времени выполнения RK4? Трудно судить.

Давайте постараемся и посмотрим, сможем ли мы найти значительное различие между двумя интеграторами. К сожалению, мы не сможем долго наблюдать за этой системой, потому что она быстро затухает до нуля, поэтому давайте перейдём к простому гармоническому осциллятору, который колеблется бесконечно и без затуханий.

Вот точный результат, к которому мы будем стремиться:

Чтобы усложнить интеграторам задачу, давайте увеличим шаг времени до 0,1 секунды.

Теперь запустим интеграторы на 90 секунд и увеличим масштаб:

Через 90 секунд симплектический метод Эйлера (оранжевая кривая) сдвинулся по фазе относительно точного решения, потому что его частота немного отличалась, в то время как зелёная кривая RK4 соответствует частоте, но теряет энергию!

Мы чётко можем это заметить, увеличив шаг времени до 0,25 секунды.

RK4 сохраняет верную частоту, но теряет энергию:

А симплектический метод Эйлера в среднем намного лучше сохраняет энергию:

Но от сдвигается от фазы. Какой интересный результат! Как вы видите, если RK4 имеет более высокий порядок точности, то он не обязательно «лучше». В этом вопросе есть множество нюансов.

Заключение

Мы реализовали три различных интегратора и сравнили результаты.

1. Явный метод Эйлера
2. Симплектический метод Эйлера
3. Метод Рунге-Кутты порядка 4 (RK4)

Так какой же интегратор стоит использовать в игре?

Я рекомендую симплектический метод Эйлера. Он «дёшев» и прост в реализации, гораздо стабильнее явного метода Эйлера и в среднем стремится к сохранению энергии даже при близких к предельным условиях.

Если вам действительно нужна бОльшая точность, чем у симплектического метода Эйлера, я рекомендую посмотреть на симплектические интеграторы более высокого порядка, рассчитанные на гамильтоновы системы. Таким образом вы изучите более современные техники интегрирования высокого порядка, которые лучше подходят для симуляций, чем RK4.

И наконец, если вы всё ещё пишете в игре такое:

То потратьте секунду и замените эти строки на:

Две основные задачи динамики точки в теоретической механике

Содержание:

Две основные задачи динамики точки:

Используя дифференциальные уравнения движения материальной точки в. той или другой системе координат, можно решать две основные задачи динамики точки.

Первая задача

Зная массу точки и ее закон движения, можно найти действующую на точку силу. Действительно, если, например, заданы уравнения движения точки в декартовой системе координат

то проекции силы на оси координат определяются из дифференциальных уравнений движения точки (9), т. е.

Зная проекции силы на координатные оси, легко определить модуль силы и косинусы углов силы с осями координат.

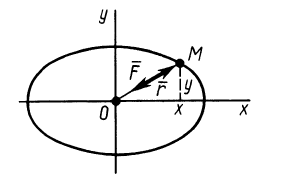
Пример 1. Точка , имеющая массу (рис. 5), движется в плоскости так, что уравнениями ее движения являются

где , , — постоянные положительные величины; — время.

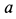
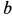
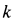
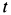
Определить силу, под действием которой точка совершает это движение.

Решение. Найдем уравнение траектории точки в координатной форме, исключая время из уравнений движения:

Траекторией точки является эллипс с полуосями 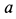и .

Рис. 5

На основании дифференциальных уравнений движения точки (10)

или, если ввести координаты движущейся точки,

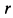
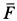
где —радиус-вектор движущейся точки. Косинусы углов силы с осями координат

Отсюда можно заключить, что сила 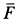имеет направление, противоположное радиусу-вектору . Окончательно

Рис. 6

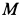
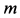
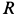
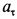
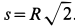
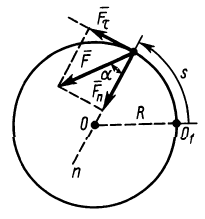
Пример 2. Точка , имеющая массу (рис. 6), движется из состояния покоя по окружности радиусом с постоянным касательным ускорением . Определить действующую на точку силу в момент, соответствующий пройденному точкой по траектории расстоянию .

Решение. Применяя дифференциальные уравнения движения точки в проекциях на естественные оси, имеем:

Так как движение происходит с постоянным касательным ускорением 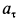без начальной скорости, то

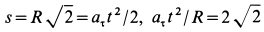
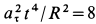
В момент, когда и, следовательно, ,

Тангенс угла 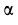между радиусом окружности и силой

Из рассмотрения первой задачи динамики точки видно, что по заданной массе точки и уравнениям ее движения сила полностью определяется как по величине, так и по направлению.

Вторая задача

По заданной массе и действующей на точку силе необходимо определить движение этой точки. Рассмотрим решение этой задачи в прямоугольной декартовой системе координат. В общем случае сила 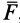, а следовательно, и ее проекции на координатные оси могут зависеть от времени, координат движущейся точки, ее скорости, ускорения и т. д. Для простоты ограничимся случаем зависимости силы и ее проекций на оси координат от времени, координат и скорости. Дифференциальные уравнения движения точки (9) имеют вид

Для нахождения уравнений движения точки в декартовых координатах необходимо проинтегрировать систему трех обыкновенных дифференциальных уравнений второго порядка. Из теории обыкновенных дифференциальных уравнений известно, что решение одного дифференциального уравнения второго порядка содержит две произвольные постоянные. Для случая системы трех обыкновенных дифференциальных уравнений второго порядка имеется шесть произвольных постоянных: .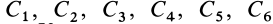

Каждая из координат 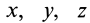движущейся точки после интегрирования системы уравнений (9) зависит от времени t и всех шести произвольных постоянных, т. е.

Если продифференцировать уравнения (13) по времени, то определяются проекции скорости точки на координатные оси:

Таким образом, задание силы не определяет конкретного движения материальной точки, а выделяет целый класс движений, характеризующийся шестью произвольными постоянными. Действующая сила определяет только ускорение движущейся точки, а скорость и положение точки на траектории могут зависеть еще от скорости, которая сообщена точке в начальный момент, и от начального положения точки. Так, например, материальная точка, двигаясь вблизи поверхности Земли под действием силы тяжести, имеет ускорение 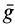, если не учитывать сопротивление воздуха. Но точка будет иметь различные скорости и положение в пространстве в один и тот же момент времени и различную форму траектории в зависимости от того, из какой точки пространства началось движение и с какой по величине и направлению начальной скоростью.

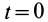
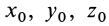
Для выделения конкретного вида движения материальной точки надо дополнительно задать условия, позволяющие определить произвольные постоянные, которых в общем случае будет шесть. В качестве таких условий обычно задают так называемые начальные условия, т.е. в какой-то определенный момент времени, например при (рис. 7), задают координаты движущейся точки и проекции ее скорости :

Рис. 7

Используя эти начальные условия и формулы (13) и (14), получаем шесть следующих уравнений для определения шести произвольных постоянных:

Если система уравнений (16) удовлетворяет условиям разрешимости, то из нее можно определить все шесть произвольных постоянных.

Начальные условия в форме (15) определяют единственное решение системы дифференциальных уравнений (9) при соблюдении соответствующих условий теории дифференциальных уравнений. Условия в других формах, как например, задание двух точек, через которые должна проходить траектория движущейся точки, могут дать или несколько решений, удовлетворяющих этих условиям, или не дать ни одного решения.

При движении точки в плоскости имеется два дифференциальных уравнения движения. В решения этих уравнений входят четыре произвольные постоянные. Постоянные определяются из начальных условий

В случае прямолинейного движения точки имеется только одно дифференциальное уравнение и в его решение входят две произвольные постоянные. Для их определения необходимо задать начальные условия:

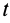
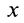
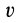
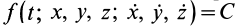
Задача интегрирования системы дифференциальных уравнений (9′) при заданных начальных условиях в общем случае является довольно трудной. Даже в простейшем случае прямолинейного движения, когда имеется только одно дифференциальное уравнение, его решение удается выразить точно в квадратурах лишь при определенной зависимости силы от времени , координаты и скорости . Поэтому важно определение таких соотношений из системы уравнений (9′), которые являются следствиями этой системы и в которые входят производные от координат точки только первого порядка. Такие соотношения, например, в виде называют первыми интегралами системы дифференциальных уравнений (9′).

Если из системы (9′) удается найти три независимых первых интеграла, то задача интегрирования упрощается, так как вместо интегрирования системы дифференциальных уравнений второго порядка достаточно проинтегрировать систему трех дифференциальных уравнений первого порядка, которую представляют эти первые интегралы.

В дальнейшем будет рассмотрен способ получения первых интегралов дифференциальных уравнений движения точки из так называемых общих теорем динамики в некоторых частных случаях движения точки.

Для выяснения особенностей решения второй основной задачи динамики, имеющей прикладное значение, рассмотрим ее решение для случая как прямолинейного, так и криволинейного движения материальной точки.

Две основные задачи динамики

Динамика имеет две основные задачи:

1. по заданному движению определить действующие силы
2. по заданным силам определить движение

Прямая и обратная задачи динамики

В динамике изучают механическое движение в связи с силами, приложенными к движущимся объектам. Следовательно, перед динамикой стоят две основные задачи:

1. по движению материального объекта (точки, твердого тела или системы точек) определить силы, производящие, данное движение. Эту задачу называют прямой, или первой основной задачей динамики;
2. вторая задача — обратная по отношению к первой, поэтому ее называют обратной, или второй основной задачей динамики: даны силы, действующие на данный материальный объект; требуется определить движение этого объекта под действием данных сил.

Наиболее просты с механической стороны эти задачи для одной материальной точки, хотя и здесь встречаются большие трудности математического характера.

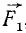
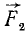
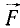
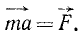
Пусть точка M массы m находится под действием сил, представленных в мгновение t векторами ,, . , или их равнодействующей . Согласно основному закону динамики ускорение, получаемое точкой M от действия сил, направлено по силе и пропорционально ей:

(123)

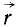
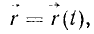
Если решают первую основную задачу динамики точки и движение точки определено в векторной форме, т. е. дан радиус-вектор как некоторая векторная функция времени t:

(54)

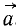
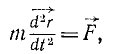
то надо определить по (57) ускорение , выражающееся второй производной от радиуса-вектора точки по времени t, и умножить его на массу т точки. Тогда мы получим следующее выражение основного закона динамики:

(125)

где правая часть даст нам искомую силу.
Если же решают вторую основную задачу динамики точки и задан вектор силы, но требуется определить радиус-вектор как функцию (54) от времени, то для решения задачи нужно интегрировать уравнение (125).

Значительно проще решать такие задачи не в векторной, а в координатной форме.

Все основные теоремы динамики точки могут быть выведены из трех дифференциальных уравнений движения материальной точки в прямоугольных координатах: mx = X; mу = Y; mz =Z

Дифференциальные уравнения движения точки в прямоугольных координатах

Пусть движение точки M задано в прямоугольных координатах кинематическими уравнениями

x = x (t), y = y (t), z = z (t). (58)

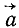
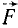
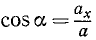
Преобразуем выражение (123) основного закона динамики; для этого определим проекции на оси координат ускорения и силы . Направляющие косинусы (67) ускорения являются вместе с тем и направляющими косинусами силы, так как направление ускорения совпадает с направлением силы. Умножая величины (123) на , получим: ma_x = F cos α.

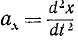
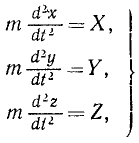
Но согласно (65) . Подставляем это значение и, пользуясь для проекции силы на ось абсцисс (и аналогично для проекций на оси у и z) знакомым нам по статике обозначением, получим

(126)

или, если обозначать вторые производные по времени двумя точками,

mx = X; mу = Y; mz =Z (126 / )

Система трех дифференциальных уравнений (126) второго порядка эквивалентна системе шести дифференциальных уравнений первого порядка:

(127)

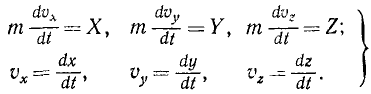
Уравнения (126) или (127) называют дифференциальными уравнениями движения материальной точки в прямоугольных координатах.

Из уравнений движения мы выведем все теоремы динамики. Они дают возможность решить и обе основные задачи динамики точки. В прямой задаче, когда кинематические уравнения движения (58) даны, решение сводится к дифференцированию этих уравнений: умножив на массу вторую производную от координаты но времени, получим проекцию силы. В обратной задаче, когда заданы проекции силы X, Y и Z, а нужно определить координаты точки х, у и z как функции времени (58), решение сводится к интегрированию трех совместных дифференциальных уравнений, где независимым переменным является время.

Три совместных дифференциальных уравнения (126) второго порядка определяют координаты х, у и z в функции времени t. Если движущаяся точка M совершенно свободна, то приложенные к ней силы могут быть функциями ее координат х, у и z, проекций ее скорости х, у и z и времени t:

Проинтегрировать их в общем виде невозможно, но при некоторых видах функции F эти интегралы могут быть получены. В очень многих случаях вычисления возможно проводить на интегрирующих машинах.

При интегрировании дифференциальных уравнений движения материальной точки появляется шесть постоянных интеграции, которые при решении каждой задачи должны быть определены из начальных условий

Постоянные интегрирования

Общие интегралы дифференциальных уравнений движения материальной точки содержат шесть постоянных интеграции: C₁, C₂, C_3, C₄, C₅, C₆. Эти постоянные величины отнюдь не являются произвольными, и в каждой частной задаче, при решении которой приходится интегрировать дифференциальные уравнения движения, постоянные интеграции должны быть определены из начальных условий. Если заданы положение и скорость движущейся точки для какого-либо мгновения t=t₀ (t₀ может быть равным или не равным нулю), то нужно определить постоянные C₁, C₂, C_3, C₄, C₅ и C₆ таким образом, чтобы при t=t₀ координаты х, у и z получили заданные значения х₀, у₀ и z₀ и производные
х, у и z — заданные значения υ_0x, υ_0y, и υ_0z.

Допускают, что данным начальным условиям соответствует только одно движение, конечно, при заданной массе m и силе F. В справедливости этого положения мы -убедимся на всех примерах, которые будем рассматривать, хотя это положение имеет и математическое доказательство. Поэтому, если мы нашли какое-либо движение точки M, удовлетворяющее уравнениям (126) и начальным данным, то, следовательно, мы определили именно то движение, которое искали.

Задача №1

Точка массы т кг движется по винтовой линии согласно кинематическим уравнениям движения: х=r cos kt, у =r sin kt, z=ut, где x, у, z и r выражены в метрах, а t — в секундах; известно, что r, k и и постоянны. Определить величину и направление силы в функции расстояния.

Решение. Задача заключается в определении силы по заданному движению, т. е. является прямой задачей динамики. Условие выражено в физической системе единиц (СИ). При решении будем выражать длину в метрах, мaccy- в килограммах и время — в секундах.

Определим по (126) проекции силы на координатные оси, для чего сначала дважды продифференцируем заданные текущие координаты точек:

х=rk 2 cos kt, у =rk 2 sin kt, z=0

Умножая на т полученные значения проекций ускорения, определим в ньютонах проекции силы:

X= — mk 2 x, Y = — mk 2 y, Z=0

Направляющие косинусы силы найдем по (6):

Ответ. Сила постоянна по величине и перпендикулярна к оси Oz.

Задача №2

Из орудия, стоящего на берегу на высоте 30 ,и над уровнем моря (рис. 160), выпущен снаряд массы m кг со скоростью 1000 м/сек под углом 30° к плоскости горизонта и под углом 60° к линии берега. Пренебрегая сопротивлением воздуха, определить точку, в которой упадет снаряд.

Решение. Единственной силой, действующей па снаряд во время полета, является его вес G = mg. Пo данной силе и по начальным данным (местоположение орудия и начальная скорость снаряда) надо определить движение снаряда и место его падения в морс. Задача относится к обратным задачам динамики. Для ее решения надо составить и проинтегрировать дифференциальные уравнения движения снаряда. Задачу будем решать в единицах СИ. Построим систему координат, взяв за начало точку О, находящуюся под орудием на уровне моря. Ось Ox направим горизонтально, перпендикулярно к берегу в сторону моря, ось Oy— вдоль берега, а ось Oz—вертикально вверх.

Для составления дифференциальных уравнений движения надо знать проекции действующей силы на оси координат. На снаряд после вылета его из орудия действовала только одна сила тяжести G = mg, направленная по вертикали вниз. Проекции действующей силы:

Дифференциальные уравнения движения снаряда напишем в виде (127):

Сокращаем на m, разделяем переменные:

откуда, интегрируя, находим:

Чтобы определить постоянные интеграции, подставим вместо t нуль, а вместо проекций скорости-их начальные значения υ_ox, υ_oy, и υ_oz, соответствующие мгновению t = 0. Получим

Таким образом, три первые постоянные интеграции в нашей задаче равны проекциям начальной скорости снаряда. Чтобы определить числовые значения этих проекций, надо знать направляющие косинусы начальной скорости. Снаряд был выпущен под углом 30° к плоскости горизонта, следовательно, угол ур> 0 начальной скорости с вертикалью равен 60°. Угол β_υ,₀, по условию задачи, тоже равен 60 o , cos _υ,₀ определим из равенства единице Суммы квадратов направляющих косинусов:

Теперь нетрудно определить и проекции начальной скорости:

Мы получили числовые значения постоянных интеграции:

Подставляя эти значения постоянных в уравнения и выражая проекции скоростей по (63), получим три новых дифференциальных уравнения:

Разделив переменные и проинтегрировав, получим

Для определения C₄, C₅ и C₆ подставим и в эти уравнения вместо t его частное значение 0, а вместо х, у и z —их частные значения x₀, у₀ и z₀:

При выбранной нами системе координат имеем x₀ =0; y_{0 =} 0; z₀ = + 30м, следовательно, C₄ = 0; C₅=0; C₆=+30.
Подставляя эти значения в уравнения, полученные после второго интегрирования, найдем кинематические уравнения движения снаряда:

Чтобы определить положение точки, в которой снаряд упадет в море, надо знать продолжительность полета снаряда. Для этого приравняем нулю аппликату z, так как в мгновение, когда снаряд коснется моря, он будет находиться в плоскости хОу. Из уравнения

4,905t 2 — 500t-30 = 0

находим два значения: t=101,6 сек и t=—0,06 сек. Второе значение отбрасываем а первое подставляем в кинематические уравнения движения. Находим ответ.
Ответ. x = 71 831 м — 71,8 км; у = 50 800 м — 50,8 км; z = 0.

Из этого примера видно, что движение точки зависит не только от действующих сил, но и от начальных данных. Если бы начальная скорость или начальные координаты были иными, то и движение снаряда отличалось бы от полученного. Оно по-прежнему было бы равномерным но горизонтали и равнопеременным по вертикали; траекторией снаряда оставалась бы парабола, но она была бы иной и иначе расположенной; иной была бы и точка попадания. Полученные значения постоянных C₁, C₂, . C₆ определены для данной задачи, и при этих значениях постоянных может быть только одно найденное нами решение. Эти постоянные величины вовсе не являются произвольными. Постоянные интеграции, являясь первоначальными значениями переменных, придают решению какой-либо задачи механики всю ту общность, какую она способна иметь.

Вариации постоянных интеграции. Пусть движение какой-либо точки M массы m происходит под действием силы 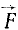. Составив и проинтегрировав дифференциальные уравнения движения точки, определим постоянные интеграции C₁, C₂, . C₆. Тогда, подставляя в полученные уравнения частные значения времени t, мы можем определить положение точки M во всякое данное мгновение. Пусть, например, в мгновение t₁ координаты точки M равны x₁, y₁, z₁. Если мы дадим постоянным интеграции бесконечно малые приращения δC₁, δC₂, . произвольного знака и произвольной величины, называемые вариациями, то положение точки M в то же мгновение t₁, но при измененных постоянных интеграции C₁ + δC₁, C₂ + δC₂, . будет иным. Точка M при неизменившемся времени получит бесконечно малое отклонение, координаты ее получат некоторые бесконечно малые приращения δx₁, δy₁, δz₁, называемые вариациями координат точки, при движении, определяемом величинами C₁, C₂, . постоянных интеграции.

Задача №3

Движение точки весом 2 Г выражается уравнениями x= 3cos2πt см; y=4sinπt см, где t выражено в секундах. Определить проекции силы, действующей на точку, в зависимости от ее координат.

Решение. Задача относится к прямым задачам динамики: по данному движению точки надо определить действующую силу. Для ее решения продифференцируем дважды кинематические уравнения движения точки и, умножив на m найденные х и у, получим X и Y.

Условие дано в технической системе единиц, и в этой задаче примем L в см, F в Г и T сек. Кинематические уравнения движения известны. Дифференцируя дважды, находим

х — 4π 2 3 cos 2πt = — 4π 2 x;
у = —4π 2 sin πt = — π 2 у.

Умножая массу 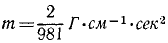на проекции ускорения, найдем проекции силы в граммах. Чтсбы перевести их в ньютоны, надо умножить число граммов на 0,00981.

Решим теперь эту же задачу в физической системе единиц. Принимать за основные единицы метр, килограмм и секунду в этой задаче нецелесообразно. Выразим L в см, M в г и T в сек.

В условии задачи дан вес точки G = 2 Г. Следовательно, ее масса m = 2 г. Умножая проекции ускорения на массу, выраженную в граммах, получим проекции силы в динах:

X = — 8π 2 x = — 78,88x [дин];
Y = — 2π 2 y = — 19,72y [дин].

Чтобы выразить их в ньютонах, надо число дин поделить на 100000.

Ответ. X =— 0,08χ Г = —78,88x дин = —0.0007888x н;
Y = —0,02x Г =— 19,72y дин = —0,0001972y н.

Обратим внимание на одно обстоятельство, которое легко усмотреть в только что решенной задаче. Определяя силу по заданному движению материальной точки, мы нашли, что движение произведено силой, являющейся функцией координат точки. Но мы могли бы выразить силу и как функцию времени. В самом деле, продифференцировав дважды кинематические уравнения движения и умножив вторые производные на m, найдем

X = — 12rnπ 2 cos 2πt; Y = —4rnπ 2 sin πt.

Так одно и то же движение может совершаться под действием различно выраженной силы.

Из этого же примера видно, что если точка движется в одной плоскости, то, приняв эту плоскость за плоскость хОу, можно описать движение точки системой первых двух дифференциальных уравнений движения (126′); третье же дифференциальное уравнение становится лишним.

Задача №4

Найти плоскую траекторию точки M массы m, притягиваемой к неподвижному центру О с силой, пропорциональной расстоянию r и равной k 2 mr, при следующих начальных данных:

Решение. Задача относится к обратным задачам динамики: по заданной силе определить движение. Точка M описывает плоскую траекторию, и нам понадобятся только два уравнения движения.

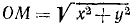
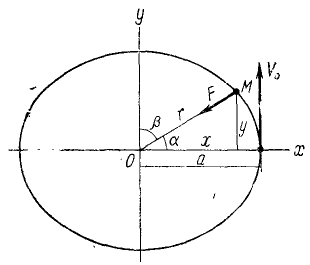
Если в какое-либо мгновение t точка M имела координаты х и у и находилась от центра на расстоянии (рис. 161), то проекции силы на оси координат:

Рис. 161

Дифференциальными уравнениями движения точки являются:

Сократим на т и умножим первое из уравнений на υ_xdt=dx, а второе—на υ_ydt = dy:

Интегрируем и умножаем на 2:

Для определения постоянных интеграции C₁ и C₂ подставляем в эти уравнения вместо переменных величин их начальные значения:

Значения постоянных вносим в уравнения, одновременно выражая υx и υy по (63):

Извлекаем квадратные корни, разделяем переменные н интегрируем:

Для определения постоянных интеграции C₃ и C₄ подставляем в эти уравнения вместо переменных величин t, х и у их начальные значения:

Эти значения постоянных интеграции вносим в уравнения:

Мы получили кинематические уравнения движения (58) точки в декартовых координатах. Чтобы определить траекторию, надо из них исключить время. Возводя в квадрат и складывая, получаем уравнение траектории

Ответ. Эллипс с полуосями a и .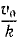

В еще более частном случае, когда сила имеет постоянное направление, а начальная скорость направлена по силе или равна нулю, движение точки прямолинейно. Направив ось Ox по этой траектории, мы обойдемся первым из уравнений (126), которое и нужно интегрировать, чтобы получить закон (58 , ) искомого движения точки. При этом нельзя забывать, что под X мы понимаем не силу, а ее проекцию F cos a, которая в данном случае по величине равна модулю силы. Если α = 0, то сила направлена в сторону положительной оси Ох, и тогда Х>0. Если же α = π, то сила направлена в сторону отрицательного направления оси Ох, тогда X 2 υ 2 .

Решение. Предположим, что тело начинает падать из начального положения О, и направим вниз из точки О ось Ох. Так как движение прямолинейное, то для его определения достаточно первого уравнения (126). На падающее тело действуют две силы: 1) постоянная сила G = mg, направленная в положительную сторону оси Ох, и 2) переменная сила R = mgk 2 υ 2 , являющаяся функцией скорости; она возрастает пропорционально квадрату скорости и направлена против скорости, а следовательно, против положительного направления оси Ох. Имеем

Перепишем это уравнение, сократив его на m:

Из этого уравнения видно, что падение не может быть равноускоренным, что по мере возрастания скорости сила сопротивления увеличивается, правая часть уравнения уменьшается и ускорение стремится к нулю.

Чтобы взять интеграл, перемножим соответственно левые и правые части этого уравнения и следующего выражения:

Это уравнение позволяет определить скорость падающего тела во всякое данное мгновение t. Оно уточняет известную формулу υ=gt, так как здесь учтено и сопротивление воздуха.

Ответ.

Движение точки можно описать в проекциях на оси естественного трехгранника двумя уравнениями:

Дифференциальные уравнения движения материальной точки в форме Эйлера. В кинематике мы изучали три способа определения движения точки: 1) векторный, 2) в прямоугольных координатах, 3) естественный. Соответственно и в динамике мы можем определить движение точки по заданным силам (или силы по заданному движению) векторным уравнением (125), в проекциях на прямоугольные оси — уравнениями (126), а также естественными уравнениями движения. Из многих форм уравнений движения эти три применяют наиболее часто.

Проецируя ускорение на оси естественного трехгранника, мы нашли (см. § 23), что проекции ускорения на касательную а_N, на главную нормаль αv и на бинормаль a_b выражаются следующими формулами:

и вместо трех составляющих полное ускорение имеет только две. Но сила всегда направлена по ускорению точки, а следовательно, проецируя силу на оси естественного трехгранника, мы и здесь получим только две составляющие (F_T — на касательную и F_N— на главную нормаль) и определим движение точки только двумя уравнениями:
(128)

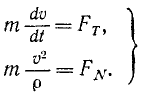
Задача №6

Горнолыжник в конце склона развил скорость 54 км/ч, после чего свободно скользил по горизонтальному прямолинейному участку пути. Определить длину и время свободного скольжения, если коэффициент трения лыж по снегу f’ = 0,051.

Решение. В задаче примем единицы СИ; тогда вес лыжника, выраженный в ньютонах, G = 9,81 ∙m, где m — его .масса в кг. Задача является обратной задачей динамики, так как требуется определить движение по заданной силе F_гp— f’G. Достаточно одного первого из уравнений (128), потому что движение прямолинейное. Проекция силы имеет отрицательный знак, так как сила трения направлена против скорости, а скорость направлена в положительном направлении (в сторону возрастания расстояния): .

Сокращаем на m и разделяем переменные:

Чтобы определить постоянную C₁, подставим вместо t нуль, а вместо υ—начальное значение скорости —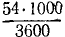= 15 м/сек:

Подставляя это значение C₁ в уравнение, полученное после интегрирования, и заменяя υ по (53), получим новое дифференциальное уравнение:

Разделим переменные и проинтегрируем:

В начальное мгновение лыжник не прошел еще никакого расстояния по горизонтальному участку, а потому C₂ = 0. Время скольжения до остановки определим, положив в уравнении, полученном для скорости,

15 — 0,50t=0, откуда t = 30.

Подставляя это значение t в последнее уравнение, найдем длину свободного скольжения.

Ответ. Время скольжения 30 сек, длина 225 м.

Задача №7

Маятник Борда для определения ускорения свободно падающих тел представляет собой латунный шарик массой 200 г, подвешенный на очень тонкой проволоке длиной 100 см. При качании шарик в наинизшем положении имеет скорость 8 см/сек. Определить натяжение проволоки в ее нижнем конце при наинизшем положении маятника.

Решение. В задаче применена физическая система единиц. Примем L в см, M в г, T в сек.

Задача относится к прямым задачам динамики. Чтобы по данному движению латунного шарика, принимаемого за материальную точку, определить действующую силу, напишем второе из естественных уравнений движения материальной точки (128). В наинизшем положении на шарик действует сила натяжения проволоки, проекцию которой T будем считать положительной, так как она направлена внутрь траектории, и сила тяжести G = 200 . 981 дин, проекцию которой будем считать отрицательной:

или, подставляя числовые значения,

откуда получаем ответ.
Ответ. T = 196 328 дин = 1,96328 н.

Движение точки в плоскости можно описать двумя уравнениями в полярных координатах.

Уравнения движения точки в полярных координатах

В ряде задач бывает удобно исследовать движение точки в полярных координатах. Примем без доказательства, что проекция ускорения точки на полярный радиус-вектор равна (r — rφ 2 ), а на перпендикулярное направление равна (rφ + 2rφ). Помножив на массу эти проекции ускорения точки и приравняв проекциям силы, напишем дифференциальные уравнения движения точки в полярных координатах:

(129)

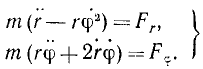
где m_k—масса k-й точки, x_k, y_k и z_k-проекции ее ускорения, a X_k, Y_k и Z_k—проекции равнодействующей всех сил, приложенных к этой точке (k = 1, 2, 3, . n).

Далеко не всегда действующие силы бывают известны. Обычно остаются неизвестными внутренние силы. Для вывода некоторых общих теорем динамики и при решении некоторых частных задач бывает удобным выделить внутренние силы уже при написании дифференциальных уравнений движения.

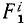
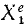
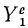
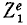
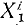
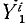
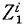
Рассмотрим сначала одну из материальных точек системы, например точку с индексом 1 , а сложив все внутренние, получим равнодействующую внутренних сил . Проекции этих сил обозначим ,, и ,, .

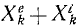
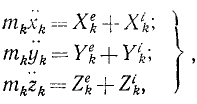
Аналогично поступим с силами, приложенными к остальным точкам, и заменим в написанных выше уравнениях проекции равнодействующей X_k суммой , то же сделаем по двум другим осям. Тогда дифференциальные уравнения примут вид:

(130)

Следовательно, движение свободной механической системы, состоящей из n материальных точек, определяется системой 3n дифференциальных уравнений второго порядка.

Если система не свободна, а на нее наложены связи, выражающие некоторую зависимость между координатами точек механической системы, то бывает возможным сократить число дифференциальных уравнений движения, о чем будет подробнее сказано в § 52 и § 53.

В ряде случаев оказывается целесообразным разделить все силы, действующие на материальные точки механической системы на две категории по иному признаку, а именно на активные силы и реакции связей. Как уже было сказано, реакции связей часто зависят от движения системы и не могут быть найдены, пока не определено движение системы. 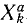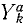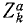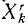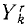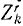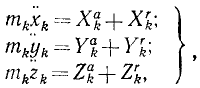Обозначая проекции равнодействующей всех активных сил, действующих на k-ю точку, , и , а проекции равнодействующей всех реакций связей, приложенных к k-й точке, , и , получим:

(130′)

Во всем вашем курсе (если это специально не оговорено) рассмотрены только свободные механические системы и механические системы с идеальными связями. Понятие идеальных связей нам уже встречалось в статике (см. § 4) и будет уточнено в динамике (см. § 51).

В дальнейшем из дифференциальных уравнений (130) и (130′) мы выведем общие теоремы динамики таких материальных систем.

Решение многих проблем по динамике механических систем сопряжено с большими трудностями математического характера. Интегрирующие машины в очень многих случаях дают возможность преодолеть эти трудности.

• Прямолинейное движение точки
• Криволинейное движение материальной точки
• Движение несвободной материальной точки
• Относительное движение материальной точки
• Сложение движение твердого тела
• Кинематика сплошной среды
• Аксиомы классической механики
• Дифференциальные уравнения движения материальной точки

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.