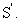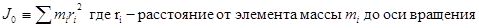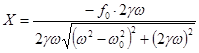Уравнения движения роль начальных условий

РОЛЬ НАЧАЛЬНЫХ УСЛОВИЙ

Векторное уравнение движения материальной точки можно записать в координатной форме:

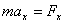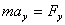(2.6)

Эти три скалярных уравнения, эквивалентные одному векторному уравнению, являются дифференциальными, то есть в них входят вторые производные от координат по времени , поэтому их недостаточно для однозначного описания движения материальной точки. Для однозначного описания движения точки к уравнениям движения надо присоединить дополнительные данные, определяющие значения шести числовых постоянных, получающихся при решении уравнений (2.6), в которые входят вторые производные. В качестве таковых обычно берут значения pадиус-вектора и скорости в момент времени . Эти значения называются начальными условиями.

Поясним этот вопрос на примере движения материальной точки под действием силы тяжести . Уравнение движения в этом случае запишется следующим образом:

(2.7)

Это уравнение эквивалентно двум уравнениям:

, .

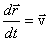
Легко проверить, что этим уравнения удовлетворяют следующие решения:

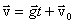(2.8)

где и – произвольные постоянные векторы. Убедиться в этом можно, если взять производные от и по времени. Решение (2.8) называется общим решением уравнения (2.7). Общее решение – это, в сущности, не одно решение, а целое семейство решений, зависящих от двух произвольных векторных постоянных и . Придавая этим постоянным какие-либо конкретные значения, мы выделяем из этого семейства определенное частное решение. Постоянная – начальная скорость движущейся точки, – ее радиус-вектор в начальный момент времени. Величины и определяются начальными условиями. В зависимости от их значений движения могут сильно отличаться друг от друга: тело может двигаться вверх или вниз по прямой линии, может описывать параболу, достигая или не достигая ее вершины. Получается довольно разнообразный класс движений. Заслуга Ньютона и состоит в том, что он подметил, что все многообразие движений может быть описано единой формулой, не содержащей никаких произвольных постоянных, если от положений и скоростей материальной точки перейти к ее ускорению.

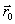
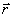
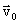
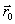
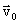
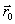
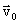
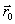
ТРЕТИЙ ЗАКОН НЬЮТОНА

Третий закон Ньютона формулируется следующим образом: силы взаимодействия двух материальных точек равны по величине, противоположно направлены и действуют вдоль прямой, соединяющей эти материальные точки.

Одну из сил, или , согласно Ньютону иногда называют действием, а другую – противодействием. Третий закон Ньютона иначе называют законом действия и противодействия. «Если кто нажимает пальцем на камень, – писал Ньютон, – то и палец его также нажимается камнем. Если лошадь тащит камень, привязанный к канату, то и обратно (если можно так выразиться) она с равным усилием оттягивается к камню. ». Всякому действию соответствует равное и противоположно направленное противодействие (рис.2.7). Следует, однако, заметить, что «действие» по своей природе ничем не отличается от «противодействия». Так, тяжелое тело, лежащее на столе, давит на стол, испытывая со стороны стола противоположно направленное противодействие. Действие – давление камня на стол – обусловлено деформацией камня, противодействие – давление стола на камень – обусловлено деформацией стола. В основе подразделения сил на «действующие» и «противодействующие» лежит представление об активных телах, производящих действие, и пассивных телах, оказывающих противодействие. Так, если мы поднимаем груз за нитку, то активным телом, производящим действие, будем мы сами, а пассивным телом, оказывающим противодействие, будет груз. Однако подразделение тел на активные и пассивные можно провести далеко не всегда. Например, когда Солнце и планета притягиваются друг к другу силами всемирного тяготения, то в этом взаимодействии они выступают совершенно равноправно, и нельзя указать, какое из взаимодействующих тел является активным, а какое – пассивным. Какую из сил, или , назвать действием, а какую – противодействием, – это в большинстве случаев вопрос соглашения.

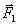
Обосновывая равенство сил действия и противодействия, Ньютон писал: «Относительно притяжений дело может быть изложено вкратце следующим образом: между двумя взаимно притягивающимися телами надо вообразить помещённым какое-либо препятствие, мешающее их сближению. Если бы одно из тел А притягивалось бы телом В сильнее, нежели тело В притягивается телом А, то препятствие испытывало бы со стороны тела А большее давление, нежели со стороны тела В и, следовательно, не осталось бы в равновесии. Преобладающее давление вызвало бы движение системы, состоящей из двух тел и препятствия, в сторону тела В, и в свободном пространстве эта система, двигаясь ускоренно, ушла бы в бесконечность. Такое заключение нелепо и противоречит первому закону, по которому система должна бы оставаться в своём состоянии покоя или равномерного и прямолинейного движения. Отсюда следует, что оба тела давят на препятствие с равными силами, а значит, и притягиваются взаимно с таковыми же».

В основу третьего закона Ньютона положено ньютоновское допущение о мгновенном распространении взаимодействия, которое носит название принципа дальнодействия в классической механике. Согласно этому принципу взаимодействие между телами распространяется в пространстве с бесконечно большой скоростью. Иначе говоря, если изменить состояние одного тела, то сразу же можно обнаружить хотя бы очень слабое изменение во взаимодействующих с ним телах, как бы далеко они не находились.

Сейчас мы знаем, что в действительности это не так – существует конечная максимальная скорость распространения взаимодействий, которая равна скорости света в вакууме. Поэтому третий закон Ньютона (а также и второй) имеет определенные границы применимости.

Примеры

	Баскетболист, забивший мяч, завис на кольце. Противодействующей силе упругости, действующей на спортсмена со стороны кольца, является сила упругой деформации кольца, действующая на кольцо со стороны спортсмена и приложенная к кольцу. Противодействующей силе тяжести, действующей на спортсмена, будет сила гравитационного притяжения Земли баскетболистом, приложенная к Земле
	Сила, с которой самосвал действует на троллейбус при столкновении, равна силе, с которой троллейбус действует на самосвал. При этом последствия действия этих сил для самосвала и троллейбуса могут сильно отличаться. Но ведь в третьем законе Ньютона речь идет только о равенстве сил действия и противодействия, но ничего не говорится о последствиях этого взаимодействия
	Сила, действующая на спортсмена со стороны строп парашюта, равна по величине силе, действующей на стропы со стороны спортсмена
	Сила, с которой спортсмен действует на штангу, и сила, с которой штанга действует на спортсмена, равны по величине и противоположны по направлению. Эти силы приложены к разным телам. Сила, действующая на штангу со стороны спортсмена, уравновешена силой тяжести штанги. Сила, действующая на спортсмена со стороны штанги, в сумме с силой тяжести и силой нормальной реакции опоры, действующими на спортсмена, дают ноль. В результате и штанга, и спортсмен в рассматриваемый момент времени покоятся
	На спортсмена и на катер действуют со стороны соединяющего их каната силы натяжения, равные по величине и противоположные по направлению. Под действием результирующих сил, действующих на катер и спортсмена, эти тела могут двигаться с разными скоростями, ускорениями и в разных направлениях

2.7. ВТОРОЙ ЗАКОН НЬЮТОНА
ДЛЯ СИСТЕМЫ МАТЕРИАЛЬНЫХ ТОЧЕК.
ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА

Тела, образующие механическую систему, могут взаимодействовать как между собой, так и с телами, не принадлежащими данной системе. В соответствии с этим силы, действующие на тела системы, можно разделить на внутренние и внешние. Внутренними называются силы, с которыми на данное тело воздействуют остальные тела системы; внешними – силы, обусловленные воздействием тел, не принадлежащих системе. В случае если внешние силы отсутствуют, система называется замкнутой или изолированной.

Во Вселенной не может быть полностью изолированных систем, поскольку все тела взаимодействуют между собой. Однако при определенных условиях можно тело считать в достаточной степени изолированным. Например, материальное тело в некоторой области космического пространства, достаточно удаленной от массивных космических тел, ведет себя как изолированная система. В других случаях движение системы в определенных направлениях можно рассматривать как движение замкнутой системы, хотя в целом система таковой не является.

Третий закон Ньютона мы сформулировали для замкнутой системы, состоящей из двух материальных точек. Постулируем теперь его справедливость для системы из произвольного числа материальных точек. Пусть – сила, с которой k-я точка системы действует на i-ю, а – сила, с которой i-я точка действует на k-ю. Третий закон Ньютона утверждает, что обе эти силы направлены вдоль прямой, соединяющей взаимодействующие точки, причем

Это соотношение позволяет выполнить переход от механики отдельной материальной точки к механике системы материальных точек.

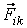
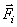
Пусть в системе из N взаимодействующих частиц кроме внутренних сил на -ю частицу действуют внешние силы, результирующая которых равна . Запишем уравнение движение для каждой из N частиц, входящих в систему:

Сложим правые и левые части этих уравнений. Так как , то

Заметим, что импульс системы материальных точек является величиной аддитивной, то есть импульс системы материальных точек равен сумме импульсов отдельных точек, входящих в систему, независимо от того, взаимодействуют они между собой или нет:

где – импульс -й частицы. Тогда

(2.9)

Согласно полученному уравнению, импульс системы материальных точек может меняться только под действием внешних сил. Внутренние силы исключаются третьим законом Ньютона, поэтому внутренние силы не могут изменить импульс системы. Уравнение (2.9) является обобщением уравнения движения для одной материальной точки.

Таким образом, производная по времени от импульса системы материальных точек равна геометрической сумме всех внешних сил, действующих на систему.

2.8. ТЕОРЕМА О ДВИЖЕНИИ ЦЕНТРА МАСС
СИСТЕМЫ МАТЕРИАЛЬНЫХ ТОЧЕК

В любой системе частиц имеется одна замечательная точка, называемая центром масс, которая обладает рядом интересных и важных свойств. Ее положение относительно начала данной системы координат характеризуется радиус-вектором , определяемым как

(2.10)

где – масса и радиус-вектор -й частицы, – масса всей системы, – полное число частиц в системе. Если взять производную по времени от обеих частей уравнения и умножить обе части на , то получится:

где – скорость движения центра масс системы. Таким образом, импульс системы материальных точек равен произведению массы системы на скорость ее центра масс:

Подставив это выражение в (2.9), получим:

(2.11)

Отсюда следует, что центр масс системы материальных точек движется как материальная точка, масса которой равна суммарной массе всей системы, а действующая сила – геометрической сумме всех внешних сил, действующих на все точки системы. Этот результат называется теоремой о движении центра масс системы материальных точек. Уравнение (2.11) по форме совпадает с основным уравнением динамики материальной точки и является его обобщением на систему материальных точек: ускорение системы как целого прямо пропорционально результирующей всех внешних сил и обратно пропорционально суммарной массе системы.

Если система замкнута, то 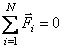и уравнение (2.11) переходит в , следовательно, . Таким образом, центр масс замкнутой системы движется прямолинейно и равномерно или покоится.

Примеры

В безвоздушном пространстве снаряд, выпущенный из пушки под некоторым углом к горизонту, будет двигаться по параболе под действием силы тяжести. Если в какой-либо момент времени снаряд разорвется на мелкие осколки, то эти осколки под действием внутренних сил будут разлетаться в разные стороны. Однако центр масс осколков и газов, образовавшихся при взрыве, будет продолжать свое движение по параболической траектории, как если бы никакого взрыва не было. Действительно, результирующая внешняя сила, действующая на продукты распада, равна силе тяжести, действовавшей на неразорвавшийся снаряд.

При взрыве праздничной ракеты центр масс продуктов распада в течение некоторого времени продолжает двигаться по траектории, по которой двигалась бы ракета, если бы взрыва не произошло

2.9. ПРИНЦИП ОТНОСИТЕЛЬНОСТИ ГАЛИЛЕЯ.
ПРЕОБРАЗОВАНИЯ ГАЛИЛЕЯ

«Открытие спутников Юпитера, фаз Венеры, солнечных пятен и т.д. потребовало лишь наличие телескопа и некоторого трудолюбия, но нужен был необыкновенный гений, чтобы открыть закон природы в таких явлениях, которые всегда пребывали перед глазами, но объяснение которых, тем не менее, всегда ускользало от изысканий философов». Ж.Л. Лагранж

Галилео Галилей (Galileo Galilei), 1564–1642

Галилео Галилей – великий итальянский физик, механик и астроном. Родился в Пизе в 1564 г. в тот самый день, когда умер Микеланджело. Галилей по праву считается одним из основоположников точного естествознания. Ряд открытий Галилея и некоторые его взгляды имели непосредственное отношение к движению небесных тел. В 1632 г. вышла его книга «Диалог о двух главнейших системах мира – Птолемеевой и Коперниковой», в которой Галилей в доступной форме изложил свои взгляды на систему мира Коперника. А годом позже Галилей был вызван на суд римской инквизиции, и там коленопреклоненный был вынужден поклясться, что отрекается от идеи о неподвижном Солнце и движущейся Земле. Он был взят под домашний арест. Однако Галилей не был сломлен. Страдая от болезней и переживаний, он все же нашел в себе силы и мужество, чтобы написать новую книгу «Беседы и математические доказательства, касающиеся двух новых отраслей наук». Это был самый значительный труд Галилея, в котором сконцентрировались плоды всех его научных поисков. Эта книга была издана в Лейдене в 1636 г.

Заслуга Галилея заключалась в том, что он опроверг ошибочное положение динамики Аристотеля и заложил основы современной механики, выдвинул идею об относительности движения, установил законы инерции, свободного падения и движения тел по наклонной плоскости. Галилей первым направил телескоп в небо, открыл горы на Луне, четыре спутника Юпитера, фазы у Венеры и пятна на Солнце.

Прожив 78 лет, совершенно потеряв зрение, Галилей умер 8 января 1642 г., того самого года, в котором на Земле суждено было появиться Ньютону.

Физики любой эпохи будут с благодарностью и уважением вспоминать Галилея, указавшего на то, что новые идеи надо искать «в великой книге – природе», опираясь только на факты.

В 1632 г. в книге «Диалог о двух главнейших системах мира – Птолемеевой и Коперниковой» Галилей обосновал принцип относительности, ставший одним из первых основных принципов физики. Согласно этому принципу все ИСО по своим механическим свойствам эквивалентны друг другу. Это значит, что никакими механическими опытами, проводимыми внутри данной ИСО, нельзя установить, покоится эта система или движется равномерно и прямолинейно. Этот принцип является обобщением опыта и подтверждается всем многообразием приложений механики Ньютона к движению тел, скорости которых значительно меньше скорости света.

Все сказанное достаточно ясно свидетельствует об исключительности свойств ИСО, в силу чего именно эти системы должны, как правило, использоваться для изучения механических явлений.

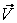
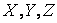
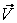
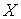
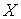
Найдем формулы преобразования координат при переходе от одной ИСО к другой. Допустим, что система отсчета S инерциальна. Рассмотрим вторую систему отсчета S’, движущуюся относительно первой поступательно с постоянной скоростью (рис. 2.8). Свяжем с каждой системой отсчета декартову систему координат. Пусть известно движение точки в одной из этих систем, например, в системе S, то есть известна зависимость координат точки от времени. Как найти движение той же точки в системе отсчета S’? Задача сводится к нахождению формул, выражающих координаты движущейся точки в системе отсчета S’ через ее координаты в системе отсчета S в один и тот же момент времени. Начало координат и направление координатных осей можно выбрать произвольно как в системе отсчета S, так и в системе отсчета S’. Для простоты можно принять, что координатные оси системы S соответственно параллельны координатным осям системы S’ и что в начальный момент начало системы координат, связанной с системой отсчета S, совпадает с началом системы координат, связанной с системой отсчета S’. Кроме того, предположим, что скорость параллельна оси . При этих условиях ось будет все время совпадать с осью .

Пусть в момент времени движущаяся точка находится в положении M. За время начало координат S’ переходит из точки О в положение , причем, так как то

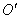
(2.12)

где и – радиус-векторы движущейся точки соответственно в системах отсчета S и

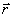
Спроецируем соотношение (2.12) на оси координат:

(2.13)

Формулы обратного преобразования имеют вид

или в координатной форме

(2.14)

Формулы (2.12–2.14) и дают решение поставленной задачи. Они называются преобразованиями Галилея. Мы присоединили к формулам преобразования координат дополнительное выражение , чтобы явно отметить, что время в механике Ньютона считается абсолютным (то есть не меняется при переходе от одной системы отсчета к другой) и поэтому не преобразуется.

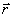
С точки зрения «здравого смысла» преобразования Галилея кажутся очевидными. Однако в основе вывода лежит предположение механики Ньютона об абсолютности длин и промежутков времени. Абсолютность времени явно отмечена в уравнении , при выводе остальных формул использовалось предположение об абсолютности длин. Действительно, формулы (2.12–2.14) были бы очевидными, если и измерялись бы в одной системе отсчета. Мы же измеряем их в разных системах отсчета. По этой причине без предположения об абсолютности расстояний и промежутков времени нельзя обойтись. Релятивистская физика отказалась от такой абсолютности.

Чтобы получить формулы сложения скоростей в нерелятивистской механике, возьмем производную по времени от (2.12):

(2.15)

где – скорость точки в системе отсчета S, а – в системе отсчета . Эта формула выражает закон сложения скоростей в классической механике.

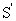
Возьмем производную по времени от (2.15), тогда получим

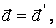(2.16)

где – ускорение точки в системе отсчета S, – в системе отсчета Таким образом, ускорение точки в обеих системах отсчета одинаково. Говорят, что ускорение инвариантно относительно преобразований Галилея.

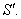
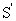
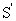
По определению ИСО свободная материальная точка движется в системе отсчета S без ускорения. Формула (2.16) показывает, что движение данной материальной точки в системе отсчета будет также неускоренным. Следовательно, – также инерциальная система отсчета. Таким образом, система отсчета, движущаяся относительно инерциальной системы отсчета прямолинейно и равномерно, также является инерциальной системой. Следовательно, если существует хотя бы одна ИСО, то существует и бесконечное множество ИСО, движущихся относительно друг друга равномерно и прямолинейно.

Сила в классической механике может зависеть от разностей координат, разностей скоростей взаимодействующих точек и от времени. Поэтому, как видно из преобразований Галилея, она не меняется при переходе от одной системы отсчета к другой. Отсюда следует, что уравнение, выражающее второй закон Ньютона, остается неизменным при переходе от одной ИСО к другой. Такие уравнения называются инвариантными. Таким образом, уравнения механики Ньютона инвариантны относительно преобразований Галилея. Это утверждение и составляет содержание принципа относительности Галилея. Равноправие ИСО дает возможность в каждом конкретном случае подбирать систему отсчета, наиболее удобную для решения рассматриваемой задачи.

Итак, принцип относительности Галилея выражает полное равноправие всех ИСО. Однако означает ли это, что одно и то же движение выглядит одинаково во всех ИСО? Конечно, нет! Движение тела, свалившегося с полки равномерно движущегося вагона, является прямолинейным, если его рассматривать относительно вагона. Но то же самое движение происходит по параболе в системе отсчета, связанной с полотном железной дороги, хотя законы механики Ньютона одинаковы в обеих системах отсчета. Движения выглядят по-разному, так как для описания движения к уравнению движения необходимо добавить начальные условия, то есть задать начальное положение тела и его начальную скорость, а они будут различными в разных системах отсчета.

РАБОТА И ЭНЕРГИЯ

Зная законы действия сил на систему частиц и состояние системы частиц (координаты и скорости всех частиц) в некоторый начальный момент времени, можно с помощью уравнений движения предсказать ее дальнейшее поведение, то есть найти состояние системы в любой момент времени. Однако детальное рассмотрение поведения системы с помощью уравнений движения часто бывает связано с большими математическими трудностями. А в тех случаях, когда законы действия сил неизвестны, такой подход оказывается в принципе неосуществимым. Поэтому возникает вопрос: нет ли каких-либо общих принципов, которые позволили бы иначе подойти к решению задачи?

Оказывается, такие принципы есть. Это законы сохранения. Законы сохранения позволяют рассмотреть общие свойства движения без решения уравнений движения и подробной информации о развитии процессов во времени. Законы сохранения были установлены опытным путем, как обобщение огромного количества экспериментальных фактов. В механике имеют значение три закона сохранения: закон сохранения энергии, закон сохранения импульса, закон сохранения момента импульса. Эти законы относятся к числу тех фундаментальных принципов физики, значение которых трудно переоценить. Их роль особенно возросла после того, как выяснилось, что они далеко выходят за рамки механики и представляют собой универсальные законы природы. Во всяком случае, до сих пор не обнаружено ни одного явления, где бы эти законы нарушались.

Открыв возможность другого подхода к рассмотрению различных механических явлений, законы сохранения стали мощным и эффективным инструментом исследования, которым повседневно пользуются физики. Эта важнейшая роль законов сохранения как инструмента исследования обусловлена следующими причинами.

Законы сохранения не зависят ни от траекторий движения, ни от характера действующих сил. Поэтому они позволяют получить ряд общих и существенных заключений о свойствах различных механических процессов, не вникая в детальное рассмотрение их с помощью уравнений движения.

Так как законы сохранения не зависят от характера действующих сил, то их можно использовать даже тогда, когда силы неизвестны. В этих случаях законы сохранения являются единственным и незаменимым инструментом исследования.

Даже в тех случаях, когда силы в точности известны, законы сохранения следует использовать при решении многих задач о движении частиц. Хотя все эти задачи могут быть решены с помощью уравнений движения, привлечение законов сохранения очень часто позволяет получить решение наиболее простым путем, избавляя нас от утомительных математических расчетов. Поэтому при решении новых задач обычно принято придерживаться следующего порядка: прежде всего, применяют законы сохранения, и только убедившись, что этого недостаточно, привлекают для решения задачи уравнения движения.

Решение уравнений движения и роль начальных условий.

Билет1. Вопрос1.

Предмет механики. Пространство и время в механике Ньютона. Система координат и тело отсчёта. Часы. Система отсчёта.

Механика – наука о движении и равновесии тел, и происходящих при этом взаимодействиях между ними.

При построении теории физика заменяет реальные обьекты их идеализированными моделями. Движение – это изменение относительнеого положения тела с течением времени. Впервые принципы механики сформулированы Ньютоном в «Математических началах натуральной философии». Тело или система тел, относительно которых определяется положение остальных тел называется простанственной системой отсчета (ПСО). В качестве ПСО можно взять произвольное твердое тело и связать с ним координатные оси, например, декартовой системы координат. Существует два вида координатных систем: 1) правая, 2) левая. Определяются они с помощью правила буравчика.

Пронстранство и время – это категории, обозначающие основные формы существования материи. Пространство выражает порядок сосуществования отдельных объектов. Время выражает порядок смены явлений.

Пространство (по Ньютону) – это совокупность физического тела и возможных его продолжений.

Время – это показание каких-то часов

Часы – устройство, с которым связан периодический процесс, положенный в основу отсчёта времени.

Основная задача механики состоит в том, чтобы, зная начальные условия, определить закон движения для тел системы.

Системы координат: примеры. Декартовы правостороняя и левосторонняя.

Система отсчёта – это система координат (вместе с телом отсчёта) плюс часы.

Билет2. Вопрос1.

Кинематика материальной точки. Система материальных точек. Уравнение кинематической связи. Закон движения.

Кинематика – раздел механики, посвящённый изучению геометрических свойств движений тел, без учёта их масс и действующих на них сил.

Материальная точка – абстрактное тело нулевых размеров.

Закон движения – зависимость координат точки от времени.

Уравнение траектории – уравнение кривой, по которой движется точка.

Эквивалентное определение траектории – годограф радиус-вектора материальной точки.

Движение материальной точки будет описано полностью, если известно ее положение в любой момент времени в выбранной системе отсчета. Полное описание движения сводится к нахождению трех координат: x = x(t); y = y(t); z = z(t); или к нахождению векторной функции r = r(t). .

– мгновенная скорость.

Производная скорости по времени называется ускорением материальной точки: ,

Понятие угловая скорость и угловое ускорение относятся к случаю движения материальной точки по окружности. Положение точки М на окружности задается углом a, который составляет радиус-вектор точки М с неизменным направлением ОХ. Производная этого угла по времени называется угловой скоростью w: . Если w = Сonst, то движение равномерно. n=w/2p – число оборотов в единицу времени (частота обращения).

Первая призводная угловой скорости и вторая производная угла по времени – это угловое ускорение: . Продифференцируем S=r´a по времени и получаем:

S’’=(w*r)’=r*w’+r’*w=re (r*w’ — тангенциальное ускорение) + (v*w =v 2 /r — центростремительное ускорение).

Уравнение кинематической связи – уравнение, связывающее кинематические характеристики системы.

Билет3. Вопрос1.

Инерциальные системы отсчёта. Преобразования Галилея.

Инерциальнойназывается такая система отсчёта, в которой изолированное тело сохраняет состояние покоя или равномерного и прямолинейного движения.

Изолированным называется такое тело, на которое не действуют другие тела.

абсолютное = переносное + кориолисово + относительное

Выводятся в лоб дифференцированием с учётом: di/dt = [w i]; dj/dt = [w j]; dk/dt = [w k];

(концепция ã ЧМЗ)

Уравнения, остающиеся неизменными при переходе от одной системы отсчета к другой, называются инвариантнымиотносительно этих систем отсчёта.

События, одновременные в одной системе, одновременны и в другой, т. е. утверждение об одновременности двух двух событий имеет абсолютный характер, независимый от системы координат.

Длина – инвариант преобразований Галлилея. Длинной движущегося стержня наз. расстояние между координатами его концов в некоторый момент времени. Следуя из этого инвариантность длинны легко доказывается.

Интервал времени явл. инвариантом преобразований Галлилея (Dt=t₂–t₁=t’₂–t’₁=Dt’)

Сложение скоростей получается из дифференциирования формул преобразования Галлилея.

Ускорение инвариантно относительно преобразований Галлилея. Это утверждение доказывается дифференциированием преобразований скорости и учитывая, что Dt=Dt’.

Билет4. Вопрос1.

Законы динамики. Первый, второй и третий законы Ньютона. Масса и сила в механике Ньютона. Уравнение движения и его решение. Роль начальных условий.

Законы динамики – три закона Ньютона и законы, описывающие индивидуальные свойства сил. (см. гравитация, упругость, трение)

Всякое тело оказывает сопротивление при попытках изменить модуль или направление его скорости. Это свойство тел называется инертностью.

Инертная Масса – это мера инертности тела (при его поступательном движении).

Сила — любая причина, изменяющая импульс движущегося тела (мера взаимодействия). Одно из количественных определений: mr¢¢=F.(имхо: бред)

I закон Ньютона – существуют такие системы отсчёта, в которых изолированное тело сохраняет состояние покоя или равномерного и прямолинейного движения.

II закон Ньютона – a = F / m, где F – равнодействующая сил, действующих на точку, a – ускорение точки, m – инертная масса точки.

III закон Ньютона – совокупность 5 утверждений:

силы взаимодействия в природе возникают парами
эти силы равны по величине
эти силы противоположны по направлению
эти силы действуют вдоль одной прямой
эти силы имеют одинаковую природу

Уравнение движения – 2-й закон Ньютона записанный в виде F = m a, где F – равнодействующая сил, a – ускорение точки, m – инертная масса.

Законы Ньютона инвариантны относительно преобразований Галилея.

Решение уравнений движения и роль начальных условий.

Первый способ решения основной задачи механики состоит в том, чтобы найти закон движения, используя законы динамики.

Система законов, описывающих индивидуальные свойства сил, действующих в системе, подставленные в систему из уравнений движений элементов системы + уравнения кинематической связи дают систему диференциальных уравнений, а законы движения для тел системы являются его решением. Отсюда очевидно, что задача не может быть решена если не известны начальные условия системы.

Билет5. Вопрос1.

Законы, описывающие индивидуальные свойства сил. Закон всемирного тяготения. Закон Гука. Законы для сил сухого и вязкого трения. Явление застоя. Явление заноса.

Закон всемирного тяготения: F₁₂ = — g m₁ m₂ r₁₂ / r₁₂ 3 , где______________.

g=6,67 * 10 -11 м 3 /кг * с 2

Закон Гука – деформация тела, если она достаточно мала, пропорциональна приложенной силе.

Для стержней: s =E e, где s — напряжение на торце стержня sºF/S, где F – продольная сила действующая на торец стержня, S – площадь поперечного сечения стердня E – модуль Юнга – характеристика материала из которого сделано тело. eºDl/l₀, где Dl изменение длины стержня, а l₀ — начальная длина стержня.

Сухое трение.Сила сухого рения покоя возникает на поверхности двух соприкасающихся тел и равна разности сил приложенных к телам. Если 2 поверхности движутся, то сила сухого трения пропорциональна силе нормального давления и направлена в сторону, противоположную скорости тела относительно соприкасающейся с ним поверхности.

Силами тренияобычно называют тангенциальные силы, вознкающие между соприкасающимися телами.

Закон Амонтона-Кулона: F = m N, где ______________, справедлив в 2-х случаях

для максимальных сил трения покоя.
для сил трения скольжения при достаточно малых скоростях.

Сила вязкого трения.В случае силы сухого трения при силах, меньших силы трения скольжения 2 поверхности не движутся относительно друг друга, а вслучае вязкого трения какова бы ни была сила – возникнет движение, причем для малых скоростей сила вязкого трения пропорциональня скорости, а на больших скоростях её квадрату. В общем случае уравнение для силы вязкого трения представляет бесконечный палином.

Явления застоя и заноса – См.

Билет6. Вопрос1.

Импульс материальной точки и импульс силы. Изолированная и замкнутая системы материальных точек. Закон сохранения импульса.

Система материальных точек – это некоторая совокупность конечного числа материальных точек.

Изолированной называется система тел, на которую не действуют другие тела.

Замкнутой называется система тел, для которой равнодействующая всех (внешних) сил равна нулю.

Импульс тела p ºmv; импульс силы P º F*Dt

Из II закона Ньютона следует: Dp=Pдля одной материальной точки. Далее рассматривается система материальных точек и всё обобщается с учётом III закона Ньютона.

Закон сохранения импульса: суммарный импульс системы тел сохраняется неизменным, если система замкнута.

2 важных случая:

Система тел замкнута вдоль какой-либо оси => суммарный импульс системы тел сохраняется неизменным в проекции на эту ось.
Взрыв. F_внутр>>F_внешн и Dt мал. (F_внешн ограничена)

Билет7. Вопрос1.

Центр масс. Теорема о движении центра масс.

Точкой приложения равнодействующей называется точка, относительно которой суммарный момент сил равен нулю.

Центр масс – точка приложения равнодействующей всех массовых сил.

(1) выводится из динамики вращения.

Массовая сила – сила, пропорциональная массам.

Теорема о движении центра масс.Ц. м. системы движется так, как двигалась бы материальная точка с массой равной сумме масс всех элементов системы под действием равнодействующей всех внешних сил, действующих на систему.

Доказывается в лоб, дифференцированием выражения (1) и подстановкой полученного выражения в закон изменения импульса.

Билет8 Вопрос1.

Движение тел с переменной массой. Уравнение Мещерского.

Движение тел с переменной массой–движение при котором тело может приобретать ускорение за счёт внешних сил, а за счёт изменения массы.

Уравнение движения тел с переменной не содержат ничего принципиально нового по сравнению с законами Ньютона, и являются их следствиями. Но они представляют большой интерес в связи с ракетной техникой.

Реактивная сила – это сила упругости, действующая на тело со стороны отбрасываемых им масс.

Выведем уравнение движения материальной точки с переменной массой на примере движения ракеты. Пусть m(t)-масса пакеты в произвольный момент времени t, а v(t)-ее скорость в тот же момент. Импульс ракеты в этот момент будет mv. Спустя dt масса и скорость ракеты получат приращение dm и dv( dm-отрицательна). Импульс ракеты станет (m+dm)(v+dv). Сюда надо добавить импульс движения газов, образовавшихся за dt. Он равен dm_газv_газ –масса и скорость газа, образовавшихся за dt. Вычитая из суммарного импульса системы в момент t+dt импульс системы в момент t, найдем приращение этой величины за dt. Это приращение равно Fdt, где F – геометрическая сумма всех внешних сил, действующих на ракету.

Время dt устремим к нулю. Поэтому, раскрывая скобки, отбрасываем dmdv. Далее dm+dm_газ=0 и v_отн=v_газ—v есть скорость истечения газов относительно ракеты. Тогда

Член v_отн(dm/dt) – реактивная сила . Уравнение (1)-уравнение Мещерского или уравнение движения точки с переменной массой.

Уравнение Мещерского.M dv/ dt = F — m v_отн; mº -dM/dt (dM ( V- Vо) / V отн . (2)

Уравнение (2) – формула Циолковского. Она справедлива для нерелятивистских движений (v и v_отн ( V- Vо) / V отн , где ___________.

Билет10. Вопрос1.

Момент импульса материальной точки. Момент силы. Закон сохранения момента импульса.

Момент силы относительно начала координат М≡[r F]

Плечом силы, действующейв плоскости, перпендикулярной оси вращения,называется расстояние между линией действия силы и осью вращения.

Момент импульса материальной точки относительно начала координат L≡m[r v]

Закон сохранения момента импульса – суммарный момент импульса относительно некоторой геометрической точки/оси сохраняется неизменным, если суммарный момент всех внешних сил относительно этой точки/оси равен нулю.

Доказывается в лоб домножением уравнения изменения импульса на радиус-вектор.

Билет11. Вопрос1.

Работа силы. Энергия системы материальных точек. Кинетическая энергия. Потенциальная энергия.

Элементарная работа силы F : dAº(F×dr), где dr –элементарное перемещение точки приложения силы F.

Работасилы Fна участке s —

Энергияесть величина работы, которую система может совершить.

Механическая энергия – запас работы системы. (имхо: не отличается от просто энергии – не корректно. Прим. корректора)

Кинетическая энергия системы – это запас той её работы, которую система может совершить двигаясь до полной остановки всех своих частей.

Потенциальная энергия системы – это запас той её работы, которую система может совершить, изменяя свою конфигурацию.

Конфигурация – взаимное расположение частей системы.

Нормировка потенциальной энергии – это выбор конфигурации системы, для которой потенциальная энергия принимается равной нулю.

Бтлет12. Вопрос1.

Консервативные силы. Консервативные системы. Связь консервативных сил с потенциальной энергией. Закон сохранения механической энергии.

Диссипативныминазываются такие силы, полная работа которых при любых движениях в замкнутой системе всегда отрицательна.

Потенциальными называют силы, работа которых по замкнутому контуру равна нулю.

Консервативные и потенциальные силы – одно и то же.

Консервативной называется система, в которой действуют только консервативные силы.

Так как работа консервативных сил зависит только от начального и конечного положения материальной точки, на которую они действуют, то их работа – это работа, совершаемая при изменении конфигурации тел, то есть изменение потенциальной энергии системы, взятое с обратным знаком. Примеры: сила упругости, сила тяжести, сила тяготения.

Закон сохранения механической энергии (он же: закон сохранения не какой попало энергии ã ЧМЗ) – механическая энергия системы тел сохраняется неизменной, если суммарная работа всех внешних сил и сил трения в системе равна нулю.

Выводится из законов Ньютона.

Билет13. Вопрос1.

Соударения тел. Абсолютно упругий и абсолютно неупругий удары. Законы сохранения при соударениях тел.

Абсолютно неупругим называется такой удар, в результате которого скорости соударяющихся тел становятся одинаковыми.

Абсолютно упругим называется такой удар, в результате которого суммарная кинетическая энергия соударяющихся тел сохраняется неизменной.

Билет14. Вопрос1.

Движение материальной точки в неинерциальной системе отсчёта. Силы инерции. Переносная и криолисова силы инерции. Центробежная сила инерции.

абсолютное = переносное + кориолисово + относительное

Переносная сила инерции – это сила, равная произведению массы материальной точки на взятое с обратным знаком её переносное ускорение. (- mA— m w [w r’]] — m [b r’])

Кориолисова сила инерции – это сила, равная произведению массы материальной точки на взятое с обратным знаком её кориолисово ускорение. (-2m [w v’])

Центробежная сила инерции – это сила, равная произведению массы материальной точки на её центростремительное ускорение, взятое с обратным знаком. (-m w [w r’]])

Билет15. Вопрос1.

Кориолисова сила инерции. Примеры её проявления на земле.

Примеры: отклонение падающих тел, маятник Фуко, стирание правого рельса и подмывание правого берега в северном полушарии. Доказывается в лоб. Главное не напутать с правилом Буравчика и не потерять минус.

Билет16. Вопрос1.

Законы сохранения в неинерциальных системах отсчёта.

Закон сохранения импульса: суммарный импульс системы тел сохраняется неизменным, если равнодействующая всех внешних сил и сил инерции равна нулю.

Закон сохранения механической энергии – механическая энергия системы тел сохраняется неизменной, если суммарная работа всех внешних сил, сил трения в системе и сил инерции равна нулю.

Вывод аналогичен выводу для инерциальных СО, только к внешним силам всюду добавляются инерциальные.

Билет17. Вопрос1.

Понятие о массовых силах. Принцип эквивалентности Эйнштейна.

Массовая сила – сила, пропорциональная массам.

Если коэффициент перед массой не равен константе, то сила не массовая.

Принцип эквивалентности: силы инерции и тяготения локально неразличимы.

Сначала рассматриваются сила тяжести и переносная сила инерции без учёта вращения. После берётся общий вид и локализация (r – const).

Билет18. Вопрос1.

Основные понятия теории относительности. Пространство и время в релятивистской механике. Два постулата Эйнштейна. Скорость света, как максимальная скорость распространения сигналов.

Время – свойство материальных процессов иметь определённую длительность, следовать друг за другом в определённой последовательности и развиваться по этапам и стадиям (Матвеев).

Как механические, так и электромагнитные явления описываются во всех инерциальных системах отсчёта одинаковыми уравнениями.
Скорость распространения электромагнитных волн в вакууме есть величина универсальная для всех инерциальных систем отсчёта и равная с.

Сигналом называется такой физеческий процесс, который может переносить информацию из одной точки пространства в другую. (Матвеев)

Темп часов одинаков, если временной интервал между посыланием сигналов измеренный по часам, расположенным в точке источника сигналов, совпадает с временным интервалом между принятыми сигналами, измеренным по часам, находящимся в точке приёмника.

Любые двое часов, находящиеся на расстоянии s друг от друга, синхронизованны,если разность показаний часов в момент прихода светового сигнала в точку нахождения одних часов и его испускания из точки нахожения других равна s/c (Матвеев).

Билет19. Вопрос1.

Учитывая

прямые преобразования Лорентца имеют вид:

Обратные преобразования Лорентца имеют вид:

(в правой части либо штрих, либо минус ã ЧМЗ)

Теоретически преобразования Лорентца выводятся из постулатов теории относительности и однородности времени и пространства.

Следствия из преобразований Лорентца:

Билет20. Вопрос1.

Собственная длина и собственное время. Лоренцево сокращение длины. Релятивистское замедление хода часов.

Собственная длина – длина покоящего отрезка.

Собственное время – время показанное часами, находящимися в покое в своей системе отсчёта.

Лорентцово сокращение длины и релятивистское замедление хода движущихся часов:

выводятся в лоб из прямых преобразований Лорентца.

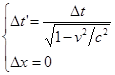
Билет21. Вопрос1.

Экспериментальные подтверждения замедления времени. «Парадокс близнецов».

Кругосветное путешествие атомных часов. 1972 г.

где: v – скорость тел на поверхности Земли. u – скорость самолёта.

Так же влияет на замедление часов влияет поле тяготения, которое затормаживает часы на поверхности Земли сильнее, чем на самолёте.

Относительное уменьшение длительности некоторого просесса над поверхностью Земли: 10 -15 /10 метров.

Было экспериментально показано, что время жизни частиц, закрученных в магнитном поле возрастает с возрастанием их скорости.

Парадокс – то, что на первый взгляд непонятно, а на 2–й – понятно.

Парадокс близнецов состоит в том, что с одной стороны первый близнец облетает второго, а с другой второй первого (в силу относительности движения). Но дело в том, что системы отсчёта не эквивалентны.

Билет22. Вопрос1.

Преобразования Галелея как предельный случай преобразований Лоренца.

Преобразования Галилея являются предельным случаем преобразований Лоренца в случае если скорость света в вакууме — с устремить к бесконечности.

Билет23. Вопрос1.

Событие: интервал между событиями. Инвариантность интервала. Свето-подобные, времени-подобные и пространственно-подобные интервалы.

Событие – совокупность 4-х размерных величин (x,y,z,t)

Интервал Ds º Sqrt ((Dx) 2 + (Dy) 2 + (Dz) 2 — (c Dt) 2 ), где ___________.

Ивариантность интервала относительно преобразований Лорентца доказывается в лоб из преобразований Лорентца, а не из формул сокращения временного и пространственного интервалов по отдельности.

Пространственноподобным называется такой интервал Ds, для которого Ds 2 >0.

Времениподобным называется такой интервал Ds, для которого Ds 2 2 =0.

Билет24 Вопрос1

Относительность одновременности. Интервал между событиями. Причинно-следственная связь между событиями.

Два события, происшедшие в различных точках системы координат называются одновременными, если если они происходят в один и тот же момент времени по часам этой сисьемы координат. События, одновременые в одной системе координат, могут быть неодновременны в другой системе координат.

Пример: при

Интервал Ds º Sqrt ((Dx) 2 + (Dy) 2 + (Dz) 2 — (c Dt) 2 ), где ___________.

Чтобы причинно-следственная связь имела объективный характер и не зависела от системы координат, в которой она рассматривается, необходимо, чтобы никакаие материальные воздействия, осуществляющие физическую связь событий, происходящих в различных точках, не могли передаваться со скорстью, большей скорости света.

Иначе говоря: причинно-следственная связь может иметь место, если Ds 2 > 0. в силу инвариантности интервала.

Кинематика твёрдого тела. Поступательное и вращательное движение твёрдого тела. Плоское движение. Мнгновенная ось вращения.

Поступательным называется такое движение твердого тела, при котором отрезок, соединяющий любые 2 точки тела, остается параллельным самому себе.

Вращательным называется такое движение твердого тела, при котором траектории всех точек тела представляют собой окружности, параллельные друг другу.

Плоским называется такое движение твёрдого тела, при котором траектории всех его точек располагаются в параллельных плоскостях.

Мгновенной называется такая ось вращения, при помощи которой движение твердого тела в данное мнгновение можно представить как только (чисто) вращательное.

Билет26. Вопрос1.

Динамика твёрдого тела. Уравнение движения и уравнение моментов. Динамика плоского движения твёрдого тела.

Теорема Гюйгенса-Штейнера: момент инерции твердого тела относительно некоторой произвольной оси равен сумме 2-х слагаемых:

момента инерции этого тела относительно оси, проходящей через его центр масс параллельно данной.
произведения массы тела на квадрат расстояния от ц.м. тела до данной оси.

Импульс твёрдого тела остаётся неизменным, если сумма всех внешних сил и сил инерции, действующих на тело равна 0.

Механическая энергия твёрдого тела сохраняется неизменной, если суммарная работа всех внешних сил и сил инерции раввна 0.

Билет27. Вопрос1.

Кинетическая энергия твёрдого тела при плоском вращении.

Теорема Кенига: кинетическая энергия твёрдого тела при его плоском движении равна сумме 2-х слагаемых:

W_кин = m v₀ 2 / 2 + J₀ w 2 / 2, где m – инертная масса тела, v₀ – скорость поступательного движения центра масс тела, J₀ — момент инерции тела относительно центральной оси, w — угловая скорость вращения тела относительно этой оси.

Центральной называется такая ось вращениятвердого тела, которая проходит через его центр масс.

Билет28. Вопрос1.

Момент импульса твёрдого тела. Тензор инерции. Осевые и центробежные моменты инерции.

расстояние от точки, относительно которой рассматривается момент импульса.

Тензором инерции называется совокупность девяти величин, характеризующих инертные свойства твёрдого тела при его вращательном движении.

доказывается в лоб, раскрытием векторного произведения

Диагональные составляющие тензора – осевые моменты, остальные – центробежные.

Билет29. Вопрос 1.

Гланые и центральные оси вращения. Силы действующие на вращающееся тело. Свободные оси вращения.

Главной называется такая ось вращениятвердого тела, в случае которой вектора угловой скорости и момента импульса коллинеарны.

Центральной называется такая ось вращениятвердого тела, которая проходит через его центр масс.

Свободной называется такая ось вращения твердого тела (эквивалентные определения),

в случае которой равнодействующая всех центробежных сил инерции равна нулю и сумма моментов этих сил также равна нулю.
которая не испытывает деформирующего влияния со стороны центробежных сил инерции.
которая является одновременно главной и центральной

Билет30. Вопрос1.

Движение тела с закреплённой точкой. Гироскопы Перецессия гироскопа. Угловая скорость прецессии.

Простой гироскоп – это тело, имеющее ось симметрии вращения и которое, кроме того, достаточно быстро вращается вокруг этой оси.

Прецессия – это процесс изменения ориентации свободной оси гироскопа под действием постоянных внешних сил.

Гироскопическими силами называют силы упругости, действующие на опору со стороны быстро вращающихся масс.

Элементарная теория гироскопа.

Ω

Постулат: гироскопическое тело ведёт себя таким образом, чтобы его свободная ось совпадала с направлением суммарного момента импульса.

Тогда:

F’

— момент импульса тела

— его изменение

— момент внешних сил

отсюда следует: — основная формула гироскопа.

Существует 3 сповоба определения

1) Физический (куда направлено …)

2) Математический (из основной формулы гироскопа)

3) Вдоль «задней» силы

Билет1. Вопрос2.

Гироскопические силы. Волчки.

Две прецесси Юлы. Первая – производная силы тяжести, вторая – трения.

Билет2. Вопрос2.

Основы механики деформируемых тел. Типы деформаций. Деформации растяжения, сжатия, сдвига, кручения, изгиба. Количественная характеристика деформаций, упругая и остаточная деформации.

Абсолютно твердым называется тело, конфигурация которого не меняется при любых воздействиях.

Абсолютно упругим называется такое тело, у которого не остается деформации после снятия нагрузки.

Пластическимназывается такое тело, у которого остаются деформации после снятия нагрузки

Закон Гука – деформация тела, если она достаточно мала, пропорциональна приложенной силе.

График зависимости деформации от силы сначала идёт по прямой, затем, начинает загибаться вверх (деформации ещё упругие), а потом идёт ещё круче вверх, переходя в зону пластических деформаций.

Деформации можно измерять углами и смещениями, как абсолютно, так и относительно.

Билет3. Вопрос2.

Модуль Юнга, коэффициент Пуассона. Модуль сдвига. Энергия деформированного тела.

Коэфф. Пуассона μ ≡ — (Δd/d)/( Δl/l) = — (λ_y/λ_x)= — (λ_z/λ_x) (при растяжении или сжатии вдоль оси x)

Сдвиг: τ=Gγ, где τ-касательное напряжение на поверхности бруска τºF/S где F – касательная сила действующая на поверхность пластины, S – площадь этой поверхности, γ – малый угол наклона боковой грани бруска, а G – модуль сдвига, характеризующий упругие свойства материала.

Энергия деформированного стержня W=kx 2 /2.

Билет4. Вопрос2.

Основы гидро- и аэростатики. Закон Паскаля, сжимаемость жидкостей и газов. Коэффициент всестороннего сжатия.

Закон Паскаля:внешнее давление передается жидкостью и газом по всем направлениям без изменений.

Доказываестся из треугольной призмы, подобия треугольников сечения и векторов сил и теоремы синусов.

Жидкости сжимаемы меньше, чем газы.

Коэффициент сжимаемости:

На сколько можно сжать одну единицу объёма среды, при изменении на единицу внешнего давления и неизменной температуре.

Коэффициент всестороннего сжатия K’≡1/K

Билет5. Вопрос2.

Распределение давления в покоящейся жидкости (газе).

dP = -ρgdh, но ρ≠const
PV = (m/μ)RT => ρ= (ρ₀/P₀)P
dP/P = -(ρ₀/P₀)gdh
ln(P)= -(ρ₀/P₀)gh+C; h=0 => P = P₀ => C = ln(P₀)

Билет6. Вопрос2.

Закон Архимеда. Условие устойчивого плавания тел.

Закон Архимеда: на тело, погруженное в жидкость/газ, действует сила, направленная вертикально вверх, численно равная весу этой жидкости/газа, вытесненной телом.

Погруженным в данную среду телом называется тело окруженное этой средой со всех сторон.

F_A=ρVg. Условие устойчивого плавания тел: P 2 /2 + rgh = const, всюду вдоль линии тока где ______________.

линии тока
трубки тока
потока в целом (если в пределах любого сечения характеристики потока одинаковы)
для 2-х сечений при условии, что в пределах этих сечений характеристики потока одинаковы

Модель: жидкость несжимаема, трение отсутствует, ток стационарный.

p – статическое давление (измеряется монометрическим зондом)

rv 2 /2 – динамическое давление (измеряется трубкой Пито)

p + rv 2 /2 – полное давление (измеряется трубкой Пито)

rgh – давление столба

Билет8. Вопрос2.

Условия применимости уравнения Бернулли. Роль вязкости. Сила внутреннего трения.

Условия применимости уравнения Бернулли:

линии тока
трубки тока
потока в целом (если в пределах любого сечения характеристики потока одинаковы)
для 2-х сечений при условии, что в пределах этих сечений характеристики потока одинаковы

При этом: жидкость несжимаема, трение отсутствует, ток стационарный, (вязкости нет?).

Явление переноса – это явление, при котором молекулами среды в их непрерывном тепловом хаотическом движении переносится некоторая физическая величина.

При вязком внутреннем трениипереносится импульс.

где η – коэффициент вязкого трения.

Коэффициент внутреннего трения средыесть величина, численно равная тому импульсу, который переносится молекулами среды в их непрерывном тепловом хаотическом движении через единичную площадку за единицу времени, при градиенте скорости слоёв среды в направлении, перпендикулярном данной площадке, численно равном единице.

Коэффициент внутреннего трения средыесть величина, численно равная той силе вязкого трения, которая действует на единичную площадку, при градиенте скорости слоёв среды в направлении, перпендикулярном данной площадке, численно равном единице.

Роль вязкого трения: если вязкого трения нет, то ламинарное течение невозможноБилет9. Вопрос2.

Билет9. Вопрос1.

Течение вязкой жидкости по трубе. Формула Пуазейля.

Билет10. Вопрос2.

Ламинарное и турбулентное течение. Число Рейнольдса. Лобовое сопротивление при обтекании тел.

Ламинарным называется такой ток жидкости или газа, при котором конфигурация линий тока остаётся неизменной.

Re – число Рейнольдса. Re≡ρvl/η – где ρ – плотность среды, v – характерная скорость, l – характерный линейный размер.

Критерий Рейнольдса: уравнение Бернулли применимо при Re >> 1

Re≡W_кин/A_трения =(1/2) ρv 2 (l 3 )/ηl 2 (v/l)l; ½ опускаем в связи со знаком >>.

Лобовое сопротивление – проекция равнодействующей всех сил, действующих со стороны среды на тело, на направление движения.

Подъёмная сила – вертикальная составляющая равнодействующей всех сил, действующих со стороны среды на тело. (записано по памяти. прим. ред.)

Билет11. Вопрос2.

Циркуляция. Подъёмная сила. Эффект Магнуса.

Пример с крылом. Угол атаки – угол между нижней поверхностью крыла и горизонталью.

Эффект Магнуса– возникновение поперечной силы, действующей на тело, вращающееся в набегающем на него потоке жидкости/газа.

Объясняется с помощью уравнения Бернулли.

Билет 12. Вопрос2.

Колебания. Число степеней свободы системы. Свободные колебания системы с одной степенью свободы. Уравнение собственных незатухающих колебаний. Его решение.

Колебания – это повторяющиеся движения.

Числом степеней свободы системыназывается количество независимых координат, при помощи которых можно полностью задать положение системы в пространстве.

Собственными называются колебания системы, предоставленной самой себе.

Система со сосредоточенными параметрами – система, различные свойства которой сосредоточены в отдельных её частях.

Уравнение гармонических незатухающих колебаний: x’’ + ω₀ 2 x=0

Квазиупругой называется возвращающая сила, пропорциональная отклонению системы от положения равновесия.

Квазиупругимназывается возвращающий момент, пропорциональный угловому отклонению системы от положения равновесия.

Решение уравнения гармонических незатухающих колебаний: x = X₀ sin (ωt+φ).

Далее следующие производные, графики, итд.

Билет13. Вопрос2.

Гармонические колебания. Амплитуда колебаний. Частота и период колебаний. Фаза и начальная фаза. Начальные условия.

Всё понятно. Начальные условия – начальные смещение и скорость.

Билет14. Вопрос2.

Сложение гармонических колебаний. Фигуры Лиссажу. Биения. Частота биений.

Так, всё ясно. Для Лиссажу првести пример.

Фигурой Лиссажу называется кривая, совпадающая с траекторией точки, движение которой можнопредставить как суперпозицию 2-х колебаний вдоль перпендикулярных друг другу напрвлений.

Система с сосредоточенными параметрами – система, различные свойства которой сосредоточены в отдельных её частях.

Биения – медленное изменение амплитуды суммарных колебаний для 2-x источников с близкими частотами.

Билет15. Вопрос2.

Затухающие колебания. Уравнение затухающих колебаний. Его решение. Показатель затухания. Логарифмический декремент затухания. Время релаксации.

Уравнение затухающих колебаний: x’’+ 2γx’ + ω₀ 2 x = 0

Решение: x = X₀ e — γt sin (ω₁t+φ) ; где ω₁ 2 = ω₀ 2 — γ 2

γ – показатель затухания.

Логарифмический декремент затухания θ ≡ ln(X_n/X_n₊₁) = ln(X₀ e — γt / X₀ e — γ( t+ T) ) = γT=1/N₀, где N₀ – количество периодов, за которое амплитуда уменьшается в e раз.

Время релаксации – время, за которое амплитуда собственных затухающих колебаний системы уменьшается в e раз.

Билет16. Вопрос2.

Вынужденные колебания. Уравнение вынужденных колебаний. Его решение. Процесс установления колколебаний.

Время релаксации — характерное время установления равновесия в системе.

Уравнение вынужденных колебаний: x’’+ 2γx’ + ω02x = f0 sin(ωt) (1)

По прошествии времени релаксации: x =X sin (ωt+φ). X=? φ=?

x’ = ωXcos (ωt+φ); x’’ = -ω2 X sin (ωt+φ);

Подставляем в (1): -ω2 X sin (ωt+φ) + 2γ ωXcos (ωt+φ) + ω02 X sin (ωt+φ) = f0 sin(ωt)

При ωt = 0: -ω2 X sin (φ) + 2γ ωXcos (φ) + ω02 X sin (φ) = 0;

tg φ = -2γ ω/ ω02- ω2

При ωt = π/2: 2γ ωX = — f₀ sin(φ);

В общем виде x = X₀ e — γt sin (ω₁t+φ) + X sin (ωt+φ).

Билет17. Вопрос2.

Резонанс. Амплитудные и фазовые резонансные кривые. Добротность.

Резонанс – резкое возрастание амлитуды вынужденных колебаний, когда частота вынуждающей силы приближается к частоте собственных колебаний системы.

Добротность Q≡ = = 2π/(1-e -2 θ ); при θ 2 =ω₀ 2 -2γ 2

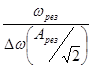
Произведение крайних равно квадрату средней.

Куда сдвигается, там и поднимается.

Билет18. Вопрос2.

Соотношение между силами при резонансе (на примере пружинного маятника).

Идея в том, что внешняя сила компенсирует силу вязкого трения, и система становится предоставленной самой себе. См. частотные графики.

Билет19. Вопрос2.

Параметрическое возбуждение колебаний. Автоколебания.

Параметрическим называется такое возбуждение колебанийсистемы, при котором меняются параметры этой системы.

Автоколебания– незатухающие колебания, которые поддерживаются стационарным внешним воздействием.

Билет20. Вопрос1.

Связанные системы. Нормальные колебания (моды). Нормальные частоты.

Нормальныминазываются такие колебания системы, при которых все части её колеблются по гармоническому закону с одинаковой частотой.

Билет21. Вопрос2.

Волны. Распространение «импульса» в среде. Продольные и поперечные волны. Уравнение бегущей волны. Скорость волны и скорости «частиц».

Волна – процесс распространения состояния.

Волновая поверхность – поверхность, во всех точках которой которой данная физическая величина имеет одно значение в любой момент времени.

Уравнение бегущей волны:

Решение уравнения бегущей волны:

Билет22. Вопрос2.

Гармоническая бегущая волна. Волны вмещений, скоростей, деформаций. Волновое уравнение. Его решение.

Гармоническая бегущая волна: ε = ε₀ sin(ωt-(2π/λ)x + φ);

— волна скоростей — волна деформаций.

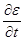
Волновое уравнение:

Его решение: y(x,t) = f(t- x/v) + g(t+x/v), где f и g — произвольные дважды дифференцирунмые по обеим переменным функции.

Билет23. Вопрос2.

Волны на струне, в стержне, в газовой среде.Связь скорости волны со свойствами среды.

Волны на струне.

ρΔx =T(α+Δα) – Tα = TΔα= => =(T/ρ) ; α= => = (T/ρ) => (T/ρ)=v 2

ρ – линейная плотность струны.

Продольные волны в твёрдом теле.

Ускорение частицы:

Получаем:

ρ — плотность тела, E – модуль Юнга.

Продольные волны в газовой среде.

PV γ =const, где γ≡c_p/c_v= (i+2)/i где i – количество степеней свободы частицы (для воздуха i=2)

∂PV γ +PγV γ -1 ∂V=0

dV/V=(-1/γP)dP сравнивая с = = получаем: v 2 = γP/ρ

Билет24. Вопрос2.

Отражение волн от границы раздела двух сред. Основные случаи граничных условий.

Импульсы, идущие «туда» и «обратно» не мешают друг другу.
Скорость «туда» такая же как «обратно».
Какими порциями эенергия поступает к границе, где нет поглощения энергии, такими же она отправляется назад.
Энергия, которую несёт импульс не зависит от полярности, поскольку она пропорциональна квадратам деформации и скорости.

Варианты граничных условий:

закреплённая граница => узел
незакреплённая граница => пучность

Билет25. Вопрос2.

Стоячие волны. Распределение амплитуд смещений, скоростей, ускорений, частиц в стоячей волне. Узлы и пучности.

Уравнение плоской волны: y(x,t) = f(t- x/v) + f(t+x/v),

Стоячая волна –периодическое во времени синфазное колебание с характерным пространственным распределением амплитуды – чередованием узлов и пучностей.

В случае стоячей волны мех. энергия оказывается локализованной в промежутках между соседними узлами и пучностями, переходя из кинетической (в пучностях) в потенциальную (в узлах)

Билет26. Вопрос2.

Нормальные колебания струны, стержня, столба газа. Акустические резонаторы.

Первый обертон – второй тон.

Тон – то же что и мода – разновидность нормальных колебаний.

Условия нормальных колебаний струны, стержня, столба газа: L=kλ, или L=(k+1)(λ/2) (в зависимости от граничных условий).

Резонатор – колебательная система, способная резонировать при воздействии внешней силы определённой частоты и формы.

Билет27. Вопрос2.

Поток энергии в бегущей волне. Вектор Умова.

В случае плоской гармонической волныВектор Умова –вектор, направленный в сторону распространения волны и равный по модулю энергии волны, переносимой через единичную площадку в единицу времени.

p=2 ω_кинv/v = ρ(∂ξ/∂x) 2 (∂x/∂t)v= -ρ (∂ξ/∂x) (∂ξ/∂t) v; (∂ξ/∂x) (∂ξ/∂t) 2 = γP/ρ Так ка при ΔQ=const, PV γ =const, а γ >1, при увеличении давления, плотность растёт, ещё сильнее, таким образом накапливается сгущение, которое формируется до тех пор, пока волна не натолкнётся на какое-нибудь препятствие, принеся с собой эффект удара.

Ударной называется волна, которая приносит с собой эффект удара.

Удар– резкое изменение параметров, характеризующих состояние среды.

Билет29. Вопрос2.

Элементы акустики. Звуковые волны. Громкость звука. Тембр звука.

Звуковыми строго говоря называются все механические волны, но если сузить понятие звуковых волн, то это механические волны частота которых может восприниматься человеческим ухом.

Частотный диапазон: 16 Гц – 6КГц. (либо 1, либо К) Длина волн: 2 см – 20 м. (либо с, либо 0)

Громкость – характеристика звука представляющая собой величину энергии/амплитуды звуковой волны.

Тембр– характеристика звука, представляющая собою спектр частот и соответствующих им амплитуд.

Билет30. Вопрос2.

Эффект Доплера– изменение частоты волны вследствие движения источника/приёмника.

Механическое состояние. Уравнение движения. Алгоритм численного решения

Механическое состояние. Уравнение движения. Алгоритм численного решения. Системы взаимодействующих тел. Разные движения по эллипсам.

Механическое состояние. Уравнение движения.

При движении материальной точки изменяются со временем ее положение в пространстве, определяемое радиусом-вектором, ее скорость, ускорение. Говорят, что происходит изменение состояния материальной точки со временем. Что же понимают под механическим состоянием и какими параметрами оно определяется? Механическое состояние материальной точки в некоторый момент времени определено, если для этого момента времени заданы ее радиус-вектор и скорость.

Если известно механическое состояние материальной точки в какой-либо момент времени и действующие на нее силы, то с помощью второго закона Ньютона можно определить механическое состояние в последующие моменты времени, т. с. полностью предсказать движение. Именно по этой причине второй закон Ньютона часто называют уравнением движения, ибо он описывает эволюцию начального состояния механической системы во времени. Уравнение движения.

Остановимся подробнее на вопросе определения механического состояния в произвольный момент времени. Второй закон Ньютона, или уравнение движения, позволяет при известных силах найти ускорение материальной точки. Но знание ускорения дает возможность определить только изменение скорости за некоторый промежуток времени. Чтобы найти само значение скорости к концу этого промежутка, нужно знать не только изменение скорости, но и значение в начальный момент. Аналогично, знание скорости позволяет найти изменение положения материальной точки за некоторое время.

Чтобы найти сам радиус-вектор, нужно знать его значение в начальный момент. Например, в случае движения под действием постоянной силы, когда ускорение также постоянно, скорость и радиус-вектор материальной точки в момент времени определяются формулами скорость и радиус-вектор в начальный момент времени. Уравнение движения даст возможность найти только тогда, когда известно начальное состояние системы,величины.

Начальные условия.

Задание начальных условий для нахождения необходимо и в том случае, когда действующие силы таковы, что ускорение не остается постоянным. При этом в некоторых случаях уравнение движения удастся решить (проинтегрировать) аналитически, найти как функции времени, которые также будут содержать начальные значения.

В качестве примеров таких случаев можно указать движение материальной точки под действием силы, обратно пропорциональной квадрату расстояния от центра силового поля (движение планеты под действием притяжения к Солнцу, движение спутника Земли, движение альфа-частицы в поле атомного ядра), движение под действием силы, пропорциональной смещению от положения равновесия (тело на пружине).

По этой ссылке вы найдёте полный курс лекций по математике:

Алгоритм численного решения.

В случаях, когда уравнение движения не удается решить аналитически, его можно решать численно. Действующая на материальную точку сила может зависеть от времени явно, от положения точки и от ее скорости. Пусть нам заданы начальные значения. Уравнение движения дает возможность найти ускорение в тот же момент времени. Зная ускорение, можно приближенно найти изменение скорости за малый промежуток времени откуда скорость к концу этого промежутка равна Зная скорость в начальный момент, можно приближенно найти изменение радиуса-вектора за то же время.

Более точное значение можно получить, если взять вместо среднее значение скорости на этом промежутке, считая ускорение на нем постоянным: Отсюда значение радиуса-вектора к концу промежутка времени получится в виде в зависимости от того, какой из приведенных выше формул для отдать предпочтение. Выбор промежутка времени определяется той точностью, которую мы хотим получить при таком приближенном вычислении.

Чем меньше промежуток времени, тем ближе к истинным будут значения вычисляемые по формулам.

Найденные значения подставляем в выражение для силы и с помощью уравнения движения находим ускорение а, материальной точки в конце промежутка времени . Теперь повторяем описанную процедуру для следующего промежутка времени, причем роль начальных условий будут играть найденные по формулам и значения Затем все повторяется еще раз и т. д. Если требуется найти изменение механического состояния материальной точки за большой промежуток времени, придется разбить этот промежуток на большое число шагов. Чем меньше размер каждого шага, тем точнее будет результат.

Но необходимое число шагов при этом увеличивастся. За повышение точности результатов приходится платить увеличением объема вычислений. Практически такие работы удобно выполнять на ЭВМ. При проведении расчетов имеют дело не с векторами, а с числами. Поэтому каждое из приведенных выше векторных уравнений записывается в виде трех скалярных уравнений, соответствующих проекциям векторного уравнения на оси выбранной системы координат.

Возможно вам будут полезны данные страницы:

Системы взаимодействующих тел.

Часто приходится рассматривать механическую систему, состоящую из нескольких взаимодействующих тел. Если известны силы взаимодействия между телами и внешние силы, действующие на каждое из тел, то для нахождения движения всех этих тел приходится решать систему уравнений, состоящую из уравнений движения для каждого тела. Механическое состояние системы частиц определяется заданием положений и скоростей всех частиц в один и тот же момент времени. Уравнения движения позволяют найти изменение этого состояния со временем.

Аналитическое решение задачи о механическом

движении системы взаимодействующих тел обычно сопряжено с огромными математическими трудностями. Так, например, до сих пор не решена в общем виде задача о движении всего лишь трех взаимодействующих тел при произвольных начальных условиях. Однако численный расчет движения системы взаимодействующих частиц не содержит ничего принципиально нового по сравнению с расчетом движения одной материальной точки.

При приближенном вычислении скорость и радиус-вектор каждой из частиц находятся с помощью той же самой процедуры по формулам, только при определении ускорений частиц в каждый момент времени с помощью уравнений движения в этих уравнениях кроме внешних сил учитываются и силы взаимодействия между частицами.

• Какой смысл вкладывается в понятие механического состояния? Какими величинами определяется механическое состояние материальной точки? системы материальных точек?

• Почему ускорение частицы не входит в число величин, определяющих ее механическое состояние?

• Опишите алгоритм численного расчета механического движения материальной точки.

• Какую роль играют начальные условия при решении уравнений движения?

А Нахождение сил по движению. Уравнения движения можно использовать для нахождения действующих сил, если известно, как происходит движение тела, т. с. задан его радиус-вектор как функция времени. Примером такой задачи может служить нахождение силы притяжения планеты к Солнцу по известному из астрономических наблюдений закону обращения этой планеты по эллиптической орбите вокруг Солнца. Именно так был установлен закон обратных квадратов для силы тяготения.

Другой пример — движение точки по эллипсу, описываемое уравнениями В том, что траектория такого движения действительно представляет собой эллипс, можно убедиться, исключив время из этих уравнений. Разделив первое из этих уравнений, возводя их в квадрат и складывая, получим, учитывая тождество , следующую связь между: Это уравнение эллипса (рис. 102) с полуосями , которое в частном случае превращается в уравнение окружности.

Легко убедиться, что материальная точка движется по этому эллипсу в направлении против часовой стрелки, причем так, что ее радиус-вектор поворачивается с постоянной угловой скоростью. Для нахождения силы, вызывающей такое движение, нужно с помощью формул определить ускорение частицы. Дифференцируя уравнения по времени, находим проекции скорости на оси координат Дифференцируя по времени соотношения, получаем проекции ускорения.

Используя второй закон Ньютона и уравнения, получаем проекции силы, действующей на материальную точку массы. Сравнивая видим, что выражения для проекций силы можно записать в виде Эти соотношения дают искомую зависимость действующей на частицу силы от ее координат. В векторном виде их можно записать следующим образом Сила в каждой точке направлена к началу координат и пропорциональна расстоянию до находящегося там центра силового поля (см. рис. 102).

Такую зависимость силы от положения можно реализовать, например, с помощью двух пар одинаковых пружин (рис. 103). Чтобы движение тела происходило именно по уравнениям, начальные условия должны быть вполне определенными из следует, что при должно быть Рис. 103. При смещении шарика из положения равновесия действующая со стороны пружин сила направлена к этому положению равновесия и пропорциональна смещению из уравнений.

Такое начальное состояние можно осуществить, оттянув шарик в направлении оси на расстояние и толчком сообщив ему начальную скорость вдоль оси. При этом оси направлены вдоль недеформированных взаимно перпендикулярных пружин, а ось перпендикулярна плоскости, в которой они расположены. В действительности оказывается, однако, что взаимно перпендикулярные оси могут быть в плоскости пружин ориентированы произвольным образом.

Более того, если к этим двум парам пружин добавить еще такую же пару, расположенную перпендикулярно плоскости, в которой они лежат (рис. 104), то в такой системе выбор направления всех трех осей совершенно произволен. По своим механическим свойствам система оказывается изотропной. При любых начальных условиях траектория шарика будет плоской. Ориентация этой плоскости определяется векторами начального смещения и начальной скорости.

Разные движения по эллипсам.

Хотя движение тела под действием силы, пропорциональной смещению из положения равновесия, как и движение планет вокруг Солнца, происходит по эллиптической траектории, характер этих движений совершенно различен. Движение планеты происходит под действием силы, обратно пропорциональной квадрату расстояния до Солнца, расположенного в одном из фокусов эллипса (рис. 105), в то время как в рассмотренном выше примере шарика на пружинах силовой центр совпадает с центром эллипса. Различие в характере движений становится особенно отчетливым, если вспомнить, что вокруг Солнца скорость в афелии меньше, чем в перигелии.

Скорости планеты в афелии и перигелии, на концах большой полуоси эллипса, различны (рис. 105), в то время как у шарика на пружинах скорости в соответствующих точках орбиты одинаковы (см. рис. 102). Отметим, что в случае движения при наложенных связях механическое состояние определяется заданием значений обобщенных координат и значений скоростей их изменения (обобщенных скоростей) в один и тот же момент времени.

Таким образом, число параметров, определяющих механическое состояние системы, в два раза больше числа ее степеней свободы. Так, при движении точки по заданной окружности, сс механическое состояние определяется всего двумя величинами, например углом и угловой скоростью.

• Как показать, что радиус-вектор частицы, движение которой описывается уравнениями, поворачивается против часовой стрелки с постоянной угловой скоростью?

• Докажите, что формулы, связывающие проекции силы с координатами шарика, подвешенного на двух парах одинаковых пружин, справедливы при произвольной ориентации осей в плоскости пружин (т. с. оси не обязательно направлять вдоль пружин).

• Чем различаются движения по эллиптическим траекториям в случаях шарика, подвешенного на трех парах взаимно перпендикулярных одинаковых пружин, и орбитального движения планеты?

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

источники:

http://arhivinfo.ru/1-98872.html

http://natalibrilenova.ru/mehanicheskoe-sostoyanie-uravnenie-dvizheniya-algoritm-chislennogo-resheniya/